Fatigue Life Analysis of Titanium Torsion Spring Based on Continuous Damage Mechanics
Abstract
:1. Introduction
2. Finite Element Analysis and Experimental Method of Torsion Spring
2.1. Establishment of Torsion Spring Finite Element
2.2. Fatigue Test Method of Titanium Alloy Torsion Spring
3. Materials and Methods
3.1. Damage-Coupled Chaboche Plastic Constitutive Model
3.2. Damage Evolution Model
3.2.1. Plastic Damage Model
3.2.2. Elastic Damage Model
3.3. Determination of Material Parameters and UMAT Calculation Method
3.3.1. Parameters of the Elastoplastic Constitutive Model
3.3.2. Parameter Identification of Damage Evolution Model
Parameter Identification of Elastic Damage Evolution Model
Parameter Identification of Plastic Damage Evolution Model
3.4. UMAT Subroutine Calculation Method
4. Analysis of Fatigue Life Results
4.1. Fatigue Fracture Prediction
4.2. Analysis of Damage Variables
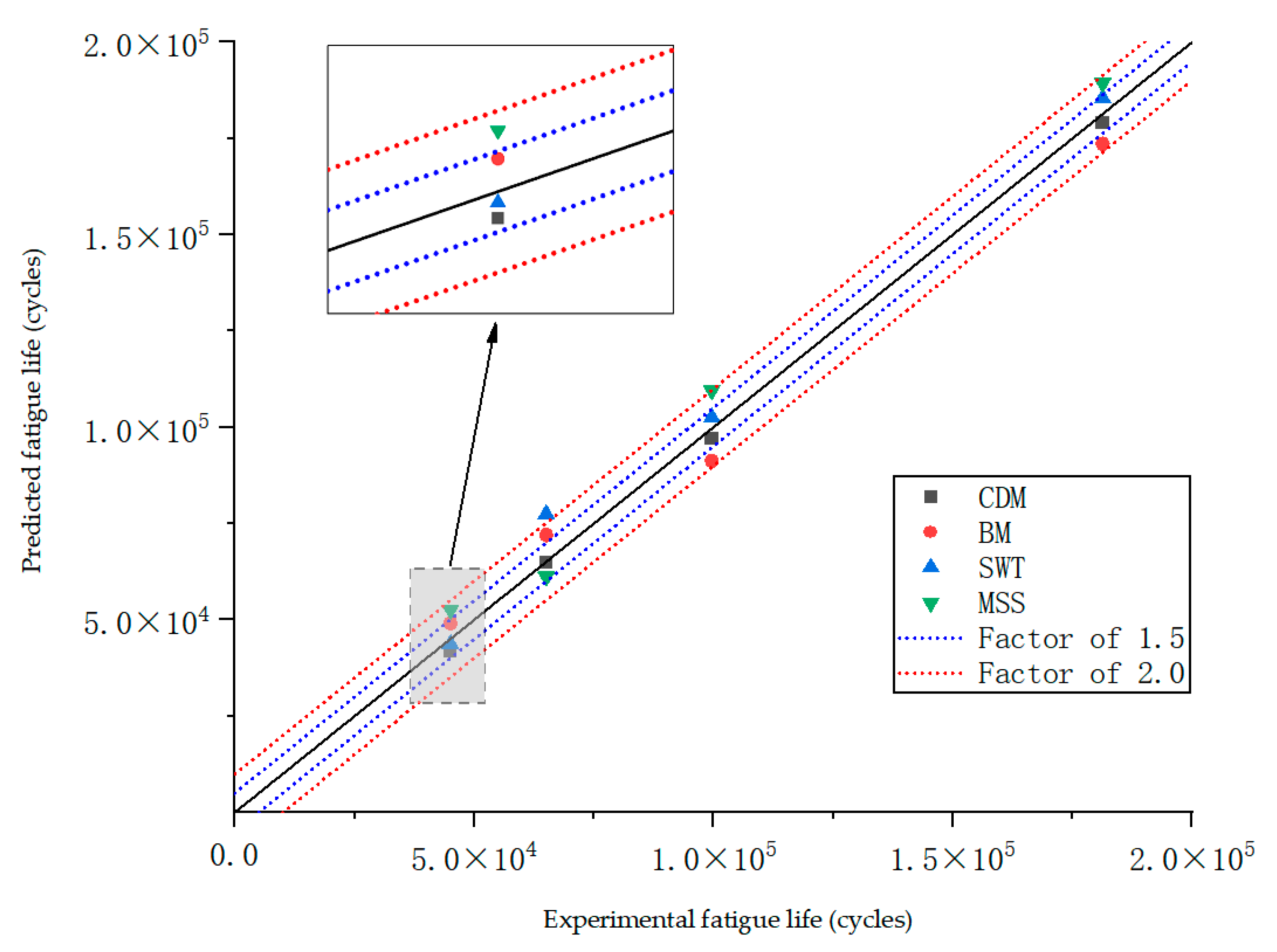
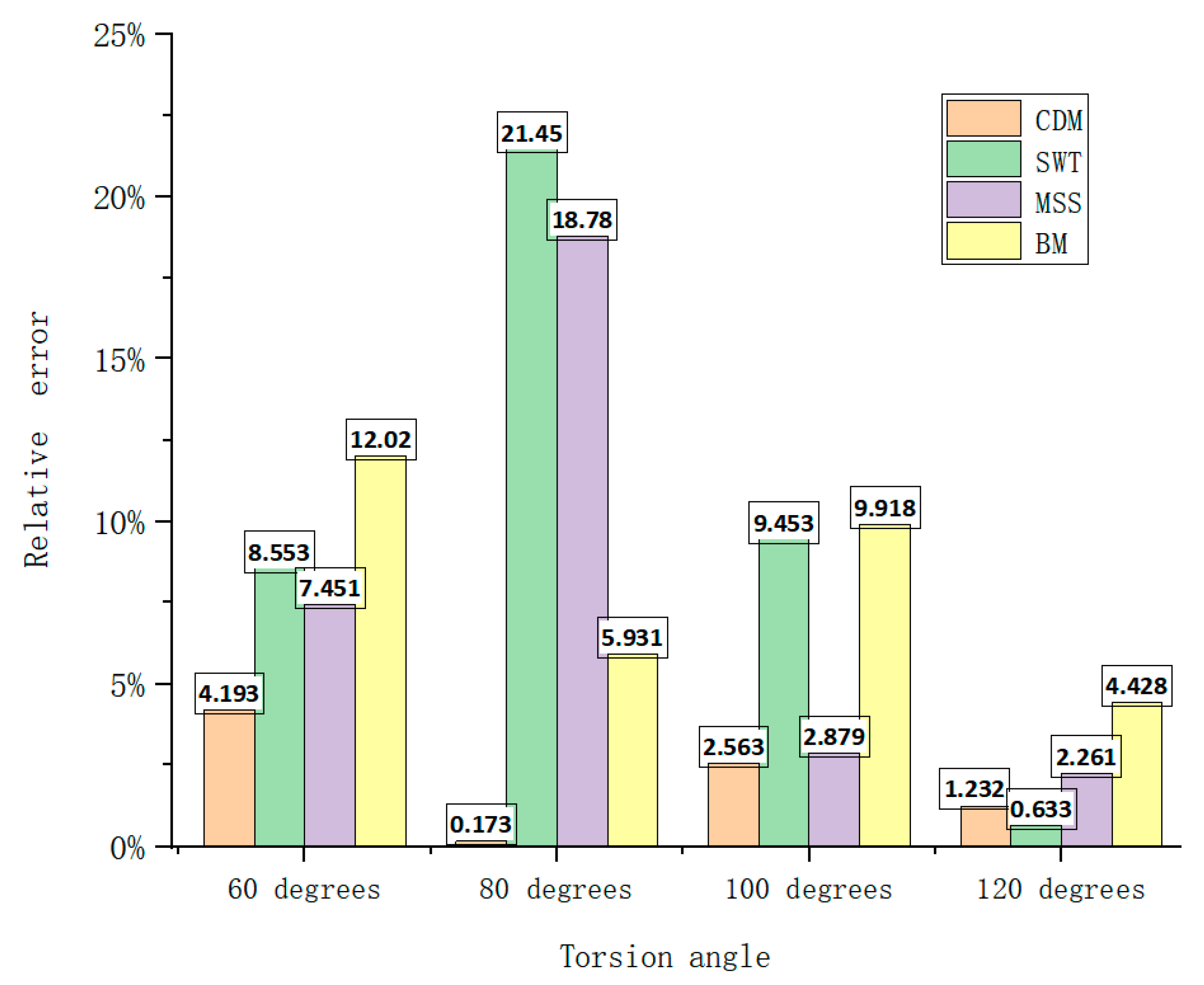
4.3. Comparison of Experimental and Theoretical Predictions
5. Conclusions
- Based on the continuous damage mechanics model combined with the secondary development of the UMAT subroutine, a damage mechanics finite element numerical method for predicting the fatigue life of torsion springs of Ti-6Al-4V alloys was established and compared with other multi-axial fatigue prediction models, and the average relative error between the customized continuum damage mechanics subroutine and the actual measured spring life was 2.04%, which shows a good prediction accuracy as compared with other prediction models.
- The finite element simulation based on the continuous damage fatigue model could represent the damage evolution process, which was of great significance for understanding the fatigue damage mechanism.
- The fracture region of the spring predicted by the model agreed with the experimentally derived fracture region of the spring. Comparing the fatigue life results of the prediction model with the experimental results in different dimensions verified the validity and applicability of the proposed model and method, reduced the time and economic costs due to the long experimental cycle, and has certain reference value for improving the accuracy of fatigue life prediction of this type of titanium alloy torsion springs. The research results can provide an effective reference for the further optimization of the design of this titanium alloy torsion spring.
- Suggestions for the future: this study did not consider the effect of surface area defects on the fatigue performance of springs, and the effects of various other surface treatments (shot peening and coatings) on the fatigue performance of springs may be investigated over time in order to improve their structural integrity and fatigue life. Suggestions for model enhancement: the parameters of the fatigue prediction model can be adjusted and optimized by combining machine learning and artificial intelligence algorithms with the experimental fatigue life to make the model predictions closer to the experimental fatigue life, which will potentially improve the accuracy of the prediction model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gürgen, S.; Kuşhan, M.C.; Diltemiz, S.F. Fatigue failure in aircraft structural components. In Handbook of Materials Failure Analysis with Case Studies from the Aerospace and Automotive Industries; Butterworth-Heinemann: Oxford, UK, 2016; pp. 261–277. [Google Scholar]
- Bhaumik, S.K.; Sujata, M.; Venkataswamy, M.A. Fatigue failure of aircraft components. Eng. Fail. Anal. 2008, 15, 675–694. [Google Scholar] [CrossRef]
- Cui, H.; Han, Q. Fatigue Damage Mechanism and Fatigue Life Prediction of Metallic Materials. Metals 2023, 13, 1752. [Google Scholar] [CrossRef]
- Findlay, S.J.; Harrison, N.D. Why aircraft fail. Mater. Today 2002, 5, 18–25. [Google Scholar] [CrossRef]
- Liu, S.; Song, X.i.; Xue, T. Application and development of titanium alloy and titanium matrix composites in aerospace. J. Aeronaut. Mater. 2020, 40, 18. [Google Scholar]
- Wang, C. Thermal coupling numerical simulation of Ti6Al4V alloy strengthened by high temperature shot peening. China Surf. Eng. 2019, 32, 11. [Google Scholar]
- Zhang, P.; Wang, D.; Guo, Y.; Cheng, P.; Shao, C.; Lang, N.; Liu, X.; Huang, J. Fatigue failure analysis and finite element assessment of the twins torsion spring. Eng. Fail. Anal. 2021, 122, 105187. [Google Scholar] [CrossRef]
- Del Llano-Vizcaya, L.; Rubio-González, C.; Mesmacque, G.; Cervantes-Hernández, T. Multiaxial fatigue and failure analysis of helical compression springs. Eng. Fail. Anal. 2006, 13, 1303–1313. [Google Scholar] [CrossRef]
- Pastorcic, D.; Vukelic, G.; Bozic, Z. Coil spring failure and fatigue analysis. Eng. Fail. Anal. 2019, 99, 310–318. [Google Scholar] [CrossRef]
- Kong, Y.S.; Omar, M.Z.; Chua, L.B.; Abdullah, S. Fatigue life prediction of parabolic leaf spring under various road conditions. Eng. Fail. Anal. 2014, 46, 92–103. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. Machine learning based fatigue life prediction with effects of additive manufacturing process parameters for printed SS 316L. Int. J. Fatigue 2021, 142, 105941. [Google Scholar] [CrossRef]
- Pandey, V.B.; Singh, I.V.; Mishra, B.K.; Ahmad, S.; Venugopal Rao, A.; Kumar, V. A new framework based on continuum damage mechanics and XFEM for high cycle fatigue crack growth simulations. Eng. Fract. Mech. 2019, 206, 172–200. [Google Scholar] [CrossRef]
- Sandoval, C.F.B.; Malcher, L.; Canut, F.A.; Araújo, L.M.; Doca, T.C.R.; Araújo, J.A. Micromechanical Gurson-based continuum damage under the context of fretting fatigue: Influence of the plastic strain field. Int. J. Plast. 2020, 125, 235–264. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Lesne, P.A. A Non-Linear Continuous Fatigue Damage Model. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 1–7. [Google Scholar] [CrossRef]
- Chaudonneret, M. A Simple and Efficient Multiaxial Fatigue Damage Model for Engineering Applications of Macro-Crack Initiation. J. Eng. Mater. Technol. 1993, 115, 373–379. [Google Scholar] [CrossRef]
- Shang, D. A nonlinear damage cumulative model for uniaxial fatigue. Int. J. Fatigue 1999, 21, 187–194. [Google Scholar] [CrossRef]
- Dattoma, V.; Giancane, S.; Nobile, R.; Panella, F. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model. Int. J. Fatigue 2006, 28, 89–95. [Google Scholar] [CrossRef]
- Lemaitre, J.; Sermage, J.P.; Desmorat, R. A two scale damage concept applied to fatigue. Int. J. Fract. 1999, 97, 67–81. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, D.; Yan, X.; Zhang, X.; Qi, M.; Fan, J. A damage coupled elastic-plastic constitutive model and its application on low cycle fatigue life prediction of turbine blade. Int. J. Fatigue 2020, 131, 105298. [Google Scholar] [CrossRef]
- Xia, Q.; Zhan, Z.; Mei, Y.; Zhang, Y.; Hu, W.; Meng, Q. Novel integration of PSO-enhanced damage mechanics and finite element method for predicting medium–low-cycle fatigue life in perforated structures. Chin. J. Aeronaut. 2024. [Google Scholar] [CrossRef]
- Liu, N.; Cui, X.; Xiao, J.; Lua, J.; Phan, N. A simplified continuum damage mechanics based modeling strategy for cumulative fatigue damage assessment of metallic bolted joints. Int. J. Fatigue 2020, 131, 105302. [Google Scholar] [CrossRef]
- Hojjati-Talemi, R.; Wahab, M.A. Fretting fatigue crack initiation lifetime predictor tool: Using damage mechanics approach. Tribol. Int. 2013, 60, 176–186. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L.; Maji, A.K. Mechanics of Solid Materials. J. Eng. Mech. 1992, 119, 642–643. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Kang, G.; Liu, Y.; Ding, J. Multiaxial ratchetting–fatigue interactions of annealed and tempered 42CrMo steels: Experimental observations. Int. J. Fatigue 2008, 30, 2104–2118. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Military Handbook-MIL-HDBK-5H: Metallic Materials and Elements for Aerospace Vehicle Structures, Knovel Interactive ed.; US Department of Defense: Arlington County, VA, USA, 1998.
- Zhang, T.; McHugh, P.E.; Leen, S.B. Finite element implementation of multiaxial continuum damage mechanics for plain and fretting fatigue. Int. J. Fatigue 2012, 44, 260–272. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Sharifimehr, S.; Phan, N.; Shamsaei, N. Multiaxial fatigue behavior of wrought and additive manufactured Ti-6Al-4V including surface finish effect. Int. J. Fatigue 2017, 100, 347–366. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. Engineering, Consistent tangent operators for rate-independent elastoplasticity. Comput. Methods Appl. Mech. Eng. 1985, 48, 101–118. [Google Scholar] [CrossRef]
- Kang, G. Finite element implementation of visco-plastic constitutive model with strain-range-dependent cyclic hardening. Commun. Numer. Methods Eng. 2005, 22, 137–153. [Google Scholar] [CrossRef]
- Kan, Q.H.; Kang, G.Z.; Zhang, J. Uniaxial time-dependent ratchetting: Visco-plastic model and finite element application. Theor. Appl. Fract. Mech. 2007, 47, 133–144. [Google Scholar] [CrossRef]
- Kang, G. A visco-plastic constitutive model for ratcheting of cyclically stable materials and its finite element implementation. Mech. Mater. 2004, 36, 299–312. [Google Scholar] [CrossRef]
- Kang, G. Ratchetting: Recent progresses in phenomenon observation, constitutive modeling and application. Int. J. Fatigue 2008, 30, 1448–1472. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Meng, Q. A non-local approach based on the hypothesis of damage dissipation potential equivalence to the effect of stress gradient in fretting fatigue. Int. J. Fatigue 2016, 90, 125–138. [Google Scholar] [CrossRef]
- Shen, F.; Hu, W.; Voyiadjis, G.Z.; Meng, Q. Effects of fatigue damage and wear on fretting fatigue under partial slip condition. Wear 2015, 338, 394–405. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, W.; Shen, F.; Meng, Q.; Xu, Y. Numerical simulations of the fatigue damage evolution at a fastener hole treated by cold expansion or with interference fit pin. Int. J. Mech. Sci. 2016, 107, 188–200. [Google Scholar] [CrossRef]
- Zhan, Z.; Meng, Q.; Hu, W.; Sun, Y.; Shen, F.; Zhang, Y. Continuum damage mechanics based approach to study the effects of the scarf angle, surface friction and clamping force over the fatigue life of scarf bolted joints. Int. J. Fatigue 2017, 102, 59–78. [Google Scholar] [CrossRef]
- Tavernelli, J.F.; Coffin, L.F. Experimental Support for Generalized Equation Predicting Low Cycle Fatigue. Trans. Am. Soc. Mech. Eng. 1962, 12, 533. [Google Scholar] [CrossRef]
- Ricotta, M. Simple expressions to estimate the Manson–Coffin curves of ductile cast irons. Int. J. Fatigue 2015, 78, 38–45. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Optimization of spring fatigue life prediction model for vehicle ride using hybrid multi-layer perceptron artificial neural networks. Mech. Syst. Signal Process. 2019, 122, 597–621. [Google Scholar] [CrossRef]
- Smith, K.N. A Stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Brown, M.W.; Miller, K.J. A Theory for Fatigue Failure under Multiaxial Stress-Strain Conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–755. [Google Scholar] [CrossRef]
- Pellinghelli, D.; Riboli, M.; Spagnoli, A.J.P.E. Full-Model Multiaxial Fatigue Life Calculations With Different Criteria. Procedia Eng. 2018, 213, 126–136. [Google Scholar] [CrossRef]
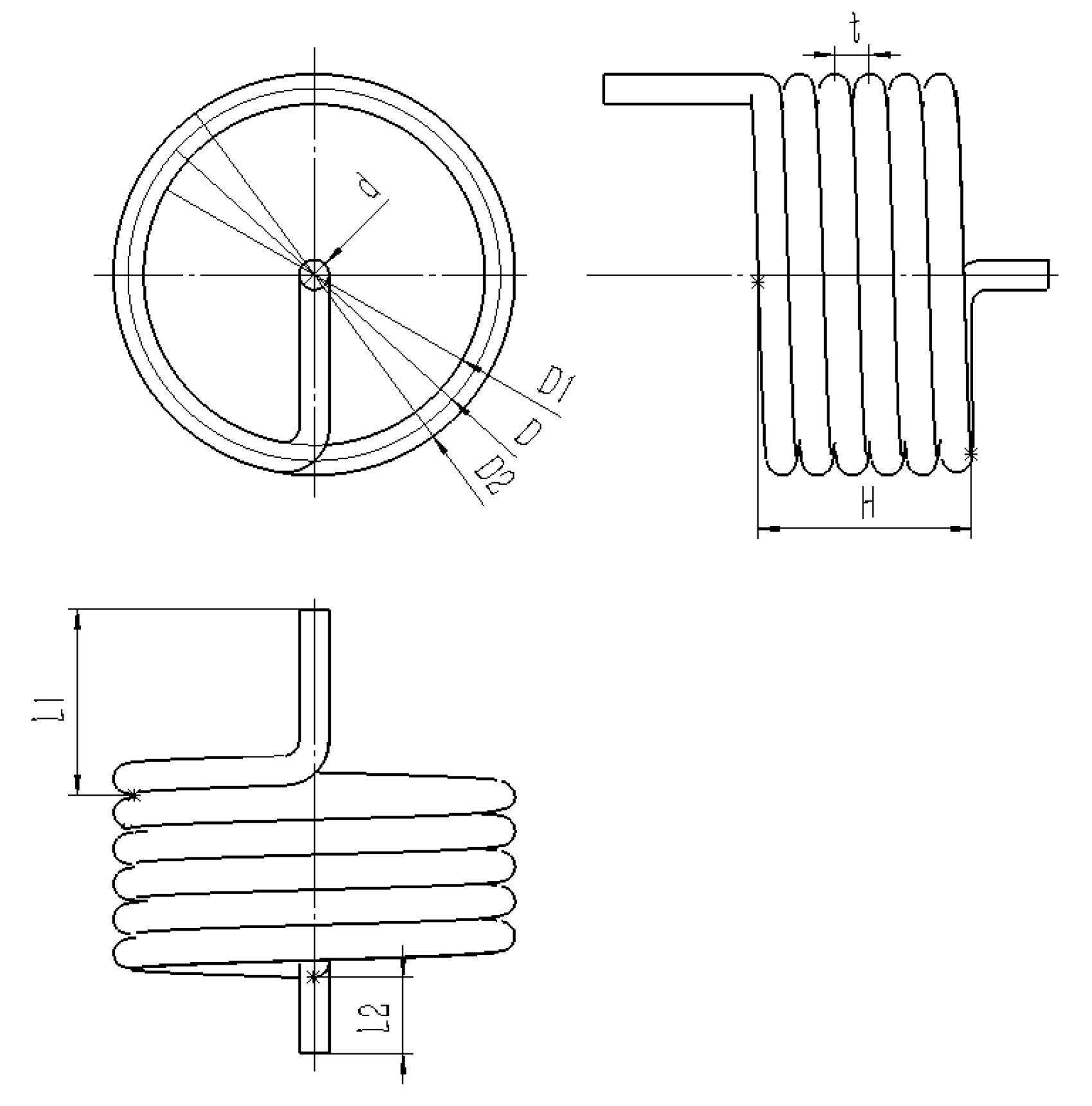

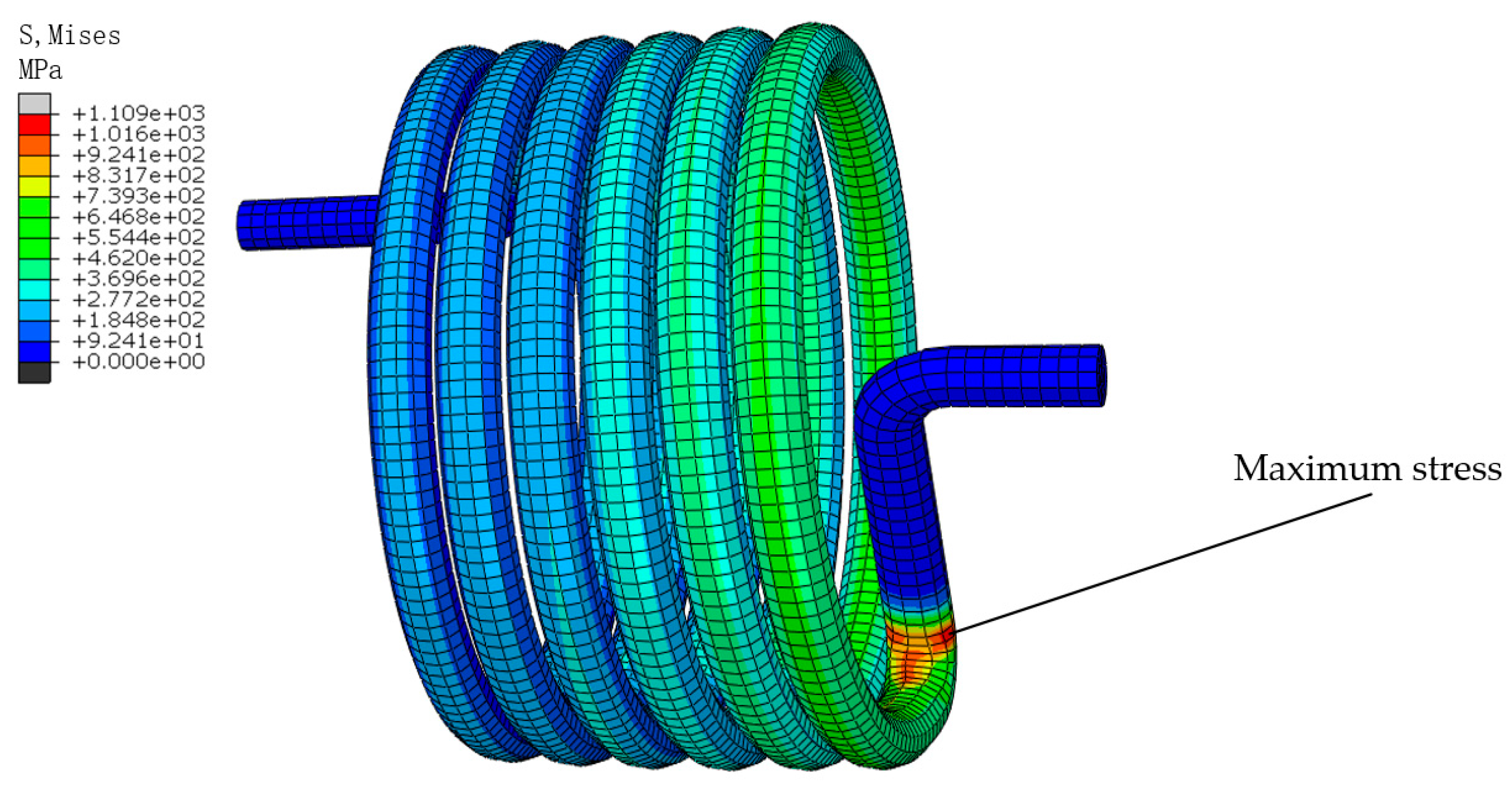


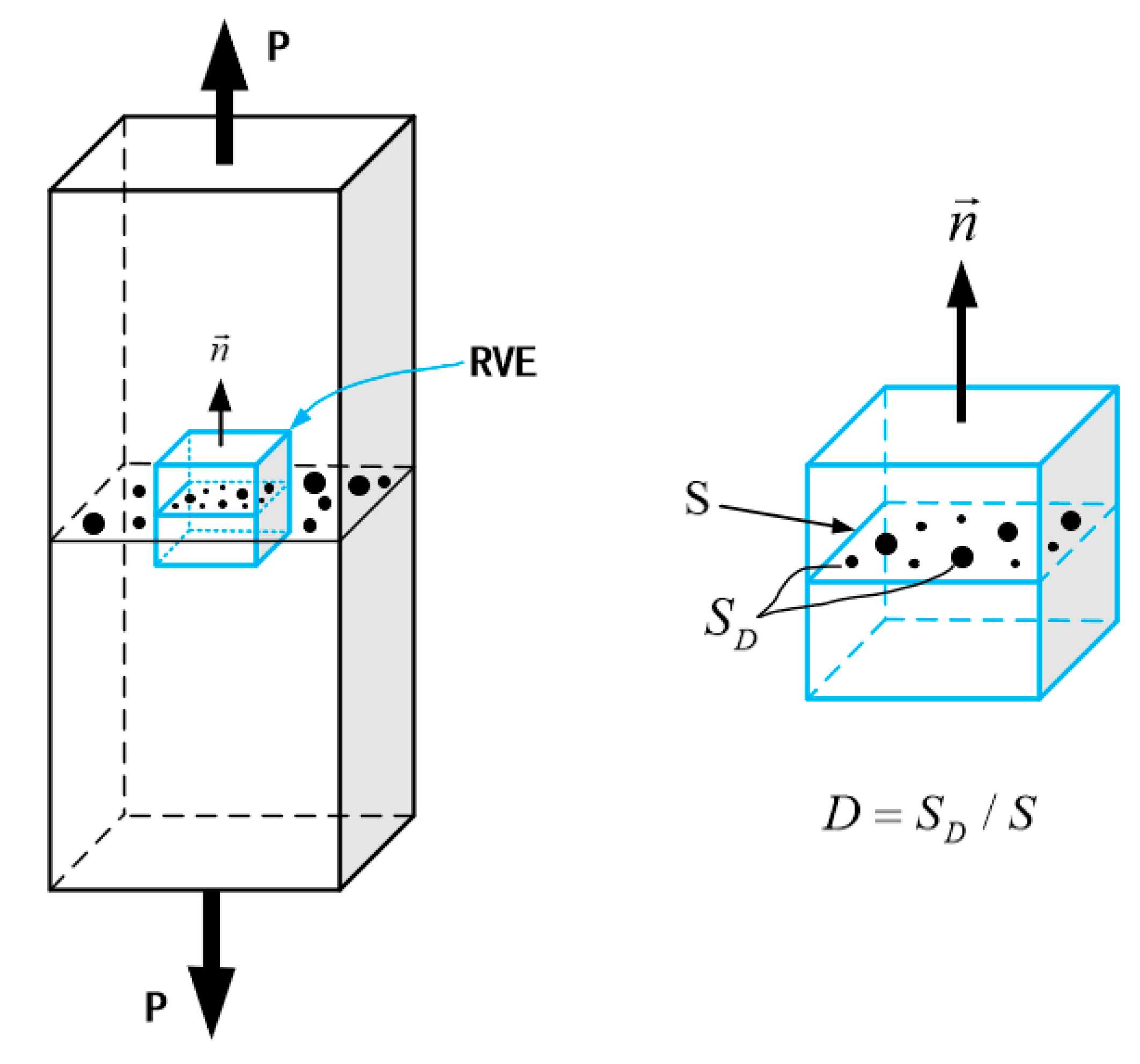


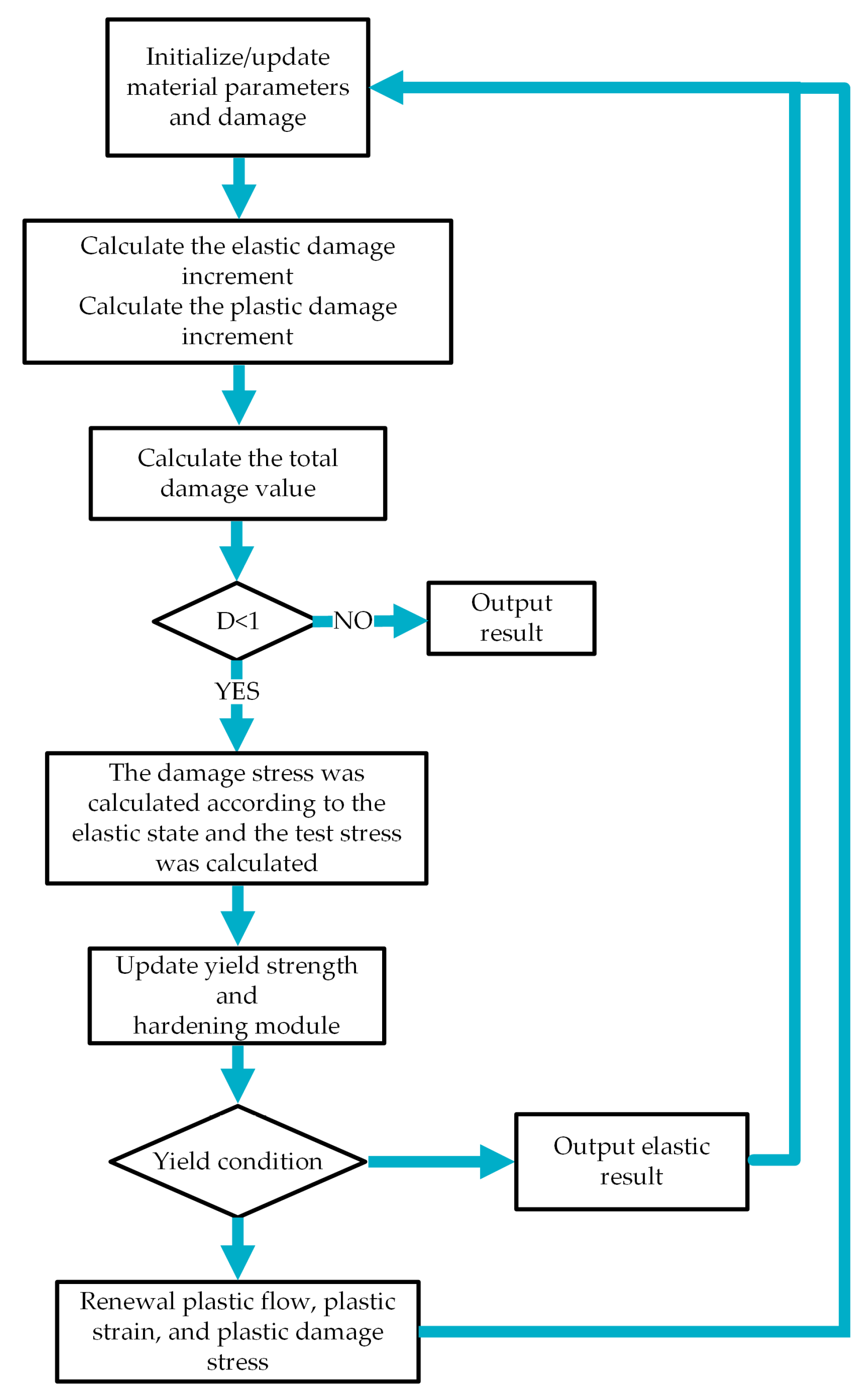
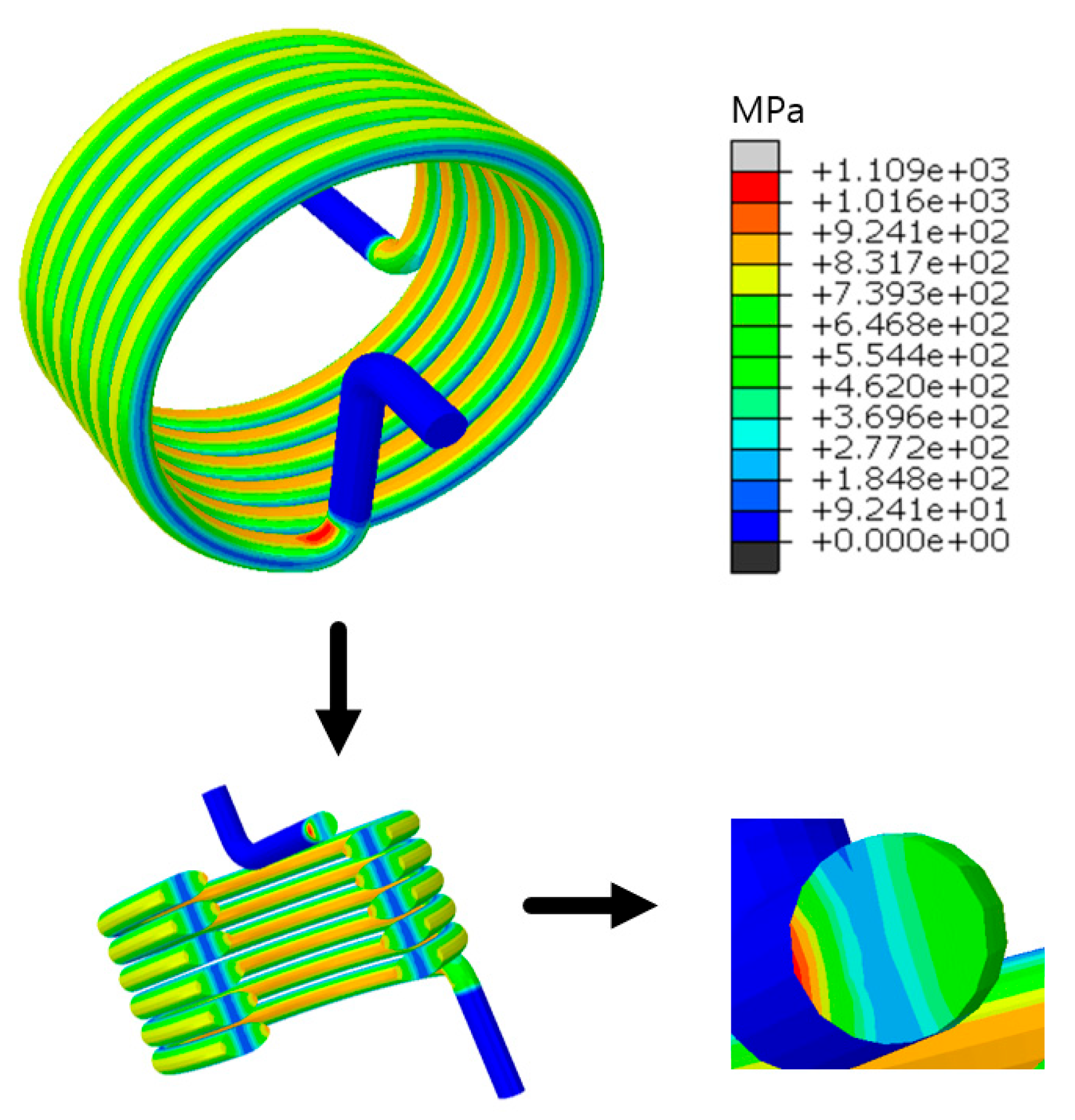


| Mesh Size/mm | Maximum Stress/MPa |
|---|---|
| 1.5 mm | 1108.7 |
| 1 mm | 1108.9 |
| 0.5 mm | 1109 |
| 0.2 mm | 1109.2 |
| Angle of Torsion | 60 Degrees | 80 Degrees | 100 Degrees | 120 Degrees |
|---|---|---|---|---|
| Fatigue life | 181,322 | 99,677 | 65,067 | 45,070 |
| (MPa) | (MPa) | (MPa) | (MPa) | |||
|---|---|---|---|---|---|---|
| 116,000 | 0.34 | 965 | 136,500 | 8100 | 1050 | 45 |
| (MPa) | (MPa) | |||||
|---|---|---|---|---|---|---|
| 1180 | 358 | 2.1 | 1.79 × 10−11 | 0.0013 | 0.00055 | 0.75 |
| 9.9293 | 4.7846 |
| Model | Mean Relative Error (MRE) |
|---|---|
| CDM | 2.04% |
| SWT | 10% |
| MSS | 7.84% |
| BM | 8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, D.; Zhang, C.; Yang, F.; Duan, F. Fatigue Life Analysis of Titanium Torsion Spring Based on Continuous Damage Mechanics. Materials 2025, 18, 221. https://doi.org/10.3390/ma18020221
Meng D, Zhang C, Yang F, Duan F. Fatigue Life Analysis of Titanium Torsion Spring Based on Continuous Damage Mechanics. Materials. 2025; 18(2):221. https://doi.org/10.3390/ma18020221
Chicago/Turabian StyleMeng, Dehai, Changming Zhang, Fan Yang, and Feixiang Duan. 2025. "Fatigue Life Analysis of Titanium Torsion Spring Based on Continuous Damage Mechanics" Materials 18, no. 2: 221. https://doi.org/10.3390/ma18020221
APA StyleMeng, D., Zhang, C., Yang, F., & Duan, F. (2025). Fatigue Life Analysis of Titanium Torsion Spring Based on Continuous Damage Mechanics. Materials, 18(2), 221. https://doi.org/10.3390/ma18020221






