A Study on the Fracture of Brittle Heterogeneous Materials Using Non-Extensive Statistical Mechanics and the Energy Distribution Function
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Preliminaries
2.2. The Experimental Protocol and the Mechanical Response of the Specimens
3. Results
3.1. Temporal Evolution of the Energy Content of the Acoustic Hits
3.2. The Energy Distribution Function of the Acoustic Hits and the Variation in the Entropic Index
4. Discussion
5. Conclusions
- From the thermodynamical point of view, the fracture process (and the respective damage mechanisms activated) of notched concrete beams (either plain or fiber-reinforced) is definitely a non-additive process, which cannot be described by traditional Boltzmann–Gibbs Statistical Mechanics.
- The discipline of Non-Extensive Statistical Mechanics, based on the Tsallis entropy concept, provides a powerful and flexible tool for the description of the mechanical response and the fracture process for such heterogeneous materials. This is the case for both intact and notched specimens. The main difference between the two configurations is the width of the range of values of the entropic index q and its evolution with increasing load.
- The energy content of the acoustic signals is a very interesting parameter for the analysis of the experimental data provided by the acoustic emission technique using NESM. Its efficiency is here proven similar to that of another parameter of the acoustic activity, namely the interevent time intervals, which has been used successfully in a long series of previous studies.
- The presence of the notch assigns a non-additive (and non-extensive) character to the fracture processes from very early loading steps, due to the early development of the process zone around the crown of the notch. On the contrary, for intact specimens, there is a smooth transition from additivity (low load levels) to non-additivity (as the load imposed tends to its maximum value and the system is about to enter into the critical stage of impending macroscopic fracture).
- The values of the entropic index, which are obtained from the Cumulative Distribution Function of the energy content of the acoustic signals before the load attains its peak value (1.39 ≤ q ≤ 1.45), are slightly smaller compared to the respective ones obtained from the energy content of the acoustic signals recorded after the maximization of the load (1.47 ≤ q ≤ 1.59).
- Finally, a correlation between the values of the entropic index and those of the average energy content of the acoustic signals is revealed. This correlation is excellently described by a power law for the whole range of values of the energy content of the acoustic signals.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grosse, C.U. Introduction. In Acoustic Emission Testing; Grosse, C.U., Ohtsu, M., Aggelis, D.G., Shiotani, T., Eds.; Springer Tracts in Civil Engineering; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced structural health monitoring of concrete structures with the aid of acoustic emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Ohtsu, M. Basics of acoustic emission and applications to concrete engineering. Mater. Sci. Res. Int. 1998, 4, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Sammonds, P.R.; Meredith, P.G.; Main, I.G. Role of pore fluids in the generation of seismic precursors to shear fracture. Nature 1992, 359, 228–230. [Google Scholar] [CrossRef]
- Burud, N.B.; Chandra Kishen, J.M. Response based damage assessment using acoustic emission energy for plain concrete. Const. Build. Mater. 2021, 269, 12124. [Google Scholar] [CrossRef]
- Jia, X.; Li, J.; Zhang, Q.; Zhang, M.; Jin, Y.; Ding, Y. Analysis of critical states based on acoustic emission signals during progressive failure of wood. PLoS ONE 2024, 19, e0302528. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Soulioti, D.V.; Sapouridis, N.; Barkoula, N.M.; Paipetis, A.S.; Matikas, T.E. Acoustic emission characterization of the fracture process in fibre reinforced concrete. Const. Build. Mater. 2011, 25, 4126–4131. [Google Scholar] [CrossRef]
- De Smedt, M.; Vandecruys, E.; Vrijdaghs, R.; Verstrynge, E.; Vandewalle, L. Acoustic emission-based damage analysis of steel fibre reinforced concrete in uniaxial tension tests. Const. Build. Mater. 2022, 321, 126254. [Google Scholar] [CrossRef]
- Vandecruys, E.; Van de Velde, M.; Reynders, E.; Lombaert, G.; Verstrynge, E. Experimental study on acoustic emission sensing and vibration monitoring of corroding reinforced concrete beams. Eng. Struct. 2023, 293, 116553. [Google Scholar] [CrossRef]
- Verstrynge, E.; Van Steen, C.; Vandecruys, E.; Wevers, M. Steel corrosion damage monitoring in reinforced concrete structures with the acoustic emission technique: A review. Const. Build. Mater. 2022, 349, 128732. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractal analysis and synthesis of fracture surface roughness and related forms of complexity and disorder. Int. J. Fract. 2006, 138, 13–17. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Z.; Chen, L.; Gu, J. Experimental study on critical characteristics of self-organized behavior of concrete under uniaxial compression based on AE characteristic parameters information entropy. J. Mater. Civ. Eng. 2022, 34, 04022141. [Google Scholar] [CrossRef]
- Diodati, P.; Piazza, S.; Marchesoni, F. Acoustic emission from periodically perturbed systems: SOC and predictability. Physica A 2004, 340, 598–606. [Google Scholar] [CrossRef]
- Sun, B.; Yan, Y.; Wang, S.; Qi, C.; Yang, H.; Zeng, S. Self-organized criticality and b-value characteristics of acoustic emission of rocks under different stress paths. Rock Mech. Rock Eng. 2025, 58, 851–866. [Google Scholar] [CrossRef]
- Triantis, D.; Pasiou, E.D.; Stavrakas, I.; Kourkoulis, S.K. Hidden affinities between electric and acoustic activities in brittle materials at near-fracture load levels. Rock Mech. Rock Eng. 2022, 55, 1325–1342. [Google Scholar] [CrossRef]
- Rao, M.V.M.S.; Prasanna Lakshimi, K.J.; Nagaraja Rao, G.M.; Kumar, K.V.; Udaykumar, S. Pre-failure damage caused by micro-cracks in rock: A laboratory study using Acoustic Emission. In Proceedings of the National Seminar and Exhibition on Nondestructive Evaluation, Tiruchirappalli, India, 10–12 December 2009; pp. 323–327. [Google Scholar]
- Dexing, L.; Enyuan, W.; Xiangguo, K.; Haishan, J.; Dongming, W.; Muhammad, A. Damage precursor of construction rocks under uniaxial cyclic loading tests analyzed by acoustic emission. Const. Build. Mater. 2019, 206, 169–178. [Google Scholar] [CrossRef]
- Ozevin, D.; Kessler, S. The dependence of acoustic emission behavior on prior fatigue loading history. Front. Built. Environ. 2022, 8, 981327. [Google Scholar] [CrossRef]
- Vu, C.C.; Amitrano, D.; Plé, O.; Weiss, J. Compressive failure as a critical transition: Experimental evidence and mapping onto the universality class of depinning. Phys. Rev. Lett. 2019, 122, 015502. [Google Scholar] [CrossRef]
- Lee, S.C. Prediction of concrete strength using artificial neural networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Thirumalaiselvi, A.; Sasmal, S. Pattern recognition enabled acoustic emission signatures for crack characterization during damage progression in large concrete structures. Appl. Acoust. 2021, 175, 107797. [Google Scholar] [CrossRef]
- Łazarska, M.; Woźniak, T.; Ranachowski, Z.; Trafarski, A.; Domek, G. Analysis of acoustic emission signals at austempering of steels using neural networks. Met. Mater. Int. 2017, 23, 426–433. [Google Scholar] [CrossRef]
- Schabowicz, K. Neural networks in the NDT identification of the strength of concrete. Arch. Civ. Eng. 2005, 51, 371–382. [Google Scholar]
- Bal, L.; Buyle-Bodin, F. Artificial neural network for predicting drying shrinkage of concrete. Const. Build. Mater. 2013, 38, 248–254. [Google Scholar] [CrossRef]
- Wang, Y.; Jie, G.; Na, W.; Chao, Y.; Li, Z.; Jun, C.L. Identification of the concrete damage degree based on the principal component analysis of acoustic emission signals and neural networks. Mater. Test. 2020, 62, 517–524. [Google Scholar] [CrossRef]
- Ai, L.; Soltangharaei, V.; Ziehl, P. Developing a heterogeneous ensemble learning framework to evaluate Alkali-silica reaction damage in concrete using acoustic emission signals. Mech. Syst. Signal Process. 2022, 172, 108981. [Google Scholar] [CrossRef]
- Main, I.; Meredith, P.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Lei, X.; Ma, S. Laboratory acoustic emission study for earthquake generation process. Earthq. Sci. 2014, 27, 627–646. [Google Scholar] [CrossRef]
- Gregori, G.P.; Paparo, G.; Poscolieri, M.; Zanini, A. Acoustic emission and released seismic energy. Nat. Hazards Earth Syst. Sci. 2005, 5, 777–782. [Google Scholar] [CrossRef]
- Zhu, Z.; Jiang, Z.; Accornero, F.; Carpinteri, A. Correlation between seismic activity and acoustic emission on the basis of in situ monitoring. Nat. Hazards Earth Syst. Sci. 2024, 24, 4133–4143. [Google Scholar] [CrossRef]
- Thurner, S.; Hanel, R.; Klimek, P. Introduction to the Theory of Complex Systems; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Santos Lima, H.; Tsallis, C. Exploring the neighborhood of q-exponentials. Entropy 2020, 22, 1402. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics-Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. On the foundations of statistical mechanics. Eur. Phys. J. Spec. Top. 2017, 226, 1433–1443. [Google Scholar] [CrossRef]
- Ludescher, J.; Tsallis, C.; Bunde, A. Universal behaviour of interoccurrence times between losses in financial markets: An analytical description. Europhys Lett 2011, 95, 68002. [Google Scholar] [CrossRef]
- Di Giovambattista, R.; Tyupkin, Y. An analysis of the process of acceleration of seismic energy emission in laboratory ex-periments on destruction of rocks and before strong earthquakes on Kamchatka and in Italy. Tectonophysics 2001, 338, 339–351. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions. Eurphys. Lett. 2012, 97, 58002. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Posadas, A. Fragment-asperity interaction model for earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Silva, R.; França, G.; Vilar, C.; Alcaniz, J. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef]
- Telesca, L. Tsallis-based nonextensive analysis of the southern California seismicity. Entropy 2011, 13, 1267–1280. [Google Scholar] [CrossRef]
- Shcherbakov, I.P.; Kuksenko, V.S.; Chmel, A.E. Nonextensive statistical analysis of the data on the high-speed impact fracture of solids. JETP Lett. 2011, 94, 378–381. [Google Scholar] [CrossRef]
- Vinciguerra, S.C.; Greco, A.; Pluchino, A.; Rapisarda, A.; Tsallis, C. Acoustic Emissions in rock deformation and failure: New insights from q-statistical analysis. Entropy 2023, 25, 701. [Google Scholar] [CrossRef]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Koumoudeli, T.; Stavrakas, I. Nonextensive statistical analysis of acoustic emissions series recorded during the uniaxial compression of brittle rocks. Physica A 2019, 528, 121498. [Google Scholar] [CrossRef]
- Loukidis, A.; Triantis, A.; Stavrakas, I. Non-extensive statistical analysis of Acoustic Emissions recorded in marble and cement mortar specimens under mechanical load until fracture. Entropy 2020, 22, 1115. [Google Scholar] [CrossRef] [PubMed]
- Loukidis, A.; Triantis, A.; Stavrakas, I. Non-extensive statistical mechanics in Acoustic Emissions: Detection of upcoming fracture in rock materials. Appl. Sci. 2023, 13, 3249. [Google Scholar] [CrossRef]
- Greco, A.; Tsallis, C.; Rapisarda, A.; Pluchino, A.; Fichera, G.; Contrafatto, L. Acoustic emissions in compression of building materials: Q-statistics enables the anticipation of the breakdown point. Eur. Phys. J. Spec. Top. 2020, 229, 841–849. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Hloupis, G.; Triantis, D.; Vallianatos, F. Electrical and Acoustic Emissions in cement mortar beams subjected to mechanical loading up to fracture. Eng. Fail. Anal. 2013, 35, 454–461. [Google Scholar] [CrossRef]
- Naukhez, K.; Vidya Sagar, R.; Chandra Kishen, J.M. Q-Statistical analysis of acoustic emissions recorded during unconfined uniaxial compression of ultra-high-performance concrete. In Proceedings of the 11th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Bangalore, India, 10–14 September 2023. [Google Scholar]
- Triantis, D.; Stavrakas, I.; Loukidis, A.; Pasiou, E.D.; Kourkoulis, S.K. Spatio-temporal distribution of the sources of acoustic events in notched fiber-reinforced concrete beams under three-point bending. Materials 2023, 16, 5118. [Google Scholar] [CrossRef]
- Available online: https://www.physicalacoustics.com/by-product/sensors/R15a-150-kHz-General-Purpose-AE-Sensor (accessed on 29 December 2024).
- Available online: https://material.karlov.mff.cuni.cz/people/mathis/Navody/PCI2.pdf (accessed on 29 December 2024).
- Sychev, V.N.; Kulkov, D.S. Energy characteristics of acoustic emission under various modes of uniaxial loading. IOP Conf. Ser. Earth Environ. Sci. 2021, 929, 012018. [Google Scholar] [CrossRef]
- Burud, N.B.; Chandra Kishen, J.M. Non-extensive statistical mechanics for acoustic emission in disordered media: Entropy, size effect, and self-organization. Int. J. Mech. Sci. 2021, 202–203, 106514. [Google Scholar] [CrossRef]
- Stavrakas, I.; Triantis, D.; Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I. Acoustic emission analysis when cement mortar specimens are subjected to three point bending repetitive cycles. Lat. Am. J. Solids Struct. 2016, 13, 2283–2297. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Stavrakas, I.; Triantis, D. Assessing structural integrity of non-homogeneous systems by means of Acoustic Emissions and Non-Extensive Statistical Mechanics. Frat. Integrità Strutt. 2024, 68, 440–457. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C. Mathematical Foundations of Nonextensive Statistical Mechanics; World Scientific: Singapore, 2022. [Google Scholar]
- Tsallis, C. Nonextensive Statistical Mechanics and Thermodynamics: Historical Background and Present Status. In Nonextensive Statistical Mechanics and its Applications; Lecture Notes in Physics; Abe, S., Okamoto, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 560. [Google Scholar]
- Abe, S.; Martínez, S.; Pennini, F.; Plastino, A. Nonextensive thermodynamic relations. Phys. Lett. A 2001, 281, 126–130. [Google Scholar] [CrossRef]
- Beck, C. Dynamical foundations of nonextensive statistical mechanics. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar] [CrossRef]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to nonextensive statistical mechanics and thermodynamics. In The Physics of Complex Systems (New Advances and Perspectives); IOS Press: Amsterdam, The Netherlands, 2004; pp. 229–252. [Google Scholar]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker-Planck equation. Physica A 1995, 222, 347354. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Rendell, R.W. Nonextensive statistical mechanics: Implications to quantum information. Europhys. News 2005, 36, 221–224. [Google Scholar] [CrossRef]
- Ruseckas, J.; Gontis, V.; Kaulakys, B. Nonextensive statistical mechanics distributions and dynamics of financial observables from the nonlinear stochastic differential equations. Adv. Complex Syst. 2012, 15, 1250073. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Triantis, D.; Vallianatos, F.; Stonham, J. Predicting fracture of mortar beams under three-point bending using non-extensive statistical modeling of electric emissions. Physica A 2015, 419, 603–611. [Google Scholar] [CrossRef]
- Shan, T.; Li, Z.; Jia, H.; Wang, E.; Wang, X.; Niu, Y.; Zhang, X.; Chen, D.; Yin, S.; Zhang, Q. Failure evolution and disaster prediction of rock under uniaxial compression based on non-extensive statistical analysis of electric potential. Int. J. Min. Sci. Technol. 2024, 34, 975–993. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Ramírez-Rojas, A.; Vargas, C.A. Tsallis q-statistics in seismology. Entropy 2023, 25, 408. [Google Scholar] [CrossRef]
- Stavrakas, I.; Triantis, D.; Agioutantis, Z.; Maurigiannakis, S.; Saltas, V.; Vallianatos, F. Pressure Stimulated Currents in rocks and their correlations with mechanical properties. Nat. Hazards Earth Syst. Sci. 2004, 4, 563–567. [Google Scholar] [CrossRef]
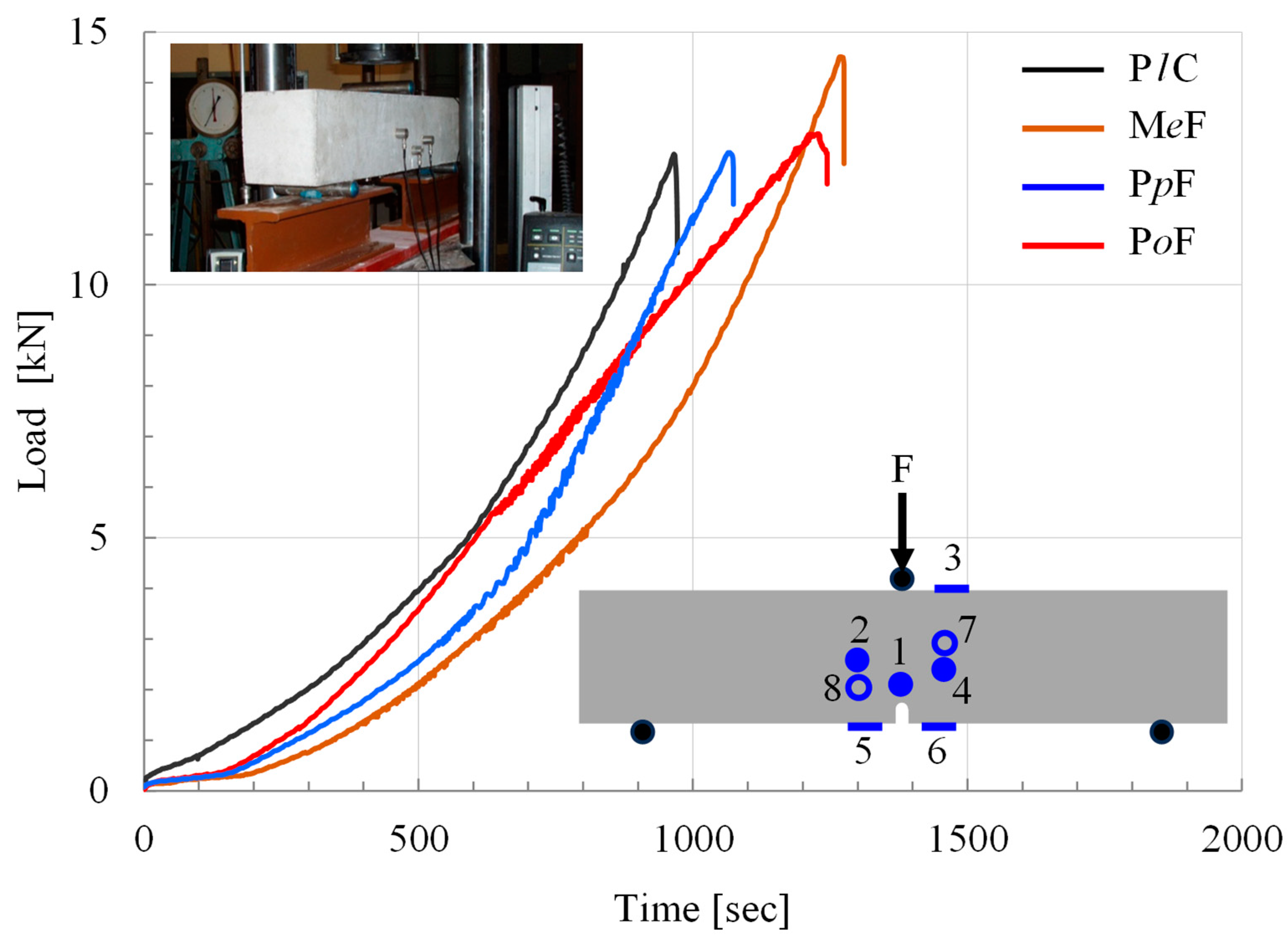
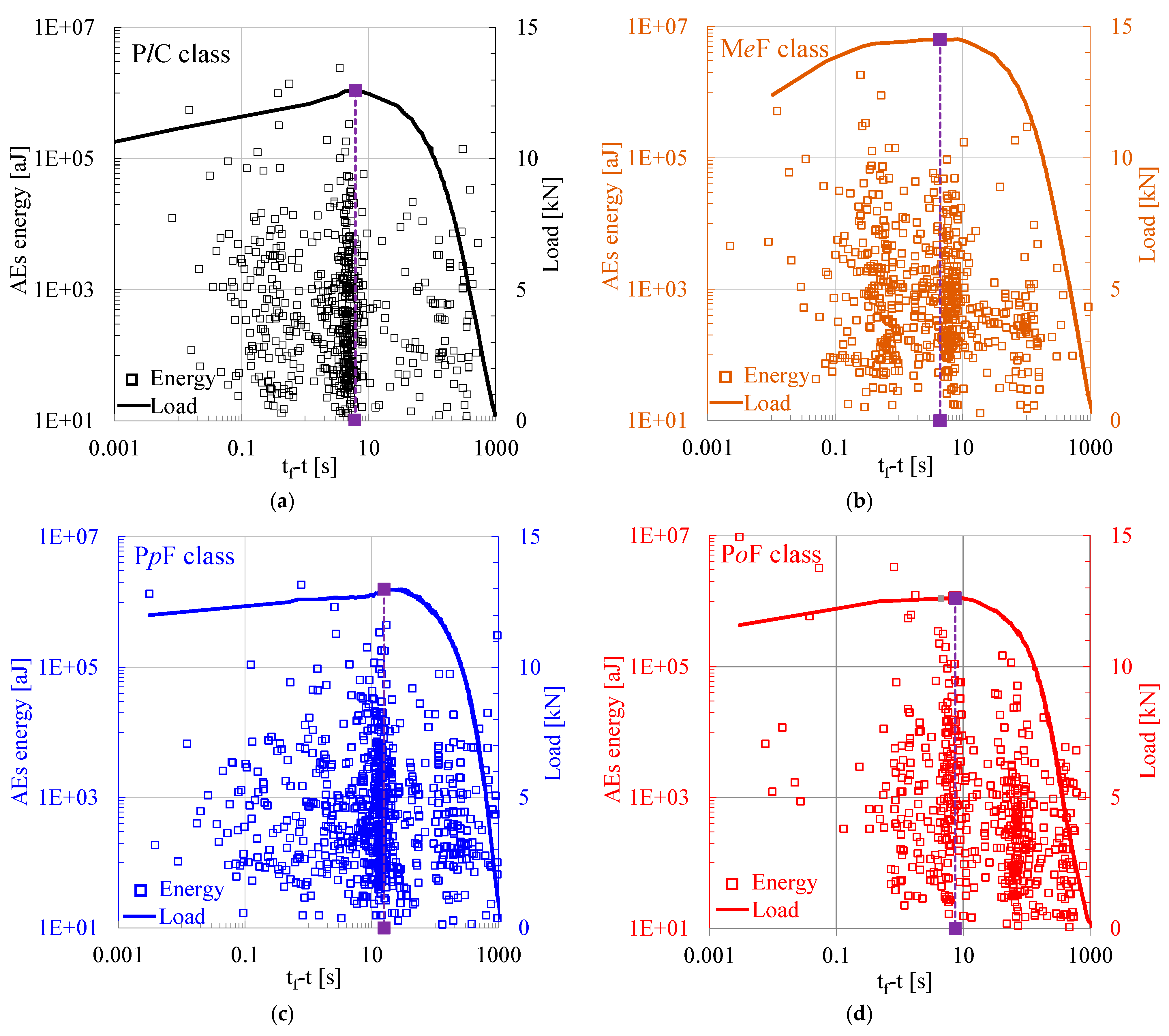
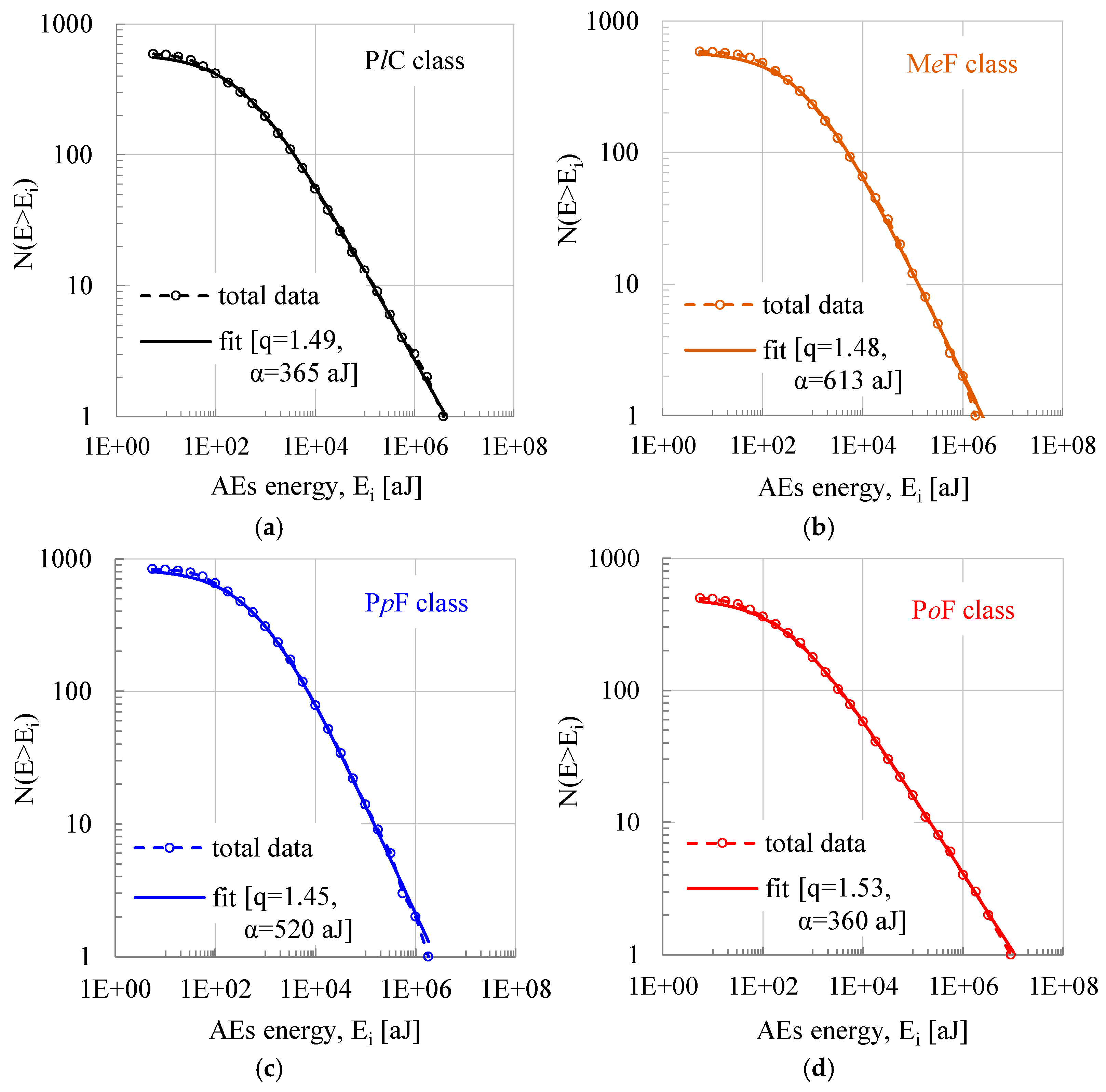
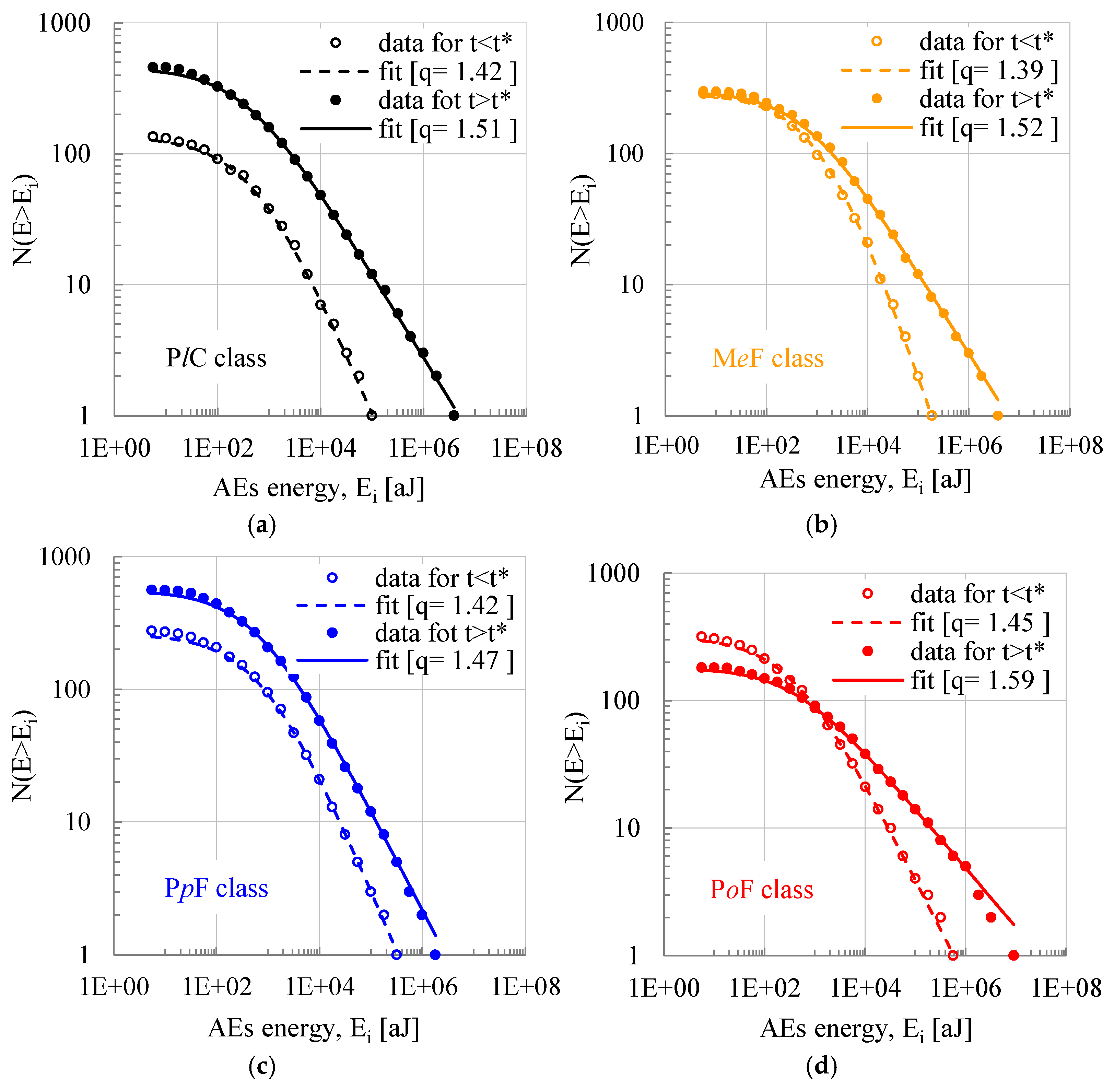
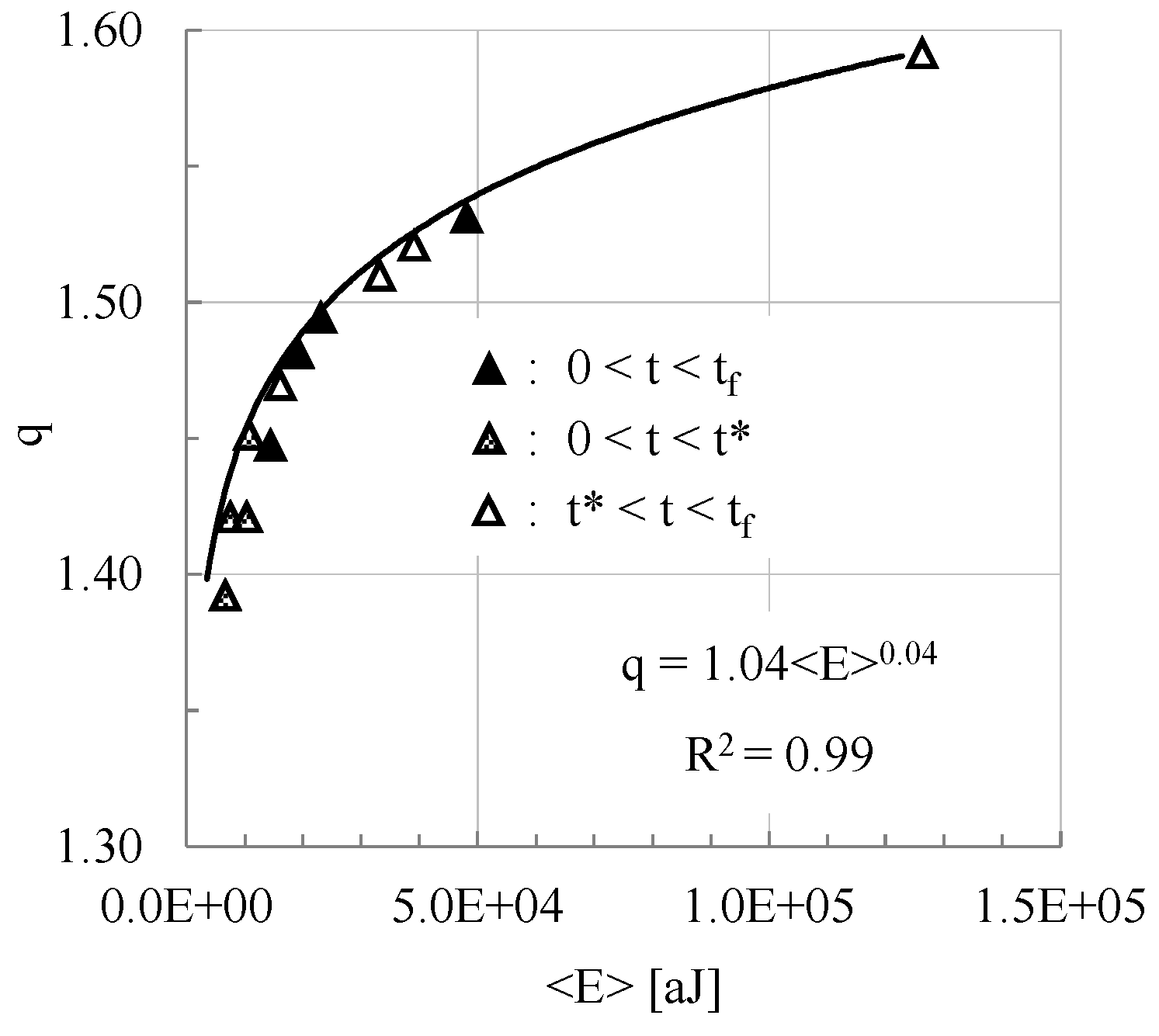

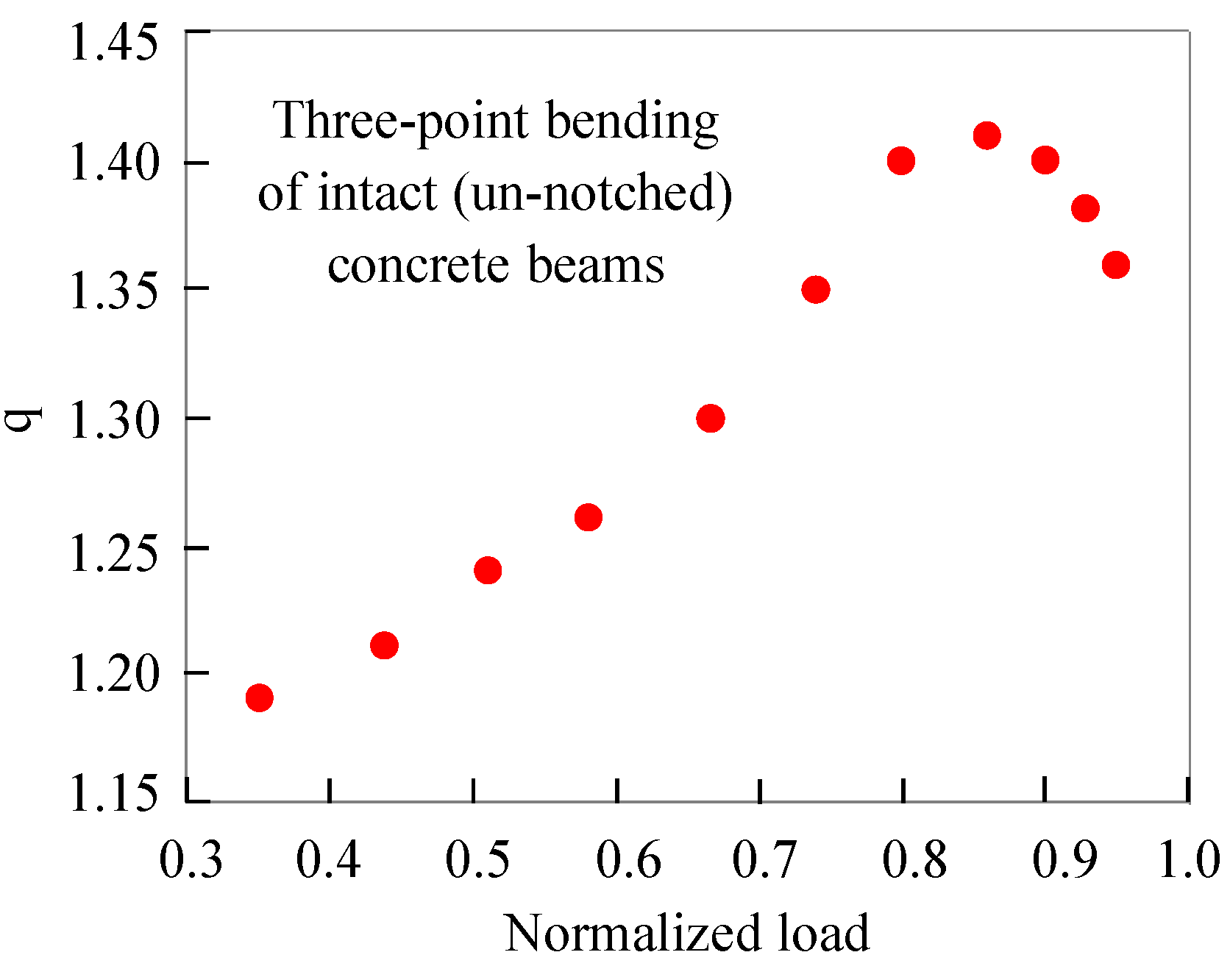
| Class of Specimens | tf [s] | t* [s] | Lmax [kN] | Nt | N1 | N2 |
|---|---|---|---|---|---|---|
| PlC | 971.2 | 965.5 | 12.6 | 590 | 135 | 455 |
| MeF | 1275.4 | 1271.0 | 14.5 | 585 | 287 | 298 |
| PpF | 1244.7 | 1229.0 | 13.0 | 836 | 276 | 560 |
| PoF | 1073.5 | 1066.0 | 12.6 | 498 | 317 | 181 |
| Class of Specimens | Overall Data 0 < t < tf | Group I 0 < t < t* | Group II t* < t < tf | ||||||
|---|---|---|---|---|---|---|---|---|---|
| q | α [aJ] | < E> [aJ] | q | α [aJ] | < E> [aJ] | q | α [aJ] | < E> [aJ] | |
| PlC | 1.49 | 365 | 20076 | 1.42 | 323 | 4611 | 1.51 | 370 | 30308 |
| MeF | 1.48 | 613 | 19452 | 1.39 | 605 | 3522 | 1.52 | 645 | 35853 |
| PpF | 1.45 | 520 | 10872 | 1.42 | 509 | 6074 | 1.47 | 525 | 13236 |
| PoF | 1.53 | 360 | 44851 | 1.45 | 293 | 7899 | 1.59 | 703 | 122788 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Triantis, D.; Stavrakas, I.; Pasiou, E.D.; Kourkoulis, S.K. A Study on the Fracture of Brittle Heterogeneous Materials Using Non-Extensive Statistical Mechanics and the Energy Distribution Function. Materials 2025, 18, 335. https://doi.org/10.3390/ma18020335
Triantis D, Stavrakas I, Pasiou ED, Kourkoulis SK. A Study on the Fracture of Brittle Heterogeneous Materials Using Non-Extensive Statistical Mechanics and the Energy Distribution Function. Materials. 2025; 18(2):335. https://doi.org/10.3390/ma18020335
Chicago/Turabian StyleTriantis, Dimos, Ilias Stavrakas, Ermioni D. Pasiou, and Stavros K. Kourkoulis. 2025. "A Study on the Fracture of Brittle Heterogeneous Materials Using Non-Extensive Statistical Mechanics and the Energy Distribution Function" Materials 18, no. 2: 335. https://doi.org/10.3390/ma18020335
APA StyleTriantis, D., Stavrakas, I., Pasiou, E. D., & Kourkoulis, S. K. (2025). A Study on the Fracture of Brittle Heterogeneous Materials Using Non-Extensive Statistical Mechanics and the Energy Distribution Function. Materials, 18(2), 335. https://doi.org/10.3390/ma18020335









