Computational Model of the Effective Thermal Conductivity of a Bundle of Round Steel Bars
Abstract
1. Introduction
2. Materials and Methods
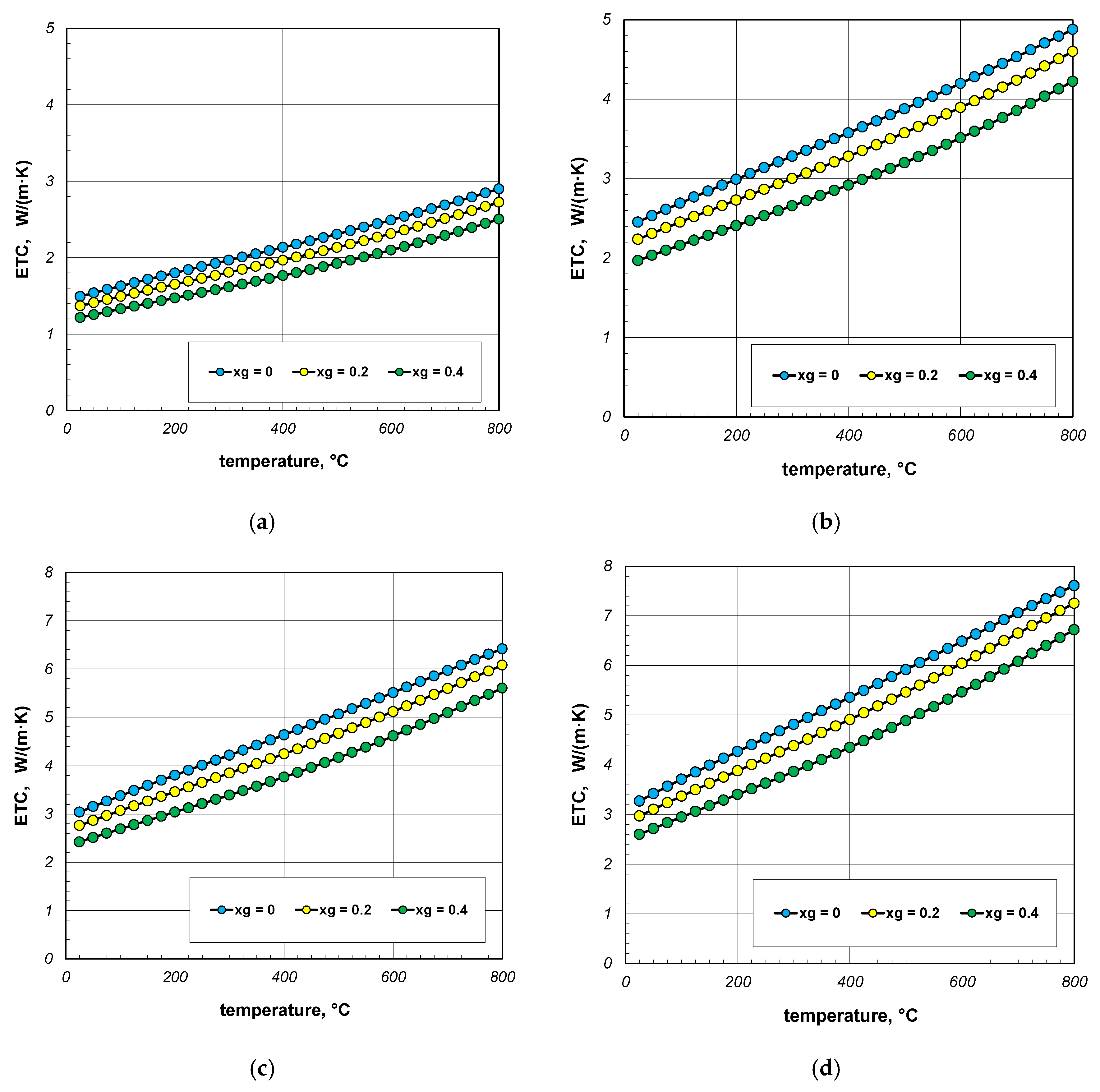
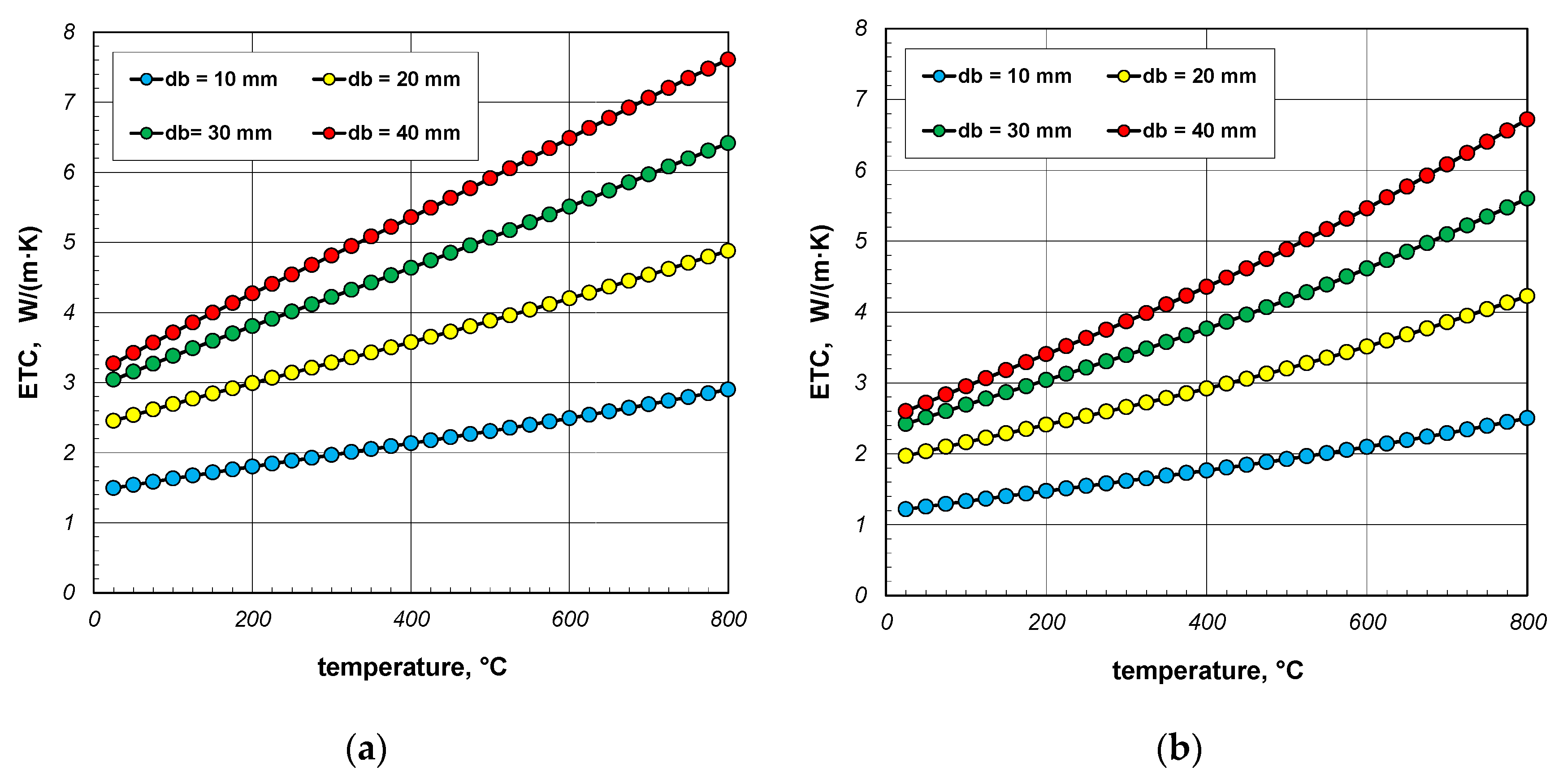
3. Results and Discussion
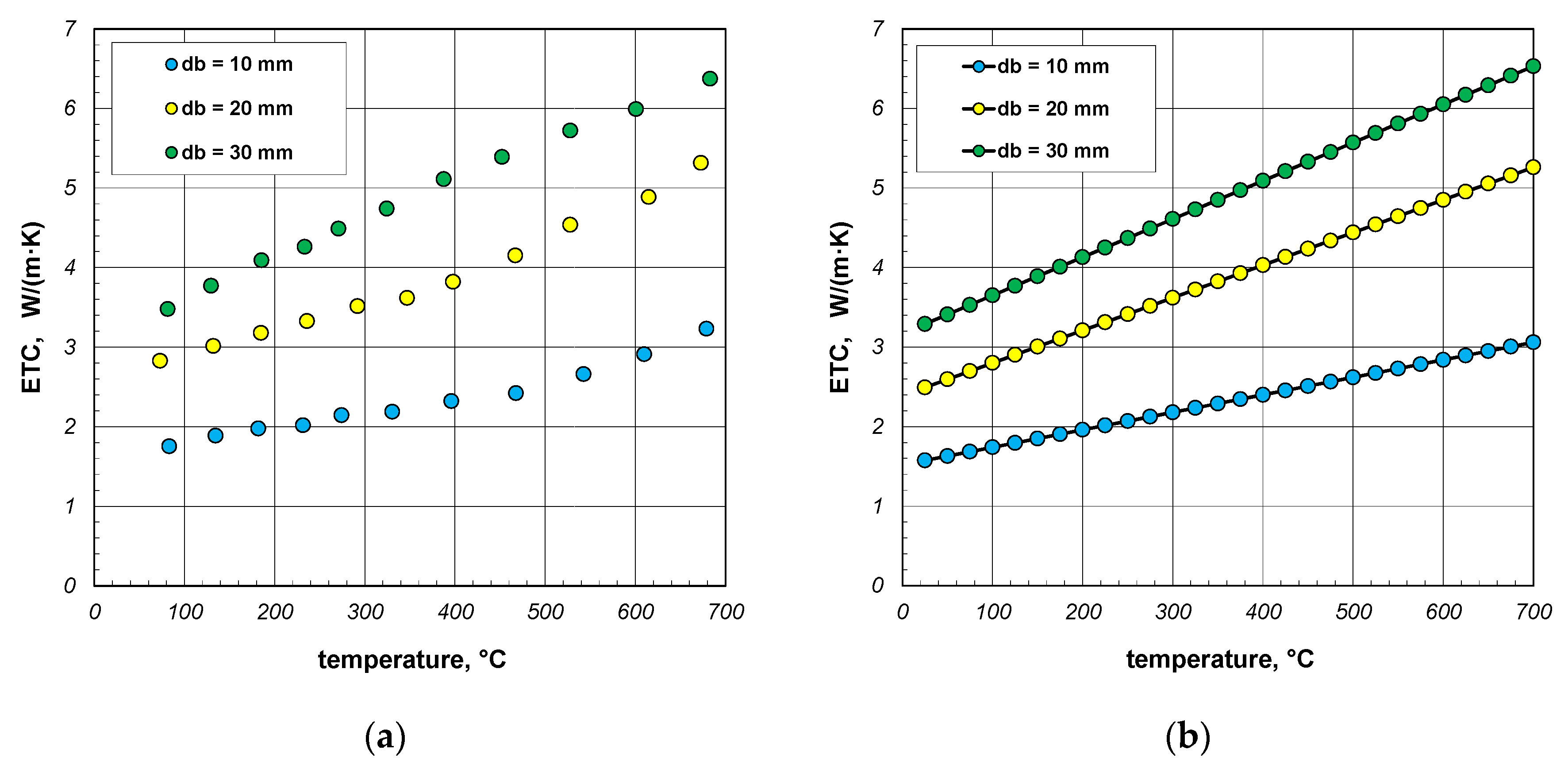
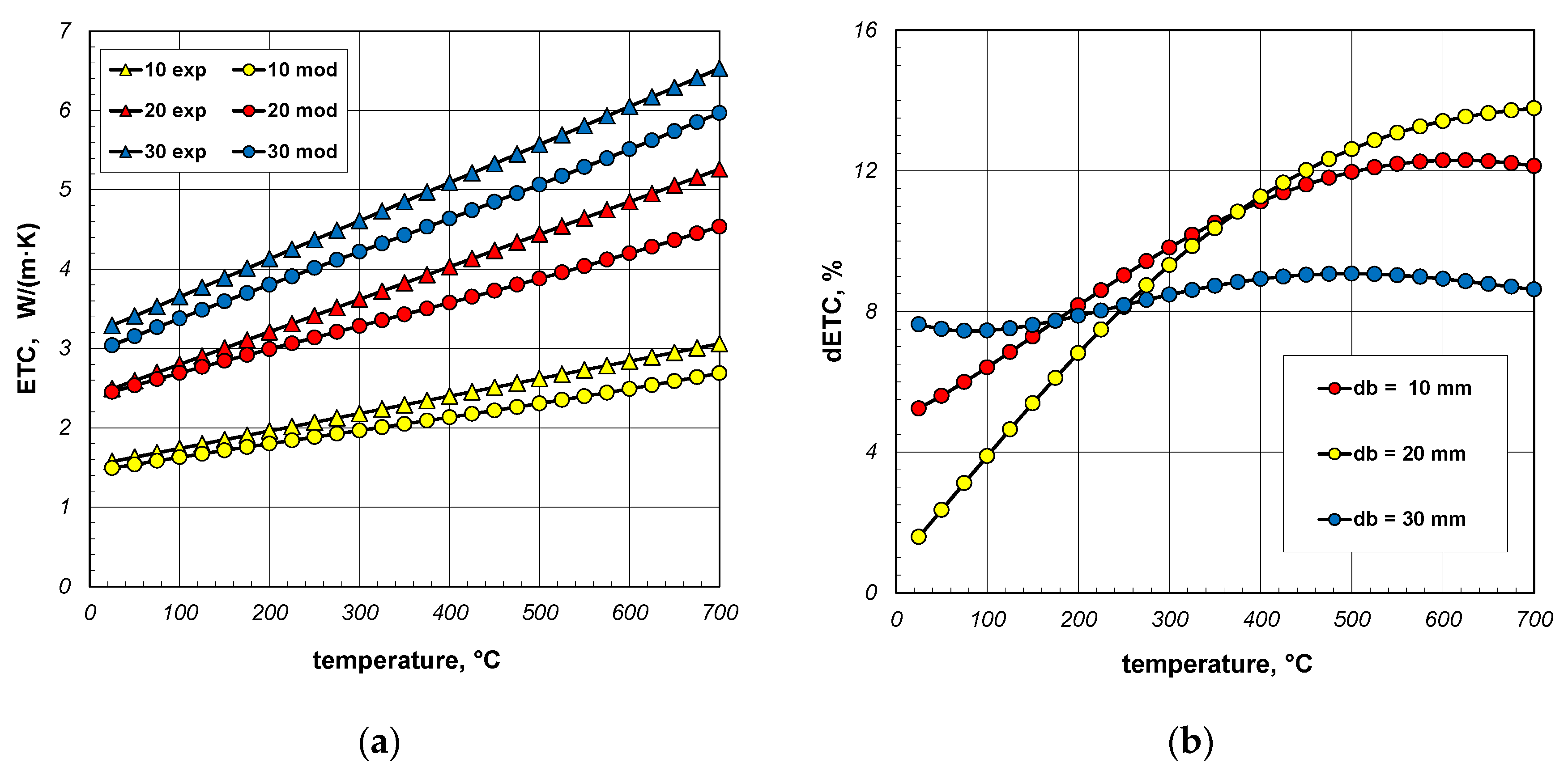
- bar diameter db;
- distance between the bars lg;
- thermal conductivity of steel ks;
- thermal conductivity of gas kg;
- thermal contact conductance hct;
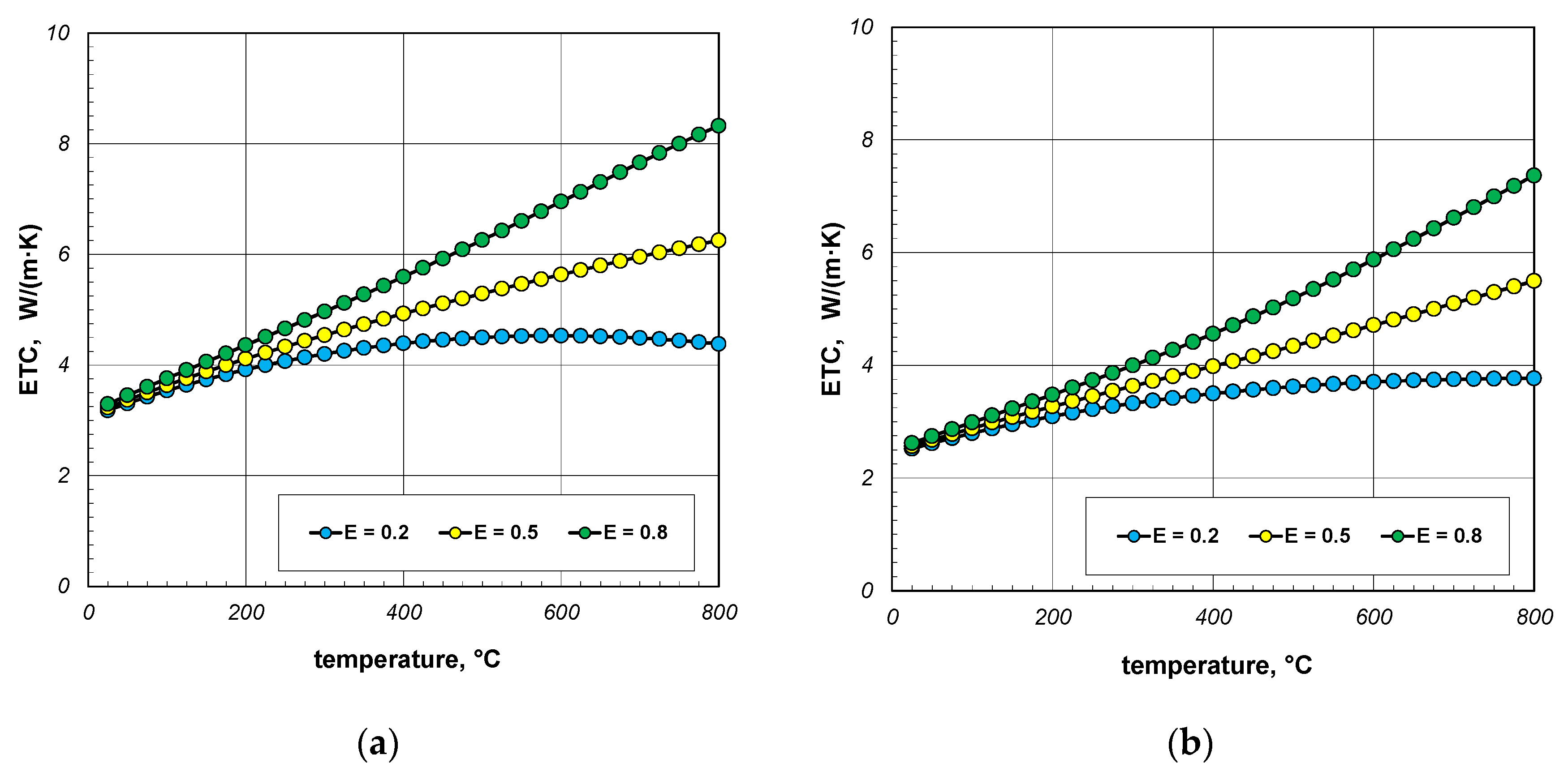
- bar surface emissivity εb.
4. Conclusions
- ETC of round steel bar bundle changes over the range of 2.2–8.5 W/(m·K);
- ETC rises linearly with temperature;
- ETC increases as a function of the bar diameter—this increase is not linear;
- The bar thermal conductivity does not have much influence on the ETC value;
- The values of ETC range from 0.02 to 0.27 of bar thermal conductivity;
- The key problem for modeling heat transfer in a bar bundle is the selection of the bar’s emissivity;
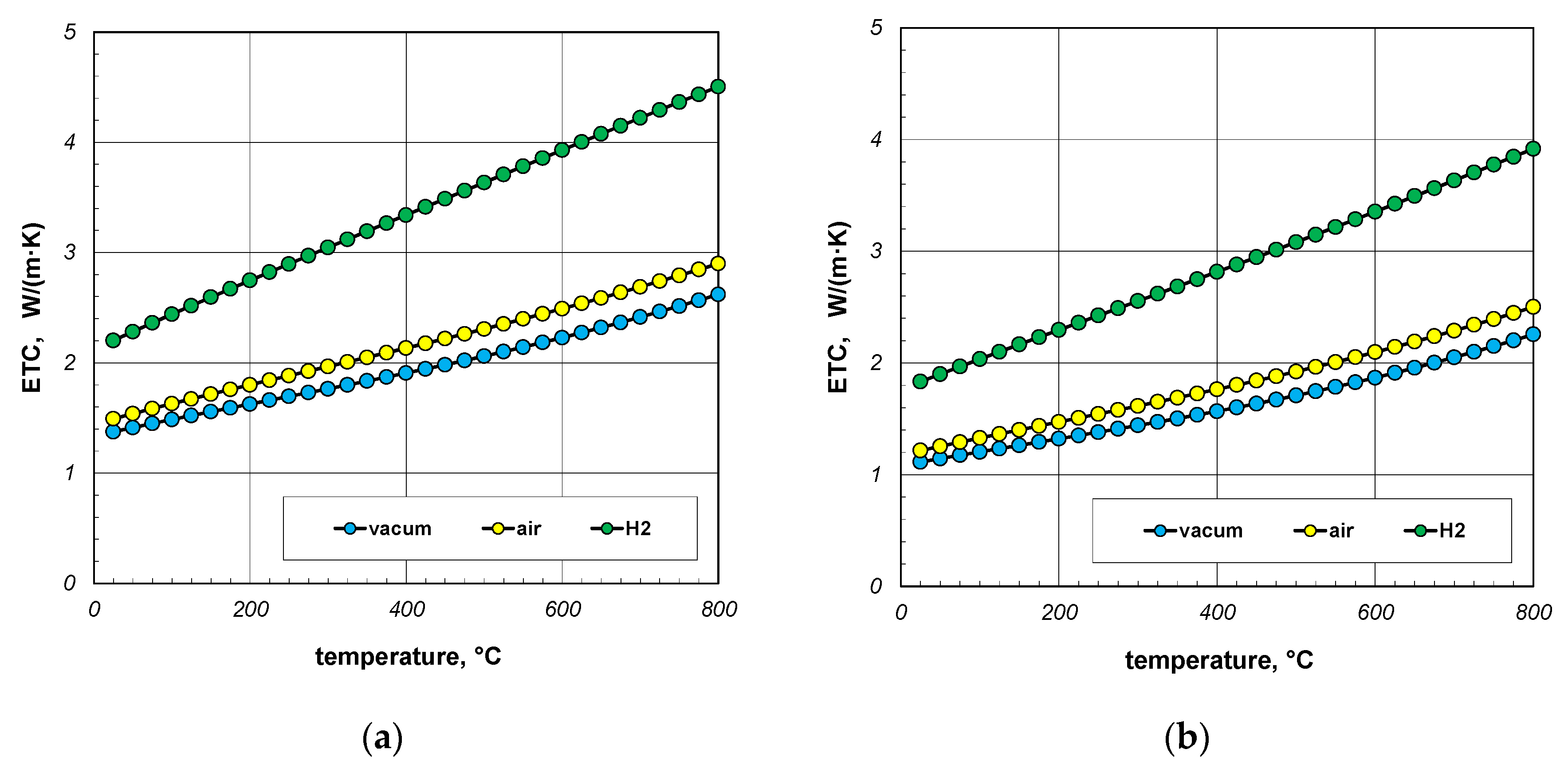
- Replacing the air with a vacuum does not have a major impact on the bundle heating;
- Replacing air with hydrogen increases the bundle heating intensity from 20% to 55%. The degree of intensification of this process is the greater the smaller the diameter of the bars;
- Changing the bundle porosity in the range of 0.1–0.2 slightly reduces the ETC value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwon, W.H.; Choi, S.W.; Lee, E.B. Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants. Energies 2024, 17, 1536. [Google Scholar] [CrossRef]
- Bataille, C.; Melton, N. Energy efficiency and economic growth: A retrospective CGE analysis for Canada from 2002 to 2012. Energy Econ. 2017, 64, 118–130. [Google Scholar] [CrossRef]
- Baig, A.A.; Fung, A.S.; Kumar, R. Auditing and Analysis of Natural Gas Consumptions in Small- and Medium-Sized Industrial Facilities in the Greater Toronto Area for Energy Conservation Opportunities. Energies 2024, 17, 1744. [Google Scholar] [CrossRef]
- Tahmasebi, M.M.; Banihashemi, S.; Hassanabadi, M.S. Assessment of the Variation Impacts on Windows on Energy Consumption and Carbon Footprint. Procedia Eng. 2011, 21, 820–828. [Google Scholar] [CrossRef]
- Górecki, J.; Berdychowski, M.; Gawrońska, E.; Wałęsa, K. Influence of PPD and Mass Scaling Parameter on the Goodness of Fit of Dry Ice Compaction Curve Obtained in Numerical Simulations Utilizing Smoothed Particle Method (SPH) for Improving the Energy Efficiency of Dry Ice Compaction Process. Energies 2023, 16, 7194. [Google Scholar] [CrossRef]
- Lohri, C.; Rajabu, H.; Sweeney, D.; Zurbrügg, C. Char fuel production in developing countries—A review of urban biowaste carbonization. Renew. Sustain. Energy Rev. 2016, 59, 1514–1530. [Google Scholar]
- Sahay, S.S.; Krishnan, K.; Kuthle, M.; Chodha, A.; Bhattacharya, A.; Das, A.K. Model-Based Optimization of a Highly Automated Industrial Batch Annealing Operation. Ironmak. Steelmak. 2006, 33, 306–314. [Google Scholar] [CrossRef]
- Saboonchi, A.; Hassanpour, S. Simulation of Cold Rolled Steel Coil Heating during Batch Annealing Process. Heat Trans. Eng. 2008, 29, 893–901. [Google Scholar] [CrossRef]
- Sahay, S.S.; Kumar, A.M.; Chatterjee, A. Development of integrated model for batch annealing of cold rolled steels. Ironmak. Steelmak. 2004, 31, 144–152. [Google Scholar] [CrossRef]
- Mathotra, C.P.; Pedenekar, N.R.; Sahay, S.S. Cost model for the steel reheating operation. Ind. Heat. 2002, 69, 67–71. [Google Scholar]
- Sahay, S.S.; Mitra, K. Cost model-based optimization of carburizing operation. Surf. Eng. 2004, 20, 379–384. [Google Scholar] [CrossRef]
- Kotrbacek, P.; Chabicovsky, M.; Resl, O.; Kominek, J.; Luks, T. The Efficient Way to Design Cooling Sections for Heat Treatment of Long Steel Products. Materials 2023, 16, 3983. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Roberts, S.; Wildgoose, J.; Philpott, W.; Jepson, M.A. Effects of post-weld heat treatment on the microstructure and properties of the matching SMAW filler metal for weld joints in MarBN steel. Weld World 2024, 68, 1549–1561. [Google Scholar] [CrossRef]
- Kulkarni, A.R.; Raju, P.V.; Sarma, P.P.; Dewangan, S.; Selvaraj, S.K. Microstructure and Mechanical Properties of 0.18%-C Steel Samples Processed Through Five Different Heat Treatment Techniques. J. Inst. Eng. India Ser. D 2024, 105, 1945–1960. [Google Scholar] [CrossRef]
- Shi, F.; Zheng, J.; Zhang, J.; Zhao, Y.; Chen, L. Heat Treatment Process, Microstructure, and Mechanical Properties of Spring Steel with Ultra-High Strength and Toughness. Metals 2024, 14, 180. [Google Scholar] [CrossRef]
- Meshkabadi, R.; Pouyafar, V.; Soltanikia, R. Investigation on Microstructure, Hardness and Fracture Energy of AISI H13 Hot Work Tool Steel by Cyclic Heat Treatment. J. Mater. Eng. Perform. 2024, 33, 6620–6629. [Google Scholar] [CrossRef]
- Talebi, F.; Jamaati, R.; Hosseinipour, S.J. Strong strain-hardening capability in plain carbon steel through cold rolling and heat treatment of lamellar structure. Arch. Civ. Mech. Eng. 2024, 24, 44. [Google Scholar] [CrossRef]
- Musiał, D. Numerical analysis of the process of heating of a bed of steel bars. Arch. Met. Mat. 2013, 58, 63–66. [Google Scholar]
- Kolmasiak, C.; Wyleciał, T. Heat treatment of steel products as an example of transport phenomenon in porous media. Metalurgija 2018, 57, 363–366. [Google Scholar]
- Qiu, J.; Xu, X.; Chen, X.; Liu, Y.; Wu, Y. Fabrication of Particle-Stacking Microporous Metal Using Laser Powder Bed Fusion. Coatings 2024, 14, 348. [Google Scholar] [CrossRef]
- Qin, J.; Chen, Q.; Yang, C. Research process on property and application of metal porous materials. J. Alloys Compd. 2016, 654, 39–44. [Google Scholar] [CrossRef]
- Nakajima, H. Fabrication, properties and application of porous metals with directional pores. Prog. Mater. Sci. 2007, 52, 1091–1173. [Google Scholar] [CrossRef]
- Sahay, S.S.; Krishnan, K. Model based optimization of continuous annealing operation for bundle of packed rods. Ironmak. Steelmak. 2007, 34, 89–94. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, T.J.; Hudson, H.P.; Jackson, J.D. The temperature dependence of effective thermal conductivity of open-celled steel alloy foams. Mat. Scen. Eng. 2004, 367, 123–131. [Google Scholar] [CrossRef]
- Van Antwerpen, W.; du Toit, C.G.; Rousseau, P.G.A. Review of Correlations to Model the Packing Structure and Effective Thermal Conductivity in Packed Beds of Mono-Sized Spherical Particles. Nucl. Engin. Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
- Carson, J.K. Review of Effective Thermal Conductivity Models for Foods. Int. J. Refrig. 2006, 29, 958–967. [Google Scholar] [CrossRef]
- Murlidhar, G.; Yang, J.; Roy, C. Modelling the Effective Thermal Conductivity in Polydispersed Bed System: A Unified Approach using the Linear Packing Theory and Unit Cell Approach. Can. J. Chem. Eng. 2002, 80, 830–839. [Google Scholar]
- Kolmasiak, C.; Bagdasaryan, V.; Wyleciał, T.; Gała, M. Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle. Materials 2021, 14, 5655. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yu, F.; Wu, W.; Zuo, Y. Application of radial effective thermal conductivity for heat transfer model of steel coils in HPH furnace. Int. J. Ther. 2003, 24, 1395–1405. [Google Scholar] [CrossRef]
- ASTM C1044-12; Standard Practice for Using a Guarded-Hot-Plate Apparatus or Thin-Heater Apparatus in the Single-Sided Mode. ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM C177-13; Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus. ASTM International: West Conshohocken, PA, USA, 2013.
- Zhao, S.-Y.; Zhang, B.-M.; He, X.-D. Temperature and pressure dependent effective thermal conductivity of fibrous insulations. Int. J. Therm. Sci. 2009, 8, 440–448. [Google Scholar] [CrossRef]
- Yang, X.H.; Lu, T.J.; Kim, T. Temperature effects on the effective thermal conductivity of phase change materials with two distinctive phases. Int. Commun. Heat Mass Transf. 2011, 38, 1344–1348. [Google Scholar] [CrossRef]
- Öchsner, A.; Murcg, G.E.; de Lemos, M.J.S. (Eds.) Cellular and Porous Materials: Thermal Properties Simulation and Prediction; WILEY-VCH Verlag GmbH & Co., KGaA: Darmstadt, Germany, 2008. [Google Scholar]
- Carson, J.K. Thermal conductivity bounds for isotropic porous materials. Int. J. Heat Mass Transf. 2005, 48, 2150–2158. [Google Scholar] [CrossRef]
- Palaniswamy, S.K.A.; Venugopal, P.R.; Palaniswamy, K. Effective thermal conductivity modeling with primary and secondary parameters for two-phase materials. Therm. Sci. 2010, 14, 393–407. [Google Scholar] [CrossRef]
- Kunii, D.; Smith, J.M. Heat transfer characteristics of porous rocks. AIChE J. 1960, 6, 71–78. [Google Scholar] [CrossRef]
- Zehner, P.; Schlunder, E.U. Thermal conductivity of granular materials at moderate temperatures. Chemie Ingr Tech. 1970, 42, 933–941. (In German) [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Bagdasaryan, V.; Tomczyk, B. Modelling of effective thermal conductivity of a packed bed of steel bars with the use of chosen literature models. Compos. Struct. 2022, 282, 115025. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Musiał, D. Analysis of the Occurrence of Natural Convection in a Bed of Bars in Vertical Temperature Gradient Conditions. Arch. Thermodyn. 2013, 34, 71–83. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Bagdasaryan, V.; Strycharska, D. Experimental and Theoretical Studies of the Thermal Contact Conductance for Bundles of Round Steel Bars. Materials 2023, 16, 6925. [Google Scholar] [CrossRef]
- Cengel, Y.A. Heat and Mass Transfer—A Practical Approach, 3rd ed.; Mc Graw Hill: New York, NY, USA, 2007. [Google Scholar]
- Tian, W.X.; Zhang, K.; Hou, Y.D.; Zhang, Y.P.; Qiu, S.Z.; Su, G.H. Hydrodynamics of two-phase flow in a rod bundle under cross-flow condition. Ann. Nucl. Energy 2016, 91, 206–214. [Google Scholar] [CrossRef]
- Faraji, H.; Teggar, M.; Arshad, A.; Arıcı, M.; Mehdi Berra, E.; Choukairy, K. Lattice Boltzmann simulation of natural convection heat transfer phenomenon for thermal management of multiple electronic components. Ther. Sci. Eng. Prog. 2023, 45, 102126. [Google Scholar] [CrossRef]
- Afaynou, I.; Faraji, H.; Choukairy, K.; Arıcı, M.; Khallaki, K. Heat transfer improvement of phase change materials by metal foams and nanoparticles for efficient electronic thermal management: A comprehensive study. Int. J. Heat Mass Transf. 2024, 227, 125534. [Google Scholar] [CrossRef]
- Sohag, F.A.; Mohanta, L.; Cheung, F.B. CFD analyses of mixed and forced convection in a heated vertical rod bundle. App. Therm. Eng. 2017, 117, 85–93. [Google Scholar] [CrossRef]
- Bahrami, M.; Yovanovich, M.M.; Culham, J.R. Effective thermal conductivity of rough spherical packed beds. Int. J. Heat Mass Transf. 2006, 49, 3691–3701. [Google Scholar] [CrossRef]
- Nellis, G.; Klein, S. Heat Transfer; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Wyczółkowski, R.; Gała, M.; Boryca, J. Computational Model of Heat Conduction in the Steel Round Bar Bundle. Act. Phys. Pol. A 2019, 136, 1001–1007. [Google Scholar] [CrossRef]
- Yovanovich, M.M.; Marotta, E.E. Chapter 4—Thermal spreading and contact resistances. In Heat Transfer Handbook; Bejan, A., Kraus, A.D., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Yovanovich, M.M. Four decades of research on thermal contact, gap, and joint resistances in microelectronics. IEEE Trans. Comp. Pack. Tech. 2005, 20, 182–206. [Google Scholar] [CrossRef]
- Furmański, P.; Wiśniewski, T.S.; Banaszek, J. Thermal Contact Resistances and Other Thermal Phenomena at Solid-Solid Interface; Institute of Heat Engineering—Warsaw University of Technology: Warsaw, Poland, 2008. [Google Scholar]
- Wyczólkowski, R.; Urbaniak, D. Modeling of Radiation in Bar Bundles Using the Thermal Resistance Concept. J. Ther. Heat Transf. 2016, 30, 721–729. [Google Scholar] [CrossRef]
- Modest, M.F. Chapter 5—Radiative Exchange Between Gray, Diffuse Surfaces. In Radiative Heat Transfer, 3rd ed.; Academic Press: New York, NY, USA; San Francisco, CA, USA; London, UK, 2013; pp. 160–198. [Google Scholar]
- Liščić, B. Steel Heat Treatment—Metallurgy and Technologies; CRC Taylor & Francis Group: Boca Raton, CA, USA; London, UK; New York, NY, USA, 2006. [Google Scholar]
- Wyczółkowski, R.; Strycharska, D.; Bagdasaryan, V. Correlations for the thermal conductivity of selected steel grades as a function of temperature in the range of 0–800 °C. Arch. Thermod. 2022, 43, 29–45. [Google Scholar]
- Saboonchi, A.; Hassanpour, S.; Abbasi, S. New heating schedule in hydrogen annealing furnace based on process simulation for less energy consumption. Energ. Cons. Manag. 2009, 49, 3211–3216. [Google Scholar] [CrossRef]
- Zuo, Y.; Wu, W.; Zhang, X.; Lin, L.; Xiang, S.; Liu, T.; Niu, L.; Huang, X. A study of heat transfer in high-performance hydrogen bell-type annealing furnace. Heat Trans. Asian Res. 2001, 30, 615–623. [Google Scholar] [CrossRef]
- Raźnjević, K. Thermal Table with Diagrams; WNT: Warsaw, Poland, 1966. (In Polish) [Google Scholar]
- Available online: https://www.flukeprocessinstruments.com/en-us/service-and-support/knowledge-center/infrared-technology/emissivity-metals (accessed on 15 October 2024).
- Available online: https://www.transmetra.ch/images/transmetra_pdf/publikationen_literatur/pyrometrie-thermografie/emissivity_table.pdf (accessed on 15 October 2024).
- Available online: https://knifemaker.com/wp-content/uploads/2020/11/TDMAW_SOS_Spring_Page_Kinetic_Vacuum_Heat_Treat_Article.pdf (accessed on 15 October 2024).
- Available online: https://polmet.zagan.pl/en/blog/31-heat-treatment-vacuum-what-is-it (accessed on 15 October 2024).
- Available online: https://www.miheuprecision.com/blog/vacuum-heat-treatment (accessed on 15 October 2024).
- European Steel and Alloy Grades/Numbers Steel Number. Available online: http://www.steelnumber.com/en/steel_composition_eu.php?name_id=645 (accessed on 15 October 2024).
- Wyczółkowski, R. Experimental Investigations of Effective Thermal Conductivity of the Selected Examples of Steel Porous Charge. Solids 2021, 2, 420–436. [Google Scholar] [CrossRef]

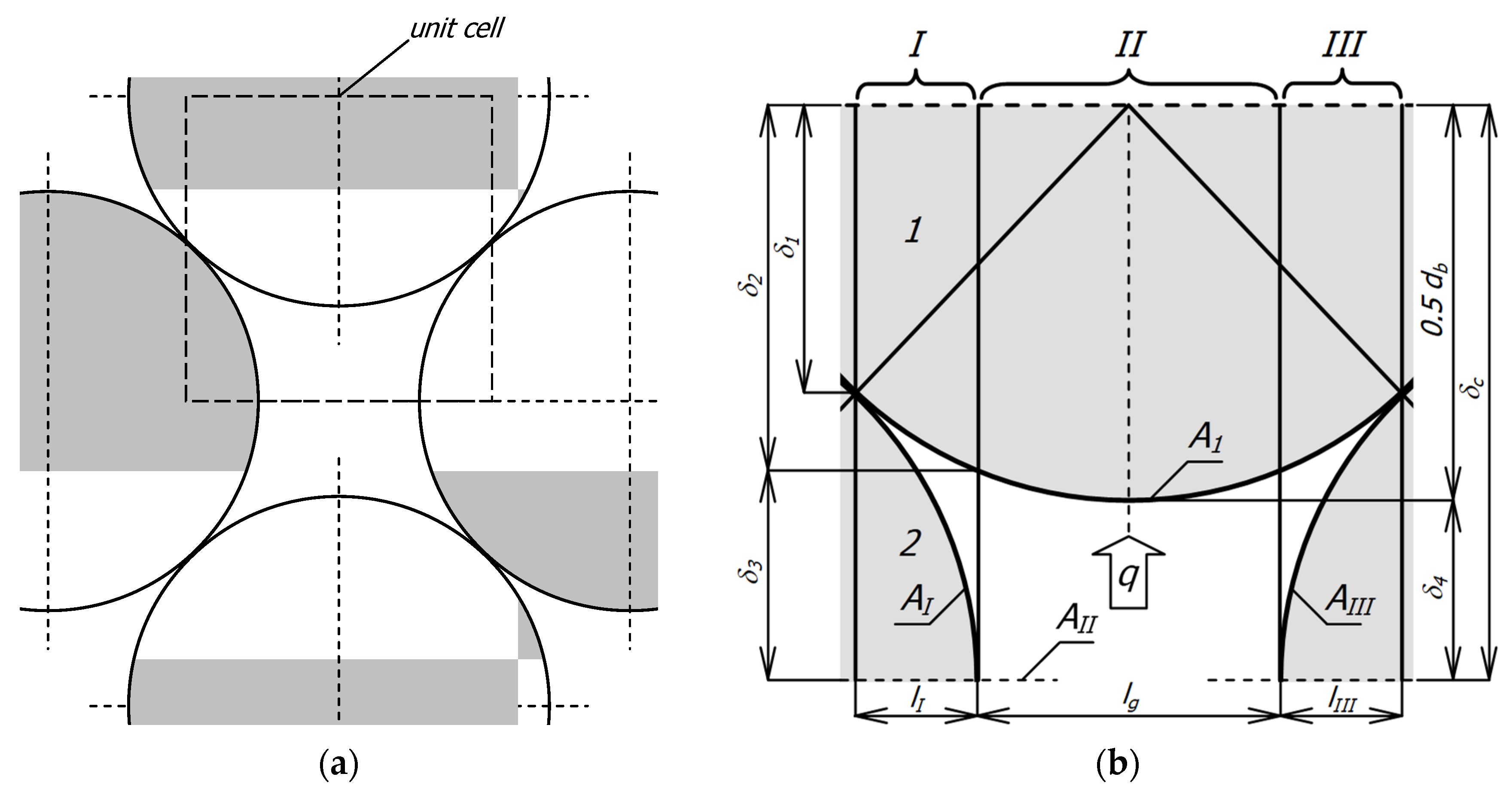
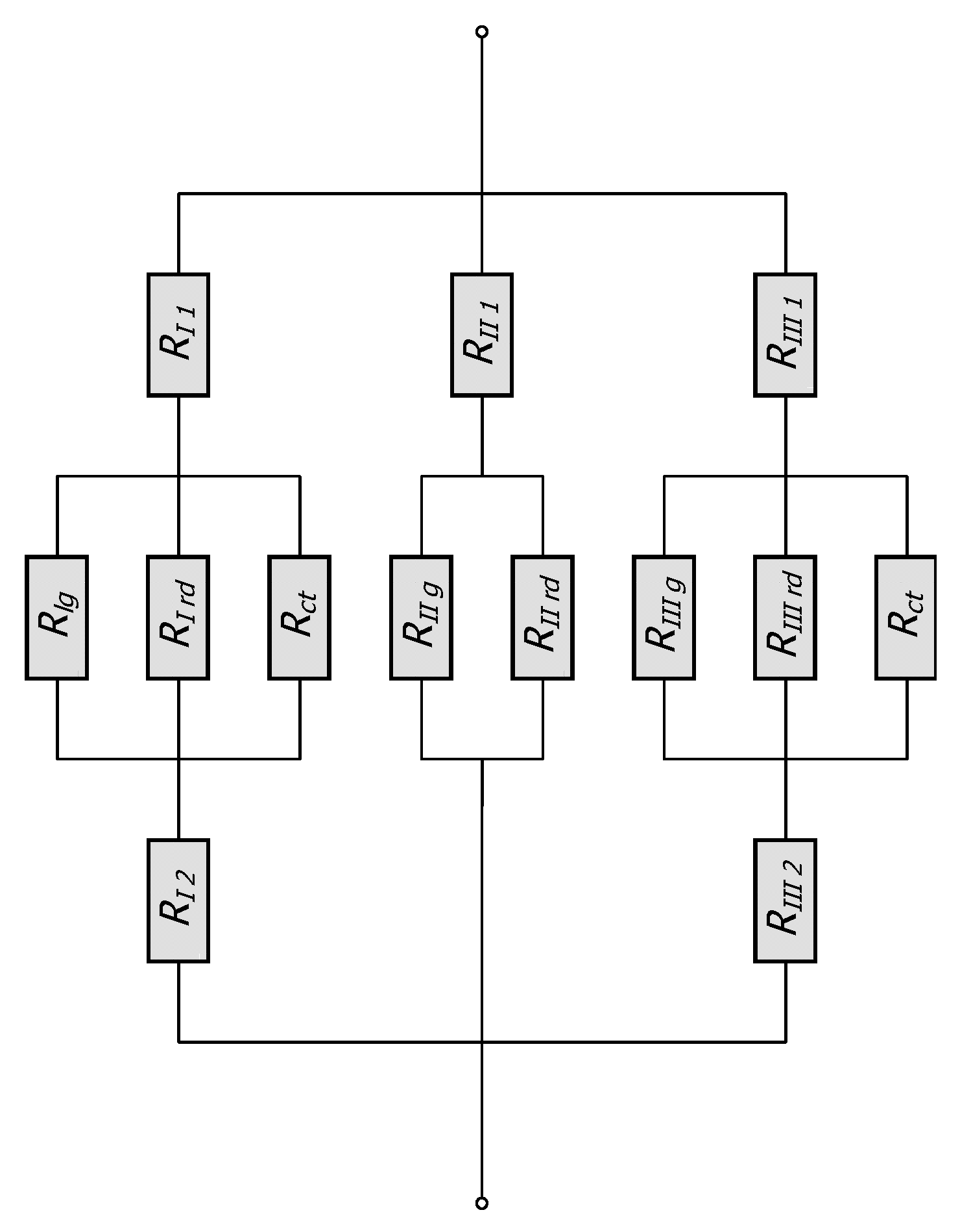
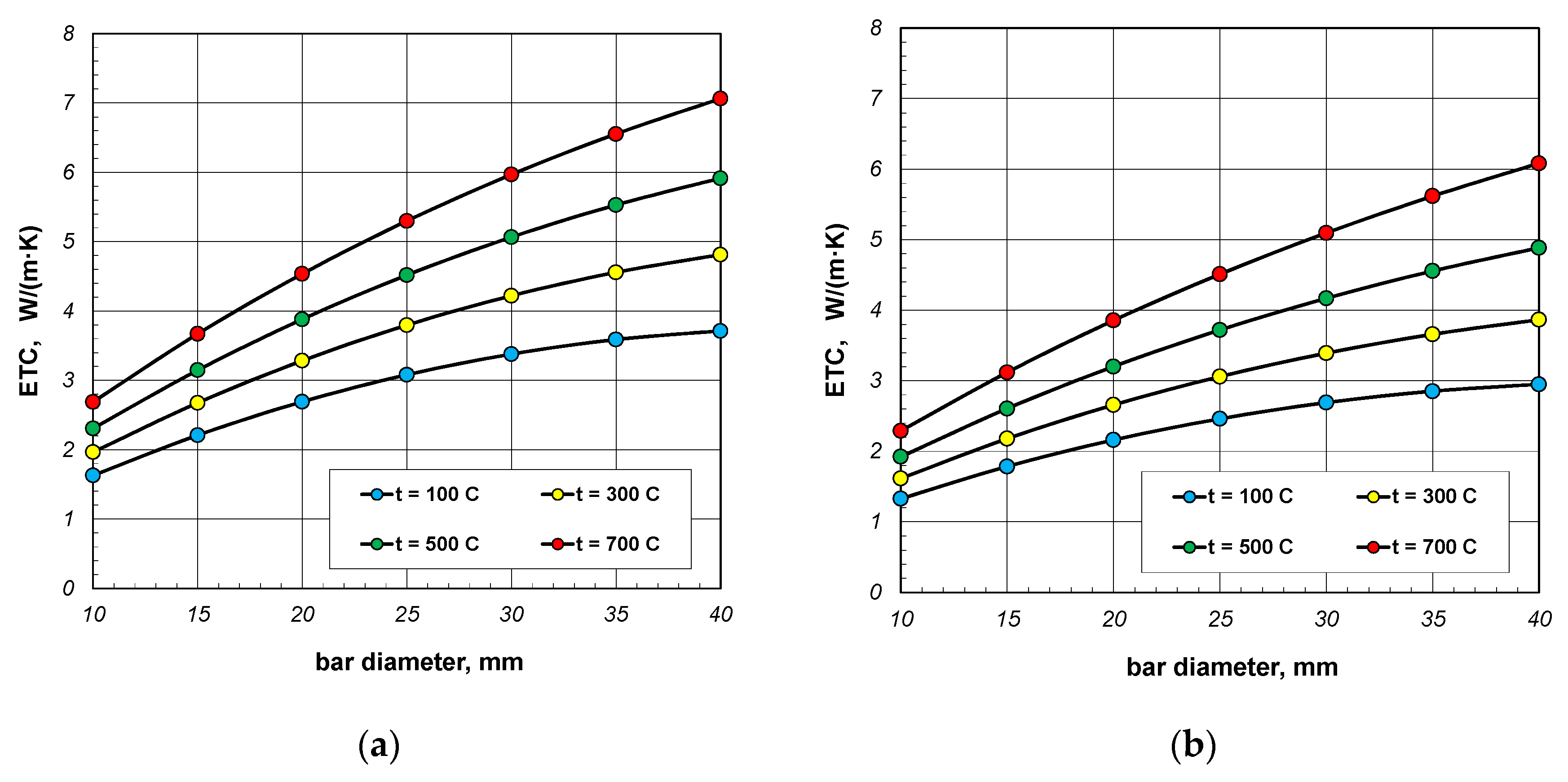

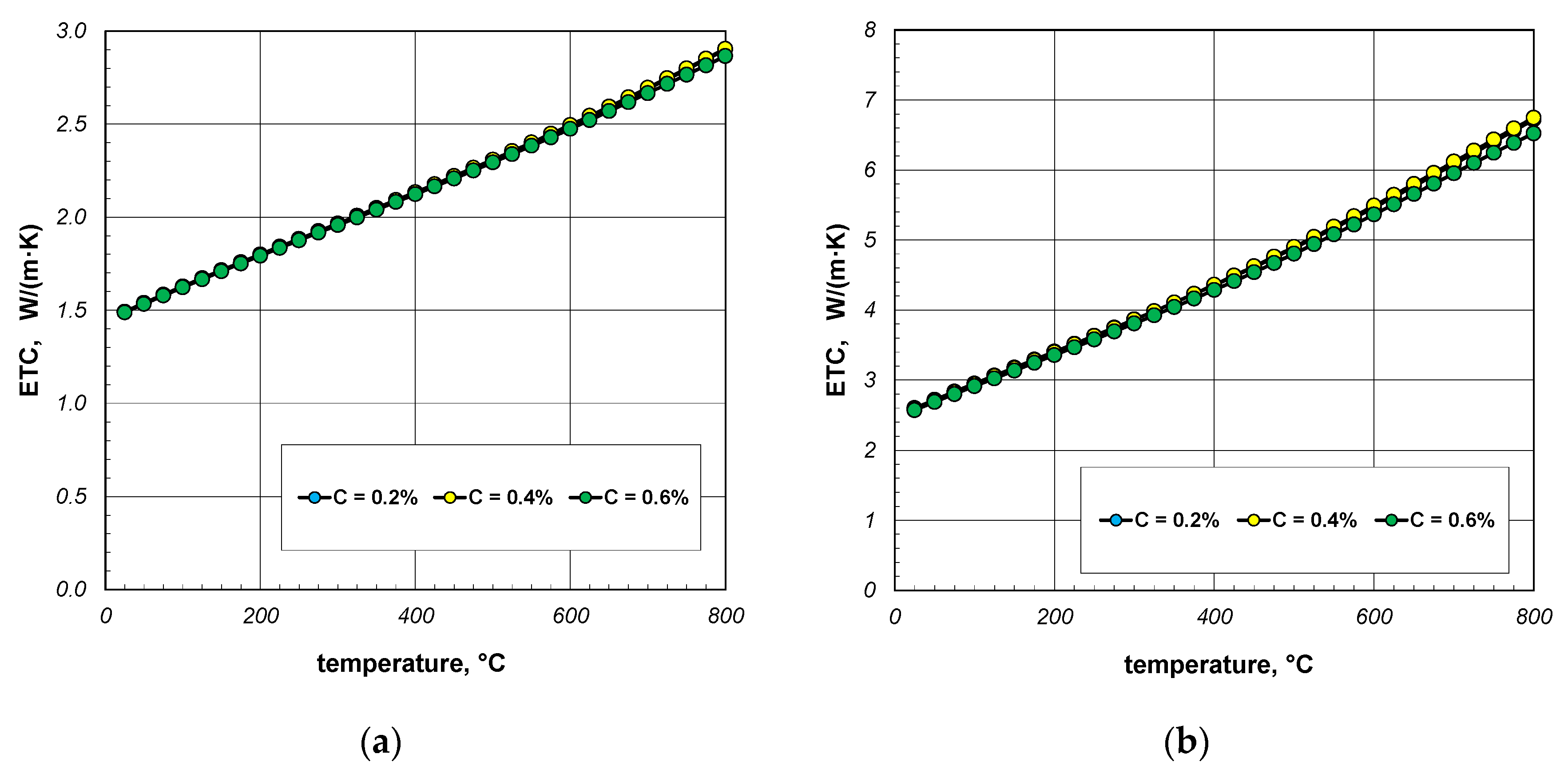
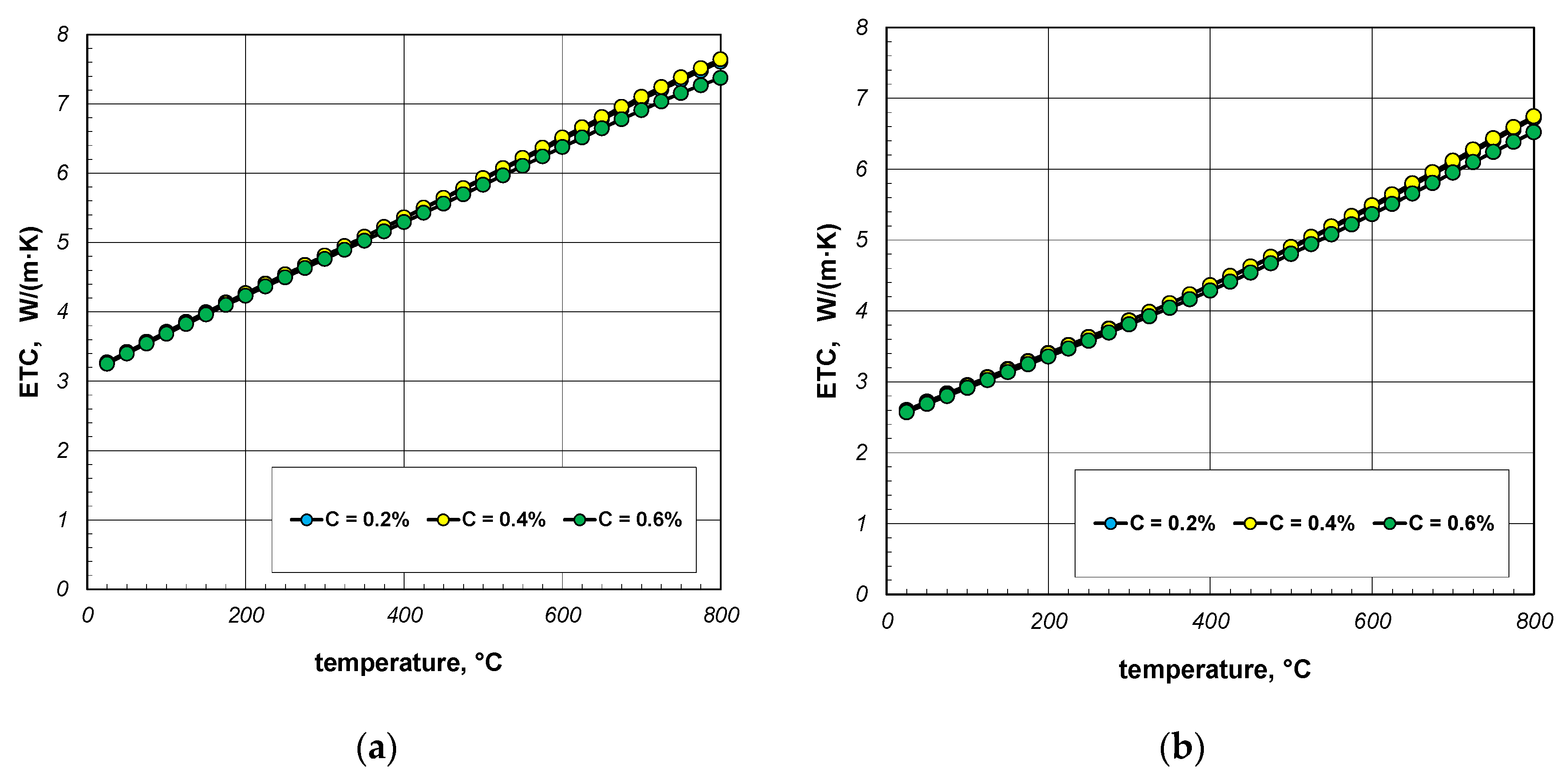
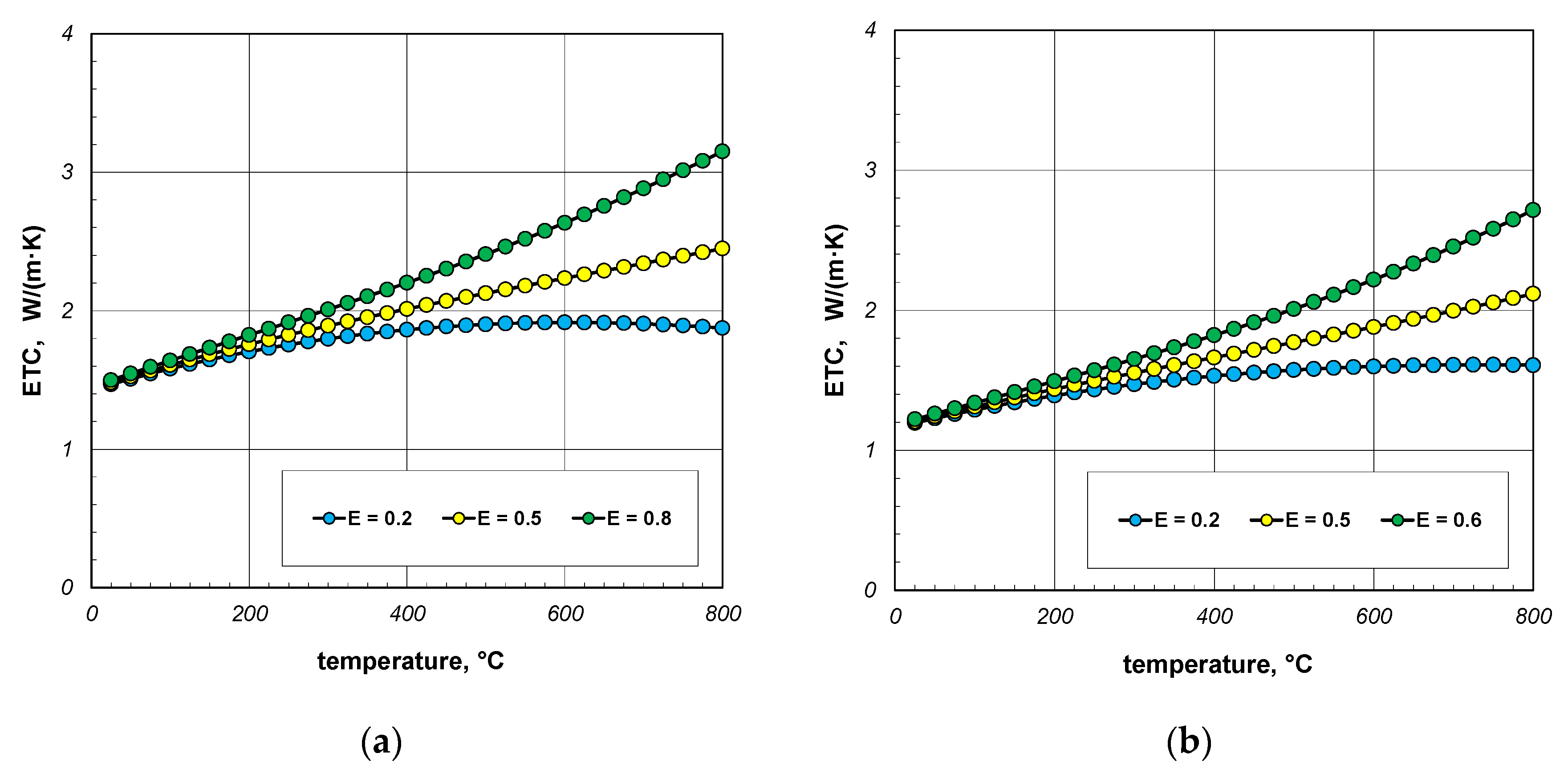


| Element | Minimum Dimension | Maximum Dimension |
|---|---|---|
| EI1, EIII1 | δ1 | δ2 |
| EIg, EIIIg | 0 | δ3 |
| EI2, EIII2 | 0 | δc − δ1 |
| EII1 | δ2 | 0.5db |
| EIIg | δ3 | δ4 |
| Temperature, °C | Thermal Conductivity, W/(m·K) | ||
|---|---|---|---|
| Steel | Air | Hydrogen | |
| 25 | 51.3 | 0.026 | 0.185 |
| 800 | 27.4 | 0.069 | 0.495 |
| xg | 0 | 0.2 | 0.4 |
| φ | 0.09 | 0.14 | 0.21 |
| Temperature, °C | ks, W/(m·K) | ||
|---|---|---|---|
| 0.2% C | 0.4% C | 0.6% C | |
| 25 | 51.3 | 48.0 | 49.2 |
| 100 | 50.8 | 47.2 | 46.4 |
| 200 | 48.3 | 46.5 | 43.8 |
| 300 | 44.6 | 43.8 | 40.6 |
| 400 | 42.6 | 41.0 | 37.6 |
| 500 | 39.2 | 38.4 | 34.9 |
| 600 | 35.4 | 36.0 | 32.2 |
| 700 | 31.8 | 31.4 | 29.1 |
| 800 | 27.4 | 26.7 | 24.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wyczółkowski, R.; Gała, M. Computational Model of the Effective Thermal Conductivity of a Bundle of Round Steel Bars. Materials 2025, 18, 373. https://doi.org/10.3390/ma18020373
Wyczółkowski R, Gała M. Computational Model of the Effective Thermal Conductivity of a Bundle of Round Steel Bars. Materials. 2025; 18(2):373. https://doi.org/10.3390/ma18020373
Chicago/Turabian StyleWyczółkowski, Rafał, and Marek Gała. 2025. "Computational Model of the Effective Thermal Conductivity of a Bundle of Round Steel Bars" Materials 18, no. 2: 373. https://doi.org/10.3390/ma18020373
APA StyleWyczółkowski, R., & Gała, M. (2025). Computational Model of the Effective Thermal Conductivity of a Bundle of Round Steel Bars. Materials, 18(2), 373. https://doi.org/10.3390/ma18020373







