The Influence of Mg Doping in α-Al2O3 Crystals Investigated with First-Principles Calculations and Experiment
Highlights
- An ideal model in which Mg substitutes for Al and incorporates an O vacancy (MgAlVO) is constructed in the calculations for the first time.
- The absorption spectra of MgAl2O4 and Mg2Al2O5 structures verified that the locally Mg-enriched spinel structure (Mg2Al2O5) affects the optical properties of α-Al2O3:Mg crystals.
- Based on experimental and computational results, the influence of Mg2+ substitutional doping in α-Al2O3 and the impact of locally Mg-rich spinels on the optical and radiation performance of α-Al2O3:Mg crystals are elucidated.
Abstract
1. Introduction
2. Theoretical Method
3. Experimental Method
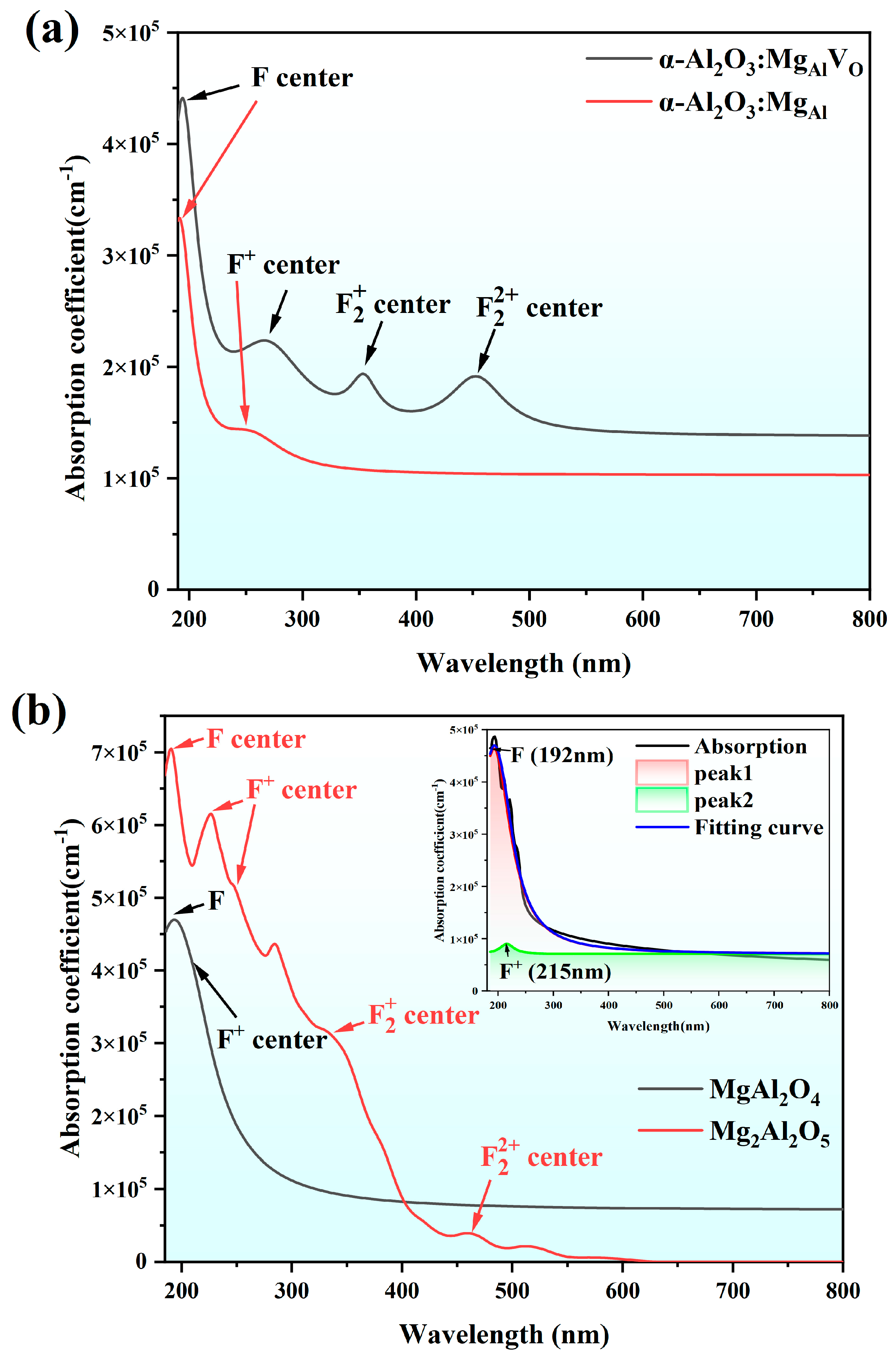
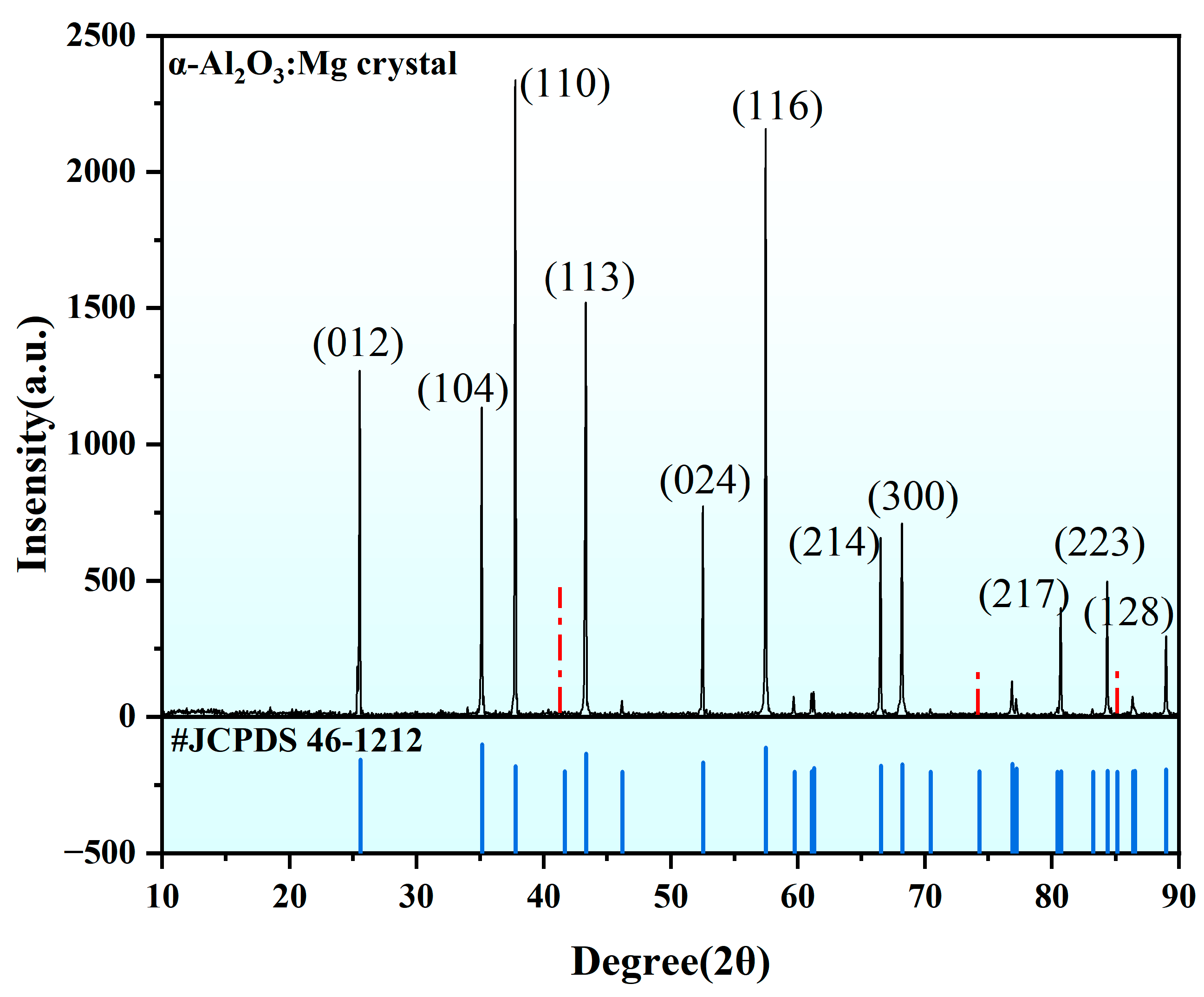
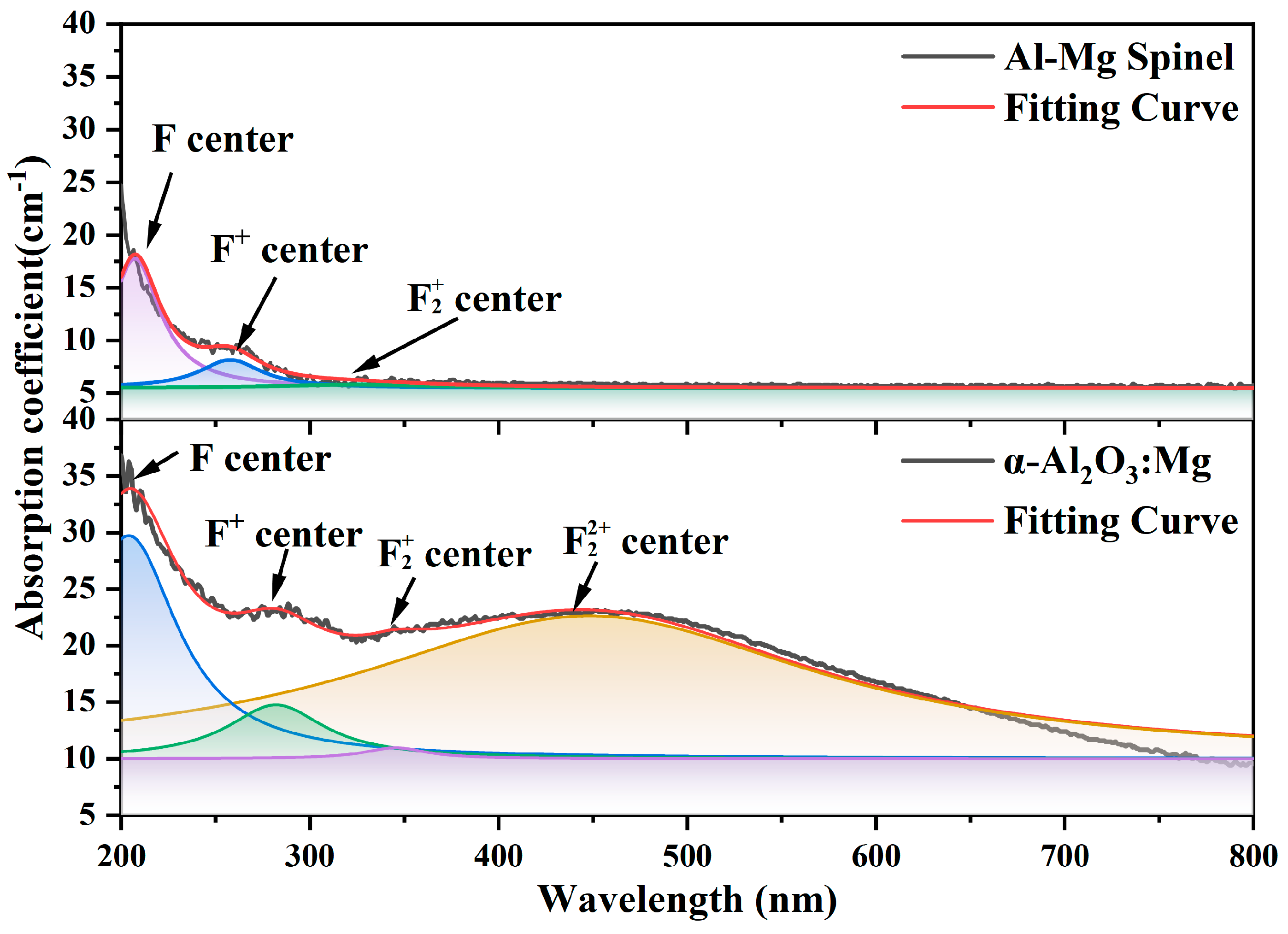
4. Results and Discussion
4.1. Calculation Section
4.2. Experimental Section
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watcharatharapong, T. First-Principles Study of Intrinsic Defects in α-Al2O3 and Their Optical Property. Master’s Thesis, Kasetsart University, Bangkok, Thailand, 2014. [Google Scholar]
- Valbis, J.; Itoh, N. Electronic Excitations, Luminescence and Lattice Defect Formation in α-Al2o3 Crystals. Radiat. Eff. Defects Solids 1991, 116, 171–189. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Q.; Sun, Y.; Liu, J.; Zhu, Z. Color Center Formation in α-Al2O3 Induced by High Energy Heavy Ions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2007, 254, 268–272. [Google Scholar] [CrossRef]
- Lee, K.H.; Crawford, J.H. Luminescence of the F Center in Sapphire. Phys. Rev. B 1979, 19, 3217–3221. [Google Scholar] [CrossRef]
- Evans, B.D.; Stapelbroek, M. Optical Properties of the F+ Center in Crystalline Al2O3. Phys. Rev. B 1978, 18, 7089–7098. [Google Scholar] [CrossRef]
- Yukihara, E.G.; Whitley, V.H.; McKeever, S.W.S.; Akselrod, A.E.; Akselrod, M.S. Effect of High-Dose Irradiation on the Optically Stimulated Luminescence of Al2O3:C. Radiat. Meas. 2004, 38, 317–330. [Google Scholar] [CrossRef] [PubMed]
- Akselrod, M.; Kouwenberg, J. Fluorescent Nuclear Track Detectors—Review of Past, Present and Future of the Technology. Radiat. Meas. 2018, 117, 35–51. [Google Scholar] [CrossRef]
- Kalita, J.M.; Chithambo, M.L. A Comparative Study of the Dosimetric Features of α-Al2O3:C,Mg and α-Al2O3:C. Radiat. Prot. Dosim. 2017, 177, 261–271. [Google Scholar] [CrossRef]
- Denis, G.; Rodriguez, M.G.; Akselrod, M.S.; Underwood, T.H.; Yukihara, E.G. Time-Resolved Measurements of Optically Stimulated Luminescence of Al2O3:C and Al2O3:C,Mg. Radiat. Meas. 2011, 46, 1457–1461. [Google Scholar] [CrossRef]
- Sun, N.; Jiang, H.; Zhao, X.; Deng, X.; Zhang, W. High-Temperature Protection Performance of Mg-Doped Al2O3 Protective Layers on the Thin Film Thermocouples. Ceram. Int. 2024, 50, 36537–36543. [Google Scholar] [CrossRef]
- Parray, M.R.; Khan, N.Z.; Manroo, S.A.; Maqbool, A. Experimental Investigation on Fabrication and Characterisation of Mg-Al2O3 Surface Composites. Adv. Mater. Process. Technol. 2024, 10, 1264–1281. [Google Scholar]
- Wang, C.; Yan, W.; Chen, Q.; Wang, X. Microstructures and Properties of Microporous MgO-MgAl2O4 Refractory Aggregates from Mg(OH)2 Powder and α-Al2O3 Micro-Powder. Constr. Build. Mater. 2024, 426, 136144. [Google Scholar] [CrossRef]
- Yang, S.; Wei, P.; Dai, Y.; Liu, S.; Han, N.; Fu, X.; Fan, L.; Zhang, M.; An, L. Effects of MgO Doping Concentration on Densification and Microstructure of Flash Sintered α-Al2O3 Ceramics. J. Eur. Ceram. Soc. 2024, 44, 4210–4215. [Google Scholar] [CrossRef]
- Ramírez, R.; Tardío, M.; González, R.; Muñoz Santiuste, J.E.; Kokta, M.R. Optical Properties of Vacancies in Thermochemically Reduced Mg-Doped Sapphire Single Crystals. J. Appl. Phys. 2007, 101, 123520. [Google Scholar] [CrossRef]
- Ramírez, R.; Tardío, M.; González, R.; Chen, Y.; Kokta, M.R. Photochromism of Vacancy-Related Defects in Thermochemically Reduced α-Al2O3:Mg Single Crystals. Appl. Phys. Lett. 2005, 86, 081914. [Google Scholar] [CrossRef]
- Cox, R.T. Electron Spin Resonance Studies of Holes Trapped at Mg2+, Li+ and Cation Vacancies in Al2O3. Solid State Commun. 1971, 9, 1989–1992. [Google Scholar] [CrossRef]
- Kulis, P.A.; Springis, M.J.; Tale, I.A.; Vainer, V.S.; Valbis, J.A. Impurity-Associated Colour Centres in Mg- and Ca-Doped Al2O3 Single Crystals. Phys. Status Solidi (B) 1981, 104, 719–725. [Google Scholar] [CrossRef]
- Ishii, M.; Hiraishi, J.; Yamanaka, T. Structure and Lattice Vibrations of Mg-Al Spinel Solid Solution. Phys. Chem. Miner. 1982, 8, 64–68. [Google Scholar] [CrossRef]
- Dupree, R.; Lewis, M.H.; Smith, M.E. A Study of the Vacancy Distribution in Non-Stoichiometric Spinels by Magic-Angle Spinning NMR. Philos. Mag. A 1986, 53, L17–L20. [Google Scholar] [CrossRef]
- Mitchell, T.E. Dislocations and Mechanical Properties of MgO-Al2O3 Spinel Single Crystals. J. Am. Ceram. Soc. 1999, 82, 3305–3316. [Google Scholar] [CrossRef]
- Summers, G.P.; White, G.S.; Lee, K.H.; Crawford, J.H. Radiation Damage in MgAl2O4. Phys. Rev. B 1980, 21, 2578–2584. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Ramzan, M.; Li, Y.; Chimata, R.; Ahuja, R. Electronic, Mechanical and Optical Properties of Y2O3 with Hybrid Density Functional (HSE06). Comput. Mater. Sci. 2013, 71, 19–24. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Biswas, T.; Singh, A.K. pyGWBSE: A High Throughput Workflow Package for GW-BSE Calculations. npj Comput. Mater. 2023, 9, 22. [Google Scholar] [CrossRef]
- Fuchs, F.; Rödl, C.; Schleife, A.; Bechstedt, F. Efficient O(N2) Approach to Solve the Bethe-Salpeter Equation for Excitonic Bound States. Phys. Rev. B 2008, 78, 085103. [Google Scholar] [CrossRef]
- Feret, F.R.; Roy, D.; Boulanger, C. Determination of Alpha and Beta Alumina in Ceramic Alumina by X-Ray Diffraction. Spectrochim. Acta Part B At. Spectrosc. 2000, 55, 1051–1061. [Google Scholar] [CrossRef]
- Hallstedt, B. Thermodynamic Assessment of the System MgO–Al2O3. J. Am. Ceram. Soc. 1992, 75, 1497. [Google Scholar] [CrossRef]

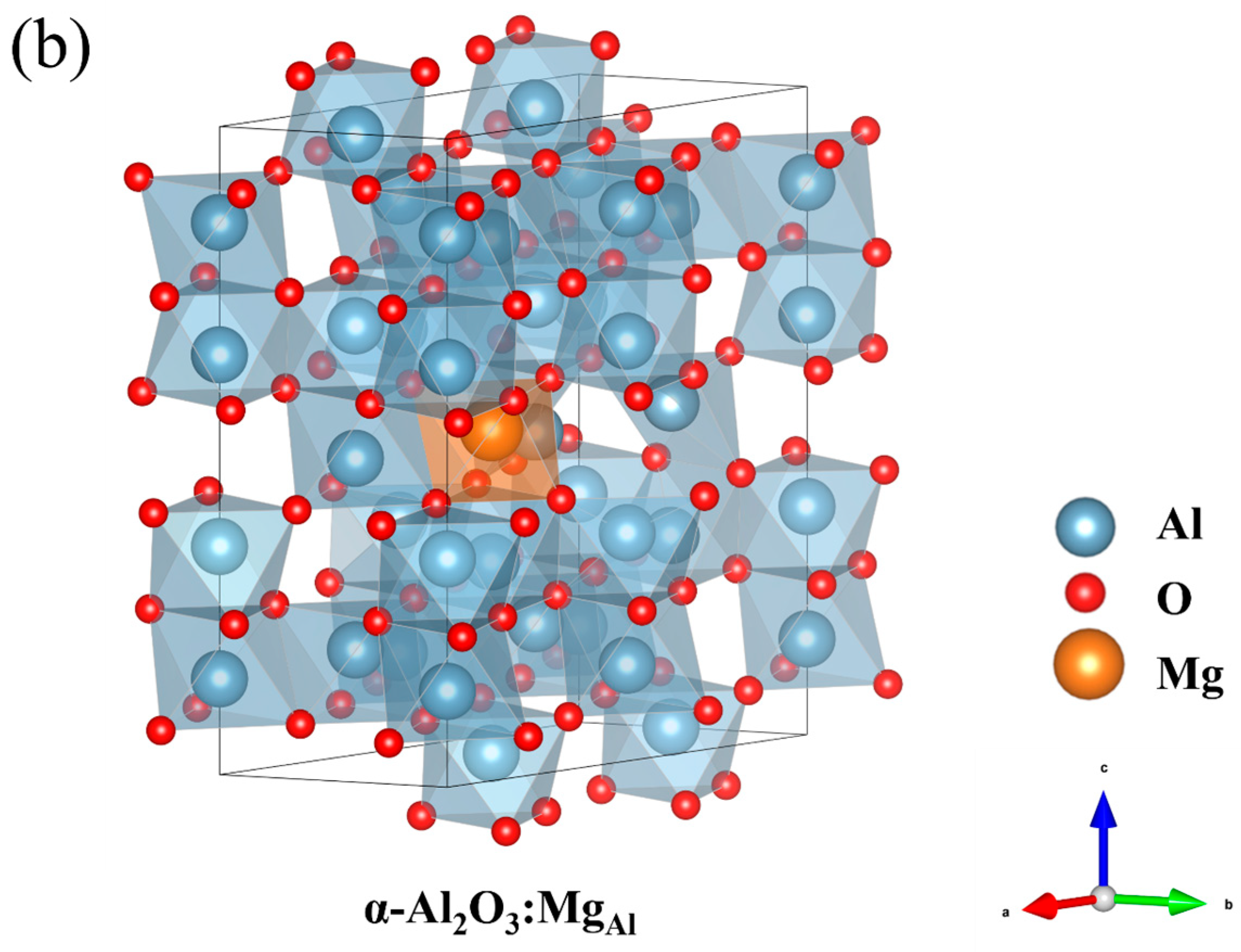
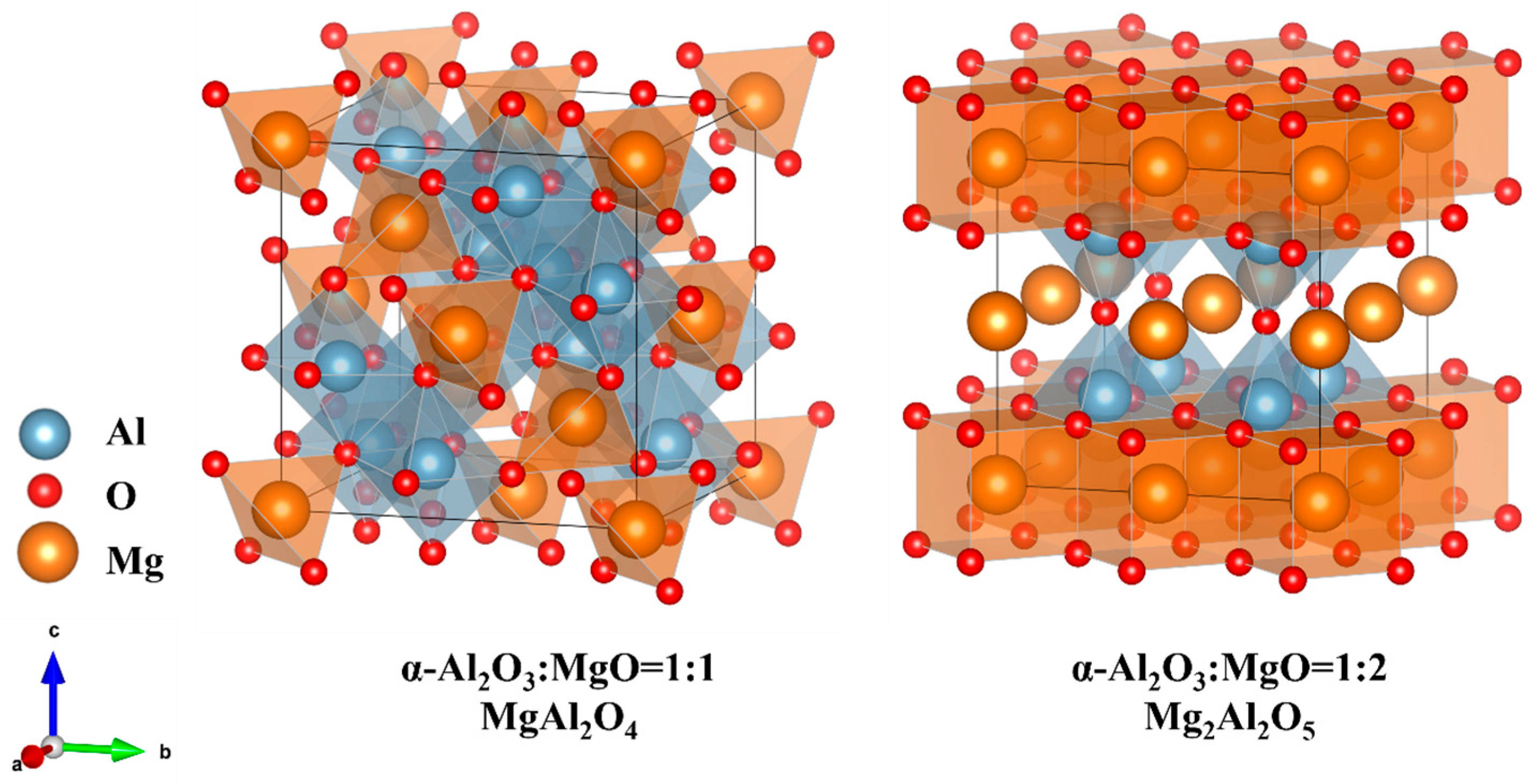

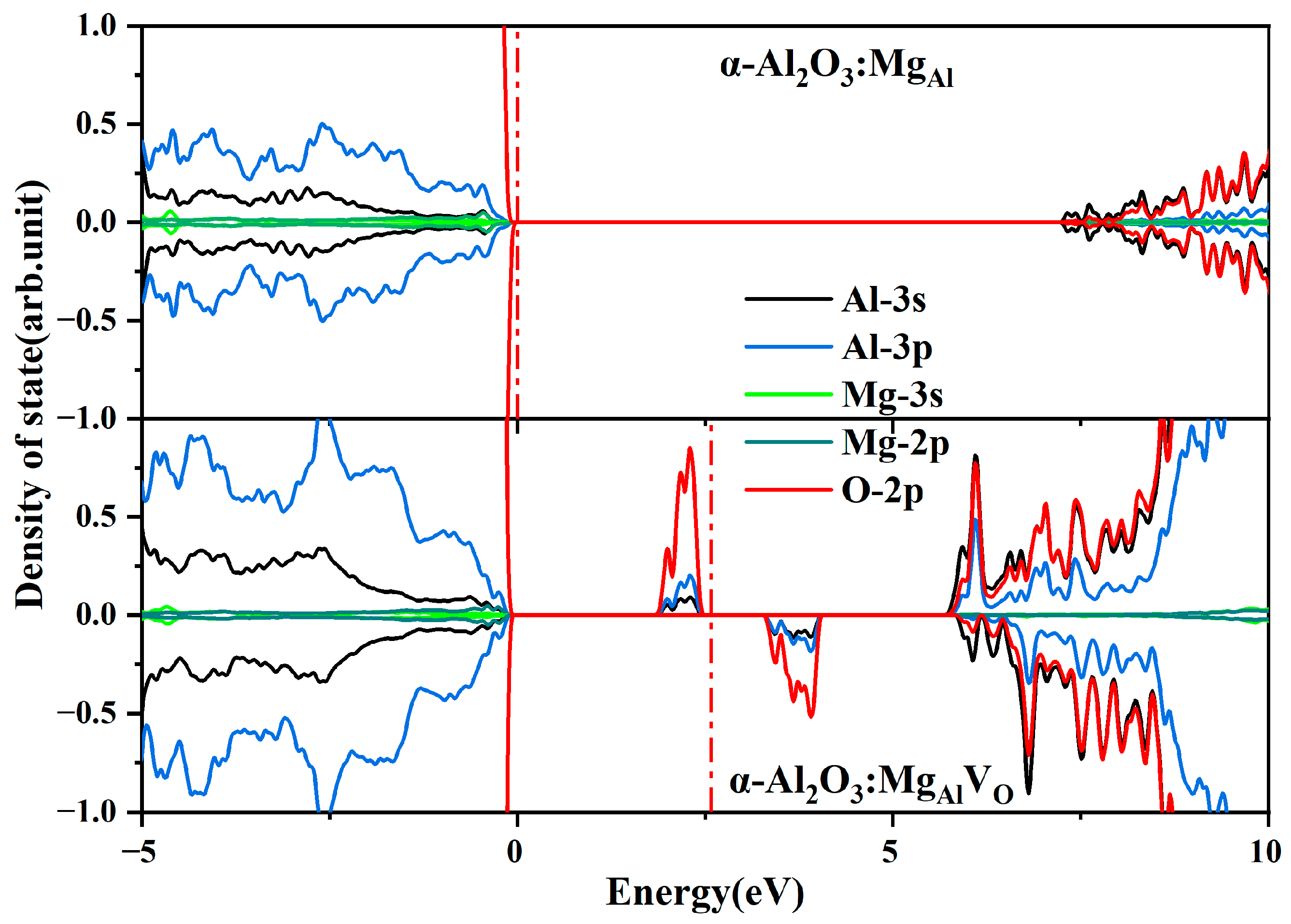
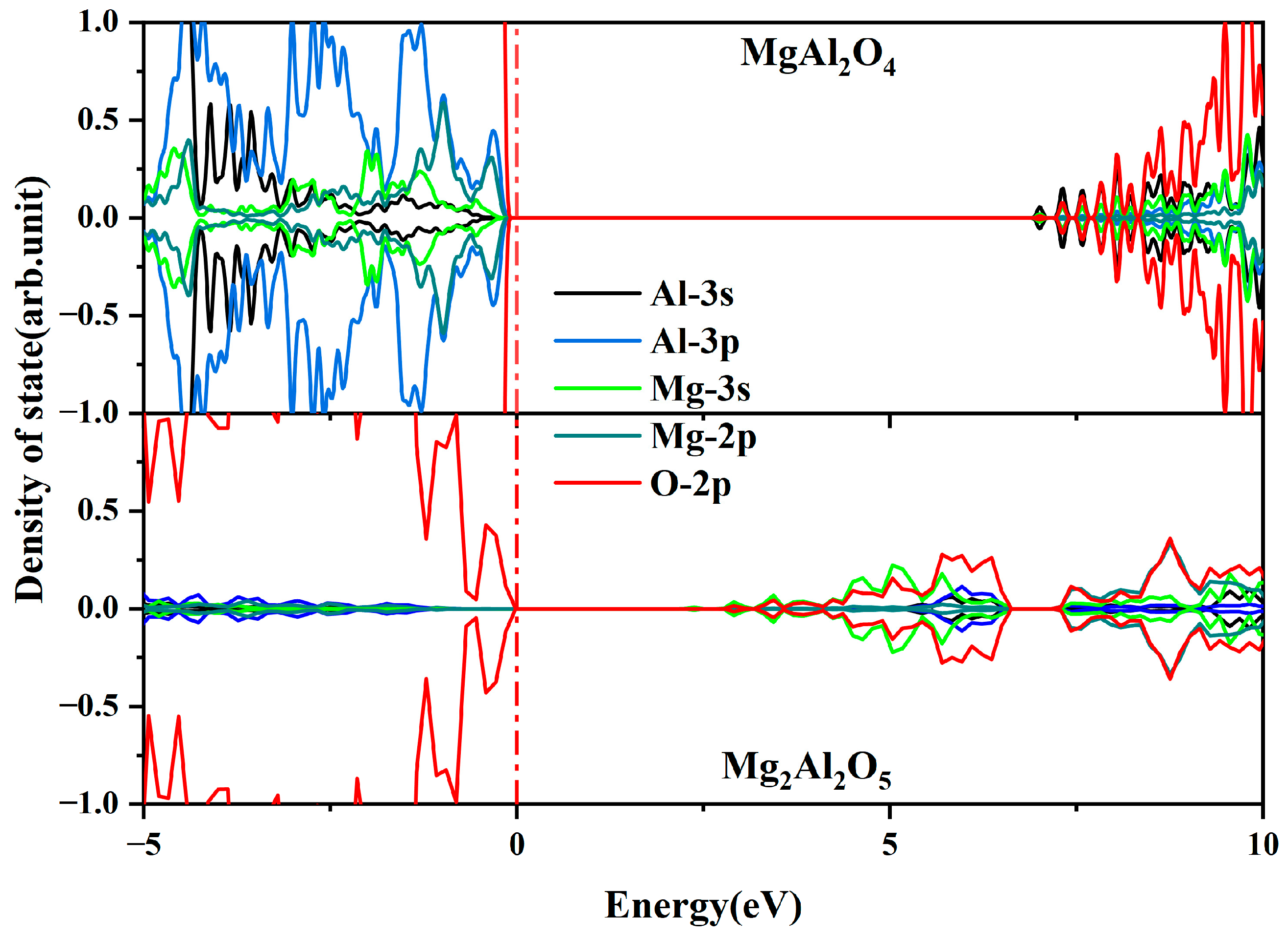


| Structure | Formation Energy (eV) |
|---|---|
| α-Al2O3:MgAl | 3.368 |
| α-Al2O3:MgAlVO | 2.189 |
| α-Al2O3:VO | 1.952 |
| Mechanical Properties | Hill’s Algorithm |
|---|---|
| Bulk Modulus B (GPa) | 230.321 |
| Young’s Modulus E (GPa) | 346.362 |
| Shear Modulus G (GPa) | 138.615 |
| Vickers Hardness (GPa) | 16.614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Fan, H.; Guo, H.; Tang, K.; Wang, Z.; Zhang, S.; Zhou, M.; Fu, L.; Feng, H. The Influence of Mg Doping in α-Al2O3 Crystals Investigated with First-Principles Calculations and Experiment. Materials 2025, 18, 407. https://doi.org/10.3390/ma18020407
Zeng Y, Fan H, Guo H, Tang K, Wang Z, Zhang S, Zhou M, Fu L, Feng H. The Influence of Mg Doping in α-Al2O3 Crystals Investigated with First-Principles Calculations and Experiment. Materials. 2025; 18(2):407. https://doi.org/10.3390/ma18020407
Chicago/Turabian StyleZeng, Yan, Haijun Fan, Haibo Guo, Kaiyong Tang, Zungang Wang, Siyuan Zhang, Mo Zhou, Li Fu, and He Feng. 2025. "The Influence of Mg Doping in α-Al2O3 Crystals Investigated with First-Principles Calculations and Experiment" Materials 18, no. 2: 407. https://doi.org/10.3390/ma18020407
APA StyleZeng, Y., Fan, H., Guo, H., Tang, K., Wang, Z., Zhang, S., Zhou, M., Fu, L., & Feng, H. (2025). The Influence of Mg Doping in α-Al2O3 Crystals Investigated with First-Principles Calculations and Experiment. Materials, 18(2), 407. https://doi.org/10.3390/ma18020407






