Shear Instability and Localization in High-Speed Cold Spray Processes: Impact on Particle Fragmentation and Bonding Mechanisms
Abstract
:1. Introduction
2. Numerical Framework
2.1. Material Elasticity
2.2. Kinetics of Plastic Deformation
2.3. Adiabatic Shear Instability and Shear Localization
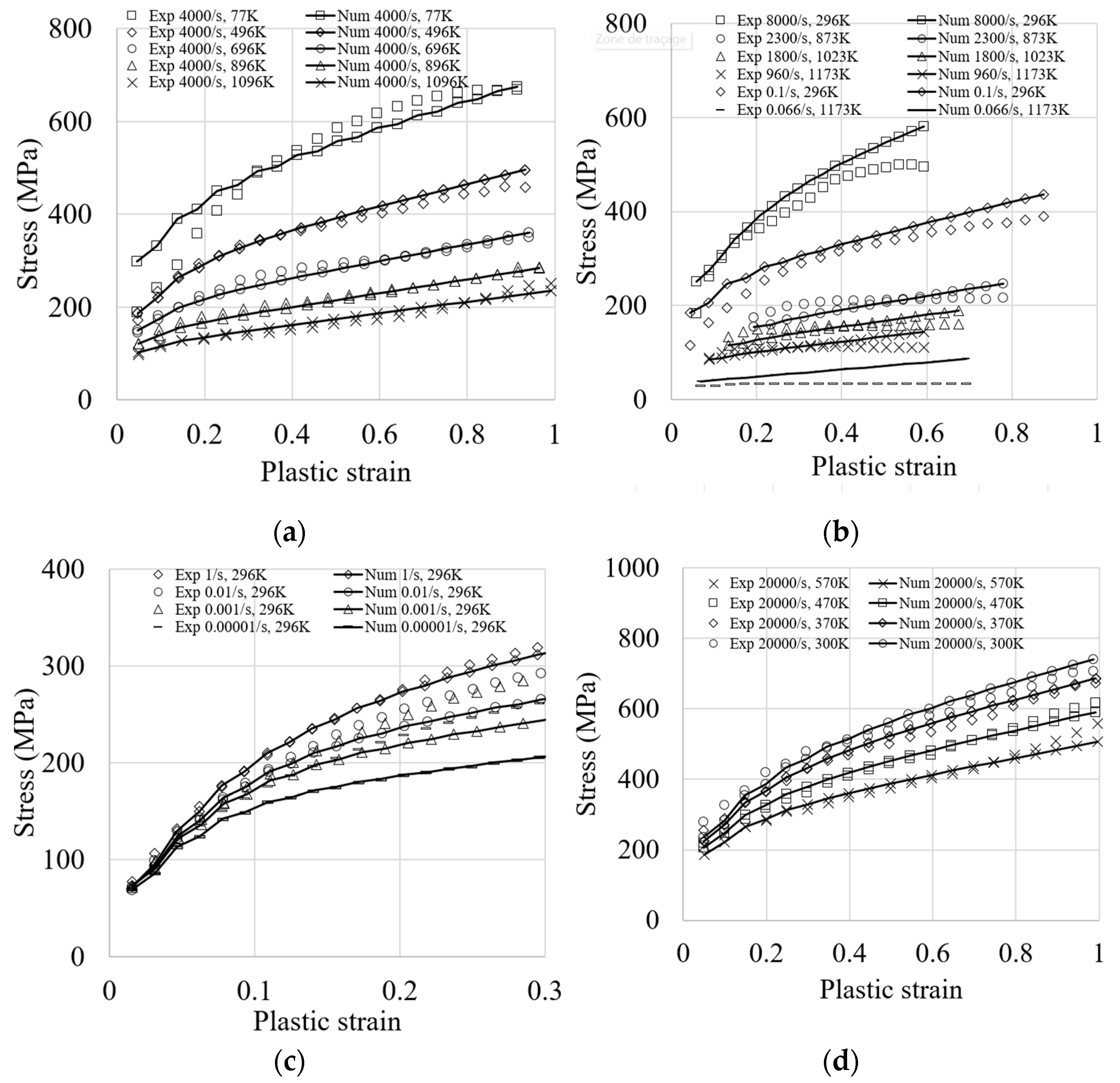
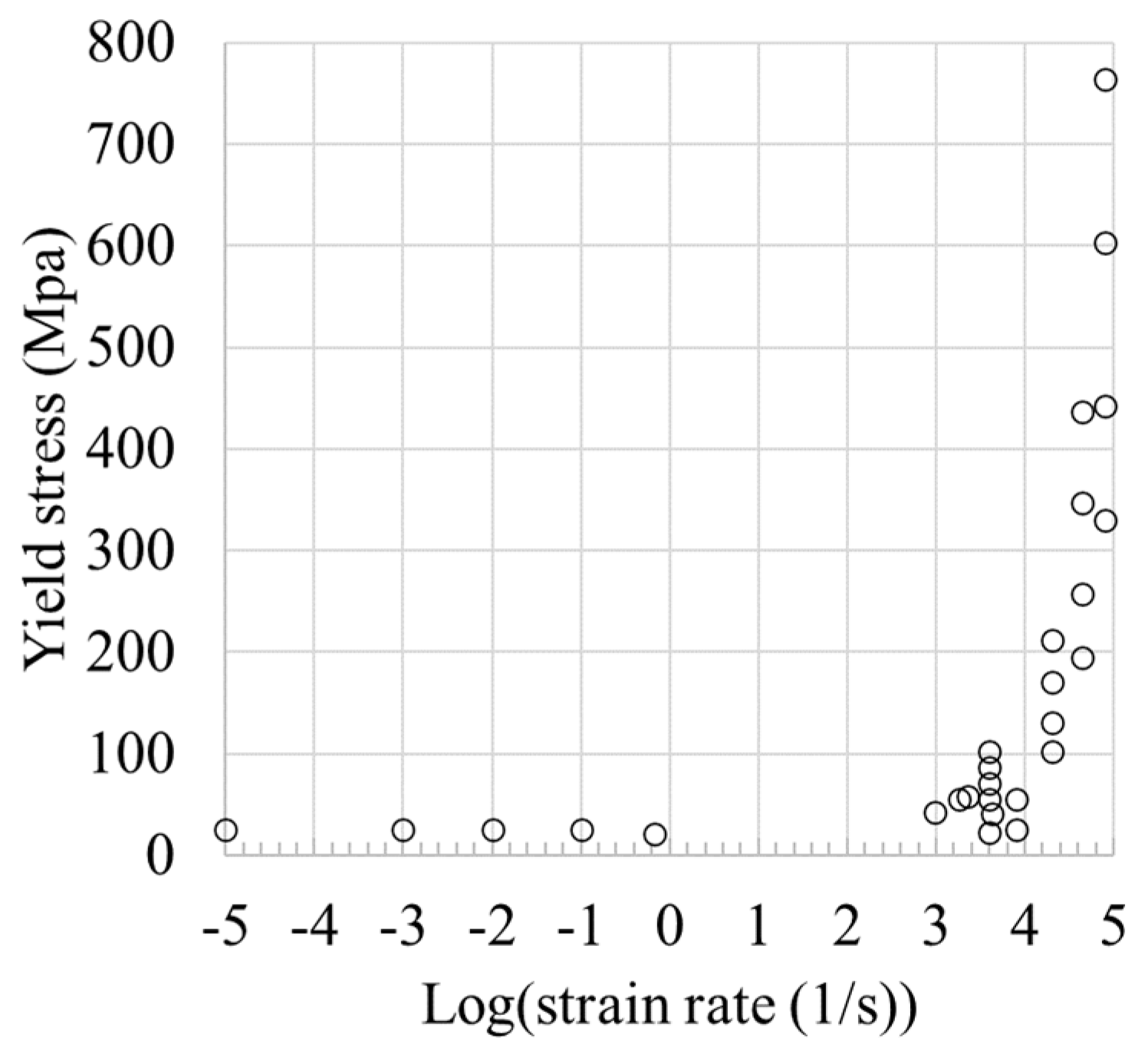
2.4. Identification of Material Parameters
2.5. Finite Element Model
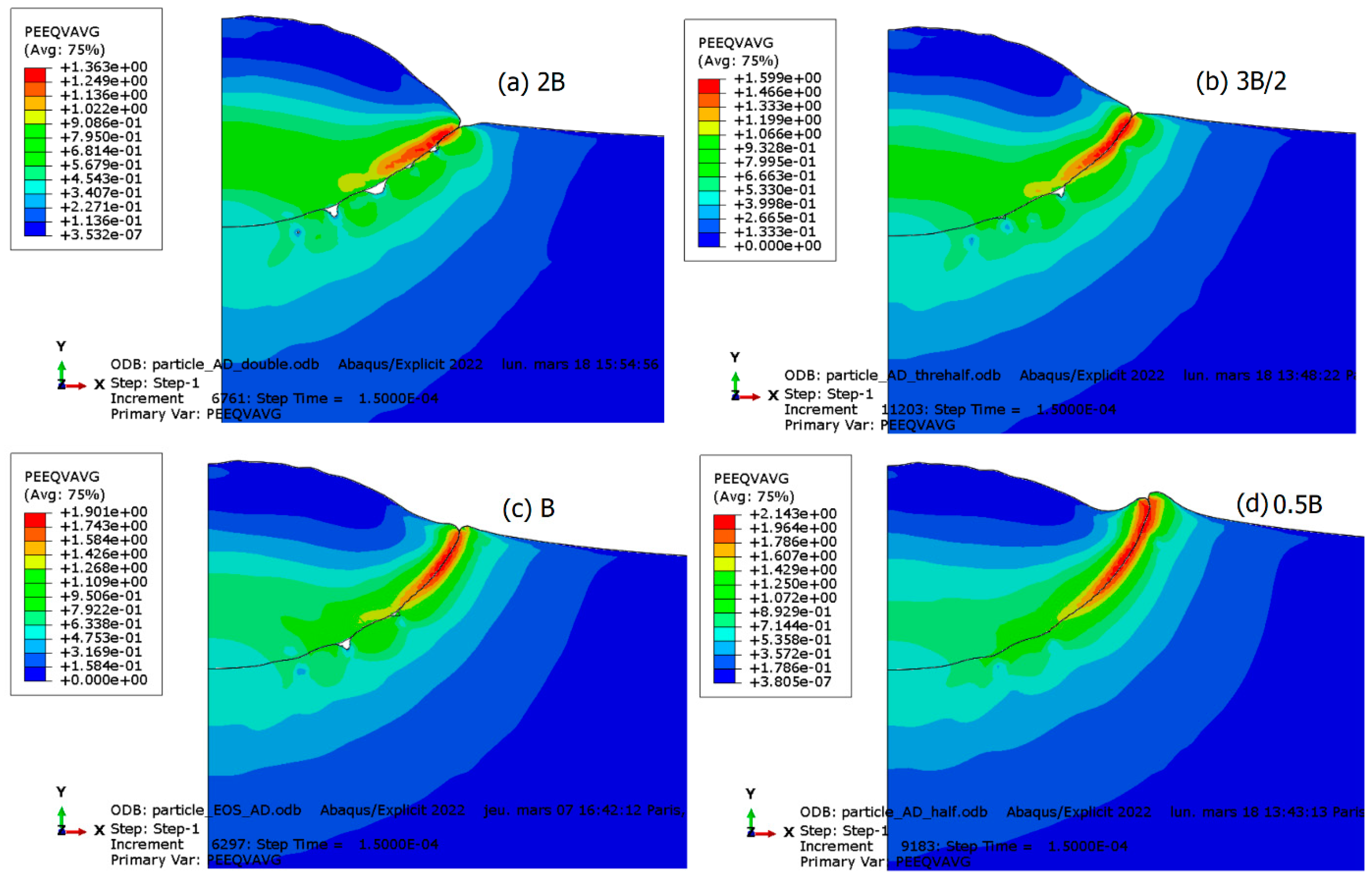
3. Results and Discussions
3.1. Shear Viscosity Effect
3.2. Drag Coefficient Effect
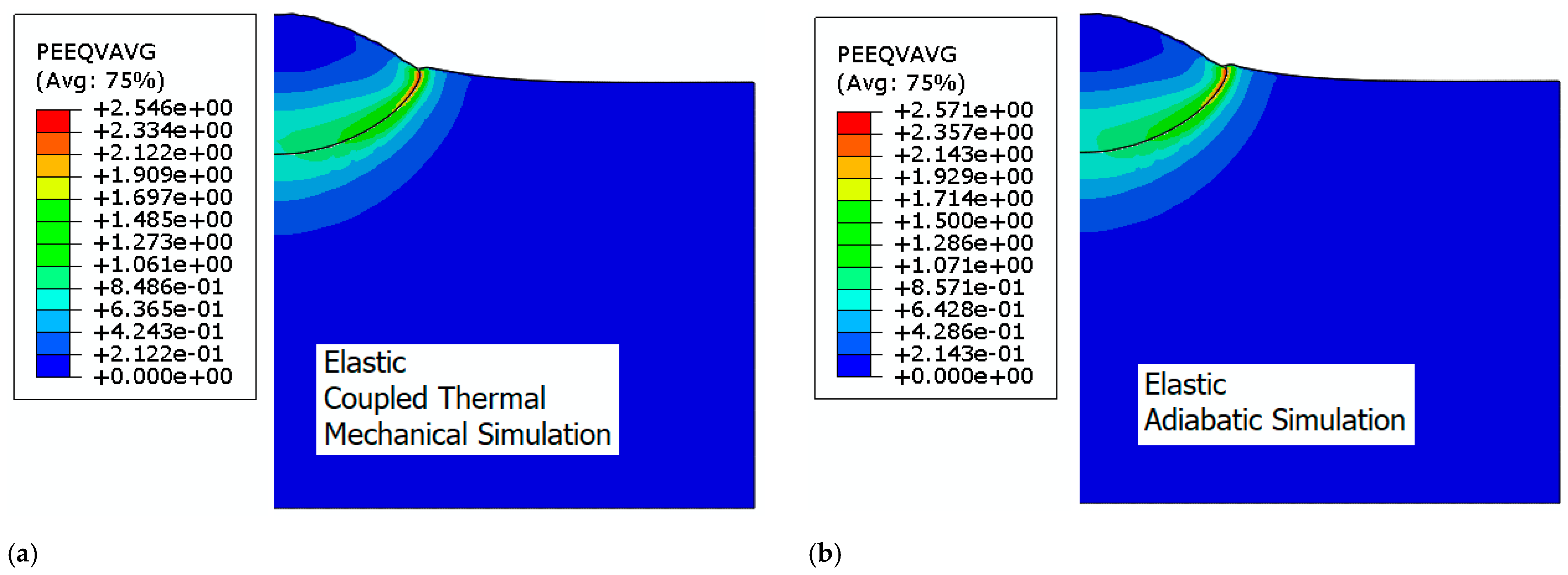
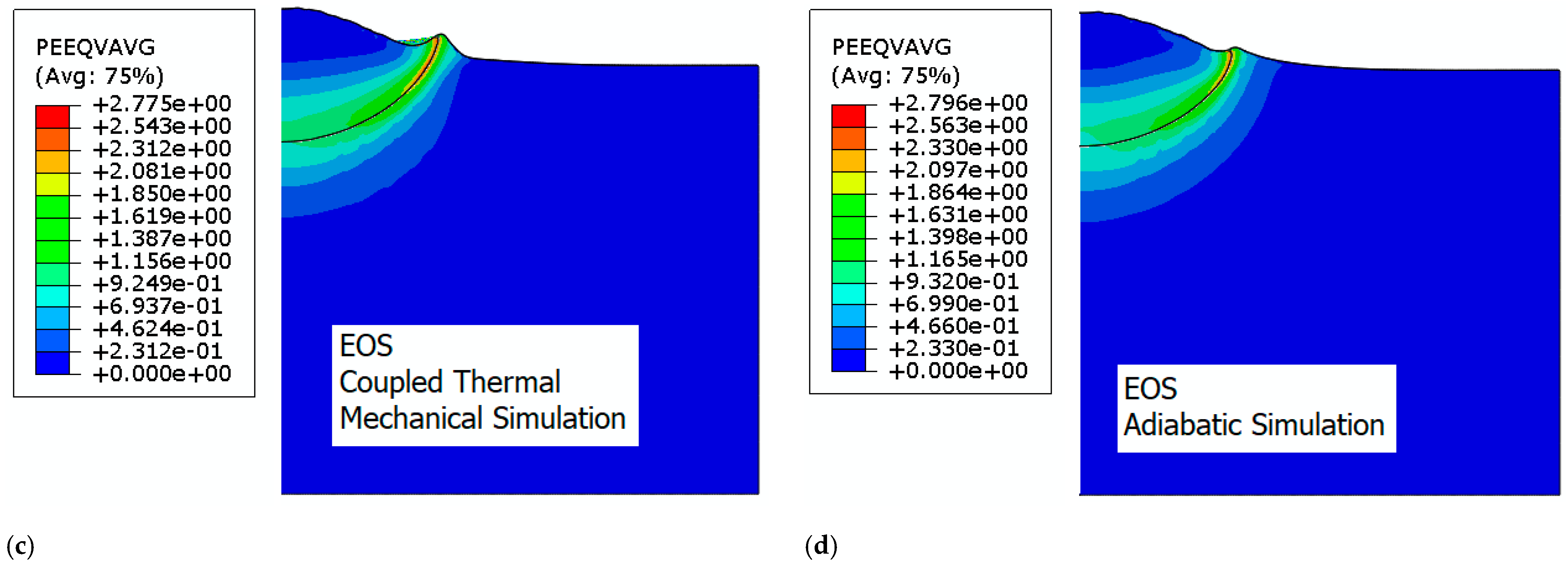
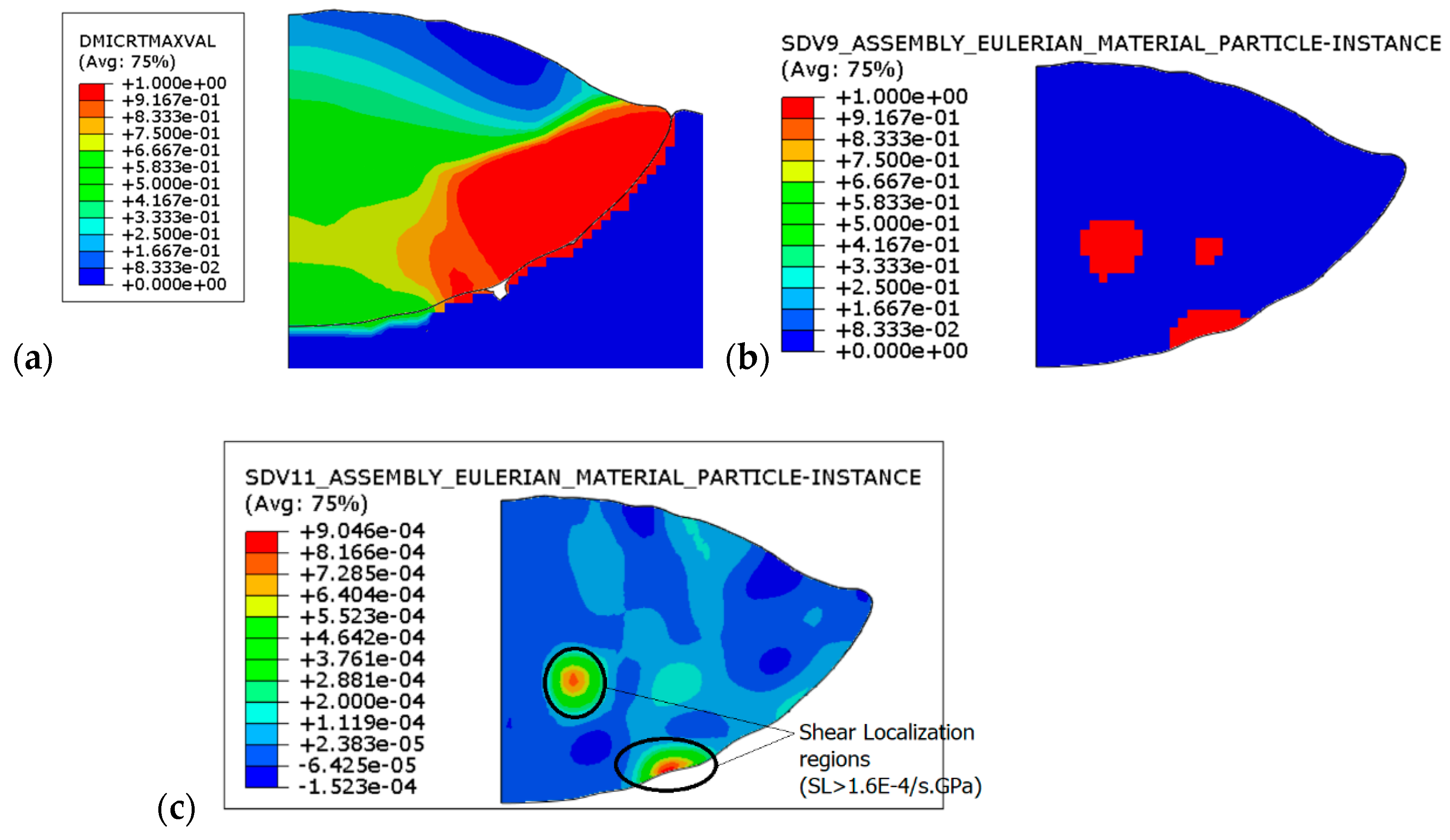
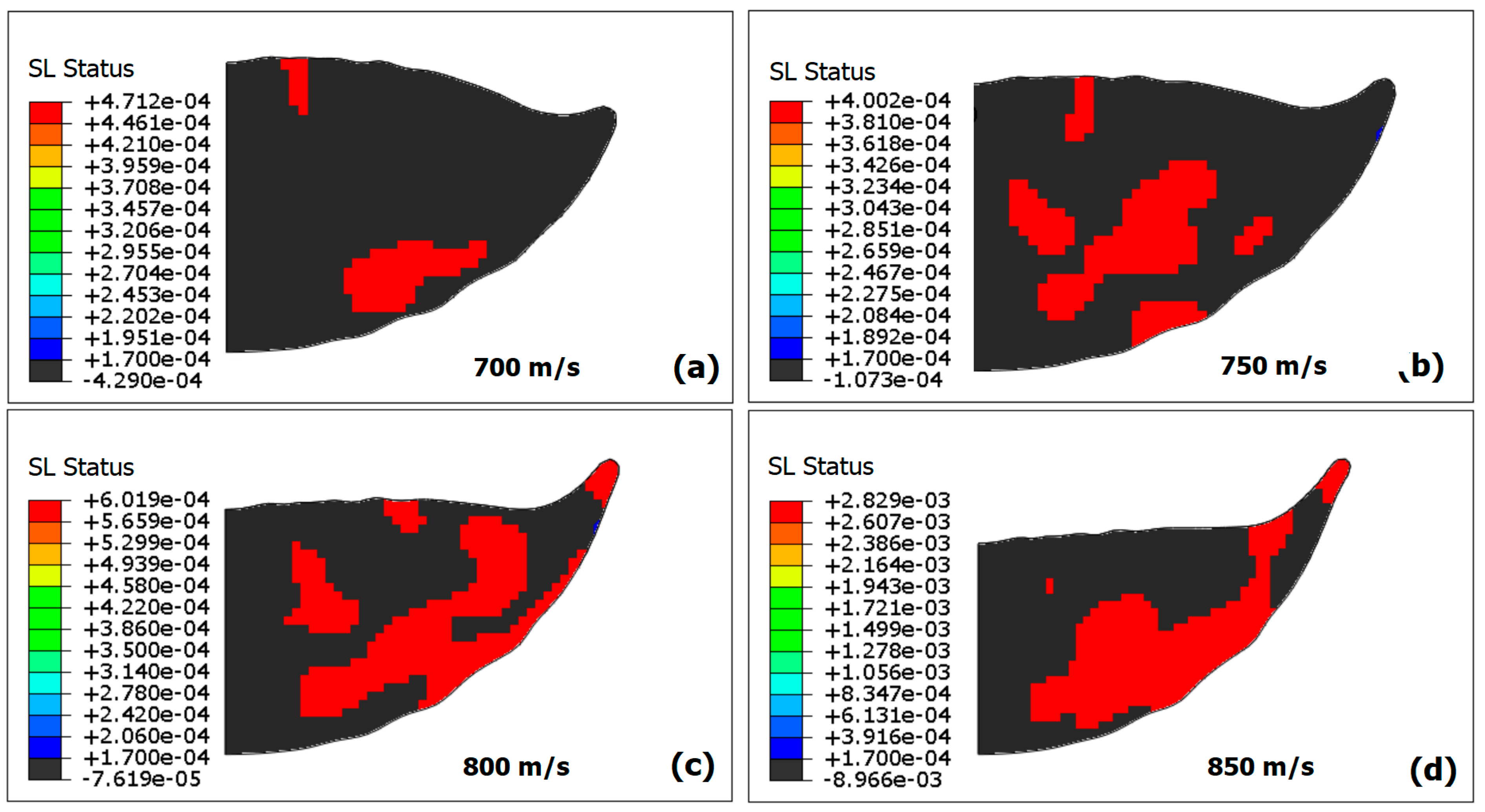
3.3. Adiabatic Shear Instability and Localization
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guetta, S.; Berger, M.H.; Borit, F.; Guipont, V.; Jeandin, M.; Boustie, M.; Ichikawa, Y.; Sakaguchi, K.; Ogawa, K. Influence of Particle Velocity on Adhesion of Cold-Sprayed Splats. J. Therm. Spray. Technol. 2009, 18, 331–342. [Google Scholar] [CrossRef]
- Moridi, A.; Hassani-Gangaraj, S.M.; Guagliano, M.; Dao, M. Cold spray coating: Review of material systems and future perspectives. Surf. Eng. 2014, 30, 369–395. [Google Scholar] [CrossRef]
- Arabgol, Z.; Villa Vidaller, M.; Assadi, H.; Gärtner, F.; Klassen, T. Influence of thermal properties and temperature of substrate on the quality of cold-sprayed deposits. Acta Mater. 2017, 127, 287–301. [Google Scholar] [CrossRef]
- Yu, M.; Li, W.-Y.; Wang, F.F.; Suo, X.K.; Liao, H. Effect of particle and substrate preheating on particle deformation behavior in cold spraying. Surf. Coat. Technol. 2013, 220, 174–178. [Google Scholar] [CrossRef]
- Koivuluoto, H.; Vuoristo, P. Effect of Powder Type and Composition on Structure and Mechanical Properties of Cu + Al2O3 Coatings Prepared by using Low-Pressure Cold Spray Process. J. Therm. Spray. Technol. 2010, 19, 1081–1092. [Google Scholar] [CrossRef]
- Lemiale, V.; Estrin, Y.; Kim, H.S.; O’Donnell, R. Forming Nanocrystalline Structures in Metal Particle Impact. Metall. Mater. Trans. A 2011, 42, 3006–3012. [Google Scholar] [CrossRef]
- Irissou, E.; Legoux, J.-G.; Arsenault, B.; Moreau, C. Investigation of Al-Al2O3 Cold Spray Coating Formation and Properties. J. Therm. Spray. Technol. 2007, 16, 661–668. [Google Scholar] [CrossRef]
- Li, W.Y.; Zhang, D.D.; Huang, C.J.; Yin, S.; Yu, M.; Wang, F.F.; Liao, H.L. Modelling of impact behaviour of cold spray particles: Review. Surf. Eng. 2014, 30, 299–308. [Google Scholar] [CrossRef]
- Yin, S.; Chen, C.; Suo, X.; Lupoi, R. Cold-Sprayed Metal Coatings with Nanostructure. Adv. Mater. Sci. Eng. 2018, 2018, 2804576. [Google Scholar] [CrossRef]
- Wang, Q.; Birbilis, N.; Huang, H.; Zhang, M.-X. Microstructure characterization and nanomechanics of cold-sprayed pure Al and Al-Al2O3 composite coatings. Surf. Coat. Technol. 2013, 232, 216–223. [Google Scholar] [CrossRef]
- Zhao, Z.; Tariq N ul, H.; Tang, J.; Ren, Y.; Liu, H.; Tong, M.; Yin, L.; Du, H.; Wang, J.; Xiong, T. Influence of annealing on the microstructure and mechanical properties of Ti/steel clad plates fabricated via cold spray additive manufacturing and hot-rolling. Mater. Sci. Eng. A 2020, 775, 138968. [Google Scholar] [CrossRef]
- Reddy, C.D.; Zhang, Z.-Q.; Msolli, S.; Guo, J.; Narayanaswamy, S. Impact induced metallurgical and mechanical interlocking in metals. Comput. Mater. Sci. 2021, 192, 110363. [Google Scholar] [CrossRef]
- Chen, C.; Xie, X.; Xie, Y.; Planche, M.-P.; Deng, S.; Ji, G.; Aubry, E.; Ren, Z.; Liao, H. Cold spraying of thermally softened Ni-coated FeSiAl composite powder: Microstructure characterization, tribological performance and magnetic property. Mater. Des. 2018, 160, 270–283. [Google Scholar] [CrossRef]
- Rokni, M.R.; Widener, C.A.; Ozdemir, O.C.; Crawford, G.A. Microstructure and mechanical properties of cold sprayed 6061 Al in As-sprayed and heat treated condition. Surf. Coat. Technol. 2017, 309, 641–650. [Google Scholar] [CrossRef]
- Gärtner, F.; Stoltenhoff, T.; Voyer, J.; Kreye, H.; Riekehr, S.; Koçak, M. Mechanical properties of cold-sprayed and thermally sprayed copper coatings. Surf. Coat. Technol. 2006, 200, 6770–6782. [Google Scholar] [CrossRef]
- Sample, C.M.; Champagne, V.K.; Nardi, A.T.; Lados, D.A. Factors governing static properties and fatigue, fatigue crack growth, and fracture mechanisms in cold spray alloys and coatings/repairs: A review. Addit. Manuf. 2020, 36, 101371. [Google Scholar] [CrossRef]
- Huang, C.; Arseenko, M.; Zhao, L.; Xie, Y.; Elsenberg, A.; Li, W.; Gärtner, F.; Simar, A.; Klassen, T. Property prediction and crack growth behavior in cold sprayed Cu deposits. Mater. Des. 2021, 206, 109826. [Google Scholar] [CrossRef]
- Wang, X.; Feng, F.; Klecka, M.A.; Mordasky, M.D.; Garofano, J.K.; El-Wardany, T.; Nardi, A.; Champagne, V.K. Characterization and modeling of the bonding process in cold spray additive manufacturing. Addit. Manuf. 2015, 8, 149–162. [Google Scholar] [CrossRef]
- Assadi, H.; Gärtner, F.; Stoltenhoff, T.; Kreye, H. Bonding mechanism in cold gas spraying. Acta. Mater. 2003, 51, 4379–4394. [Google Scholar] [CrossRef]
- Kumar, S.; Bae, G.; Lee, C. Influence of substrate roughness on bonding mechanism in cold spray. Surf. Coat. Technol. 2016, 304, 592–605. [Google Scholar] [CrossRef]
- Sun, W.; Tan, A.W.Y.; Bhowmik, A.; Marinescu, I.; Song, X.; Zhai, W.; Li, F.; Liu, E. Deposition characteristics of cold sprayed Inconel 718 particles on Inconel 718 substrates with different surface conditions. Mater. Sci. Eng. A 2018, 720, 75–84. [Google Scholar] [CrossRef]
- Ghelichi, R.; Bagherifard, S.; Guagliano, M.; Verani, M. Numerical simulation of cold spray coating. Surf. Coat. Technol. 2011, 205, 5294–5301. [Google Scholar] [CrossRef]
- Fardan, A.; Berndt, C.C.; Ahmed, R. Numerical modelling of particle impact and residual stresses in cold sprayed coatings: A review. Surf. Coat. Technol. 2021, 409, 126835. [Google Scholar] [CrossRef]
- Henao, J.; Concustell, A.; Dosta, S.; Bolelli, G.; Cano, I.G.; Lusvarghi, L.; Guilemany, J.M. Deposition mechanisms of metallic glass particles by Cold Gas Spraying. Acta Mater. 2017, 125, 327–339. [Google Scholar] [CrossRef]
- Grujicic, M.; Zhao, C.L.; DeRosset, W.S.; Helfritch, D. Adiabatic shear instability based mechanism for particles/substrate bonding in the cold-gas dynamic-spray process. Mater. Des. 2004, 25, 681–688. [Google Scholar] [CrossRef]
- Grujicic, M. 9—Particle/substrate interaction in the cold-spray bonding process. In The Cold Spray Materials Deposition ProcessFundamentals and Applications; Woodhead Publishing Series in Metals and Surface Engineering; Woodhead Publishing: Cambridge, UK, 2007; pp. 148–177. [Google Scholar]
- Schmidt, T.; Assadi, H.; Gärtner, F.; Richter, H.; Stoltenhoff, T.; Kreye, H.; Klassen, T. From Particle Acceleration to Impact and Bonding in Cold Spraying. J. Therm. Spray Technol. 2009, 18, 794. [Google Scholar] [CrossRef]
- Boruah, D.; Robinson, B.; London, T.; Wu, H.; de Villiers-Lovelock, H.; McNutt, P.; Doré, M.; Zhang, X. Experimental evaluation of interfacial adhesion strength of cold sprayed Ti-6Al-4V thick coatings using an adhesive-free test method. Surf. Coat. Technol. 2020, 381, 125130. [Google Scholar] [CrossRef]
- Chen, C.; Xie, Y.; Yin, S.; Planche, M.-P.; Deng, S.; Lupoi, R.; Liao, H. Evaluation of the interfacial bonding between particles and substrate in angular cold spray. Mater. Lett. 2016, 173, 76–79. [Google Scholar] [CrossRef]
- Song, X.; Jin, X.-Z.; Zhai, W.; Wei-Yee Tan, A.; Sun, W.; Li, F.; Marinescu, I.; Liu, E. Correlation between the macroscopic adhesion strength of cold spray coating and the microscopic single-particle bonding behaviour: Simulation, experiment and prediction. Appl. Surf. Sci. 2021, 547, 149165. [Google Scholar] [CrossRef]
- Wang, F.F.; Li, W.Y.; Yu, M.; Liao, H.L. Prediction of Critical Velocity During Cold Spraying Based on a Coupled Thermomechanical Eulerian Model. J. Therm. Spray Technol. 2014, 23, 60–67. [Google Scholar] [CrossRef]
- Chakrabarty, R.; Song, J. A modified Johnson-Cook material model with strain gradient plasticity consideration for numerical simulation of cold spray process. Surf. Coat. Technol. 2020, 397, 125981. [Google Scholar] [CrossRef]
- Mishra, A.; Martin, M.; Thadhani, N.N.; Kad, B.K.; Kenik, E.A.; Meyers, M.A. High-strain-rate response of ultra-fine-grained copper. Acta Mater. 2008, 56, 2770–2783. [Google Scholar] [CrossRef]
- Wang, F.; Wang, J.; Qi, Z.; Wu, X.; Zeng, X.; Yang, X. Evaluation of copper spall response using Mie-Grüneisen equation-of-state parameters determined from molecular dynamics. Comput. Mater. Sci. 2023, 216, 111883. [Google Scholar] [CrossRef]
- Rokni, M.R.; Widener, C.A.; Champagne, V.R. Microstructural stability of ultrafine grained cold sprayed 6061 aluminum alloy. Appl. Surf. Sci. 2014, 290, 482–489. [Google Scholar] [CrossRef]
- Cinca, N.; Drehmann, R.; Dietrich, D.; Gärtner, F.; Klassen, T.; Lampke, T.; Guilemany, J.M. Mechanically induced grain refinement, recovery and recrystallization of cold-sprayed iron aluminide coatings. Surf. Coat. Technol. 2019, 380, 125069. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Haché, M.; Irissou, E.; Zou, Y. Formation of refined grains below 10 nm in size and nanoscale interlocking in the particle–particle interfacial regions of cold sprayed pure aluminum. Scr. Mater. 2020, 177, 96–100. [Google Scholar] [CrossRef]
- Msolli, S.; Zhang, Z.-Q.; Seng, D.H.L.; Zhang, Z.; Guo, J.; Reddy, C.D.; Sridhar, N.; Pan, J.; Tan, B.H.; Loi, Q. An experimentally validated dislocation density based computational framework for predicting microstructural evolution in cold spray process. Int. J. Solids Struct. 2021, 225, 111065. [Google Scholar] [CrossRef]
- Zhang, Z.; Seng Hwee Leng, D.; Lin, M.; Siew, L.T.; Meng, T.L.; Jing Jun Lee, C.; Zhang, Z.-Q.; Ba, T.; Guo, J.; Sundaravadivelu, K.; et al. Cold Spray Deposition of Inconel 718 in Comparison with Atmospheric Plasma Spray Deposition. Appl. Surf. Sci. 2020, 535, 147704. [Google Scholar] [CrossRef]
- Lin, Q.; Liu, H.; Zhu, C.; Chen, D.; Zhou, S. Effects of different shot peening parameters on residual stress, surface roughness and cell size. Surf. Coat. Technol. 2020, 398, 126054. [Google Scholar] [CrossRef]
- Liu, T.; Vaudin, M.D.; Bunn, J.R.; Ungár, T.; Brewer, L.N. Quantifying dislocation density in Al-Cu coatings produced by cold spray deposition. Acta Mater. 2020, 193, 115–124. [Google Scholar] [CrossRef]
- Ding, H.; Shen, N.; Shin, Y.C. C. Predictive modeling of grain refinement during multi-pass cold rolling. J. Mater. Process Technol. 2012, 212, 1003–1013. [Google Scholar] [CrossRef]
- Ding, H.; Shen, N.; Shin, Y.C. Modeling of grain refinement in aluminum and copper subjected to cutting. Comput. Mater. Sci. 2011, 50, 3016–3025. [Google Scholar] [CrossRef]
- Ding, H.; Shin, Y.C. Dislocation Density-Based Grain Refinement Modeling of Orthogonal Cutting of Titanium. J. Manuf. Sci. Eng. 2014, 136, 041003. [Google Scholar] [CrossRef]
- Wang, C.; Hu, X.; Cheng, Y.; Wang, X.; Deng, H.; Wang, S.; Yao, S. Experimental investigation and numerical study on ultrasonic impact treatment of pure copper. Surf. Coat. Technol. 2021, 428, 127889. [Google Scholar] [CrossRef]
- Tóth, L.S.; Molinari, A.; Estrin, Y. Strain hardening at large strains as predicted by dislocation based polycrystal plasticity model. J. Eng. Mater. Technol. 2002, 124, 71–77. [Google Scholar] [CrossRef]
- Lapovok, R.; Dalla Torre, F.H.; Sandlin, J.; Davies, C.H.J.; Pereloma, E.V.; Thomson, P.F.; Estrin, Y. Gradient plasticity constitutive model reflecting the ultrafine micro-structure scale: The case of severely deformed copper. J. Mech. Phys. Solids 2005, 53, 729–747. [Google Scholar] [CrossRef]
- Estrin, Y.; Brechet, Y.; Kim, H.S. Modelling of the Evolution of Dislocation Cell Misorientation under Severe Plastic Deformation. Mater. Sci. Forum 2006, 504, 675–680. [Google Scholar] [CrossRef]
- Estrin, Y.; Toth, L.S.; Molinari, A.; Brechet, Y. A Dislocation-Based Model for All Hardening Stages in Large Strain Deformation. Acta Mater. 1998, 46, 5509–5522. [Google Scholar] [CrossRef]
- Holt, D.L. Dislocation Cell Formation in Metals. J. Appl. Phys. 1970, 41, 3197–3201. [Google Scholar] [CrossRef]
- Nasrollahnejad, M.; Miresmaeili, R.; Abdollah-Zadeh, A. Prediction of grain size and dislocation density in the cold spraying process using a dislocation-based model. J. Mater. Res. Technol. 2024, 28, 244–254. [Google Scholar] [CrossRef]
- Tóth, L.S.; Estrin, Y.; Lapovok, R.; Gu, C. A model of grain fragmentation based on lattice curvature. Acta Mater. 2010, 58, 1782–1794. [Google Scholar] [CrossRef]
- Gu, C.F.; Tóth, L.S.; Beausir, B. Modeling of large strain hardening during grain refinement. Scr. Mater. 2012, 66, 250–253. [Google Scholar] [CrossRef]
- Tóth, L.S.; Beausir, B.; Gu, C.F.; Estrin, Y.; Scheerbaum, N.; Davies, C.H.J. Effect of grain refinement by severe plastic deformation on the next-neighbor misorientation distribution. Acta Materialia 2010, 20, 6706–6716. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Q.; El-Awady, J.A.; Raabe, D.; Zaiser, M. Strain rate dependency of dislocation plasticity. Nat. Commun. 2021, 12, 1845. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Chen, S.R.; Gray, G.T. Constitutive behavior of tantalum and tantalum-tungsten alloys. Metall. Mater. Trans. A 1996, 27, 2994–3006. [Google Scholar] [CrossRef]
- Razavipour, M.; Jodoin, B. Material Model for Predicting Dynamic Response of Copper and Nickel at Very High Strain Rates Under Cold Spray Conditions. J. Therm. Spray Technol. 2021, 30, 324–343. [Google Scholar] [CrossRef]
- Mao, Z.N.; An, X.H.; Liao, X.Z.; Wang, J.T. Opposite grain size dependence of strain rate sensitivity of copper at low vs high strain rates. Mater. Sci. Eng. A 2018, 738, 430–438. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodríguez-Martínez, J.A.; Arias, A. A thermo-viscoplastic constitutive model for FCC metals with application to OFHC copper. Int. J. Mech. Sci. 2010, 52, 120–135. [Google Scholar] [CrossRef]
- Jassby, K.M.; Vreeland, T. Dislocation Mobility in Pure Copper at 4.2 K. Phys. Rev. B 1973, 8, 3537–3541. [Google Scholar] [CrossRef]
- Mordehai, D.; Ashkenazy, Y.; Kelson, I.; Makov, G. Dynamic properties of screw dislocations in Cu: A molecular dynamics study. Phys. Rev. B 2003, 67, 24112. [Google Scholar] [CrossRef]
- Zaretsky, E.B.; Kanel, G.I. Response of copper to shock-wave loading at temperatures up to the melting point. J. Appl. Phys. 2013, 114, 83511. [Google Scholar] [CrossRef]
- Leibfried, G. Über den Einfluß thermisch angeregter Schallwellen auf die plastische Deformation. Z. Phys. 1950, 127, 344–356. [Google Scholar] [CrossRef]
- Swegle, J.W.; Grady, D.E. Shock viscosity and the prediction of shock wave rise times. J. Appl. Phys. 1985, 58, 692–701. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Shear viscosity of liquid copper at experimentally accessible shear rates: Application of the transient-time correlation function formalism. J. Chem. Phys. 2008, 128, 84506. [Google Scholar] [CrossRef]
- Yan, N.; Li, Z.; Xu, Y.; Meyers, M.A. Shear localization in metallic materials at high strain rates. Prog. Mater. Sci. 2021, 119, 100755. [Google Scholar] [CrossRef]
- Rice, J.R. The localization of plastic deformation. In Proceedings of the 14th International Congress on Theoratical and Applied Mechanics 1976; pp. 207–220. Available online: http://esag.harvard.edu/rice/062_Rice_LocalPlasDef_IUTAM76.pdf (accessed on 10 January 2025).
- Rudnicki, J.W.; Rice, J.R. Conditions for the localization of deformation in pressure-sensitive dilatant materials. J. Mech. Phys. Solids 1975, 23, 371–394. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Post-bifurcation behavior in the plastic range. J. Mech. Phys. Solids 1973, 21, 163–190. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Tvergaard, V. Surface instabilities on statically strained plastic solids. Int. J. Mech. Sci. 1980, 22, 339–354. [Google Scholar] [CrossRef]
- Miguélez, M.H.; Soldani, X.; Molinari, A. Analysis of adiabatic shear banding in orthogonal cutting of Ti alloy. Int. J. Mech. Sci. 2013, 75, 212–222. [Google Scholar] [CrossRef]
- Molinari, A. Collective behavior and spacing of adiabatic shear bands. J. Mech. Phys. Solids 1997, 45, 1551–1575. [Google Scholar] [CrossRef]
- Molinari, A.; Soldani, X.; Miguélez, M.H. Adiabatic shear banding and scaling laws in chip formation with application to cutting of Ti–6Al–4V. J. Mech. Phys. Solids 2013, 61, 2331–2359. [Google Scholar] [CrossRef]
- Fressengeas, C.; Molinari, A. Instability and localization of plastic flow in shear at high strain rates. J. Mech. Phys. Solids 1987, 35, 185–211. [Google Scholar] [CrossRef]
- Bonnet-Lebouvier, A.-S.; Molinari, A.; Lipinski, P. Analysis of the dynamic propagation of adiabatic shear bands. Int. J. Solids Struct. 2002, 39, 4249–4269. [Google Scholar] [CrossRef]
- Recht, R.F. Catastrophic Thermoplastic Shear. J. Appl. Mech. 1964, 31, 189–193. [Google Scholar] [CrossRef]
- Culver, R.S. Thermal Instability Strain in Dynamic Plastic Deformation. In Metallurgical Effects at High Strain Rates; Rohde, R.W., Butcher, B.M., Holland, J.R., Karnes, C.H., Eds.; Springer: Boston, MA, USA, 1973; pp. 519–530. [Google Scholar]
- Gurrutxaga-Lerma, B. Adiabatic shear banding and the micromechanics of plastic flow in metals. Int. J. Solids Struct. 2018, 132–133, 153–170. [Google Scholar] [CrossRef]
- Wright, T.W. Shear band susceptibility: Work hardening materials. Int. J. Plast. 1992, 8, 583–602. [Google Scholar] [CrossRef]
- Wright, T.W. Toward a defect invariant basis for susceptibility to adiabatic shear bands. Mech. Mater. 1994, 17, 215–222. [Google Scholar] [CrossRef]
- Schoenfeld, S.E.; Wright, T.W. A failure criterion based on material instability. Int. J. Solids Struct. 2003, 40, 3021–3037. [Google Scholar] [CrossRef]
- Tanner, A.B.; McDowell, D.L. Deformation, temperature and strain rate sequence experiments on OFHC Cu. Int. J. Plast. 1999, 15, 375–399. [Google Scholar] [CrossRef]
- Tanner, A.B.; McGinty, R.D.; McDowell, D.L. Modeling temperature and strain rate history effects in OFHC Cu. Int. J. Plast. 1999, 15, 575–603. [Google Scholar] [CrossRef]
- Banerjee, B. An evaluation of plastic flow stress models for the simulation of high-temperature and high-strain-rate deformation of metals. arXiv 2005. [Google Scholar] [CrossRef]
- Nemat-Nasser, S. Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials; Department of Mechanical and Aerospace Engineering, University of California: San Diego, CA, USA, 2003. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder—Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Samanta, S.K. Dynamic deformation of aluminium and copper at elevated temperatures. J. Mech. Phys. Solids 1971, 19, 117–135. [Google Scholar] [CrossRef]
- Khan, A.S.; Zhang, H. Mechanically alloyed nanocrystalline iron and copper mixture: Behavior and constitutive modeling over a wide range of strain rates. Int. J. Plast. 2000, 16, 1477–1492. [Google Scholar] [CrossRef]
- Lea, L.J.; Jardine, A.P. Characterisation of high rate plasticity in the uniaxial deformation of high purity copper at elevated temperatures. Int. J. Plast 2018, 102, 41–52. [Google Scholar] [CrossRef]
- Loke, K.; Guo, J.; Zhang, Z.; Narayanaswamy, S.; Koh, P.K.; Lim, T.C.; Ning, P.C.H.; Kwok, W.O.R. Analysis of Cold Spray Coating Sprayed at Angles. In Proceedings of the 9th (ATSC-2018), Singapore, 16–18 November 2018. [Google Scholar]
- Chen, C.; Xie, Y.; Yin, S.; Li, W.; Luo, X.; Xie, X.; Zhao, R.; Deng, X.; Wang, J.; Liao, H.; et al. Ductile and high strength Cu fabricated by solid-state cold spray additive manufacturing. J. Mater. Sci. Technol. 2023, 134, 234–243. [Google Scholar] [CrossRef]
- Zheng, L.; Haché, M.J.R.; Poirier, D.; Legoux, J.-B.; Giallonardo, J.D.; Zou, Y.; Howe, J.Y.; Erb, U. Submicrometer scale mapping of microstructure and mechanical properties of cold sprayed copper. Mater. Sci. Eng. A 2025, 920, 147556. [Google Scholar] [CrossRef]
- Zheng, L.; Poirier, D.; Legoux, J.-G.; Giallonardo, J.D.; Howe, J.Y.; Erb, U. Microstructural characterization of interfaces between cold sprayed copper and electrodeposited copper corrosion barrier coatings for used nuclear fuel containers. Surf. Coat. Technol. 2024, 494, 131396. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J.; Huang, C. Prediction of deformation characteristics and critical velocities during cold-spray: A new 3D model. Surf. Coat. Technol. 2024, 478, 130492. [Google Scholar] [CrossRef]
- Pereira, L.M.; Zúñiga, A.; Jodoin, B.; Vega, R.G.A.; Rahmati, S. Unraveling jetting mechanisms in high-velocity impact of copper particles using molecular dynamics simulations. Addit. Manuf. 2023, 75, 103755. [Google Scholar] [CrossRef]
- Schmidt, T.; Gärtner, F.; Assadi, H.; Kreye, H. Development of a generalized parameter window for cold spray deposition. Acta Mater. 2006, 54, 729–742. [Google Scholar] [CrossRef]
- King, P.C.; Bae, G.; Zahiri, S.H.; Jahedi, M.; Lee, C. An Experimental and Finite Element Study of Cold Spray Copper Impact onto Two Aluminum Substrates. J. Therm. Spray Technol. 2010, 19, 620–634. [Google Scholar] [CrossRef]
- Kumar Reddy Sirigiri, V.; Yadav Gudiga, V.; Shankar Gattu, U.; Suneesh, G.; Buddaraju, K.M. A review on Johnson Cook material model. Mater. Today Proc. 2022, 62, 3450–3456. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact. Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]

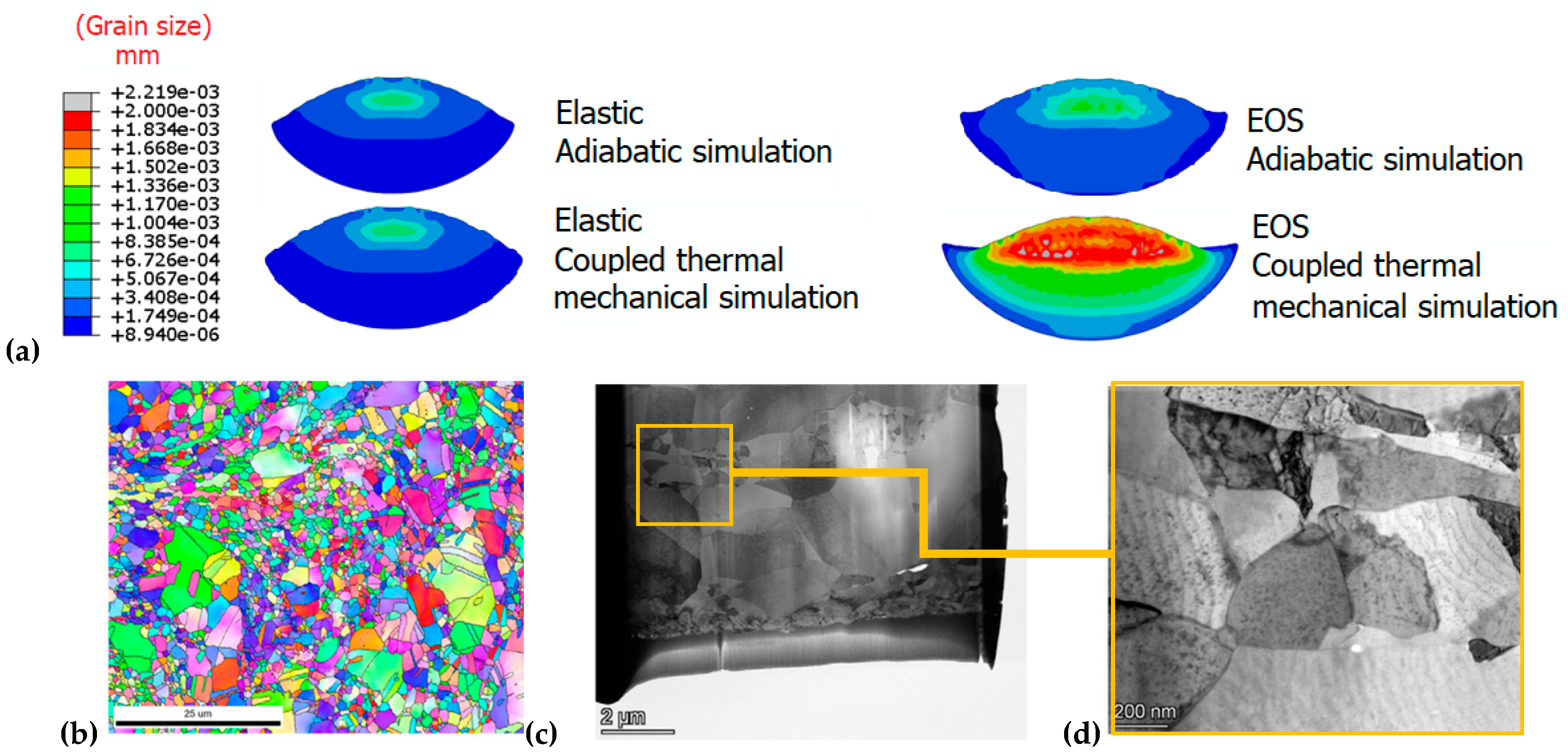


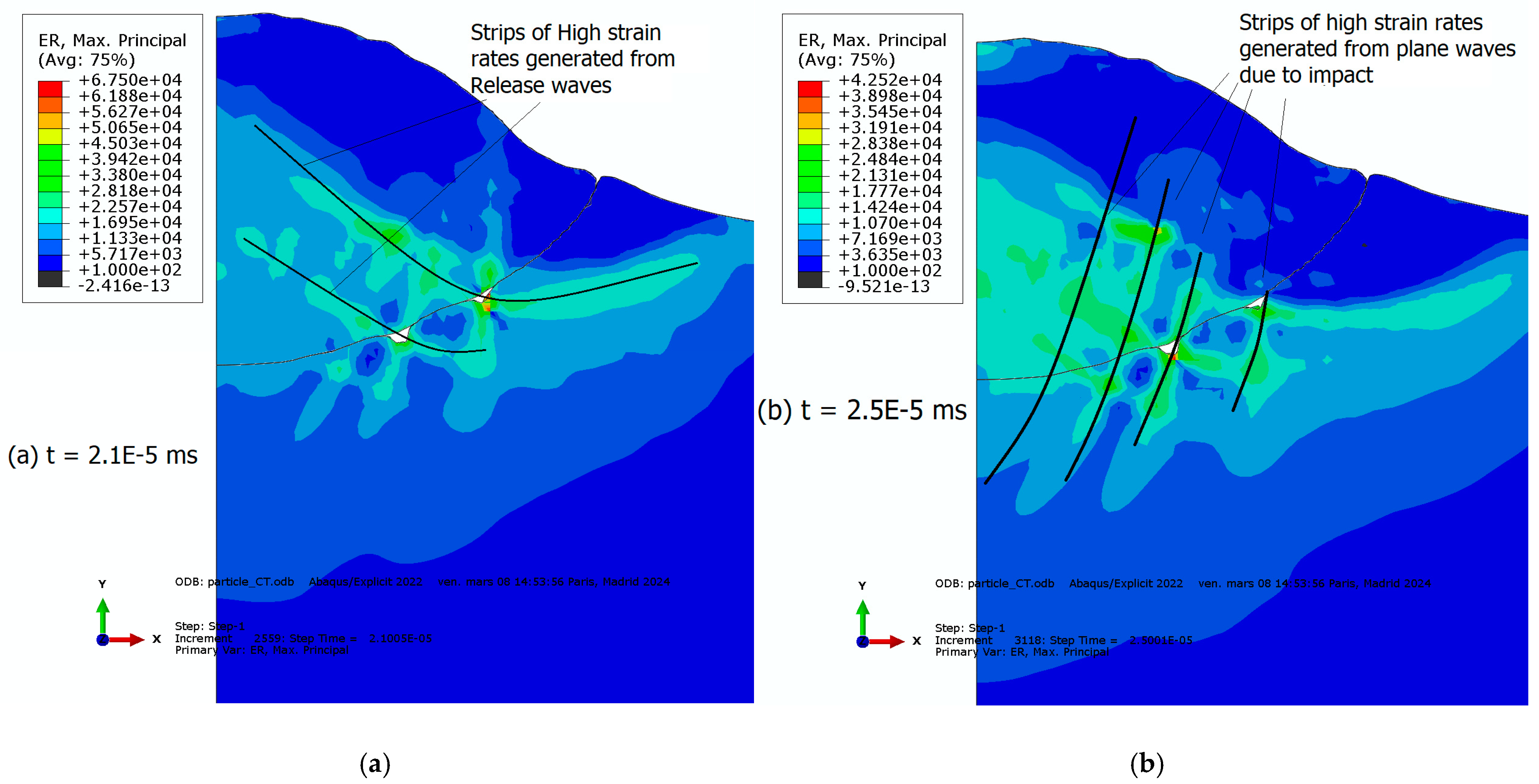

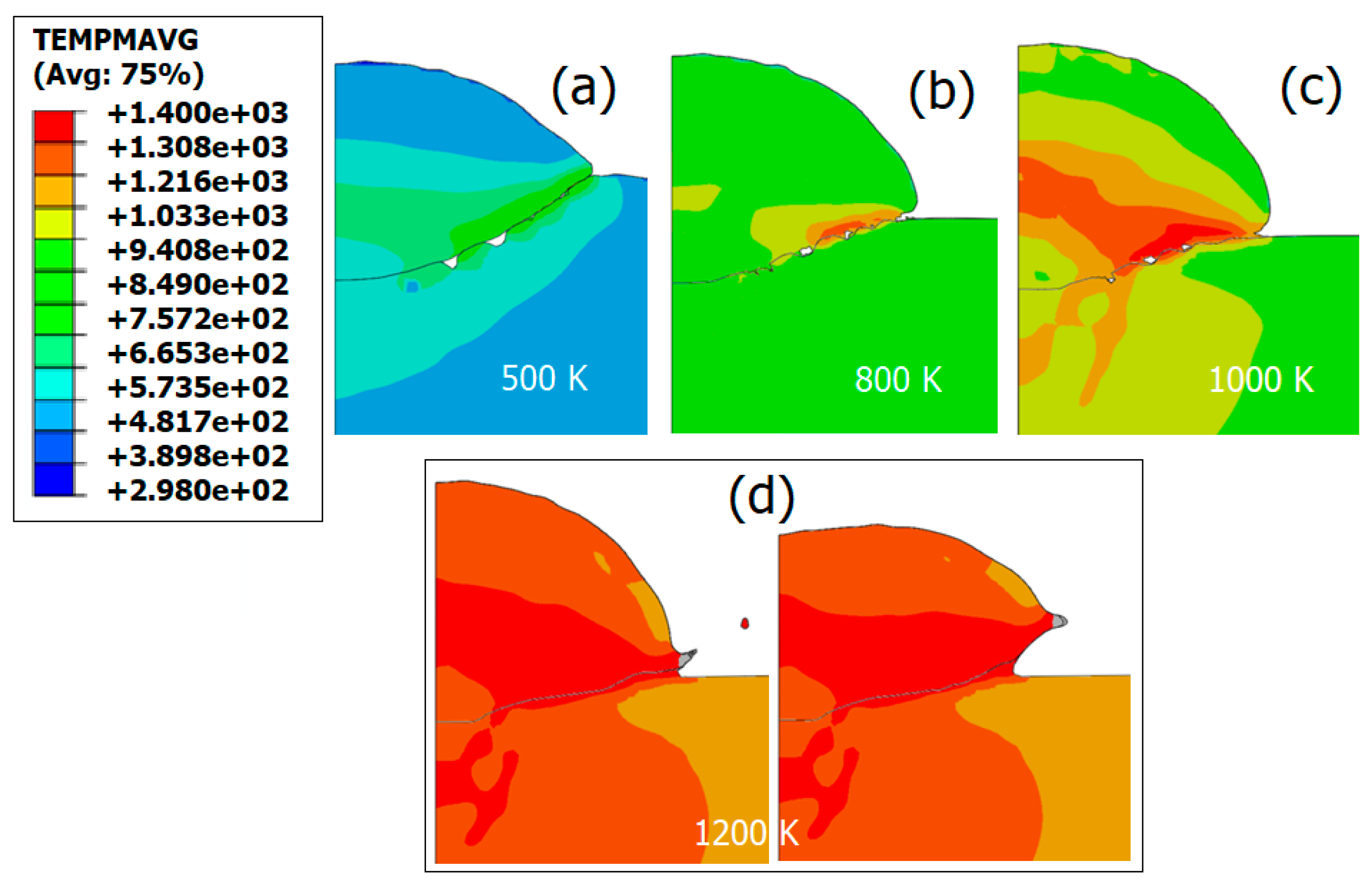

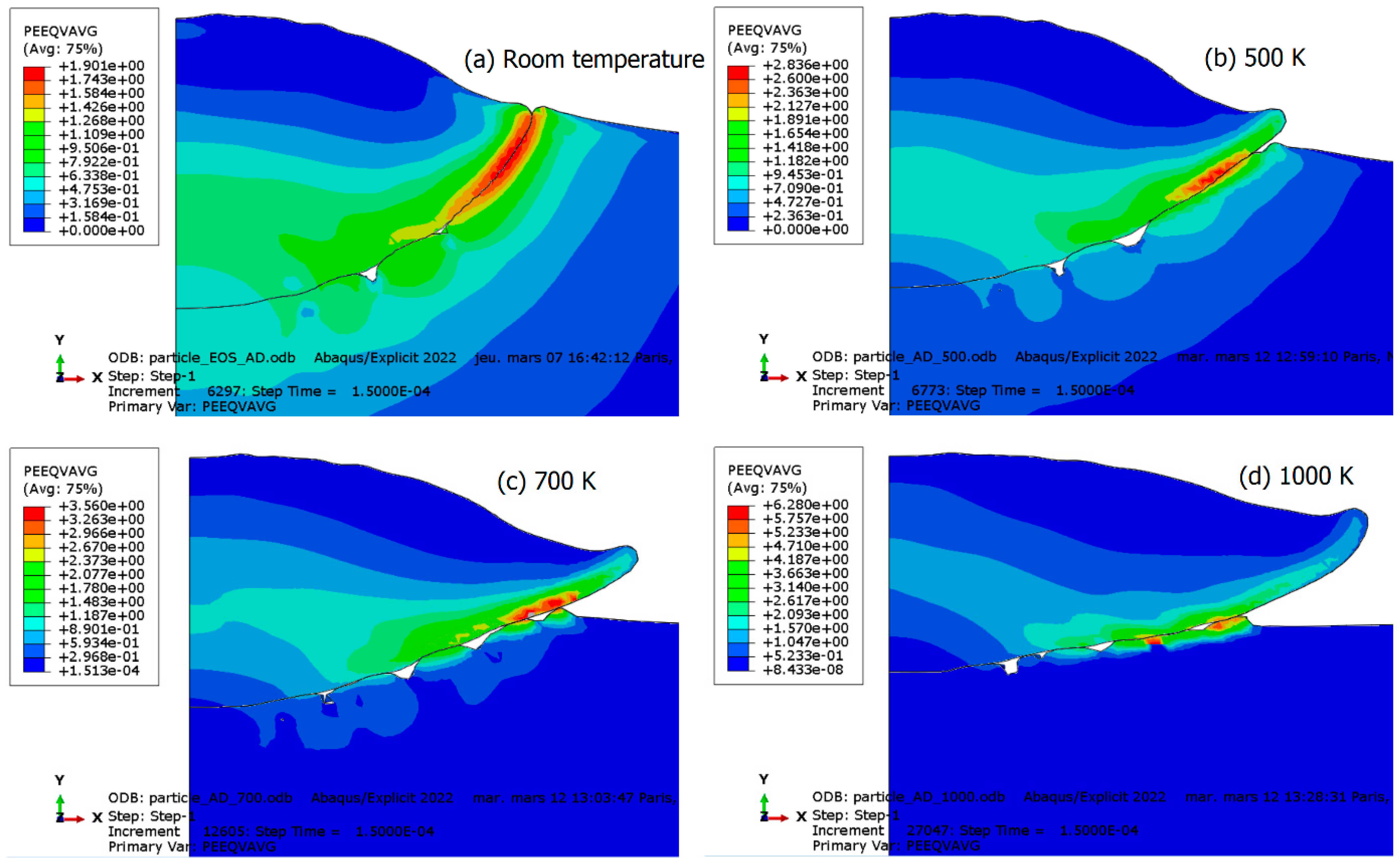
| T (K) | ρ (kg.m−3) | Cp (J Kg−1 K−1) | λ (W m−1.K−1) | α | E (GPa) |
|---|---|---|---|---|---|
| 300 | 8960 | 385 | 395 | 16 × 10−6 | 115 |
| 1300 | 8420 | 700 | 335 | 23 × 10−6 | 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Msolli, S. Shear Instability and Localization in High-Speed Cold Spray Processes: Impact on Particle Fragmentation and Bonding Mechanisms. Materials 2025, 18, 490. https://doi.org/10.3390/ma18030490
Msolli S. Shear Instability and Localization in High-Speed Cold Spray Processes: Impact on Particle Fragmentation and Bonding Mechanisms. Materials. 2025; 18(3):490. https://doi.org/10.3390/ma18030490
Chicago/Turabian StyleMsolli, Sabeur. 2025. "Shear Instability and Localization in High-Speed Cold Spray Processes: Impact on Particle Fragmentation and Bonding Mechanisms" Materials 18, no. 3: 490. https://doi.org/10.3390/ma18030490
APA StyleMsolli, S. (2025). Shear Instability and Localization in High-Speed Cold Spray Processes: Impact on Particle Fragmentation and Bonding Mechanisms. Materials, 18(3), 490. https://doi.org/10.3390/ma18030490







