Effect of the Alkali-Sulphate Activators on the Hydration Process of Blast-Furnace Slag Mortars and Pastes
Abstract
1. Introduction
2. Materials and Methods
- (1)
- (2)
- (3)
3. Results and Discussion
3.1. Properties in the Fresh State
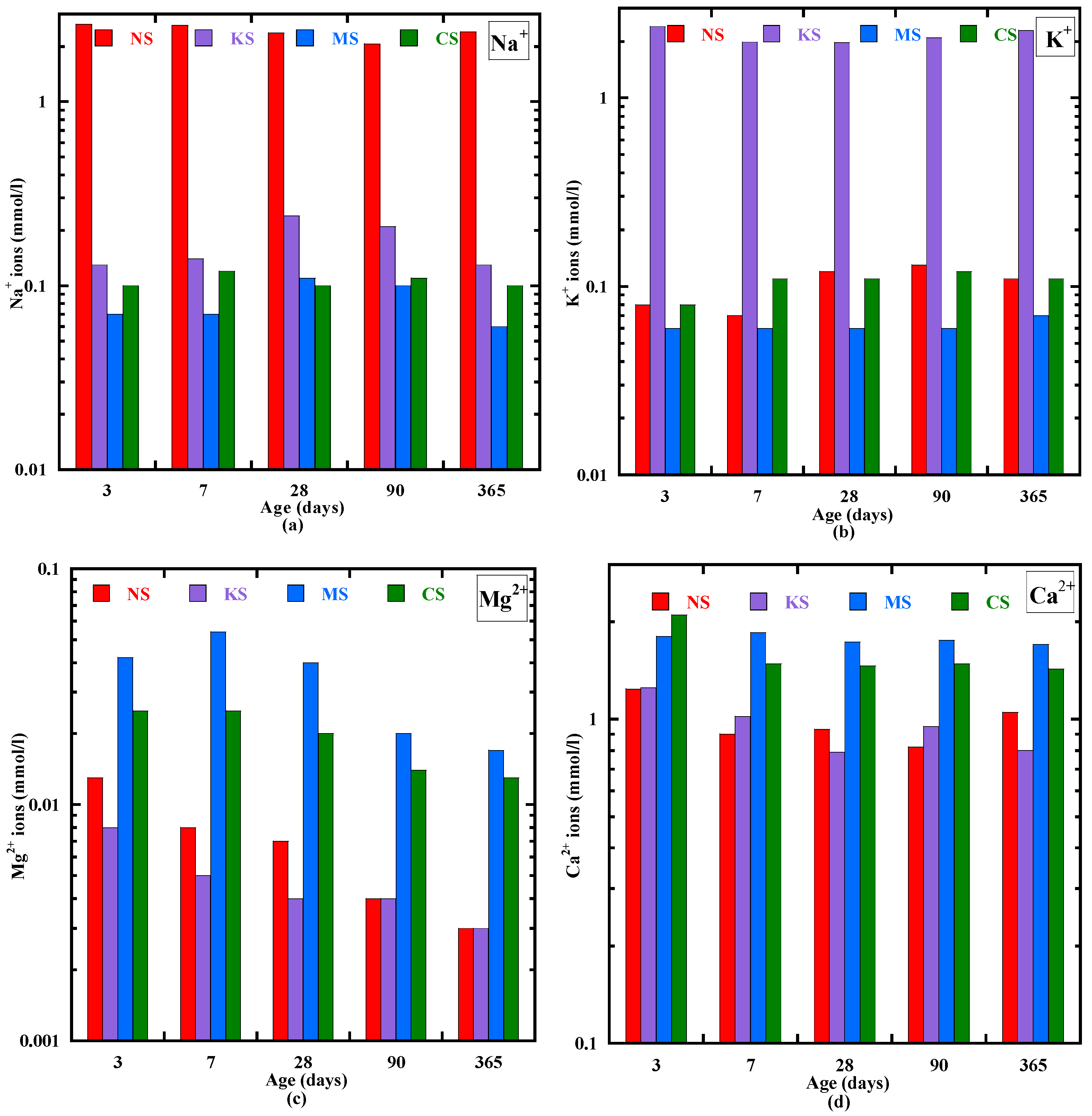
3.2. Pore Solution Chemistry
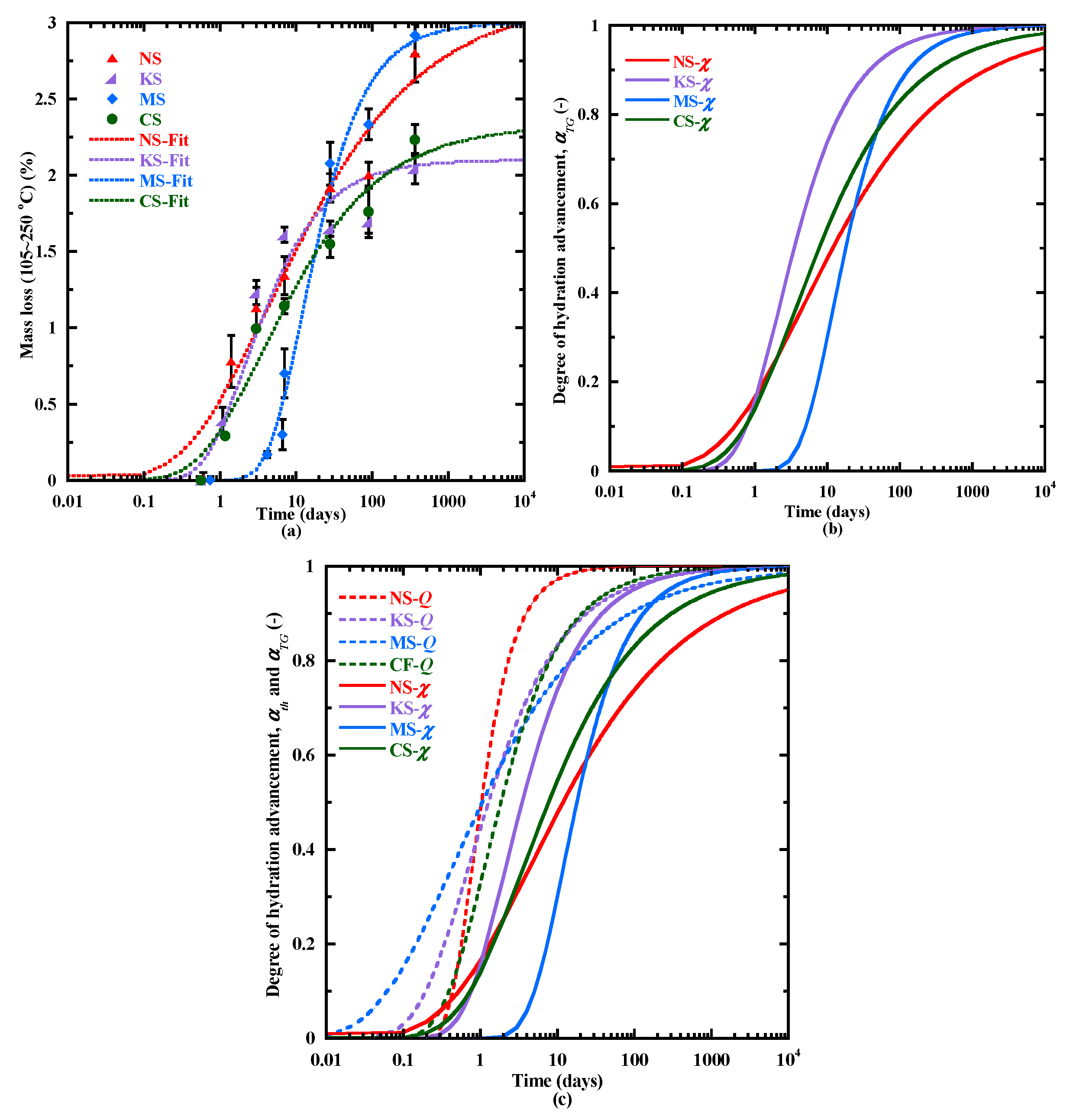
3.3. Hydration Process at Early Age
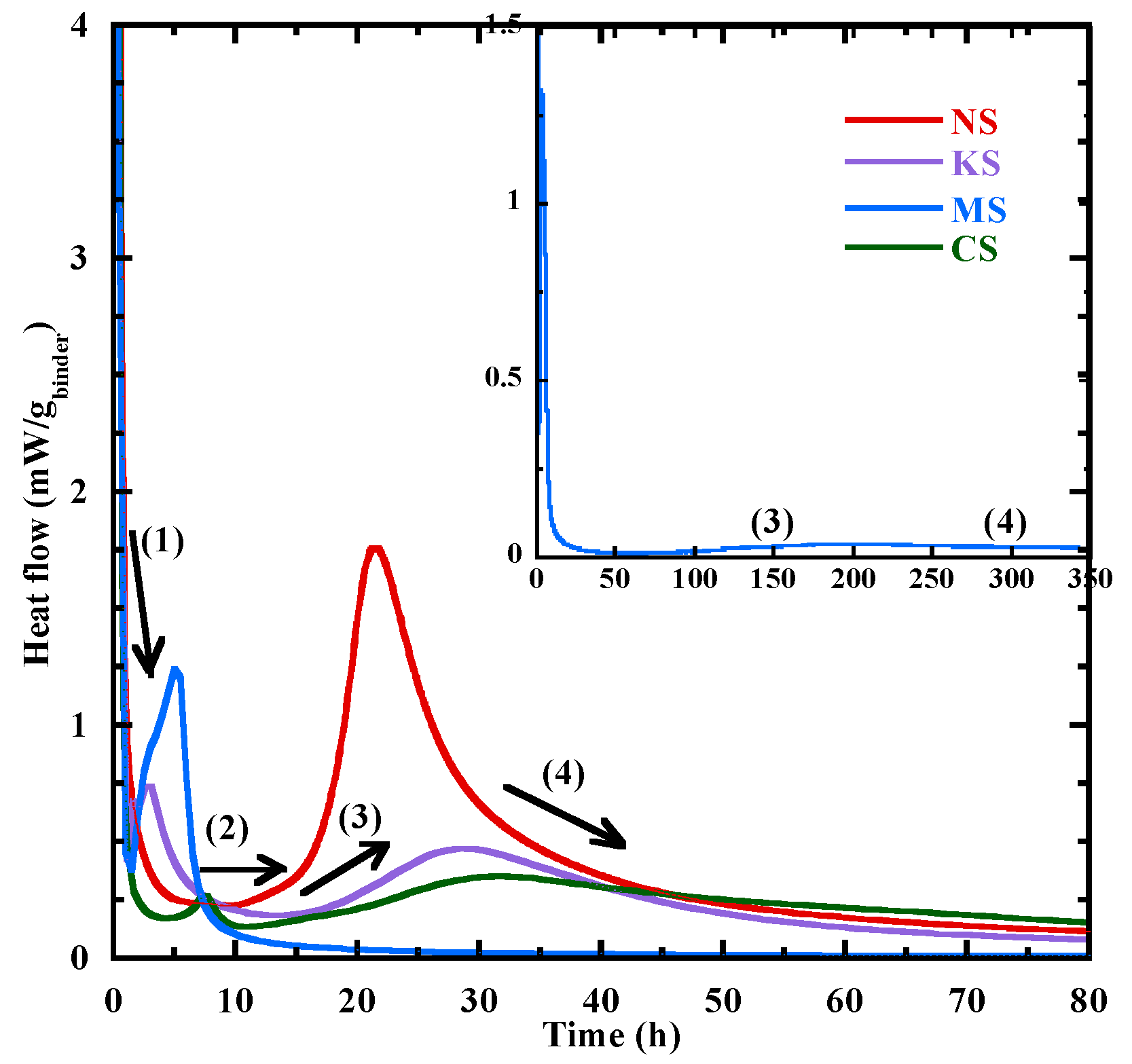
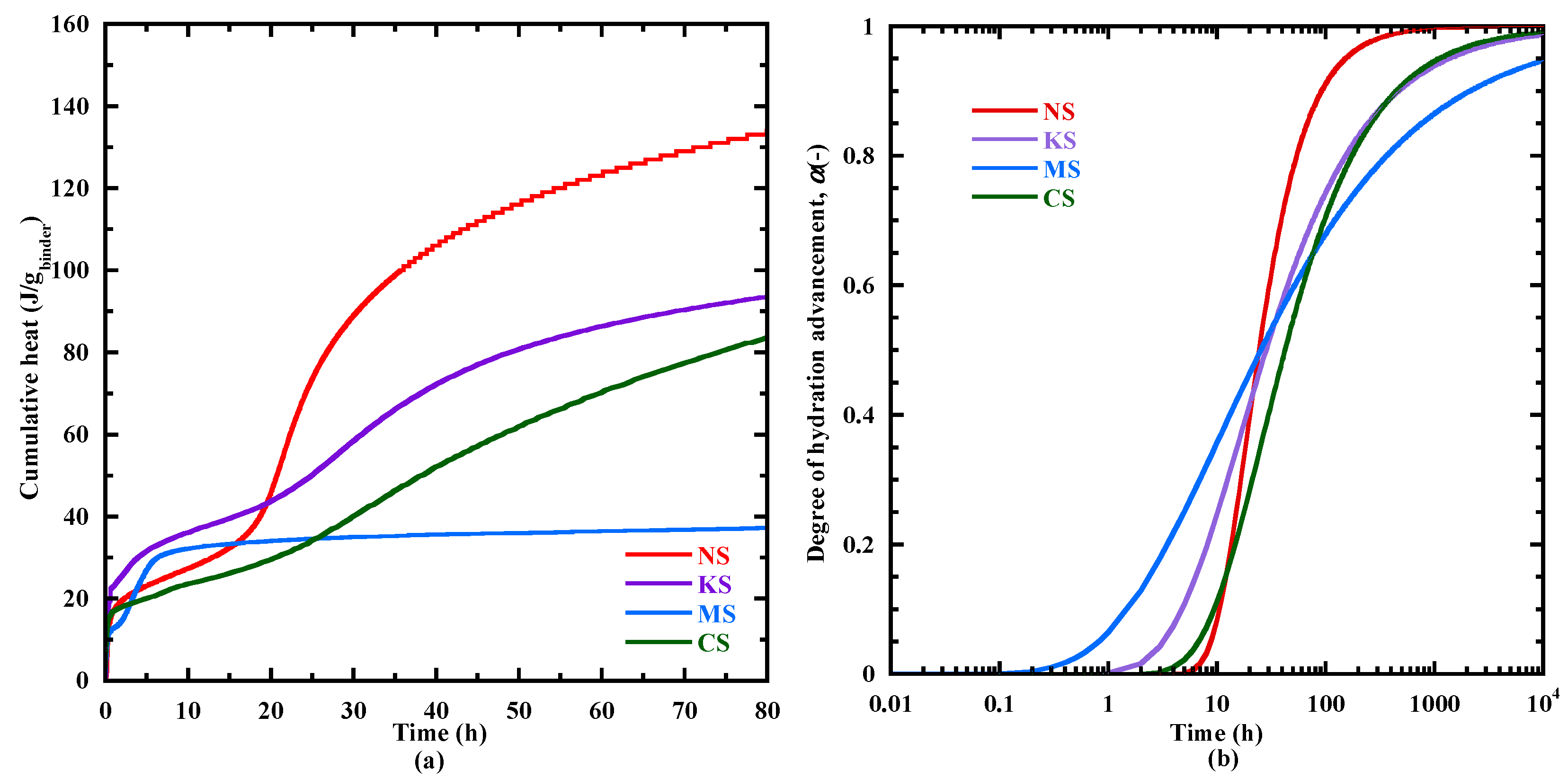
3.3.1. Hydration Kinetics
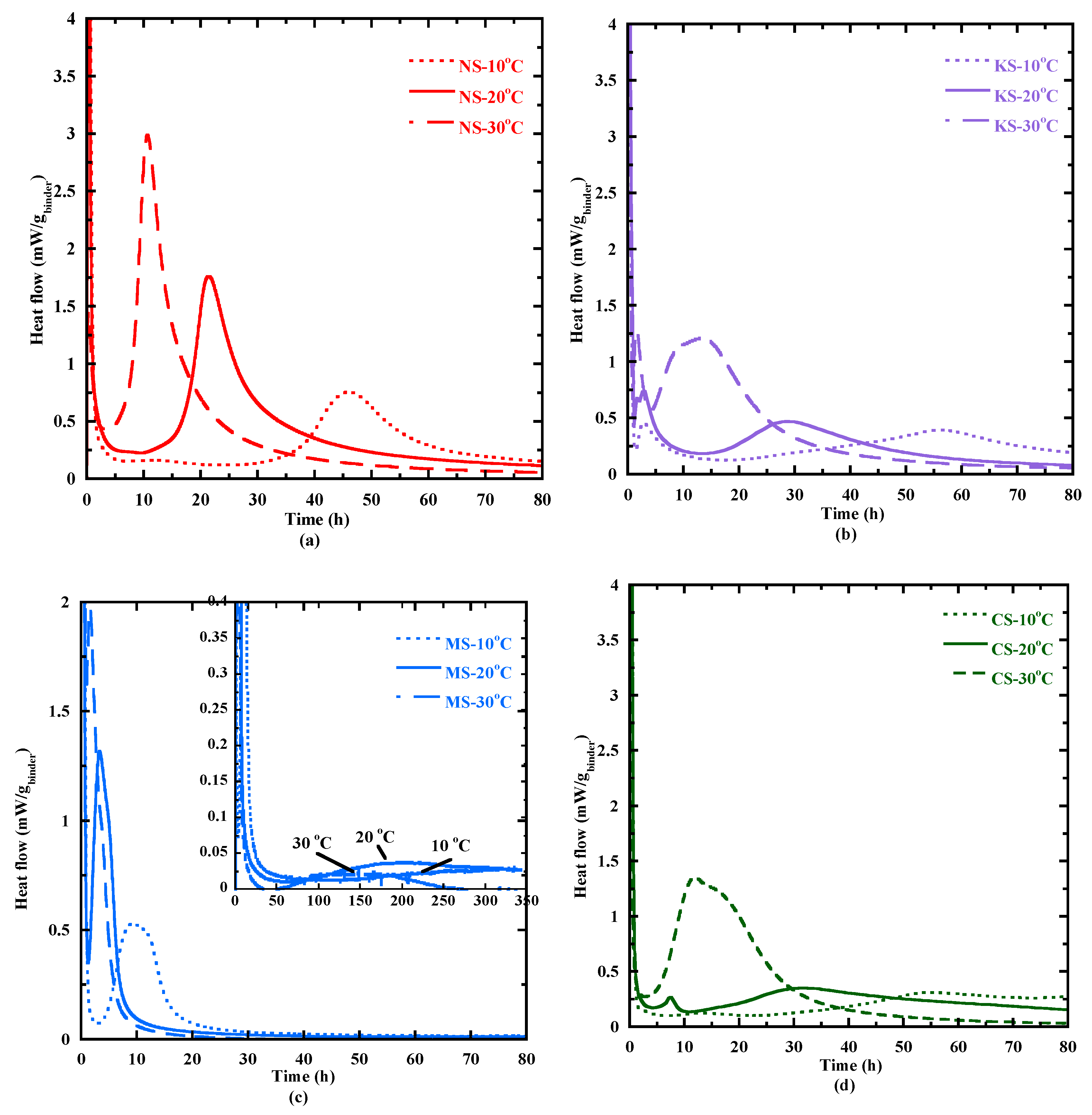
3.3.2. Temperature Effect on the Hydration Process
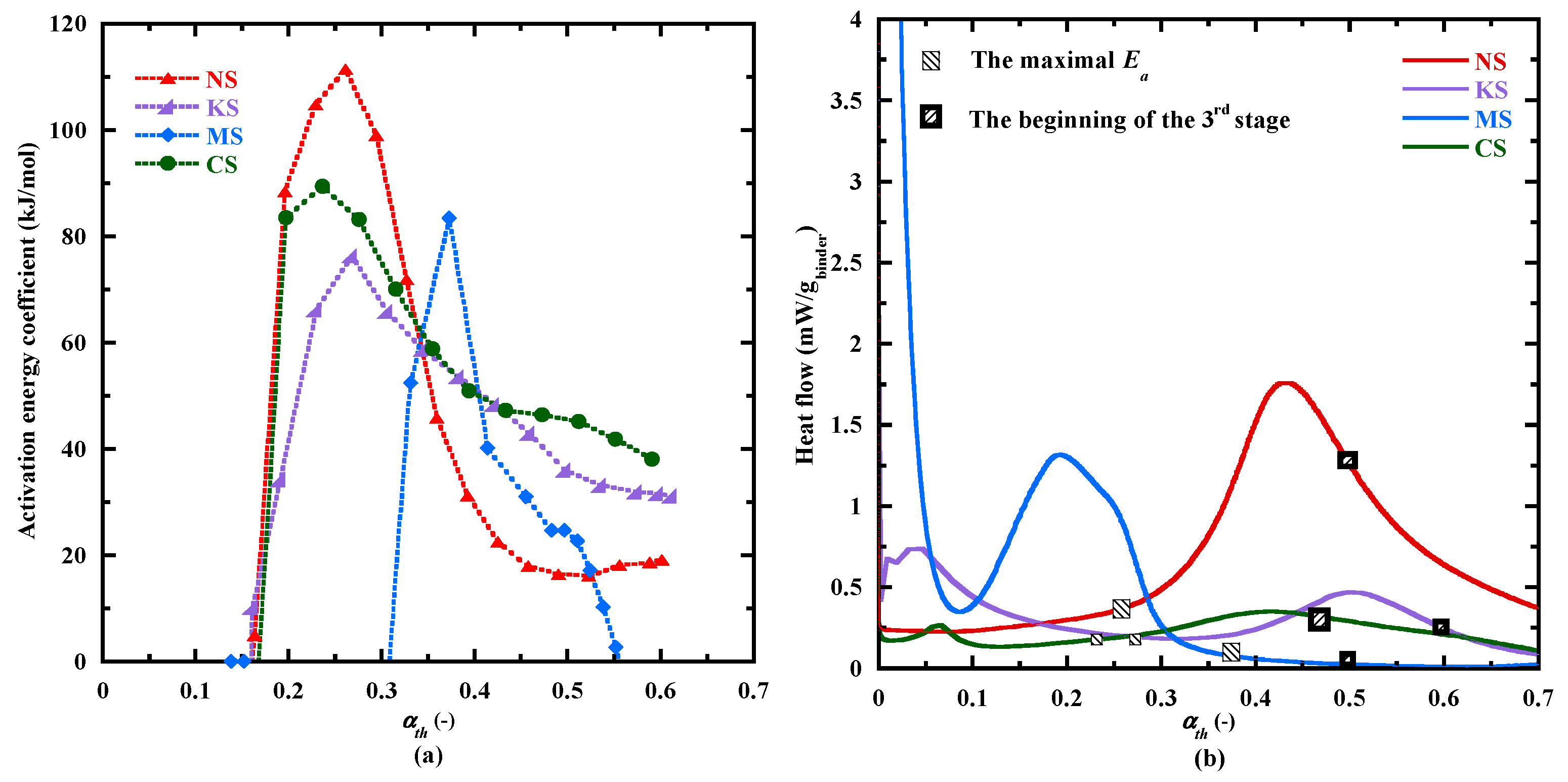
- The first stage is characterized by a fast increase in Ea. It begins at a equal to about 0.16 for NS, KS and CS and to a higher value for MS (0.31) (Table 7). The highest value of Ea (111 kJ/mol—Table 7) is reached by NS at equal to 0.26. For NS, KS and CS, the maximal Ea values are reached near the end of the dormant period, indicating a similar kinetic behavior during the early hydration phase (Figure 7b). Indeed, under a similar (0.25), Ea is equal to 76 kJ/mol for KS and 89 kJ/mol for CS. For MS, the slightly delayed peak could be attributed to its slow reaction kinetics (Figure 3), affecting its dormancy duration (Figure 7b).
- During the second stage, Ea decreases until it reaches a quite stationary state (beginning of the third stage). This stage happens during the acceleration period for NS, KS and CS, highlighting the important effect of physical and chemical changes during this stage (Figure 7b). The drop in Ea confirms an increased ease of reaction and a stable establishment of hydration products.
- The third stage begins at an equal to about 0.46 for CS, 0.49 for NS, 0.5 for MS and 0.6 for KS. The average value of Ea calculated on this stage is equal to 46, 18, 24 and 32 kJ/mol, respectively. In this stage, the hydration process of CS and KS are more sensitive to thermal activation.
- For CS and MS, a second decrease is observed (fourth stage), possibly related to their larger duration of the characteristic times (Appendix A) and their lower evolution rate of heat flow at 10 °C (Figure 6). This secondary reduction could be associated with the prolonged hydration and diminished thermal sensitivity [86].
3.3.3. Setting
- During the 3 first days, the sodium sulphate activator proves to be the most effective activator for BFS hydration. It is followed by the potassium sulphate, while dihydrated calcium sulphate and magnesium sulphate lead to slower hydration. This difference of behavior is due to their lower pH and their cation nature.
- The thermal activation can accelerate the hydration process, particularly for BFS activated with sodium, potassium and dihydrated calcium sulphate as shown by their activation energy coefficients.
- The good correlations between the heat flow evolution and two characteristic times of setting, IST and PT, lead to propose a time of final setting equal to the “Plateau time” determined with the ultrasonic waves for the alkali activation of BFS. This approach is also in good agreement with the evolution of the hydration advancement degree αth and the formation kinetics of C-(N)-A-S-H- and M-S-H-type gels.
- The coupling of the studied parameters (heat flow, hydration advancement degree, kinetics of hydrates formation, setting) indicate an important delay of the hydration process of MS. This behavior is investigated more in depth with thermodynamic modeling (Section 3.6.1).
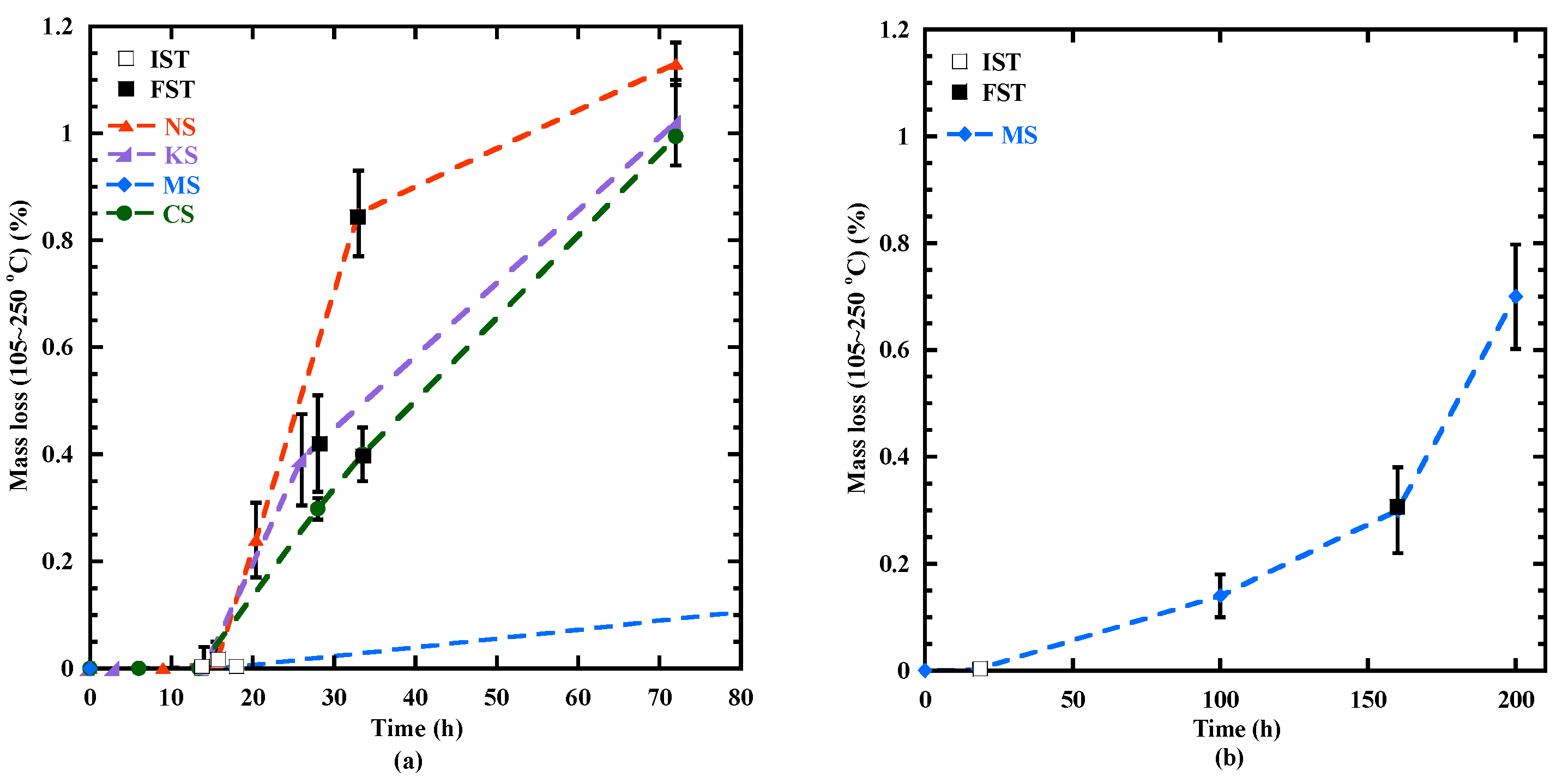
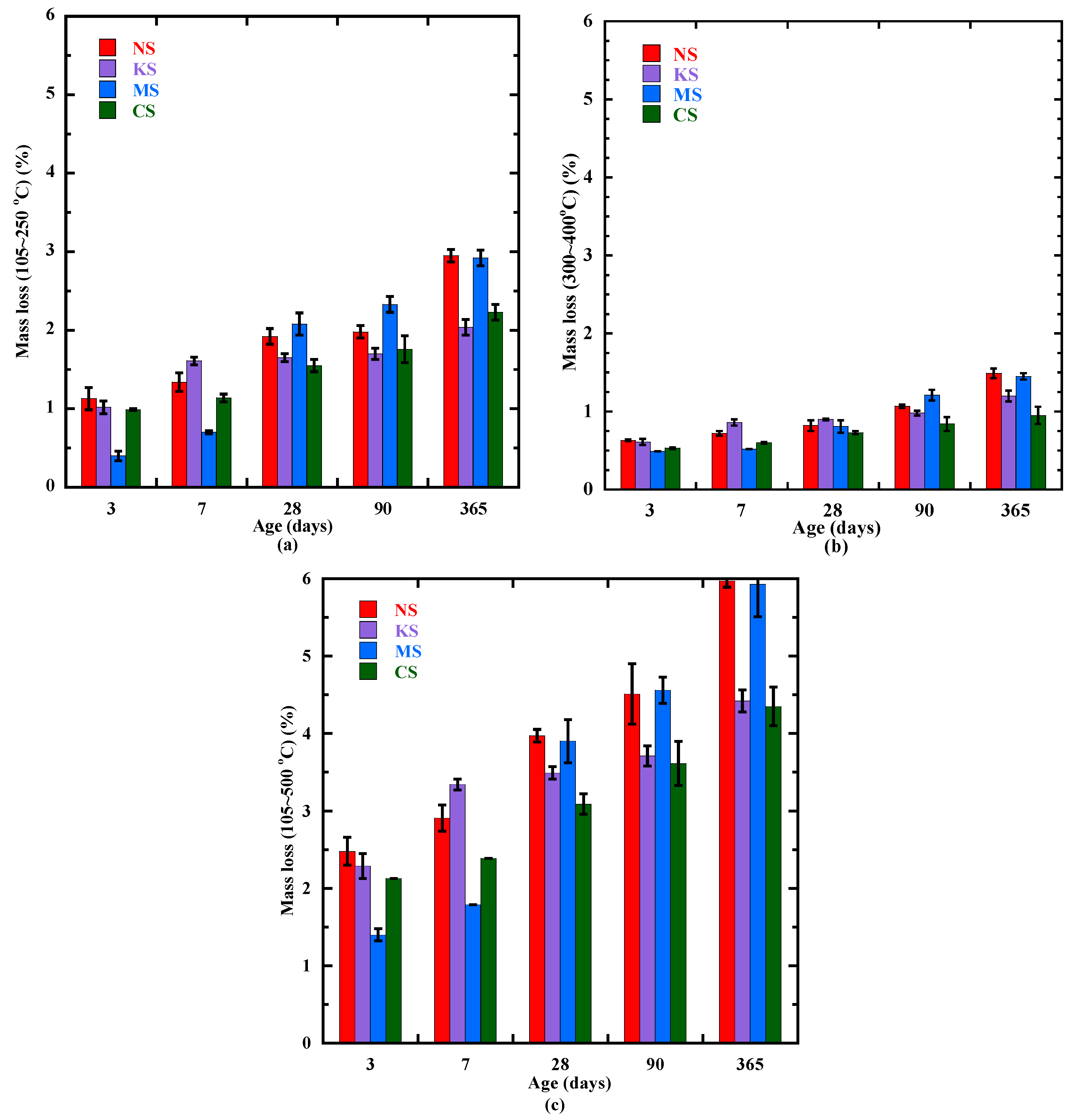
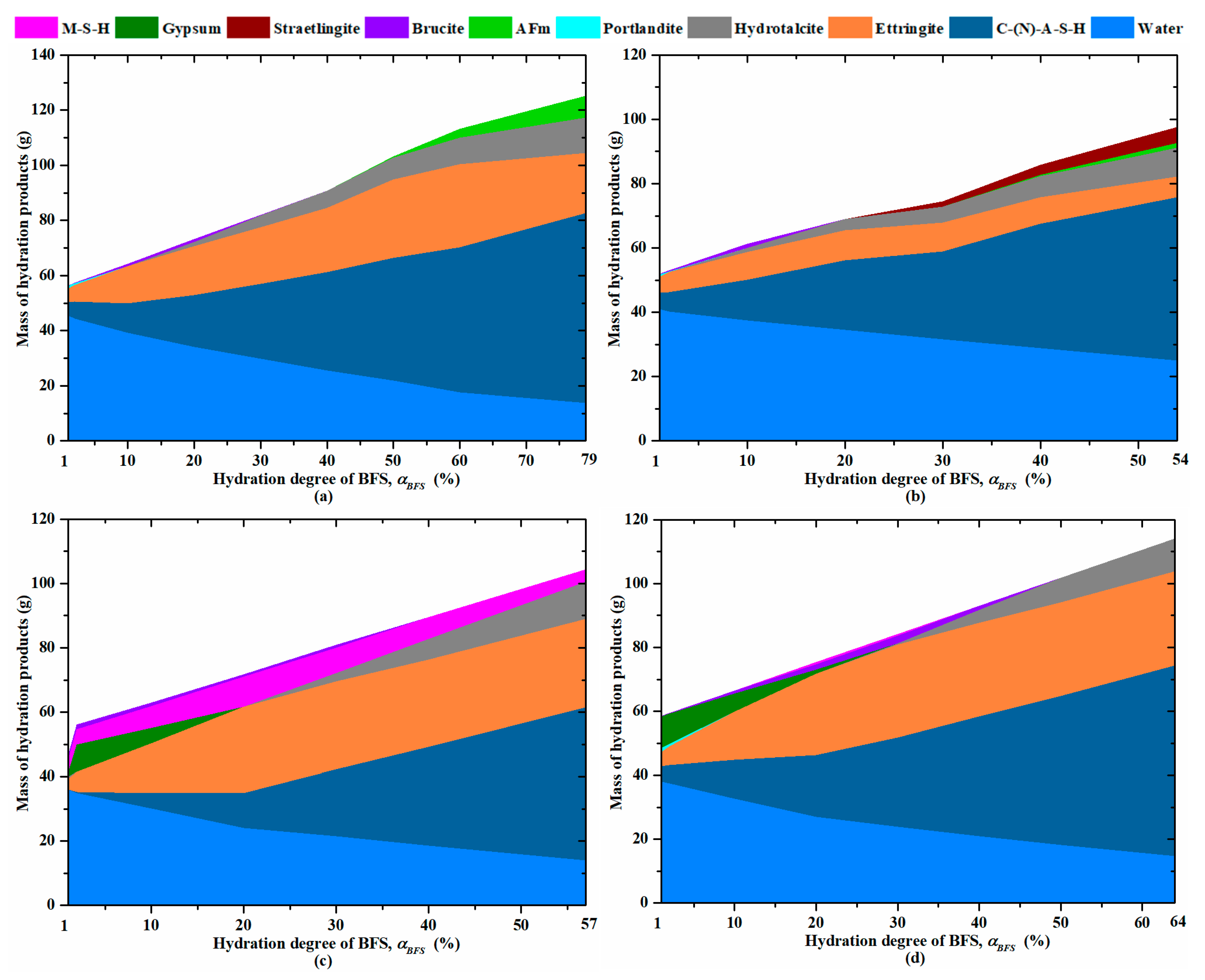
3.4. Formation of the Hydration Products Beyond 3 Days
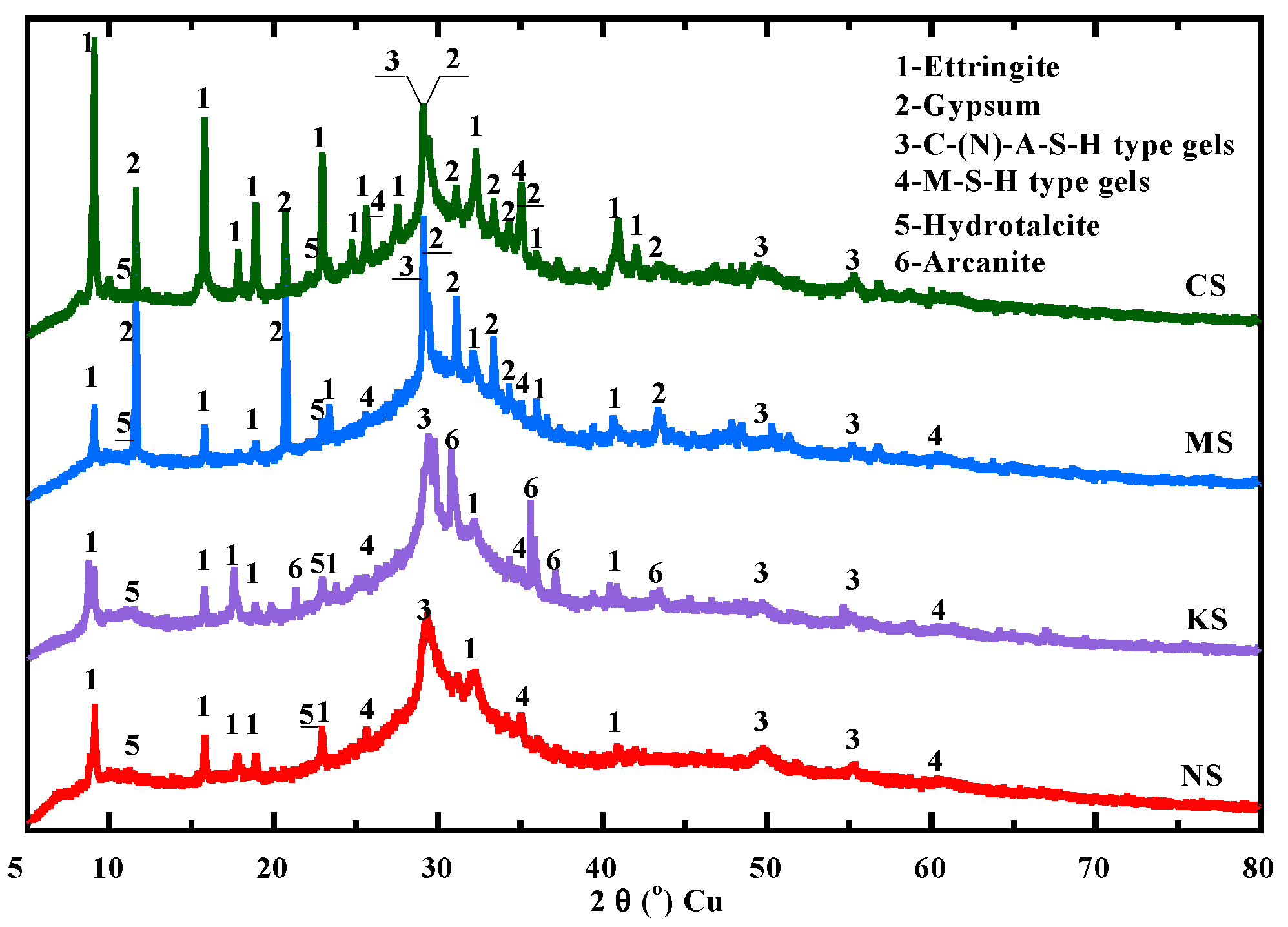
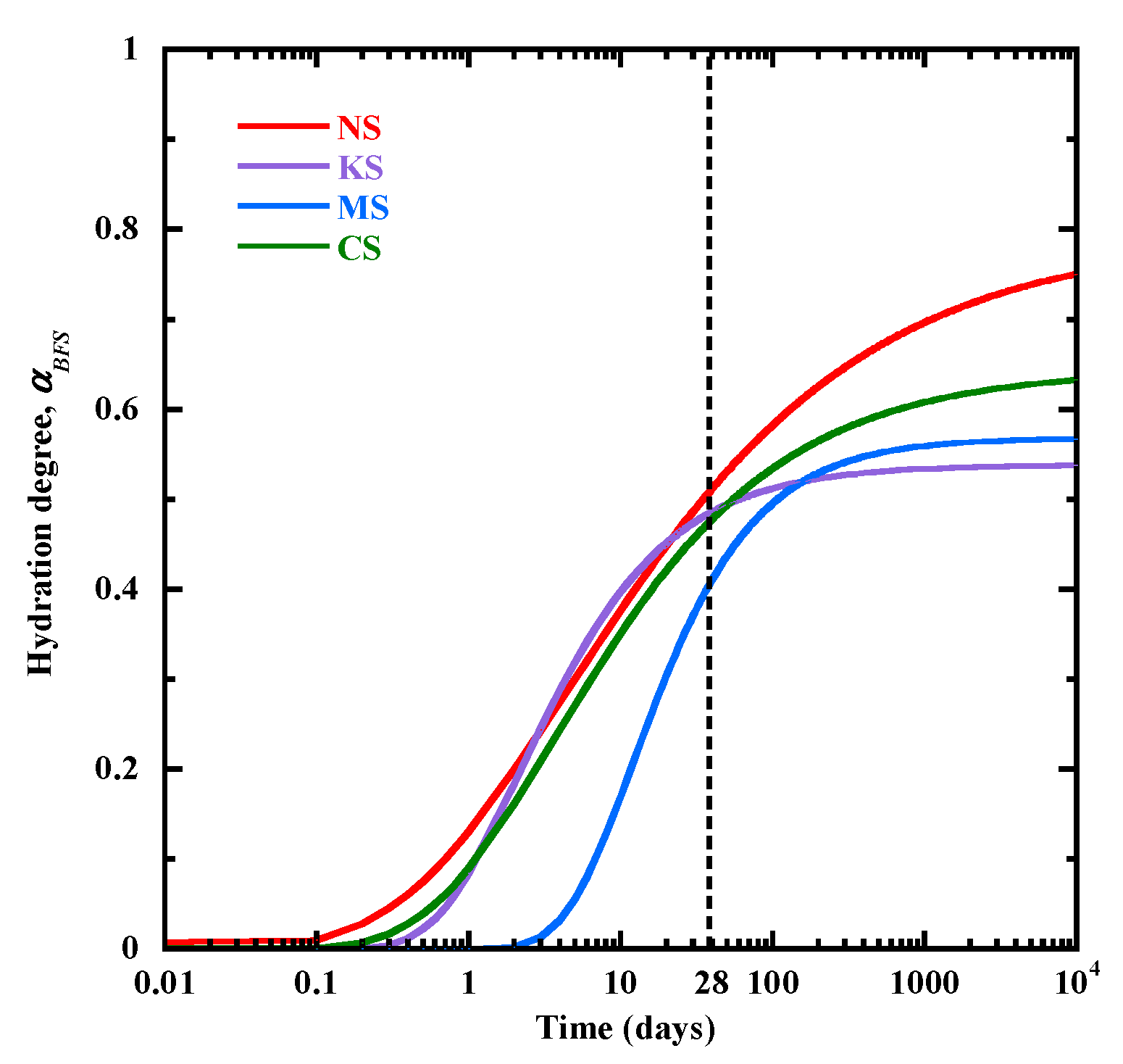
3.5. Hydration of BFS
3.6. Applications for the Hydration Degree of BFS
3.6.1. Hydration Modeling
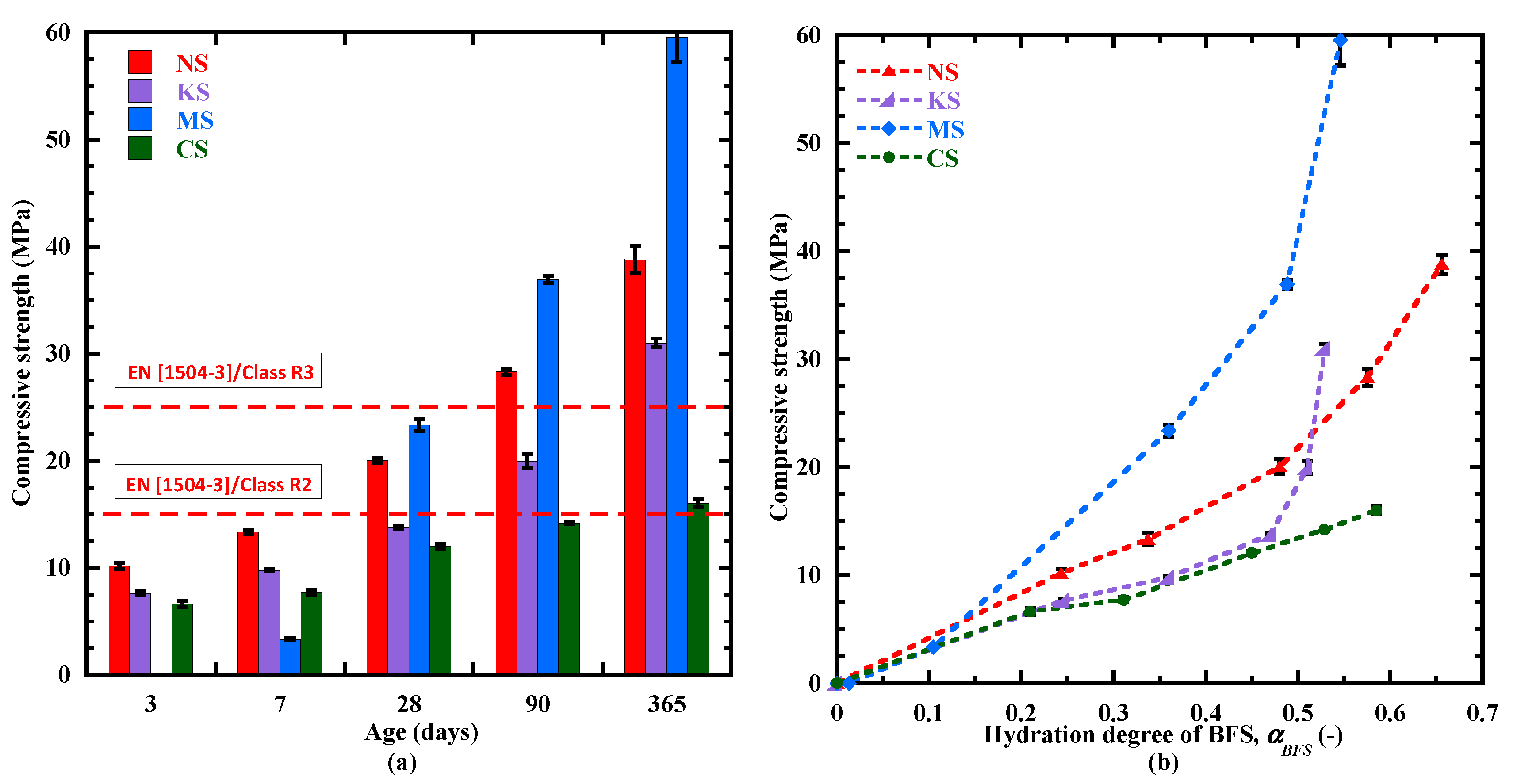
3.6.2. Evolution of the Compressive Strength
4. Conclusions
- Three experimental techniques (calorimetry, TGA, ultrasonic measurement) applied on the sulphate-activated mortars indicate that sodium sulphate is the most effective activator for the BFS hydration at early age (≤3 days). This is evidenced by its fast hydration kinetics and setting due to the fast formation of C-(N)-A-S-H-type gel and ettringite. For the potassium sulphate and dihydrated calcium sulphate activators, their hydration kinetics is slower due to slower C-(N)-A-S-H-type gel formation and a lower initial pH of the pore solution, leading to a lower rate of hydration advancement evolution. For these three activators, the thermal activation is significant, as shown by their higher coefficient of activation energy. A different behavior characterizes the mortar activated with magnesium sulphate: a delay in the hydration process and the largest setting times due to the absence of portlandite and the delay in the formation of C-(N)-A-S-H-type gel.
- Beyond 28 days, the kinetics of hydration products is the most significant for mortars activated with sodium and magnesium sulphate. In the long term, they present a larger content of hydrates, such as C-(N)-A-S-H-type gels, ettringite and hydrotalcite. Moreover, magnesium sulphate contributes to the formation of a large content of M-S-H-type gel due to an increase in the pH of the pore solution and a continuous consumption of Mg2+. All these hydrates provide a denser matrix, leading to a satisfying compressive strength for standard repaired mortars.
- The new approach proposed to predict the hydration degree of blast-furnace slag as a function of time is based on the evolution to C-(N)-A-S-H/M-S-H-type gels measured with TGA and the content of unhydrated particles of blast-furnace slag quantified by the SEM technique. The relevance of this approach is confirmed by the results from thermodynamic modeling, confirming a continuous increase in C-(N)-A-S-H for the mortars activated with alkali sulphates.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Temperature Effect on the Hydration Process
| Characteristics Times | NS | KS | MS | CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | |
| Duration of the dormant period (h) | 20.8 | 5.4 | 2.4 | 9.5 | 7.0 | 2.0 | 80.0 | 31.0 | 22.0 | 9.8 | 2.5 | 1.8 |
| the 2nd peak (h) | 46.3 | 21.2 | 10.6 | 2.8 | 3.1 | 1.6 | 9.2 | 3.3 | 1.6 | 13.2 | 7.6 | 11.5 |
| the 3rd peak (h) | - | - | - | 55.5 | 28.6 | 13.5 | 328 | 199 | 130 | 54.5 | 32.1 | 15.3 |
| The beginning of the acceleration period (b.a.p) (h) | 25.6 | 9.4 | 4.3 | 17.5 | 13.6 | 4.5 | 130 | 63.0 | 42.0 | 23.0 | 11.1 | 2.9 |
| Duration from the end of the dormant period to the 3rd peak (h) | 20.7 | 11.8 | 6.3 | 38 | 15 | 9 | 198 | 136 | 88 | 31.5 | 21 | 8.6 |
| (J/gbinder) | 159 | 161 | 137 | 143 | 110 | 133 | 85 | 83 | 60 | 144 | 122 | 119 |
| (J/gbinder) | 152 | 129 | 76 | 128 | ||||||||
References
- Provis, J.L. Alkali-Activated Materials. Cem. Concr. Res. 2018, 114, 40–48. [Google Scholar] [CrossRef]
- Tu, W.; Zhang, M. Multiscale Microstructure and Micromechanical Properties of Alkali-Activated Concrete: A Critical Review. Cem. Concr. Compos. 2024, 152, 105664. [Google Scholar] [CrossRef]
- Sun, B.; Ye, G.; De Schutter, G. A Review: Reaction Mechanism and Strength of Slag and Fly Ash-Based Alkali-Activated Materials. Constr. Build. Mater. 2022, 326, 126843. [Google Scholar] [CrossRef]
- Bernal, S.A.; Provis, J.L. Durability of Alkali-Activated Materials: Progress and Perspectives. J. Am. Ceram. Soc. 2014, 97, 997–1008. [Google Scholar] [CrossRef]
- Coppola, L.; Coffetti, D.; Crotti, E.; Gazzaniga, G.; Pastore, T. The Durability of One-Part Alkali-Activated Slag-Based Mortars in Different Environments. Sustainability 2020, 12, 3561. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, C.; Zhang, Z.; Ou, Z. Durability of Alkali-Activated Materials in Aggressive Environments: A Review on Recent Studies. Constr. Build. Mater. 2017, 152, 598–613. [Google Scholar] [CrossRef]
- Darquennes, A.; Staquet, S.; Delplancke-Ogletree, M.-P.; Espion, B. Effect of Autogenous Deformation on the Cracking Risk of Slag Cement Concretes. Cem. Concr. Compos. 2011, 33, 368–379. [Google Scholar] [CrossRef]
- Darquennes, A.; Espion, B.; Staquet, S. How to Assess the Hydration of Slag Cement Concretes? Constr. Build. Mater. 2013, 40, 1012–1020. [Google Scholar] [CrossRef]
- Provis, J.L.; Palomo, A.; Shi, C. Advances in Understanding Alkali-Activated Materials. Cem. Concr. Res. 2015, 78, 110–125. [Google Scholar] [CrossRef]
- He, T.; Li, Z.; Zhao, S.; Zhao, X.; Qu, X. Study on the Particle Morphology, Powder Characteristics and Hydration Activity of Blast Furnace Slag Prepared by Different Grinding Methods. Constr. Build. Mater. 2021, 270, 121445. [Google Scholar] [CrossRef]
- Li, Y.; Fang, J.; Cheng, L.; He, X.; Su, Y.; Tan, H. Mechanical Performance, Hydration Characteristics and Microstructures of High Volume Blast Furnace Ferronickel Slag Cement Mortar by Wet Grinding Activation. Constr. Build. Mater. 2022, 320, 126148. [Google Scholar] [CrossRef]
- Wang, Y.; He, X.; Su, Y.; Yang, J.; Strnadel, B.; Wang, X. Efficiency of Wet-Grinding on the Mechano-Chemical Activation of Granulated Blast Furnace Slag (GBFS). Constr. Build. Mater. 2019, 199, 185–193. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, H.; He, X.; Yang, W.; Deng, X.; Su, Y.; Yang, J. Compressive Strength and Hydration Process of Ground Granulated Blast Furnace Slag-Waste Gypsum System Managed by Wet Grinding. Constr. Build. Mater. 2019, 228, 116777. [Google Scholar] [CrossRef]
- Tu, W.; Zhang, M. Behaviour of Alkali-Activated Concrete at Elevated Temperatures: A Critical Review. Cem. Concr. Compos. 2023, 138, 104961. [Google Scholar] [CrossRef]
- Uppalapati, S.; Vandewalle, L.; Cizer, Ö. Autogenous Shrinkage of Slag-Fly Ash Blends Activated with Hybrid Sodium Silicate and Sodium Sulfate at Different Curing Temperatures. Constr. Build. Mater. 2020, 265, 121276. [Google Scholar] [CrossRef]
- Altan, E.; Erdoğan, S.T. Alkali Activation of a Slag at Ambient and Elevated Temperatures. Cem. Concr. Compos. 2012, 34, 131–139. [Google Scholar] [CrossRef]
- Song, Q.; Guo, M.-Z.; Ling, T.-C. A Review of Elevated-Temperature Properties of Alternative Binders: Supplementary Cementitious Materials and Alkali-Activated Materials. Constr. Build. Mater. 2022, 341, 127894. [Google Scholar] [CrossRef]
- Li, P.; Tang, J.; Chen, X.; Bai, Y.; Li, Q. Effect of Temperature and pH on Early Hydration Rate and Apparent Activation Energy of Alkali-Activated Slag. Adv. Mater. Sci. Eng. 2019, 2019, 3531543. [Google Scholar] [CrossRef]
- Uppalapati, S.; Vandewalle, L.; Cizer, Ö. Monitoring the Setting Process of Alkali-Activated Slag-Fly Ash Cements with Ultrasonic P-Wave Velocity. Constr. Build. Mater. 2021, 271, 121592. [Google Scholar] [CrossRef]
- Li, Z.; Delsaute, B.; Lu, T.; Kostiuchenko, A.; Staquet, S.; Ye, G. A Comparative Study on the Mechanical Properties, Autogenous Shrinkage and Cracking Proneness of Alkali-Activated Concrete and Ordinary Portland Cement Concrete. Constr. Build. Mater. 2021, 292, 123418. [Google Scholar] [CrossRef]
- Duran Atiş, C.; Bilim, C.; Çelik, Ö.; Karahan, O. Influence of Activator on the Strength and Drying Shrinkage of Alkali-Activated Slag Mortar. Constr. Build. Mater. 2009, 23, 548–555. [Google Scholar] [CrossRef]
- Aydın, S.; Baradan, B. Effect of Activator Type and Content on Properties of Alkali-Activated Slag Mortars. Compos. Part B Eng. 2014, 57, 166–172. [Google Scholar] [CrossRef]
- Navarro, R.; Zornoza, E.; Sánchez, I.; Alcocel, E.G. Influence of the Type and Concentration of the Activator on the Microstructure of Alkali Activated SiMn Slag Pastes. Constr. Build. Mater. 2022, 342, 128067. [Google Scholar] [CrossRef]
- De Filippis, U.; Prud’homme, E.; Meille, S. Relation between Activator Ratio, Hydration Products and Mechanical Properties of Alkali-Activated Slag. Constr. Build. Mater. 2021, 266, 120940. [Google Scholar] [CrossRef]
- Fernández-Jiménez, A.; Puertas, F.; Sobrados, I.; Sanz, J. Structure of Calcium Silicate Hydrates Formed in Alkaline-Activated Slag: Influence of the Type of Alkaline Activator. J. Am. Ceram. Soc. 2003, 86, 1389–1394. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiu, J.; Zhang, S.; Guo, Z.; Ma, Z.; Sun, X.; Xing, J. Effect of Sodium Sulfate on the Hydration and Mechanical Properties of Lime-Slag Based Eco-Friendly Binders. Constr. Build. Mater. 2020, 250, 118603. [Google Scholar] [CrossRef]
- Rashad, A.M.; Bai, Y.; Basheer, P.A.M.; Milestone, N.B.; Collier, N.C. Hydration and Properties of Sodium Sulfate Activated Slag. Cem. Concr. Compos. 2013, 37, 20–29. [Google Scholar] [CrossRef]
- Ke, X.; Bernal, S.A.; Provis, J.L. Controlling the Reaction Kinetics of Sodium Carbonate-Activated Slag Cements Using Calcined Layered Double Hydroxides. Cem. Concr. Res. 2016, 81, 24–37. [Google Scholar] [CrossRef]
- Rashad, A.M. Influence of Different Additives on the Properties of Sodium Sulfate Activated Slag. Constr. Build. Mater. 2015, 79, 379–389. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Provis, J.L.; Cizer, Ö.; Ye, G. Autogenous Shrinkage of Alkali-Activated Slag: A Critical Review. Cem. Concr. Res. 2023, 172, 107244. [Google Scholar] [CrossRef]
- Brough, A.R.; Atkinson, A. Sodium Silicate-Based, Alkali-Activated Slag Mortars Part I. Strength, Hydration and Microstructure. Cem. Concr. Res. 2002, 32, 865–879. [Google Scholar] [CrossRef]
- Luukkonen, T.; Sreenivasan, H.; Abdollahnejad, Z.; Yliniemi, J.; Kantola, A.; Telkki, V.-V.; Kinnunen, P.; Illikainen, M. Influence of Sodium Silicate Powder Silica Modulus for Mechanical and Chemical Properties of Dry-Mix Alkali-Activated Slag Mortar. Constr. Build. Mater. 2020, 233, 117354. [Google Scholar] [CrossRef]
- Ravikumar, D.; Neithalath, N. Reaction Kinetics in Sodium Silicate Powder and Liquid Activated Slag Binders Evaluated Using Isothermal Calorimetry. Thermochim. Acta 2012, 546, 32–43. [Google Scholar] [CrossRef]
- Cheah, C.B.; Tan, L.E.; Ramli, M. Recent Advances in Slag-Based Binder and Chemical Activators Derived from Industrial by-Products—A Review. Constr. Build. Mater. 2021, 272, 121657. [Google Scholar] [CrossRef]
- Angulo-Ramírez, D.E.; Mejía De Gutiérrez, R.; Puertas, F. Alkali-Activated Portland Blast-Furnace Slag Cement: Mechanical Properties and Hydration. Constr. Build. Mater. 2017, 140, 119–128. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, Z.; Yang, J.; Yang, H.; Ji, Y.; Hu, K. Mechanical Performance and Reaction Mechanism of Copper Slag Activated with Sodium Silicate or Sodium Hydroxide. Constr. Build. Mater. 2021, 266, 120900. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, L.; Xu, J.; Zu, Y. Effect of Na2SiO3 Content on Passivation and Corrosion Behaviour of Steel in a Simulated Pore Solution of Na2SiO3-Activated Slag. Constr. Build. Mater. 2017, 146, 156–164. [Google Scholar] [CrossRef]
- Adesina, A. Performance and Sustainability Overview of Sodium Carbonate Activated Slag Materials Cured at Ambient Temperature. Resour. Environ. Sustain. 2021, 3, 100016. [Google Scholar] [CrossRef]
- Mobasher, N.; Bernal, S.A.; Provis, J.L. Structural Evolution of an Alkali Sulfate Activated Slag Cement. J. Nucl. Mater. 2016, 468, 97–104. [Google Scholar] [CrossRef]
- Deng, X.; Li, M.; Wang, Y.; Wang, J.; Zhang, J.; Yang, Z.; He, X.; Yang, J.; Tan, H. Impact of Ettringite Seeding on Hydration, Strength and Shrinkage of Na2SO4 Activated Slag. Compos. Part B Eng. 2024, 276, 111374. [Google Scholar] [CrossRef]
- Fu, J.; Bligh, M.W.; Shikhov, I.; Jones, A.M.; Holt, C.; Keyte, L.M.; Moghaddam, F.; Arns, C.H.; Foster, S.J.; Waite, T.D. A Microstructural Investigation of a Na2SO4 Activated Cement-Slag Blend. Cem. Concr. Res. 2021, 150, 106609. [Google Scholar] [CrossRef]
- Adesina, A.; Rodrigue Kaze, C. Physico-Mechanical and Microstructural Properties of Sodium Sulfate Activated Materials: A Review. Constr. Build. Mater. 2021, 295, 123668. [Google Scholar] [CrossRef]
- Fu, J.; Jones, A.M.; Bligh, M.W.; Holt, C.; Keyte, L.M.; Moghaddam, F.; Foster, S.J.; Waite, T.D. Mechanisms of Enhancement in Early Hydration by Sodium Sulfate in a Slag-Cement Blend—Insights from Pore Solution Chemistry. Cem. Concr. Res. 2020, 135, 106110. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Liu, L.; Kuang, L.; Zhang, S.; Chen, Z.; Li, J.; Shi, C. Effects of Different Activators on Autogenous Shrinkage of Alkali-Activated Slag Cement. Constr. Build. Mater. 2024, 446, 138018. [Google Scholar] [CrossRef]
- Zhai, Q.; Kurumisawa, K. Effects of Cation in Sulfate Chloride and Nitrite on Ca(OH)2 Activated Ground Granulated Blast-Furnace Slag. Cem. Concr. Compos. 2022, 133, 104648. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Q.; Lu, J. The Effects of Cations and Concentration on Reaction Mechanism of Alkali-Activated Blast Furnace Ferronickel Slag. Compos. Part B Eng. 2022, 236, 109825. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, L.; He, X. Hydration Characteristics and Mechanic Properties of Basic Magnesium Sulfate Cement Containing Steel Slag. ACT 2022, 20, 277–286. [Google Scholar] [CrossRef]
- Pane, I.; Hansen, W. Investigation of Blended Cement Hydration by Isothermal Calorimetry and Thermal Analysis. Cem. Concr. Res. 2005, 35, 1155–1164. [Google Scholar] [CrossRef]
- Tailhan, J.L.; D’aloia, L.; Autuori, P. Simulations Numériques Du Comportement Au Jeune Âge Des Structures En Béton: Modélisation et Retour d’expérience. Bull. Lab. Ponts Chaussées 2011, 278, 65–77. [Google Scholar]
- Ben Haha, M.; Le Saout, G.; Winnefeld, F.; Lothenbach, B. Influence of Activator Type on Hydration Kinetics, Hydrate Assemblage and Microstructural Development of Alkali Activated Blast-Furnace Slags. Cem. Concr. Res. 2011, 41, 301–310. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, J.; Yan, N. Microstructural Evolution and Characterization of Ground Granulated Blast Furnace Slag in Variant pH. Constr. Build. Mater. 2020, 251, 118978. [Google Scholar] [CrossRef]
- Ye, H.; Chen, Z.; Huang, L. Mechanism of Sulfate Attack on Alkali-Activated Slag: The Role of Activator Composition. Cem. Concr. Res. 2019, 125, 105868. [Google Scholar] [CrossRef]
- Fu, Q.; Bu, M.; Zhang, Z.; Xu, W.; Yuan, Q.; Niu, D. Hydration Characteristics and Microstructure of Alkali-Activated Slag Concrete: A Review. Engineering 2023, 20, 162–179. [Google Scholar] [CrossRef]
- Wei, Y.; Gao, X.; Liang, S. Nanoindentation-Based Study of the Micro-Mechanical Properties, Structure, and Hydration Degree of Slag-Blended Cementitious Materials. J. Mater. Sci. 2016, 51, 3349–3361. [Google Scholar] [CrossRef]
- Robeyst, N.; Gruyaert, E.; Grosse, C.U.; De Belie, N. Monitoring the Setting of Concrete Containing Blast-Furnace Slag by Measuring the Ultrasonic p-Wave Velocity. Cem. Concr. Res. 2008, 38, 1169–1176. [Google Scholar] [CrossRef]
- Heng, S. Étude de la Sensibilité à la Fissuration de Géopolymères; INSA: Rennes, France, 2022. [Google Scholar]
- Naqi, A.; Delsaute, B.; Königsberger, M.; Staquet, S. Effect of Solution-to-Binder Ratio and Alkalinity on Setting and Early-Age Properties of Alkali-Activated Slag-Fly Ash Binders. Materials 2022, 16, 373. [Google Scholar] [CrossRef]
- Durdziński, P.T.; Dunant, C.F.; Haha, M.B.; Scrivener, K.L. A New Quantification Method Based on SEM-EDS to Assess Fly Ash Composition and Study the Reaction of Its Individual Components in Hydrating Cement Paste. Cem. Concr. Res. 2015, 73, 111–122. [Google Scholar] [CrossRef]
- Kocaba, V.; Gallucci, E.; Scrivener, K.L. Methods for Determination of Degree of Reaction of Slag in Blended Cement Pastes. Cem. Concr. Res. 2012, 42, 511–525. [Google Scholar] [CrossRef]
- Kulik, D.A.; Wagner, T.; Dmytrieva, S.V.; Kosakowski, G.; Hingerl, F.F.; Chudnenko, K.V.; Berner, U.R. GEM-Selektor Geochemical Modeling Package: Revised Algorithm and GEMS3K Numerical Kernel for Coupled Simulation Codes. Comput. Geosci. 2013, 17, 1–24. [Google Scholar] [CrossRef]
- Wagner, T.; Kulik, D.A.; Hingerl, F.F.; Dmytrieva, S.V. GEM-Selektor geochemical modelling package: TSolMod library and date interface for multicomponent phase models. Can. Mineral. 2012, 50, 1173–1195. [Google Scholar] [CrossRef]
- Lothenbach, B.; Zajac, M. Application of Thermodynamic Modelling to Hydrated Cements. Cem. Concr. Res. 2019, 123, 105779. [Google Scholar] [CrossRef]
- Liu, Z.; Van Den Heede, P.; Zhang, C.; Shi, X.; Wang, L.; Li, J.; Yao, Y.; Lothenbach, B.; De Belie, N. Carbonation of Blast Furnace Slag Concrete at Different CO2 Concentrations: Carbonation Rate, Phase Assemblage, Microstructure and Thermodynamic Modelling. Cem. Concr. Res. 2023, 169, 107161. [Google Scholar] [CrossRef]
- Thoenen, T.; Kulik, D. Nagra/PSI Chemical Thermodynamic Data Base 01/01 for the GEM-Selektor (V.2-PSI) Geochemical Modeling Code: Release 28-02-03; Paul Scherrer Institut: Villigen, Switzerland, 2003. [Google Scholar]
- Myers, R.J.; Bernal, S.A.; San Nicolas, R.; Provis, J.L. Generalized Structural Description of Calcium–Sodium Aluminosilicate Hydrate Gels: The Cross-Linked Substituted Tobermorite Model. Langmuir 2013, 29, 5294–5306. [Google Scholar] [CrossRef]
- Okoronkwo, M.U.; Glasser, F.P. Stability of Strätlingite in the CASH System. Mater. Struct. 2016, 49, 4305–4318. [Google Scholar] [CrossRef]
- Helgeson, H.C.; Kirkham, D.H.; Flowers, G.C. Theoretical Prediction of the Thermodynamic Behavior of Aqueous Electrolytes by High Pressures and Temperatures; IV, Calculation of Activity Coefficients, Osmotic Coefficients, and Apparent Molal and Standard and Relative Partial Molal Properties to 600 Degrees C and 5kb. Am. J. Sci. 1981, 281, 1249–1516. [Google Scholar]
- Nied, D.; Enemark-Rasmussen, K.; L’Hopital, E.; Skibsted, J.; Lothenbach, B. Properties of Magnesium Silicate Hydrates (M-S-H). Cem. Concr. Res. 2016, 79, 323–332. [Google Scholar] [CrossRef]
- Parrot, L.J.; Killoh, D.C. Prediction of Cement Hydration. Br. Cermamic Proc. 1984, 35, 41–53. [Google Scholar]
- NF EN 196-1; Méthodes D’essais des Ciments-Partie 1: Détermination des Résistances—196–1. Laboratoire CBTP: Noyal-sur-Vilaine, France, 2016.
- NF EN 1015-11; Méthodes D’essai des Mortiers pour Maçonnerie-Partie 11: Détermination de la Résistance en Flexion et en Compression Du Mortier Durci—1015–11. Laboratoire CBTP: Noyal-sur-Vilaine, France, 2019.
- Dai, X.; Aydin, S.; Yardimci, M.Y.; Lesage, K.; De Schutter, G. Early Age Reaction, Rheological Properties and Pore Solution Chemistry of NaOH-Activated Slag Mixtures. Cem. Concr. Compos. 2022, 133, 104715. [Google Scholar] [CrossRef]
- Almakhadmeh, M.; Soliman, A.M. Effects of Mixing Water Temperatures on Properties of One-Part Alkali-Activated Slag Paste. Constr. Build. Mater. 2021, 266, 121030. [Google Scholar] [CrossRef]
- Boscaro, F.; Palacios, M.; Flatt, R.J. Formulation of Low Clinker Blended Cements and Concrete with Enhanced Fresh and Hardened Properties. Cem. Concr. Res. 2021, 150, 106605. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Li, S.; Gao, Y.; Liu, C.; Qi, Y. Effect of Different Gypsums on the Workability and Mechanical Properties of Red Mud-Slag Based Grouting Materials. J. Clean. Prod. 2020, 245, 118759. [Google Scholar] [CrossRef]
- Kang, C.; Kim, T. Investigation of the Effects of Magnesium-Sulfate as Slag Activator. Materials 2020, 13, 305. [Google Scholar] [CrossRef] [PubMed]
- Puertas, F.; Fernández-Jiménez, A.; Blanco-Varela, M.T. Pore Solution in Alkali-Activated Slag Cement Pastes. Relation to the Composition and Structure of Calcium Silicate Hydrate. Cem. Concr. Res. 2004, 34, 139–148. [Google Scholar] [CrossRef]
- Weng, L.; Sagoe-Crentsil, K. Dissolution Processes, Hydrolysis and Condensation Reactions during Geopolymer Synthesis: Part I—Low Si/Al Ratio Systems. J. Mater. Sci. 2007, 42, 2997–3006. [Google Scholar] [CrossRef]
- Snellings, R.; Chwast, J.; Cizer, Ö.; De Belie, N.; Dhandapani, Y.; Durdzinski, P.; Elsen, J.; Haufe, J.; Hooton, D.; Patapy, C.; et al. RILEM TC-238 SCM Recommendation on Hydration Stoppage by Solvent Exchange for the Study of Hydrate Assemblages. Mater. Struct. 2018, 51, 172. [Google Scholar] [CrossRef]
- Andrade Neto, J.D.S.; De La Torre, A.G.; Kirchheim, A.P. Effects of Sulfates on the Hydration of Portland Cement—A Review. Constr. Build. Mater. 2021, 279, 122428. [Google Scholar] [CrossRef]
- Skibsted, J.; Andersen, M.D. The Effect of Alkali Ions on the Incorporation of Aluminum in the Calcium Silicate Hydrate (C–S–H) Phase Resulting from Portland Cement Hydration Studied by 29Si MAS NMR. J. Am. Ceram. Soc. 2013, 96, 651–656. [Google Scholar] [CrossRef]
- Burciaga-Díaz, O.; Escalante-García, J.I. Structure, Mechanisms of Reaction, and Strength of an Alkali-Activated Blast-Furnace Slag. J. Am. Ceram. Soc. 2013, 96, 3939–3948. [Google Scholar] [CrossRef]
- Chen, W.; Brouwers, H.J.H. Alkali Binding in Hydrated Portland Cement Paste. Cem. Concr. Res. 2010, 40, 716–722. [Google Scholar] [CrossRef]
- Zhang, Y.; Wan, Z.; De Lima Junior, L.M.; Çopuroğlu, O. Early Age Hydration of Model Slag Cement: Interaction among C3S, Gypsum and Slag with Different Al2O3 Contents. Cem. Concr. Res. 2022, 161, 106954. [Google Scholar] [CrossRef]
- Torréns-Martín, D.; Fernández-Carrasco, L. Effect of Sulfate Content on Cement Mixtures. Constr. Build. Mater. 2013, 48, 144–150. [Google Scholar] [CrossRef]
- Buyle-bodin, F.; Cussigh, F. Résistance du Béton Dans L’ouvrage: La Maturométrie: Guide Technique; Techniques et Methodes des Laboratoire des Ponts et Chaussess Guide Techinque, LCPC: Paris, France, 2003; ISBN 978-2-7208-3109-6. [Google Scholar]
- Jonathan, L.P.; Kyle, A.R.; Kevin, J.F.; Maria, C.G.J.; Anton, K.S. Methods for Calculating Activation Energy for Portland Cement. ACI Mater. J. 2007, 104, 303–311. [Google Scholar] [CrossRef]
- Darquennes, A.; Staquet, S.; Robeyst, R.; De Belie, N.; Espion, B. Autogenous Shrinkage Development and Setting Monitoring of Slag Cement Concrete. In Proceedings of the 8th International Conference on Creep, Shrinkage and Durability of Concrete and Concrete Structures (ConCreep’08), Ise-Shima, Japan, 30 September–2 October 2008; pp. 315–319. [Google Scholar]
- Ouvrier-Buffet, F.; Eiras, J.N.; Garnier, V.; Payan, C.; Ranaivomanana, N.; Durville, B.; Marquie, C. Linear and Nonlinear Resonant Ultrasonic Techniques Applied to Assess Delayed Ettringite Formation on Concrete Samples. Constr. Build. Mater. 2021, 275, 121545. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, L.; Li, Z. Hydration Monitoring of Cement-Based Materials with Resistivity and Ultrasonic Methods. Mater. Struct. 2009, 42, 15–24. [Google Scholar] [CrossRef]
- Darquennes, A.; Staquet, S.; Espion, B.; Germain, O.; PIERRE, C. Comparison between Different Techniques for Monitoring Setting and Hardening of Concrete. In Proceedings of the NDTCE’09, Nantes, France, 30 June–3 July 2009; pp. 661–667. [Google Scholar]
- Richardson, I.G.; Brough, A.R.; Groves, G.W.; Dobson, C.M. The Characterization of Hardened Alkali-Activated Blast-Furnace Slag Pastes and the Nature of the Calcium Silicate Hydrate (C-S-H) Phase. Cem. Concr. Res. 1994, 24, 813–829. [Google Scholar] [CrossRef]
- Roosz, C.; Grangeon, S.; Blanc, P.; Montouillout, V.; Lothenbach, B.; Henocq, P.; Giffaut, E.; Vieillard, P.; Gaboreau, S. Crystal Structure of Magnesium Silicate Hydrates (M-S-H): The Relation with 2:1 Mg–Si Phyllosilicates. Cem. Concr. Res. 2015, 73, 228–237. [Google Scholar] [CrossRef]
- Dewitte, C.; Bertron, A.; Neji, M.; Lacarrière, L.; Dauzères, A. Chemical and Microstructural Properties of Designed Cohesive M-S-H Pastes. Materials 2022, 15, 547. [Google Scholar] [CrossRef] [PubMed]
- Frank, M. Powder Diffraction File; International Centre for Diffraction Data, 12 Campus Boulevard: Newtown Square, PA, USA, 2013. [Google Scholar]
- Goetz-Neunhoeffer, F.; Neubauer, J. Refined Ettringite (Ca6Al2(SO4)3(OH)12∙26H2O) Structure for Quantitative X-Ray Diffraction Analysis. Powder Diffr. 2006, 21, 4–11. [Google Scholar] [CrossRef]
- Black, L.; Breen, C.; Yarwood, J.; Deng, C.-S.; Phipps, J.; Maitland, G. Hydration of Tricalcium Aluminate (C3A) in the Presence and Absence of Gypsum—Studied by Raman Spectroscopy and X-Ray Diffraction. J. Mater. Chem. 2006, 16, 1263. [Google Scholar] [CrossRef]
- Gamage McEvoy, J.; Thibault, Y.; Beauchemin, S. Iron and Sulphur Management Options during Ni Recovery from (Bio)Leaching of Pyrrhotite Tailings Part 2: Strategies for Sulphur Fixation during Biomass-Induced Magnetization of Goethite and Jarosite. Miner. Eng. 2020, 150, 106266. [Google Scholar] [CrossRef]
- Wang, S.-D.; Scrivener, K.L. Hydration Products of Alkali Activated Slag Cement. Cem. Concr. Res. 1995, 25, 561–571. [Google Scholar] [CrossRef]
- Lootens, D.; Bentz, D.P. On the Relation of Setting and Early-Age Strength Development to Porosity and Hydration in Cement-Based Materials. Cem. Concr. Compos. 2016, 68, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Alharbi, N.; Varela, B.; Hailstone, R. Alkali-Activated Slag Characterization by Scanning Electron Microscopy, X-Ray Microanalysis and Nuclear Magnetic Resonance Spectroscopy. Mater. Charact. 2020, 168, 110504. [Google Scholar] [CrossRef]
- Lothenbach, B.; Le Saout, G.; Ben Haha, M.; Figi, R.; Wieland, E. Hydration of a Low-Alkali CEM III/B–SiO2 Cement (LAC). Cem. Concr. Res. 2012, 42, 410–423. [Google Scholar] [CrossRef]
- Park, J.; Kim, S.; Moon, J. Substantially Enhanced Reaction of Steel Slag Binder Stimulated by the Addition of Sodium Sulfate and Thermal Treatment. Cem. Concr. Compos. 2024, 152, 105679. [Google Scholar] [CrossRef]
- Bortnovsky, O.; Dědeček, J.; Tvarůžková, Z.; Sobalík, Z.; Šubrt, J. Metal Ions as Probes for Characterization of Geopolymer Materials. J. Am. Ceram. Soc. 2008, 91, 3052–3057. [Google Scholar] [CrossRef]
- Myers, R.J.; Bernal, S.A.; Provis, J.L. Phase Diagrams for Alkali-Activated Slag Binders. Cem. Concr. Res. 2017, 95, 30–38. [Google Scholar] [CrossRef]
- Cavani, F.; Trifirb, F.; Vaccari, A. Hydrotalcite-type anionic clays: Preparation, properties and applications. Catal. Today 1991, 11, 173–301. [Google Scholar] [CrossRef]
- Bernard, E.; Lothenbach, B.; Rentsch, D.; German, A.; Winnefeld, F. Effect of Carbonates on the Formation of Magnesium Silicate Hydrates. Mater. Struct. 2022, 55, 183. [Google Scholar] [CrossRef]
- Frost, R.L.; Spratt, H.J.; Palmer, S.J. Infrared and Near-Infrared Spectroscopic Study of Synthetic Hydrotalcites with Variable Divalent/Trivalent Cationic Ratios. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2009, 72, 984–988. [Google Scholar] [CrossRef] [PubMed]
- NF EN 1504-3; Produits et Systèmes pour La Protection et la Réparation des Structures en Béton—Définitions, Exigences, Maîtrise de la Qualité et Évaluation de la Conformité—Partie 3: Réparation Structurale et Réparation Non Structurale. Laboratoire CBTP: Noyal-sur-Vilaine, France, 2010.
- Peng, Y.; Unluer, C. Magnesium-Silicate-Hydrate Cement Pastes: Rheological Behavior and Strength Development. Case Stud. Constr. Mater. 2024, 20, e03400. [Google Scholar] [CrossRef]
- Mabroum, S.; Garcia-Lodeiro, I.; Blanco-Varela, M.T.; Taha, Y.; Chhaiba, S.; Indris, S.; Benzaazoua, M.; Mansori, M.; Hakkou, R. Formation of C S H and M S H Gels in Alkali-Activated Materials Based on Marl by-Products from Phosphate Mines. Constr. Build. Mater. 2023, 365, 130029. [Google Scholar] [CrossRef]





| Chemical Activators | Na2SO4 | K2SO4 | MgSO4 | CaSO4.2H2O |
|---|---|---|---|---|
| Density (g/cm3) | 2.70 | 2.66 | 2.65 | 2.32 |
| Molar mass (g/mol) | 142 | 174 | 120 | 172 |
| Solubility (g/100 mL) | 19.5 | 11.0 | 35.0 | 2.0 |
| pH in distilled water | 10.2 | 10.4 | 9.5 | 9.2 |
| Purity (%) | 99 | - | 98 | 98 |
| Chemical Composition | SiO2 | CaO | Fe2O3 | Al2O3 | MgO | T2O | SO3 | Na2O | Cl− | K2O | Fineness (cm2/g) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BFS | 35.1 | 42.1 | 0.4 | 11.1 | 7.0 | 0.8 | 0.1 | 0.2 | 0.03 | 0.4 | 4200 |
| PC | 20.8 | 65.9 | 2.2 | 5.4 | 1.1 | - | 3.4 | 0.2 | - | 0.3 | 4682 |
| Compositions | NS | KS | MS | CS |
|---|---|---|---|---|
| PC (kg/m3) | 29 | 29 | 29 | 26 |
| Activator (kg/m3) | 46 | 56 | 39 | 60 |
| BFS (kg/m3) | 502 | 492 | 509 | 433 |
| Water (kg/m3) | 243 | 242 | 242 | 247 |
| Sand (kg/m3) | 1444 | 1444 | 1444 | 1444 |
| Binder (kg/m3) | 577 | 577 | 577 | 519 |
| PC/B | 0.05 | 0.05 | 0.05 | 0.05 |
| A/B | 0.08 | 0.10 | 0.07 | 0.11 |
| BFS/B | 0.87 | 0.85 | 0.88 | 0.84 |
| Water/B | 0.42 | 0.42 | 0.42 | 0.50 |
| Paste volume (L/m3) | 443 | 443 | 443 | 443 |
| SO42− concentration (mol/L) | 1.4 | 1.4 | 1.4 | 1.4 |
| Activator state a | TD | PD | TD | SP |
| Average slump (mm) | 26.0 | 13.0 | 6.3 | 6.1 |
| Average air content (%) | 4.9 | 4.5 | 4.5 | 4.4 |
| Characteristic Times of the Hydration Kinetics | NS | KS | MS | CS |
|---|---|---|---|---|
| Duration of the dormant period (h) | 5.4 | 7.0 | 31.0 | 2.5 |
| The peak before the dormant period named “the 2nd peak”(h) | - | 3.1 | 3.3 | 7.6 |
| The peak during the acceleration period named “the 3rd peak” (h) | 21.2 | 28.6 | 199 | 32.1 |
| The beginning of the acceleration period (b.a.p) (h) | 9.4 | 13.6 | 63.0 | 11.1 |
| Duration from the end of the dormant period to the 3rd peak (h) | 11.8 | 15.0 | 136 | 21 |
| (J/gbinder) | 161 | 110 | 84 | 122 |
| Mass Loss (%) | NS | KS | MS | CS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beginning of the Acceleration Period (9 h) | 3rd Peak (21 h) | 72 h | 2nd Peak (3 h) | Beginning of the Acceleration Period (14 h) | 3rd Peak (29 h) | 72 h | 2nd Peak (3 h) | Beginning of the Acceleration Period (63 h) | 72 h | 3rd Peak (199 h) | 2nd Peak (7 h) | Beginning of the Acceleration Period (11 h) | 3rd Peak (32 h) | 72 h | |
| C-(N)-A-S-H and M-S-H-type gel (105–250 °C) | 0 | 0.2 | 1.13 | 0 | 0 | 0.4 | 1.02 | 0 | 0.3 | 0.4 | 0.5 | 0 | 0 | 0.3 | 0.99 |
| Hydrotalcite and brucite (300–450 °C) | 0.1 | 0.3 | 0.60 | 0 | 0.06 | 0.3 | 0.59 | 0.01 | 0.4 | 0.48 | 0.5 | 0.03 | 0.05 | 0.3 | 0.53 |
| Portlandite (400–500 °C) | 0.1 | 0.2 | 0.36 | 0.02 | 0.05 | 0.2 | 0.32 | 0.01 | 0.3 | 0.33 | 0.35 | 0.03 | 0.06 | 0.2 | 0.33 |
| Chemical-bound water (105–500 °C) | 0.3 | 0.9 | 2.43 | 0.02 | 0.1 | 1.0 | 2.29 | 0.02 | 1.0 | 1.3 | 1.4 | 0.05 | 0.13 | 0.8 | 2.13 |
| Mixtures | Evolution Rate of Mass Loss from 105 to 250 °C (‰/h) | (-) Acceleration Period | pH After Mixing | pH at 3 Days | |
|---|---|---|---|---|---|
| Acceleration Period | Deceleration Period | ||||
| NS | 4.7 | 0.7 | 3.8 | 12.77 | 12.07 |
| KS | 3.0 | 1.5 | 3.3 | 12.65 | 12.26 |
| MS | 0.02 | - | 0.6 | 11.91 | 11.50 |
| CS | 2.0 | 1.6 | 2.0 | 11.93 | 12.25 |
| Parameters | NS | KS | MS | CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | 10 °C | 20 °C | 30 °C | |
| (J/gbinder) | 159 | 161 | 137 | 143 | 110 | 133 | 85 | 83 | 60 | 144 | 122 | 119 |
| (J/gbinder) | 152 | 129 | 76 | 128 | ||||||||
| Qinf (J/gbinder) | 24 | 21 | 22 | 21 | ||||||||
| Qsup (J/gbinder) | 91 | 77 | 42 | 76 | ||||||||
| Rc,28 (MPa) | 20 | 14 | 23 | 12 | ||||||||
| Ea,SM (kJ/mol) | 38 | 40 | 33 | 39 | ||||||||
| Ea,VM (kJ/mol) | 46 | 45 | 37 | 52 | ||||||||
| Maximal value of Ea,VM (kJ/mol) | 111 | 76 | 83 | 89 | ||||||||
| Time corresponding to the beginning of the 1st Stage (h) | 12 | 7 | 8 | 13 | ||||||||
| Time (h) and αth (-) corresponding to the maximal Ea | 15–0.26 | 11–0.27 | 12–0.38 | 17–0.24 | ||||||||
| Mixtures | NS | KS | MS | CS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time (h) | Velocity (m/s) | (%) | Time (h) | Velocity (m/s) | (%) | Time (h) | Velocity (m/s) | (%) | Time (h) | Velocity (m/s) | (%) | |
| Initial Setting Time (IST) | 15.5 | 2167 | 0.00 ± 0.0 | 14.0 | 2480 | 0.00 ± 0.0 | 17.0 | 1940 | 0.00 ± 0.0 | 13.4 | 1691 | 0.00 ± 0.0 |
| Interval from IST to FST | 17.5 | 630 | 0.85 | 12.0 | 400 | 0.40 | 140.0 | 715 | 0.26 | 20.1 | 640 | 0.40 |
| Final Setting Time (FST) | 33.0 | 2797 | 0.85 ± 0.08 | 26.0 | 2879 | 0.40 ± 0.06 | 157.0 | 2655 | 0.26 ± 0.07 | 33.5 | 2331 | 0.40 ± 0.05 |
| Interval from FST to PT | 6.7 | 358 | 0.10 | 14.0 | 291 | 0.18 | 56.0 | 461 | 0.56 | 13.1 | 554 | 0.2 |
| Plateau Time (PT) | 39.7 | 3155 | 0.90 ± 0.05 | 40.0 | 3170 | 0.58 ± 0.05 | 213.0 | 3116 | 0.82 ± 0.1 | 46.6 | 2885 | 0.60 ± 0.02 |
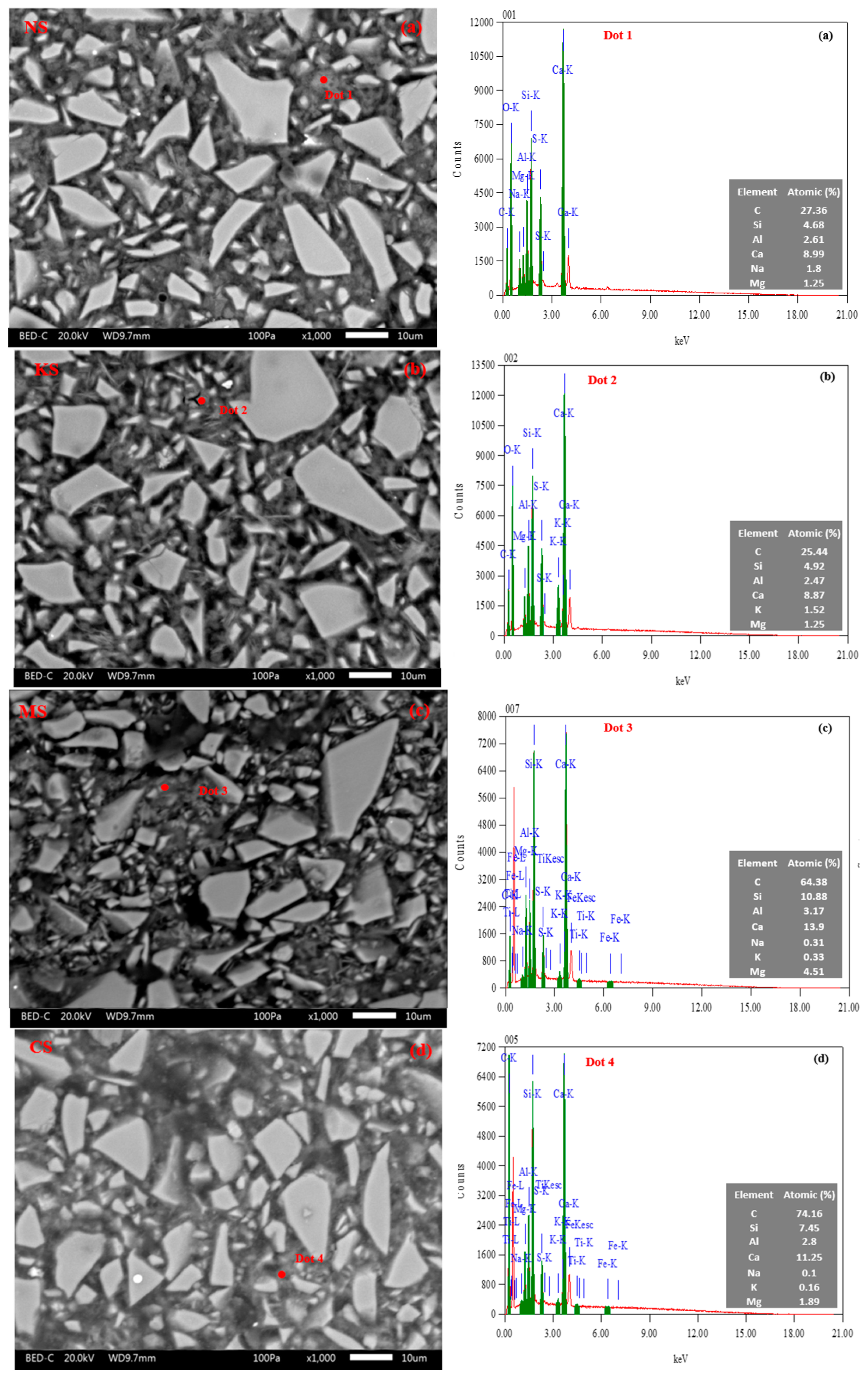
| Element (Atom%) a | Ca | Si | Al | Na | K | Mg |
|---|---|---|---|---|---|---|
| NS | 8.3 ± 0.5 | 5.7 ± 0.8 | 2.2 ± 0.3 | 1.9 ± 0.1 | - | 1.7 ± 0.4 |
| KS | 8.6 ± 0.2 | 5.4 ± 0.4 | 2.4 ± 0.2 | - | 1.8 ± 0.2 | 1.4 ± 0.2 |
| MS | 12.7 ± 1.8 | 8.8 ± 1.0 | 2.6 ± 0.3 | 0.3 ± 0.1 | 0.3 ± 0.0 | 3.7 ± 0.6 |
| CS | 12.6 ± 0.5 | 8.3 ± 3.7 | 2.0 ± 0.2 | 0.1 ± 0.1 | 0.2 ± 0.2 | 1.3 ± 0.2 |
| Element Ratio (-) | Ca/Si | Al/Si | Ca/(Si+Al) | Al/(Na or K or Mg or Ca) | Mg/Al |
|---|---|---|---|---|---|
| NS | 1.5 ± 0.3 | 0.4 ± 0.1 | 1.1 ± 0.1 | 0.20 ± 0.0 | 0.8 ± 0.3 |
| KS | 1.6 ± 0.2 | 0.5 ± 0.1 | 1.1 ± 0.0 | 0.18 ± 0.0 | 0.7 ± 0.1 |
| MS | 1.5 ± 0.3 | 0.3 ± 0.0 | 1.1 ± 0.1 | 0.15 ± 0.1 | 1.5 ± 0.1 |
| CS | 1.5 ± 0.4 | 0.3 ± 0.1 | 1.2 ± 0.1 | 0.16 ± 0.0 | 0.6 ± 0.1 |
| AAS [50,101,102] | 1.2~2.0 | 0.0~0.2 | 0.6 | - | 1.0~1.8 |
| PC [99] | 1.5~2.0 | 0.0~0.1 | 1.3 | - | - |
| BFS/PC [58,102] | 1.0~2.0 | - | - | 1.7~2.7 |
| Mixtures | NS | KS | MS | CS |
|---|---|---|---|---|
| (%) | 3.1 | 2.1 | 3 | 2.3 |
| (h) | 4.6 | 2.2 | 12.2 | 3.8 |
| (-) | 0.4 | 0.8 | 0.9 | 0.5 |
| Mixtures | NS | KS | MS | CS |
|---|---|---|---|---|
| Vanhyd-BFS (t = 28) (%) | 34.0 ± 1.4 | 34.8 ± 2.0 | 42.0 ± 2.9 | 33.4 ± 0.7 |
| Vpores + hydrates (t = 28) (%) | 66.0 ± 3.0 | 65.2 ± 3.2 | 58.0 ± 4.9 | 65.6 ± 1.8 |
| Vfanhyd-BFS (t = 0) (%) | 65.4 | 65.9 | 66.2 | 62.3 |
| (t = 28) | 0.48 | 0.47 | 0.36 | 0.45 |
| (t = 28) | 0.61 | 0.87 | 0.63 | 0.70 |
| 0.79 | 0.54 | 0.57 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Darquennes, A.; Hannawi, K.; Che, C. Effect of the Alkali-Sulphate Activators on the Hydration Process of Blast-Furnace Slag Mortars and Pastes. Materials 2025, 18, 514. https://doi.org/10.3390/ma18030514
Li L, Darquennes A, Hannawi K, Che C. Effect of the Alkali-Sulphate Activators on the Hydration Process of Blast-Furnace Slag Mortars and Pastes. Materials. 2025; 18(3):514. https://doi.org/10.3390/ma18030514
Chicago/Turabian StyleLi, Lei, Aveline Darquennes, Kinda Hannawi, and Caigan Che. 2025. "Effect of the Alkali-Sulphate Activators on the Hydration Process of Blast-Furnace Slag Mortars and Pastes" Materials 18, no. 3: 514. https://doi.org/10.3390/ma18030514
APA StyleLi, L., Darquennes, A., Hannawi, K., & Che, C. (2025). Effect of the Alkali-Sulphate Activators on the Hydration Process of Blast-Furnace Slag Mortars and Pastes. Materials, 18(3), 514. https://doi.org/10.3390/ma18030514






