Assessing the Effectiveness of Dowel Bars in Jointed Plain Concrete Pavements Using Finite Element Modelling
Abstract
1. Introduction
- = the load transfer efficiency based on deflection
- = the deflection of the unloaded slab at the joint
- = the deflection of the loaded slab at the joint
2. Research Significance
3. Finite Element Modelling of Dowelled Jointed Plain Concrete Pavement
4. Results and Discussion
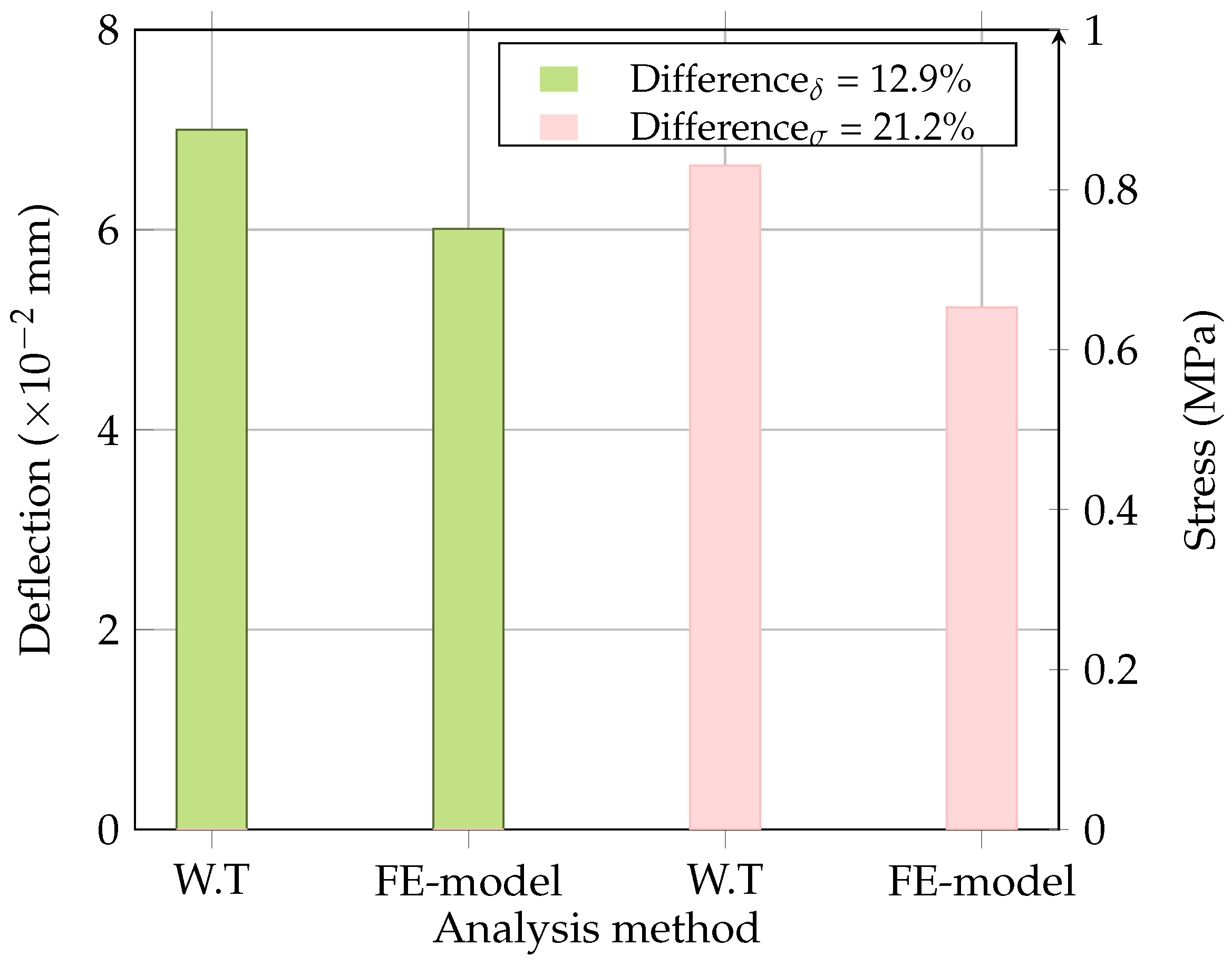
4.1. Comparison of FE Analysis with Westergaard’s Central Loading Case
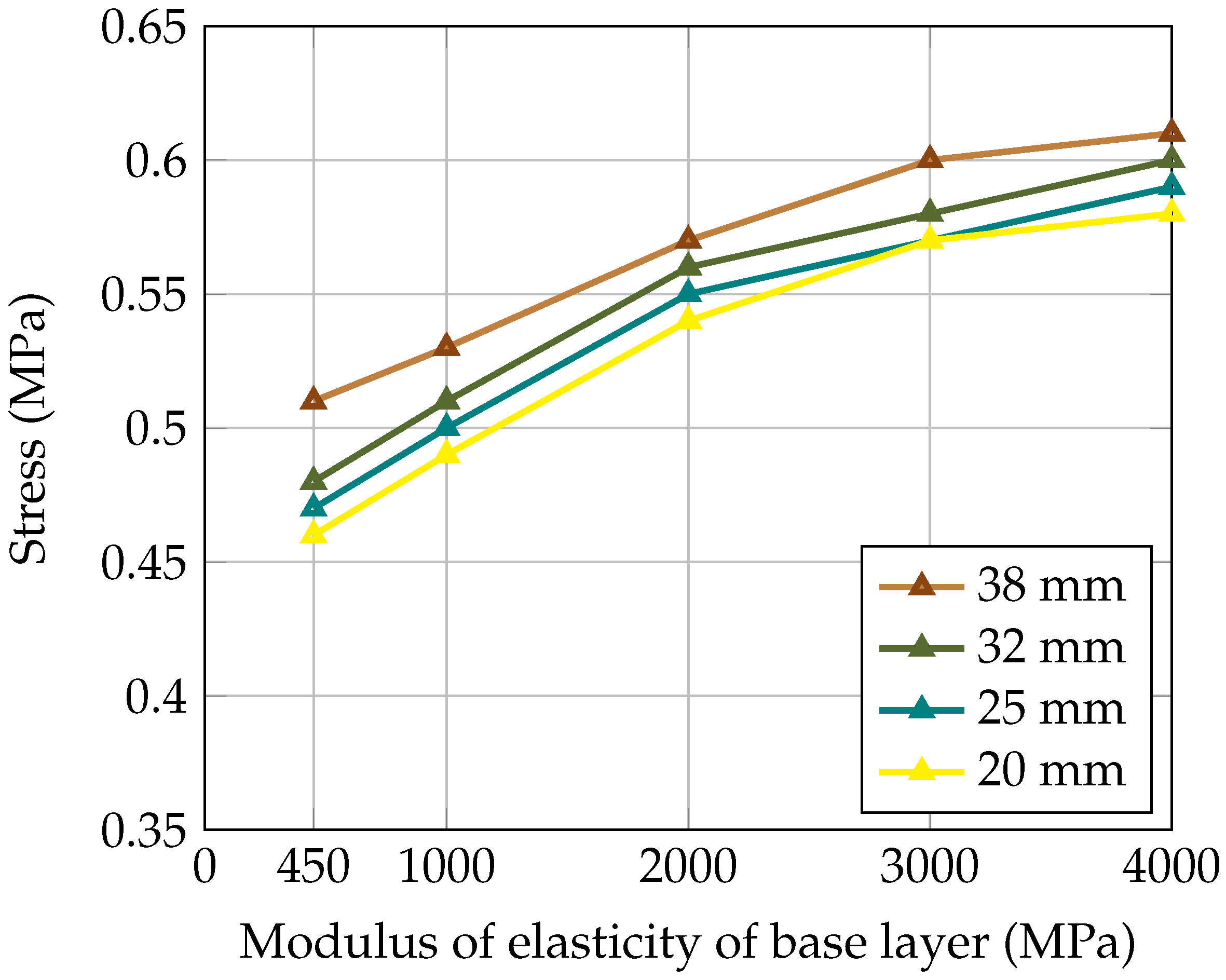
4.2. The Effect of the Base Layer’s Stiffness on the Load Transfer and Flexural Stress at the Bottom of the Concrete Slab
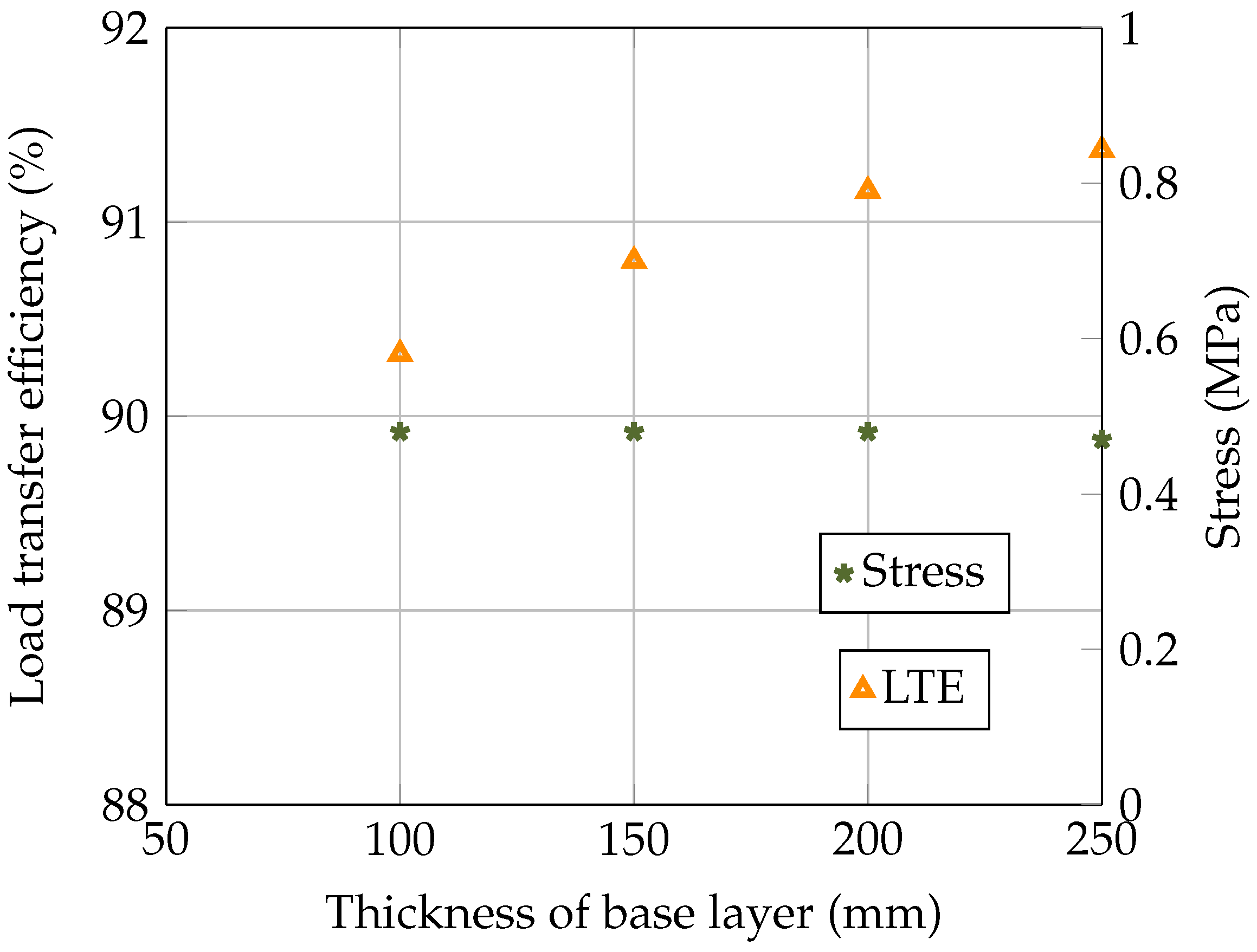
4.3. The Effect of the Base Layer’s Thickness on the Load Transfer and Flexural Stress at the Bottom of the Concrete Slab
4.4. The Effect of the Dowel Bar’s Diameter on the Load Transfer and the Flexural Stress at the Bottom of the Concrete Slab
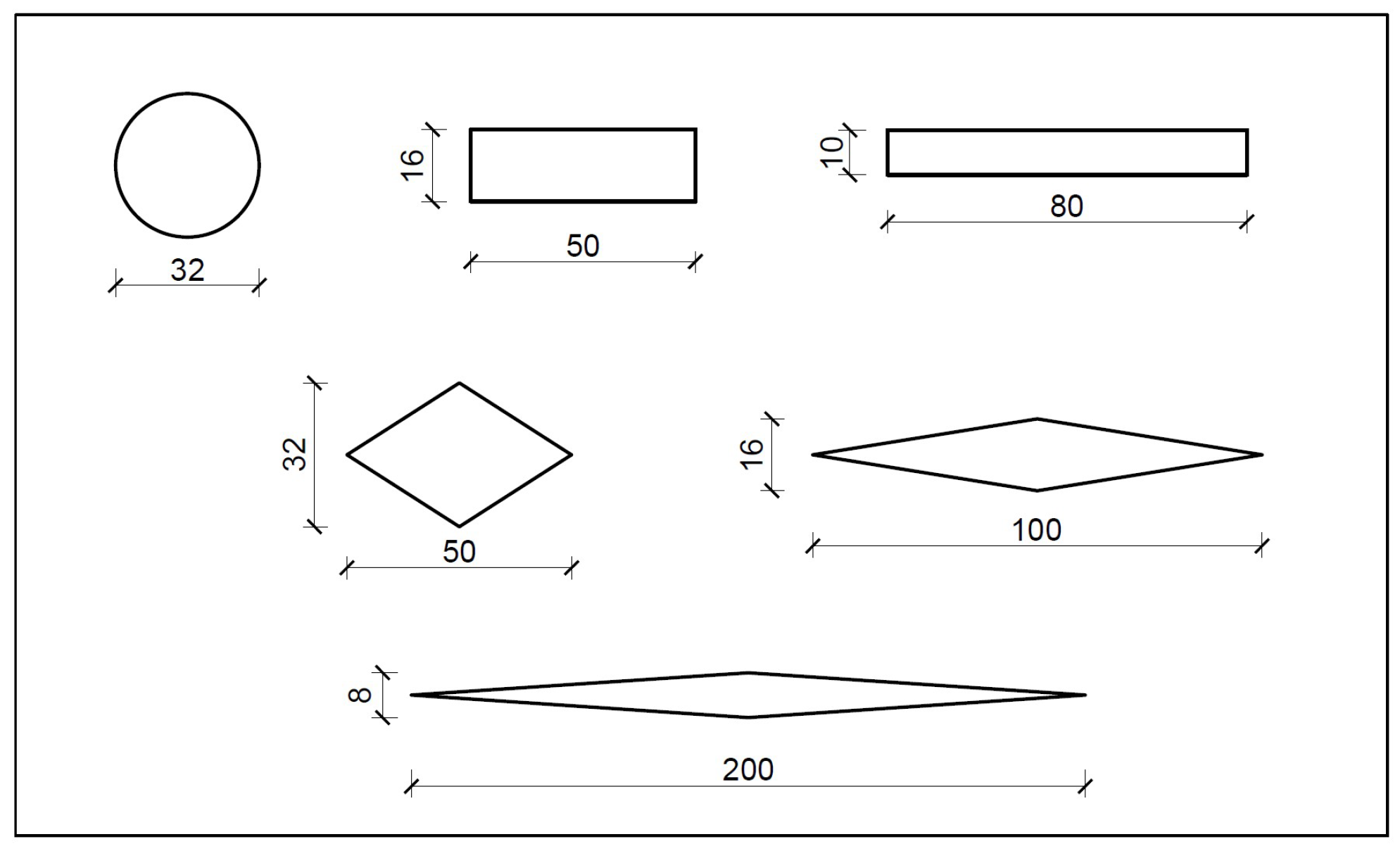
4.5. The Effect of the Dowel Bar’s Shape on the Load Transfer and Flexural Stress at the Bottom of the Concrete Slab
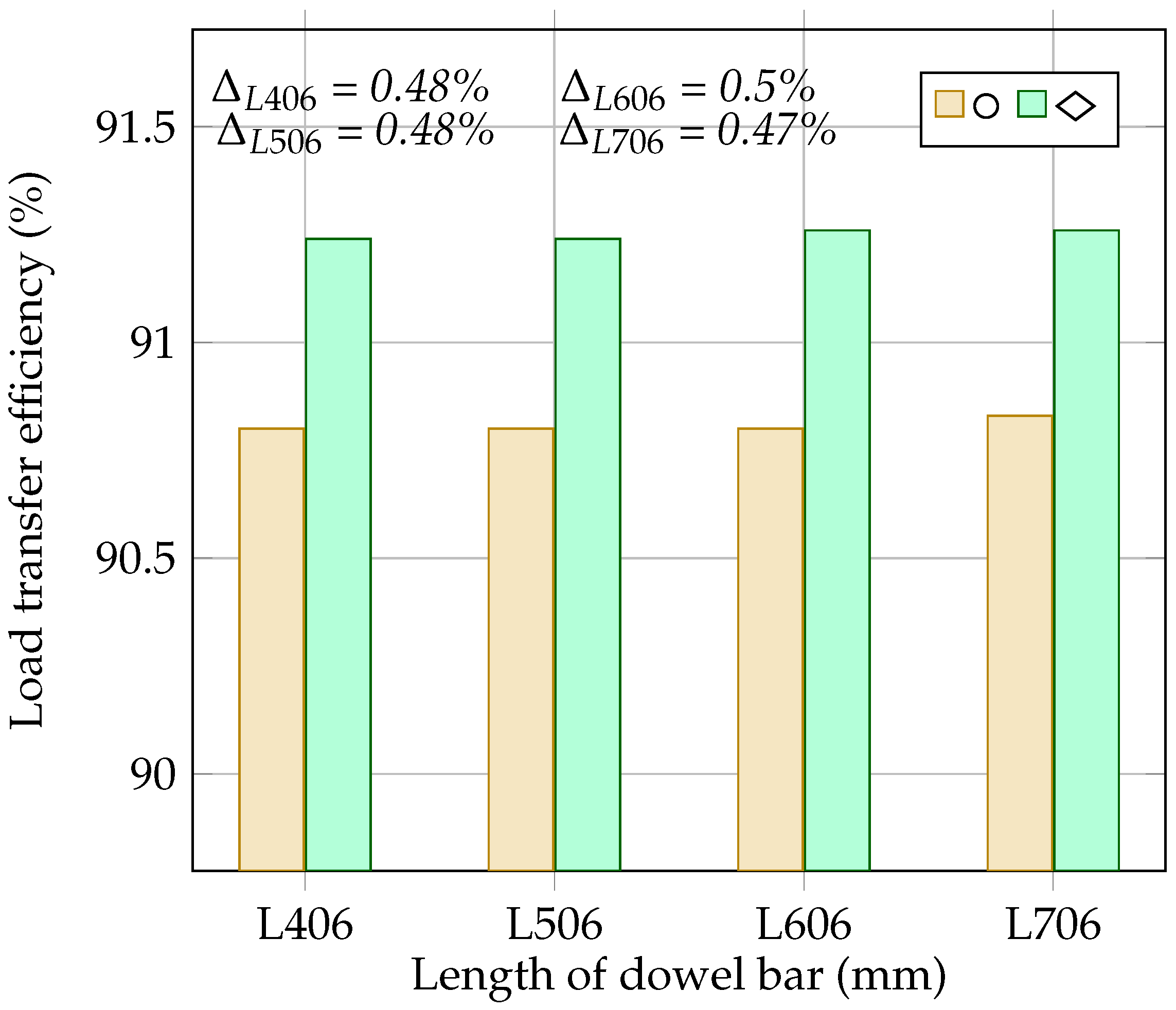
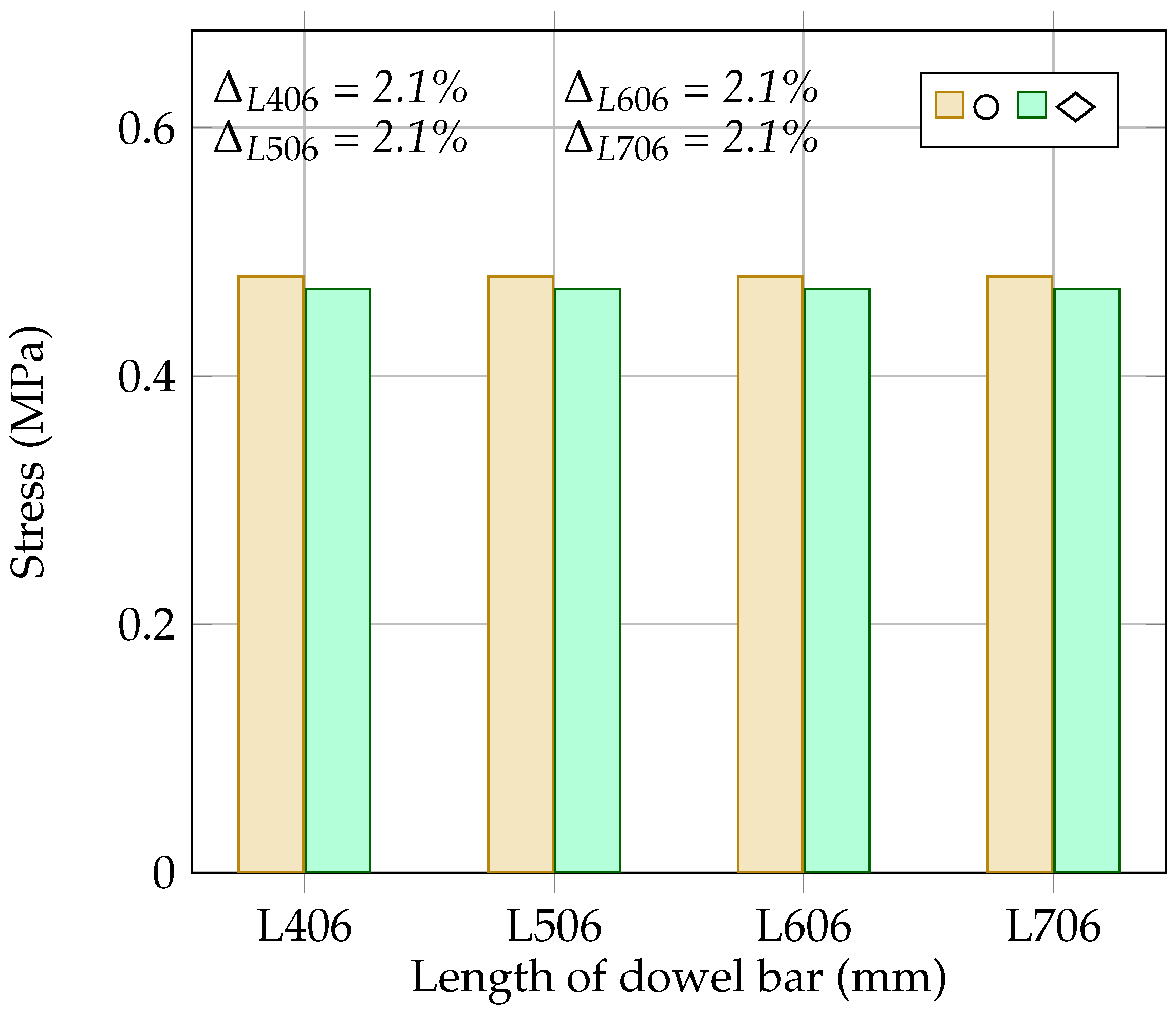
4.6. The Effect of Dowel Bar Length on the Load Transfer Efficiency and Flexural Stress at the Bottom of the Concrete Slab
5. Conclusions
- With an increase in the modulus of elasticity of the base layer from 450 MPa to 6000 MPa, this study shows a 4% increase in the LTE and a 23% increase in stress. However, beyond 3000 MPa, the difference in the LTE and stress become more gradual, reaching approximately 0.38% and 3.2%, respectively.
- The results demonstrate that as the base layer’s thickness increases from 100 mm to 250 mm, the LTE improves by 1.2%. Conversely, the stress remains the same for thicknesses of 100 mm, 150 mm, and 200 mm, while a 2.1% decrease in stress is noticed at a thickness of 250 mm.
- The results show that increasing the dowel bar’s diameter significantly improves the LTE but also increases the stress in the concrete slab. However, the differences in the LTE and stress are more notable for smaller diameters and relatively flexible base layers. For base layer moduli of 450 MPa and 4000 MPa, the increase in the LTE and stress from a 20 mm to a 38 mm dowel bar were 4.3% and 3.8% and 10% and 5%, respectively.
- With a diamond-shaped dowel bar of a 50 × 32 mm size, a 0.48% increase in the LTE and a 2.1% decrease in stress are observed compared to these values for the rounded dowel bar, whereas diamond-shaped dowel bars with sizes of 100 × 16 and 200 × 8 show 0.74% and 2.0% decreases in the LTE, respectively, along with significant stress reductions of 6.7% and 23.1%. For a rectangular dowel bar with a size of 50 × 16, the LTE is approximately similar to that for the rounded dowel bar, while for a size of 80 × 10 mm, a 0.53% reduction in the LTE is noted. However, a 4% increase in stress is seen for both rectangular sizes.
- The diamond-shaped dowel bar improves the LTE by 0.48% for lengths of 406 mm and 506 mm and by 0.5% and 0.47% for lengths of 606 mm and 706 mm, respectively, compared to that with the rounded dowel bar. Additionally, the diamond-shaped dowel bar reduces the stress in the concrete slab by 2.1% relative to that with the rounded dowel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caltrans. Concrete Pavement Guide; California Department of Transportation: Sacramento, CA, USA, 2015. [Google Scholar]
- FHWA. Concrete Pavement Joints; Federal Highway Administration: Washington, DC, USA, 2019. [Google Scholar]
- Yaqoob, S. Concrete Pavements Repair Techniques and Numerical Assessment of Dowel Bar Load Transfer Efficiency. Licentiate Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2024. [Google Scholar]
- Yaqoob, S.; Silfwerbrand, J. Rapid repair of concrete pavement using precast technology. In Proceedings of the 14th International Symposium on Concrete Roads, Krakow, Poland, 25–28 June 2023. [Google Scholar]
- Khichad, J.S.; Vishwakarma, R.J.; Ingle, R.K. Load transfer mechanism for jointed plain concrete pavements: A review. Indian Concr. J. 2022, 96, 35–45. [Google Scholar]
- Shoukry, S.N.; William, G.W.; Riad, M.Y. Evaluation of Load Transfer Efficiency Measurement; West Virginia University, Department of Civil and Environmental Engineering: Morgantown, WV, USA, 2005. [Google Scholar]
- Rens, L. Guide for Design of “Jointed Plain Concrete Pavements”; EUPAVE (European Concrete Paving Association): Brussels, Belgium, 2020. [Google Scholar]
- EN 13877-1; Concrete Pavements—Part 1: Materials. Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006.
- EN 13877-2; Concrete Pavements—Part 2: Functional Requirements for Concrete Pavement. Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006.
- EN 13877-3; Concrete Pavements—Part 3: Specification for Dowels to Be Used in Concrete Pavements. Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2006.
- ČSN 736123-1; Road Building—Concrete Pavements—Part 1: Construction and Conformity Assessment. Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2014.
- Smith, P.; Snyder, M.B. Manual for Jointed Precast Concrete Pavement; NPCA (National Precast Concrete Association): Carmel, IN, USA, 2019. [Google Scholar]
- Tayabji, S. Guide Specification for Jointed Precast Concrete Pavement Introduction [Techbrief]; FHWA (Federal Highway Administration): Washington, DC, USA, 2019. [Google Scholar]
- Tayabji, S. Overview of Precast Concrete Pavement Practices & Recent Innovations; United States. 2016. Available online: https://www.researchgate.net/publication/303920954_OVERVIEW_OF_PRECAST_CONCRETE_PAVEMENT_PRACTICES_RECENT_INNOVATIONS?channel=doi&linkId=575dcf9b08aec91374aef87d&showFulltext=true (accessed on 25 October 2024).
- Yaqoob, S.; Silfwerbrand, J.; Strömberg, L. Overnight Rehabilaition of Concrete Pavements Using Precast Concrete Technology. In Proceedings of the XXIV Nordic Research Symposium, Stockholm, Sweden, 16–19 August 2022. [Google Scholar]
- Yaqoob, S. Report on 12th International Conference on Concrete Pavements: “Making Waves with Durable and Resilient Concrete Pavements”; KTH Royal Institute of Technology: Stockholm, Sweden, 2022. [Google Scholar]
- Pierce, L.M.; Weston, J.; Uhlmeyer, J.S. Dowel Bar Retrofit-Do’s and Don’ts; Washington State Department of Transportation: Washington, DC, USA, 2009. [Google Scholar]
- Smith, K.; Harrington, D.; Pierce, L.M.; Preshant, R.; Smith, K. Concrete Pavement Preservation Guide; National Concrete Pavement Technology Center: Ames, IA, USA, 2014. [Google Scholar]
- Priddy, L.P. Evaluation of Precast Portland Cement Concrete Panels for Airfield Pavement Repairs; U.S. Army Engineer Research and Development Center: Vicksburg, USA, 2015. [Google Scholar]
- ACPA. Concrete Pavement Field Reference Preservation and Repair; American Concrete Pavement Association: Rosemont, IL, USA, 2008. [Google Scholar]
- Shoukry, S.N.; William, G.W.; Riad, M.Y.; Motamarri, S.V.S. Effect of Bonding Force on Stresses in Concrete Slabs; West Virginia Department of Transportation: Morgantown, WV, USA, 2003. [Google Scholar]
- Breemen, W.V. Experimental Dowel Installations in New Jersey. Bull. Highw. Res. Board 1955, 34, 8–33. [Google Scholar]
- Nishizawa, T.; Koyanagawa, M.; Takeuchi, Y.; Kimura, M. Study on mechanical behaviour of dowel bar in transverse joint of concrete pavement. In Proceedings of the 7th International Conference on Concrete Pavements, Orlando, FL, USA, 9–13 September 2001. [Google Scholar]
- Keymanesh, M.R.; Babaki, M.M.; Shahriari, N.; Pirhadi, A. Evaluating the Performance of Dowel in PCC Pavement of Roads Using ABAQUS Finite Element Software. Int. J. Transp. Eng. 2018, 5, 349–365. [Google Scholar]
- Sadeghi, V.; Hesami, S. Investigation of load transfer efficiency in jointed plain concrete pavements (JPCP) using FEM. Int. J. Pavement Res. Technol. 2018, 11, 245–252. [Google Scholar] [CrossRef]
- Kim, K.; Chun, S.; Han, S.; Tia, M. Effect of dowel bar arrangements on performance of jointed plain concrete pavement (JPCP). Int. J. Concr. Struct. and Mater. 2018, 12, 39. [Google Scholar]
- Swarna, S.T.; Gali, R.R.L.; Reddy, M.A.; Mehta, Y. The Analysis and Design of Jointed Plain Concrete Pavements with Wider Slabs. Road Mater. Pavement Des. 2024, 25, 2664–2684. [Google Scholar]
- Yaqoob, S.; Silfwerbrand, J.; Balieu, R.G.R. A Parametric Study Investigating the Dowel Bar Load Transfer Efficiency in Jointed Plain Concrete Pavement Using a Finite Element Model. Building 2024, 14, 1039. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Huang, X.; Ye, Y.; Ruan, S. Analysis on Effects of Joint Spacing on the Performance of Jointed Plain Concrete Pavements Based on Long-Term Pavement Performance Database. Materials 2022, 15, 8132. [Google Scholar] [CrossRef]
- Li, C.; Lei, S.; Xiao, Q.; Pan, Y.; Han, X.; Chen, Q. An Experimental and Numerical Investigation on the Load Transfer Efficiency of a Novel Prefabricated Cement Concrete Pavement. Structures 2023, 53, 963–972. [Google Scholar] [CrossRef]
- Mackiewicz, P. Analysis of Stresses in Concrete Pavement Under a Dowel According to Its diameter and Load transfer Efficiency. Can. J. Civ. Eng 2015, 42, 845–853. [Google Scholar] [CrossRef]
- Murison, S.; Shalaby, A.; Mufti, A. Concrete-Filled, Glass Fiber-Reinforced Polymer Dowels for Load Transfer in Jointed Rigid Pavements. Transp. Res. Rec. 2005, 1919, 54–64. [Google Scholar] [CrossRef]
- Al-Humeidawi, B.H.; Mandal, P. Experimental Investigation on the Combined Effect of Dowel Misalignment and Cyclic Wheel Loading on Dowel Bar Performance in JPCP. Eng. Struct. 2018, 174, 256–266. [Google Scholar] [CrossRef]
- Brown, V.; Bartholomew, C. FRP Dowel Bars in Reinforced Concrete Pavements. Spec. Publ. 1993, 138, 813–830. [Google Scholar]
- Benmokrane, B.; Ahmed, E.A.; Montaigu, M. Thebeau, D. Performance of Glass Fiber-Reinforced Polymer-Doweled Jointed Plain Concrete Pavement Under Static and Cyclic Loadings. ACI Struct. J. 2014, 111, 331–342. [Google Scholar]
- Al-Humeidawi, B.H.; Mandal, P. Numerical Evaluation of the Combined Effect of Dowel Misalignment and Wheel Load on Dowel Bars Performance in JPCP. Eng. Struct. 2022, 252, 113655. [Google Scholar] [CrossRef]
- Rabah, M.; Eisa, M.; Mohamed Elghanam, A. Influence of Misalignment Method on Performance of Dowel Bars in Joints of Rigid Pavement. Mansoura Eng. J. 2021, 46, 26–39. [Google Scholar]
- Smith, A.R.; Benham, S.W. Effect of Dowel-Bar Misalignment Across Concrete Pavement Joints. Trans. Am. Soc. Civ. Eng. 1938, 103, 1133–1144. [Google Scholar] [CrossRef]
- Segner, E.P.; Cobb, J.R. Study of Misaligned Dowels in Concrete Pavements; Alabama Highway Department: Montgomery, AL, USA, 1967. [Google Scholar]
- Cong, Z.Y.; Ling, G.L. Effect of Dowel Bar Position Deviation on Joint Load-Transfer Ability of Cement Concrete Pavement. Int. J. Pavement Res. Technol. 2016, 9, 30–36. [Google Scholar]
- Peng, P.; Bo, T.; Kaimin, N. A Study on the Working Performance of Dowel Bars with Horizontal Installation Errors. J. Highw. Transp. Res. Dev. 2012, 6, 33–38. [Google Scholar] [CrossRef]
- Leong, P.; Tighe, S.; Rothenburg, L.; Hein, D. Finite Difference Modelling of Misaligned Dowel bars and Their Effects on Joint Performance. J. Transp. Res. Board 2006, 1946, 101–110. [Google Scholar] [CrossRef]
- ACPA. In Dowel Bar Alignment and Location for Placement by Mechanical Dowel Bar Insertion; American Concrete Pavement Association Guide Specification: Rosemont, IL, USA, 2013.
- ACPA. Evaluating and Optimizing Dowel Bar Alignment; American Concrete Pavement Association: Rosemont, IL, USA, 2006. [Google Scholar]
- Kivi, A.K. Dowel bar alignment in concrete pavements-21st century standards and methods. In Proceedings of the Transportation Association of Canada 2020 Conference and Exhibition—The Journey to Safer Roads, Ottawa, ON, Canada, 21 September–8 October 2020. [Google Scholar]
- Silfwerbrand, J. Concrete pavements for modern Swedish highways. In Proceedings of the 14th International Symposium on Concrete Roads, Krakow, Poland, 25–28 June 2023. [Google Scholar]
- Silfwerbrand, J. The advantages of concrete pavements in tunnels. In Proceedings of the 12th International Symposium on Concrete Roads, Prague, Czech Republic, 24–26 September 2014. [Google Scholar]
- Hultqvist, B.Å.; Dolk, E. Handbok—Drift, Underhåll Och Reparation av Betongvägar, Technical Report; Swedish National Road and Transport Institute (VTI): Stockholm, Sweden, 2014. [Google Scholar]
- Nilsson, R.; Saleh, I.; Gustafsson, M. Hällbara Betongvägar—Underhåll (Etapp I); Svenska Byggbranschens Utvecklingsfond (SBUF): Stockholm, Sweden, 2022. [Google Scholar]
- Petersson, Ö.; Johansson, A.; Sundbom, S. Provväg av Cementbrtong vid Arlanda, 1990; Cement och Betong Institute (CBI): Stockholm, Sweden, 1991. [Google Scholar]
- Yaqoob, S.; Silfwerbrand, J.; Strömberg, L. Evaluation of Rapid Repair of Concrete Pavements Using Precast Concrete Technology: A Sustainable and Cost-Effective Solution. Nordic Concr. Res. 2021, 65, 107–128. [Google Scholar] [CrossRef]
- Dassault Systems. Simulia User Assistance 2021. Available online: https://help.3ds.com/2021/English/DSSIMULIA_Established/SIMULIA_Established_FrontmatterMap/sim-r-DSDocAbaqus.htm?contextscope=all&redirect_lang=English (accessed on 25 September 2024).
- AB Svensk Byggtjänst. Betong på mark. In Concrete Slabs on Grade; AB Svensk Byggtjänst: Stockholm, Sweden, 2002; 253p. (In Swedish) [Google Scholar]
- STA. ATBVÄG: Allmän Teknisk Beskrivning för Vägkonstruktioner; Swedish Transport Administration: Stockholm, Sweden, 2003. (In Swedish) [Google Scholar]
- Petersson, Ö. Svensk Metod för Dimensionering av Betongvägar; Licentiatavhandlig, Kungl Tekniska Högsklan Institutioen för Byggkonstruktion: Stockholm, Sweden, 1996. [Google Scholar]
- Silfwerbrand, J. Dimensionering av Betongbeläggningar, (Design of Concrete Pavements); KTH Royal Institute of Technology, Department of Structural Mechanics and Engineering: Stockholm, Sweden, 1995. [Google Scholar]
- Liu, Y.; Glass, G. Effects of Mesh Density on Finite Element Analysis; Technical Paper; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
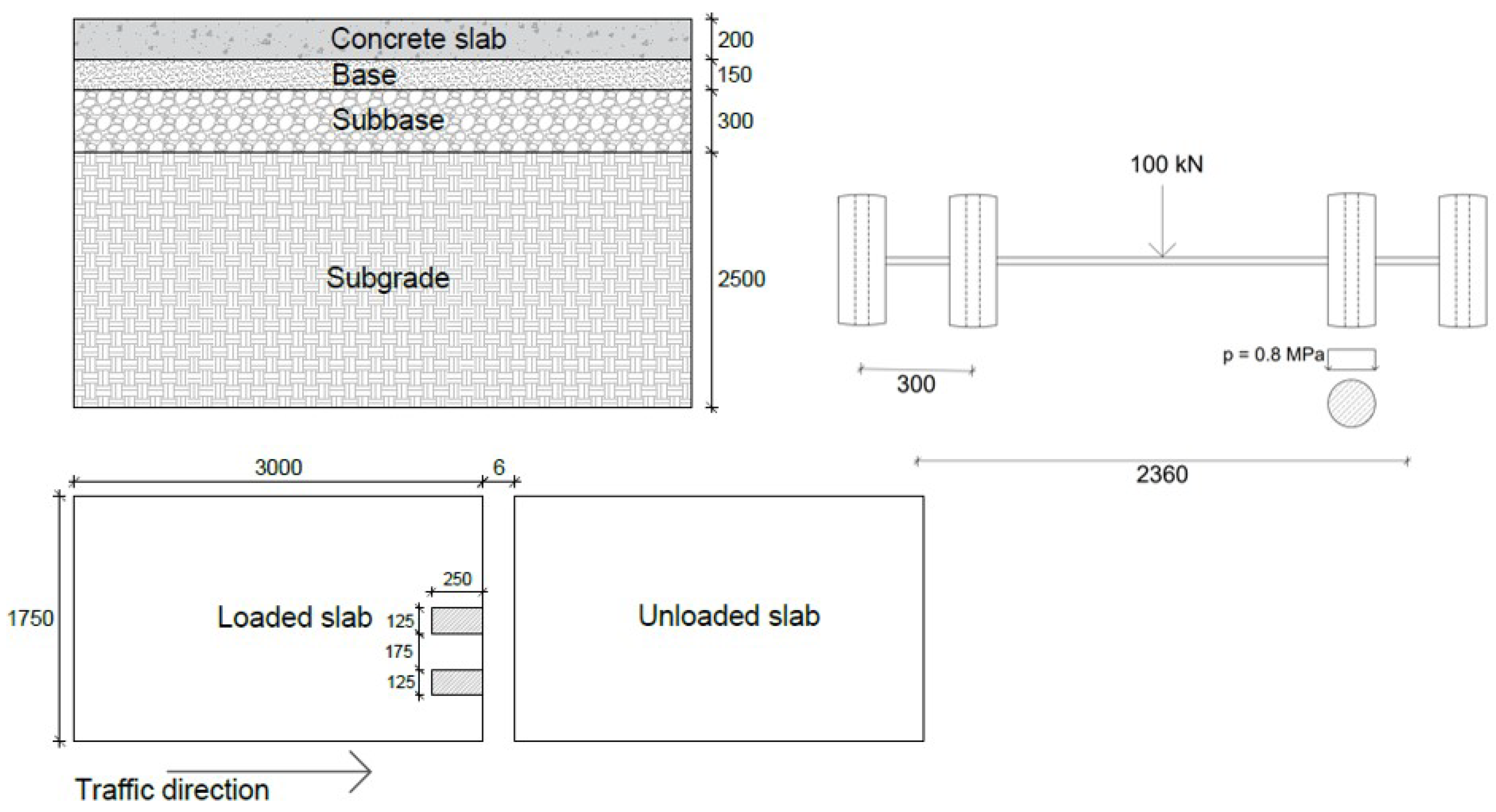
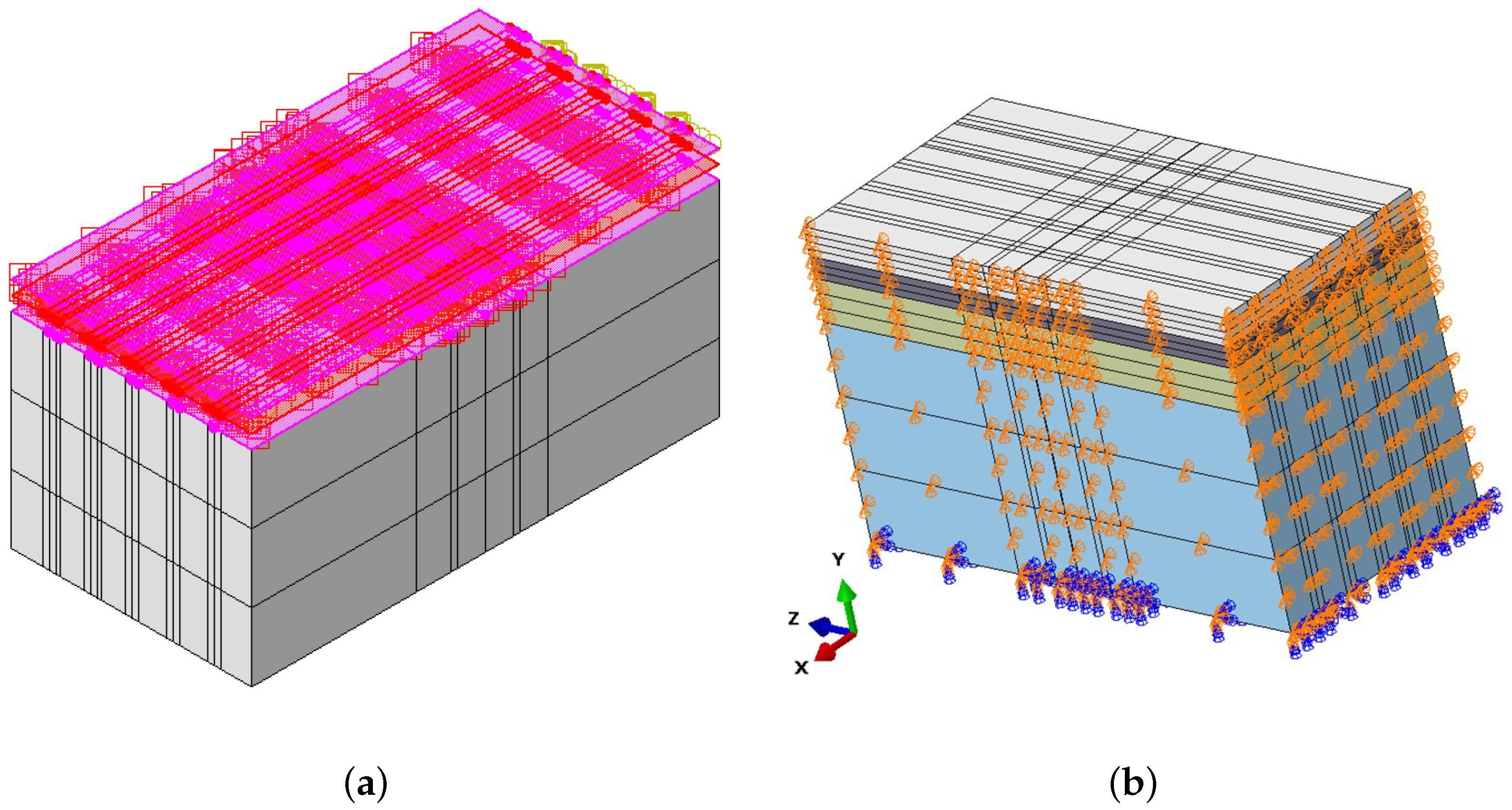




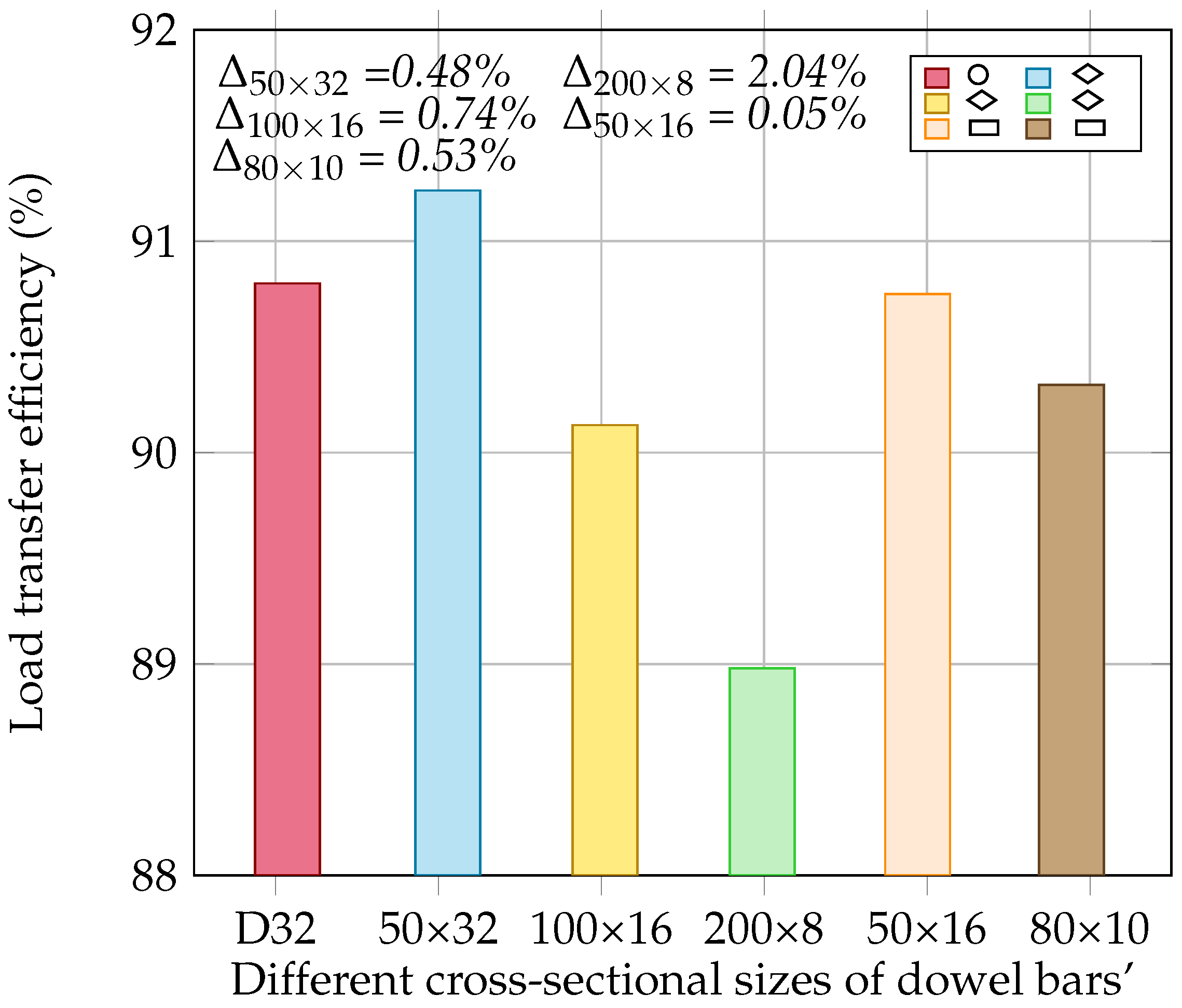

| Materials | Modulus of Elasticity | Poisson’s Ratio |
|---|---|---|
| - | MPa | - |
| Concrete | 33,000 | 0.2 |
| Unbound gravel (base) | 450 | 0.35 |
| Gravel (subbase) | 150 | 0.35 |
| Sand (subgrade) | 100 | 0.35 |
| Steel dowel bar | 200,000 | 0.35 |
| Elastic Modulus | Deflection at the | Deflection at the | Stress in |
|---|---|---|---|
| of the Base Layer | Loaded Slab () | Unloaded Slab () | the Concrete Slab |
| MPa | mm | mm | MPa |
| 450 | 0.3860 | 0.3505 | 0.48 |
| 1000 | 0.3742 | 0.3451 | 0.51 |
| 2000 | 0.3624 | 0.3383 | 0.56 |
| 3000 | 0.3542 | 0.3326 | 0.58 |
| 4000 | 0.3475 | 0.3276 | 0.60 |
| 5000 | 0.3418 | 0.3230 | 0.61 |
| 6000 | 0.3368 | 0.3187 | 0.62 |
| Thickness | Deflection at the | Deflection at the | Stress in |
|---|---|---|---|
| of the Base Layer | Loaded Slab () | Unloaded Slab () | the Concrete Slab |
| mm | mm | mm | MPa |
| 100 | 0.3914 | 0.3535 | 0.48 |
| 150 | 0.3860 | 0.3505 | 0.48 |
| 200 | 0.3799 | 0.3463 | 0.48 |
| 250 | 0.3730 | 0.3408 | 0.47 |
| Diameter of the Dowel Bar | Elastic Modulus of the Base Layer | Deflection at the Loaded Slab ) | Deflection at the Unloaded Slab | Stress in the Concrete Slab |
|---|---|---|---|---|
| mm | MPa | mm | mm | MPa |
| 20 | 450 | 0.3927 | 0.3446 | 0.46 |
| 1000 | 0.3796 | 0.3389 | 0.49 | |
| 2000 | 0.3668 | 0.3319 | 0.54 | |
| 3000 | 0.3580 | 0.3261 | 0.57 | |
| 4000 | 0.3510 | 0.3210 | 0.58 | |
| 25 | 450 | 0.3896 | 0.3478 | 0.47 |
| 1000 | 0.3772 | 0.3422 | 0.50 | |
| 2000 | 0.3648 | 0.3353 | 0.55 | |
| 3000 | 0.3562 | 0.3295 | 0.57 | |
| 4000 | 0.3494 | 0.3245 | 0.59 | |
| 32 | 450 | 0.3860 | 0.3505 | 0.48 |
| 1000 | 0.3742 | 0.3451 | 0.51 | |
| 2000 | 0.3624 | 0.3383 | 0.56 | |
| 3000 | 0.3542 | 0.3326 | 0.58 | |
| 4000 | 0.3475 | 0.3276 | 0.60 | |
| 38 | 450 | 0.3833 | 0.3515 | 0.51 |
| 1000 | 0.3720 | 0.3463 | 0.53 | |
| 2000 | 0.3605 | 0.3397 | 0.57 | |
| 3000 | 0.3525 | 0.3341 | 0.60 | |
| 4000 | 0.3460 | 0.3291 | 0.61 |
| Shape of the Dowel Bar | Cross-Sectional Size of the Dowel Bar | Deflection at the Loaded Slab ) | Deflection at the Unloaded Slab | Stress in the Concrete Slab | |
|---|---|---|---|---|---|
| Width | Height | ||||
| - | mm | mm | mm | mm | MPa |
| Rounded dowel bar (D32) | - | - | 0.3860 | 0.3505 | 0.48 |
| Diamond-shaped dowel bar | 50 | 32 | 0.3857 | 0.3519 | 0.47 |
| 100 | 16 | 0.3891 | 0.3507 | 0.45 | |
| 200 | 8 | 0.3938 | 0.3504 | 0.39 | |
| Rectangular dowel bar | 50 | 16 | 0.3741 | 0.3395 | 0.5 |
| 80 | 10 | 0.3702 | 0.3360 | 0.5 | |
| Shape of the Dowel Bar | Length of the Dowel Bar | Deflection at the Loaded Slab ) | Deflection at the Unloaded Slab | Stress in the Concrete Slab |
|---|---|---|---|---|
| - | mm | mm | mm | MPa |
| Rounded dowel bar (D32) | 406 | 0.3860 | 0.3505 | 0.48 |
| 506 | 0.3860 | 0.3505 | 0.48 | |
| 606 | 0.3860 | 0.3505 | 0.48 | |
| 706 | 0.3873 | 0.3518 | 0.48 | |
| Diamond-shaped dowel bar | 406 | 0.3857 | 0.3519 | 0.47 |
| 506 | 0.3857 | 0.3519 | 0.47 | |
| 606 | 0.3857 | 0.3520 | 0.47 | |
| 706 | 0.3857 | 0.3520 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaqoob, S.; Silfwerbrand, J. Assessing the Effectiveness of Dowel Bars in Jointed Plain Concrete Pavements Using Finite Element Modelling. Materials 2025, 18, 588. https://doi.org/10.3390/ma18030588
Yaqoob S, Silfwerbrand J. Assessing the Effectiveness of Dowel Bars in Jointed Plain Concrete Pavements Using Finite Element Modelling. Materials. 2025; 18(3):588. https://doi.org/10.3390/ma18030588
Chicago/Turabian StyleYaqoob, Saima, and Johan Silfwerbrand. 2025. "Assessing the Effectiveness of Dowel Bars in Jointed Plain Concrete Pavements Using Finite Element Modelling" Materials 18, no. 3: 588. https://doi.org/10.3390/ma18030588
APA StyleYaqoob, S., & Silfwerbrand, J. (2025). Assessing the Effectiveness of Dowel Bars in Jointed Plain Concrete Pavements Using Finite Element Modelling. Materials, 18(3), 588. https://doi.org/10.3390/ma18030588










