Study on Bending Performance of High-Ductility Composite Slab Floor with Composite Ribs
Abstract
:1. Introduction
2. Test Overview
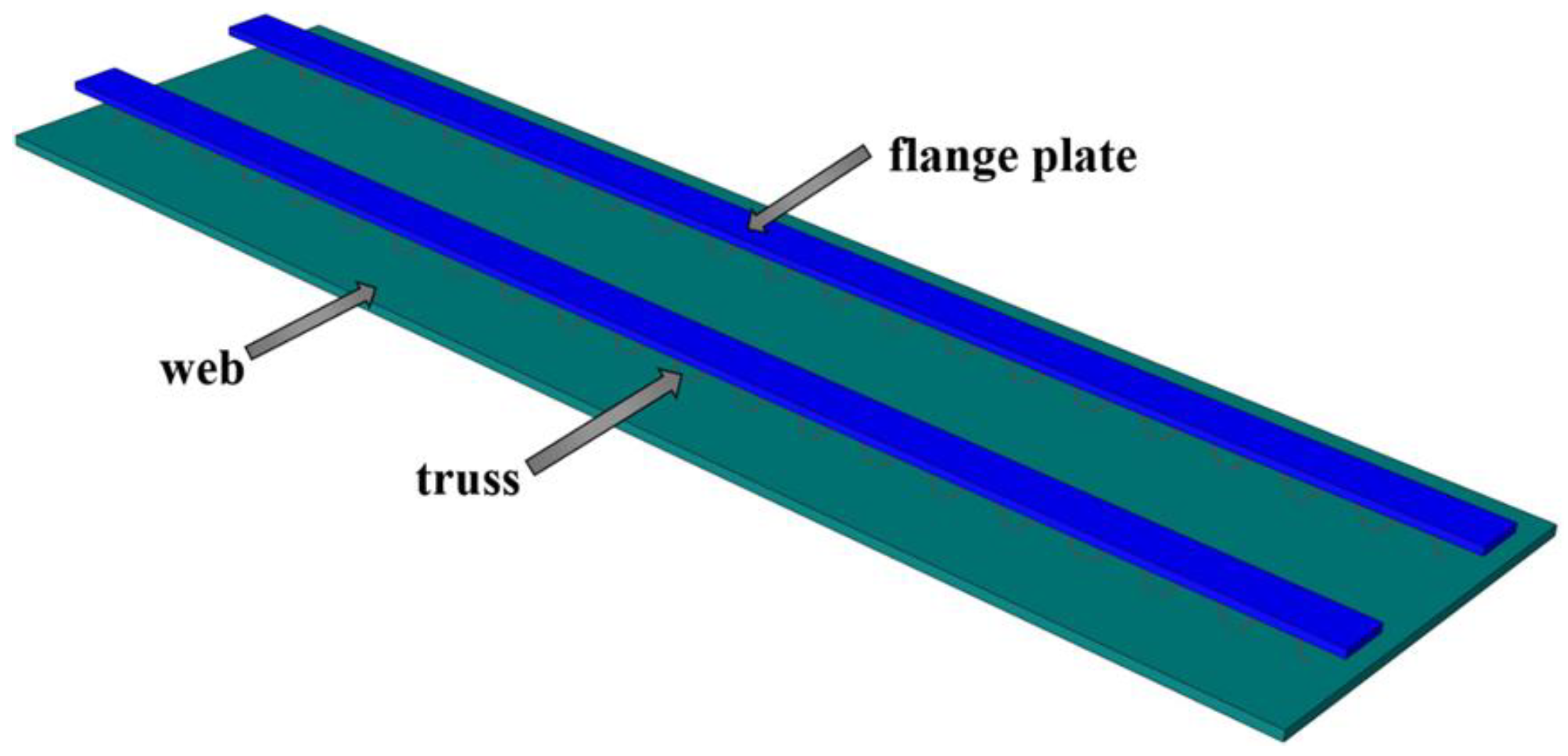
2.1. Material Parameters and Overview of the Specimen
2.1.1. Material Properties of Specimen
2.1.2. Overview of the Specimen
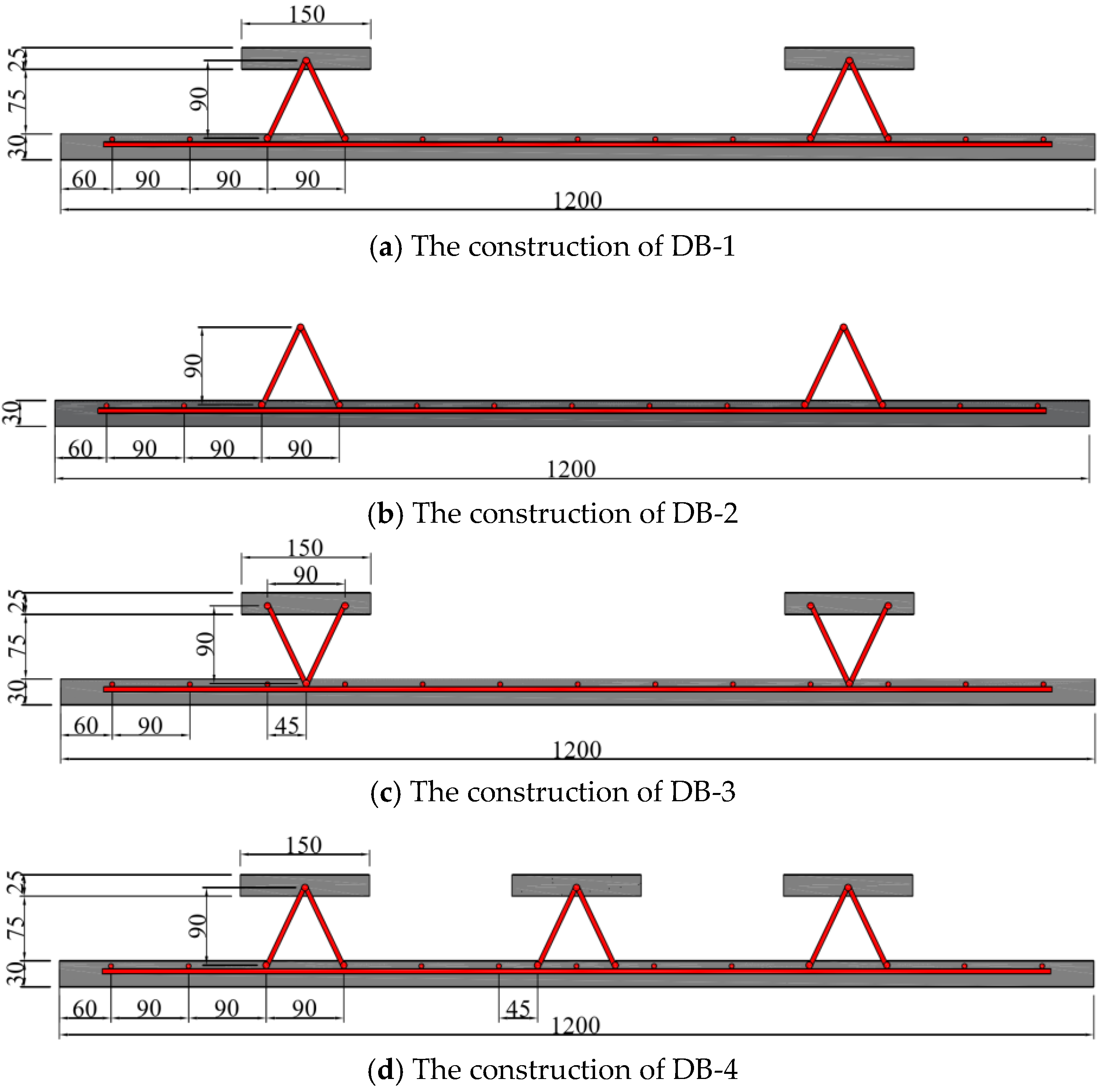
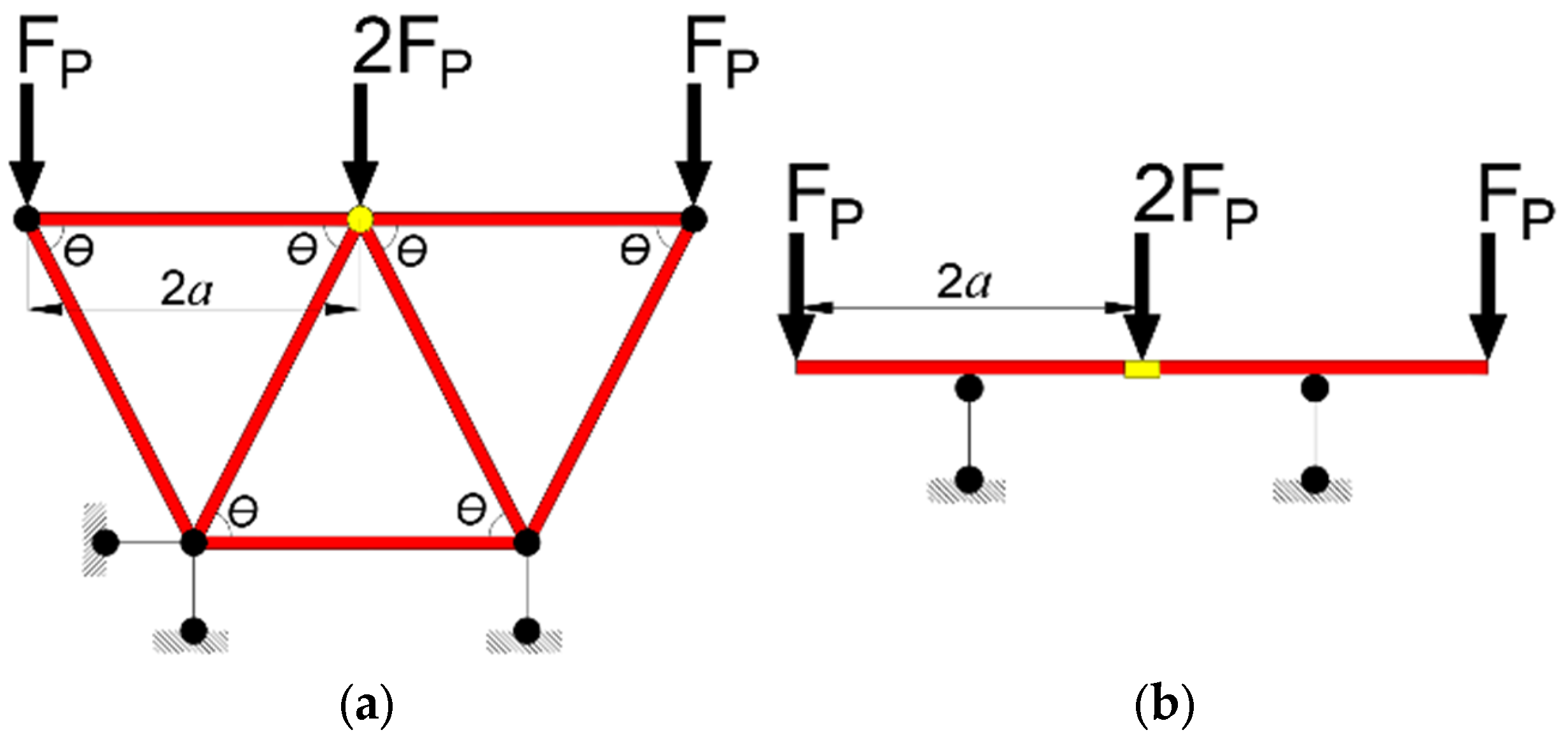
2.2. Test Scheme
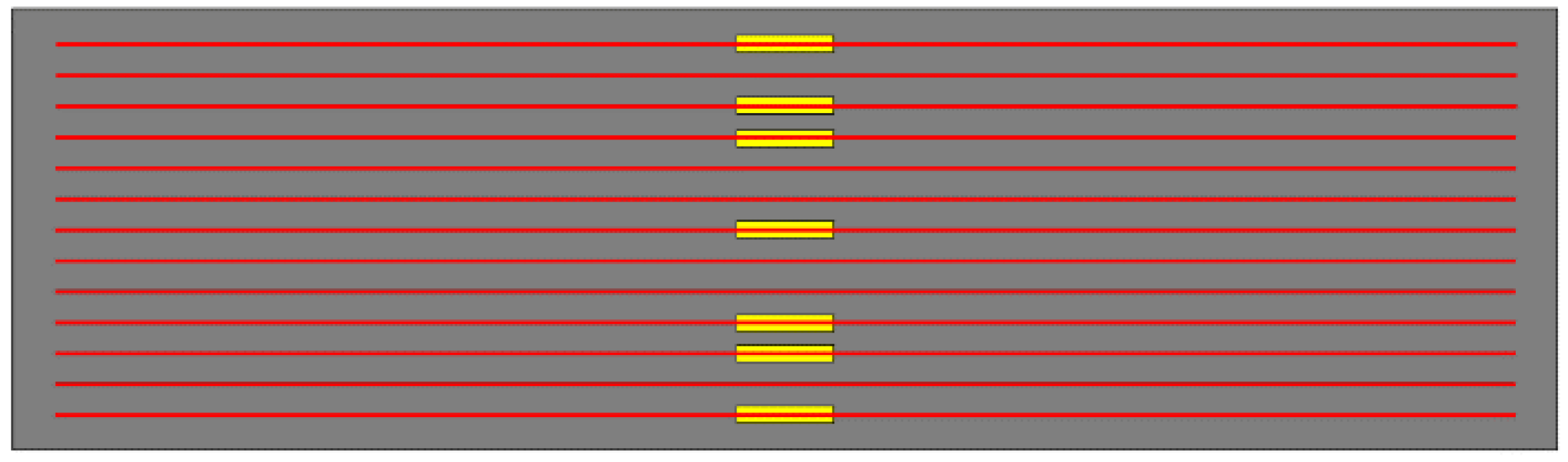
2.3. Layout of Measuring Points
3. Test Results and Analysis
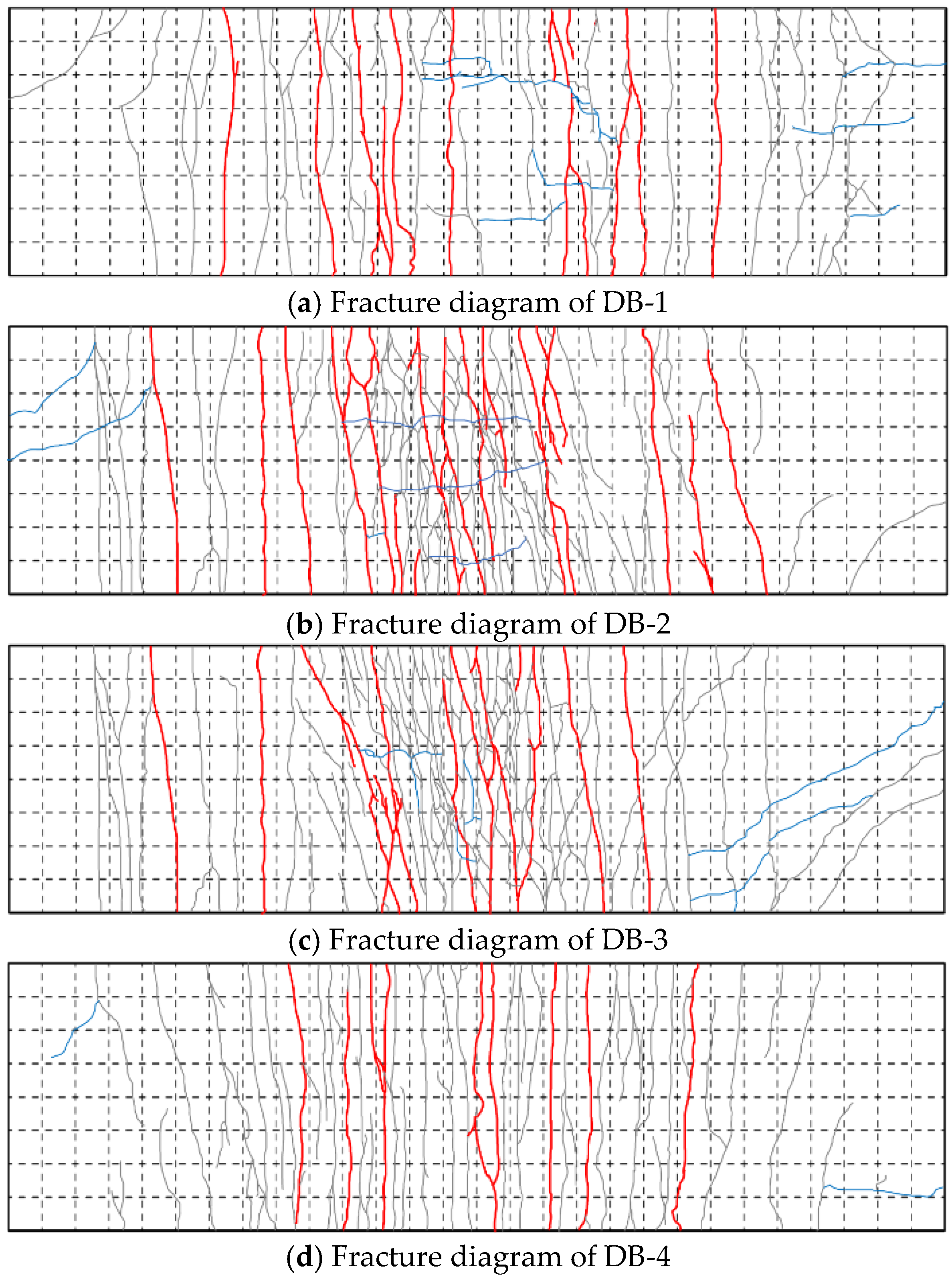
3.1. Failure Characteristics and Fracture Distribution
3.1.1. Failure Characteristics of Specimens
3.1.2. Crack Distribution of Specimens
3.2. Analysis of Bending Properties
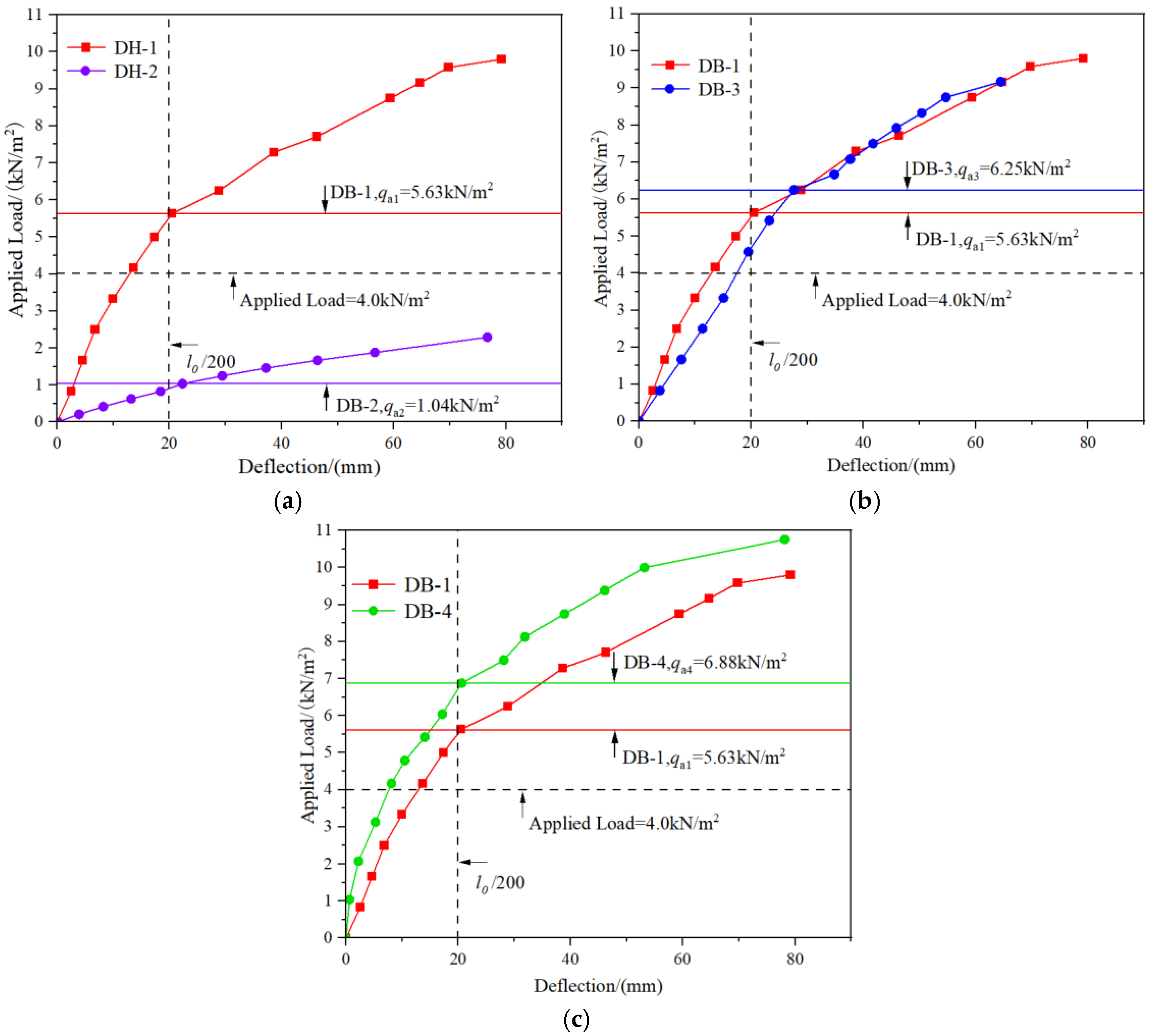
3.2.1. Analysis of Applied Load and Mid-Span Deflection
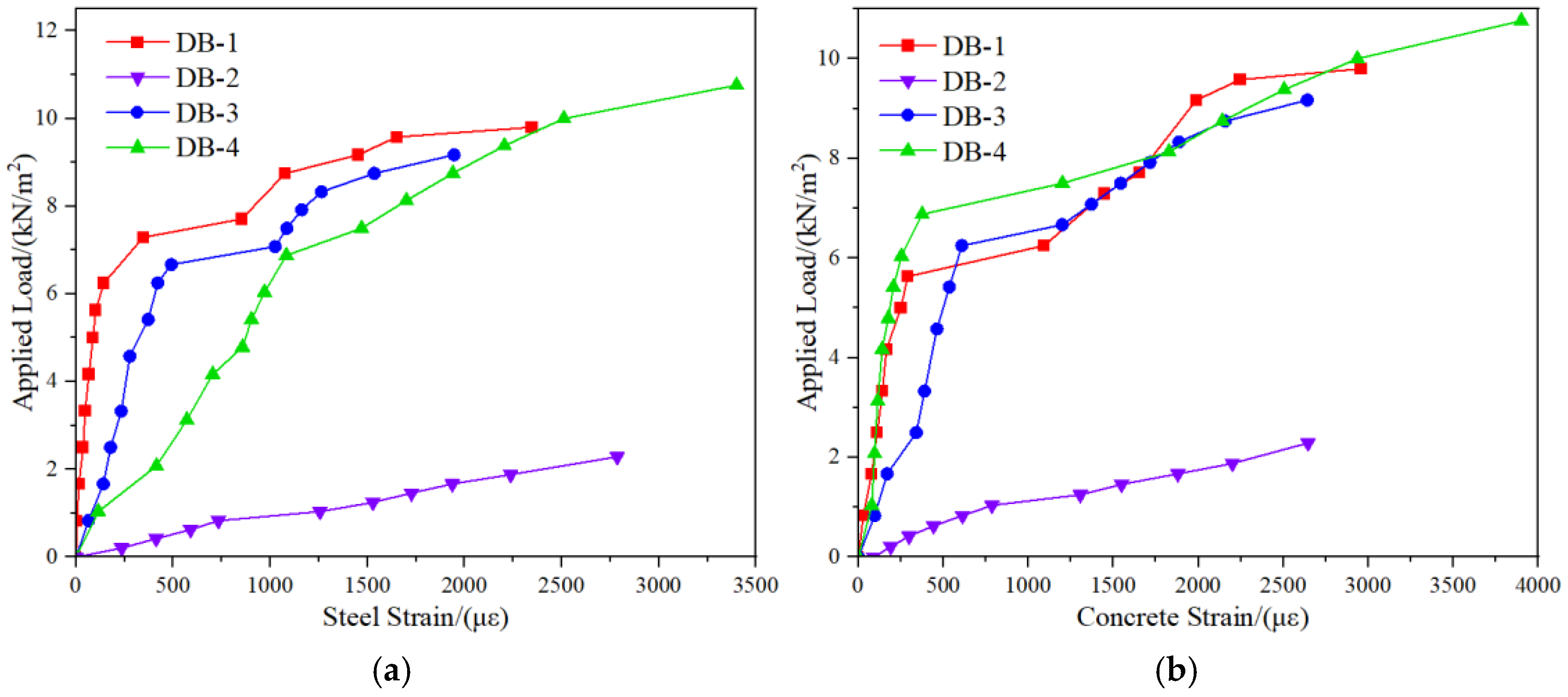
3.2.2. Analysis of Applied Load and Mid-Span Strain
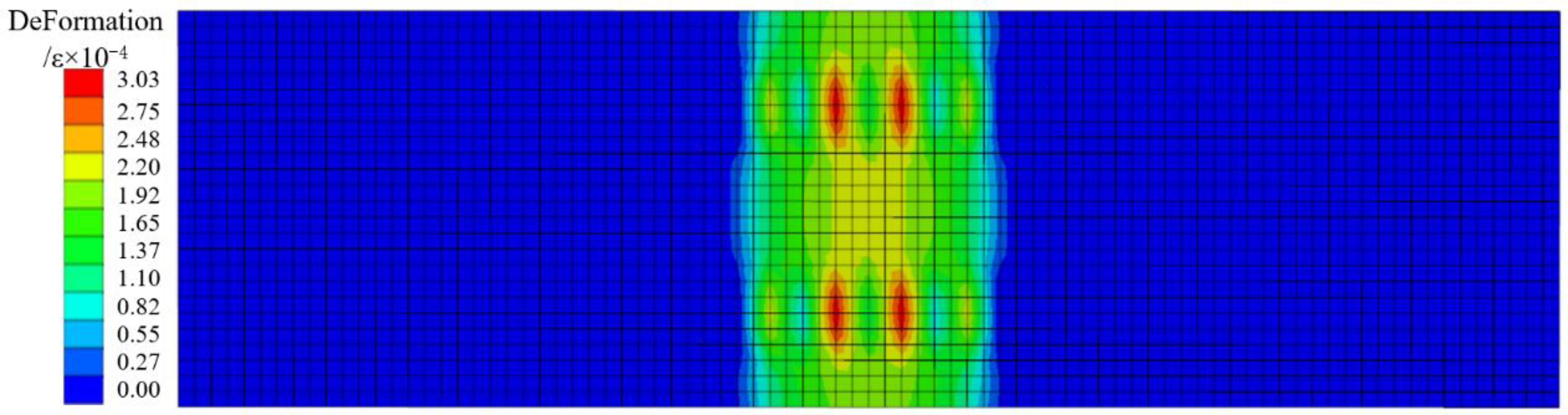
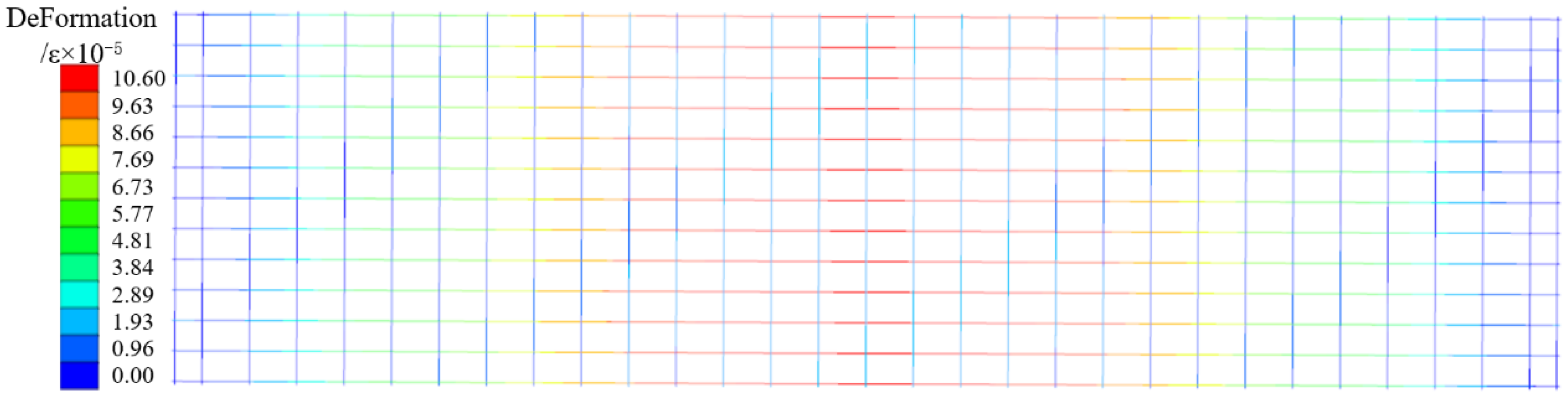
4. Numerical Analysis
5. Non-Support Calculation Method
5.1. Derivation of Related Parameters of Support-Free Theory
5.2. Method Validation and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rueda-García, L.; Bonet, J.L.; Miguel, P.; Fernández-Prada, M.A. Experimental analysis of the shear resistance of precast concrete T-beams with a top cast-in-place slab. Eng. Struct. 2023, 291, 15. [Google Scholar] [CrossRef]
- Lou, F.; Chen, X.L.; Luo, B.; Chen, Z. Mechanical behavior of a new type of reinforced concrete composite slab with a joint. Case Stud. Constr. Mater. 2024, 20, 18. [Google Scholar] [CrossRef]
- Wang, G.M.; Zhu, L.; Zhou, G.P.; Han, B.; Ji, W.Y. Experimental Research of the Time-Dependent Effects of Steel-Concrete Composite Girder Bridges during Construction and Operation Periods. Materials 2020, 13, 2123. [Google Scholar] [CrossRef] [PubMed]
- Masoudnia, R.; Hashemi, A.; Quenneville, P. Predicting the Effective Flange Width of a CLT Slab in Timber Composite Beams. J. Struct. Eng. 2018, 144, 18. [Google Scholar] [CrossRef]
- Jun, S.C.; Lee, C.H.; Bae, C.J.; Chung, G.T. Experimental Evaluation of Negative Flexural Capacity of Composite Slabs Embedded with Truss Girders. Int. J. Steel Struct. 2024, 24, 644–657. [Google Scholar] [CrossRef]
- Candido, D.C.D.; Gomes, A.V.S.; Favarato, L.F.; Ferrareto, J.A.; Vianna, J.D.; Calenzani, A.F.G. Flexural behavior of composite ribbed slabs employing cold-formed steel lipped channels. Eng. Struct. 2024, 298, 14. [Google Scholar] [CrossRef]
- Wu, H.P.; Qiao, G.P.; Qiao, Y.J.; Zhong, Z.W.; Zhou, Z.Y.; Ye, T.P. Experimental and theoretical research on flexural performance of truss reinforced concrete two-way composite slab with prefabricated baseplate. Structures 2023, 58, 16. [Google Scholar] [CrossRef]
- Zheng, C.Y.; Xiong, F.; Liu, Y.; Yu, M.J. Study on the flexural behavior of precast concrete multi-ribbed sandwich slabs under different boundary conditions. Eng. Struct. 2023, 291, 17. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.M.; Han, G.H.; Shi, D.R. Experimental and analytical investigation on flexural behaviour of glulam-concrete composite beams with interlayer. J. Build. Eng. 2021, 38, 102193. [Google Scholar] [CrossRef]
- Fang, J.P.; Zhou, L.Y.; Zhu, Y.B.; Li, F.G.; Dai, C.H.; Zhou, Q.; Liao, F. Experimental study on flexural behavior of modular prefabricated channel-concrete composite beams with dry connections. J. Build. Eng. 2023, 68, 106194. [Google Scholar] [CrossRef]
- Joo, H.E.; Han, S.J.; Kim, K.S. Analytical model for shear strength of prestressed hollow-core slabs reinforced with core-filling concrete. J. Build. Eng. 2021, 42, 102819. [Google Scholar] [CrossRef]
- Yoo, S.W.; Choi, Y.C.; Choi, J.H.; Choo, J.F. Nonlinear flexural analysis of composite beam with Inverted-T steel girder and UHPC slab considering partial interaction. J. Build. Eng. 2021, 34, 12. [Google Scholar] [CrossRef]
- Crocetti, R.; Sartori, T.; Tomasi, R. Innovative Timber-Concrete Composite Structures with Prefabricated FRC Slabs. J. Struct. Eng. 2015, 141, 10. [Google Scholar] [CrossRef]
- Guan, Y.; Wang, J.Q.; Li, Q.L.; Shi, Y.; Yao, X.M. Study on In-Plane and Out-of-Plane Stiffness of Cold-Formed Steel Composite Floor with Opening. J. Struct. Eng. 2024, 150, 16. [Google Scholar] [CrossRef]
- Zhang, D.S.; Lin, X.H.; Wang, H.Q.; Dong, Y.L.; Zhang, J.C.; Hu, H.C. Experimental Investigation on Fire Behavior and Quantitative Restraint Forces of Steel-Concrete Composite Floor Systems. J. Struct. Eng. 2022, 148, 14. [Google Scholar] [CrossRef]
- Liu, E.M.; Lin, M.Q.; Xie, Q.; Zhang, Y. Flexural Performance of Prestressed Composite Recycled Aggregate Slabs with Steel Tube Trusses. KSCE J. Civ. Eng. 2022, 26, 5253–5263. [Google Scholar] [CrossRef]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef]
- Liejy, M.C.; Al Zand, A.W.; Mutalib, A.A.; Abdulhameed, A.A.; Kaish, A.; Tawfeeq, W.M.; Baharom, S.; Al-Attar, A.A.; Hanoon, A.N.; Yaseen, Z.M. Prediction of the Bending Strength of a Composite Steel Beam-Slab Member Filled with Recycled Concrete. Materials 2023, 16, 2748. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Li, X.J.; Liu, C. Study on the Flexural Performance of Ultrahigh-Performance Concrete-Normal Concrete Composite Slabs. Materials 2024, 17, 4675. [Google Scholar] [CrossRef]
- Wang, X.W.; Xu, B.; Mu, R.; Qing, L.B.; Liu, Y.L.; Chen, X.S.; Chen, J.; Lei, Z.H. Flexural properties of a 2D-distributed steel fiber reinforced cement-based composite two-way slab. J. Build. Eng. 2023, 73, 106792. [Google Scholar] [CrossRef]
- Deng, B.Y.; Tan, D.; Li, L.Z.; Zhang, Z.; Cai, Z.W.; Yu, K.Q. Flexural behavior of precast ultra-lightweight ECC-concrete composite slab with lattice girders. Eng. Struct. 2023, 279, 14. [Google Scholar] [CrossRef]
- Fayed, S.; Madenci, E.; Özkiliç, Y.O.; Basha, A. The flexural behaviour of multi-layered steel fiber reinforced or ultra-high performance-normal concrete composite ground slabs. J. Build. Eng. 2024, 95, 19. [Google Scholar] [CrossRef]
- Li, T.; Deng, M.K.; Zhang, Y.X.; Zhang, W.; Guo, L.Y.; Hu, X.; Li, P.P. Study on flexural behavior of BFRCM-autoclaved aerated concrete composite slabs: Effects of slab and strengthening thickness. J. Build. Eng. 2023, 76, 14. [Google Scholar] [CrossRef]
- Mahdi, S.; Ali, M.S.M.; Sheikh, A.H.; Elchalakani, M.; Xie, T. An investigation into the feasibility of normal and fibre-reinforced ultra-high performance concrete multi-cell and composite sandwich panels. J. Build. Eng. 2021, 41, 102728. [Google Scholar] [CrossRef]
- Altoubat, S.; Ousmane, H.; Barakat, S. Experimental Study of In-Plane Shear Behavior of Fiber-Reinforced Concrete Composite Slabs. J. Struct. Eng. 2016, 142, 11. [Google Scholar] [CrossRef]
- Noshiravani, T.; Brühwiler, E. Analytical Model for Predicting Response and Flexure- Shear Resistance of Composite Beams Combining Reinforced Ultrahigh Performance Fiber- Reinforced Concrete and Reinforced Concrete. J. Struct. Eng. 2014, 140, 10. [Google Scholar] [CrossRef]
- Rajchel, M.; Kulpa, M.; Siwowski, T. Experimental Study on a Novel Shear Connection System for FRP-Concrete Hybrid Bridge Girder. Materials 2020, 13, 2045. [Google Scholar] [CrossRef]
- Sadowska-Buraczewska, B.; Szafraniec, M.; Barnat-Hunek, D.; Lagód, G. Flexural Behavior of Composite Concrete Slabs Made with Steel and Polypropylene Fibers Reinforced Concrete in the Compression Zone. Materials 2020, 13, 3616. [Google Scholar] [CrossRef]
- Soares, P.R.R.; Maciel, P.S.; Barreto, R.R.; Neto, J.T.D.; Siqueira Corrêa, E.C.; Bezerra, A.C.D. Thin Slabs Made of High-Performance Steel Fibre-Reinforced Cementitious Composite: Mechanical Behaviour, Statistical Analysis and Microstructural Investigation. Materials 2019, 12, 3297. [Google Scholar] [CrossRef]
- Park, M.K.; Lee, D.; Yang, Y.G.; Zhang, D.C.A.; Kim, K.S. Composite Performance of Prestressed Hollow-Core Slabs with Cast-in-Place Topping Concrete. ACI Struct. J. 2022, 119, 153–164. [Google Scholar] [CrossRef]
- He, Y.L.; Shen, H.B.; Zhao, W.J.; Wu, Q.Q.; Lou, T.J. Experimental study of prestressed steel-HFRC composite girders under hogging moment. Case Stud. Constr. Mater. 2024, 21, 18. [Google Scholar] [CrossRef]
- Kaspary, J.; Ehrenbring, H.Z.; Pacheco, F.; Christ, R.; Quinino, U.C.D.; Tutikian, B.F. Theoretical and experimental analysis of precast slabs composed of pre-stressed joists. Materia 2022, 27, 14. [Google Scholar] [CrossRef]
- Tahar, H.D.; Tayeb, B.; Abderezak, R.; Tounsi, A. New approach of composite wooden beam- reinforced concrete slab strengthened by external bonding of prestressed composite plate: Analysis and modeling. Struct. Eng. Mech. 2021, 78, 319–332. [Google Scholar] [CrossRef]
- GB 50010−2010; Code for the Design of Concrete Structures. China Building Industry Press: Beijing, China, 2010.
- GB/T 50081-2019; Standard for Test Methods of Mechanical and Physical Properties of Concrete. China Building Industry Press: Beijing, China, 2019.
- GB/T 50152-2012; Standard for Test Methods of Concrete Structures. China Building Industry Press: Beijing, China, 2012.
- CECS 38-2004; Technical Specification for Fiber Reinforced Concrete Structures. China Building Industry Press: Beijing, China, 2004.
- Liu, Y.L. Experimental Study and Numerical Simulation of the Stress Mechanism at the Joints of Two-Way Composite Floors; Hefei University of Technology: Hefei, China, 2014. (In Chinese) [Google Scholar]










| Mechanical Property | fcc/(N/mm2) | fcp/(N/mm2) | fts/(N/mm2) | ff/(N/mm2) |
|---|---|---|---|---|
| measured value | 75.70 | 55.60 | 5.81 | 11.38 |
| Reinforcement Location | Configuration Details |
|---|---|
| Web longitudinal reinforcement | A6@90 |
| Web distribution of steel bars | A6@140 |
| Truss upper and lower chord steel bar | C8 |
| Truss web reinforcement | A6 |
| Parameter | Expansion Angle | Eccentricity | K Coefficient | Viscosity Parameter |
|---|---|---|---|---|
| The value | 30° | 0.1 | 2/3 | 0.00045 |
| Test Piece | qt/kN/m2 | qa/kN/m2 | qa/qt |
|---|---|---|---|
| DB-1 | 5.63 | 5.25 | 0.93 |
| DB-2 | 1.04 | 1.01 | 0.97 |
| DB-3 | 6.25 | 5.63 | 0.90 |
| DB-4 | 6.88 | 6.27 | 0.91 |
| Test Piece | Mt (kN/m) | Mc (kN/m) | Mt/Mc |
|---|---|---|---|
| DB-1 | 13.51 | 14.01 | 0.96 |
| DB-2 | 2.50 | 2.53 | 0.99 |
| DB-3 | 15.00 | 14.14 | 1.06 |
| DB-4 | 16.51 | 16.04 | 1.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Liu, L.; Wang, X.; Liu, R.; Yang, H. Study on Bending Performance of High-Ductility Composite Slab Floor with Composite Ribs. Materials 2025, 18, 658. https://doi.org/10.3390/ma18030658
Jiang Y, Liu L, Wang X, Liu R, Yang H. Study on Bending Performance of High-Ductility Composite Slab Floor with Composite Ribs. Materials. 2025; 18(3):658. https://doi.org/10.3390/ma18030658
Chicago/Turabian StyleJiang, Yuchen, Libo Liu, Xiaolei Wang, Run Liu, and Haibo Yang. 2025. "Study on Bending Performance of High-Ductility Composite Slab Floor with Composite Ribs" Materials 18, no. 3: 658. https://doi.org/10.3390/ma18030658
APA StyleJiang, Y., Liu, L., Wang, X., Liu, R., & Yang, H. (2025). Study on Bending Performance of High-Ductility Composite Slab Floor with Composite Ribs. Materials, 18(3), 658. https://doi.org/10.3390/ma18030658








