Enhancing the Thermoelectric Performance of n-Type PbTe via Mn Doping
Abstract
:1. Introduction
2. Materials and Methods
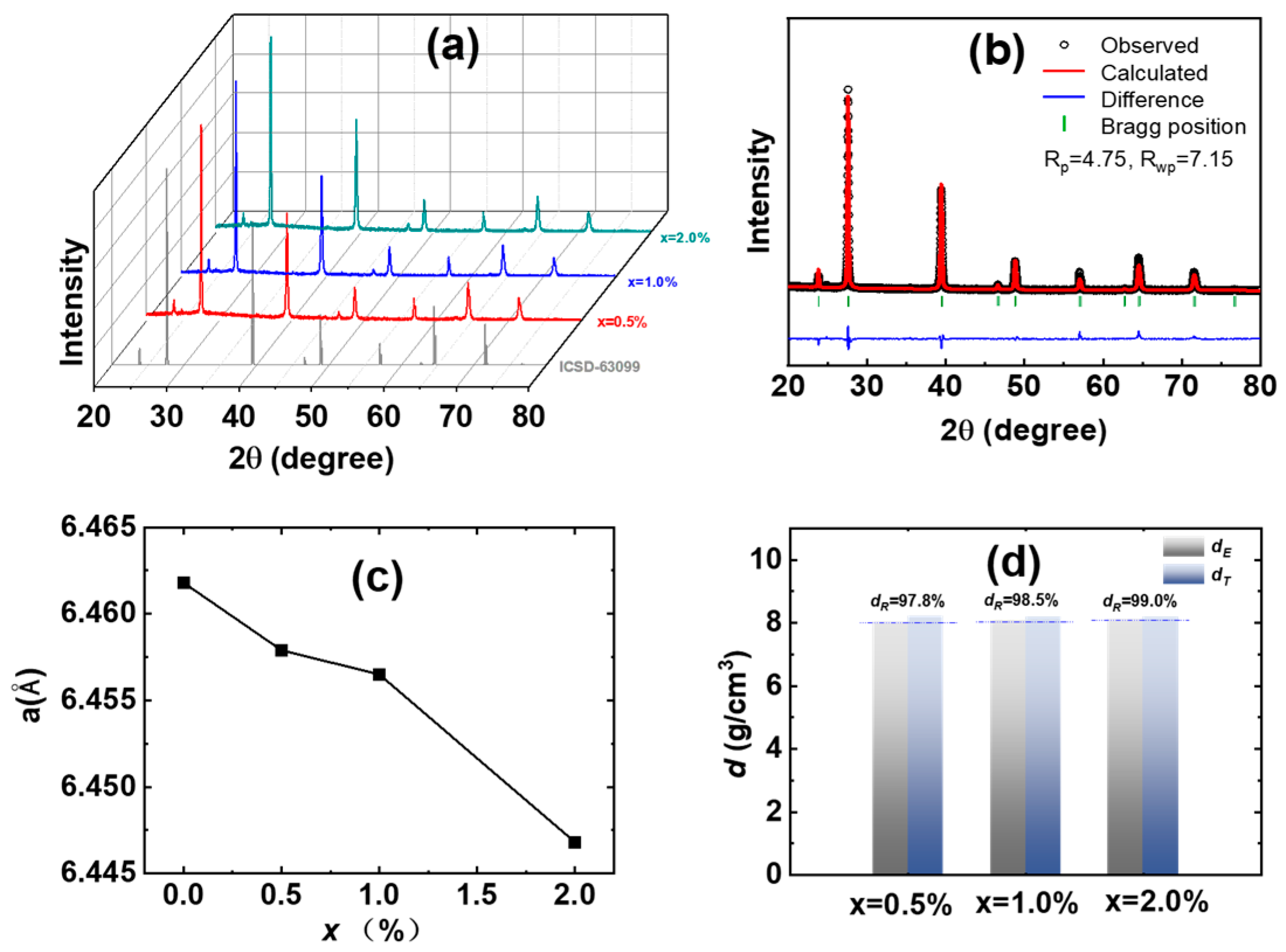
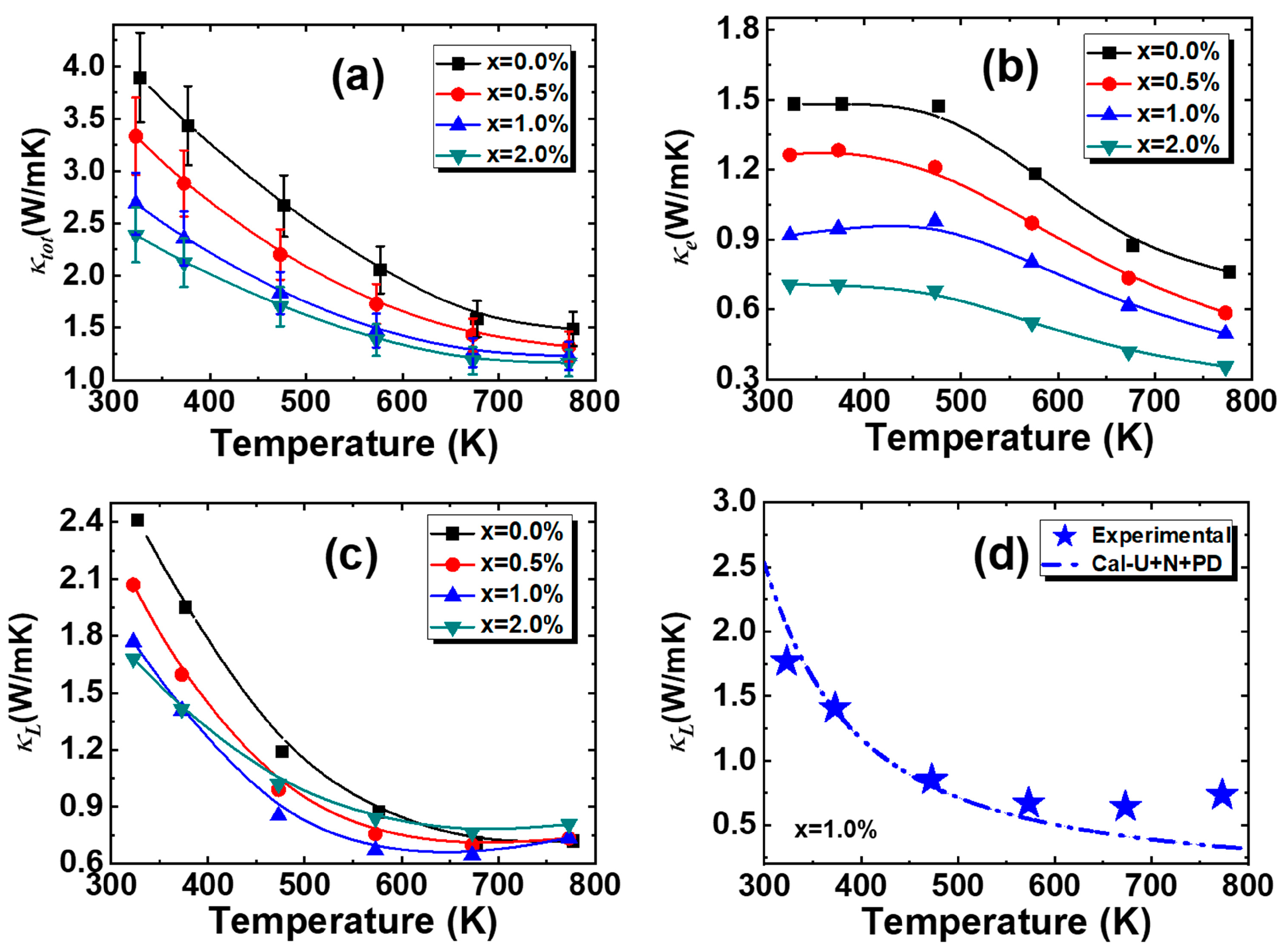
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Shi, X.-L.; Li, M.; Liu, T.; Mao, Y.; Liu, Q.; Dargusch, M.; Zou, J.; Lu, G.Q.; Chen, Z.-G. Nanobinders advance screen-printed flexible thermoelectrics. Science 2024, 386, 1265–1271. [Google Scholar] [CrossRef] [PubMed]
- Deng, T.; Gao, Z.; Li, Z.; Qiu, P.; Li, Z.; Yuan, X.; Ming, C.; Wei, T.-R.; Chen, L.; Shi, X. Room-temperature exceptional plasticity in defective Bi2Te3-based bulk thermoelectric crystals. Science 2024, 386, 1112–1117. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yu, Y.; Cui, J.; Liu, X.; Xie, L.; Liao, J.; Zhang, Q.; Huang, Y.; Ning, S.; Jia, B.; et al. High-entropy-stabilized chalcogenides with high thermoelectric performance. Science 2021, 371, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Liu, Z.; Sun, Z.; Zhang, Q.; Wei, P.; Mu, X.; Zhou, H.; Li, C.; Ma, S.; He, D.; et al. Superparamagnetic enhancement of thermoelectric performance. Nature 2017, 549, 247–251. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Wang, D.; Wang, S.; Qin, B.; Wang, Y.; Qin, Y.; Jin, Y.; Chang, C.; Zhao, L.-D. High thermoelectric performance realized through manipulating layered phonon-electron decoupling. Science 2022, 375, 1385–1389. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Zhang, K.; Wang, H.; Su, W.; Mehmood, F.; Wang, T.; Zhai, J.; Wang, X.; Huo, T.; Wang, C. The high thermoelectric performance of slightly Sb doped PbTe alloys. J. Mater. Chem. C 2020, 8, 1679–1685. [Google Scholar] [CrossRef]
- Chen, T.; Wang, H.; Su, W.; Wang, X.; Mehmood, F.; Zhang, K.; Huo, T.; Wang, C. Thermoelectric performance of Dy/Y co-doped SrTiO3 ceramic composites with submicron A2Ti2O7 (A = Dy, Y) pyrochlore. J. Phys. D Appl. Phys. 2021, 54, 155501. [Google Scholar] [CrossRef]
- Shi, X.L.; Zou, J.; Chen, Z.G. Advanced thermoelectric design: From materials and structures to devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef]
- Zhong, Y.; Tang, J.; Liu, H.; Chen, Z.; Lin, L.; Ren, D.; Liu, B.; Ang, R. Optimized strategies for advancing n-Type PbTe thermoelectrics: A review. ACS Appl. Mater. Interfaces 2020, 12, 49323–49334. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef]
- Wang, H.; Bahk, J.H.; Kang, C.; Hwang, J.; Kim, K.; Kim, J.; Burke, P.; Bowers, J.E.; Gossard, A.C.; Shakouri, A.; et al. Right sizes of nano- and microstructures for high-performance and rigid bulk thermoelectrics. Proc. Natl. Acad. Sci. USA 2014, 111, 10949–10954. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Wu, H.; Wang, D.; Niu, C.; Pei, Y.; Zhang, Y.; Spanopoulos, I.; Witting, I.T.; Li, X.; Pennycook, S.J.; et al. Amphoteric indium enables carrier engineering to enhance the power factor and thermoelectric performance in n-Type AgnPb100InnTe100+2n(LIST). Adv. Energy Mater. 2019, 9, 1900414. [Google Scholar] [CrossRef]
- Jia, B.; Huang, Y.; Wang, Y.; Zhou, Y.; Zhao, X.; Ning, S.; Xu, X.; Lin, P.; Chen, Z.; Jiang, B.; et al. Realizing high thermoelectric performance in non-nanostructured n-type PbTe. Energy Environ. Sci. 2022, 5, 1920–1929. [Google Scholar] [CrossRef]
- Luo, Z.-Z.; Cai, S.; Hao, S.; Bailey, T.P.; Luo, Y.; Luo, W.; Yu, Y.; Uher, C.; Wolverton, C.; Dravid, V.P.; et al. Extraordinary role of Zn in enhancing thermoelectric performance of Ga-doped n-type PbTe. Energy Environ. Sci. 2022, 1, 368–375. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, D.; He, D.; Feng, D.; Yin, M.; Qin, X.; He, J. Extraordinary thermoelectric performance realized in n-Type PbTe through multiphase nanostructure engineering. Adv. Mater. 2017, 29, 1703148. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Yin, M.; Wu, D.; Li, W.; Feng, D.; Huang, L.; He, J. Large enhancement of thermoelectric properties in n-type PbTe via dual-site point defects. Energy Environ. Sci. 2017, 10, 2030–2040. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, L.-D. Charge and phonon transport in PbTe-based thermoelectric materials. NPJ Quantum Mater. 2018, 3, 55. [Google Scholar] [CrossRef]
- Lee, K.H.; Oh, M.-W.; Kim, H.-S.; Shin, W.H.; Lee, K.; Lim, J.-H.; Kim, J.-I.; Kim, S.-I. Enhanced thermoelectric transport properties of n-type InSe due to the emergence of the flat band by Si doping. Inorg. Chem. Front. 2019, 6, 1475–1481. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Li, J.; Bu, Z.; Meng, X.; Ang, R.; Li, W. Band and phonon engineering for thermoelectric enhancements of rhombohedral GeTe. ACS Appl. Mater. Interfaces 2019, 11, 30756–30762. [Google Scholar] [CrossRef] [PubMed]
- Dutta, M.; Biswas, R.K.; Pati, S.K.; Biswas, K. Discordant Gd and electronic band flattening synergistically induce high thermoelectric performance in n-type PbTe. ACS Energy Lett. 2021, 6, 1625–1632. [Google Scholar] [CrossRef]
- Hong, T.; Wang, D.; Qin, B.; Zhang, X.; Chen, Y.; Gao, X.; Zhao, L.-D. Band convergence and nanostructure modulations lead to high thermoelectric performance in SnPb0.04Te-y% AgSbTe2. Mater. Today Phys. 2021, 21, 100505. [Google Scholar] [CrossRef]
- Wang, H.; Hu, H.; Man, N.; Xiong, C.; Xiao, Y.; Tan, X.; Liu, G.; Jiang, J. Band flattening and phonon-defect scattering in cubic SnSe-AgSbTe2 alloy for thermoelectric enhancement. Mater. Today Phys. 2021, 16, 100298. [Google Scholar] [CrossRef]
- Zhi, S.; Li, J.; Hu, L.; Li, J.; Li, N.; Wu, H.; Liu, F.; Zhang, C.; Ao, W.; Xie, H.; et al. Medium entropy-enabled high performance cubic gete thermoelectrics. Adv. Sci. 2021, 8, 2100220. [Google Scholar] [CrossRef]
- Zeng, X.; Ma, Z.; Li, W.; Yang, B.; Qian, Y.; Luo, Y.; Yang, J.; Liu, Y.; Jiang, Q. Entropy engineering for superior performance in BiCuSeO by band flattening and all-scale hierarchical microstructures. Chem. Eng. J. 2023, 474, 145663. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H.; Cui, J.; Wang, D.; Fu, L.; Zhang, Y.; Chen, Y.; He, J.; Pennycook, S.J.; Zhao, L.-D. Realizing high performance n-type PbTe by synergistically optimizing effective mass and carrier mobility and suppressing bipolar thermal conductivity. Energy Environ. Sci. 2018, 11, 2486–2495. [Google Scholar] [CrossRef]
- Tan, G.; Stoumpos, C.C.; Wang, S.; Bailey, T.P.; Zhao, L.-D.; Uher, C.; Kanatzidis, M.G. Subtle roles of Sb and S in regulating the thermoelectric properties of N-Type PbTe to high performance. Adv. Energy Mater. 2017, 7, 1700099. [Google Scholar] [CrossRef]
- Blachnik, R.; Igel, R. Thermodynamic properties of IV-VI-compounds: Leadchalcogenides. Z. Für Naturforschung B 1974, 29, 625–629. [Google Scholar] [CrossRef]
- Heremans, J.P.; Martin, J. Thermoelectric measurements. Nat. Mater. 2024, 23, 18–19. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Chen, S.; Zhong, Y.; Cai, J.; Zhang, Z.; Gao, F.; Huo, S.; Wu, J.; Cui, C.; Tan, X.; Liu, G.; et al. High thermoelectric performance of GeTe-MnTe alloy driven by spin degree of freedom. Mater. Today Phys. 2024, 43, 101393. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Su, W.; Wang, T.; Wang, X.; Chen, T.; Huo, T.; Dang, F.; Dong, M.; Wang, C.; et al. Trace bismuth and iodine co-doping enhanced thermoelectric performance of PbTe alloys. J. Phys. D Appl. Phys. 2020, 53, 245501. [Google Scholar] [CrossRef]
- Wang, H.; Charoenphakdee, A.; Kurosaki, K.; Yamanaka, S.; Snyder, G.J. Reduction of thermal conductivity in PbTe:Tl by alloying withTlSbTe2. Phys. Rev. B 2011, 83, 024303. [Google Scholar] [CrossRef]
- He, H.; Song, J.; Liang, R.; Yan, G.; Geng, Y.; Hu, L.; Liu, F.; Ao, W.; Zhang, C. Multicomponent synergistic doping enables high-efficiency n-type pbte thermoelectric devices. Small 2024, 21, 2408864. [Google Scholar] [CrossRef] [PubMed]
- Jood, P.; Ohta, M.; Kunii, M.; Hu, X.; Nishiate, H.; Yamamoto, A.; Kanatzidis, M.G. Enhanced average thermoelectric figure of merit of n-type PbTe1−xIx—MgTe. J. Mater. Chem. C 2015, 3, 10401–10408. [Google Scholar] [CrossRef]
- Kim, H.-S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef]
- Gao, F.; Cai, J.; Li, M.; Chen, Z.; Wang, Y.; Zhang, Z.; Chen, L.; Hu, D.; Tan, X.; Wu, J.; et al. Thermoelectric performance optimization of n-type PbTe by In and Cu2Te co-doping and anomalous temperature-dependent transport. J. Mater. Chem. A 2024, 12, 11875–11882. [Google Scholar] [CrossRef]
- Chen, Z.; Li, M.; Chen, Z.; Wang, Y.; Zhou, D.; Huang, X.; Zhang, X.; Guo, R.; Liu, X.; Wang, Z. Enhancing n-type PbTe thermoelectric performance through Cd alloying and strategic defects management. J. Alloys Compd. 2024, 1002, 175183. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H.; Shi, H.; Xu, L.; Zhu, Y.; Qin, Y.; Peng, G.; Zhang, Y.; Ge, Z.-H.; Ding, X.; et al. High-ranged ZT value promotes thermoelectric cooling and power generation in n-Type PbTe. Adv. Energy Mater. 2022, 12, 2200204. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Shao, Y.; Feng, R.; Zhang, J.; Wang, Q.; Dong, Y.; Ma, H.; Sun, B.; Ao, D. Enhancing the Thermoelectric Performance of n-Type PbTe via Mn Doping. Materials 2025, 18, 1029. https://doi.org/10.3390/ma18051029
Chen T, Shao Y, Feng R, Zhang J, Wang Q, Dong Y, Ma H, Sun B, Ao D. Enhancing the Thermoelectric Performance of n-Type PbTe via Mn Doping. Materials. 2025; 18(5):1029. https://doi.org/10.3390/ma18051029
Chicago/Turabian StyleChen, Tingting, Yaqi Shao, Ruilin Feng, Junxiang Zhang, Qidong Wang, Yanan Dong, Hongan Ma, Bing Sun, and Dongwei Ao. 2025. "Enhancing the Thermoelectric Performance of n-Type PbTe via Mn Doping" Materials 18, no. 5: 1029. https://doi.org/10.3390/ma18051029
APA StyleChen, T., Shao, Y., Feng, R., Zhang, J., Wang, Q., Dong, Y., Ma, H., Sun, B., & Ao, D. (2025). Enhancing the Thermoelectric Performance of n-Type PbTe via Mn Doping. Materials, 18(5), 1029. https://doi.org/10.3390/ma18051029





