Theoretical Investigation and Parametric Sensitivity Analysis of Polypropylene–Polyester Fiber-Reinforced Recycled Brick Aggregate Concrete Pavement Humidity Warping Stress During the Service Life
Abstract
1. Introduction
2. Theoretical Methods
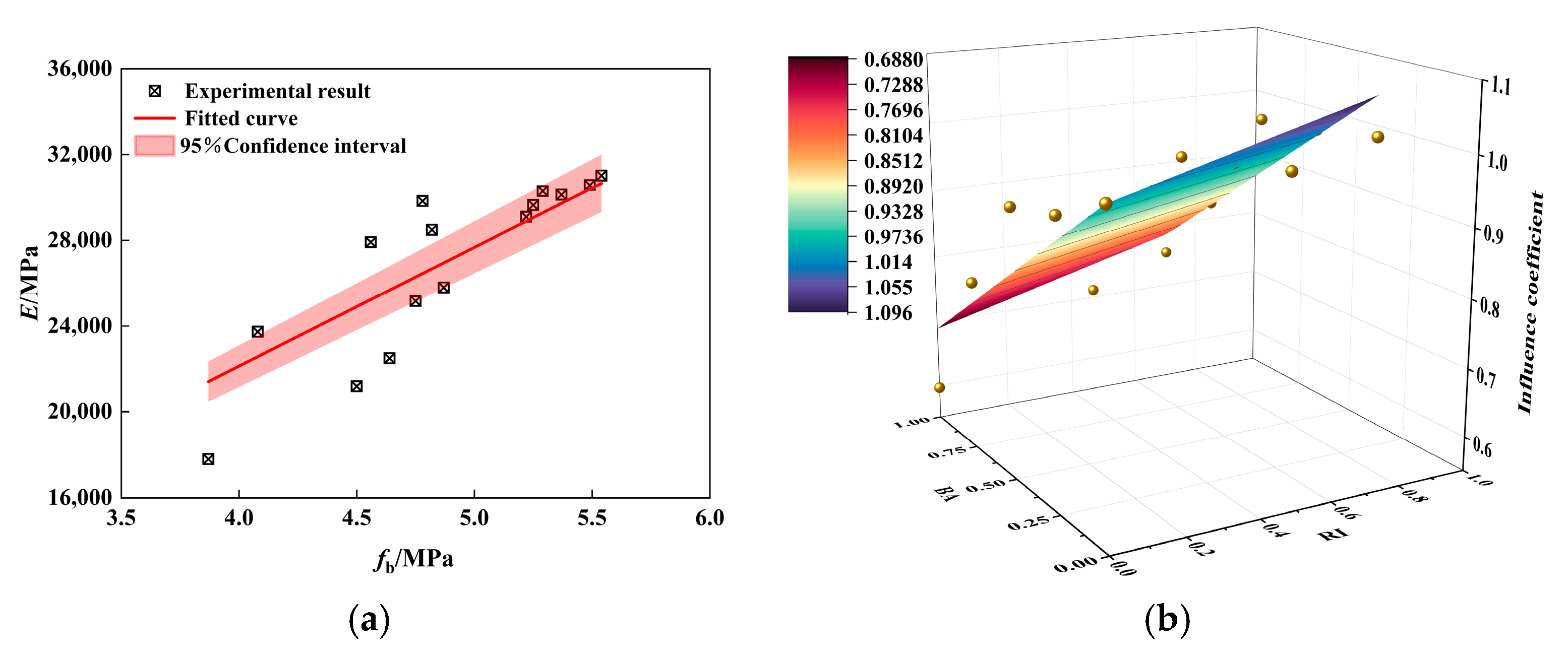
2.1. Elastic Modulus Prediction Model of PPRBAC
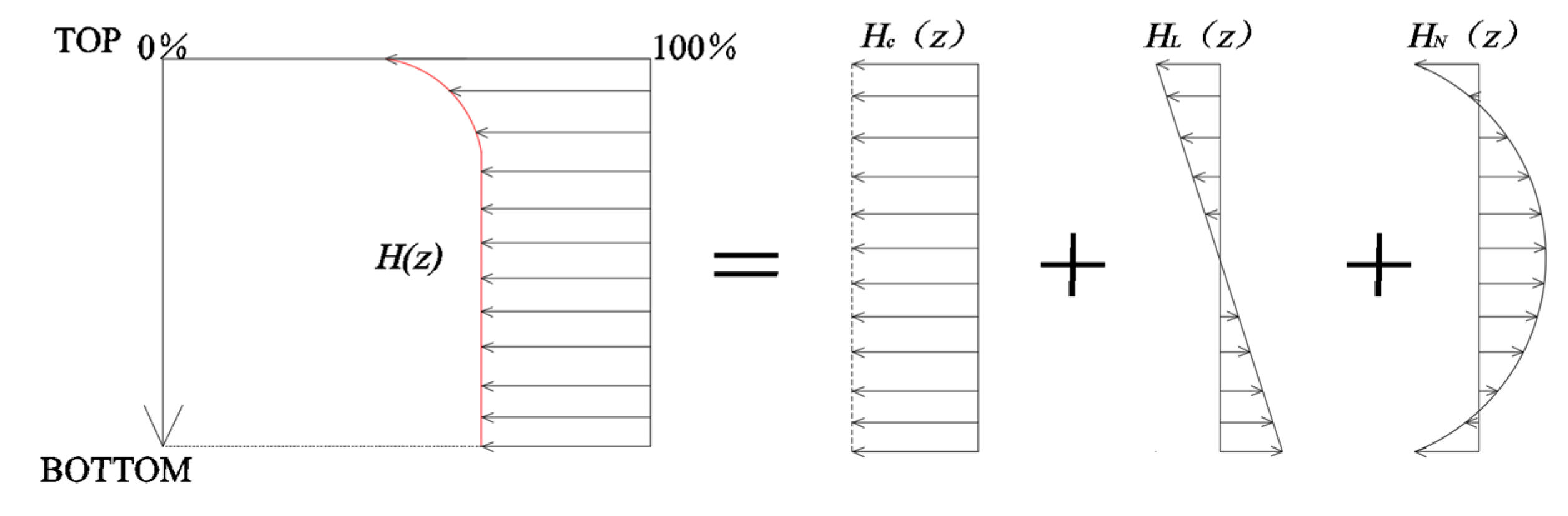
2.2. Calculation Method for Nonlinear Humidity Warping of PPFRAC Slabs
2.3. Gray Relational Computing Theory
3. Results and Discussion
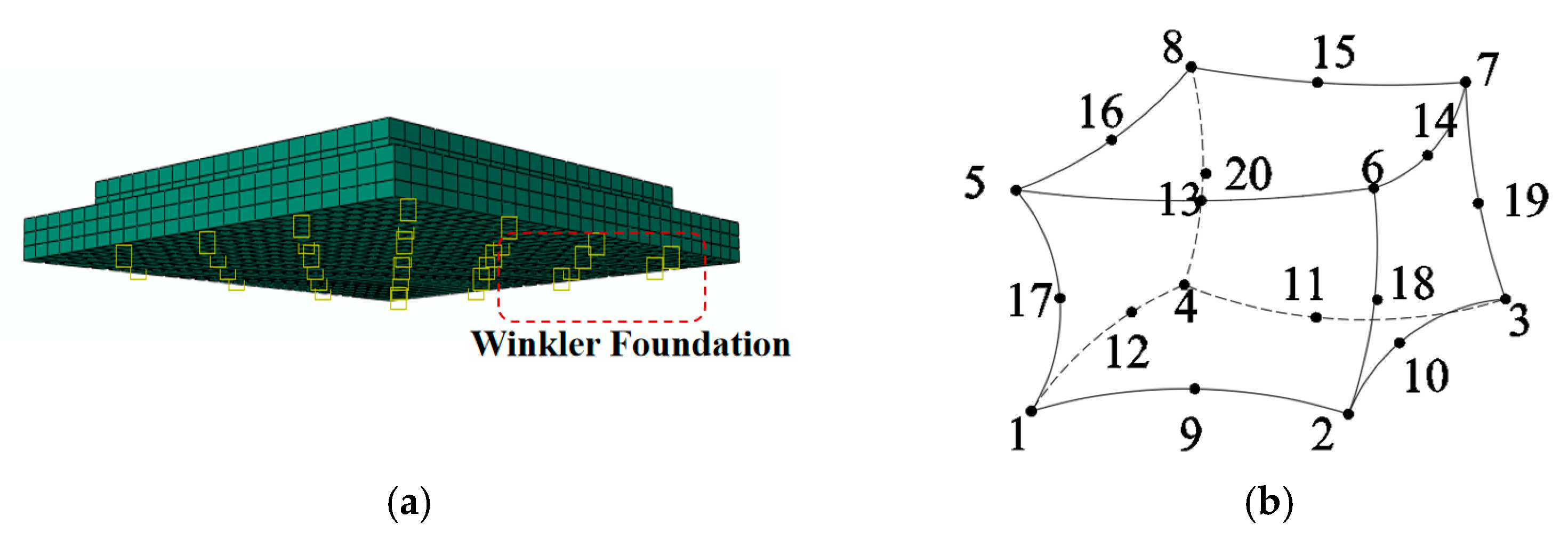
3.1. PPRBAC Pavement Humidity Warping Stress Theoretical Analytical Method
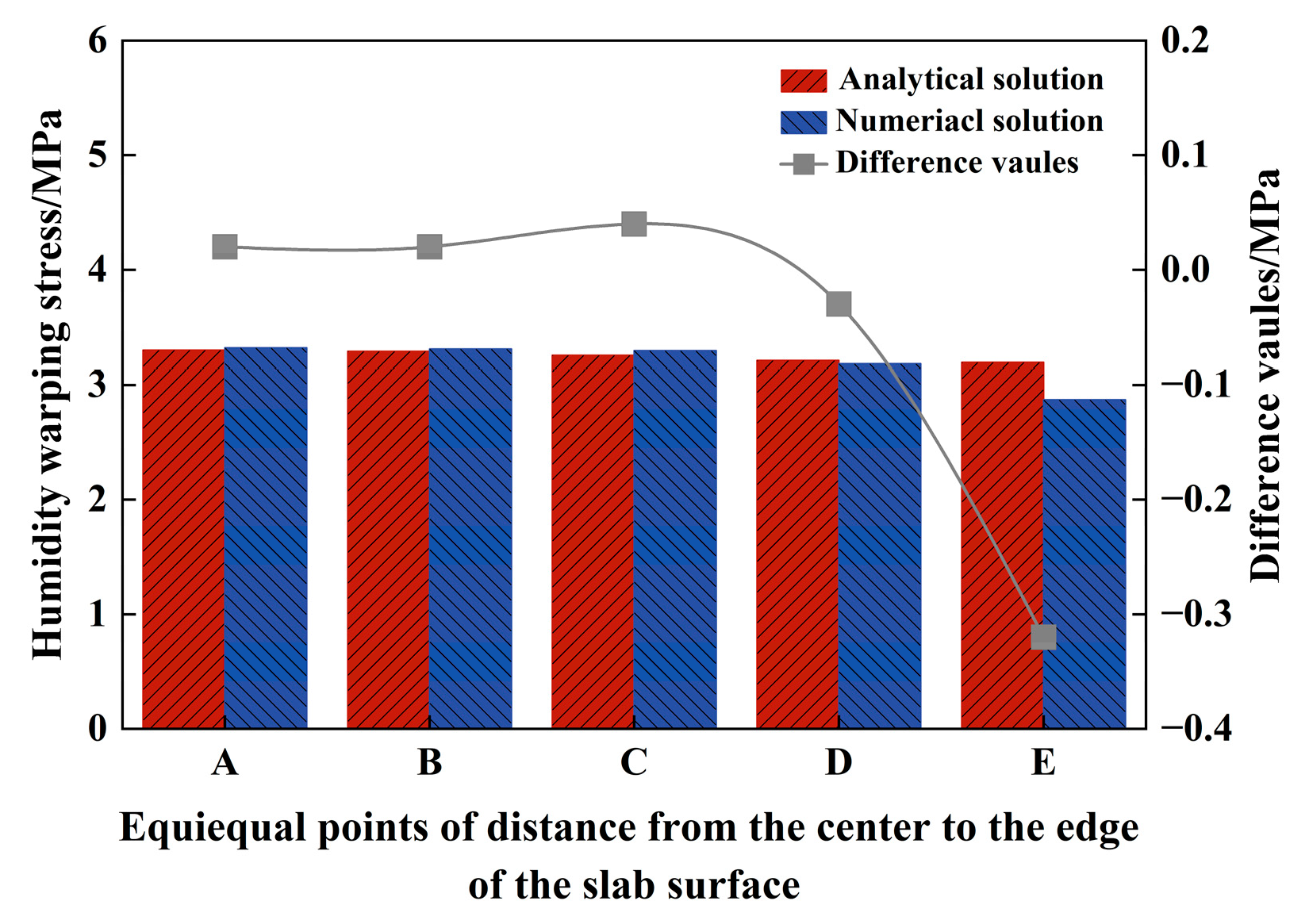
3.2. Reliability Verification of Shrinkage Equivalent Calculation Method
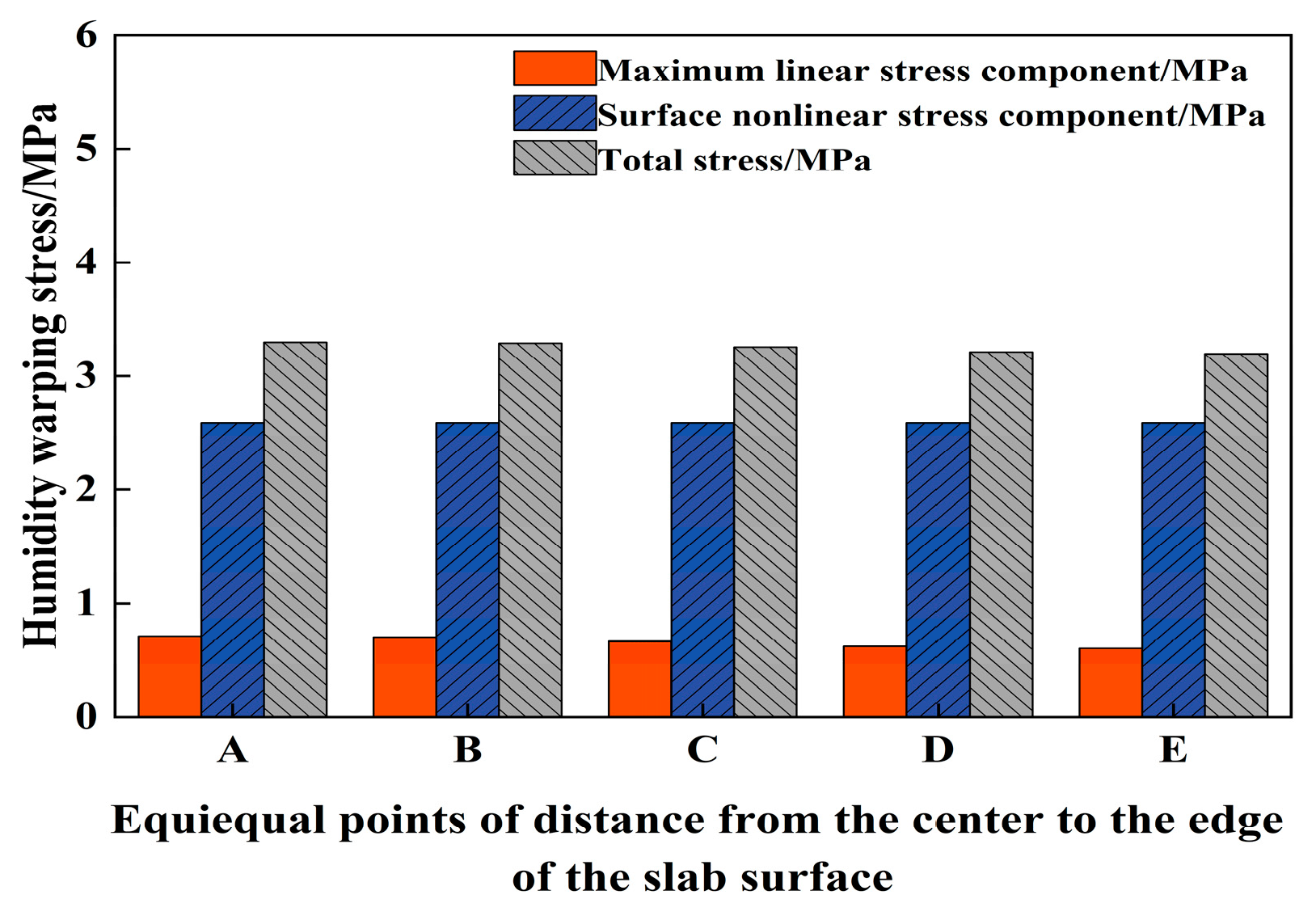
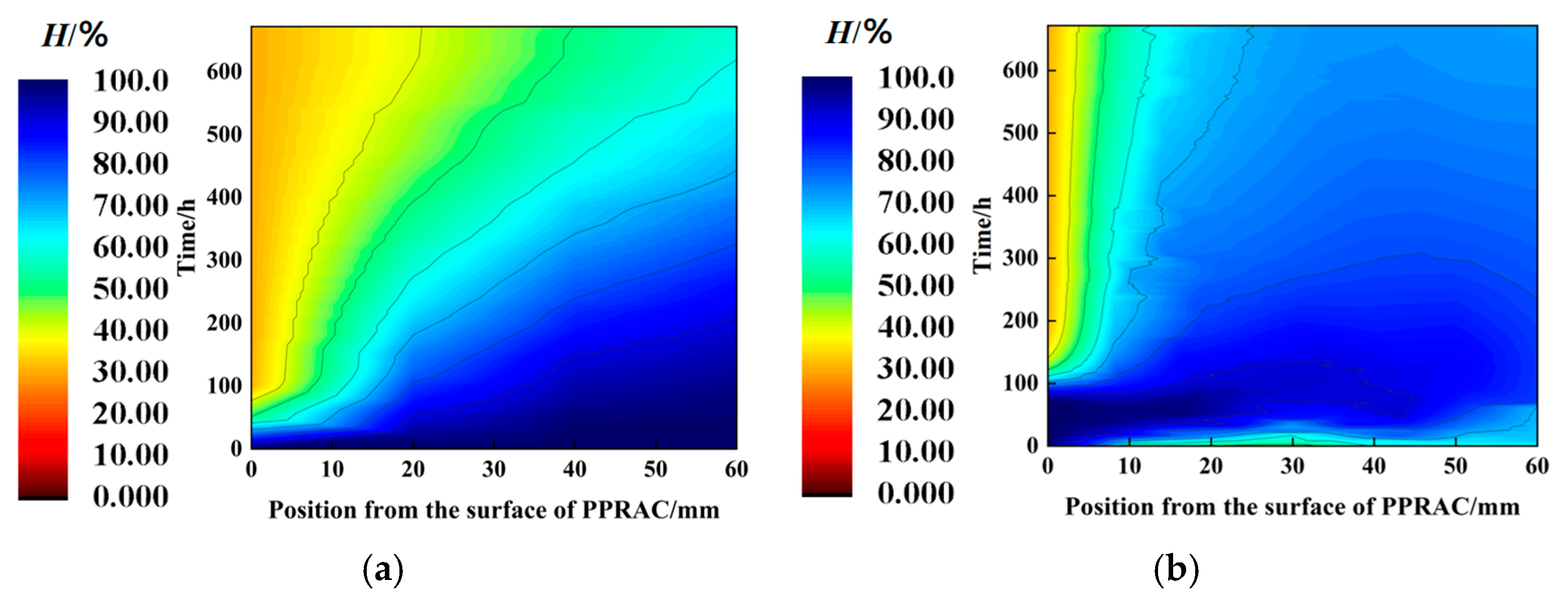
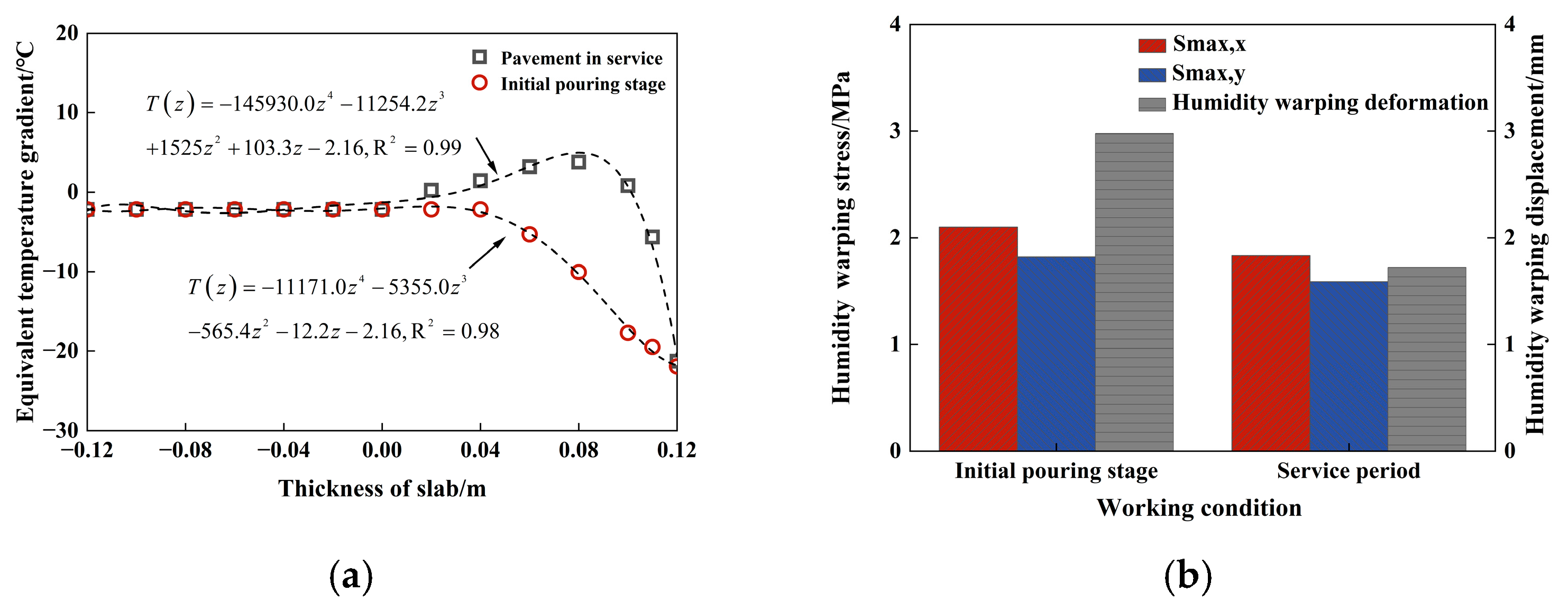
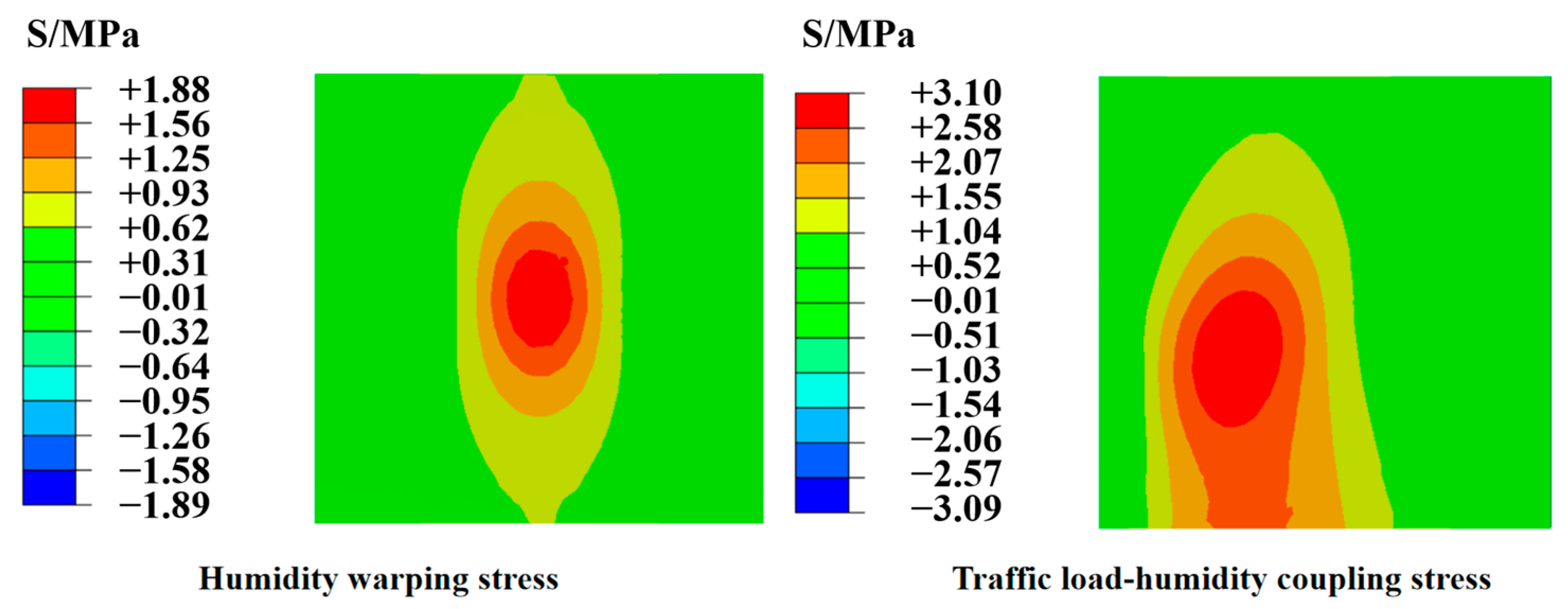
3.3. Calculation of PPRBAC Pavement Moisture Warping Stress During Service Period
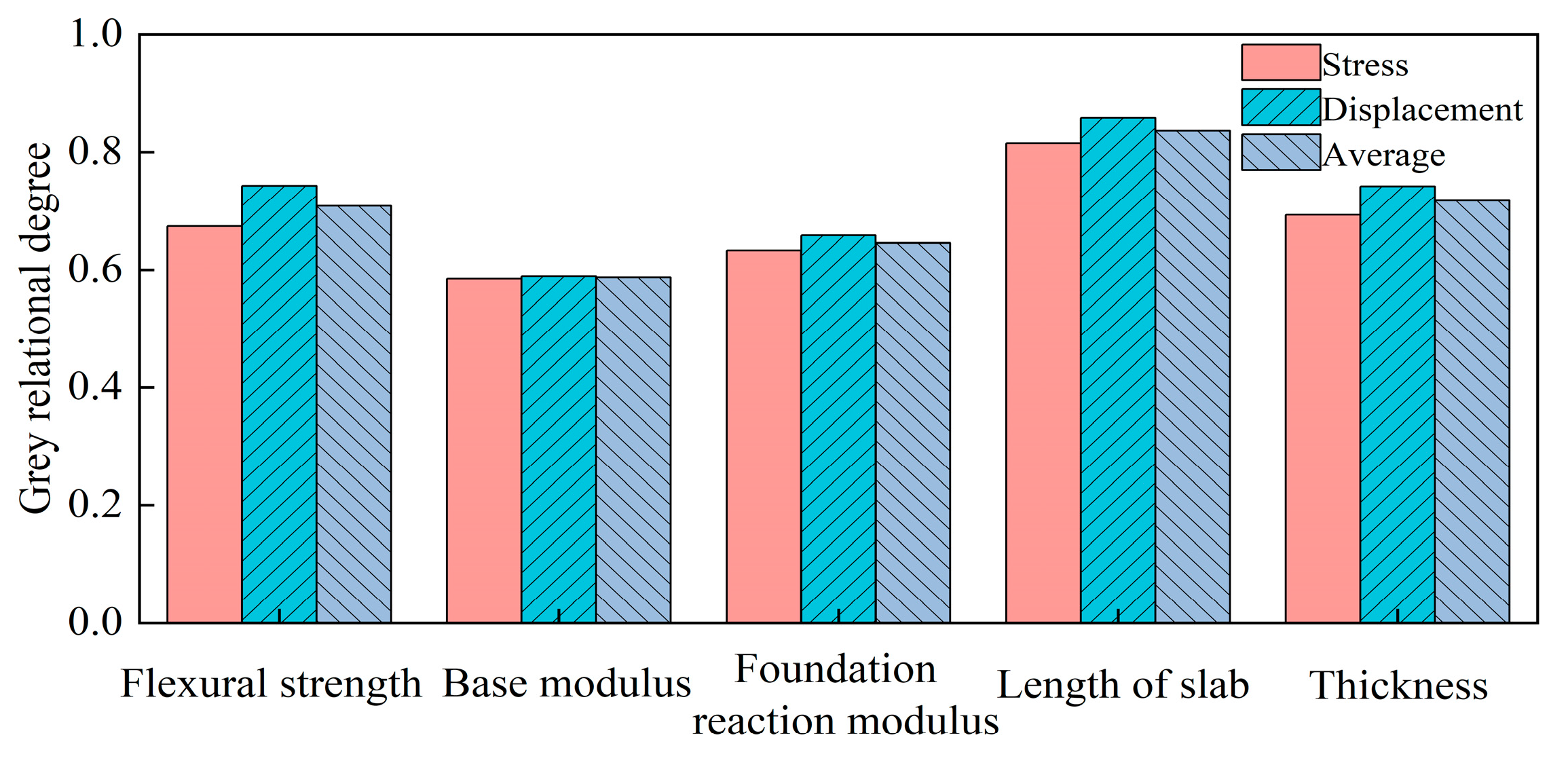
3.4. Parameter Sensitivity Analysis Based on Taguchi–GRA
4. Conclusions
- (1)
- In conjunction with prior research findings, the conversion relationship established between flexural strength and elastic modulus demonstrates high accuracy, with a correlation coefficient R2 reaching 0.85. The predictive model incorporates adjustments for the BA substitution rate and PPF content, ensuring high reliability.
- (2)
- The nonlinear humidity warping stress formula for PPRBAC pavement slabs is derived based on flexural strength considerations. A comparison between the bending moment equivalent method and the contraction equivalent method reveals that the former fails to accurately capture the nonlinearity of PPRBAC wetness warping stress, leading to a significant underestimation of this stress. Furthermore, numerical simulations validate the rationality and accuracy of the contraction equivalent method.
- (3)
- The PPRBAC pavement slab will experience humidity-induced warping stress and deformation due to the uneven distribution of moisture gradients. The stress state during the service life is calculated based on the assumption of initial pouring conditions (initial saturation, without considering subsequent wetting and drying cycles). This approach tends to overestimate the impact of the wetting phase on the drying phase. Specifically, the final calculated values for warping stress and displacement under this assumption are approximately 1.1 and 1.7 times higher, respectively, compared to the scenario where wetting precedes drying. Therefore, it is essential to account for the influence of the wetting stage on the drying stage when evaluating the humidity-induced warping stress of PPRBAC pavement slabs in service.
- (4)
- The Taguchi–gray relational analysis (Taguchi–GRA) method was employed to determine the weights of each influencing factor associated with PPRBAC road wet-warping. Based on the indices of warping displacement and warping stress, the length, thickness, and flexural strength have a more significant impact on PPRBAC pavement humidity warping than other factors. Therefore, these parameters should be prioritized as key control indices during the design and construction phases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akbarnezhad, A.; Ong, K.C.G.; Tam, C.T.; Zhang, M.H. Effects of the parent concrete properties and crushing procedure on the properties of coarse recycled concrete aggregates. J. Mater. Civ. Eng. 2013, 25, 1795–1802. [Google Scholar] [CrossRef]
- Bao, J.; Yu, Z.; Zhang, P.; Li, S.; Zhao, T. Research progress on frost resistance of recycled coarse aggregate concrete and its components. J. Build. Struct. 2020, 4, 142–157. [Google Scholar]
- Visintin, P.; Xie, T.; Bennett, B. A large-scale life-cycle assessment of recycled aggregate concrete: The influence of functional unit, emissions allocation and carbon dioxide uptake. J. Clean. Prod. 2020, 248, 119243. [Google Scholar] [CrossRef]
- Kim, H.K.; Lim, Y.; Tafesse, M.; Kim, G.M.; Yang, B. Micromechanics-integrated machine learning approaches to predict the mechanical behaviors of concrete containing crushed clay brick aggregates. Constr. Build. Mater. 2022, 317, 125840. [Google Scholar] [CrossRef]
- Meng, T.; Yang, X.; Wei, H.; Meng, R.; Zhou, W. Study of the relationship between the water binder ratio and strength of mixed recycled aggregate concrete based on brick content. Constr. Build. Mater. 2023, 394, 132148. [Google Scholar] [CrossRef]
- Tan, G.; Gong, S.; Wang, T.; Li, M.; Li, J.; Ren, X.; Zhang, W.; Wang, C.; Cao, F.; Su, T. Mechanical Damage and Freeze–Thaw Damage of Concrete with Recycled Brick Coarse Aggregate. Sustainability 2024, 16, 5643. [Google Scholar] [CrossRef]
- Omidinasab, F.; Moazami Goodarzi, S.; Sahraei, M.A. Characterization and optimization of mechanical and impact properties of steel fiber reinforced recycled concrete. Int. J. Civ. Eng. 2022, 20, 41–55. [Google Scholar] [CrossRef]
- Toghroli, A.; Mehrabi, P.; Shariati, M.; Trung, N.T.; Jahandari, S.; Jahandari, H. Evaluating the use of recycled concrete aggregate and pozzolanic additives in fiber-reinforced pervious concrete with industrial and recycled fibers. Constr. Build. Mater. 2020, 252, 118997. [Google Scholar] [CrossRef]
- Mehrabi, P.; Shariati, M.; Kabirifar, K.; Jarrah, M.; Rasekh, H.; Trung, N.T.; Shariati, A.; Jahandari, S. Effect of pumice powder and nano-clay on the strength and permeability of fiber-reinforced pervious concrete incorporating recycled concrete aggregate. Constr. Build. Mater. 2021, 287, 122652. [Google Scholar] [CrossRef]
- Rishav, G.; Rajni, G. Performance evaluation of polypropylene fiber waste reinforced concrete in presence of silica fume. Mater. Today Proc. 2021, 43, 809–816. [Google Scholar]
- Yuan, Z.; Jia, Y. Mechanical properties and microstructure of glass fiber and polypropylene fiber reinforced concrete: An experimental study. Constr. Build. Mater. 2021, 266, 121048. [Google Scholar] [CrossRef]
- Małek, M.; Jackowski, M.; Łasica, W.; Kadela, M. Characteristics of recycled polypropylene fibers as an addition to concrete fabrication based on portland cement. Materials 2020, 13, 1827. [Google Scholar] [CrossRef] [PubMed]
- Jorbat, M.H.; Hosseini, M.; Mahdikhani, M. Effect of polypropylene fibers on the mode I, mode II, and mixed-mode fracture toughness and crack propagation in fiber-reinforced concrete. Theor. Appl. Fract. Mech. 2020, 109, 102723. [Google Scholar] [CrossRef]
- Li, F.; Jin, S.; Cheng, P.; Wang, Z.; Yang, Z. Study on Mechanical Properties and Carbon Emission Analysis of Polypropylene Fiber-Reinforced Brick Aggregate Concrete. Polymers 2024, 16, 3535. [Google Scholar] [CrossRef]
- Rao, S.; Roesler, J.R. Characterizing effective built-in curling from concrete pavement field measurements. J. Transp. Eng. 2005, 131, 320–327. [Google Scholar] [CrossRef]
- Wei, Y.; Liang, S.; Gao, X. Numerical Evaluation of Moisture Warping and Stress in Concrete Pavement Slabs with Different Water-to-Cement Ratio and Thickness. J. Eng. Mech. 2017, 143, 0401611. [Google Scholar] [CrossRef]
- Wei, Y.; Gao, X.; Hansen, W. Influential depth by water absorption and surface drying in concrete slabs. Transp. Res. Rec. J. Transp. Res. Board 2013, 2342, 76–82. [Google Scholar] [CrossRef]
- JTG D40-2011; Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Cement Concrete Pavement. China Standard Press: Beijing, China, 2011.
- Wang, X.; Zhang, Y.; Liu, Z. Influence of Temperature and Moisture Warping on Reinforcement Design of CRCP. J. Highw. Transp. Res. Dev. 2021, 38, 33–40. [Google Scholar]
- Zhu, H.; Zeng, X.; Liu, H.; Ling, C.; Pan, Z.; Chen, L.; Kang, J.; Chen, H.; Peng, C.; Wang, J. Structural Design and Analysis of Concrete Pavement with Portland cement for road. HIGHWAY 2019, 64, 1–8. [Google Scholar]
- Chen, X.; Zhu, H.; Fan, S.; Wang, W.; Chen, R. Analysis on Mechanical Response of Void beneath Cement Concrete Pavement Slab under load-temperature-water Interaction. J. Highw. Transp. Res. Dev. 2022, 39, 11–19. [Google Scholar]
- Wei, Y. Mechanism of moisture warping and deformation calculations in concrete pavements. Eng. Mech. 2012, 29, 266–271. [Google Scholar]
- Gong, S.; Bai, L.; Tan, Z.; Xu, L.; Bai, X.; Huang, Z. Mechanical Properties of Polypropylene Fiber Recycled Brick Aggregate Concrete and Its Influencing Factors by Gray Correlation Analysis. Sustainability 2023, 15, 11135. [Google Scholar] [CrossRef]
- Gurpreet, S.; Navdeep, S. Destructive and non-destructive strength performance of iron slag recycled aggregate concrete using regression and grey correlation analysis. Measurement 2025, 239, 115422. [Google Scholar]
- Tang, Y.; Qiu, W.; Liu, D.; Zhang, W.; Zhang, R. Experimental Study on the Properties of Mortar and Concrete Made with Tunnel Slag Machine-Made Sand. Materials 2022, 15, 4817. [Google Scholar] [CrossRef]
- Zhu, C.; He, N.; Zhang, X.; Liu, X. Experimental Study on Deformation Properties of Basalt Fiber Reinforced Recycled Aggregate Concrete. Coatings 2022, 12, 632. [Google Scholar] [CrossRef]
- Liu, X. Research on Moisture Migration and Humidity Wappage of Cement Concrete Pavement Slab; Harbin Institute of Technology: Harbin, China, 2020. [Google Scholar]
- Yao, Z. Highway Design Manual-Pavement; China Communications Press: Beijing, China, 2006. [Google Scholar]
- Sun, J. Research on Moisture Transport Under Wetting and Drying Conditions; Zhejiang University: Hangzhou, China, 2012. [Google Scholar]
- Liang, S.; Wei, Y. Modelling of creep effect on moisture warping and stress developments in concrete pavement slabs. Int. J. Pavement Eng. 2018, 19, 429–438. [Google Scholar] [CrossRef]




| Number | Flexural Strength /MPa | Base Modulus /MPa | Foundation Reaction Modulus/MPa | Length of Slab /m | Thickness of Slab/m |
|---|---|---|---|---|---|
| 1 | 5.5 | 2000 | 125 | 3.0 | 0.20 |
| 2 | 5.5 | 1500 | 100 | 3.5 | 0.22 |
| 3 | 5.5 | 1000 | 75 | 4.0 | 0.24 |
| 4 | 5.5 | 500 | 50 | 4.5 | 0.26 |
| 5 | 5.0 | 2000 | 75 | 4.0 | 0.26 |
| 6 | 5.0 | 1500 | 125 | 4.5 | 0.24 |
| 7 | 5.0 | 1000 | 50 | 3.0 | 0.22 |
| 8 | 5.0 | 500 | 100 | 3.5 | 0.20 |
| 9 | 4.5 | 2000 | 50 | 4.5 | 0.22 |
| 10 | 4.5 | 1500 | 125 | 4.0 | 0.20 |
| 11 | 4.5 | 1000 | 100 | 3.5 | 0.26 |
| 12 | 4.5 | 500 | 75 | 3.0 | 0.24 |
| 13 | 4.0 | 2000 | 50 | 3.5 | 0.24 |
| 14 | 4.0 | 1500 | 75 | 3.0 | 0.26 |
| 15 | 4.0 | 1000 | 100 | 4.5 | 0.20 |
| 16 | 4.0 | 500 | 125 | 4.0 | 0.22 |
| Number | Flexural Strength /MPa | Base Modulus /MPa | Foundation Reaction Modulus/MPa | Length of Slab /m | Thickness of Slab/m | Warping Stress/MPa | Warping Displacement/mm |
|---|---|---|---|---|---|---|---|
| 1 | 5.5 | 2000 | 125 | 3.0 | 0.20 | 1.299 | 1.667 |
| 2 | 5.5 | 1500 | 100 | 3.5 | 0.22 | 1.502 | 2.252 |
| 3 | 5.5 | 1000 | 75 | 4.0 | 0.24 | 1.730 | 2.885 |
| 4 | 5.5 | 500 | 50 | 4.5 | 0.26 | 1.876 | 3.578 |
| 5 | 5.0 | 2000 | 75 | 4.0 | 0.26 | 1.733 | 2.935 |
| 6 | 5.0 | 1500 | 125 | 4.5 | 0.24 | 2.231 | 3.341 |
| 7 | 5.0 | 1000 | 50 | 3.0 | 0.22 | 1.040 | 1.747 |
| 8 | 5.0 | 500 | 100 | 3.5 | 0.20 | 1.415 | 2.103 |
| 9 | 4.5 | 2000 | 50 | 4.5 | 0.22 | 2.326 | 3.026 |
| 10 | 4.5 | 1500 | 125 | 4.0 | 0.20 | 1.981 | 2.465 |
| 11 | 4.5 | 1000 | 100 | 3.5 | 0.26 | 1.204 | 2.301 |
| 12 | 4.5 | 500 | 75 | 3.0 | 0.24 | 0.866 | 1.758 |
| 13 | 4.0 | 2000 | 50 | 3.5 | 0.24 | 1.378 | 2.197 |
| 14 | 4.0 | 1500 | 75 | 3.0 | 0.26 | 0.917 | 1.744 |
| 15 | 4.0 | 1000 | 100 | 4.5 | 0.20 | 2.127 | 2.645 |
| 16 | 4.0 | 500 | 125 | 4.0 | 0.22 | 1.982 | 2.917 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Jin, S.; Cheng, P.; Wang, Z. Theoretical Investigation and Parametric Sensitivity Analysis of Polypropylene–Polyester Fiber-Reinforced Recycled Brick Aggregate Concrete Pavement Humidity Warping Stress During the Service Life. Materials 2025, 18, 1093. https://doi.org/10.3390/ma18051093
Li F, Jin S, Cheng P, Wang Z. Theoretical Investigation and Parametric Sensitivity Analysis of Polypropylene–Polyester Fiber-Reinforced Recycled Brick Aggregate Concrete Pavement Humidity Warping Stress During the Service Life. Materials. 2025; 18(5):1093. https://doi.org/10.3390/ma18051093
Chicago/Turabian StyleLi, Fei, Shenghao Jin, Peifeng Cheng, and Zehui Wang. 2025. "Theoretical Investigation and Parametric Sensitivity Analysis of Polypropylene–Polyester Fiber-Reinforced Recycled Brick Aggregate Concrete Pavement Humidity Warping Stress During the Service Life" Materials 18, no. 5: 1093. https://doi.org/10.3390/ma18051093
APA StyleLi, F., Jin, S., Cheng, P., & Wang, Z. (2025). Theoretical Investigation and Parametric Sensitivity Analysis of Polypropylene–Polyester Fiber-Reinforced Recycled Brick Aggregate Concrete Pavement Humidity Warping Stress During the Service Life. Materials, 18(5), 1093. https://doi.org/10.3390/ma18051093





