Static Liquefaction of Tailings Containing Fines: Experimental Exploration, Mechanism Analysis and Evaluation
Abstract
1. Introduction
- (i)
- The impact of fines on the static liquefaction of coarse-grained soil is still unclear, and there is a lack of experimental data on the effect of FC;
- (ii)
- The compressibility evaluation parameters of soil are not uniform, and there is a lack of systematic research on their relationship with static liquefaction;
- (iii)
- There is still a lack of experimental research on the static liquefaction problems pertaining to tailings, a special granular material.
- (i)
- To study the effects of the initial state and FC of tailings on the critical state, the instability line, undrained shear strength, and the brittleness index;
- (ii)
- To compare two existing compressibility parameters and analyze their advantages and disadvantages;
- (iii)
- To identify the relationship between tailings’ compressibility and static liquefaction and evaluate static liquefaction using compressibility parameters within the critical state framework.
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. CUTC Tests
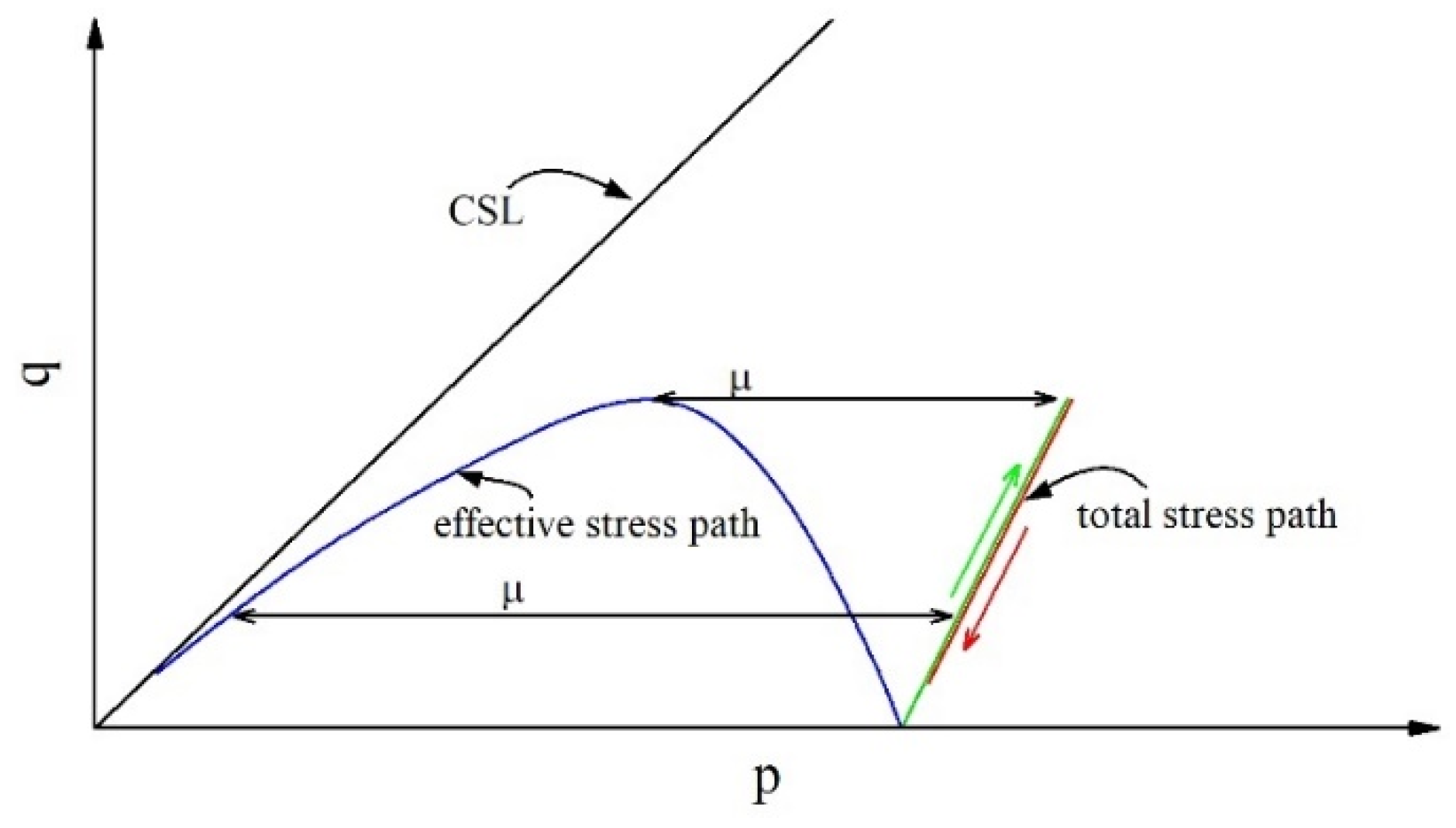
2.2.2. OC Tests
3. Results and Analysis
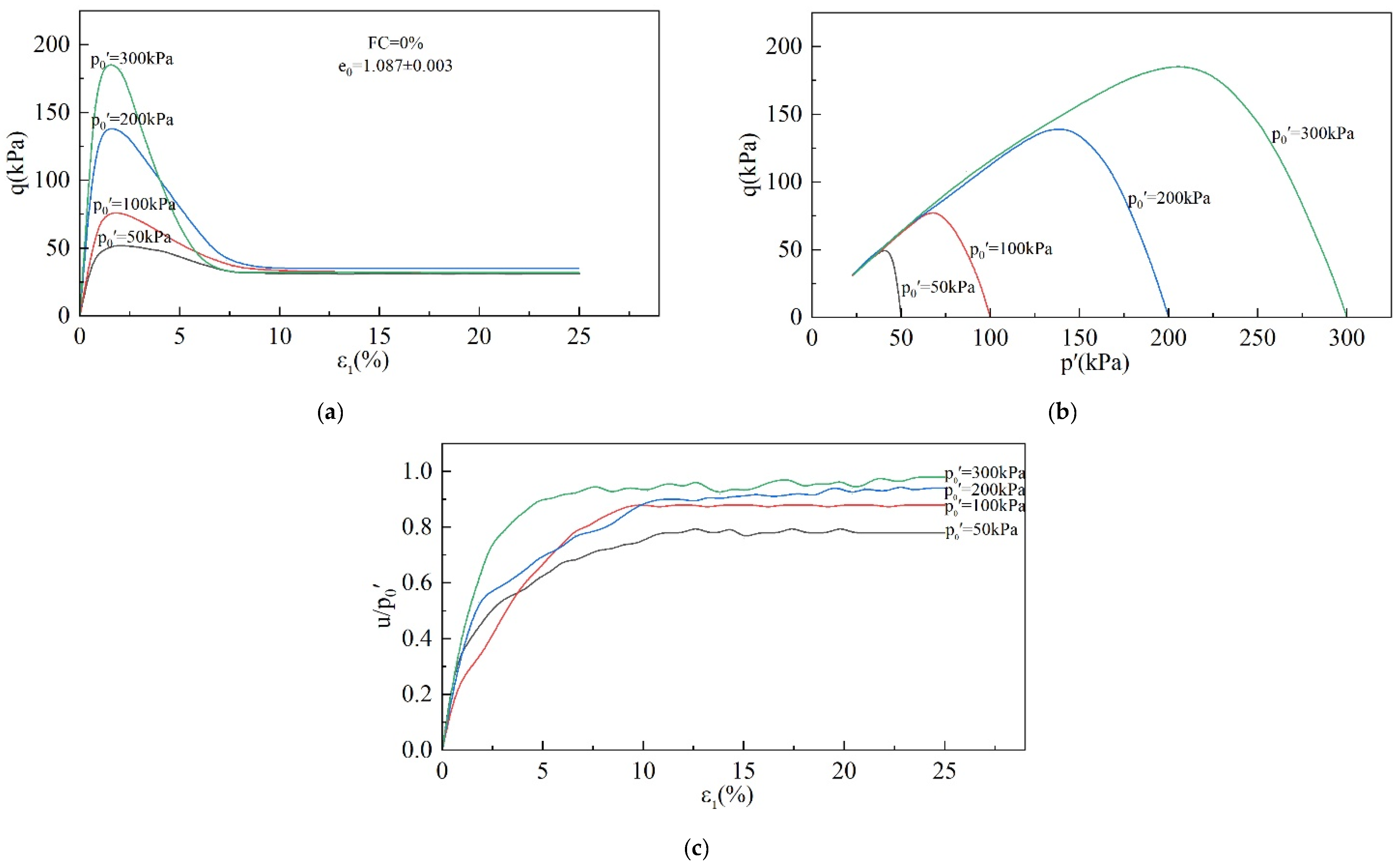
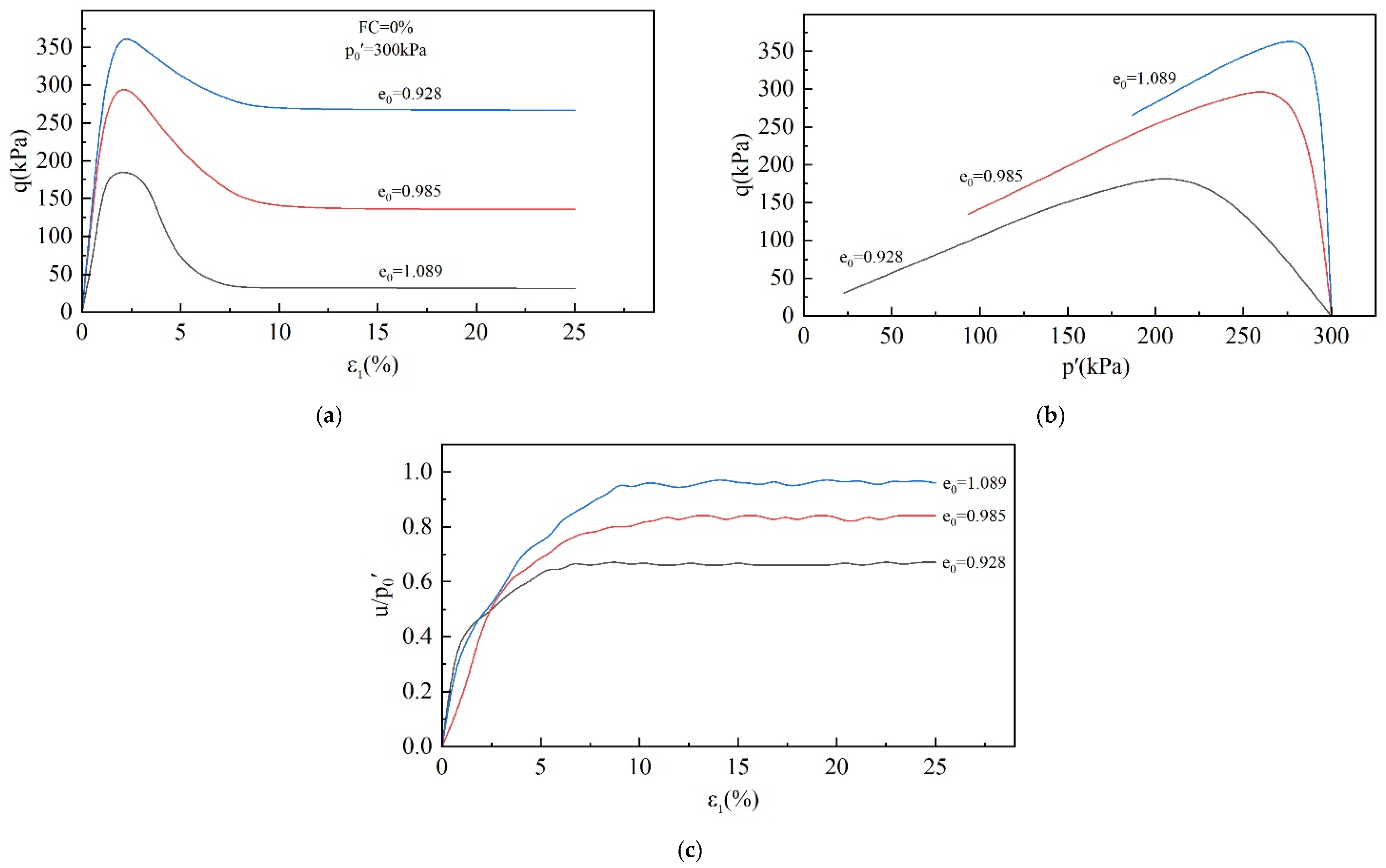
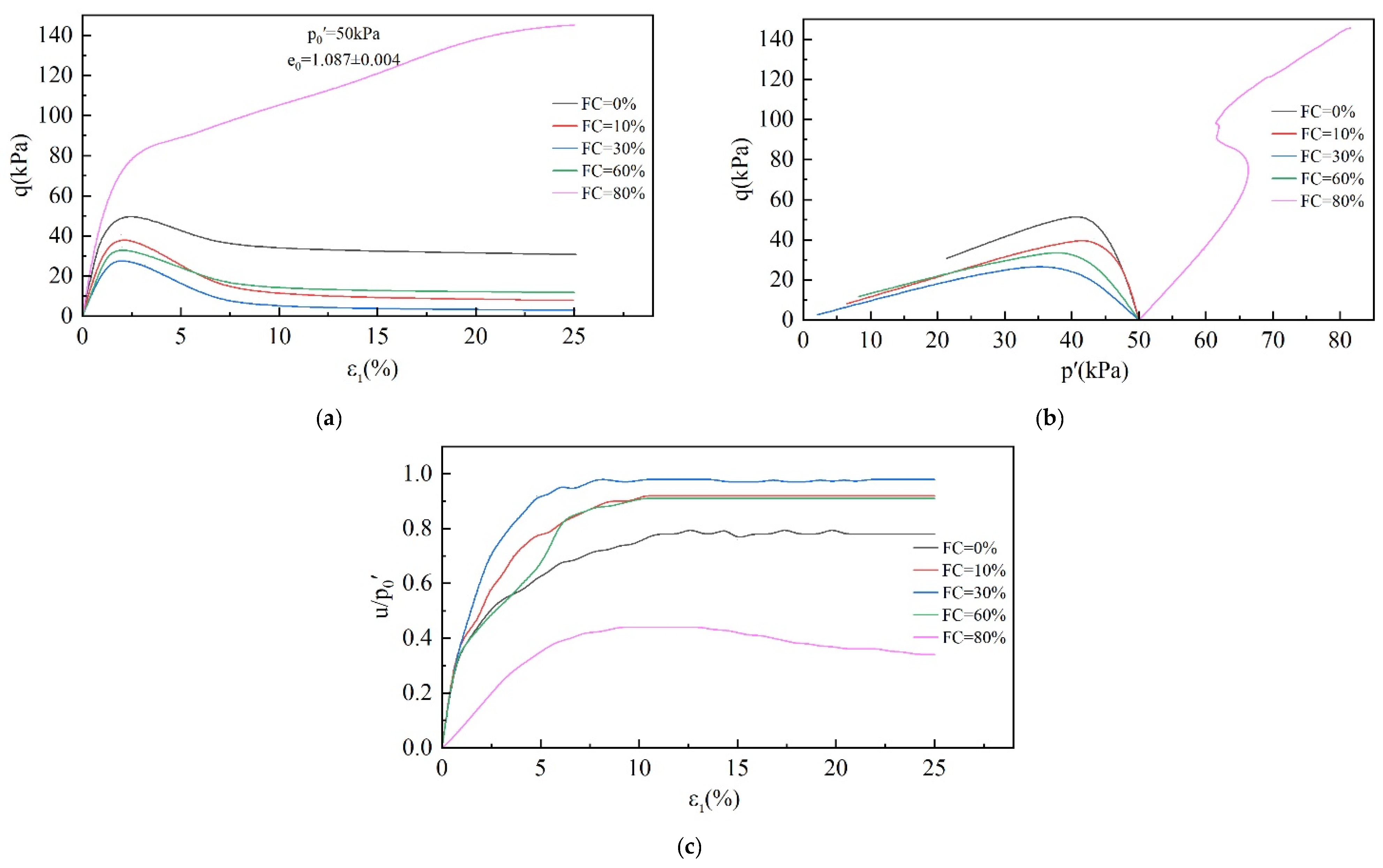
3.1. Analysis of CUTC Tests
3.1.1. Critical State
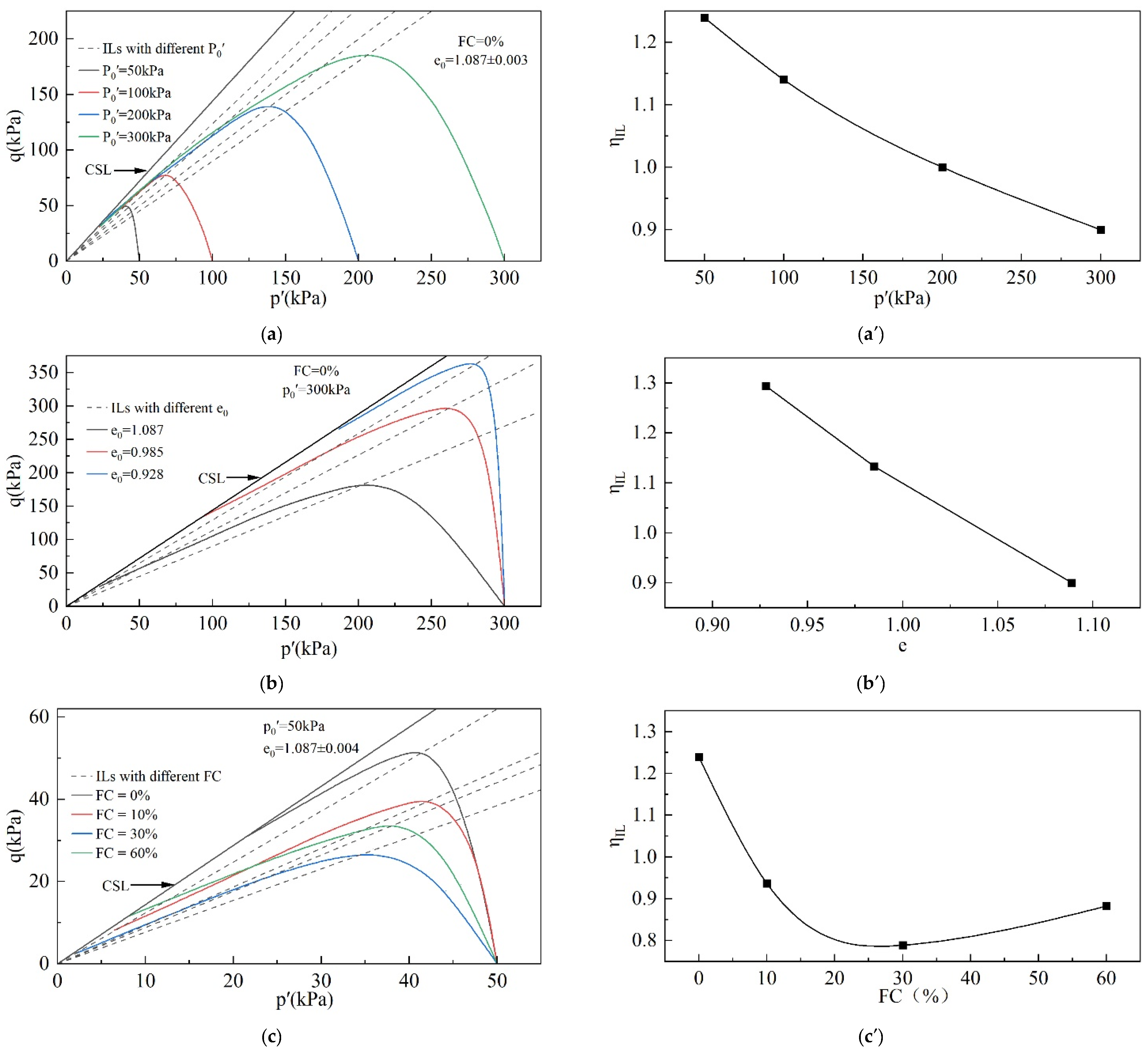
3.1.2. IL
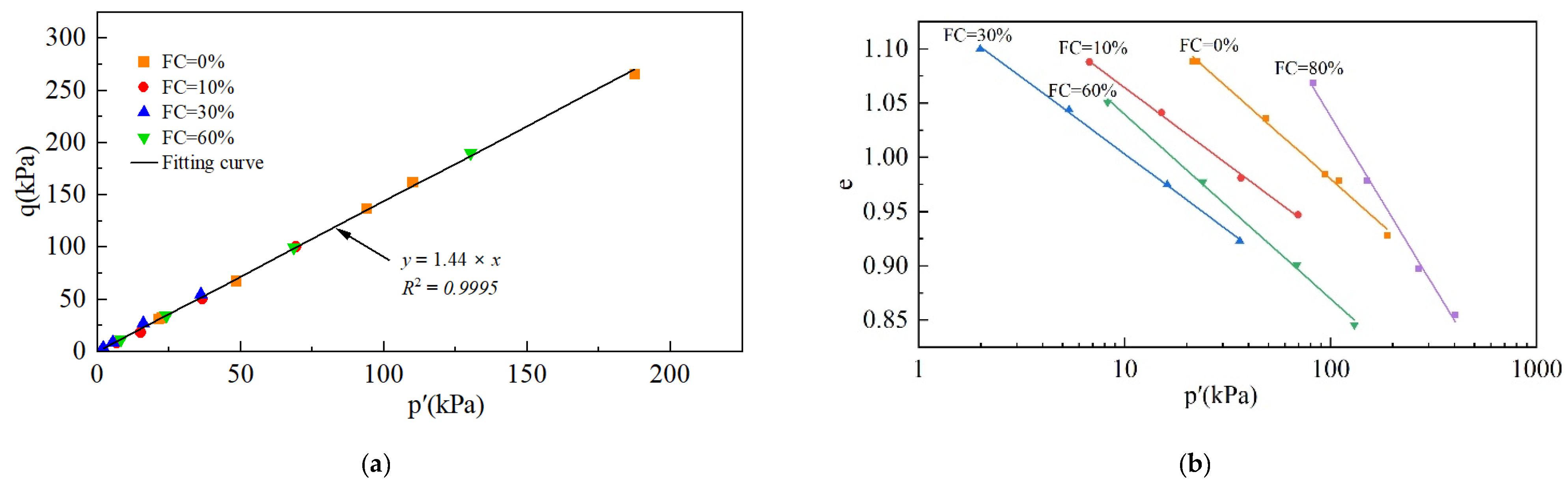
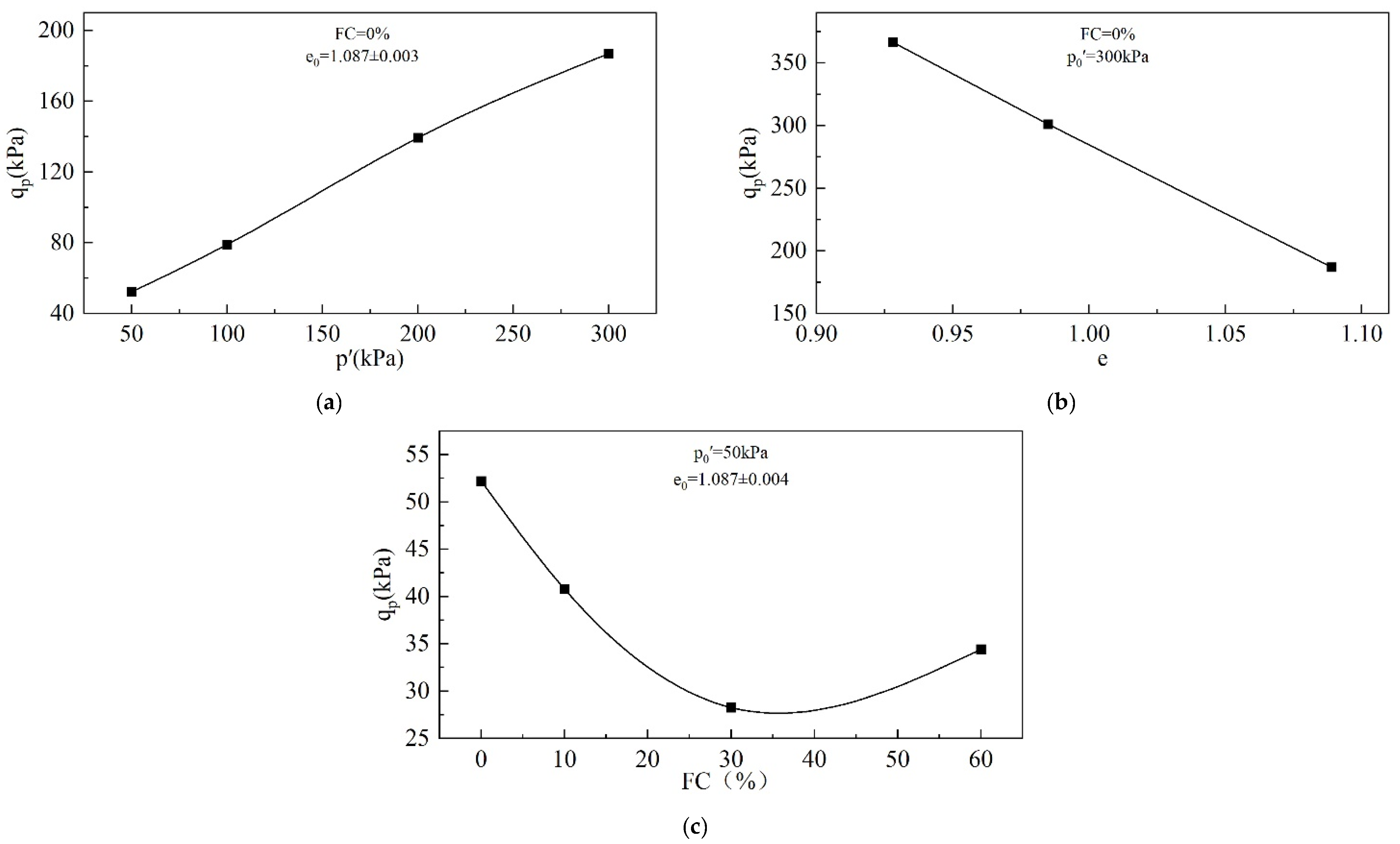
3.1.3. Undrained Shear Strength
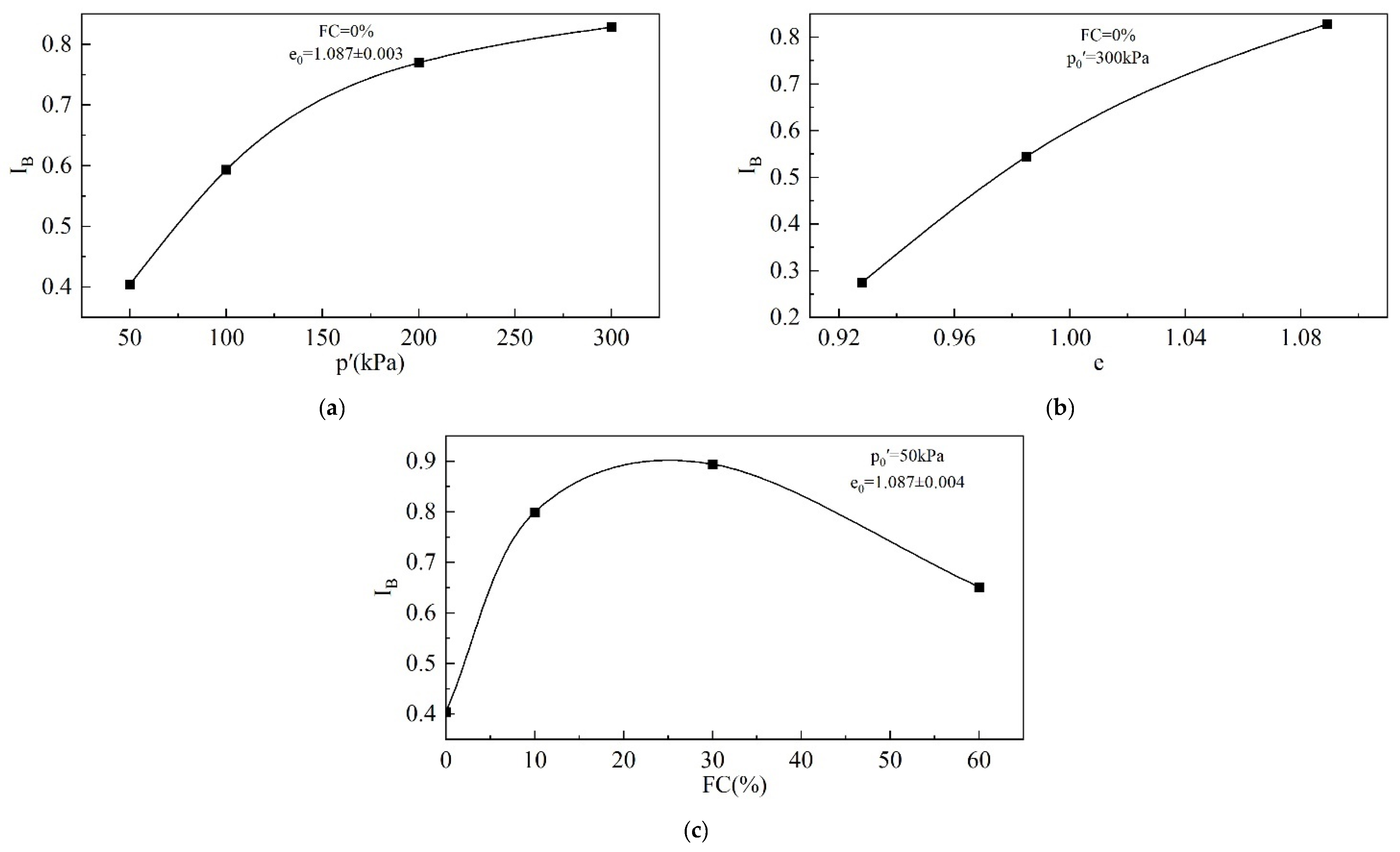
3.1.4. Brittleness Index
3.2. Analysis of OC Tests
4. Discussion
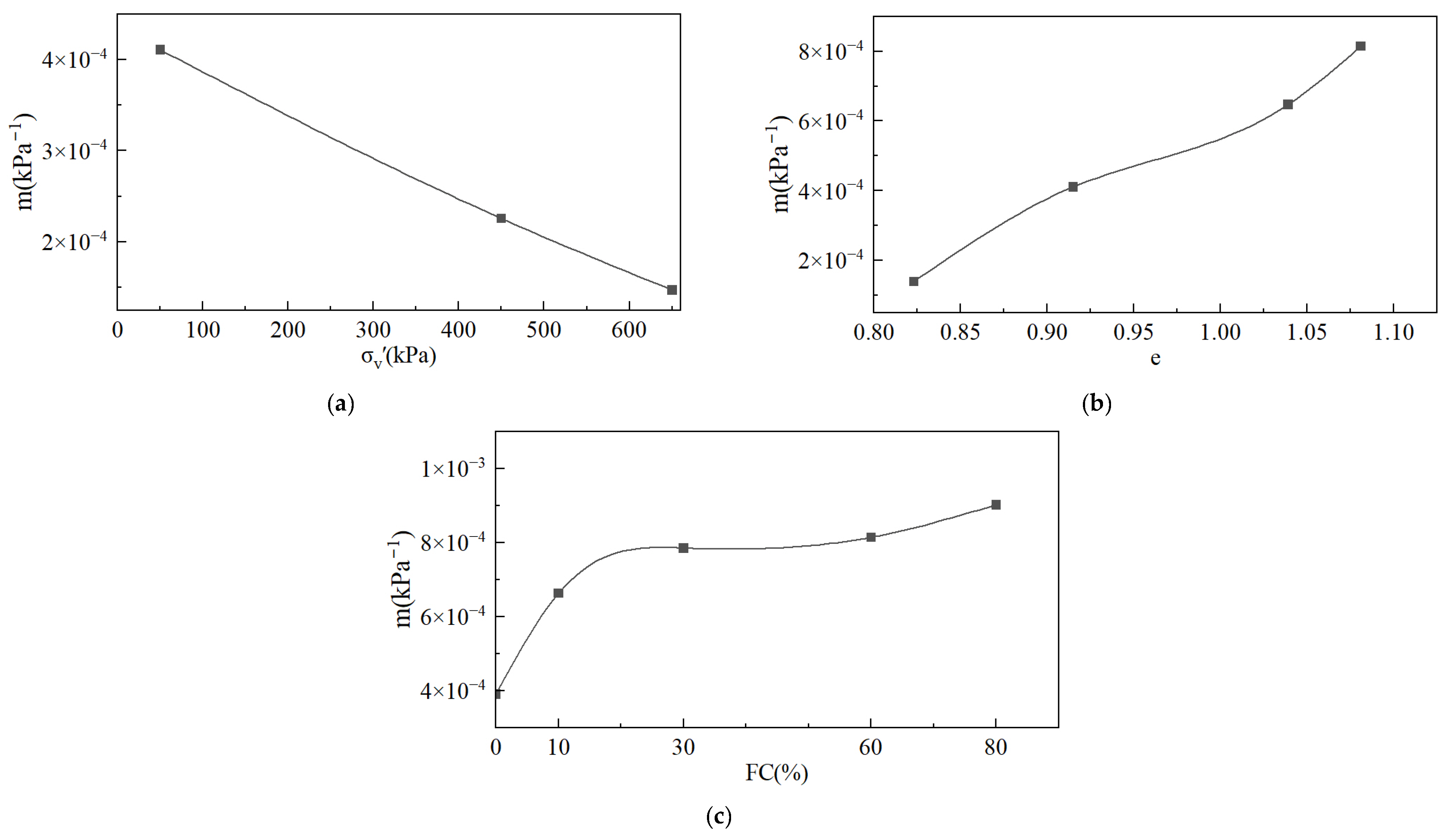
4.1. Relationship Between Compressibility and Static Liquefaction
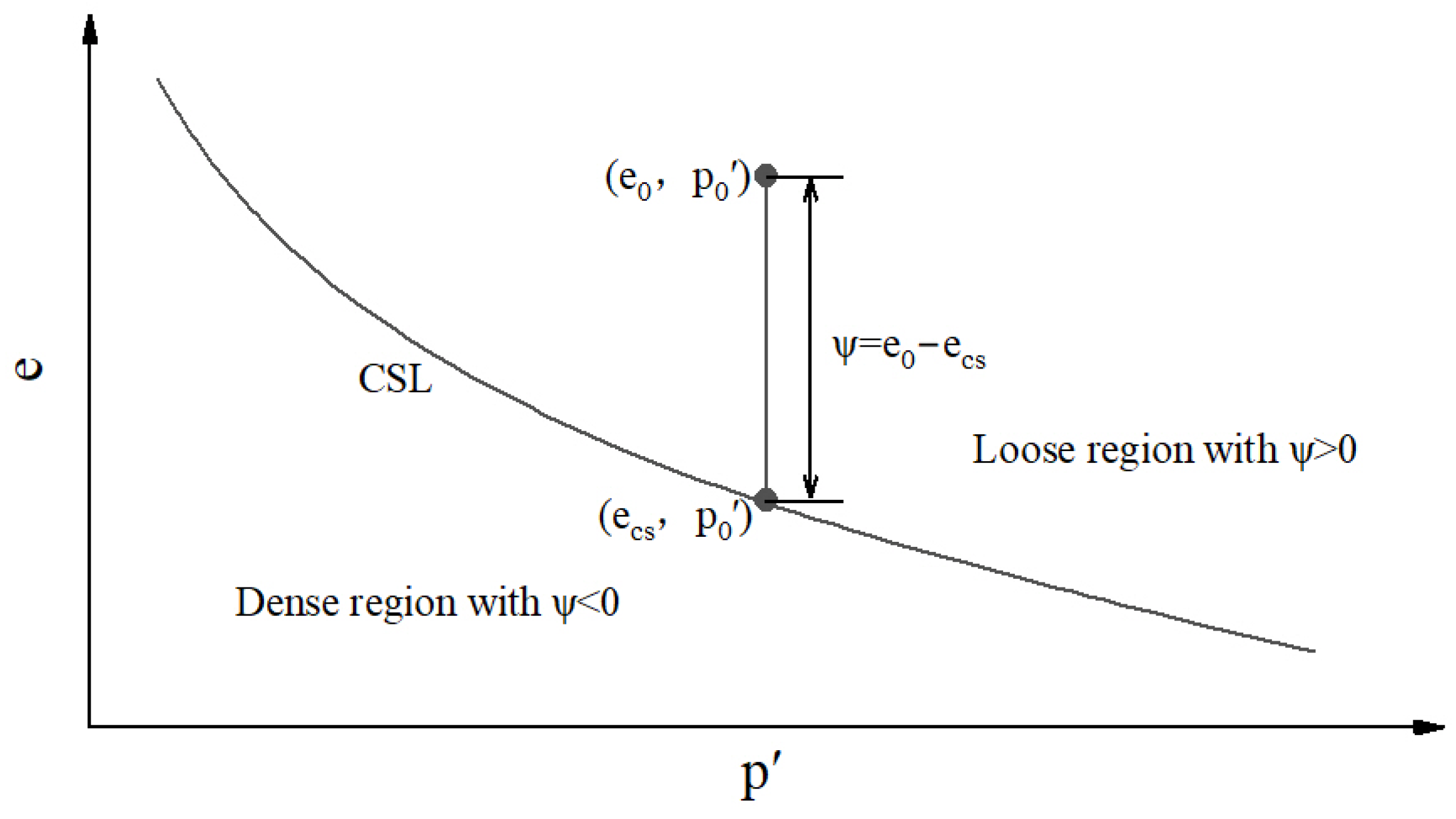
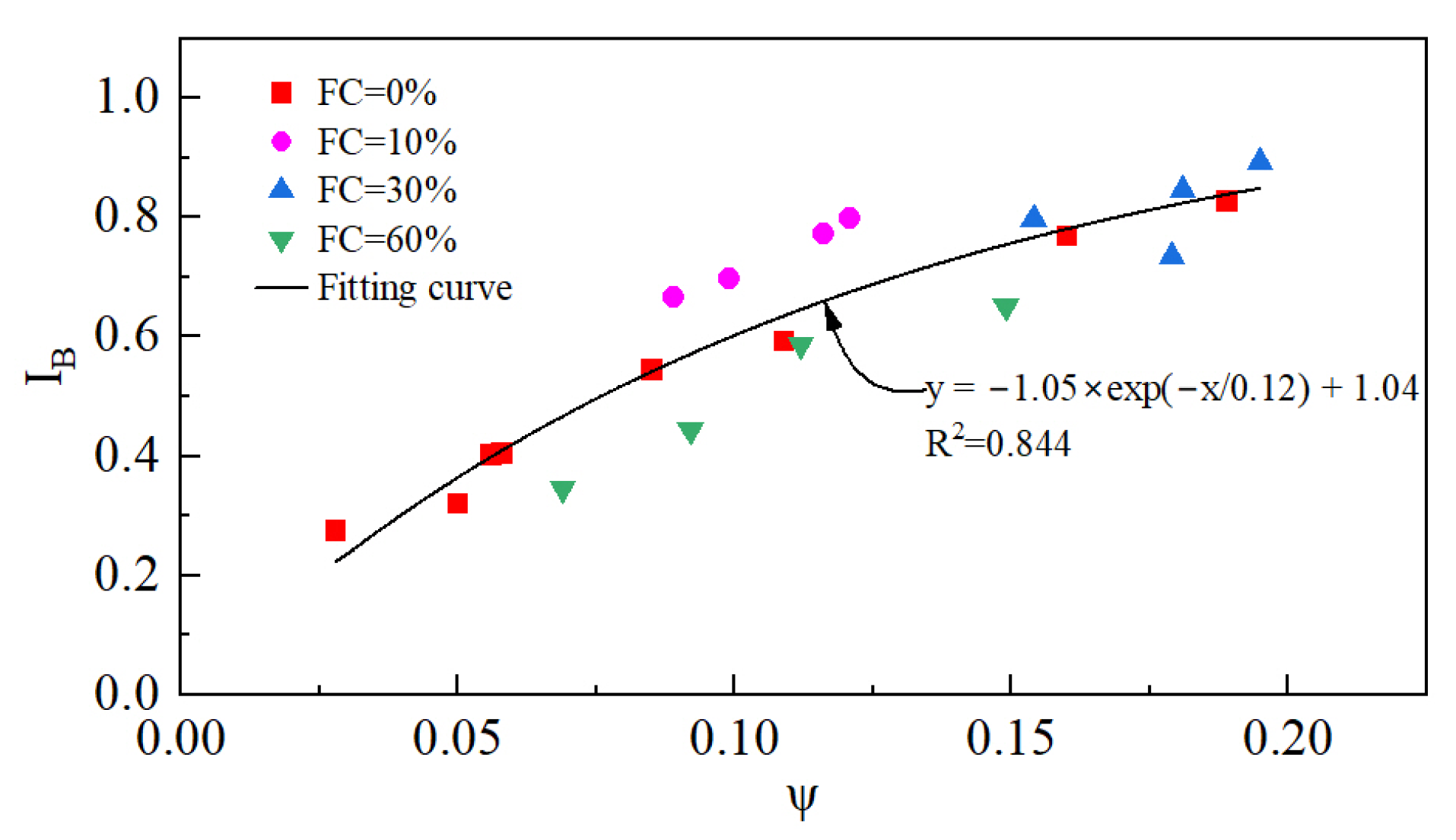
4.2. Relationship Between ψ and Static Liquefaction
5. Conclusions
- (1)
- Saturated loose tailings can undergo static liquefaction in undrained conditions. The instability line, undrained shear strength, critical state strength, and brittleness index are associated with the initial state and the fines content. A larger void ratio and higher mean effective stresses are more likely to initiate static liquefaction. There exists a fines content that is most likely to initiate static liquefaction, which is 30% in this study.
- (2)
- The instability line slope decreases with an increasing void ratio and mean effective stress. The fines content has a threshold, and the instability line slope decreases and then increases with an increasing fines content and reaches a minimum at an FC = 30%. The brittleness index has an opposite variation pattern to the instability line slope and reaches a peak at an FC = 30%.
- (3)
- The fines content has no effect on the critical state stress ratio. In the e-lnp′ space, the critical-state lines at different fines contents are approximately parallel, and the position of the critical-state line drops and then rises with an increasing fines content.
- (4)
- The compressibility of the tailings increases with an increasing void ratio and fines content and decreases with increasing pressure. Compressibility poses limitations in evaluating the static liquefaction of tailings and has little contribution to the constitutive description and prediction of static liquefaction.
- (5)
- The state parameter is an effective indicator for evaluating the static liquefaction of tailings containing fines. The comprehensive influence of the initial state and fines content on static liquefaction can be normalized by the state parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishihara, K. Post-Earthquake Failure of a Tailings Dam Due to Liquefaction of Pond Deposit. In Proceedings of the 1st Conference of the International Conference on Case Histories in Geotechnical Engineering, St. Louis, MO, USA, 30 May 1984. [Google Scholar]
- Lyu, Z.; Chai, J.; Xu, Z.; Qin, Y.; Cao, J. A comprehensive review on reasons for tailings dam failures based on case history. Adv. Civ. Eng. 2019, 2019, 4159306. [Google Scholar] [CrossRef]
- Vergaray, L.; Macedo, J.; Arnold, C. Static and Cyclic Liquefaction of Copper Mine Tailings. J. Geotech. Geoenviron. 2023, 149, 04023021. [Google Scholar] [CrossRef]
- Ishihara, K.; Troncoso, J.; Kawase, Y.; Takahashi, Y. Cyclic Strength Characteristics of Tailings Materials. Soils Found. 1980, 20, 127–142. [Google Scholar] [CrossRef] [PubMed]
- James, M.; Aubertin, M.; Wijewickreme, D.; Wilson, G.W. A laboratory investigation of the dynamic properties of tailings. Can. Geotech. J. 2011, 48, 1587–1600. [Google Scholar] [CrossRef]
- Suazo, G.; Fourie, A.; Doherty, J.; Hasan, A. Effects of confining stress, density and initial static shear stress on the cyclic shear response of fine-grained unclassified tailings. Géotechnique 2016, 66, 401–412. [Google Scholar] [CrossRef]
- Arnold, C.; Macedo, J. A novel experimental database on the cyclic response of mine tailings. Earthq. Spectra 2024, 40, 828–846. [Google Scholar] [CrossRef]
- Castro, G.; Poulos, S.J. Factors Affecting Liquefaction and Cyclic Mobility. J. Geotech. Eng. Div. 1977, 103, 501–516. [Google Scholar] [CrossRef]
- Poulos, S.J.; Robinsky, E.I.; Keller, T.O. Liquefaction Resistance of Thickened Tailings. J. Geotech. Eng. 1985, 111, 1380–1394. [Google Scholar] [CrossRef]
- Mróz, Z.; Boukpeti, N.; Drescher, A. Constitutive Model for Static Liquefaction. Int. J. Geomech. 2003, 3, 133–144. [Google Scholar] [CrossRef]
- Sabbar, A.S.; Chegenizadeh, A.; Nikraz, H. Static liquefaction of very loose sand–slag–bentonite mixtures. Soils Found. 2017, 57, 341–356. [Google Scholar] [CrossRef]
- Fourie, A.B.; Blight, G.E.; Papageorgiou, G. Static liquefaction as a possible explanation for the Merriespruit tailings dam failure. Can. Geotech. J. 2001, 38, 707–719. [Google Scholar] [CrossRef]
- Rafael, H.M.M.; Romanel, C. Static Liquefaction Analysis of the Limonar Tailings Dam in Peru. In Numerical Analysis of Nonlinear Coupled Problems; Springer: Cham, Switzerland, 2018; pp. 41–56. [Google Scholar]
- Sadrekarimi, A.; Riveros, G.A. Static Liquefaction Analysis of the Fundão Dam Failure. Geotech. Geol. Eng. 2020, 38, 6431–6446. [Google Scholar] [CrossRef]
- Riveros, G.A.; Sadrekarimi, A. Static liquefaction behaviour of gold mine tailings. Can. Geotech. J. 2021, 58, 889–901. [Google Scholar] [CrossRef]
- Verdugo, R. Static liquefaction in the context of steady state/critical state and its application in the stability of tailings dams. Soil Dyn. Earthq. Eng. 2024, 176, 108270. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Wroth, C.P. On the Yielding of Soils. Géotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Poulos, S.J. The Steady State of Deformation. J. Geotech. Eng. Div. 1981, 107, 553–562. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Kramer, S.L.; Seed, H.B. Initiation of Soil Liquefaction Under Static Loading Conditions. J. Geotech. Eng. 1988, 114, 412–430. [Google Scholar] [CrossRef]
- Leong, W.; Chu, J.; Teh, C. Liquefaction and Instability of a Granular Fill Material. Geotech. Test. J. 2000, 23, 178–192. [Google Scholar] [CrossRef]
- Fourie, A.B.; Tshabalala, L. Initiation of static liquefaction and the role of K0 consolidation. Can. Geotech. J. 2005, 42, 892–906. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.R. Undrained Behavior of Sand-Fines Mixtures and Their State Parameter. J. Geotech. Geoenviron. 2014, 140, 04014036. [Google Scholar] [CrossRef]
- Monkul, M.M.; Etminan, E.; Şenol, A. Influence of coefficient of uniformity and base sand gradation on static liquefaction of loose sands with silt. Soil Dyn. Earthq. Eng. 2016, 89, 185–197. [Google Scholar] [CrossRef]
- Ishihara, K. Liquefaction and flow failure during earthquakes. Géotechnique 1993, 43, 351–451. [Google Scholar] [CrossRef]
- Jefferies, M.; Been, K. Soil liquefaction: A critical state approach, 2nd edition. Environ. Earth Sci. 2016, 75, 1014. [Google Scholar] [CrossRef]
- Bouckovalas, G.D.; Andrianopoulos, K.I.; Papadimitriou, A.G. A critical state interpretation for the cyclic liquefaction resistance of silty sands. Soil Dyn. Earthq. Eng. 2003, 23, 115–125. [Google Scholar] [CrossRef]
- Sladen, J.A.; D’Hollander, R.D.; Krahn, J. The liquefaction of sands, a collapse surface approach. Can. Geotech. J. 1985, 22, 564–578. [Google Scholar] [CrossRef]
- Ishihara, K. Characterization of cyclic behavior of sand and post-seismic stability analyses. In Proceedings of the 9th Asian Regional Conference on Soil Mechanics and Foundation Engineering, Bangkok, Thailand, 9–13 December 1991. [Google Scholar]
- Lade, P.V. Static Instability and Liquefaction of Loose Fine Sandy Slopes. J. Geotech. Eng. 1992, 118, 51–71. [Google Scholar] [CrossRef]
- Lade, P.V. Initiation of static instability in the submarine Nerlerk berm. Can. Geotech. J. 1993, 30, 895–904. [Google Scholar] [CrossRef]
- Yamamuro, J.A.; Lade, P.V. Static liquefaction of very loose sands. Can. Geotech. J. 1997, 34, 905–917. [Google Scholar] [CrossRef]
- Chu, J.; Leroueil, S.; Leong, W.K. Unstable behaviour of sand and its implication for slope instability. Can. Geotech. J. 2003, 40, 873–885. [Google Scholar] [CrossRef]
- Yang, J. Non-uniqueness of flow liquefaction line for loose sand. Géotechnique 2002, 52, 757–760. [Google Scholar] [CrossRef]
- Yang, J.; Liang, L.B.; Chen, Y. Instability and liquefaction flow slide of granular soils: The role of initial shear stress. Acta Geotech. 2022, 17, 65–79. [Google Scholar] [CrossRef]
- Poulos, S.J.; Castro, G.; France, J.W. Liquefaction Evaluation Procedure. J. Geotech. Eng. 1985, 111, 772–792. [Google Scholar] [CrossRef]
- Castro, G.; Seed, R.B.; Keller, T.O.; Seed, H.B. Steady-State Strength Analysis of Lower San Fernando Dam Slide. J. Geotech. Eng. 1992, 118, 406–427. [Google Scholar] [CrossRef]
- Sadrekarimi, A. Influence of fines content on liquefied strength of silty sands. Soil Dyn. Earthq. Eng. 2013, 55, 108–119. [Google Scholar] [CrossRef]
- Zhu, J.Q. Strength Properties and Steady-State Behavior of Sandy Soil. Ph.D. Thesis, Chinese Academy of Sciences, Beijing, China, 2007. [Google Scholar]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of Liquefaction Potential Using Field Performance Data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Pitman, T.D.; Robertson, P.K.; Sego, D.C. Influence of fines on the collapse of loose sands. Can. Geotech. J. 1994, 31, 728–739. [Google Scholar] [CrossRef]
- Amini, F.; Qi, G.Z. Liquefaction Testing of Stratified Silty Sands. J. Geotech. Geoenviron. 2000, 126, 208–217. [Google Scholar] [CrossRef]
- Sladen, J.A.; D’Hollander, R.D.; Krahn, J.; Mitchell, D.E. Back analysis of the Nerlerk berm liquefaction slides. Can. Geotech. J. 1985, 22, 579–588. [Google Scholar] [CrossRef]
- Singh, S. Liquefaction characteristics of silts. Geotech. Geol. Eng. 1996, 14, 1–19. [Google Scholar] [CrossRef]
- Bouferra, R.; Shahrour, I. Influence of fines on the resistance to liquefaction of a clayey sand. Proc. Inst. Civ. Eng. Gr. 2004, 8, 1–5. [Google Scholar] [CrossRef]
- Choo, H.; Burns, S.E. Shear wave velocity of granular mixtures of silica particles as a function of finer fraction, size ratios and void ratios. Granul. Matter 2015, 17, 567–578. [Google Scholar] [CrossRef]
- Chen, Z.P. Effect of Fine Content on Mechanical Properties of Tailings. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2023. [Google Scholar]
- Yamamuro, J.A.; Lade, P.V. Steady-State Concepts and Static Liquefaction of Silty Sands. J. Geotech. Geoenviron. 1998, 124, 868–877. [Google Scholar] [CrossRef]
- Lade, P.V.; Yamamuro, J.A. Effects of fines content on void ratio, compressibility, and static liquefaction of silty sand. Geomech. Eng. 2009, 1, 1–15. [Google Scholar] [CrossRef]
- JTG 3430-2020; Test Methods of Soils for Highway Engineering. People’s Communications Publishing House: Beijing, China, 2020.
- Li, X.S.; Wang, Y. Linear Representation of Steady-State Line for Sand. J. Geotech. Geoenviron. 1998, 124, 1215–1217. [Google Scholar] [CrossRef]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics, 1st ed.; Press Syndicate of the University of Cambridge: Cambridge, UK, 1991. [Google Scholar] [CrossRef]
- Lade, P.V.; Yamamuro, J.A. Effects of nonplastic fines on static liquefaction of sands. Can. Geotech. J. 1997, 34, 918–928. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Dilatancy for Cohesionless Soils. Géotechnique 2000, 50, 449–460. [Google Scholar] [CrossRef]
- Kuerbis, R.; Negussey, D.; Vaid, Y.P. Effect of gradation and fines content on the undrained response of sand. Geotech. Spec. Publ. 1988, 21, 330–345. [Google Scholar] [CrossRef]

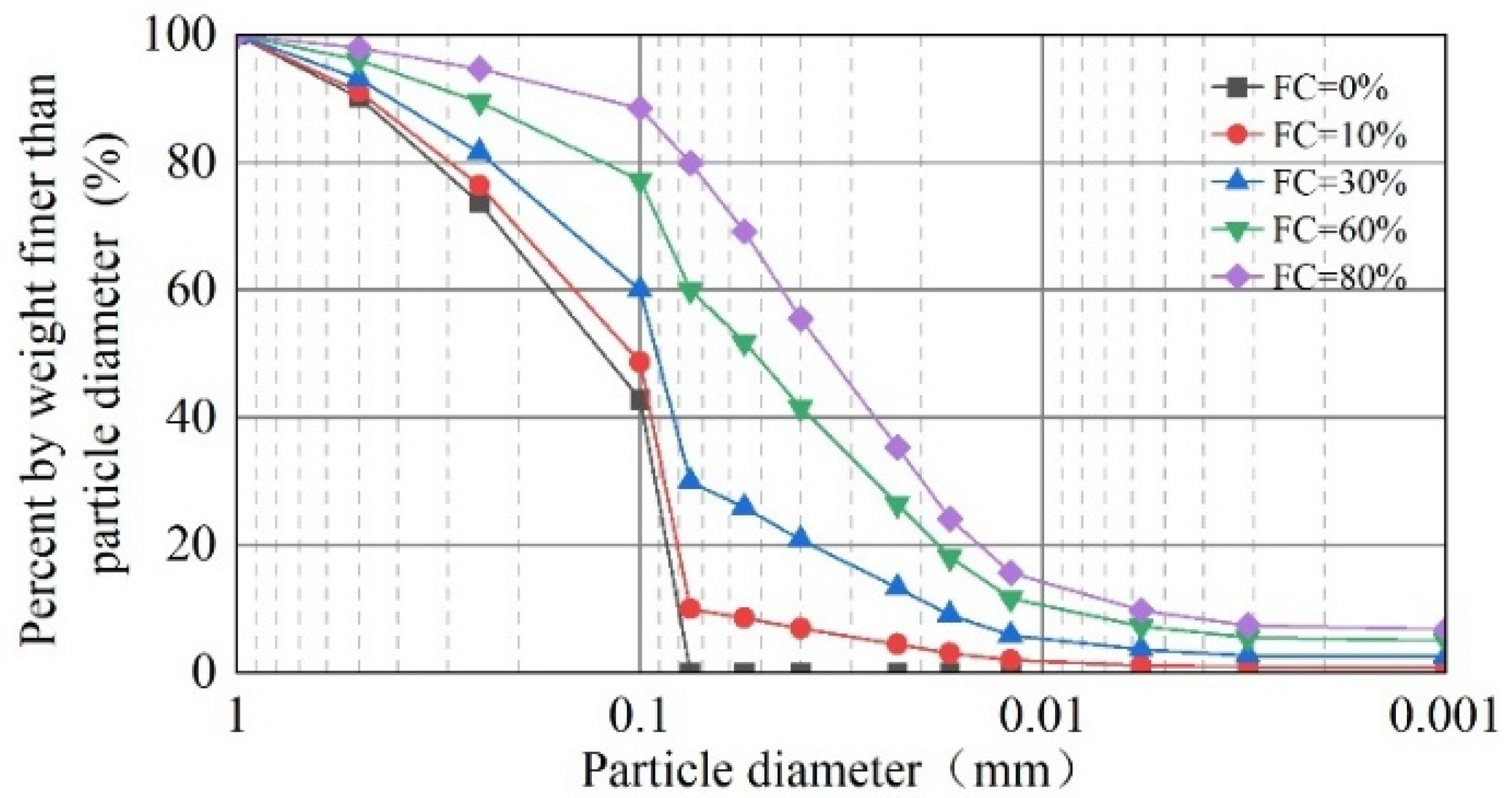
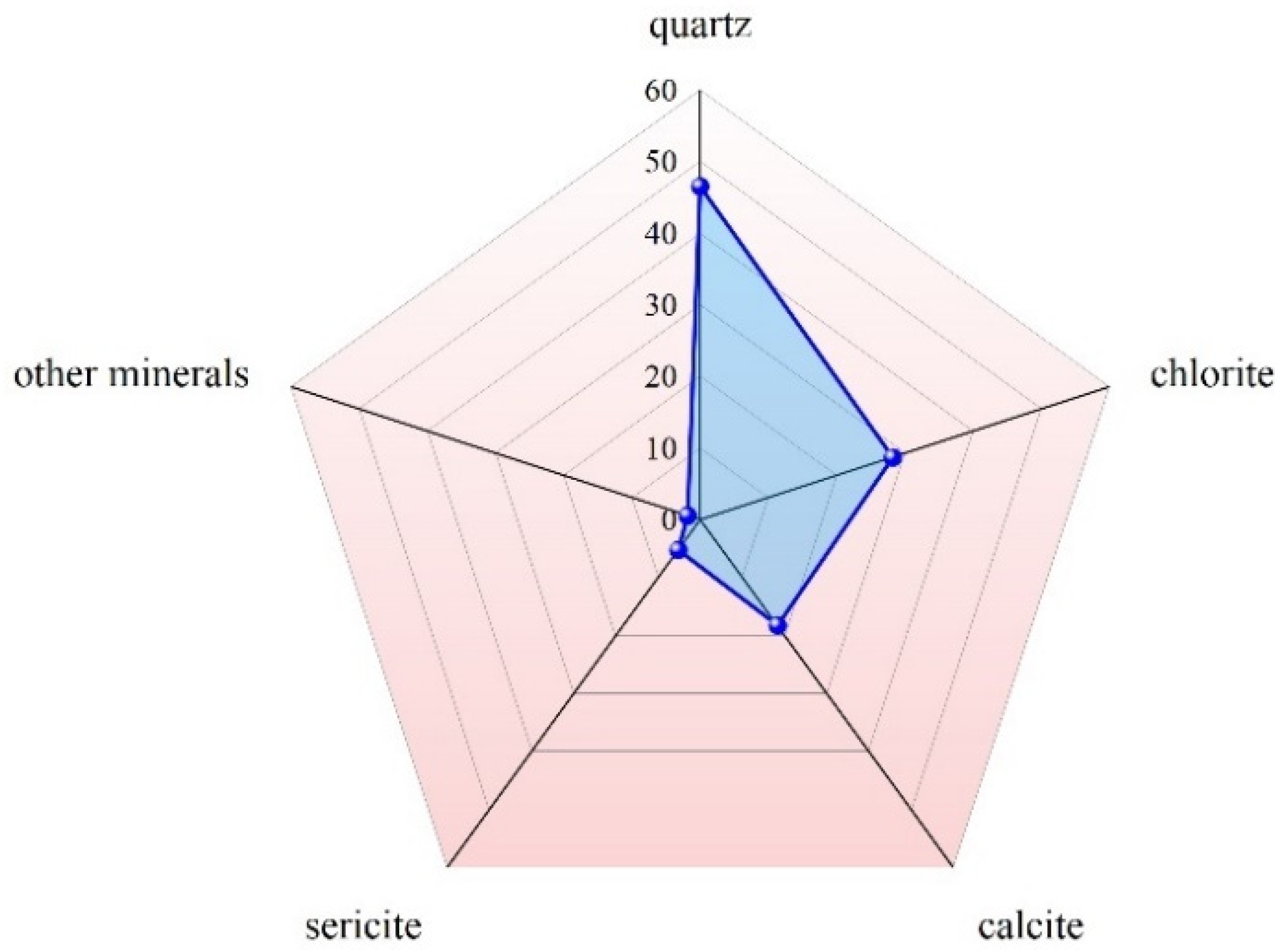


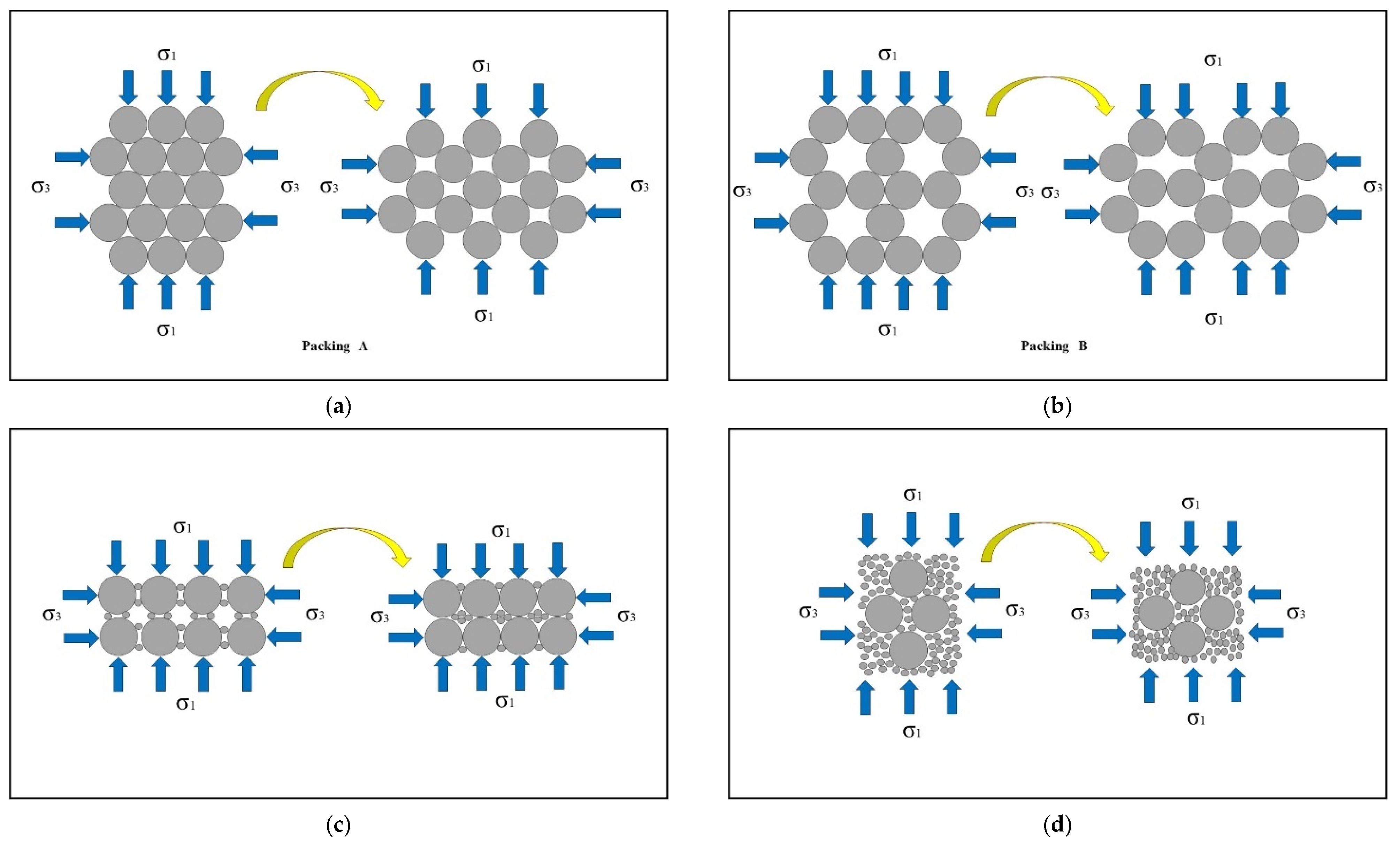
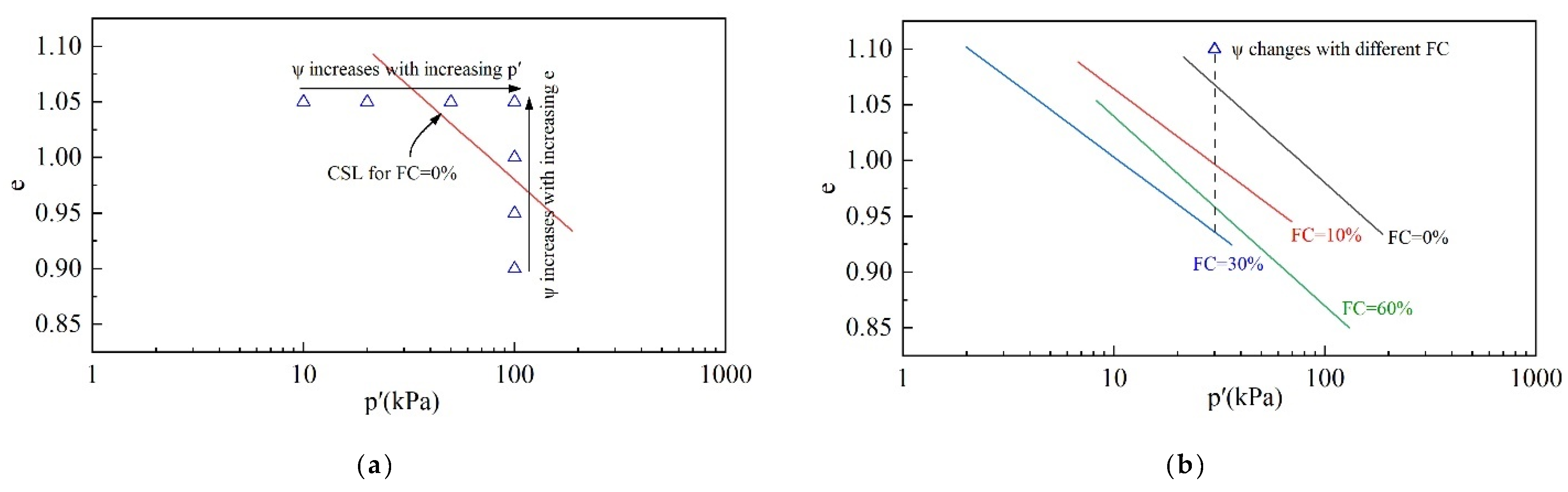
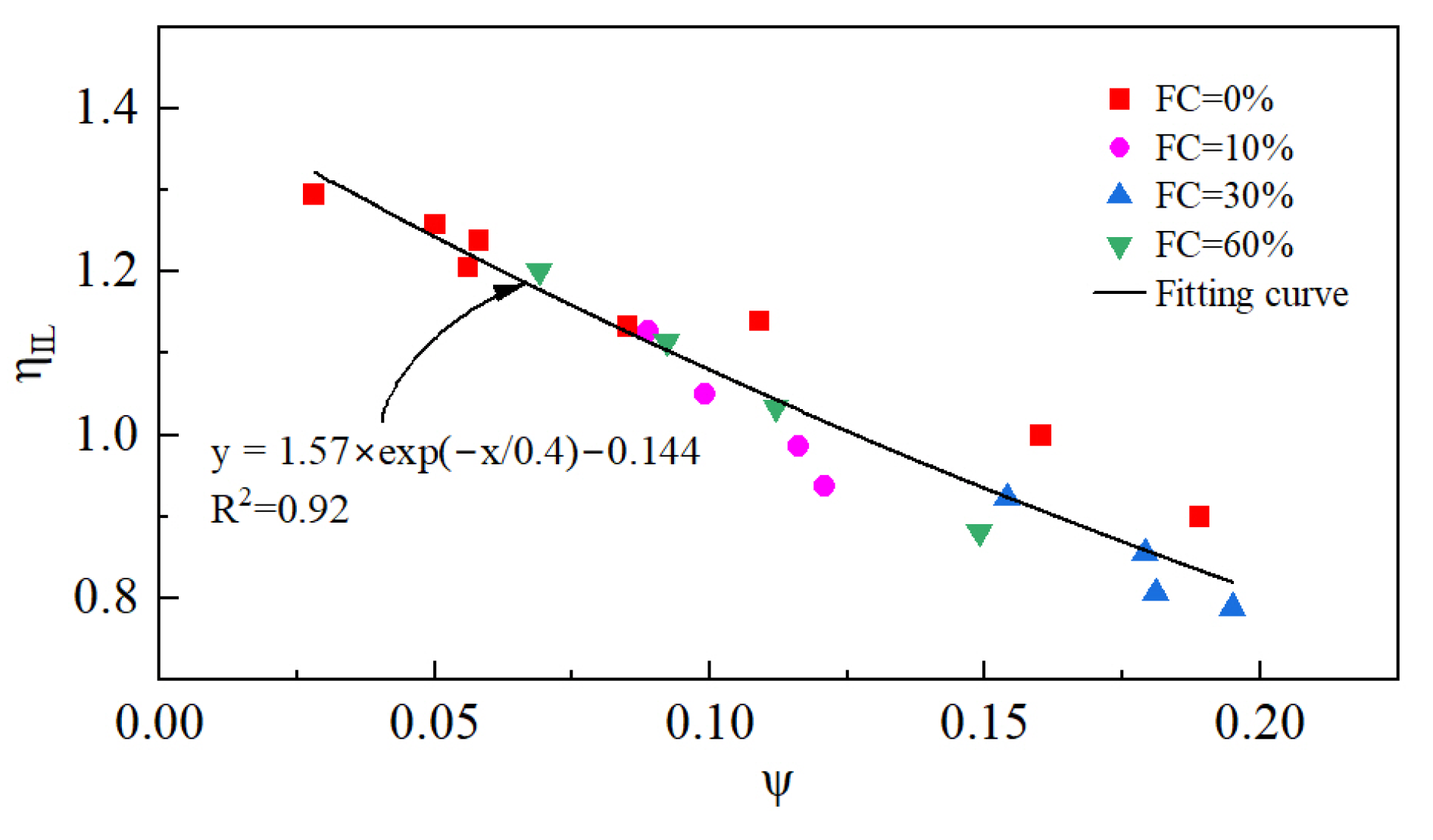
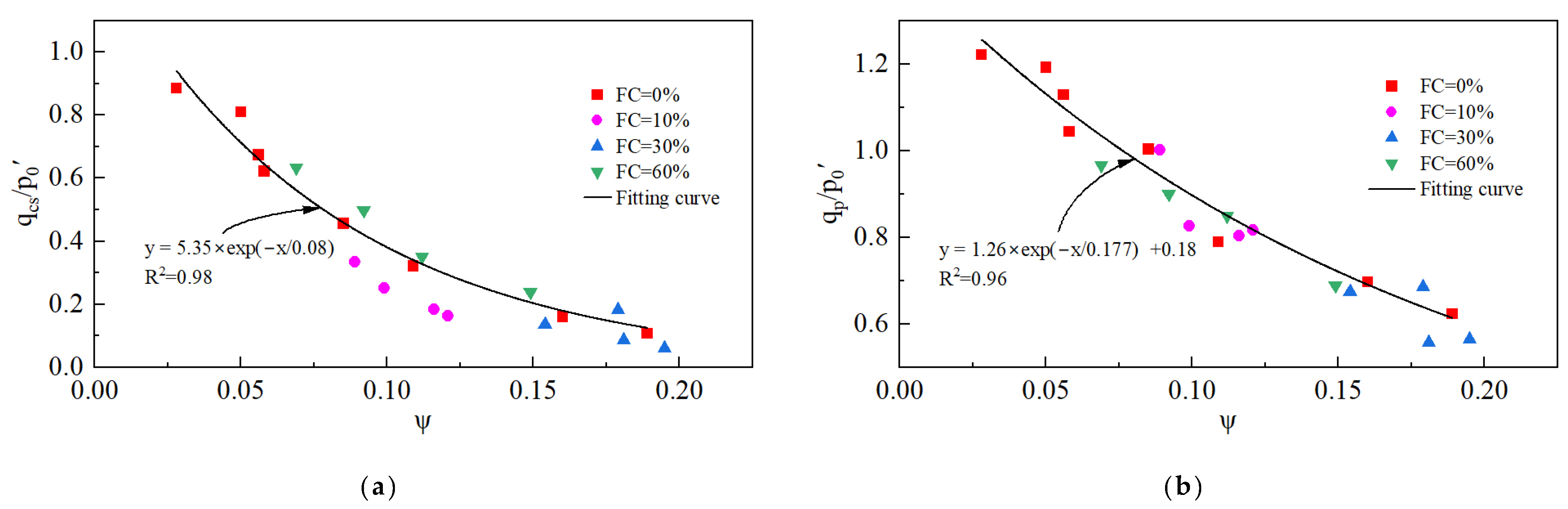
| Sampling Point | Particle Mass Percentage (%) | Median Size d50 (mm) | Particle Specific Gravity | Minimum Dry Density (g/cm3) | Maximum Dry Density (g/cm3) | ||
|---|---|---|---|---|---|---|---|
| <0.005 mm | 0.005 mm–0.075 mm | >0.075 mm | |||||
| P1 | 3.56 | 68.97 | 27.47 | 0.039 | 2.79 | 1.158 | 1.567 |
| P2 | 4.33 | 70.29 | 25.38 | 0.038 | 2.79 | 1.143 | 1.548 |
| P3 | 5.05 | 71.72 | 23.23 | 0.037 | 2.80 | 1.127 | 1.527 |
| P4 | 5.86 | 73.03 | 21.11 | 0.036 | 2.80 | 1.111 | 1.502 |
| P5 | 6.69 | 74.36 | 18.95 | 0.034 | 2.80 | 1.094 | 1.469 |
| FC (%) | e0 | p0′ (kPa) | ψ0 |
|---|---|---|---|
| 0 | 1.089 | 50 | 0.058 |
| 1.085 | 100 | 0.109 | |
| 1.090 | 200 | 0.16 | |
| 1.087 | 300 | 0.189 | |
| 0.958 | 300 | 0.085 | |
| 0.928 | 300 | 0.028 | |
| 1.036 | 100 | 0.056 | |
| 0.979 | 200 | 0.05 | |
| 10 | 1.088 | 50 | 0.121 |
| 1.041 | 100 | 0.116 | |
| 0.981 | 200 | 0.099 | |
| 0.947 | 300 | 0.089 | |
| 30 | 1.101 | 50 | 0.195 |
| 1.044 | 100 | 0.181 | |
| 0.975 | 200 | 0.154 | |
| 0.923 | 300 | 0.179 | |
| 60 | 1.071 | 50 | 0.149 |
| 0.978 | 100 | 0.112 | |
| 0.901 | 200 | 0.092 | |
| 0.846 | 300 | 0.069 | |
| 80 | 1.085 | 50 | −0.102 |
| 0.979 | 100 | −0.12 | |
| 0.898 | 200 | −0.109 | |
| 0.855 | 300 | −0.099 |
| FC (%) | ei | |||
|---|---|---|---|---|
| 0 | 1.128 | 1.050 | 0.879 | 0.799 |
| 10 | 1.128 | 0.945 | 0.830 | 0.691 |
| 30 | 1.128 | 0.915 | 0.828 | 0.717 |
| 60 | 1.128 | 1.076 | 0.940 | 0.837 |
| 80 | 1.128 | 1.228 | 1.050 | 0.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, H.; Chen, Z.; Zhong, Y.; Hu, Z.; Yang, X.; Zhang, M. Static Liquefaction of Tailings Containing Fines: Experimental Exploration, Mechanism Analysis and Evaluation. Materials 2025, 18, 1123. https://doi.org/10.3390/ma18051123
Wang X, Li H, Chen Z, Zhong Y, Hu Z, Yang X, Zhang M. Static Liquefaction of Tailings Containing Fines: Experimental Exploration, Mechanism Analysis and Evaluation. Materials. 2025; 18(5):1123. https://doi.org/10.3390/ma18051123
Chicago/Turabian StyleWang, Xiaoliang, Hongru Li, Zhenpeng Chen, Yue Zhong, Zaiqiang Hu, Xi Yang, and Miaozhi Zhang. 2025. "Static Liquefaction of Tailings Containing Fines: Experimental Exploration, Mechanism Analysis and Evaluation" Materials 18, no. 5: 1123. https://doi.org/10.3390/ma18051123
APA StyleWang, X., Li, H., Chen, Z., Zhong, Y., Hu, Z., Yang, X., & Zhang, M. (2025). Static Liquefaction of Tailings Containing Fines: Experimental Exploration, Mechanism Analysis and Evaluation. Materials, 18(5), 1123. https://doi.org/10.3390/ma18051123






