Experimental Study on the Dynamic Properties of Granite with Filled Joints of Different Thicknesses
Abstract
1. Introduction
2. The Experimental Design
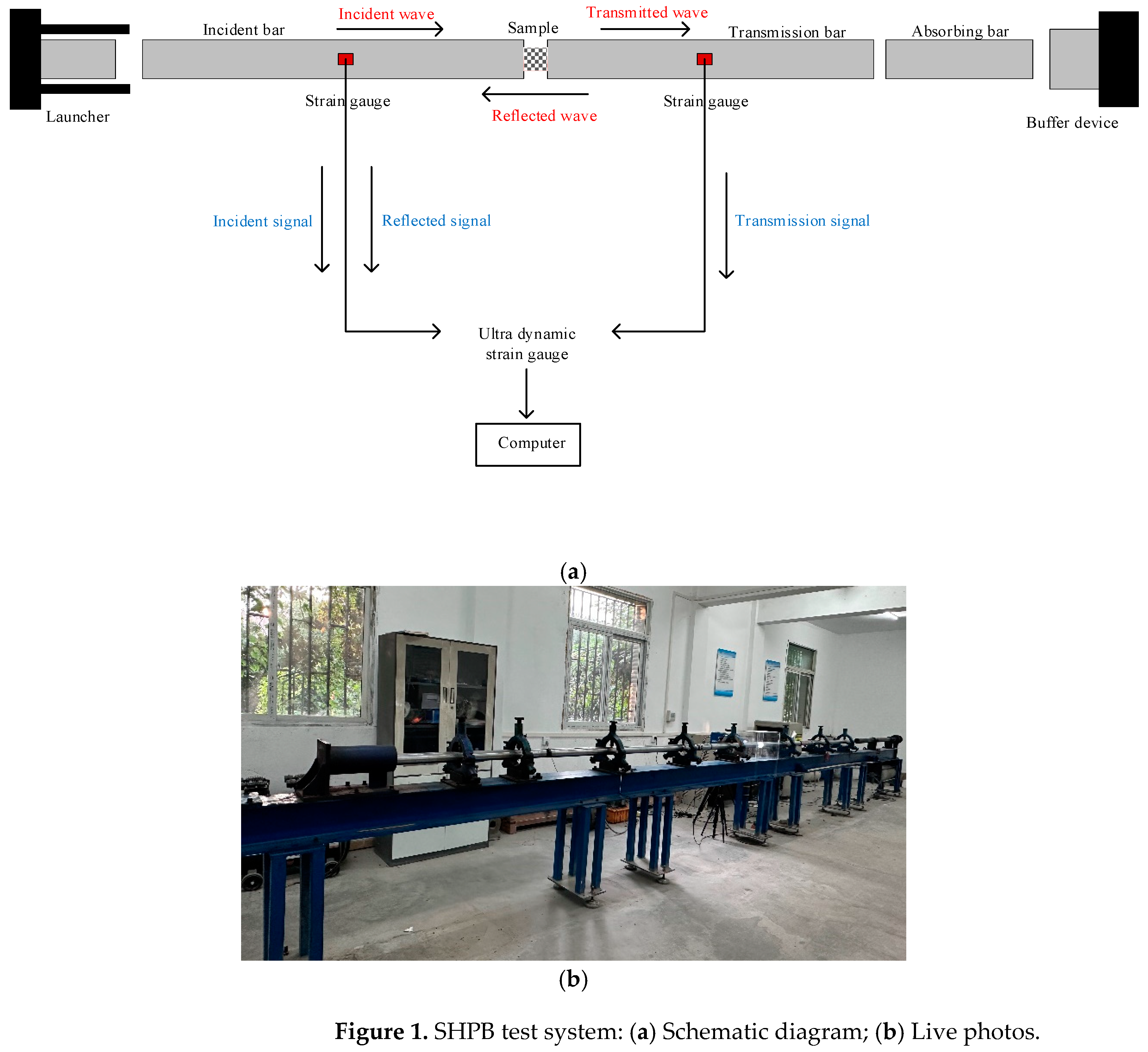
2.1. The Experimental Setup
2.2. Sample Preparation
2.3. Experimental Principle
3. The SHPB Testing Process for Filled Jointed Granite
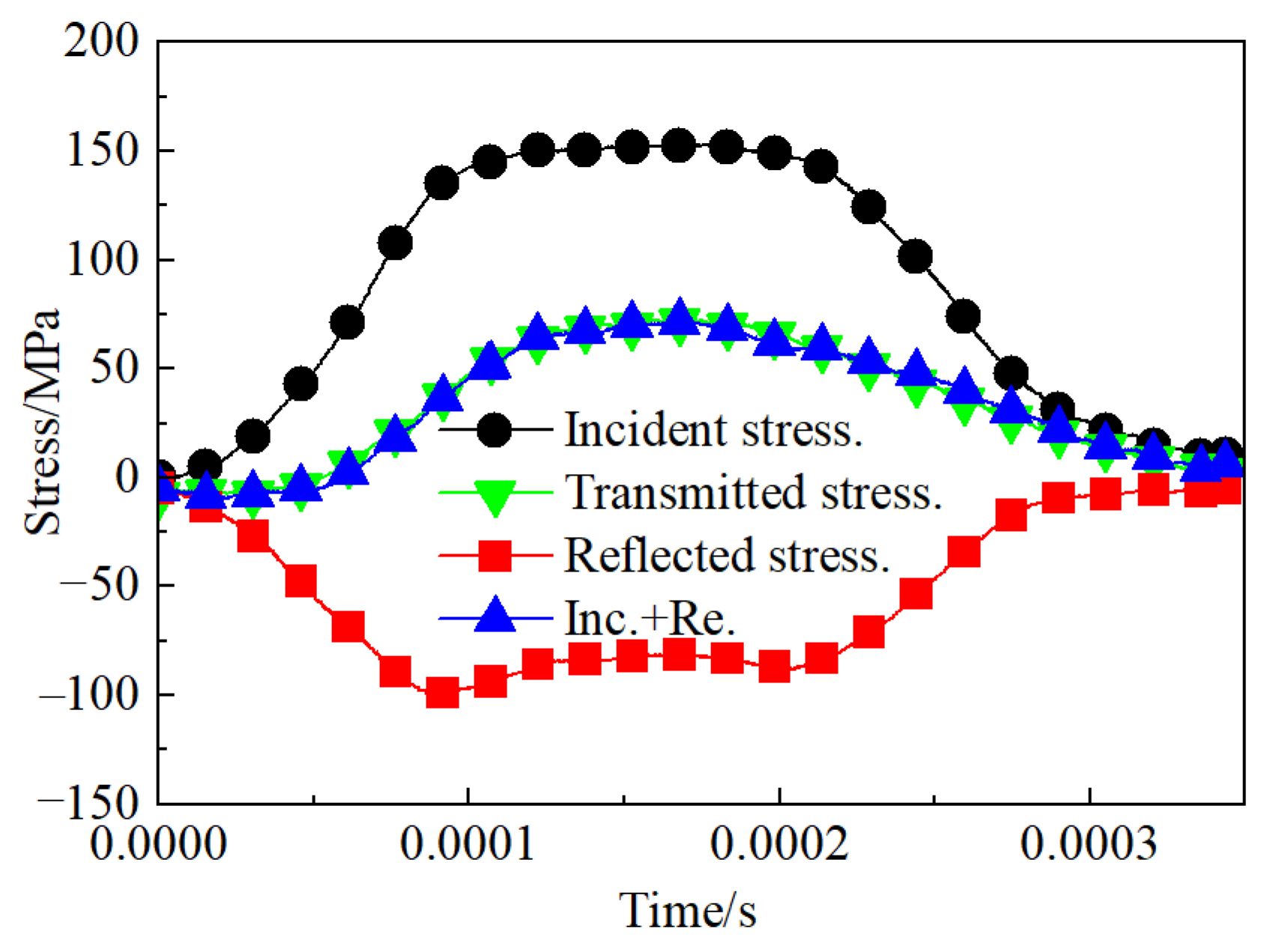
3.1. Dynamic Stress Equilibrium Verification
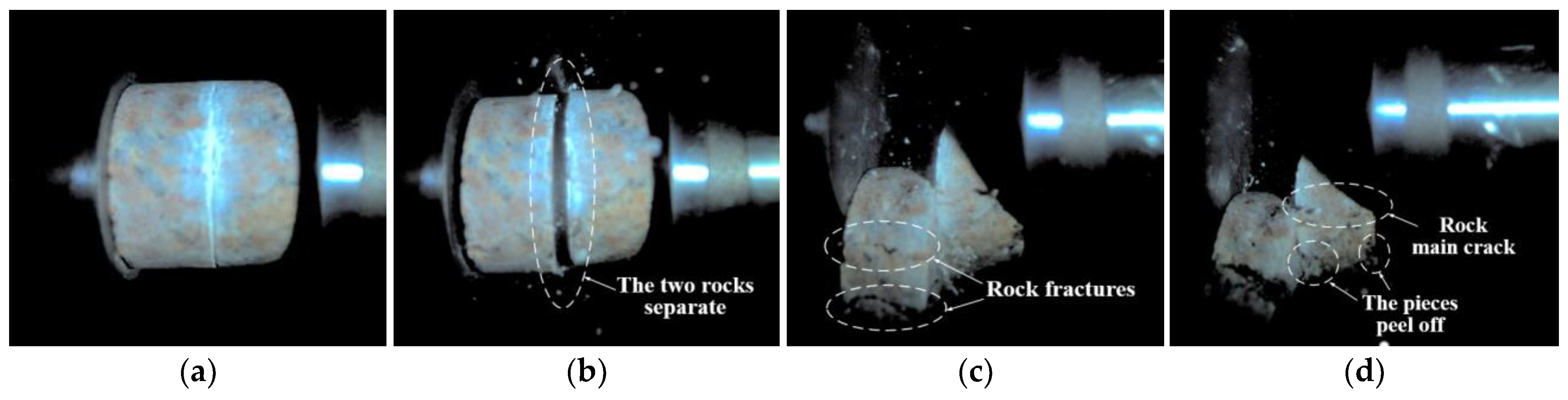
3.2. The Dynamic Failure and Crack Propagation Process of Jointed Granite
4. Experimental Results and Discussion
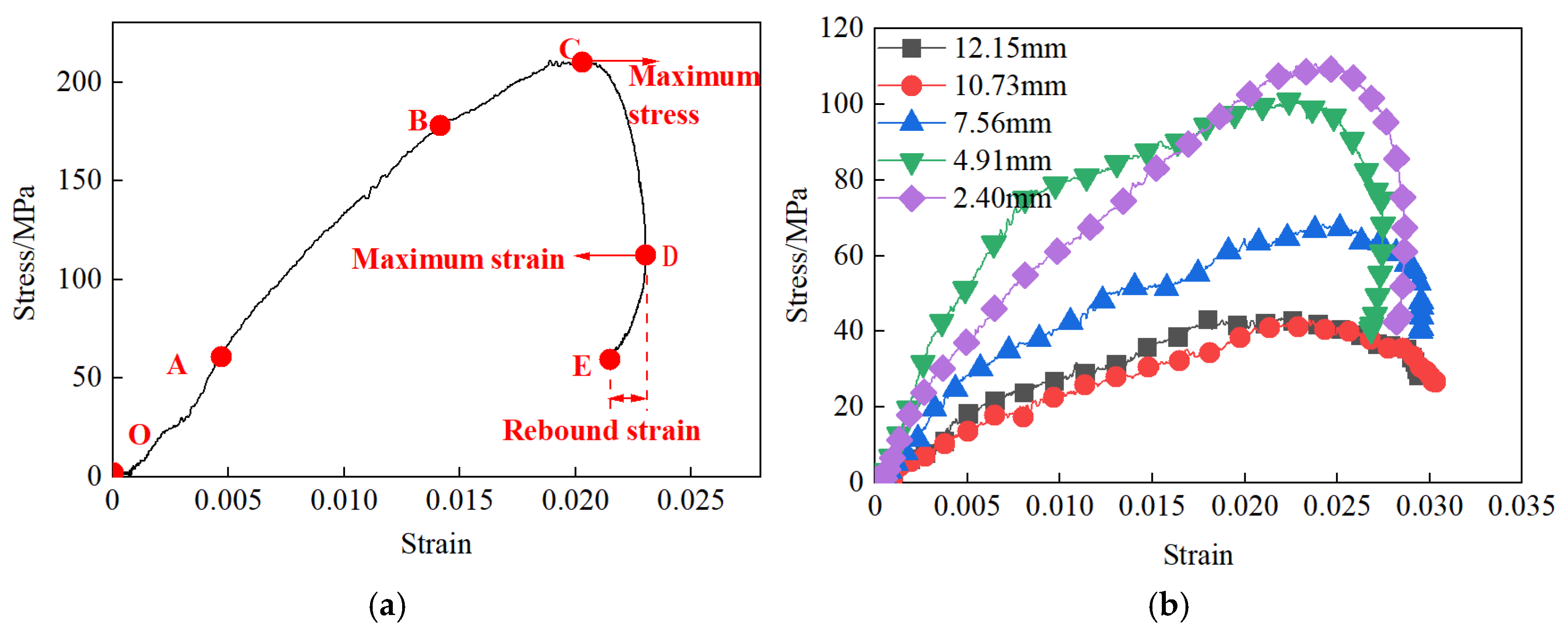
4.1. Stress–Strain Curve Characteristics
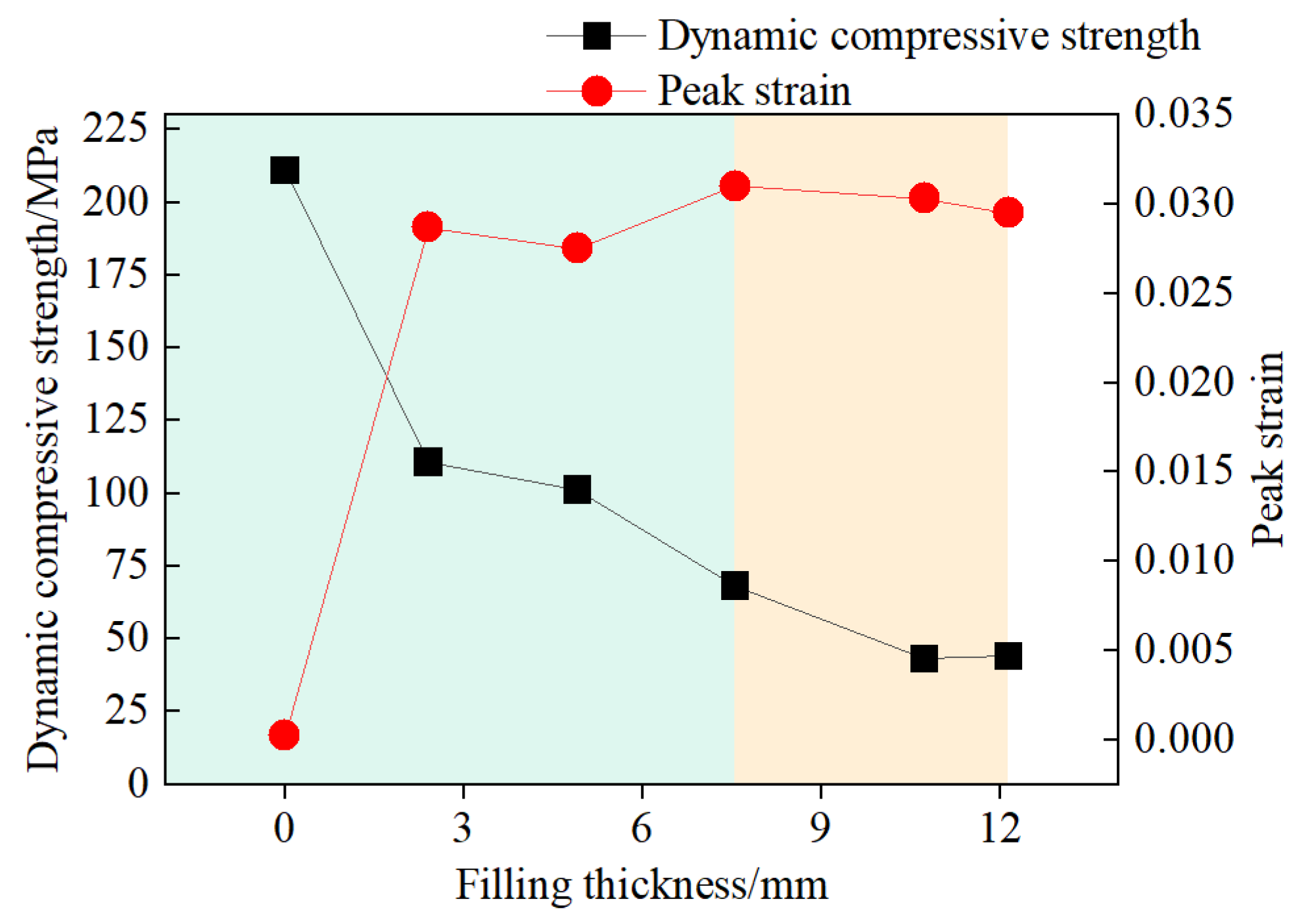
4.2. The Relationship Between Dynamic Properties and Filling Thickness
5. Patterns of Energy Evolution
5.1. Principle of Energy Dissipation in Jointed Rock Mass
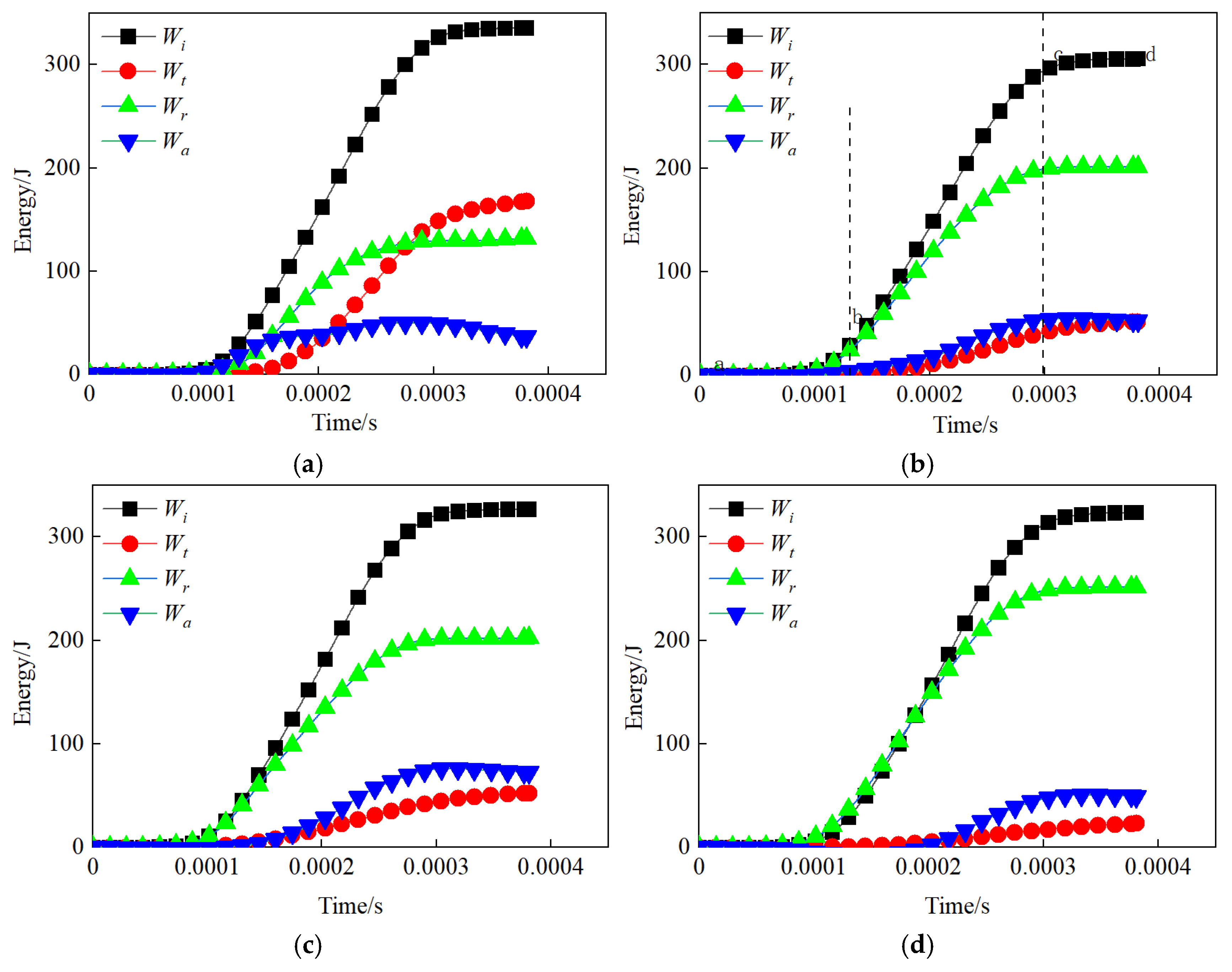
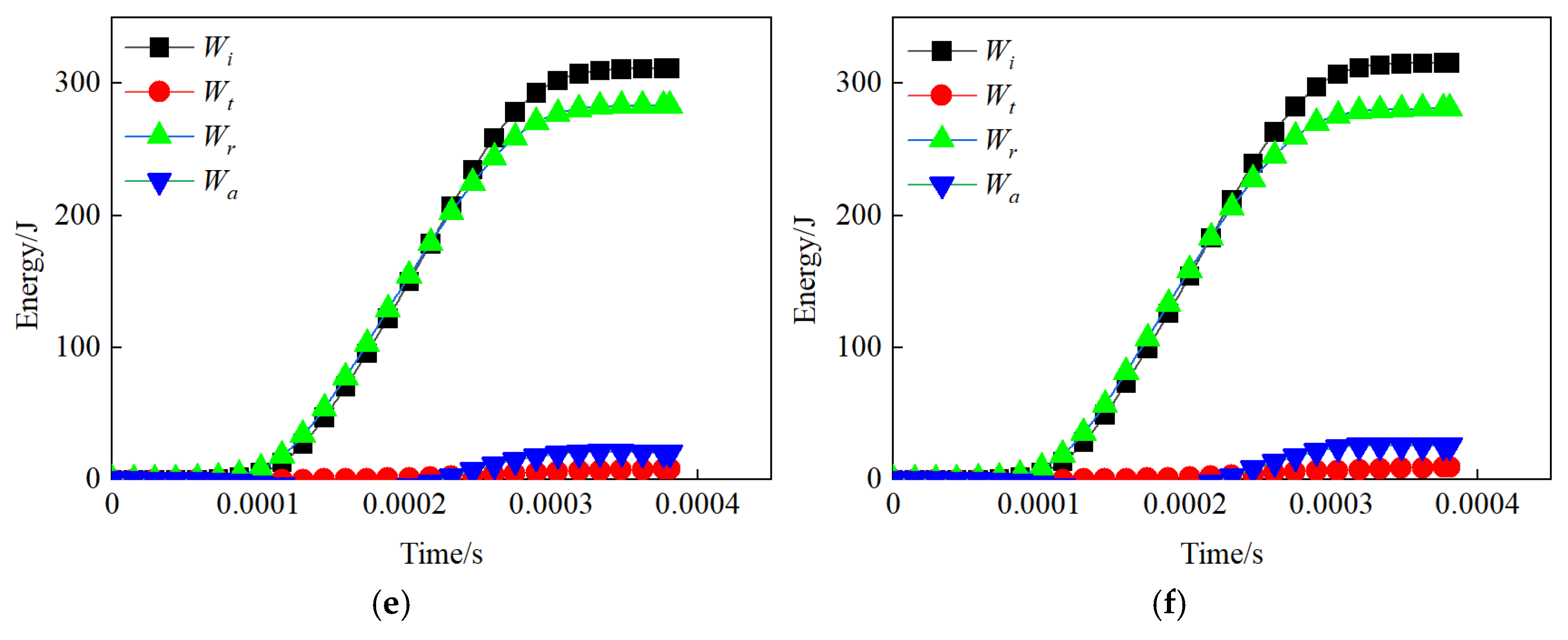
5.2. Energy–Time Curve
5.3. The Impact of Filling Thickness on Energy Dissipation
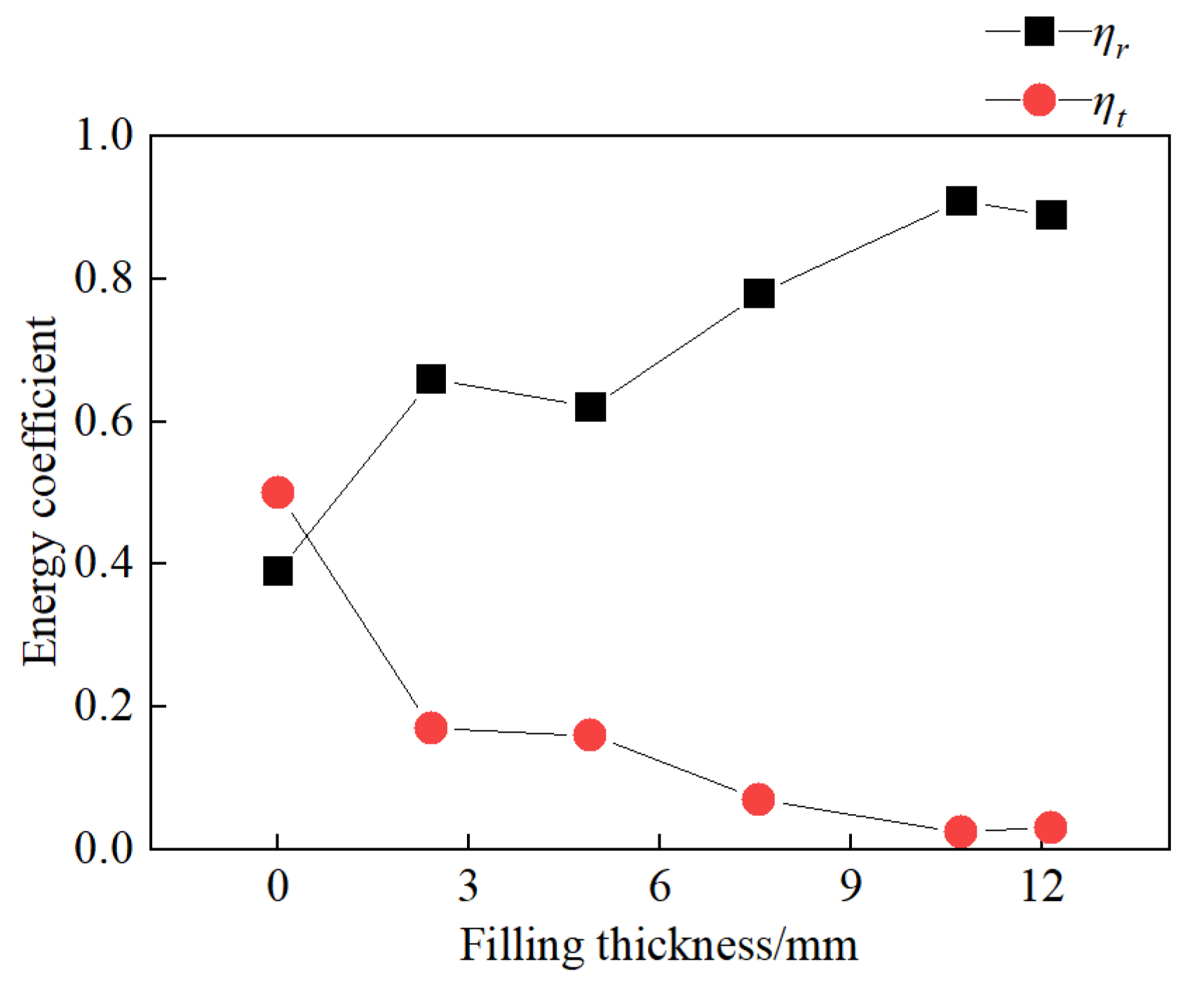
5.3.1. The Relationship Between Energy Coefficients and Filling Thickness
5.3.2. The Relationship Between the Energy Dissipation Ratio and Filling Thickness
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, P.; Verma, A.K.; Negi, A.; Jha, M.K.; Gautam, P. Stability assessment of jointed rock slope with different crack infillings under various thermomechanical loading. Arab. J. Geosci. 2018, 11, 15. [Google Scholar] [CrossRef]
- Azarfar, B.; Ahmadvand, S.; Sattarvand, J.; Abbasi, B. Stability Analysis of Rock Structure in Large Slopes and Open-Pit Mine: Numerical and Experimental Fault Modeling. Rock Mech. Rock Eng. 2019, 52, 4889–4905. [Google Scholar] [CrossRef]
- Hamid, R.M.A.; Hamid, M.; Olivier, F. Coupling of two methods, waveform superposition and numerical, to model blast vibration effect on slope stability in jointed rock masses. Comput. Geotech. 2014, 61, 42–49. [Google Scholar]
- Dai, J.; Yang, J.; Yao, C.; Hu, Y.; Zhang, X.; Jiang, Q.; Zhou, C. Study on the mechanism of displacement mutation for jointed rock slopes during blasting excavation. Int. J. Rock Mech. Min. Sci. 2022, 150, 105032. [Google Scholar] [CrossRef]
- Hong, Z.H.; Tao, M.; Li, X.D.; Zhao, H.T.; Zhao, M.S. Experimental study on the influences of charging structure with various filling mediums on rock blasting performances. Powder Technology. 2023, 429, 118952. [Google Scholar] [CrossRef]
- Mishra, S.; Khetwal, A.; Chakraborty, T.; Basu, D. Effect of loading characteristics and specimen size in split Hopkinson pressure bar test on high-rate behavior of phyllite. Arch. Civ. Mech. Eng. 2022, 22, 212. [Google Scholar] [CrossRef]
- Liu, X.; Wang, G.; Liu, T.; Lin, M.; Lei, H.; Mandal, A.K. Study on dynamic mechanical properties of phosphate rock through experimental tests and mesoscale simulation. Arab. J. Geosci. 2020, 13, 969. [Google Scholar] [CrossRef]
- Mishra, S.; Chakraborty, T.; Matsagar, V.; Loukus, J.; Bekkala, B. High Strain-Rate Characterization of Deccan Trap Rocks Using SHPB Device. J. Mater. Civ. Eng. 2018, 30, 04018059. [Google Scholar] [CrossRef]
- Hou, S.; Liang, S.; Liu, D. Study on dynamic mechanical properties and constitutive model of granite under constant strain rate loading. Constr. Build. Mater. 2023, 363, 129975. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, G.; Das, A. Dynamic Behavior of Ungrouted and Grouted Rocks of Different Morphologies Containing a Flaw Subjected to Different Thermal Treatments. Rock Mech. Rock Eng. 2024, 57, 261–286. [Google Scholar] [CrossRef]
- Li, D.; Han, Z.; Sun, X.; Zhou, T.; Li, X. Dynamic Mechanical Properties and Fracturing Behavior of Marble Specimens Containing Single and Double Flaws in SHPB Tests. Rock Mech. Rock Eng. 2019, 52, 1623–1643. [Google Scholar] [CrossRef]
- Swboda, G.; Shen, X.; Rosas, L. Damage Model for Jointed Rock Mass and Its Application to Tunnelling. Comput. Geotech. 1998, 22, 183–203. [Google Scholar] [CrossRef]
- Li, J.C.; Rong, L.F.; Li, H.B.; Hong, S.N. An SHPB Test Study on Stress Wave Energy Attenuation in Jointed Rock Masses. Rock Mech. Rock Eng. 2019, 52, 403–420. [Google Scholar] [CrossRef]
- Li, D.; Han, Z.; Zhu, Q.; Zhang, Y.; Ranjith, P. Stress wave propagation and dynamic behavior of red sandstone with single bonded planar joint at various angles. Int. J. Rock Mech. Min. Sci. 2019, 117, 162–170. [Google Scholar] [CrossRef]
- Yan, Y.; Li, J.; Li, X. Dynamic viscoelastic model for rock joints under compressive loading. Int. J. Rock Mech. Min. Sci. 2022, 1554, 105123. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, G.; Parameswaran, V. Rate-dependent mechanical behavior of jointed rock with an impersistent joint under different infill conditions. J. Rock Mech. Geotech. Eng. 2022, 14, 1380–1393. [Google Scholar] [CrossRef]
- Chai, S.; Wang, H.; Yu, L.; Shi, J.; Abi, E. Experimental Study on Static and Dynamic Compression Mechanical Properties of Filled Rock Joints. Lat. Am. J. Solids Struct. 2020, 17, 264. [Google Scholar] [CrossRef]
- Li, J.C.; Ma, G.W. Experimental study of stress wave propagation across a filled rock joint. Int. J. Rock Mech. Min. Sci. 2009, 46, 471–478. [Google Scholar] [CrossRef]
- Han, Z.; Li, D.; Zhou, T.; Zhu, Q.; Ranjith, P. Experimental study of stress wave propagation and energy characteristics across rock specimens containing cemented mortar joint with various thicknesses. Int. J. Rock Mech. Min. Sci. 2020, 131, 104352. [Google Scholar] [CrossRef]
- Mahdi, S.; Abbas, T. A cohesive discrete element based approach to characterizing the shear behavior of cohesive soil and clay-infilled rock joints. Comput. Geotech. 2019, 114, 103109. [Google Scholar]
- Chai, S.; Wang, H.; Jin, Y.; Jia, N. Experimental study on dynamic compression characteristics of rock with filled joints after cumulative damage. Chin. J. Rock Mech. Eng. 2020, 39, 2025–2037. [Google Scholar]
- T/CSRME 001-2019; Technical Specification for Testing Method of Rock Dynamic Properties. Chinese Society for Rock Mechanics and Engineering: Beijing, China, 2019.
- Liao, Z.Y.; Zhu, J.B.; Xia, K.W.; Tang, C.A. Determination of Dynamic Compressive and Tensile Behavior of Rocks from Numerical Tests of Split Hopkinson Pressure and Tension Bars. Rock Mech. Rock Eng. 2016, 49, 3917–3934. [Google Scholar] [CrossRef]
- Chakraborty, T.; Mishra, S.; Loukus, J.; Halonen, B.; Bekkala, B. Characterization of three Himalayan rocks using a split Hopkinson pressure bar. Int. J. Rock Mech. Min. Sci. 2016, 85, 112–118. [Google Scholar] [CrossRef]
- Shan, R.L.; Jiang, Y.S.; Li, B.Q. Obtaining dynamic complete stress-strain curves for rock using the Split Hopkinson Pressure Bar technique. Int. J. Rock Mech. Min. Sci. 2000, 37, 983–992. [Google Scholar] [CrossRef]
- Xia, K.W.; Jiang, W. Dynamic rock tests using split Hopkinson (Kolsky) bar system—A review. J. Rock Mech. Geotech. Eng. 2015, 7, 27–59. [Google Scholar] [CrossRef]









| Materials | Mix Ratio | Density/(kg·m3) | Uniaxial Tensile Strength/MPa | Elastic Modulus/GPa | Poisson’s Ratio | Wave Velocity/(m/s) |
|---|---|---|---|---|---|---|
| Granite | - | 2586 | 121.56 | 28.47 | 0.22 | 5357 |
| Gypsum filling | Water:Gypsum = 3:2 | 1800 | 12.18 | 0.35 | 0.25 | 2485 |
| Type of Rock Samples | Diameter/mm | Length/mm | Filling Thickness/mm | Volume/×10−3 m3 | Quality/g |
|---|---|---|---|---|---|
| nfilled jointed rock samples | 50 | 41.08 41.10 41.18 | - - - | 80.66 80.70 80.86 | 200.57 200.35 200.78 |
| Filled jointed rock samples | 50 | 44.40 44.56 44.60 46.10 46.18 46.20 49.10 49.15 49.22 51.50 52.00 52.30 53.00 53.00 53.30 | 2.40 2.40 2.40 4.82 4.91 5.00 7.44 7.56 7.60 10.50 10.73 10.80 12.00 12.10 12.15 | 87.18 87.49 87.57 90.52 90.67 90.71 96.41 96.50 96.64 101.12 102.10 102.69 104.07 104.06 104.65 | 215.50 215.58 215.60 215.59 216.08 216.00 223.52 223.87 224.27 228.72 228.97 229.68 230.71 230.74 230.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; An, J.; Xia, Y.; Si, Y. Experimental Study on the Dynamic Properties of Granite with Filled Joints of Different Thicknesses. Materials 2025, 18, 936. https://doi.org/10.3390/ma18050936
Wang Z, An J, Xia Y, Si Y. Experimental Study on the Dynamic Properties of Granite with Filled Joints of Different Thicknesses. Materials. 2025; 18(5):936. https://doi.org/10.3390/ma18050936
Chicago/Turabian StyleWang, Zhide, Jiaxing An, Yuanyou Xia, and Yingying Si. 2025. "Experimental Study on the Dynamic Properties of Granite with Filled Joints of Different Thicknesses" Materials 18, no. 5: 936. https://doi.org/10.3390/ma18050936
APA StyleWang, Z., An, J., Xia, Y., & Si, Y. (2025). Experimental Study on the Dynamic Properties of Granite with Filled Joints of Different Thicknesses. Materials, 18(5), 936. https://doi.org/10.3390/ma18050936






