Dynamical Projective Operatorial Approach (DPOA): Theory and Applications to Pump–Probe Setups and Semiconductors
Abstract
:1. Introduction
2. Theory
2.1. Dynamical Projective Operatorial Approach (DPOA): General Theory
2.2. Pumped Lattice Systems out of Equilibrium
2.3. Green’s Functions and TR-ARPES Signal
2.4. Out-of-Equilibrium Optical Properties
3. The Case Study of a Three-Band Semiconductor
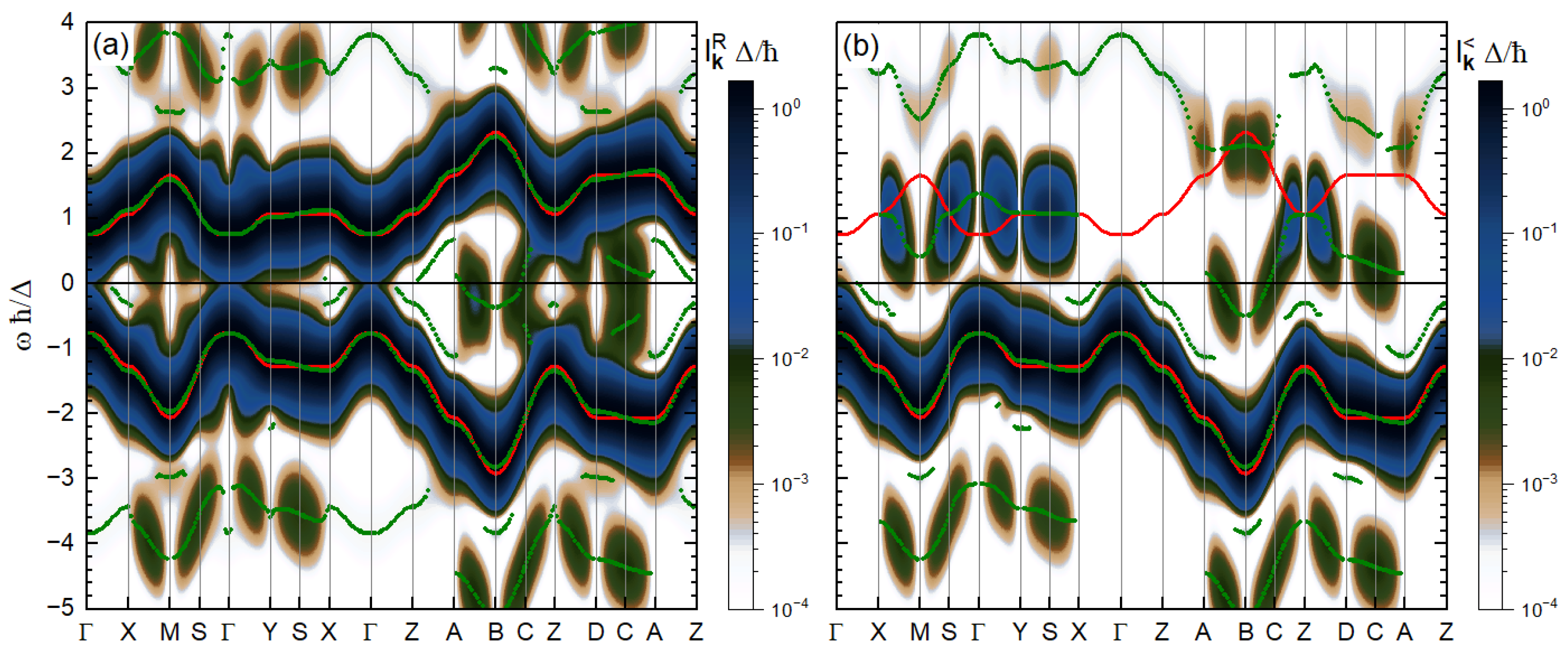
3.1. TR-ARPES Signals
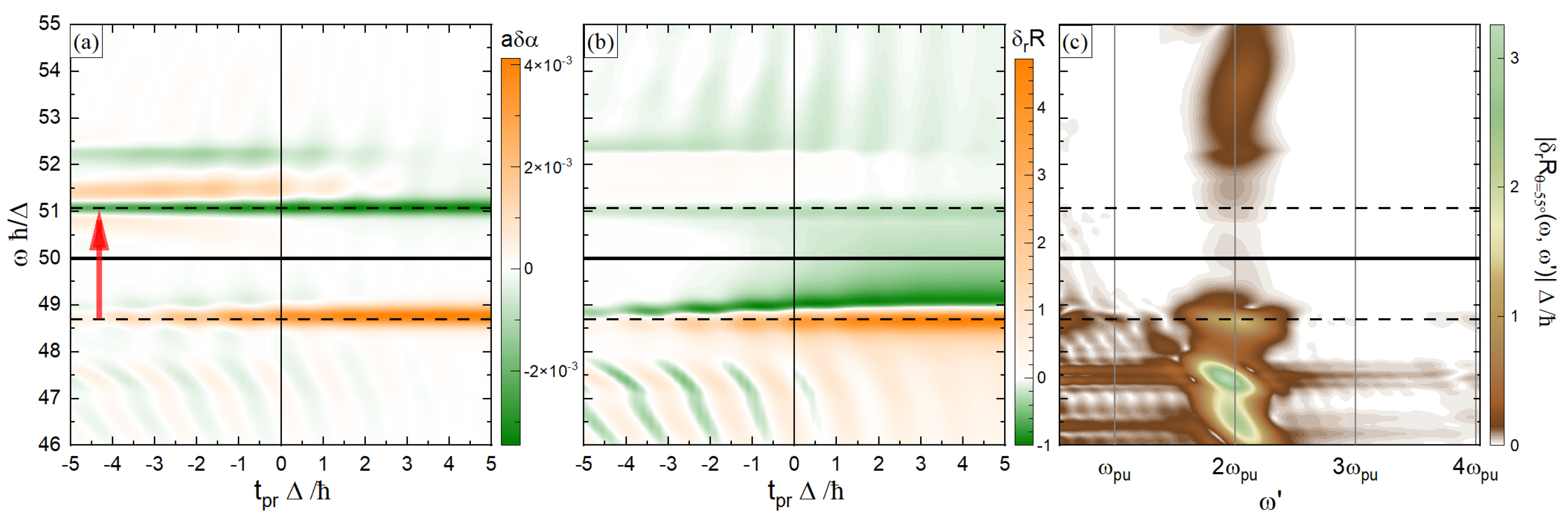
3.2. Transient Optical Properties
4. Summary and Perspectives
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163. [Google Scholar] [CrossRef]
- Schnyder, A.P.; Manske, D.; Avella, A. Resonant generation of coherent phonons in a superconductor by ultrafast optical pump pulses. Phys. Rev. B 2011, 84, 214513. [Google Scholar] [CrossRef]
- Krausz, F.; Stockman, M.I. Attosecond metrology: From electron capture to future signal processing. Nat. Photonics 2014, 8, 205–213. [Google Scholar] [CrossRef]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779–837. [Google Scholar] [CrossRef]
- Calegari, F.; Sansone, G.; Stagira, S.; Vozzi, C.; Nisoli, M. Advances in attosecond science. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 062001. [Google Scholar] [CrossRef]
- Gandolfi, M.; Celardo, G.L.; Borgonovi, F.; Ferrini, G.; Avella, A.; Banfi, F.; Giannetti, C. Emergent ultrafast phenomena in correlated oxides and heterostructures. Phys. Scr. 2017, 92, 034004. [Google Scholar] [CrossRef]
- Borrego-Varillas, R.; Lucchini, M.; Nisoli, M. Attosecond spectroscopy for the investigation of ultrafast dynamics in atomic, molecular and solid-state physics. Rep. Prog. Phys. 2022, 85, 066401. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Chang, H.T.; Borja, L.J.; Kraus, P.M.; Cushing, S.K.; Gandman, A.; Kaplan, C.J.; Oh, M.H.; Prell, J.S.; Prendergast, D.; et al. Direct and simultaneous observation of ultrafast electron and hole dynamics in germanium. Nat. Commun. 2017, 8, 15734. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Chang, H.T.; Kraus, P.M.; Cushing, S.K.; Borja, L.J.; Gandman, A.; Kaplan, C.J.; Oh, M.H.; Prell, J.S.; Prendergast, D.; et al. Ultrafast carrier thermalization and trapping in silicon-germanium alloy probed by extreme ultraviolet transient absorption spectroscopy. Struct. Dyn. 2017, 4, 044029. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, C.J.; Kraus, P.M.; Ross, A.D.; Zürch, M.; Cushing, S.K.; Jager, M.F.; Chang, H.T.; Gullikson, E.M.; Neumark, D.M.; Leone, S.R. Femtosecond tracking of carrier relaxation in germanium with extreme ultraviolet transient reflectivity. Phys. Rev. B 2018, 97, 205202. [Google Scholar] [CrossRef]
- Perfetti, L.; Loukakos, P.A.; Lisowski, M.; Bovensiepen, U.; Wolf, M.; Berger, H.; Biermann, S.; Georges, A. Femtosecond dynamics of electronic states in the Mott insulator 1T-TaS2 by time resolved photoelectron spectroscopy. New J. Phys. 2008, 10, 053019. [Google Scholar] [CrossRef]
- Schmitt, F.; Kirchmann, P.S.; Bovensiepen, U.; Moore, R.G.; Rettig, L.; Krenz, M.; Chu, J.H.; Ru, N.; Perfetti, L.; Lu, D.; et al. Transient electronic structure and melting of a charge density wave in TbTe3. Science 2008, 321, 1649–1652. [Google Scholar] [CrossRef]
- von der Linde, D.; Engers, T.; Jenke, G.; Agostini, P.; Grillon, G.; Nibbering, E.; Mysyrowicz, A.; Antonetti, A. Generation of high-order harmonics from solid surfaces by intense femtosecond laser pulses. Phys. Rev. A 1995, 52, R25. [Google Scholar] [CrossRef]
- Norreys, P.A.; Zepf, M.; Moustaizis, S.; Fews, A.P.; Zhang, J.; Lee, P.; Bakarezos, M.; Danson, C.N.; Dyson, A.; Gibbon, P.; et al. Efficient Extreme UV Harmonics Generated from Picosecond Laser Pulse Interactions with Solid Targets. Phys. Rev. Lett. 1996, 76, 1832–1835. [Google Scholar] [CrossRef] [PubMed]
- Chin, A.H.; Calderón, O.G.; Kono, J. Extreme midinfrared nonlinear optics in semiconductors. Phys. Rev. Lett. 2001, 86, 3292. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, S.; DiChiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141. [Google Scholar] [CrossRef]
- Luu, T.T.; Garg, M.; Kruchinin, S.Y.; Moulet, A.; Hassan, M.T.; Goulielmakis, E. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 2015, 521, 498–502. [Google Scholar] [CrossRef]
- Han, S.; Kim, H.; Kim, Y.W.; Kim, Y.J.; Kim, S.; Park, I.Y.; Kim, S.W. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. Nat. Commun. 2016, 7, 13105. [Google Scholar] [CrossRef]
- Borja, L.J.; Zürch, M.; Pemmaraju, C.D.; Schultze, M.; Ramasesha, K.; Gandman, A.; Prell, J.S.; Prendergast, D.; Neumark, D.M.; Leone, S.R. Extreme ultraviolet transient absorption of solids from femtosecond to attosecond timescales. J. Opt. Soc. Am. B 2016, 33, C57–C64. [Google Scholar] [CrossRef]
- You, Y.S.; Reis, D.A.; Ghimire, S. Anisotropic high-harmonic generation in bulk crystals. Nat. Phys. 2017, 13, 345–349. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; You, Y.S.; Ghimire, S.; Heinz, T.F.; Reis, D.A. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 2017, 13, 262–265. [Google Scholar] [CrossRef]
- Jiang, S.; Gholam-Mirzaei, S.; Crites, E.; Beetar, J.E.; Singh, M.; Lu, R.; Chini, M.; Lin, C. Crystal symmetry and polarization of high-order harmonics in ZnO. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 225601. [Google Scholar] [CrossRef]
- Rohwer, T.; Hellmann, S.; Wiesenmayer, M.; Sohrt, C.; Stange, A.; Slomski, B.; Carr, A.; Liu, Y.; Avila, L.M.; Kalläne, M.; et al. Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 2011, 471, 490–493. [Google Scholar] [CrossRef]
- Smallwood, C.L.; Hinton, J.P.; Jozwiak, C.; Zhang, W.; Koralek, J.D.; Eisaki, H.; Lee, D.H.; Orenstein, J.; Lanzara, A. Tracking Cooper pairs in a cuprate superconductor by ultrafast angle-resolved photoemission. Science 2012, 336, 1137–1139. [Google Scholar] [CrossRef]
- Hellmann, S.; Rohwer, T.; Kalläne, M.; Hanff, K.; Sohrt, C.; Stange, A.; Carr, A.; Murnane, M.; Kapteyn, H.; Kipp, L.; et al. Time-domain classification of charge-density-wave insulators. Nat. Commun. 2012, 3, 1069. [Google Scholar] [CrossRef]
- Papalazarou, E.; Faure, J.; Mauchain, J.; Marsi, M.; Taleb-Ibrahimi, A.; Reshetnyak, I.; van Roekeghem, A.; Timrov, I.; Vast, N.; Arnaud, B.; et al. Coherent Phonon Coupling to Individual Bloch States in Photoexcited Bismuth. Phys. Rev. Lett. 2012, 108, 256808. [Google Scholar] [CrossRef]
- Wang, Y.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch states on the surface of a topological insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef]
- Johannsen, J.C.; Ulstrup, S.; Cilento, F.; Crepaldi, A.; Zacchigna, M.; Cacho, C.; Turcu, I.C.E.; Springate, E.; Fromm, F.; Raidel, C.; et al. Direct View of Hot Carrier Dynamics in Graphene. Phys. Rev. Lett. 2013, 111, 027403. [Google Scholar] [CrossRef]
- Rameau, J.; Freutel, S.; Kemper, A.; Sentef, M.A.; Freericks, J.; Avigo, I.; Ligges, M.; Rettig, L.; Yoshida, Y.; Eisaki, H.; et al. Energy dissipation from a correlated system driven out of equilibrium. Nat. Commun. 2016, 7, 13761. [Google Scholar] [CrossRef]
- Reimann, J.; Schlauderer, S.; Schmid, C.; Langer, F.; Baierl, S.; Kokh, K.; Tereshchenko, O.; Kimura, A.; Lange, C.; Güdde, J.; et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 2018, 562, 396–400. [Google Scholar] [CrossRef]
- Smith, N.; Traum, M. Angular-resolved ultraviolet photoemission spectroscopy and its application to the layer compounds Ta Se 2 and Ta S 2. Phys. Rev. B 1975, 11, 2087. [Google Scholar] [CrossRef]
- Himpsel, F.J.; Eastman, D.E. Experimental energy dispersions for valence and conduction bands of palladium. Phys. Rev. B 1978, 18, 5236–5239. [Google Scholar] [CrossRef]
- Kampf, A.P.; Schrieffer, J.R. Spectral function and photoemission spectra in antiferromagnetically correlated metals. Phys. Rev. B 1990, 42, 7967–7974. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.E.; Kevan, S.D. The electronic structure of solids studied using angle resolved photoemission spectroscopy. Prog. Solid State Chem. 1991, 21, 49–131. [Google Scholar] [CrossRef]
- Damascelli, A.; Hussain, Z.; Shen, Z.X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473. [Google Scholar] [CrossRef]
- Hüfner, S. Photoelectron Spectroscopy: Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sobota, J.A.; He, Y.; Shen, Z.X. Angle-resolved photoemission studies of quantum materials. Rev. Mod. Phys. 2021, 93, 025006. [Google Scholar] [CrossRef]
- Schultze, M.; Bothschafter, E.M.; Sommer, A.; Holzner, S.; Schweinberger, W.; Fiess, M.; Hofstetter, M.; Kienberger, R.; Apalkov, V.; Yakovlev, V.S.; et al. Controlling dielectrics with the electric field of light. Nature 2013, 493, 75–78. [Google Scholar] [CrossRef]
- Stojchevska, L.; Vaskivskyi, I.; Mertelj, T.; Kusar, P.; Svetin, D.; Brazovskii, S.; Mihailovic, D. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 2014, 344, 177–180. [Google Scholar] [CrossRef]
- Schultze, M.; Ramasesha, K.; Pemmaraju, C.; Sato, S.; Whitmore, D.; Gandman, A.; Prell, J.S.; Borja, L.; Prendergast, D.; Yabana, K.; et al. Attosecond band-gap dynamics in silicon. Science 2014, 346, 1348–1352. [Google Scholar] [CrossRef]
- Lucchini, M.; Sato, S.A.; Ludwig, A.; Herrmann, J.; Volkov, M.; Kasmi, L.; Shinohara, Y.; Yabana, K.; Gallmann, L.; Keller, U. Attosecond dynamical Franz-Keldysh effect in polycrystalline diamond. Science 2016, 353, 916–919. [Google Scholar] [CrossRef]
- Mashiko, H.; Oguri, K.; Yamaguchi, T.; Suda, A.; Gotoh, H. Petahertz optical drive with wide-bandgap semiconductor. Nat. Phys. 2016, 12, 741–745. [Google Scholar] [CrossRef]
- Avella, A.; Buonavolontà, C.; Guarino, A.; Valentino, M.; Leo, A.; Grimaldi, G.; de Lisio, C.; Nigro, A.; Pepe, G. Disorder-sensitive pump-probe measurements on Nd1.83Ce0.17CuO4±δ films. Phys. Rev. B 2016, 94, 115426. [Google Scholar] [CrossRef]
- Nembrini, N.; Peli, S.; Banfi, F.; Ferrini, G.; Singh, Y.; Gegenwart, P.; Comin, R.; Foyevtsova, K.; Damascelli, A.; Avella, A.; et al. Tracking local magnetic dynamics via high-energy charge excitations in a relativistic Mott insulator. Phys. Rev. B 2016, 94, 201119. [Google Scholar] [CrossRef]
- Novelli, F.; Giovannetti, G.; Avella, A.; Cilento, F.; Patthey, L.; Radovic, M.; Capone, M.; Parmigiani, F.; Fausti, D. Localized vibrations in superconducting YBa2Cu3O7 revealed by ultrafast optical coherent spectroscopy. Phys. Rev. B 2017, 95, 174524. [Google Scholar] [CrossRef]
- Schlaepfer, F.; Lucchini, M.; Sato, S.A.; Volkov, M.; Kasmi, L.; Hartmann, N.; Rubio, A.; Gallmann, L.; Keller, U. Attosecond optical-field-enhanced carrier injection into the GaAs conduction band. Nat. Phys. 2018, 14, 560–564. [Google Scholar] [CrossRef]
- Giusti, F.; Marciniak, A.; Randi, F.; Sparapassi, G.; Boschini, F.; Eisaki, H.; Greven, M.; Damascelli, A.; Avella, A.; Fausti, D. Signatures of Enhanced Superconducting Phase Coherence in Optimally Doped Bi2Sr2Y0.08Ca0.92Cu2O8+δ Driven by Midinfrared Pulse Excitations. Phys. Rev. Lett. 2019, 122, 067002. [Google Scholar] [CrossRef]
- Kaplan, C.J.; Kraus, P.M.; Gullikson, E.M.; Borja, L.J.; Cushing, S.K.; Zürch, M.; Chang, H.T.; Neumark, D.M.; Leone, S.R. Retrieval of the complex-valued refractive index of germanium near the M4,5 absorption edge. J. Opt. Soc. Am. B 2019, 36, 1716. [Google Scholar] [CrossRef]
- Geneaux, R.; Marroux, H.J.; Guggenmos, A.; Neumark, D.M.; Leone, S.R. Transient absorption spectroscopy using high harmonic generation: A review of ultrafast X-ray dynamics in molecules and solids. Philos. Trans. R. Soc. A 2019, 377, 20170463. [Google Scholar] [CrossRef]
- Giusti, F.; Montanaro, A.; Marciniak, A.; Randi, F.; Boschini, F.; Glerean, F.; Jarc, G.; Eisaki, H.; Greven, M.; Damascelli, A.; et al. Anisotropic time-domain electronic response in cuprates driven by midinfrared pulses. Phys. Rev. B 2021, 104, 125121. [Google Scholar] [CrossRef]
- Inzani, G.; Adamska, L.; Eskandari-asl, A.; Palo, N.D.; Dolso, G.L.; Moio, B.; D’Onofrio, L.J.; Lamperti, A.; Molle, A.; Borrego-Varillas, R.; et al. Field-driven attosecond charge dynamics in germanium. Nat. Photonics 2023, 17, 1059. [Google Scholar] [CrossRef]
- Inzani, G.; Eskandari-asl, A.; Adamska, L.; Moio, B.; Dolso, G.L.; Palo, N.D.; D’Onofrio, L.J.; Lamperti, A.; Molle, A.; Rozzi, C.A.; et al. Photoinduced charge carrier dynamics in germanium. Il Nuovo Cimento C 2023, 46, 110. [Google Scholar]
- Neufeld, O.; Tancogne-Dejean, N.; De Giovannini, U.; Hübener, H.; Rubio, A. Attosecond magnetization dynamics in non-magnetic materials driven by intense femtosecond lasers. NPJ Comput. Mater. 2023, 9, 39. [Google Scholar] [CrossRef]
- De Giovannini, U.; Brunetto, G.; Castro, A.; Walkenhorst, J.; Rubio, A. Inside Cover: Simulating Pump–Probe Photoelectron and Absorption Spectroscopy on the Attosecond Timescale with Time-Dependent Density Functional Theory (ChemPhysChem 7/2013). ChemPhysChem 2013, 14, 1298. [Google Scholar] [CrossRef]
- De Giovannini, U.; Hubener, H.; Rubio, A. Monitoring electron-photon dressing in WSe2. Nano Lett. 2016, 16, 7993–7998. [Google Scholar] [CrossRef] [PubMed]
- Wopperer, P.; De Giovannini, U.; Rubio, A. Efficient and accurate modeling of electron photoemission in nanostructures with TDDFT. Eur. Phys. J. B 2017, 90, 51. [Google Scholar] [CrossRef]
- De Giovannini, U.; Hübener, H.; Rubio, A. A first-principles time-dependent density functional theory framework for spin and time-resolved angular-resolved photoelectron spectroscopy in periodic systems. J. Chem. Theory Comput. 2017, 13, 265–273. [Google Scholar] [CrossRef]
- Pemmaraju, C.D.; Vila, F.D.; Kas, J.J.; Sato, S.A.; Rehr, J.J.; Yabana, K.; Prendergast, D. Velocity-gauge real-time TDDFT within a numerical atomic orbital basis set. Comput. Phys. Commun. 2018, 226, 30–38. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Rubio, A. Atomic-like high-harmonic generation from two-dimensional materials. Sci. Adv. 2018, 4, eaao5207. [Google Scholar] [CrossRef]
- De Giovannini, U.; Castro, A. Real-time and real-space time-dependent density-functional theory approach to attosecond dynamics. Attosecond Mol. Dyn. 2018, 13, 424–461. [Google Scholar]
- Armstrong, G.S.; Khokhlova, M.A.; Labeye, M.; Maxwell, A.S.; Pisanty, E.; Ruberti, M. Dialogue on analytical and ab initio methods in attoscience. Eur. Phys. J. D 2021, 75, 209. [Google Scholar] [CrossRef] [PubMed]
- Sato, S.A.; Lucchini, M.; Volkov, M.; Schlaepfer, F.; Gallmann, L.; Keller, U.; Rubio, A. Role of intraband transitions in photocarrier generation. Phys. Rev. B 2018, 98, 035202. [Google Scholar] [CrossRef]
- Broers, L.; Mathey, L. Detecting light-induced Floquet band gaps of graphene via trARPES. Phys. Rev. Res. 2022, 4, 013057. [Google Scholar] [CrossRef]
- D’Onofrio, L.J.; Eskandari-asl, A.; Avella, A. Time evolution of energies and populations in germanium perturbed by a near-infrared pulse on the atto-second scale. J. Magn. Magn. Mater. 2022, 546, 168785. [Google Scholar] [CrossRef]
- Schüler, M.; Marks, J.A.; Murakami, Y.; Jia, C.; Devereaux, T.P. Gauge invariance of light-matter interactions in first-principle tight-binding models. Phys. Rev. B 2021, 103, 155409. [Google Scholar] [CrossRef]
- Eskandari-asl, A.; Avella, A. Time-resolved ARPES signal in pumped semiconductors within the dynamical projective operatorial approach. Phys. Rev. B 2024, 110, 094309. [Google Scholar] [CrossRef]
- Eskandari-asl, A.; Avella, A. Generalized linear response theory for pumped systems and its application to transient optical properties. Phys. Rev. A 2024, 110, 043520. [Google Scholar] [CrossRef]
- Mancini, F.; Avella, A. The Hubbard model within the equations of motion approach. Adv. Phys. 2004, 53, 537–768. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F. Underdoped cuprate phenomenology in the two-dimensional Hubbard model within the composite operator method. Phys. Rev. B 2007, 75, 134518. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F. The Composite Operator Method (COM). In Strongly Correlated Systems: Theoretical Methods; Avella, A., Mancini, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 103–141. [Google Scholar] [CrossRef]
- Avella, A. The Hubbard model beyond the two-pole approximation: A composite operator method study. Eur. Phys. J. B 2014, 87, 45. [Google Scholar] [CrossRef]
- Avella, A. Composite operator method analysis of the underdoped cuprates puzzle. Adv. Condens. Matter Phys. 2014, 2014, 515698. [Google Scholar] [CrossRef]
- Di Ciolo, A.; Avella, A. The composite operator method route to the 2D Hubbard model and the cuprates. Condens. Matter. Phys. 2018, 21, 33701. [Google Scholar] [CrossRef]
- Eskandari-asl, A.; Avella, A. Out-of-equilibrium Hubbard dimer within DPOA. In Proceedings of the Advances in Ultrafast Condensed Phase Physics IV, Strasbourg, France, 7–11 April 2024; Volume 12992, pp. 65–68. [Google Scholar]
- Inzani, G.; Adamska, L.; D’Onofrio, L.J.; Moio, B.; Dolso, G.L.; Di Palo, N.; Eskandari-asl, A.; Lamperti, A.; Molle, A.; Rozzi, C.A.; et al. Attosecond Inter-and Intra-Band Charge Carrier Dynamics in Germanium. In Proceedings of the International Conference on Ultrafast Phenomena, Montreal, QC, Canada, 18–22 July 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. W4A-32. [Google Scholar]
- Inzani, G.; Adamska, L.; Eskandari-asl, A.; Di Palo, N.; Dolso, G.L.; Moio, B.; D’Onofrio, L.J.; Lamperti, A.; Molle, A.; Borrego-Varillas, R.; et al. Light-Driven Attosecond Photoinjection in Germanium. In Proceedings of the The European Conference on Lasers and Electro-Optics, Munich, Germany, 26–30 June 2023; Optica Publishing Group: Washington, DC, USA, 2023; p. cg_2_2. [Google Scholar]
- Di Palo, N.; Inzani, G.; Adamska, L.; Eskandari-asl, A.; Dolso, G.; Moio, B.; D’Onofrio, L.; Lamperti, A.; Molle, A.; Borrego-Varillas, R.; et al. Attosecond photoinjection dynamics in germanium. In Proceedings of the Advances in Ultrafast Condensed Phase Physics IV, Strasbourg, France, 7–11 April 2024; p. PC129920O. [Google Scholar]
- Eskandari-asl, A.; Avella, A. Dynamical projective operatorial approach (DPOA) for pump-probe setups in the ultrafast regime. In Proceedings of the Advances in Ultrafast Condensed Phase Physics IV, Strasbourg, France, 7–11 April 2024; Volume 12992, pp. 69–73. [Google Scholar]
- Inzani, G.; Adamska, L.; Eskandari-asl, A.; Di Palo, N.; Dolso, G.L.; Moio, B.; D’Onofrio, L.J.; Lamperti, A.; Molle, A.; Borrego-Varillas, R.; et al. Photoexcitation in germanium probed by attosecond transient reflectivity spectroscopy. In Proceedings of the Ultrafast Phenomena and Nanophotonics XXVIII, San Francisco, CA, USA, 29 January–1 February 2023; Volume 12884, pp. 31–36. [Google Scholar]
- Avella, A.; Mancini, F.; Villani, D.; Matsumoto, H. The superconducting gap in the two-dimensional Hubbard model. Phys. C Supercond. 1997, 282, 1757–1758. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Villani, D. The overdoped regime in La2- xSrxCuO4. Solid State Commun. 1998, 108, 723–725. [Google Scholar] [CrossRef]
- Sanchez, M.; Avella, A.; Mancini, F. The half-filled Hubbard chain in the Composite Operator Method: A comparison with Bethe Ansatz. Europhys. Lett. 1998, 44, 328. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Villani, D. Incommensurate spin fluctuations in the two-dimensional t-t’-U model. Phys. Lett. A 1998, 240, 235–240. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Villani, D.; Siurakshina, L.; Yushankhai, V.Y. The Hubbard model in the two-pole approximation. Int. J. Mod. Phys. B 1998, 12, 81–97. [Google Scholar] [CrossRef]
- Villani, D.; Lange, E.; Avella, A.; Kotliar, G. Two-Scale Analysis of the SU(N) Kondo Model. Phys. Rev. Lett. 2000, 85, 804–807. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Villani, D.; Matsumoto, H. The two-dimensional t-t’-U model as a minimal model for cuprate materials. Eur. Phys. J. B-Condens. Matter Complex Syst. 2001, 20, 303–311. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Münzner, R. Antiferromagnetic phase in the Hubbard model by means of the composite operator method. Phys. Rev. B 2001, 63, 245117. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Turkowski, V. Bosonic sector of the two-dimensional Hubbard model studied within a two-pole approximation. Phys. Rev. B 2003, 67, 115123. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Saikawa, T. The 2-site Hubbard and t-J models. Eur. Phys. J. B-Condens. Matter Complex Syst. 2003, 36, 445–473. [Google Scholar] [CrossRef]
- Mancini, F.; Avella, A. Equation of motion method for composite field operators. Eur. Phys. J. B-Condens. Matter Complex Syst. 2003, 36, 37–56. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F. The Hubbard model with intersite interaction within the Composite Operator Method. Eur. Phys. J. B-Condens. Matter Complex Syst. 2004, 41, 149–162. [Google Scholar] [CrossRef]
- Avella, A.; Krivenko, S.; Mancini, F.; Plakida, N. Self-energy corrections to the electronic spectrum of the Hubbard model. J. Magn. Magn. Mater. 2004, 272, 456–457. [Google Scholar] [CrossRef]
- Odashima, S.; Avella, A.; Mancini, F. High-order correlation effects in the two-dimensional Hubbard model. Phys. Rev. B 2005, 72, 205121. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F. Exact solution of the one-dimensional spin-3/2 Ising model in magnetic field. Eur. Phys. J. B-Condens. Matter Complex Syst. 2006, 50, 527–539. [Google Scholar] [CrossRef]
- Avella, A.; Mancini, F.; Mancini, F.P.; Plekhanov, E. Emery vs. Hubbard model for cuprate superconductors: A composite operator method study. Eur. Phys. J. B 2013, 86, 265. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Pizzi, G.; Lee, Y.S.; Souza, I.; Vanderbilt, D.; Marzari, N. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2014, 185, 2309. [Google Scholar] [CrossRef]
- Peierls, R. Zur theorie des diamagnetismus von leitungselektronen. Z. Phys. 1933, 80, 763–791. [Google Scholar] [CrossRef]
- Ismail-Beigi, S.; Chang, E.K.; Louie, S.G. Coupling of nonlocal potentials to electromagnetic fields. Phys. Rev. Lett. 2001, 87, 087402. [Google Scholar] [CrossRef] [PubMed]
- Freericks, J.K.; Krishnamurthy, H.R.; Pruschke, T. Theoretical Description of Time-Resolved Photoemission Spectroscopy: Application to Pump-Probe Experiments. Phys. Rev. Lett. 2009, 102, 136401. [Google Scholar] [CrossRef] [PubMed]
- Sentef, M.; Kemper, A.F.; Moritz, B.; Freericks, J.K.; Shen, Z.X.; Devereaux, T.P. Examining electron-boson coupling using time-resolved spectroscopy. Phys. Rev. X 2013, 3, 041033. [Google Scholar] [CrossRef]
- Freericks, J.; Krishnamurthy, H.; Sentef, M.; Devereaux, T. Gauge invariance in the theoretical description of time-resolved angle-resolved pump/probe photoemission spectroscopy. Phys. Scr. 2015, 2015, 014012. [Google Scholar] [CrossRef]
- Schüler, M.; Sentef, M.A. Theory of subcycle time-resolved photoemission: Application to terahertz photodressing in graphene. J. Electron Spectrosc. Relat. Phenom. 2021, 253, 147121. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eskandari-asl, A.; Avella, A. Dynamical Projective Operatorial Approach (DPOA): Theory and Applications to Pump–Probe Setups and Semiconductors. Materials 2025, 18, 1310. https://doi.org/10.3390/ma18061310
Eskandari-asl A, Avella A. Dynamical Projective Operatorial Approach (DPOA): Theory and Applications to Pump–Probe Setups and Semiconductors. Materials. 2025; 18(6):1310. https://doi.org/10.3390/ma18061310
Chicago/Turabian StyleEskandari-asl, Amir, and Adolfo Avella. 2025. "Dynamical Projective Operatorial Approach (DPOA): Theory and Applications to Pump–Probe Setups and Semiconductors" Materials 18, no. 6: 1310. https://doi.org/10.3390/ma18061310
APA StyleEskandari-asl, A., & Avella, A. (2025). Dynamical Projective Operatorial Approach (DPOA): Theory and Applications to Pump–Probe Setups and Semiconductors. Materials, 18(6), 1310. https://doi.org/10.3390/ma18061310






