Innovative Machine Learning Approaches for Predicting the Asphalt Content During Marshall Design of Asphalt Mixtures
Abstract
1. Introduction
2. Methodology
2.1. Sample Preparation
2.2. Machine Learning Models and Analysis
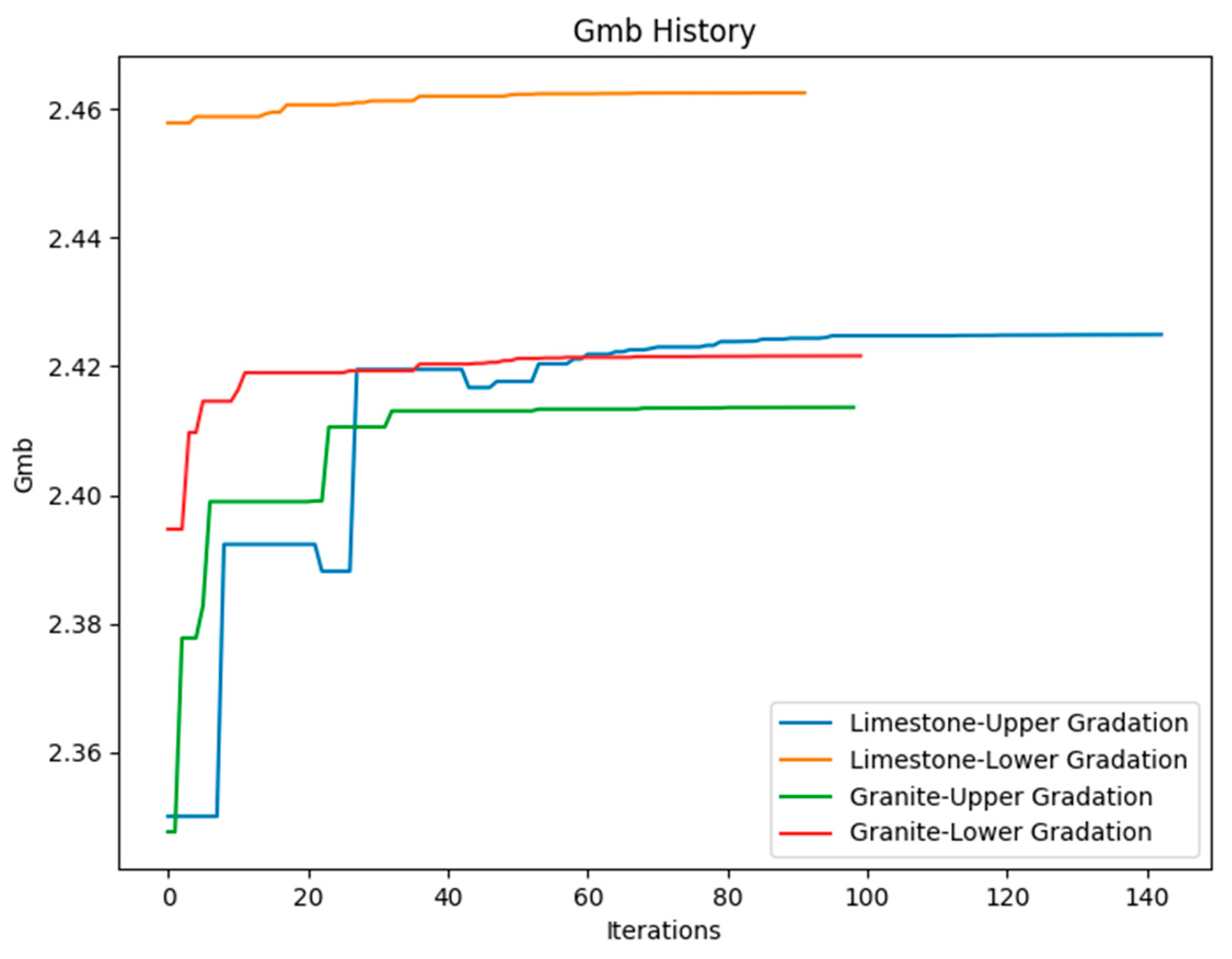
2.3. Differential Evolution Algorithm
3. Key Steps in the Differential Evolution Algorithm
- Initialization: A population of candidate solutions is randomly generated within specified bounds (minimum and maximum values for the asphalt amount and other properties).
- Mutation: For each candidate solution, a new candidate is created by applying mutation, which typically involves adding weighted differences between two randomly selected solutions to a third solution.
- Crossover: The newly mutated candidate is combined with the original candidate to form a new solution. The crossover operation defines the proportion of the original and mutated solutions retained in the new candidate.
- Selection: The new candidate is evaluated against the original solution, and the superior solution—based on the objective function, such as maximizing bulk specific gravity—is selected for the next generation.
- Iteration: These steps are repeated over multiple generations until a convergence criterion is achieved.
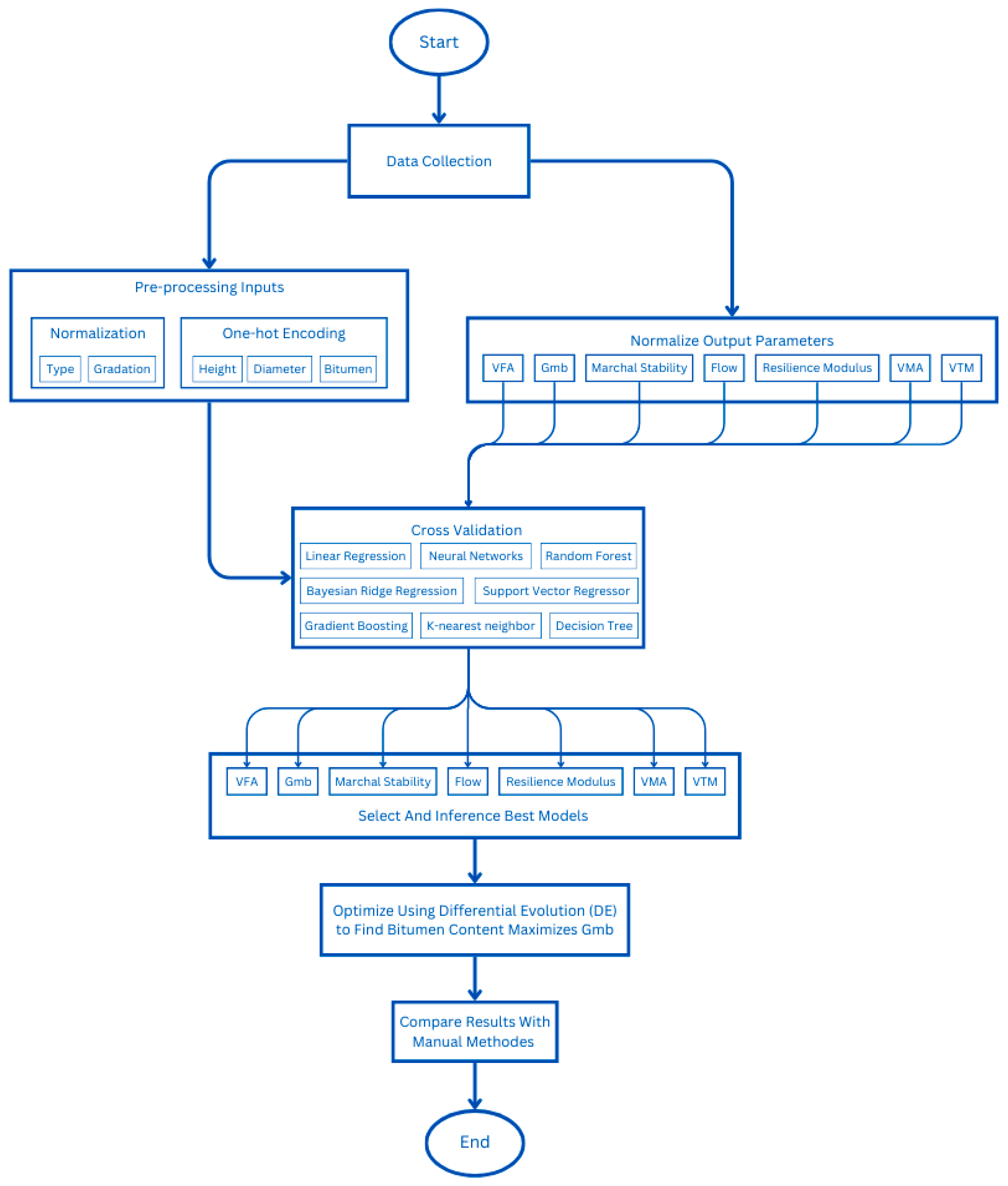
3.1. Data Preprocessing
3.2. Linear Regression
3.3. Bayesian Ridge Regression
3.4. Support Vector Regressor (SVR)
3.5. Decision Tree Regressor
3.6. Random Forest Regressor
3.7. Gradient Boosting Regressor
3.8. K-Neighbors Regressor
3.9. Neural Network Regressor
4. Results and Discussion
4.1. First Phase: Marshall Parameter Testing
Analysis Tests for (OAC)
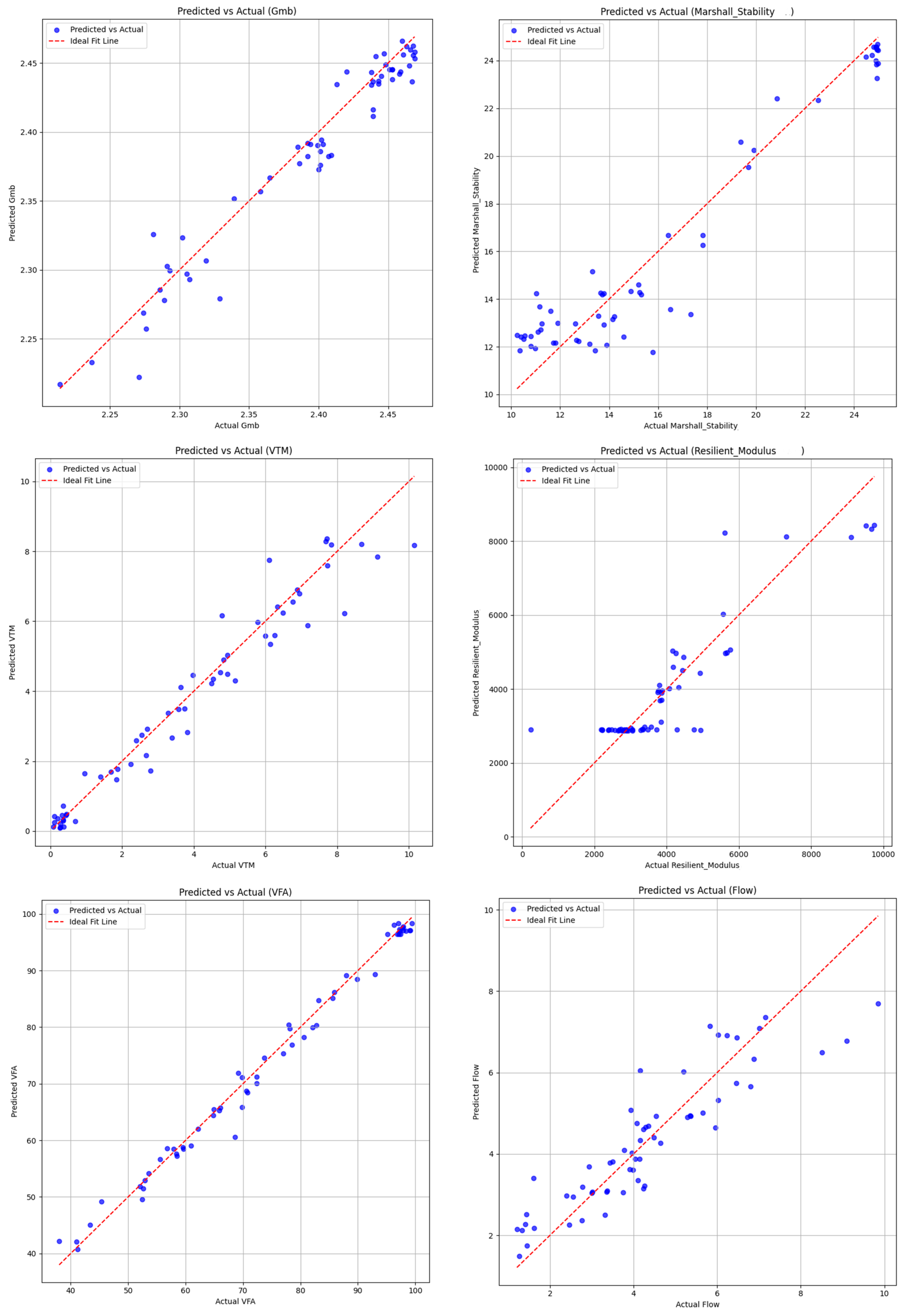
4.2. Second Phase: Analysis of Machine Learning Models
4.2.1. Cross-Validation
4.2.2. Neural Network Regression (NNR)
4.2.3. Summary of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, C.; Liu, J.; Yaohui, S.; Wang, L.; Wang, X. Optimizing Asphalt Mix Design Using Machine Learning Methods Based on RIOCHTrack Data; Research Square: Durham, NC, USA, 2023; in review. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Mei, Z.; Huang, B. Improving accuracy of rutting prediction for mechanistic-empirical pavement design guide with deep neural networks. Constr. Build. Mater. 2018, 190, 710–718. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Buttlar, W.G.; Alavi, A.H. New machine learning-based prediction models for fracture energy of asphalt mixtures. Measurement 2019, 135, 438–451. [Google Scholar] [CrossRef]
- Moussa, G.S.; Owais, M. Pre-trained deep learning for hot-mix asphalt dynamic modulus prediction with laboratory effort reduction. Constr. Build. Mater. 2020, 265, 120239. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Dong, Y.; Han, B.; Polaczyk, P.; Hu, W.; Huang, B. Improved estimation of dynamic modulus for hot mix asphalt using deep learning. Constr. Build. Mater. 2020, 263, 119912. [Google Scholar] [CrossRef]
- Behnood, A.; Daneshvar, D. A machine learning study of the dynamic modulus of asphalt concretes: An application of M5P model tree algorithm. Constr. Build. Mater. 2020, 262, 120544. [Google Scholar] [CrossRef]
- Barugahare, J.; Amirkhanian, A.N.; Xiao, F.; Amirkhanian, S.N. Predicting the dynamic modulus of hot mix asphalt mixtures using bagged trees ensemble. Constr. Build. Mater. 2020, 260, 120468. [Google Scholar] [CrossRef]
- Rahman, S.; Bhasin, A.; Smit, A. Exploring the use of machine learning to predict metrics related to asphalt mixture performance. Constr. Build. Mater. 2021, 295, 123585. [Google Scholar] [CrossRef]
- Baldo, N.; Miani, M.; Rondinella, F.; Valentin, J.; Vackova, P.; Manthos, E. Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning. Coatings 2022, 12, 54. [Google Scholar] [CrossRef]
- Emig, J.; Reuter, U.; Bolz, P.; Leischner, S.; Canon Falla, G. A stochastic neural network based approach for metamodelling of mechanical asphalt concrete properties. Int. J. Pavement Eng. 2023, 24, 2177650. [Google Scholar] [CrossRef]
- Le, T.-H.; Nguyen, H.-L.; Pham, C.-T. Artificial intelligence approach to predict the dynamic modulus of asphalt concrete mixtures. J. Sci. Transp. Technol. 2022, 2, 22–31. [Google Scholar] [CrossRef]
- Mirzaiyanrajeh, D.; Dave, E.; Sias, J.; Ramsey, P. Developing a prediction model for low-temperature fracture energy of asphalt mixtures using machine learning approach. Int. J. Pavement Eng. 2022, 24, 1–12. [Google Scholar] [CrossRef]
- Upadhya, A.; Thakur, M.S.; Mashat, A.; Gupta, G.; Abdo, M.S. Prediction of Binder Content in Glass Fiber Reinforced Asphalt Mix Using Machine Learning Techniques. IEEE Access 2022, 10, 33866–33881. [Google Scholar] [CrossRef]
- Al-Sabaeei, A.M.; Alhussian, H.; Abdulkadir, S.J.; Giustozzi, F.; Jakarni, F.M.; Yusoff, N.I.M. Predicting the rutting parameters of nanosilica/waste denim fiber composite asphalt binders using the response surface methodology and machine learning methods. Constr. Build. Mater. 2023, 363, 129871. [Google Scholar] [CrossRef]
- Upadhya, A.; Thakur, M.S.; Sihag, P.; Kumar, R.; Kumar, S.; Afeeza, A.; Afzal, A.; Saleel, C.A. Modelling and prediction of binder content using latest intelligent machine learning algorithms in carbon fiber reinforced asphalt concrete. Alex. Eng. J. 2023, 65, 131–149. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Zheng, C.; Zhou, D.; Wang, L. Optimizing asphalt mix design through predicting effective asphalt content and absorbed asphalt content using machine learning. Constr. Build. Mater. 2022, 325, 126607. [Google Scholar] [CrossRef]
- Khan, A.; Huyan, J.; Zhang, R.; Zhu, Y.; Zhang, W.; Ying, G.; Ahmad, K.N.; Shah, S.K. An ensemble tree-based prediction of Marshall mix design parameters and resilient modulus in stabilized base materials. Constr. Build. Mater. 2023, 401, 132833. [Google Scholar] [CrossRef]
- Hosseinian, S.M.; Bazoobandi, P.; Mousavi, S.R.; Karimi, F. Presentation of machine learning methods and multi-objective optimization of fracture indices for asphalt rubber mixtures containing wax-based warm mix additives modified by nano calcium carbonate. Constr. Build. Mater. 2023, 409, 134136. [Google Scholar] [CrossRef]
- Gomez-Flores, A.; Cho, H.; Hong, G.; Nam, H.; Kim, H.; Chung, Y. A critical review on machine learning applications in fiber composites and nanocomposites: Towards a control loop in the chain of processes in industries. Mater. Des. 2024, 245, 113247. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, S.; Cui, Q.; Luan, D.; Xiao, F.; Xu, C. Prediction of moisture content ratio of emulsified asphalt chip seal based on machine learning and electrical parameters. Constr. Build. Mater. 2024, 450, 138633. [Google Scholar] [CrossRef]
- Talebi, H.; Bahrami, B.; Ahmadian, H.; Nejati, M.; Ayatollahi, M.R. An investigation of machine learning algorithms for estimating fracture toughness of asphalt mixtures. Constr. Build. Mater. 2024, 435, 136783. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.; Cao, J.; Shi, X. Modeling rutting depth on RIOHTrack asphalt pavement using Circle LSTMs. Expert Syst. Appl. 2024, 253, 124184. [Google Scholar] [CrossRef]
- Alnaqbi, A.J.; Zeiada, W.; Al-Khateeb, G.; Abttan, A.; Abuzwidah, M. Predictive models for flexible pavement fatigue cracking based on machine learning. Transp. Eng. 2024, 16, 100243. [Google Scholar] [CrossRef]
- Mansour, E.; Dhasmana, H.; Mousa, M.R.; Hassan, M. Machine learning-based technology for asphalt concrete pavement performance decision-making in hot and humid climates. Constr. Build. Mater. 2024, 442, 137625. [Google Scholar] [CrossRef]
- Kaloop, M.R.; El-Badawy, S.M.; Hu, J.W.; El-Hakim, R.T.A. International Roughness Index prediction for flexible pavements using novel machine learning techniques. Eng. Appl. Artif. Intell. 2023, 122, 106007. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Rath, P.; Contreras, L.U.; Buttlar, W.G.; Alavi, A.H. Developing a prediction model for rutting depth of asphalt mixtures using gene expression programming. Constr. Build. Mater. 2021, 267, 120543. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, K.; Zhang, Y.; Luo, Y.; Wang, S. Prediction of air voids of asphalt layers by intelligent algorithm. Constr. Build. Mater. 2022, 317, 125908. [Google Scholar] [CrossRef]
- Moussa, G.S.; Owais, M. Modeling Hot-Mix asphalt dynamic modulus using deep residual neural Networks: Parametric and sensitivity analysis study. Constr. Build. Mater. 2021, 294, 123589. [Google Scholar] [CrossRef]
- Tangga, A.A.; Mufargi, H.A.L.; Milad, A.; Ali, A.A.; Al-Sabaeei, A.M.; Md Yusoff, N.I. Utilising machine learning algorithms to predict the Marshall characteristics of asphalt pavement layers. Innov. Infrastruct. Solut. 2024, 9, 381. [Google Scholar] [CrossRef]
- Riyad, R.H.; Jaiswal, R.; Muhit, I.B.; Shen, J. Optimizing modified asphalt binder performance at high and intermediate temperatures using experimental and machine learning approaches. Constr. Build. Mater. 2024, 449, 138350. [Google Scholar] [CrossRef]
- Gardezi, H.; Ikrama, M.; Usama, M.; Iqbal, M.; Jalal, F.E.; Hussain, A.; Li, X. Predictive modeling of rutting depth in modified asphalt mixes using gene-expression programming (GEP): A sustainable use of RAP, fly ash, and plastic waste. Constr. Build. Mater. 2024, 443, 137809. [Google Scholar] [CrossRef]
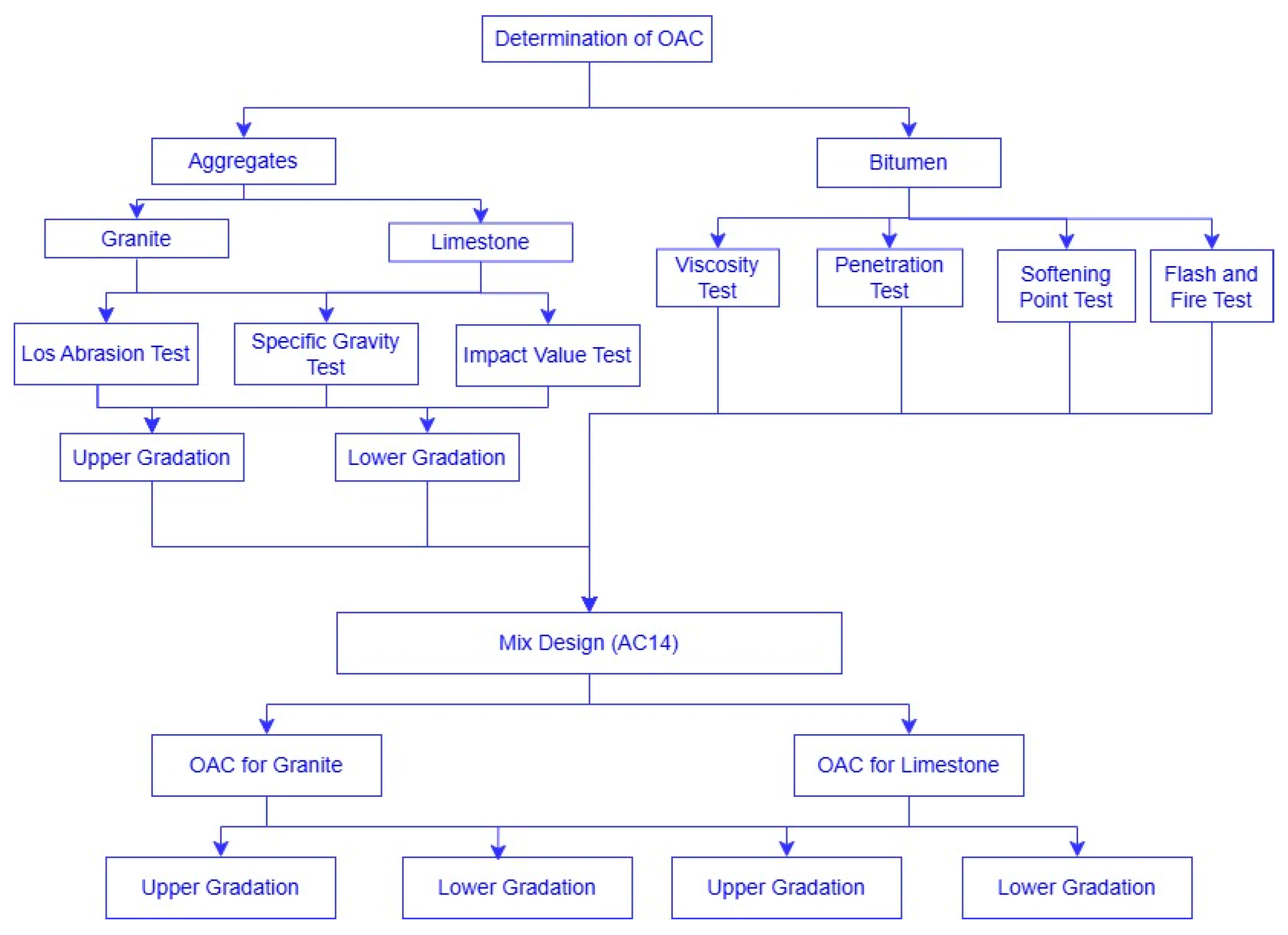
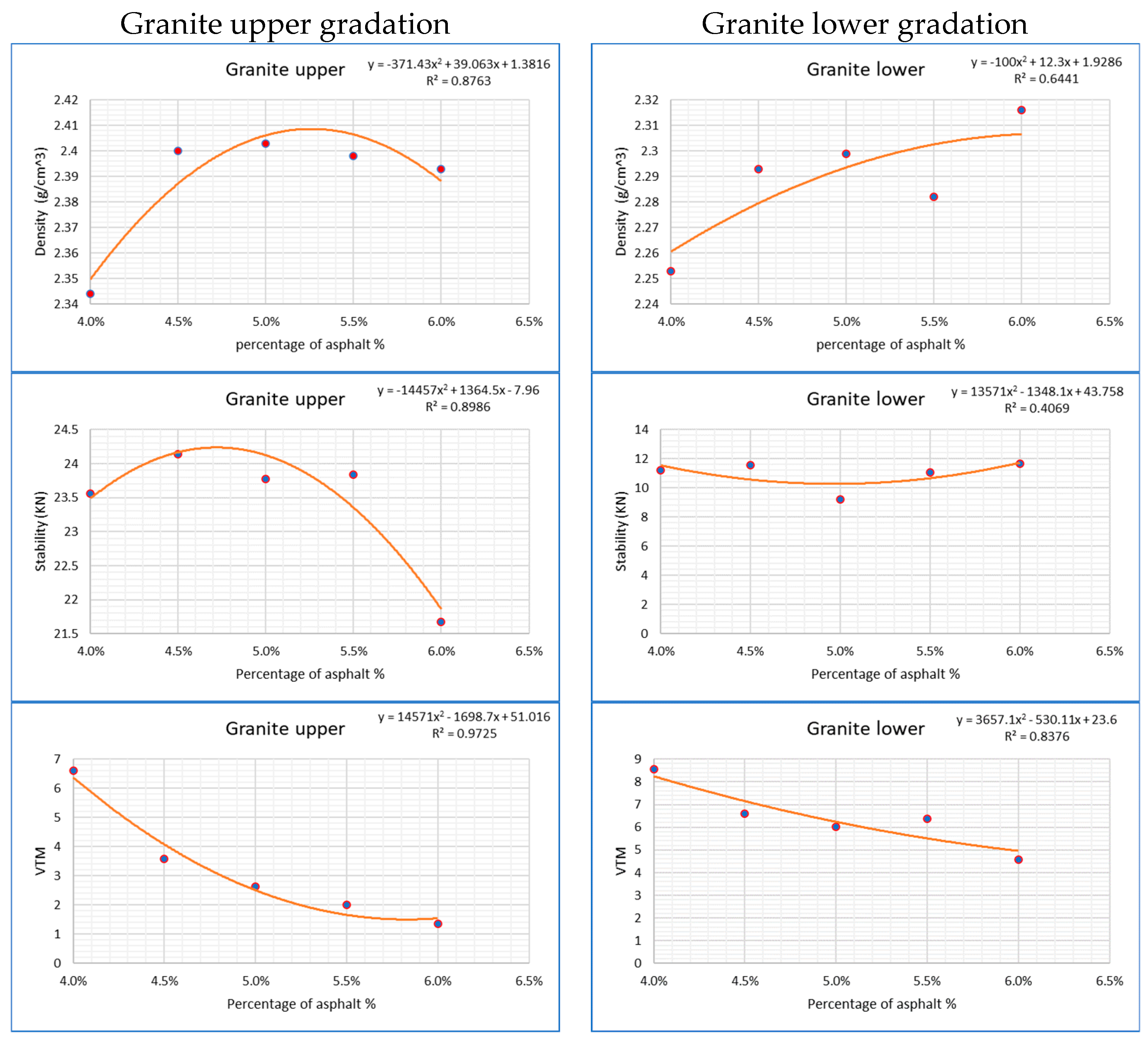
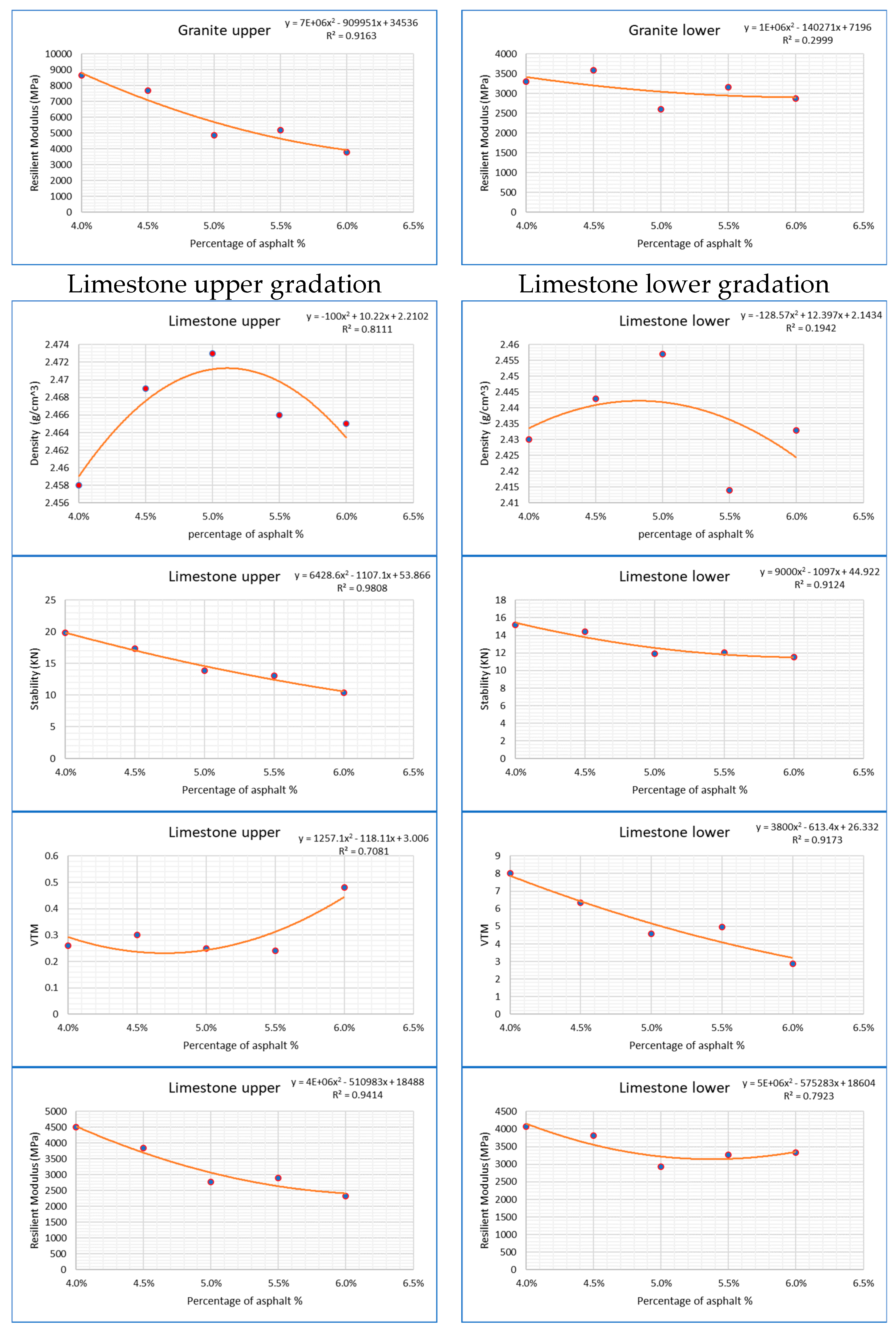

| Type of Aggregate | OAC (%) for Density | OAC (%) for Stability | OAC (%) for VTM | OAC (%) for Resilient Modulus | Average Optimum Asphalt Content |
|---|---|---|---|---|---|
| Granite upper gradation | 5.3 | 4.7 | 4.5 | 4.5 | 4.8 |
| Granite lower gradation | 6 | 5 | 6.8 * | 4.5 | 5.2 |
| Limestone upper gradation | 5.1 | 4.3 | NA | 4.3 | 4.6 |
| Limestone lower gradation | 4.8 | 4.3 | 5.5 | 4 | 4.7 |
| Type of Mixture | OAC (%) | Density (Kg/cm3) | Stability (KN) | VTM (%) | Resilient Modulus (MPa) |
|---|---|---|---|---|---|
| JKR/SPJ/2008 Specification | 4–6 | - | >8 KN | 3–5 | >2000 |
| Granite upper gradation | 4.8 | 2.401 | 24.23 | 3.05 | 6200 |
| Granite lower gradation | 5.2 | 2.298 | 12.49 | 5.92 | 3100 |
| Limestone upper gradation | 4.6 | 2.469 | 16.1 | NA | 3800 |
| Limestone lower gradation | 4.7 | 2.442 | 12.53 | 5.9 | 3845 |
| Model | Flow MSE | Gmb MSE | Marshall Stability MSE | Resilient Modulus MSE | VFA MSE | VMA MSE | VTM MSE |
|---|---|---|---|---|---|---|---|
| Linear Regression | 1.1282 | 0.0003 | 8.6917 | 2,022,443.2421 | 89.3324 | 0.3683 | 1.8881 |
| Bayesian Ridge Regression | 1.1212 | 0.0003 | 8.6839 | 1,998,274.0914 | 89.1263 | 0.3692 | 1.8676 |
| Support Vector Regressor (SVR) | 1.3895 | 0.0007 | 7.2507 | 1,327,800.8528 | 42.2544 | 0.7462 | 1.3124 |
| Decision Tree Regressor | 2.5272 | 0.0005 | 4.2419 | 1,098,981.8458 | 41.1321 | 0.6064 | 1.4373 |
| Random Forest Regressor | 1.6286 | 0.0003 | 2.9487 | 896,862.0808 | 30.2089 | 0.3532 | 1.1686 |
| Gradient Boosting Regressor | 1.7801 | 0.0004 | 4.0591 | 858,300.1841 | 25.6149 | 0.5399 | 1.2474 |
| K-Neighbors Regressor | 1.0595 | 0.0004 | 3.8122 | 1,404,392.5592 | 60.3673 | 0.6225 | 1.5999 |
| Neural Network Regressor | 0.9493 | 0.0003 | 2.9841 | 893,475.1084 | 15.4153 | 0.3753 | 0.8226 |
| Model | Flow | Gmb | Marshall Stability | Resilient Modulus | VFA | VMA | VTM |
|---|---|---|---|---|---|---|---|
| R2 | R2 | R2 | R2 | R2 | R2 | R2 | |
| Linear Regression | 0.6952 | 0.9432 | 0.6848 | 0.4133 | 0.7293 | 0.8827 | 0.7636 |
| Bayesian Ridge Regression | 0.6971 | 0.9433 | 0.6851 | 0.4203 | 0.7299 | 0.8825 | 0.7662 |
| Support Vector Regressor (SVR) | 0.6246 | 0.8655 | 0.7371 | 0.6148 | 0.8719 | 0.7624 | 0.8357 |
| Decision Tree Regressor | 0.3173 | 0.8922 | 0.8462 | 0.6812 | 0.8753 | 0.8068 | 0.8201 |
| Random Forest Regressor | 0.56 | 0.9384 | 0.8931 | 0.7398 | 0.9085 | 0.8885 | 0.8537 |
| Gradient Boosting Regressor | 0.5191 | 0.9187 | 0.8528 | 0.751 | 0.9224 | 0.828 | 0.8438 |
| K-Neighbors Regressor | 0.7138 | 0.914 | 0.8618 | 0.5926 | 0.8171 | 0.8017 | 0.7997 |
| Neural Network Regressor | 0.7435 | 0.9408 | 0.8918 | 0.7408 | 0.9533 | 0.8805 | 0.897 |
| Type of Aggregate | Optimum Asphalt Content (%) | Height (mm) | Diameter (mm) | Gmb |
|---|---|---|---|---|
| Granite upper gradation | 4.35027885 | 62.7005655 | 101.0006294 | 2.4136278 |
| Granite lower gradation | 5.3300419 | 62.7009352 | 101.6999504 | 2.4216117 |
| Limestone upper gradation | 4.00002129 | 64.0433294 | 101.0000297 | 2.4249282 |
| Limestone lower gradation | 5.40446488 | 62.7000285 | 101.6998767 | 2.4624772 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ammari, M.; Dong, R.; Nasser, M.; Al-Maswari, A. Innovative Machine Learning Approaches for Predicting the Asphalt Content During Marshall Design of Asphalt Mixtures. Materials 2025, 18, 1474. https://doi.org/10.3390/ma18071474
Al-Ammari M, Dong R, Nasser M, Al-Maswari A. Innovative Machine Learning Approaches for Predicting the Asphalt Content During Marshall Design of Asphalt Mixtures. Materials. 2025; 18(7):1474. https://doi.org/10.3390/ma18071474
Chicago/Turabian StyleAl-Ammari, Mutahar, Ruikun Dong, Mohammed Nasser, and Abdullah Al-Maswari. 2025. "Innovative Machine Learning Approaches for Predicting the Asphalt Content During Marshall Design of Asphalt Mixtures" Materials 18, no. 7: 1474. https://doi.org/10.3390/ma18071474
APA StyleAl-Ammari, M., Dong, R., Nasser, M., & Al-Maswari, A. (2025). Innovative Machine Learning Approaches for Predicting the Asphalt Content During Marshall Design of Asphalt Mixtures. Materials, 18(7), 1474. https://doi.org/10.3390/ma18071474






