Study on the Erosion Law and Erosion Prediction Model of Pipe Columns During Gas Storage Reservoir Injection and Production Processes
Abstract
1. Introduction
2. Mathematical Models
2.1. Model Assumption
- (1)
- The content of solid particles is less than 10%.
- (2)
- The incident particles are spherical, independent, and uniform in shape, and collisions between particles and possible binding and destruction of particles during collisions are not considered.
- (3)
- Changes in physical properties due to phase transitions are not considered.
- (4)
- Particles do not slide when in contact with the wall, thus simplifying the calculation of friction and impact load.
2.2. Continuous Phase Models
2.3. Turbulence Models
2.4. Discrete Phase Models
2.5. Erosion Models
2.6. Model Validation
3. Geometrical Modeling and Meshing
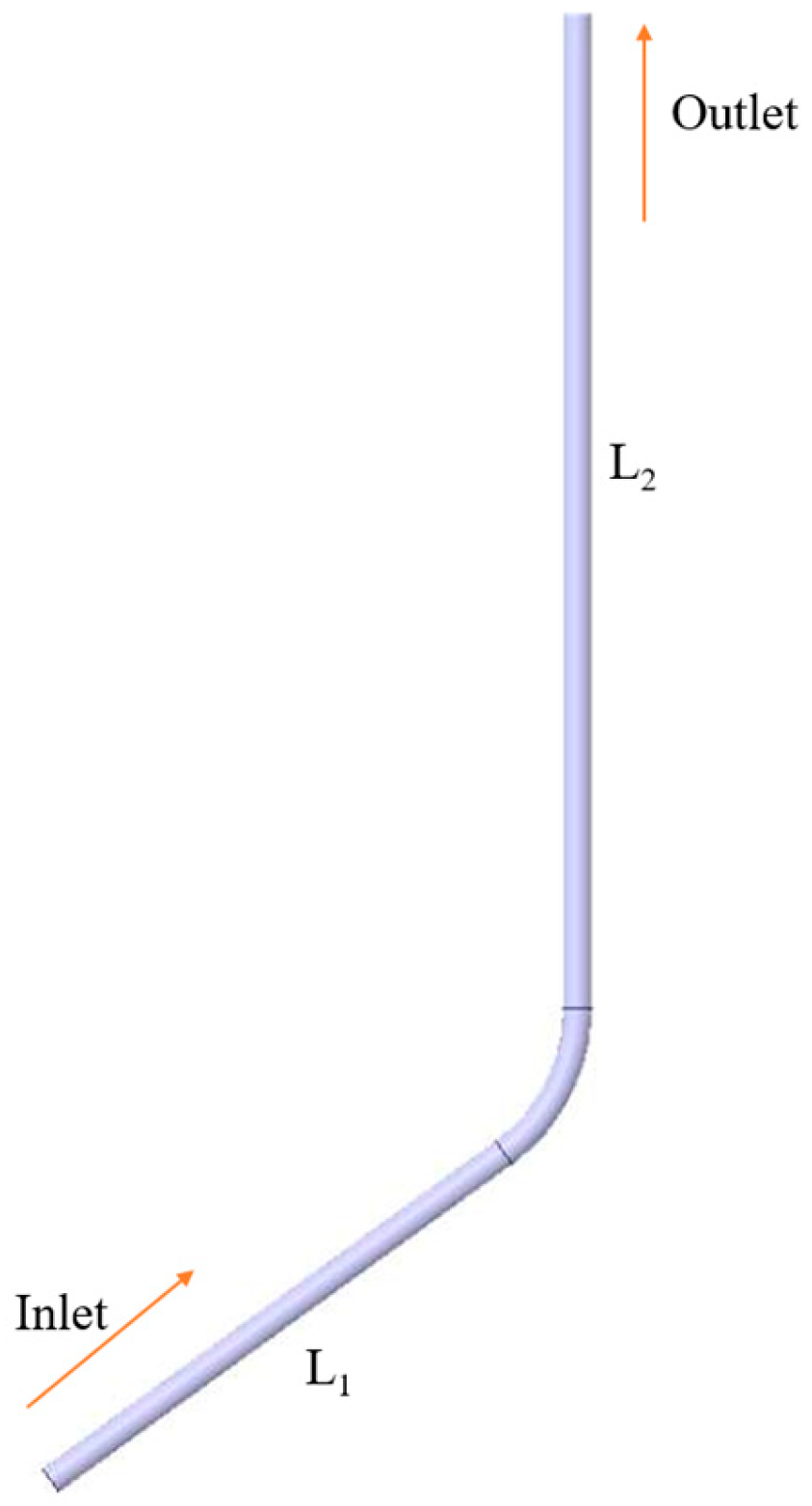
3.1. Geometrical Modeling of Gas Storage Columns
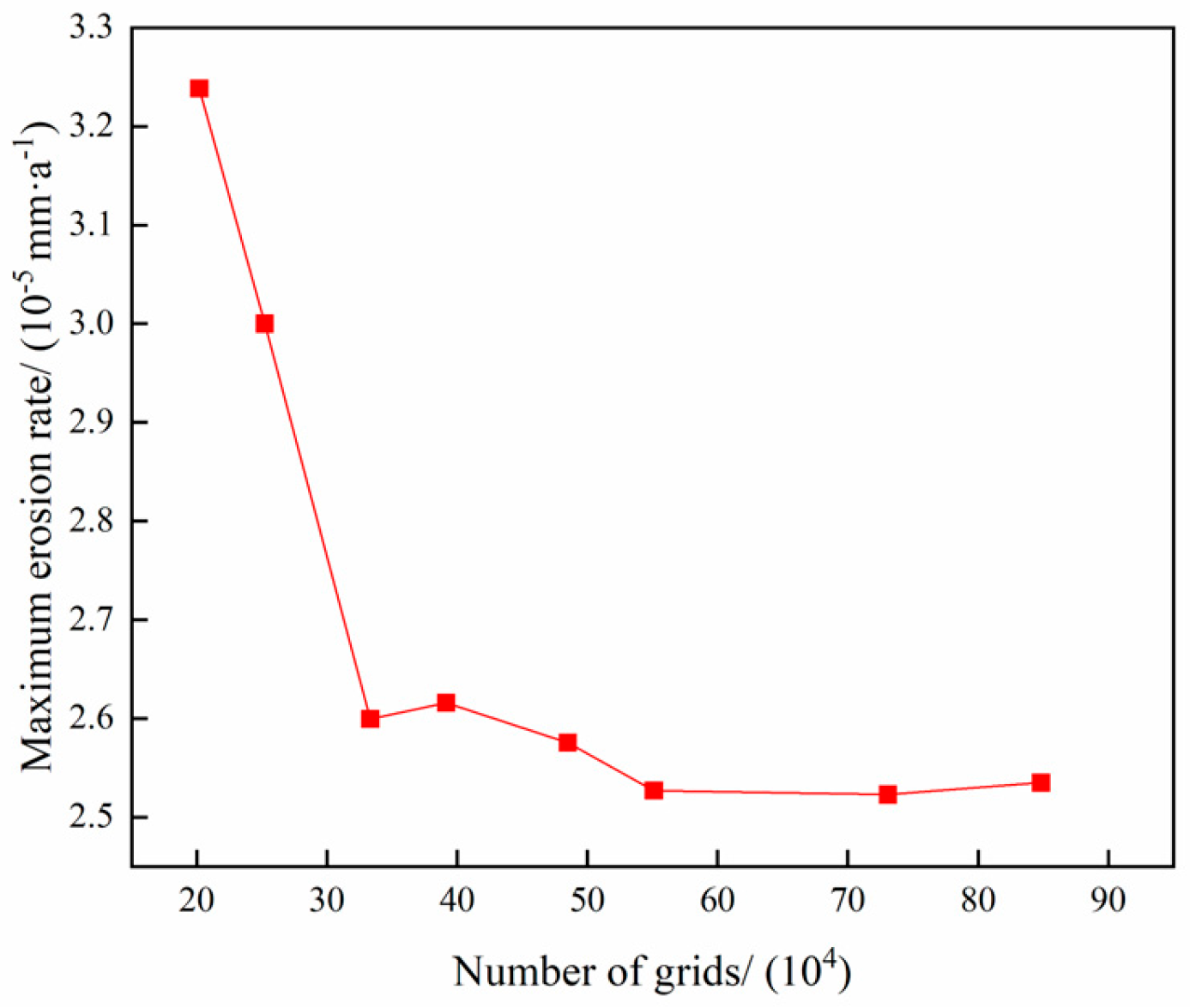
3.2. Grid Division and Irrelevance Verification
4. Single-Factor Analysis and Predictive Model Regression of the Gas Storage Reservoir Column Injection Process
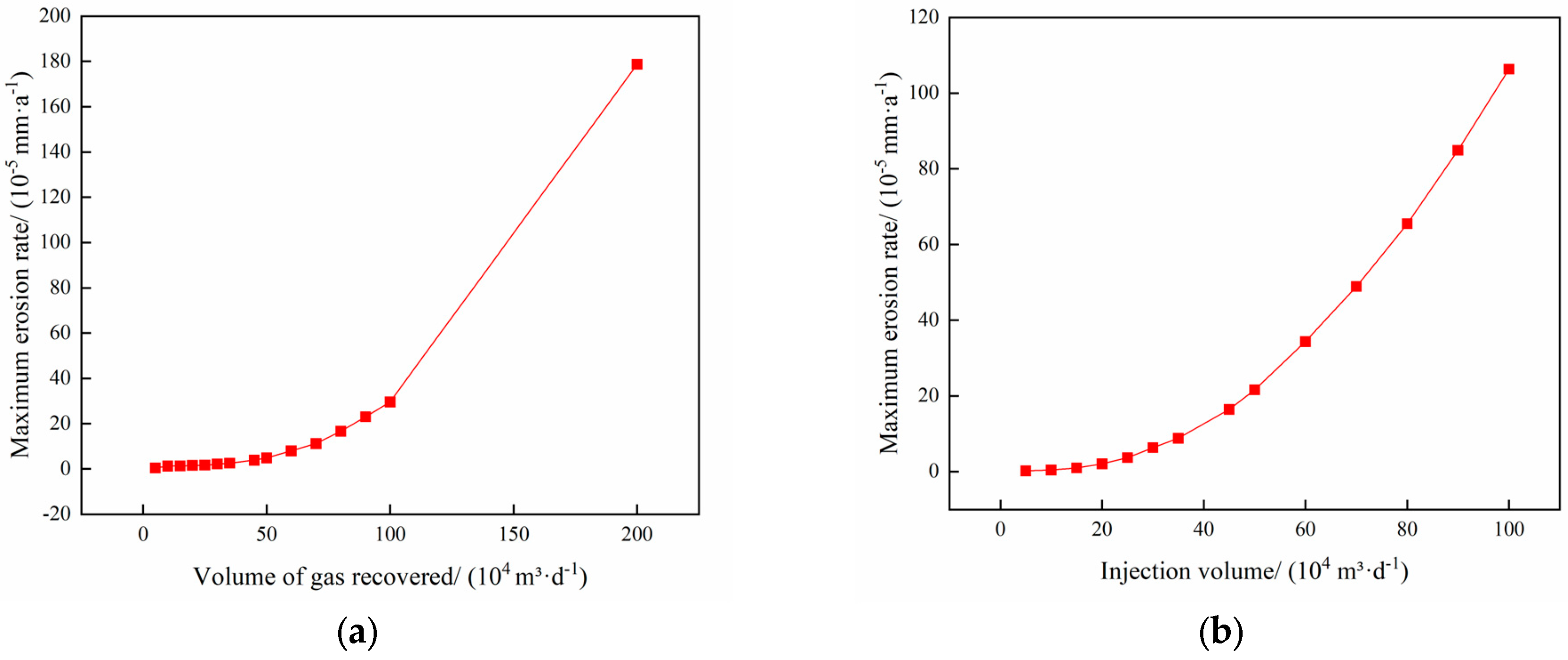
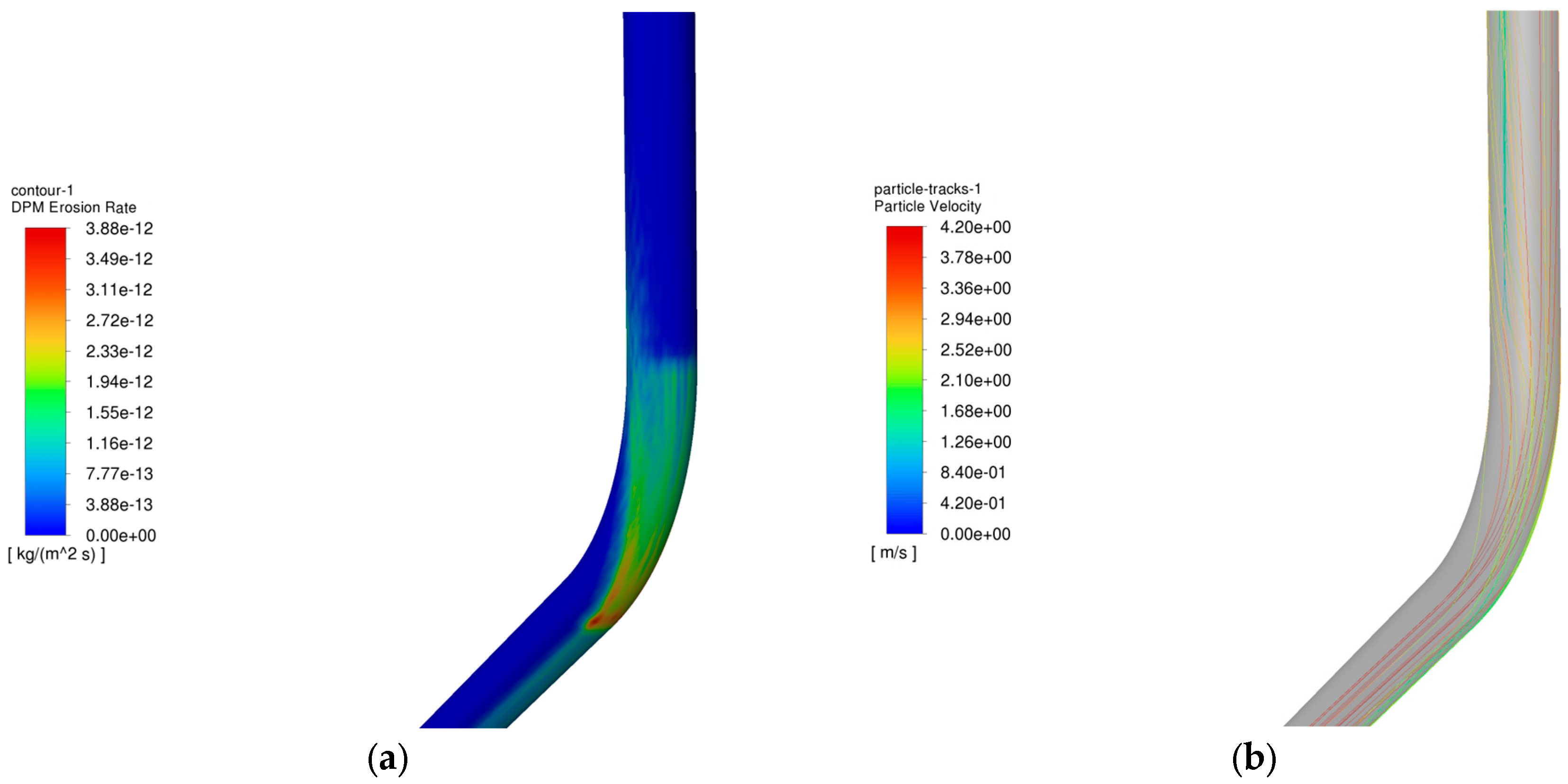
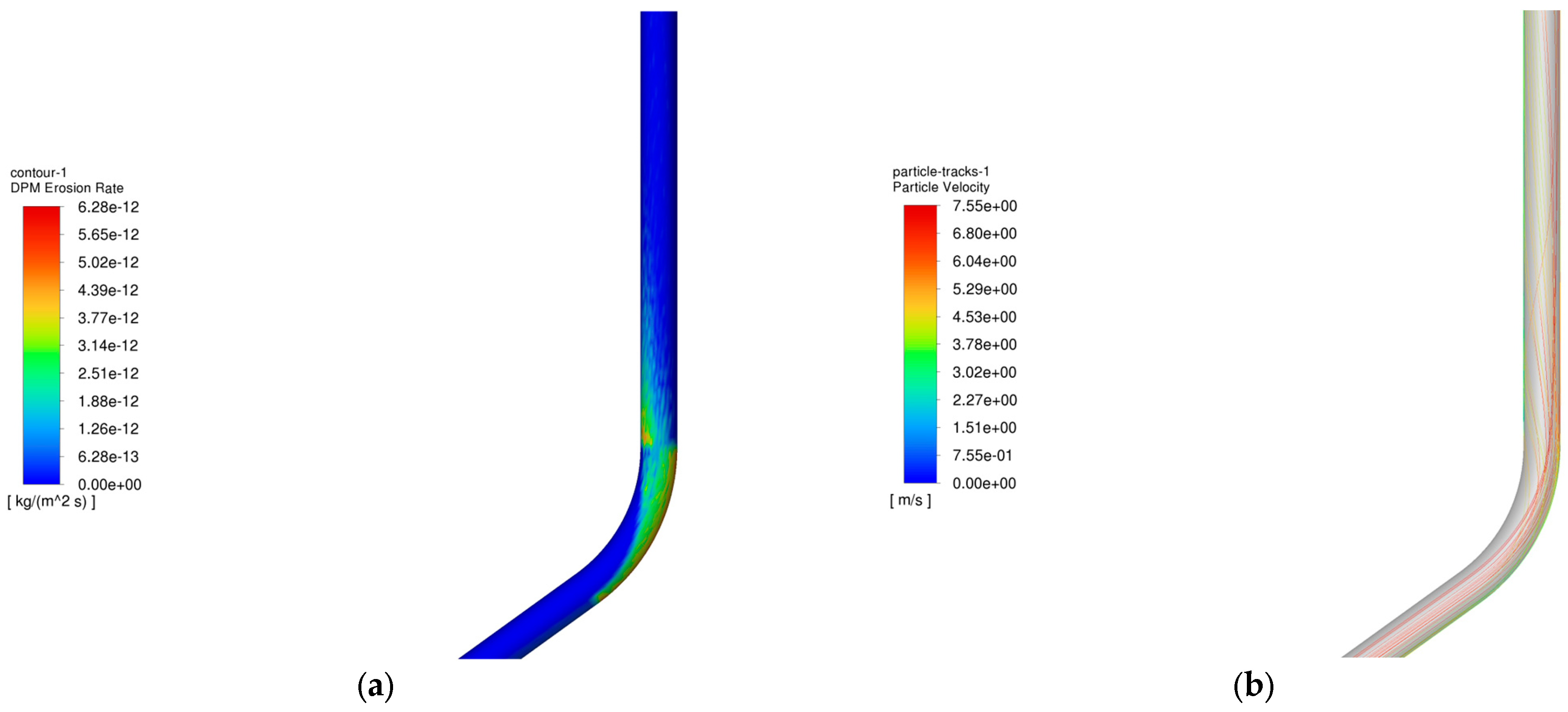
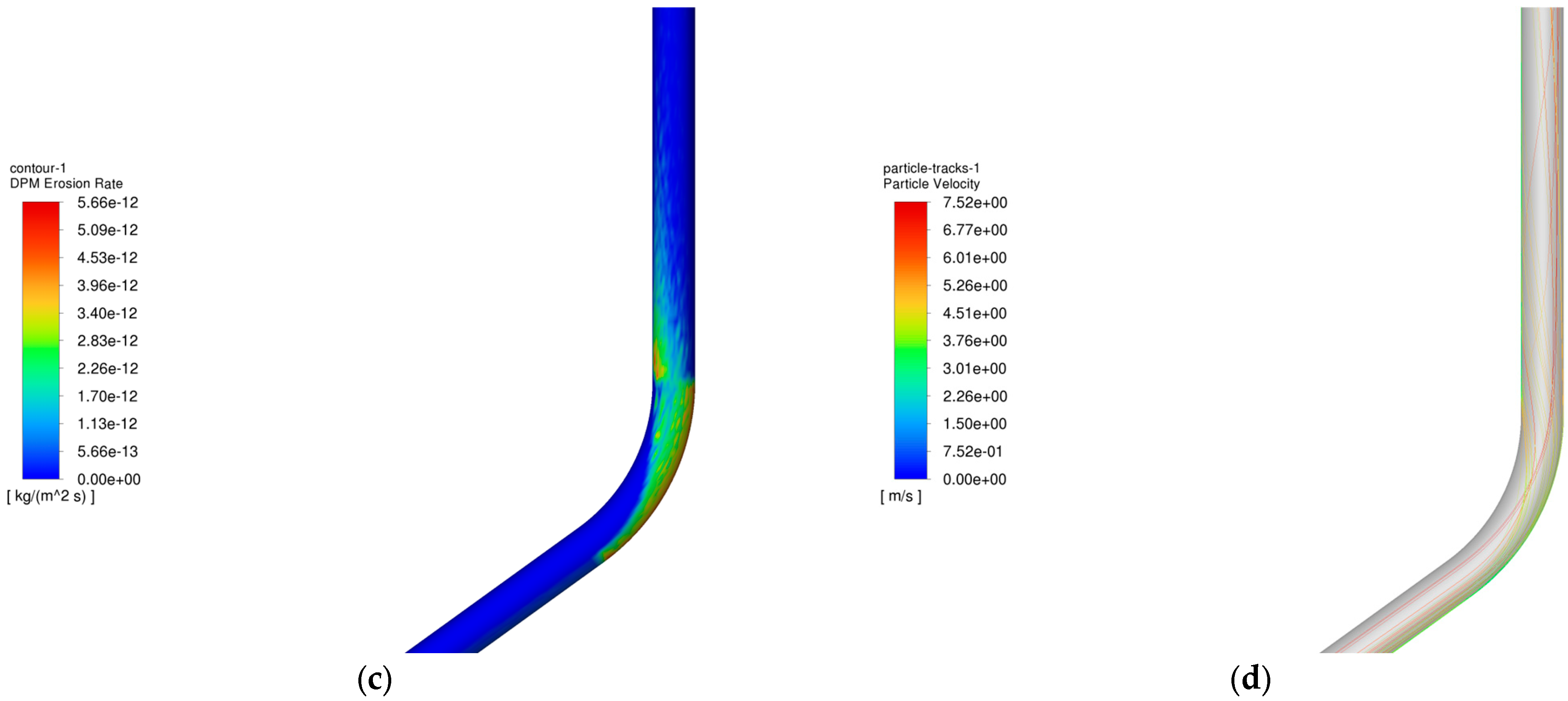
4.1. Analysis of the Influence of Gas Injection and Recovery on the Erosion Pattern of Pipe Columns
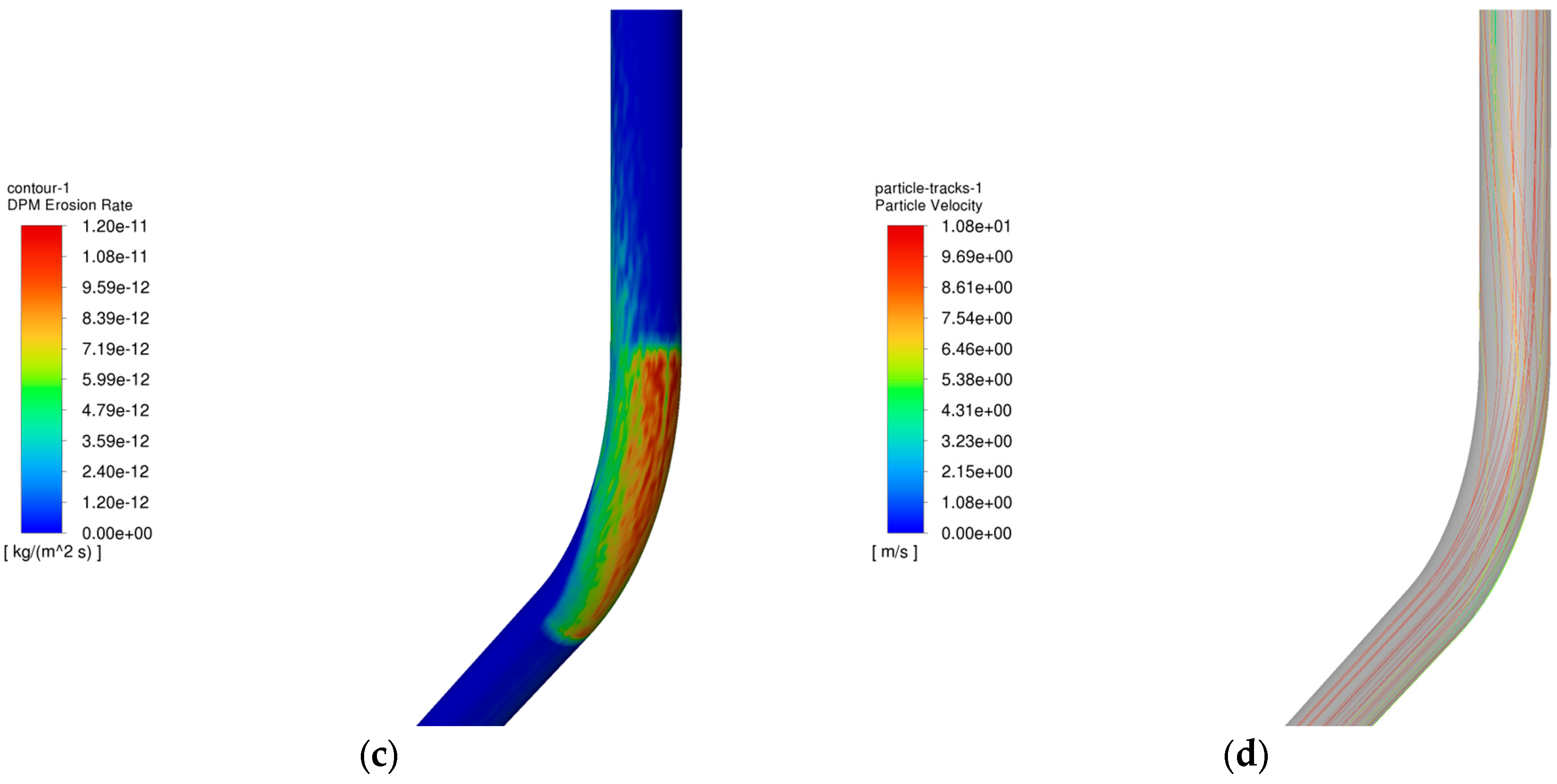
4.2. Analysis of the Influence of Particle Mass Flow Rate on Column Erosion in the Injection and Extraction Process
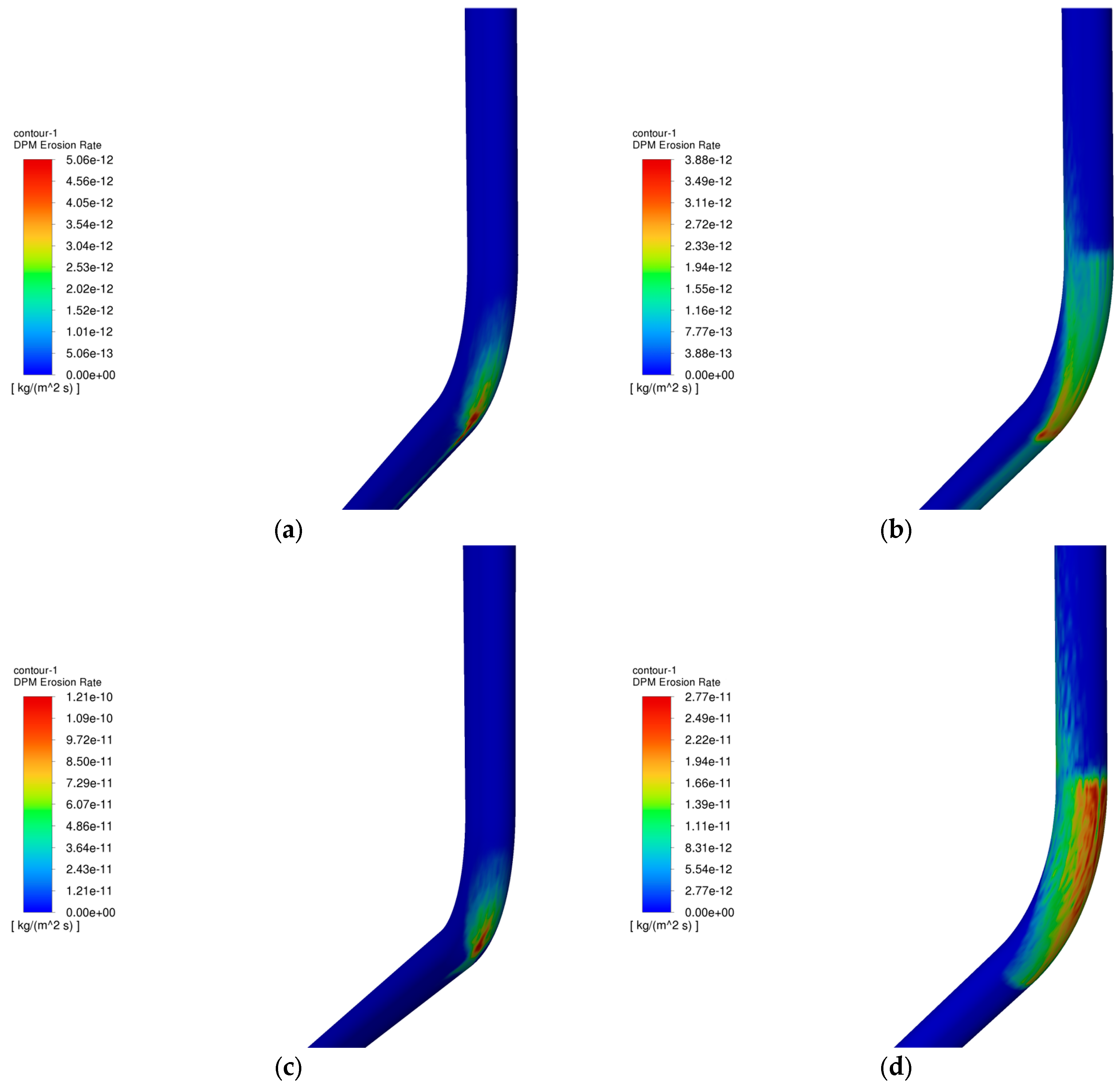
4.3. Analysis of the Influence of Particle Size on Column Erosion in the Process of Injection and Extraction
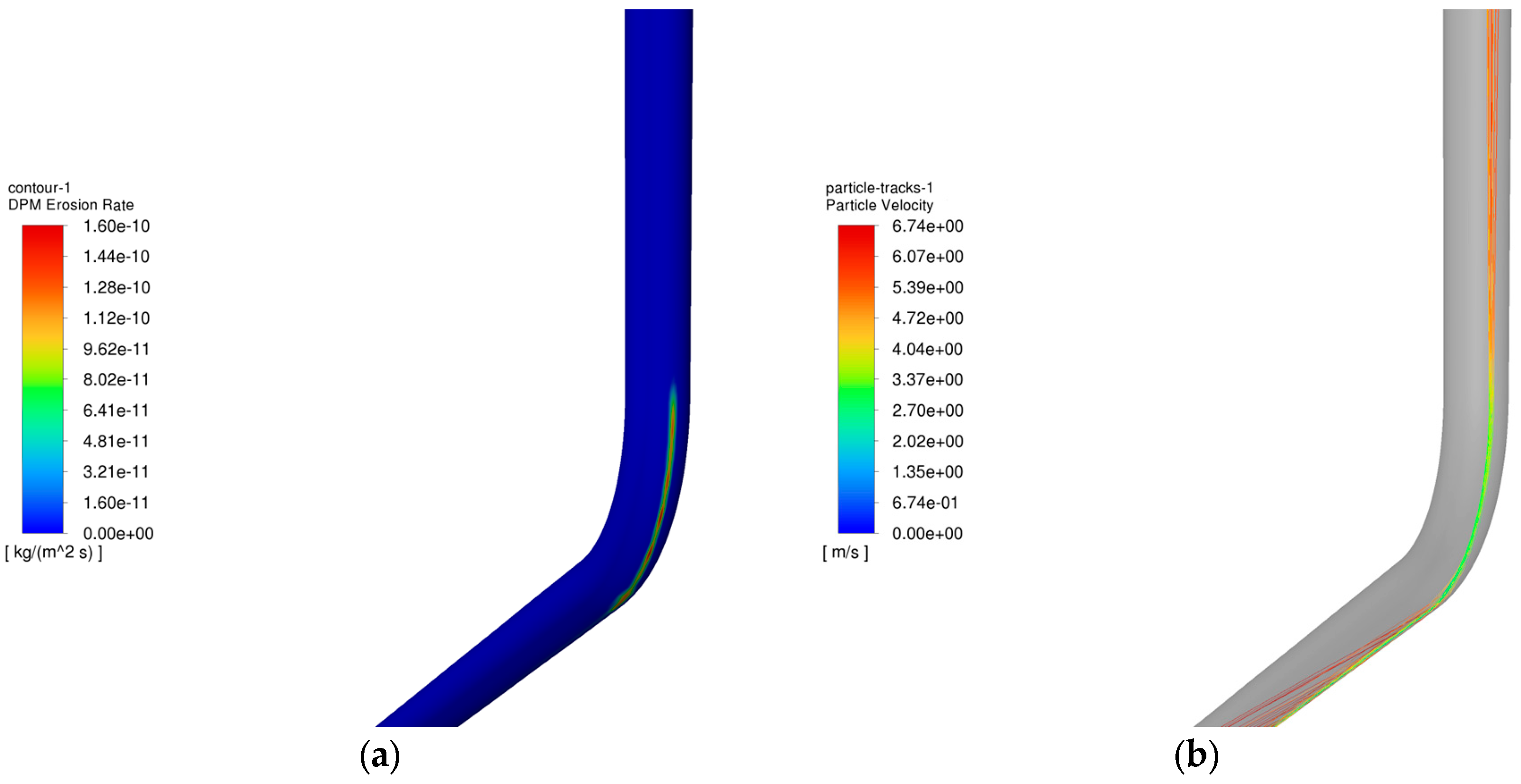
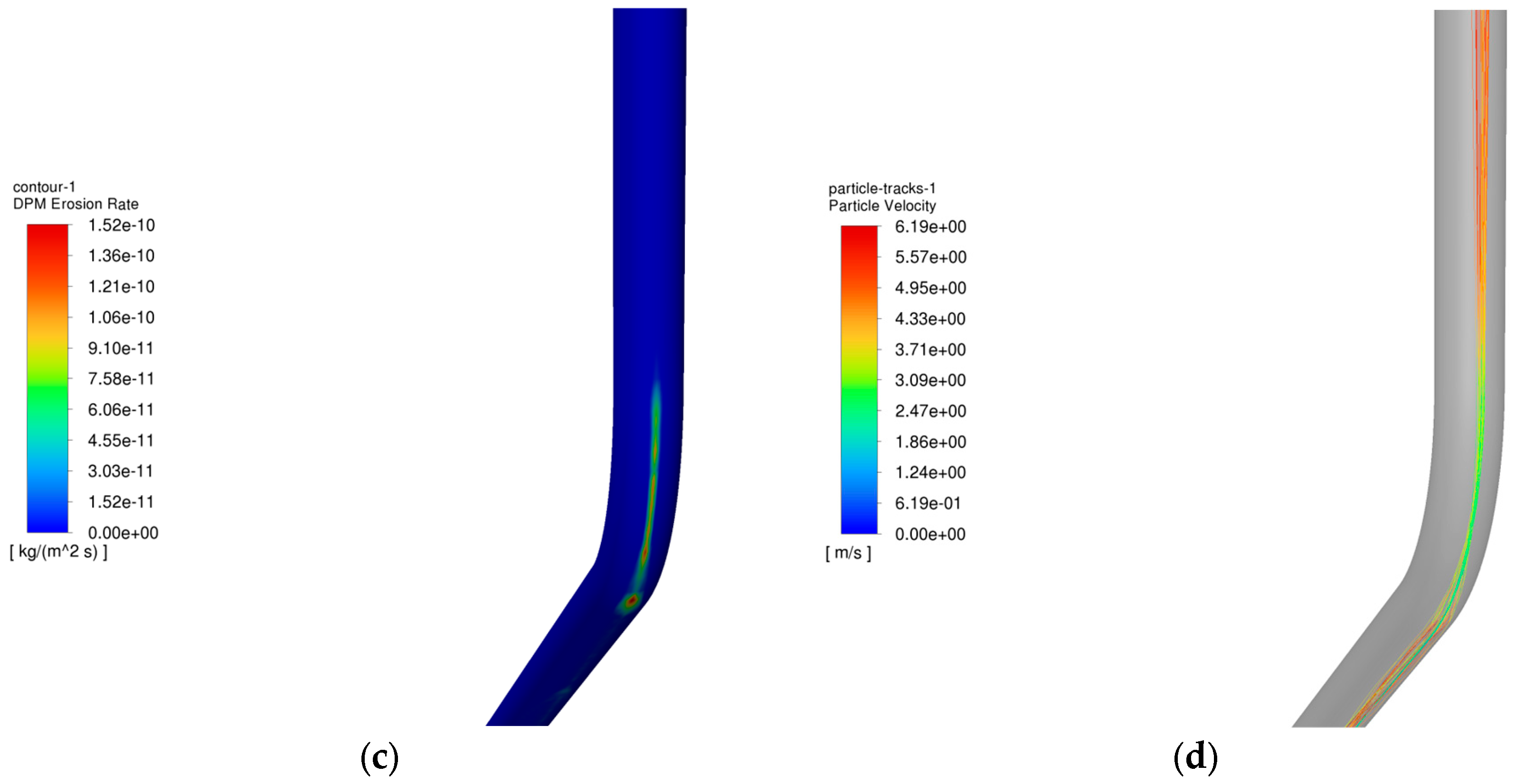
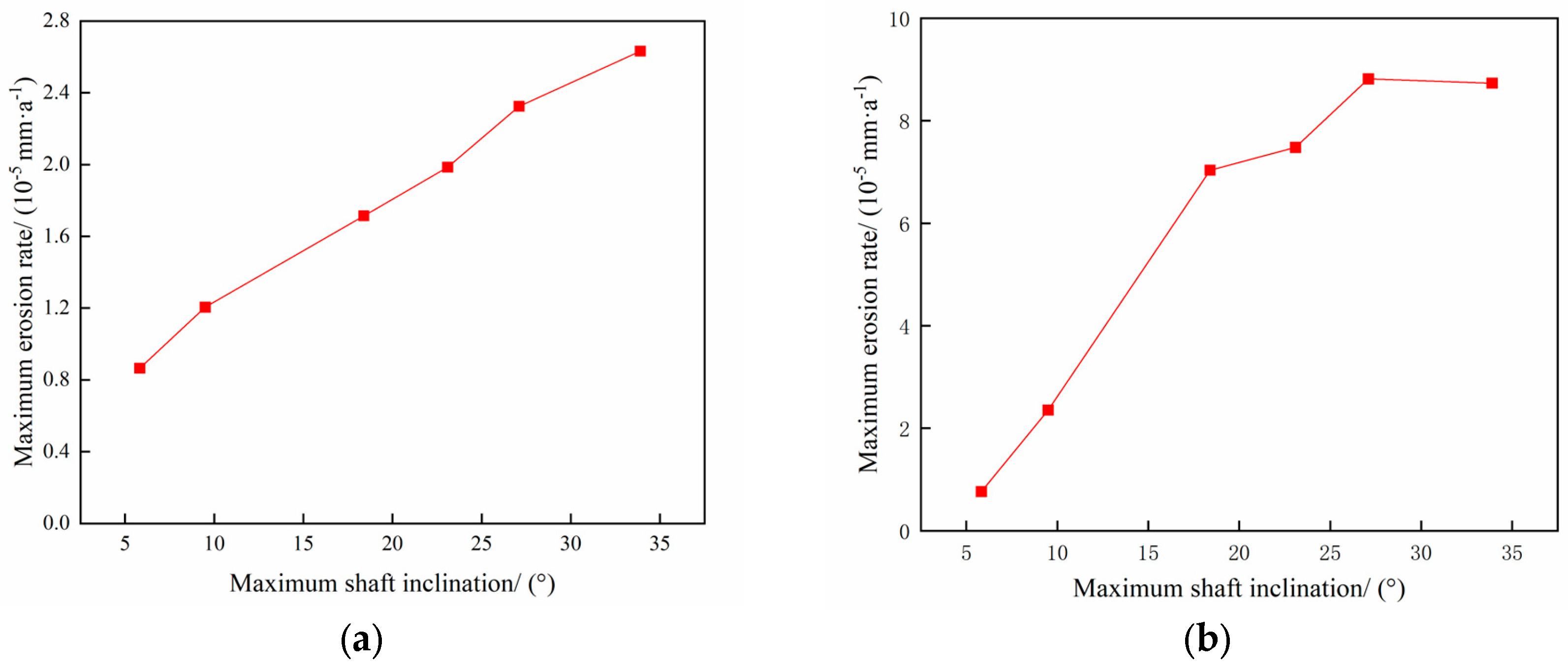
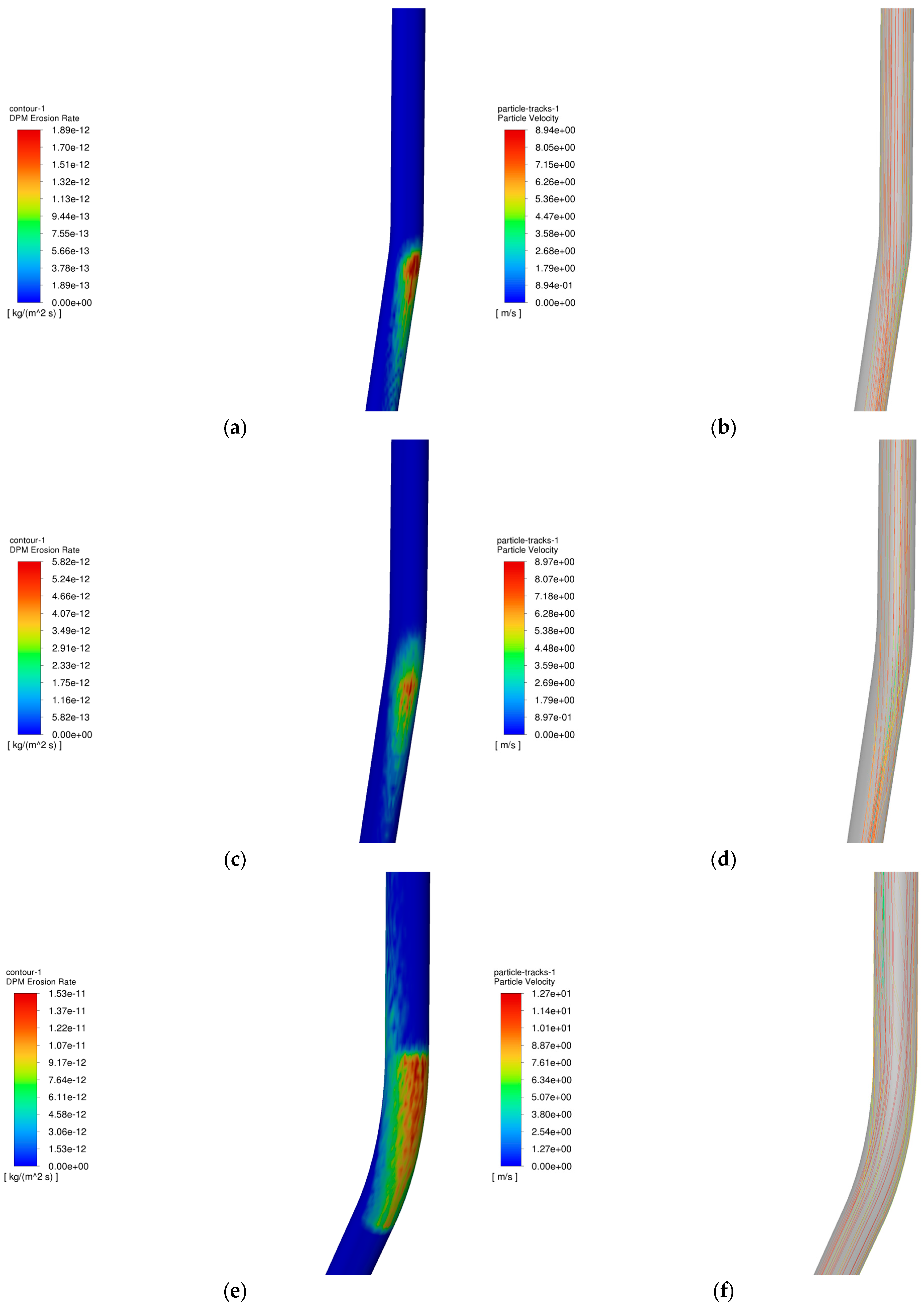
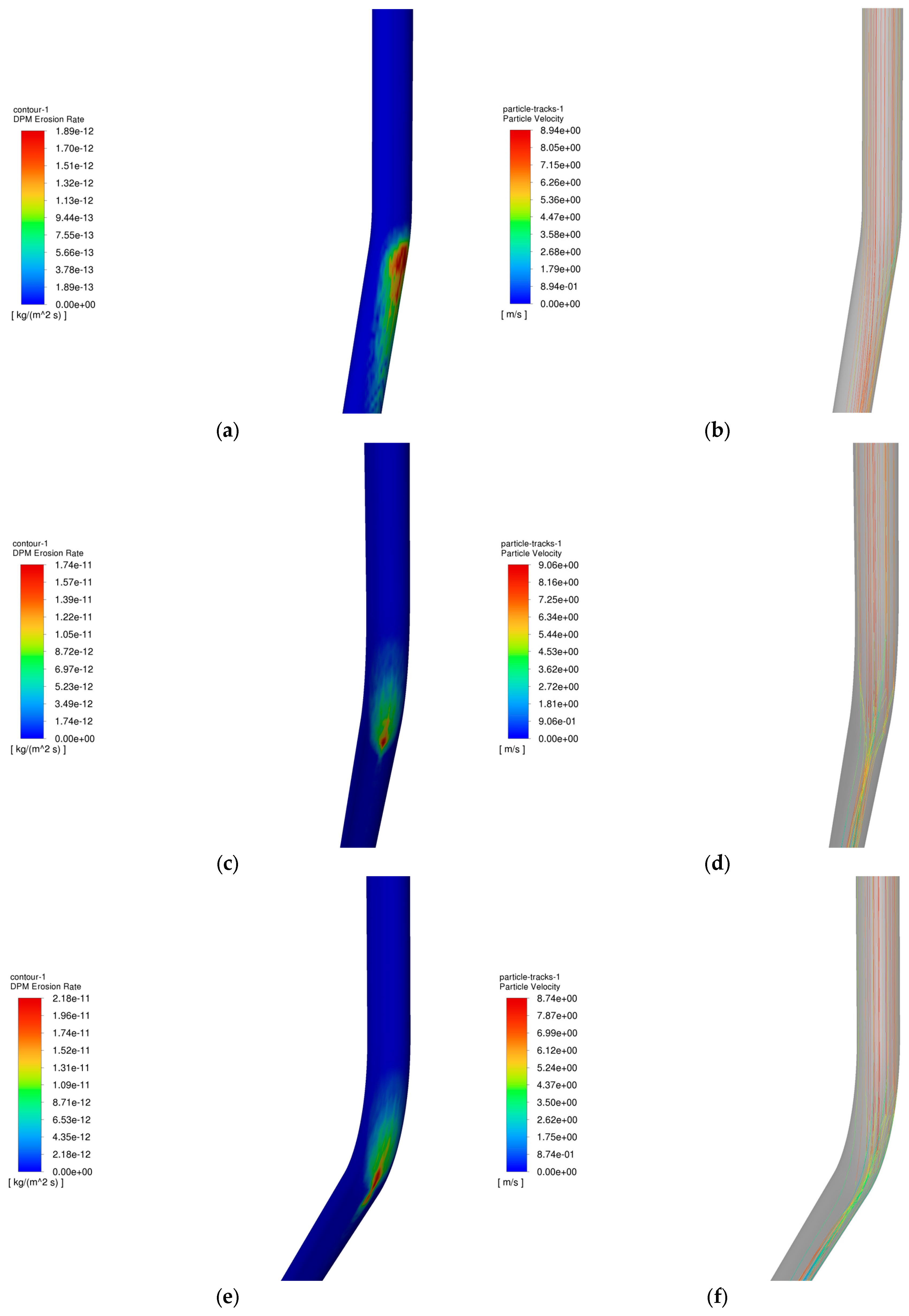
4.4. Analysis of the Influence of Well Inclination Angle on the Erosion Pattern of the Tubular Column in the Process of Injection and Extraction
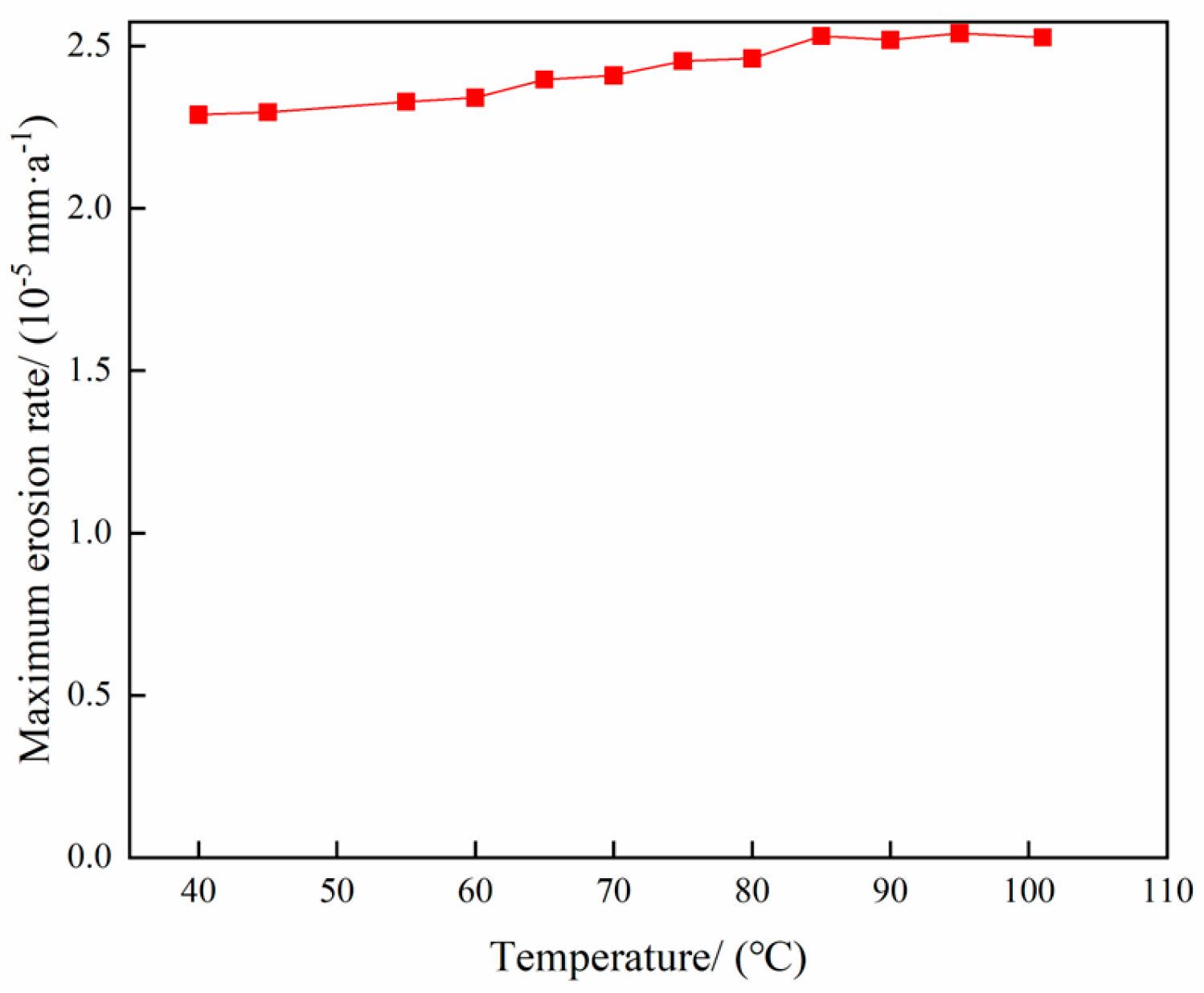
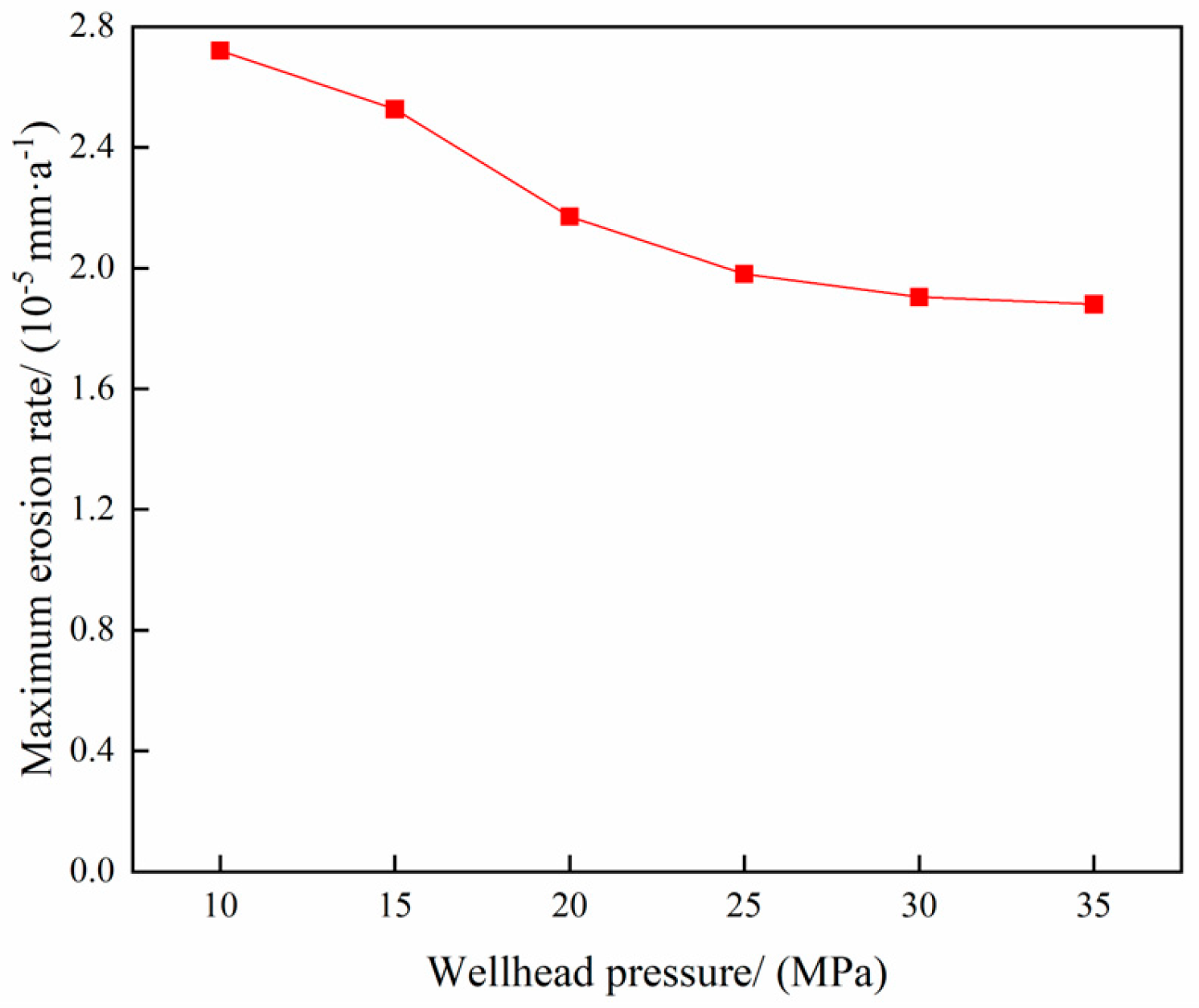
4.5. Analysis of the Influence of Temperature and Pressure on Column Erosion in the Process of Gas Extraction
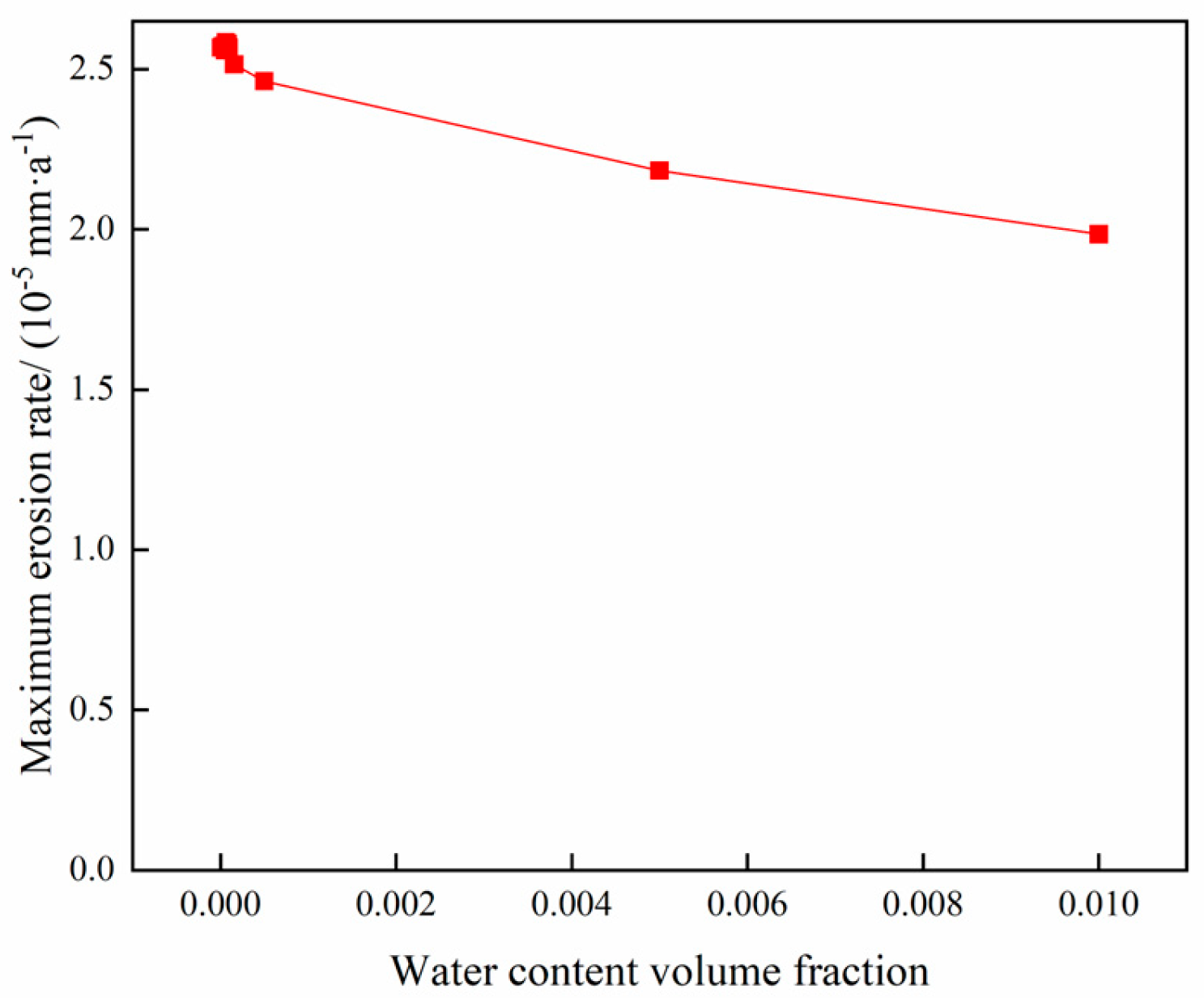
4.6. Analysis of the Effect of Water Volume Fraction on Column Erosion During Gas Extraction
4.7. Erosion Rate Prediction Modeling
5. Conclusions
- In the process of gas extraction, the erosion of the tubing column is influenced by several factors. The study shows that the larger the gas extraction volume, the more serious the erosion, and the two have an exponential relationship; the larger the mass flow rate of particles, the more significant the erosion, which has a linear relationship; as the particle size increases, the erosion first increases and then decreases; the larger the angle of well inclination, the higher the degree of erosion; the volume fraction of water content slightly reduces the maximum rate of erosion; and the temperature and wellhead pressure have little effect on erosion.
- In the gas injection process, the erosion law of the pipe column is similar to that of the gas extraction process, but the degree of erosion in the gas injection process is higher than that of the gas extraction process. This is mainly because in the gas injection process, the particles under the action of gravity and airflow to obtain the kinetic energy is greater than in the gas extraction process, and at the same time, the location of the erosion effect of the particles in the gas injection process is more concentrated, resulting in more severe erosion damage.
- Under the single-factor analysis, the principal controlling factors of tubular column erosion were ascertained to be gas extraction, particle mass flow rate, particle size, and well slope angle. Consequently, the influential factors were analyzed through orthogonal experiments, and a prediction model for the erosion rate of gas storage reservoir tubing columns was established by the least squares method. The relative error between the predicted and simulated values is minimal, thereby validating the adequacy of the prediction model. The established prediction formula can be used as an empirical formula to predict the erosion rate under different gas extraction, particle size, particle mass flow rate, and well inclination angle, thus avoiding the time-consuming and complicated numerical calculations using Fluent.
- The shortcoming of this paper is that the erosion prediction model is established by numerical simulation and verified by physical experiments, but it has not been verified by field data. The next step will be to optimize the erosion model in combination with field data to obtain a model suitable for the field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the density of the mixture | the diffusive flux of substance j in phase k | ||
| the velocity of the mixture | the effective thermal conductivity | ||
| the volume fraction | the turbulent kinetic energy | ||
| the viscosity of the mixture | the dissipation rate | ||
| the drift velocity of sub-phase k | the mean velocity | ||
| the enthalpy of substance j in phase k | the spatial coordinate | ||
| the turbulent kinetic energy generation term | the turbulent viscosity coefficient | ||
| the turbulent kinetic energy generation term caused by buoyancy | the fluctuating energy | ||
| the empirical constant | the empirical constant | ||
| the drag force per unit mass of the particle | the gas phase velocity, m/s | ||
| the particle velocity | the particle diameter | ||
| the Reynolds number of the particle | The drag force coefficient | ||
| the erosion rate | the particle mass flow | ||
| the particle size function | the impact angle function | ||
| The speed function | The sand particles impact the wall area. | ||
| Column inner diameter | incidence velocity v/(m·s−1) | ||
| Column outer diameter | mass flow rate | ||
| well inclination angle | particle diameter | ||
| kg·m−3 | Tube Density | particle density | |
| the gas extraction volume | The particle mass flow rate | ||
| the particle size | the well slope angle° | ||
| The experimental results in the dataset | The predicted results in the dataset | ||
| represents the sample size |
References
- Wang, Z.; Yang, H.; Zhang, Y.; Liu, X. Progress in the theory and prediction of gas storage column erosion research. Surf. Technol. 2023, 52, 91–110. [Google Scholar]
- Guo, M.; Dong, Z.; Meng, W.; Cui, S.; Zhang, Q. Risk assessment of erosion-corrosion coupling in sand control tubular columns of offshore high-production gas wells. J. Complex Hydrocarb. Reserv. 2021, 14, 111–118. [Google Scholar]
- Meng, W.; Zhang, J.; Zhang, C.; Huang, L.; Zhang, R.; Zhang, L.; Ren, S. Coupled erosion-CO2 corrosion test of downhole tubular column steel J. J. China Univ. Pet. (Ed. Nat. Sci.) 2021, 45, 104–110. [Google Scholar]
- Zhang, N.; Li, D.; Li, J.; He, H.; Huang, W. Study on the erosion law of super 13Cr tubing in large-scale fracturing construction. J. Sino-Global Energy 2020, 25, 64–67. [Google Scholar]
- Wang, Y.; Wanyan, Q.; Bao, C.; Li, K.; Li, D.; Li, Y.; Ran, L.; Bai, S. Study on the erosion law of 13Cr tubing by solid-phase particles under high-speed injection and extraction conditions. In Proceedings of the 33rd Annual National Natural Gas Conference (2023), (04 Drilling Engineering), Nanning, China, 1–2 June 2023; Chinese Petroleum Society, Natural Gas Professional Committee: Beijing, China; Research Institute of Exploration and Development: Beijing, China; China National Petroleum Corporation; Key Laboratory of Oil and Gas Underground Reservoir Engineering: Beijing, China; China National Petroleum Corporation: Beijing, China, 2023; Volume 9. [Google Scholar]
- Zhang, Z.; Feng, X.; Xiang, S. Effect of erosion on structural integrity of tubular column in high temperature and high production gas wells J. China Sciencepap. 2022, 17, 31–38. [Google Scholar]
- Tan, H.; Yang, J.; Ye, C.; Xiao, F.; Wang, W.; Cai, R. Experimental study of liquid-solid two-phase flow erosion in CT80 continuous oil pipe J. Pet. Tub. Goods Instr. 2023, 9, 70–74. [Google Scholar]
- Cui, L.; Li, X.; Li, J.; Li, M.; Chang, W.; Cheng, J. Liquid-solid two-phase flow erosion resistance of QT1100 continuous oil pipeline steel. Mater. Mech. Eng. 2024, 48, 55–60. [Google Scholar]
- Huang, D.Q.; Wang, W.D.; Xian, L.Y.; Wang, H.T.; Qin, S.X. Analysis of erosion resistance of CT110 continuous oil pipe plates under liquid-solid two-phase flow. Welded Pipe Tube 2024, 47, 52–57. [Google Scholar]
- He, M.; Yang, Y.; Dan, D.; Wang, J.; Duan, J.; Yu, X.; Kan, C. Simulation study on critical erosion of sand-carrying gas extraction from Y-shape wellhead of gas storage reservoir. J. Surf. Technol. 2024, 53, 160–170. [Google Scholar]
- Yang, Y.; He, M.; Yu, P.; Kan, C.; Wang, X.; Yu, X.; Chen, X.; Tao, S.; Zhao, C.; Duan, J.; et al. Investigation on critical erosion of gas production channel for sand carrying during injection and production process in gas storage. Geoenergy Sci. Eng. 2024, 239, 212945. [Google Scholar] [CrossRef]
- Li, M.X.; Liu, G.S.; Wang, N.; Zhu, F.H.; Li, W.S.; Fu, A.Q. Gas-solid erosion performance of production strings in gas storage reservoirs. Corros. Prot. 2025, 46, 66–72. [Google Scholar]
- Peng, T.; Zhang, F.; Fang, H. Effect of gravel shape on wellbore erosion in gas storage reservoirs. Sci. Technol. Eng. 2020, 20, 14908–14913. [Google Scholar]
- He, Z.; Yi, W.; Li, J.; Sun, P.; Liu, P.; Jiang, J. Wen23 Analysis of the erosion pattern of gas storage reservoir injection columns and the limiting gas injection and extraction volumes. Pet. Tubul. Goods Instrum. 2022, 55, 1–8. [Google Scholar]
- Wu, Y.H.; Jiao, X.Y.; Ma, C.L.; Niu, H.Z.; Wei, Q.; Chen, Y.R.; Tan, C.D. Erosion simulation of injection-production strings in gas storage reservoirs and design study of ultimate injection-production gas volume. In Proceedings of the 2024 Young Green Intelligent Oil Production Technology Symposium, Changsha, China, 24–25 November 2024; School of Artificial Intelligence, China University of Petroleum (Beijing): Beijing, China; School of Petroleum Engineering, China University of Petroleum (Beijing): Beijing, China; Engineering Technology Operation Center, Tianjin Branch, CNOOC (China) Limited: Tianjin, China; Beijing Yadan Petroleum Technology Development Co., Ltd.: Beijing, China, 2024; pp. 54–63. [Google Scholar]
- Wu, Z.; He, X.; Hu, S.; Jiang, W.; Shen, F. Nonlinear regression analysis of erosion rate of space type pipeline under the influence of different parameters. J. Lubr. Eng. 2024, 49, 148–155. [Google Scholar]
- Parsi, M.; Agrawal, M.; Srinivasan, V.; Vieira, R.E.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A. CFD simulation of sand particle erosion in gas-dominant multiphase flow. J. Nat. Gas Sci. Eng. 2015, 27, 706–718. [Google Scholar]
- Liu, E.; Li, D.; Zhao, W.; Peng, S.; Chen, Q. Correlation analysis of pipeline corrosion and liquid accumulation in gas gathering station based on computational fluid dynamics. J. Nat. Gas Sci. Eng. 2022, 102, 104564. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar]
- Wen, Q.; Liu, Y.; Chen, Z.; Wang, W. Numerical simulation and experimental validation of flow characteristics for a butterfly check valve in small modular reactor. Nucl. Eng. Des. 2022, 391, 111732. [Google Scholar]
- Liu, E.; Li, D.; Li, W.; Liao, Y.; Qiao, W.; Liu, W.; Azimi, M. Erosion simulation and improvement scheme of separator blowdown system—A case study of Changning national shale gas demonstration area. J. Nat. Gas Sci. Eng. 2021, 88, 103856. [Google Scholar]
- Solnordal, C.B.; Wong, C.Y.; Boulanger, J. An experimental and numerical analysis of erosion caused by sand pneumatically conveyed through a standard pipe elbow. Wear 2015, 336, 43–57. [Google Scholar]
- Finnie, I. Erosion of Surfaces by Solid Particles. Wear 1960, 3, 87–103. [Google Scholar]
- Edwards, J.K.; McLaury, B.S.; Shirazi, S.A. Evaluation of alternative pipe bend fittings in erosive service. ASME 2000, 253, 959–966. [Google Scholar]
- Eyler, R.L. Design and Analysis of a Pneumatic Flow Loop; West Virginia University: Morgantown, WV, USA, 1987. [Google Scholar]
- Peng, J.H.; Yue, M.; Lou, Y.S.; Liang, Y.K.; Wen, M.; Zhai, X.P. Three-dimensional simulation study on erosion life of metal mesh screen based on Fluent-DPM method. Pet. Drill. Technol. 2025, 53, 115–121. [Google Scholar]
- Wang, B.; Guo, H.; Geng, X.; Du, S.; Zhang, H.; Wang, W. Simulation of gas-solid mixed flow erosion on gathering pipeline bends. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2020, 47, 46–52. [Google Scholar]
- Wang, X.G.; Tian, B.; Qi, J.J.; Zhang, H.; Zhao, N.; Li, J.X.; Li, M.Q. Numerical analysis of erosion and wear of fractured elbow. J. Chem. Equip. Pipeline 2024, 61, 103–110. [Google Scholar]

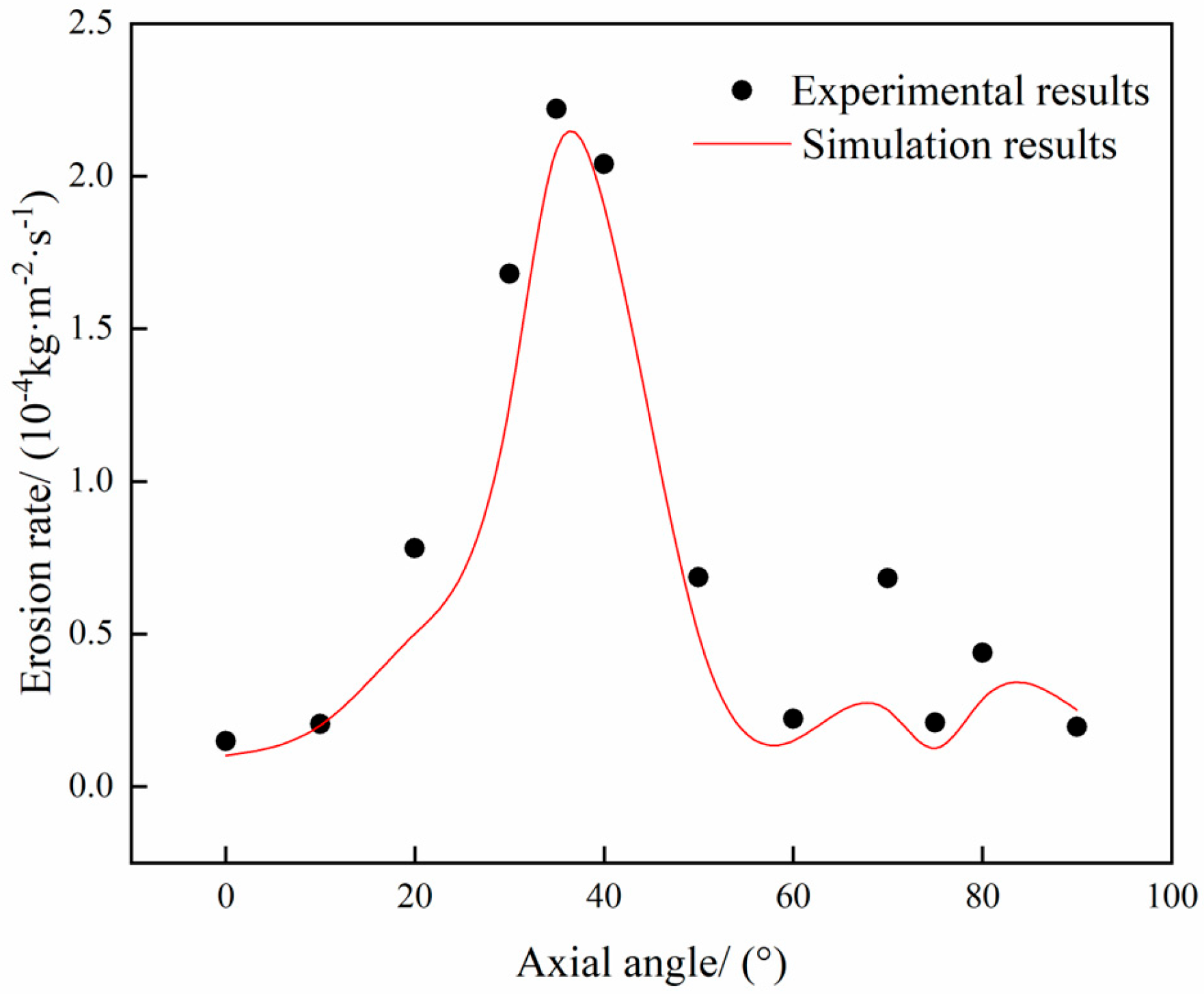




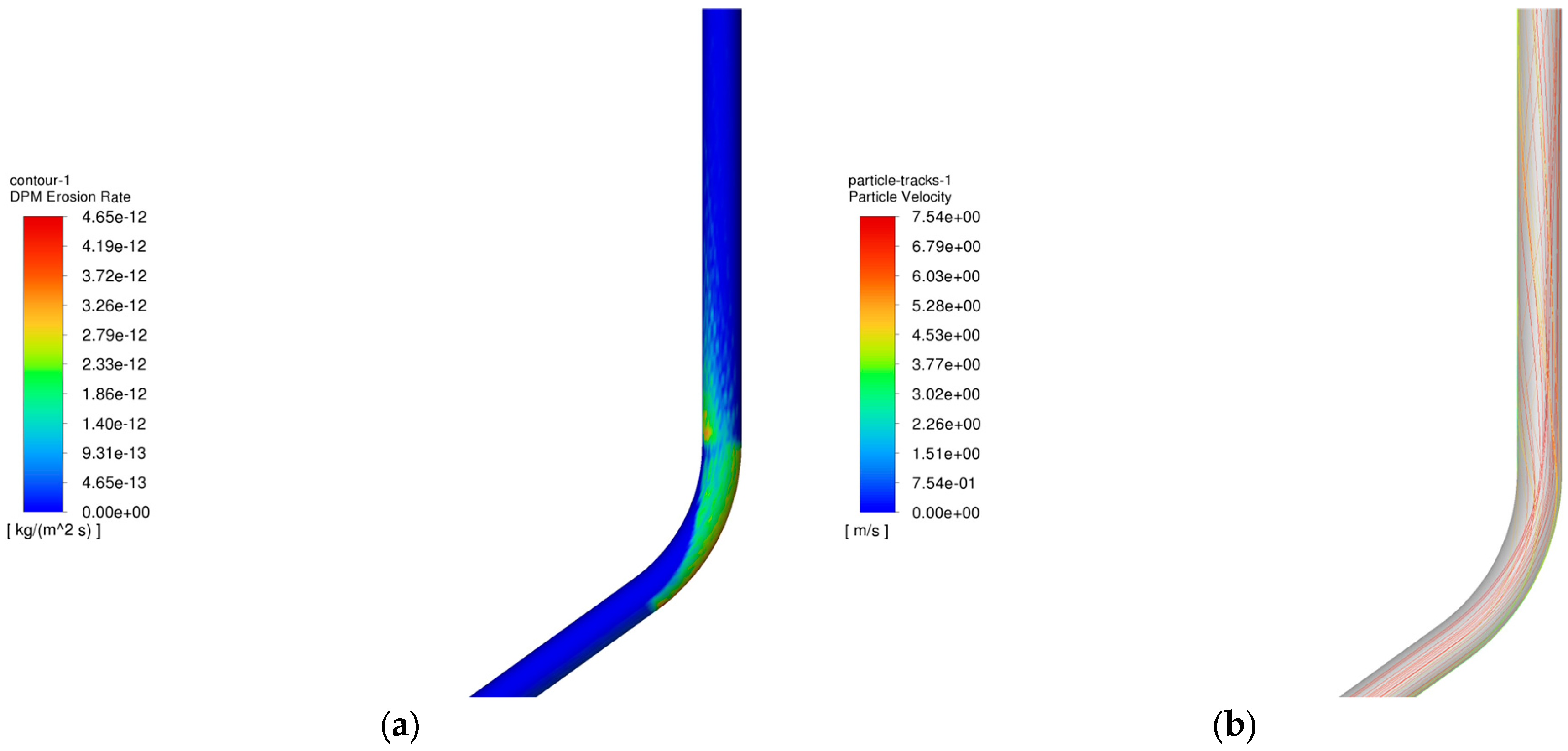
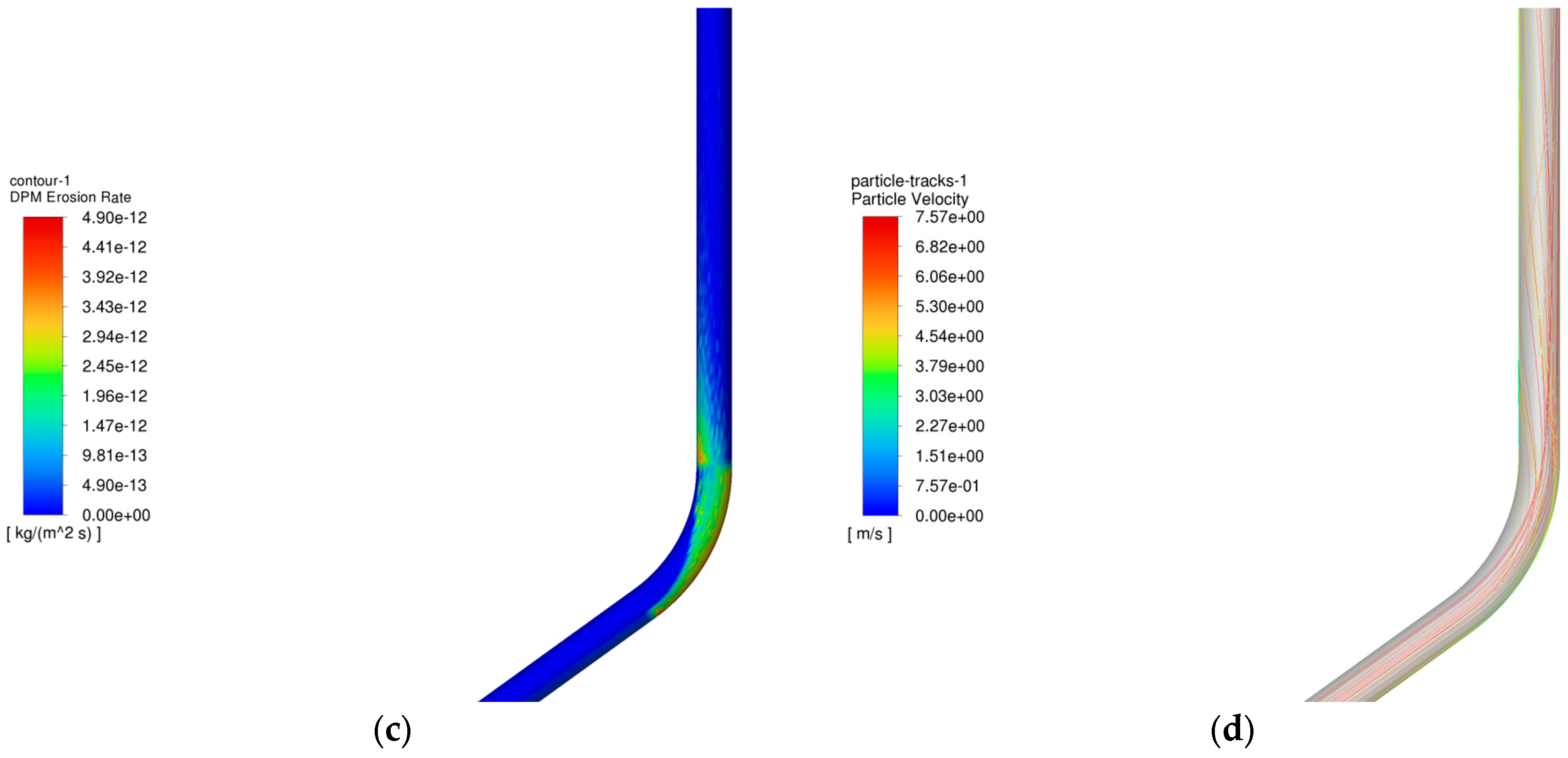
| Pipe Diameter/mm | Aspect Ratio | Sand Density/(kg·m−3) | Pipe Density/(kg·m−3) | Fluid Velocity/(m·s−1) | Sand Particle Size/mm | Maximum Erosion Rate /(mm·h−1) | Sand Mass Flow Rate/(kg·s−1) | |
|---|---|---|---|---|---|---|---|---|
| Simulation Results | Experimental Results | |||||||
| 41 | 1.25 | 2650 | 7800 | 25.24 | 0.1 | 0.097 | 0.1036 | 0.015 |
| Column Parameters | Values |
|---|---|
| Column inner diameter di/mm | 76 |
| Column outer diameter do/mm | 88.9 |
| well, inclination angle α/° | 27.1 |
| Tube density ρ/kg·m−3 | 7800 |
| Project | Project Name | Content |
|---|---|---|
| Boundary condition | Entrance boundary | Velocity |
| Export boundary | Pressure | |
| Wall | Standard wall function | |
| Calculation settings | Solver | Pressure-based solvers |
| Multiphase flow model | Mixture model | |
| Turbulence modeling | Realizable k-ε Model | |
| Solver algorithms | SIMPLE | |
| Spatial discretization method | Gradient term | The least squares method based on control bodies |
| Pressure term | PRESTO | |
| Momentum term | First order windward | |
| Volume fraction term | Geometric reconstruction | |
| Turbulent momentum term | Second order windward | |
| Turbulent dissipation rate term | Second order windward |
| Medium Parameters | Values |
|---|---|
| incidence velocity v/(m·s−1) | 6.6 |
| /(kg·d−1) | 0.432 |
| particle diameter dp/mm | 0.07 |
| particle density ρ/kg·m−3 | 2650 |
| Parameters | Values |
|---|---|
| Gas production (104 m3/d) | 5, 10, 15, 20, 25, 30, 35, 45, 50, 60, 70, 80, 90, 100, 150, 200 |
| Grain size of the sand (mm) | 0.01, 0.03, 0.05, 0.07, 0.1, 0.3, 0.5, 0.8, 1, 2, 3, 4, 5, 6 |
| Sand density (kg/m3) | 2650 kg/m3 |
| Sand mass flow rate (kg/d) | 0.000864, 0.00432, 0.00864, 0.0432, 0.0864, 0.432, 0.864 |
| Well inclination angle (°) | 5.83, 9.5, 18.4, 23.1, 27.1, 33.9 |
| Wellhead pressure (MPa) | 35, 30, 25, 20, 15, 10 |
| Inlet temperature (℃) | 101, 95, 90, 85, 80, 75, 70, 65, 60, 55, 50, 45, 40 |
| Parameters | Values |
|---|---|
| Injected quantity (104 m3/d) | 5, 10, 15, 20, 25, 30, 35, 45, 50, 60, 70, 80, 90, 100, 200 |
| Grain size of the sand (mm) | 0.01, 0.03, 0.05, 0.07, 0.1, 0.3, 0.5, 0.8, 1, 2, 3, 4, 5, 6 |
| Sand density (kg/m3) | 2650 kg/m3 |
| Sand mass flow rate (kg/d) | 0.000864, 0.00432, 0.00864, 0.0432, 0.0864 |
| Well inclination angle (°) | 5.83, 9.5, 18.4, 23.1, 27.1, 33.9 |
| Number | Flow Rate (104 m3/d) | Mass Flow (kg/d) | Grain Size (mm) | Well Inclination Angle (°) | Maximum Erosion Rate 10−5 (mm/a) |
|---|---|---|---|---|---|
| 1 | 10 | 0.000864 | 0.07 | 5.83 | 0.0001 |
| 2 | 10 | 0.0864 | 3 | 9.5 | 0.1027 |
| 3 | 10 | 0.864 | 0.5 | 18.4 | 3.3841 |
| 4 | 10 | 0.00864 | 5 | 27.1 | 0.0473 |
| 5 | 10 | 0.432 | 1 | 33.9 | 3.5175 |
| 6 | 20 | 0.864 | 3 | 33.9 | 18.8407 |
| 7 | 20 | 0.00864 | 0.5 | 5.83 | 0.0105 |
| 8 | 20 | 0.432 | 5 | 9.5 | 10.2290 |
| 9 | 20 | 0.000864 | 1 | 18.4 | 0.0118 |
| 10 | 20 | 0.0864 | 0.07 | 27.1 | 0.4447 |
| 11 | 35 | 0.432 | 0.5 | 27.1 | 52.1557 |
| 12 | 35 | 0.000864 | 5 | 33.9 | 0.1027 |
| 13 | 35 | 0.0864 | 1 | 5.83 | 0.8207 |
| 14 | 35 | 0.864 | 0.07 | 9.5 | 2.6159 |
| 15 | 35 | 0.00864 | 3 | 18.4 | 1.2331 |
| 16 | 45 | 0.0864 | 5 | 18.4 | 25.1884 |
| 17 | 45 | 0.864 | 1 | 27.1 | 64.6892 |
| 18 | 45 | 0.00864 | 0.07 | 33.9 | 0.3133 |
| 19 | 45 | 0.432 | 3 | 5.83 | 27.8972 |
| 20 | 45 | 0.000864 | 0.5 | 9.5 | 0.0280 |
| 21 | 60 | 0.00864 | 1 | 9.5 | 0.6509 |
| 22 | 60 | 0.432 | 0.07 | 18.4 | 6.1859 |
| 23 | 60 | 0.000864 | 3 | 27.1 | 0.7763 |
| 24 | 60 | 0.0864 | 0.5 | 33.9 | 10.1481 |
| 25 | 60 | 0.864 | 5 | 5.83 | 137.0603 |
| Case | u (104 m3/d) | mp (kg/d) | dp (mm) | Θ (°) | Experiment Data/(mm·a−1) | Erosion Model Prediction Results/(mm·a−1) |
|---|---|---|---|---|---|---|
| 1 | 25 | 86.4 | 0.07 | 27.1 | 0.0032 | 0.0031 |
| 2 | 35 | 86.4 | 0.07 | 27.1 | 0.0050 | 0.0051 |
| 3 | 45 | 86.4 | 0.07 | 27.1 | 0.0080 | 0.0075 |
| 4 | 60 | 86.4 | 0.07 | 27.1 | 0.0159 | 0.0142 |
| 5 | 45 | 43.2 | 0.07 | 27.1 | 0.0037 | 0.0041 |
| 6 | 45 | 172.8 | 0.07 | 27.1 | 0.0147 | 0.0152 |
| 7 | 45 | 86.4 | 0.1 | 27.1 | 0.0095 | 0.0084 |
| 8 | 50 | 86.4 | 0.07 | 27.1 | 0.0089 | 0.0097 |
| 9 | 35 | 259.2 | 0.07 | 27.1 | 0.01453 | 0.0169 |
| 10 | 60 | 259.2 | 0.05 | 27.1 | 0.046495 | 0.0471 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Zhang, C.; Jin, W.; Luo, X.; Fan, Z.; Zhang, F. Study on the Erosion Law and Erosion Prediction Model of Pipe Columns During Gas Storage Reservoir Injection and Production Processes. Materials 2025, 18, 1510. https://doi.org/10.3390/ma18071510
Ren Z, Zhang C, Jin W, Luo X, Fan Z, Zhang F. Study on the Erosion Law and Erosion Prediction Model of Pipe Columns During Gas Storage Reservoir Injection and Production Processes. Materials. 2025; 18(7):1510. https://doi.org/10.3390/ma18071510
Chicago/Turabian StyleRen, Zongxiao, Chenyu Zhang, Wenbo Jin, Xuemei Luo, Zhaoyang Fan, and Fan Zhang. 2025. "Study on the Erosion Law and Erosion Prediction Model of Pipe Columns During Gas Storage Reservoir Injection and Production Processes" Materials 18, no. 7: 1510. https://doi.org/10.3390/ma18071510
APA StyleRen, Z., Zhang, C., Jin, W., Luo, X., Fan, Z., & Zhang, F. (2025). Study on the Erosion Law and Erosion Prediction Model of Pipe Columns During Gas Storage Reservoir Injection and Production Processes. Materials, 18(7), 1510. https://doi.org/10.3390/ma18071510






