Numerical Simulation of Temperature Field Distribution During Directional Annealing of TiAl Alloy with Different Parameters
Abstract
:1. Introduction
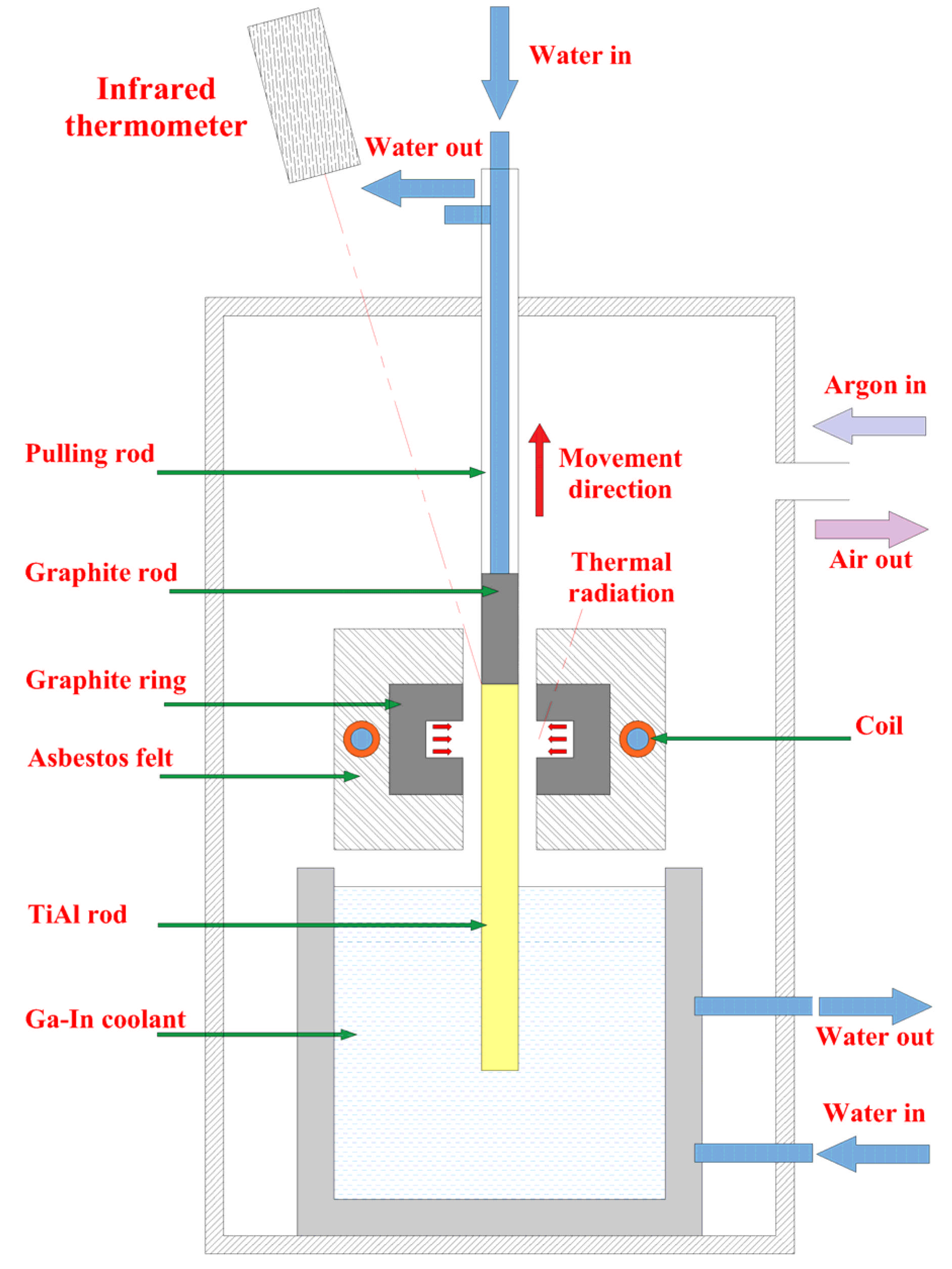
2. Bidirectional Temperature Gradient Directional Annealing Principle
3. Numerical Model of Directional Annealing
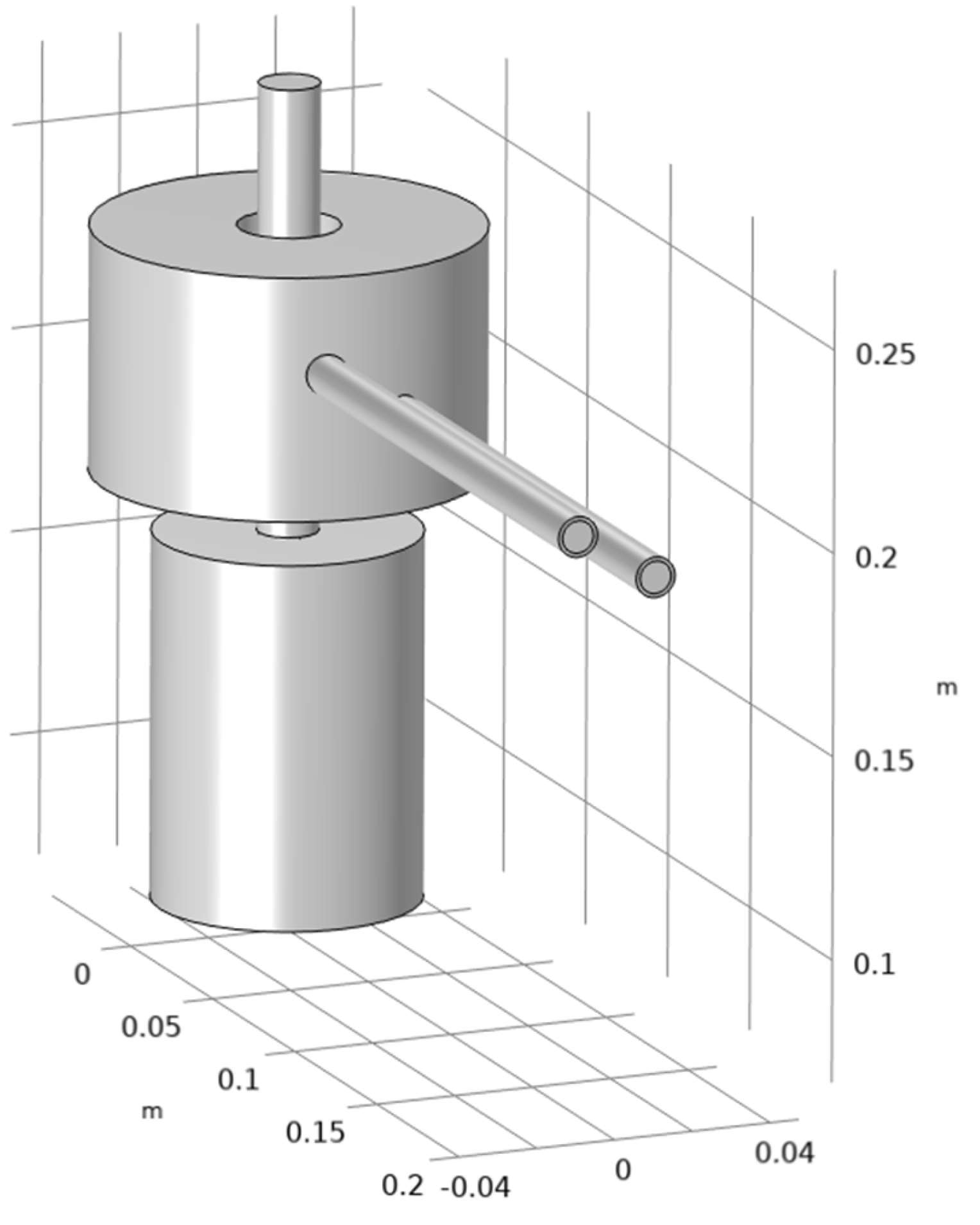
3.1. Establishment of Model
3.2. Simulation Parameters
3.3. Governing Equations and Boundary Conditions
4. Results and Discussion
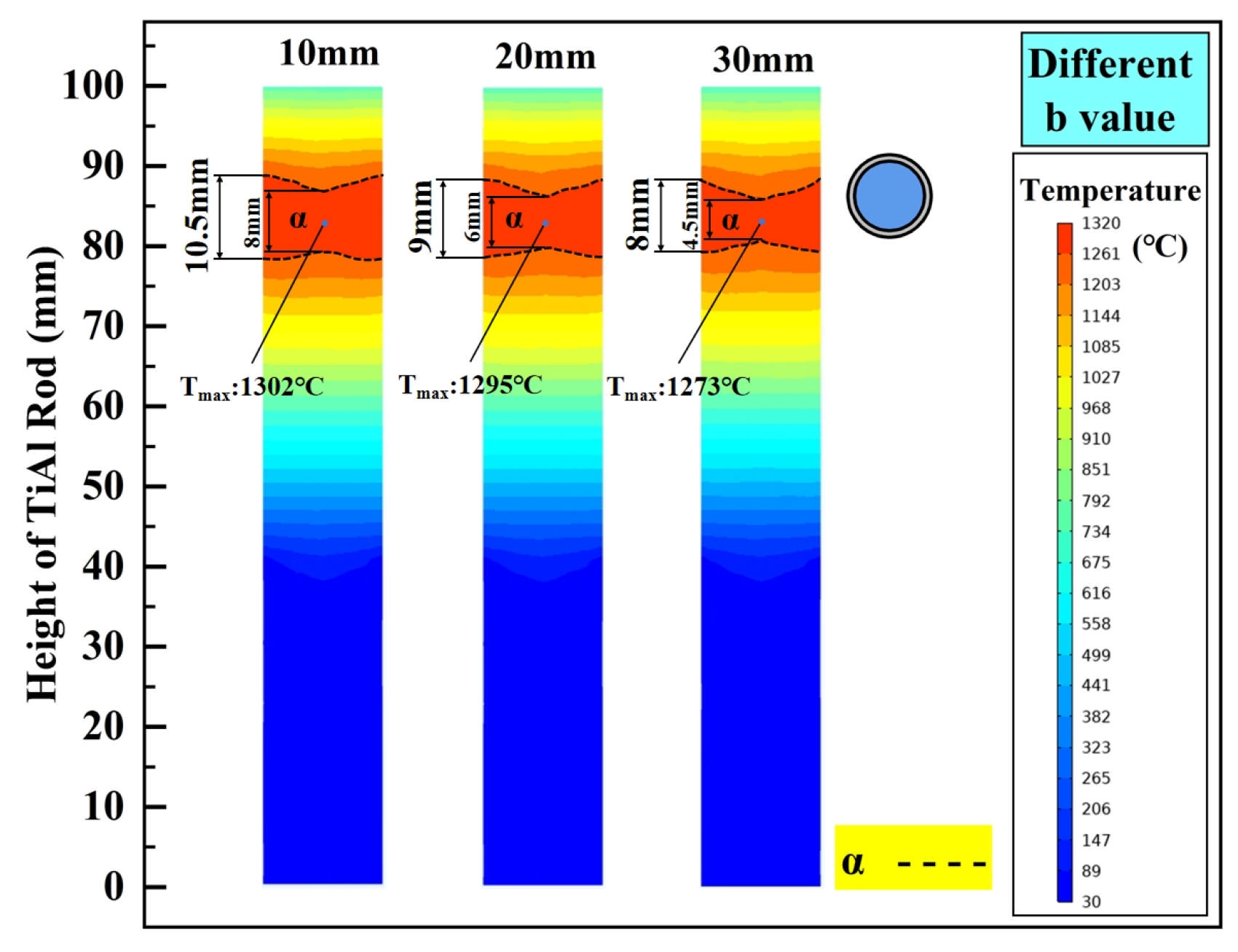
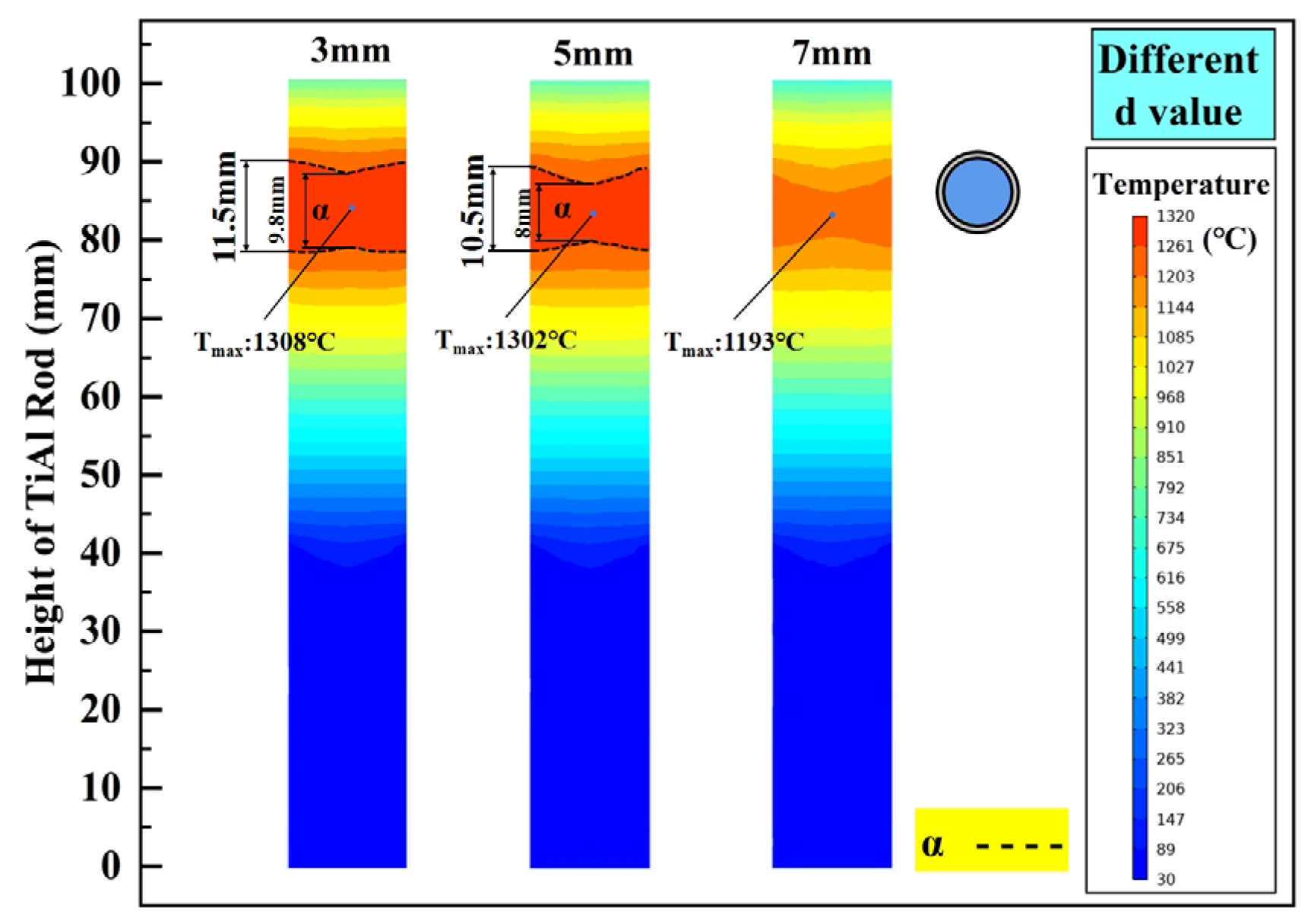
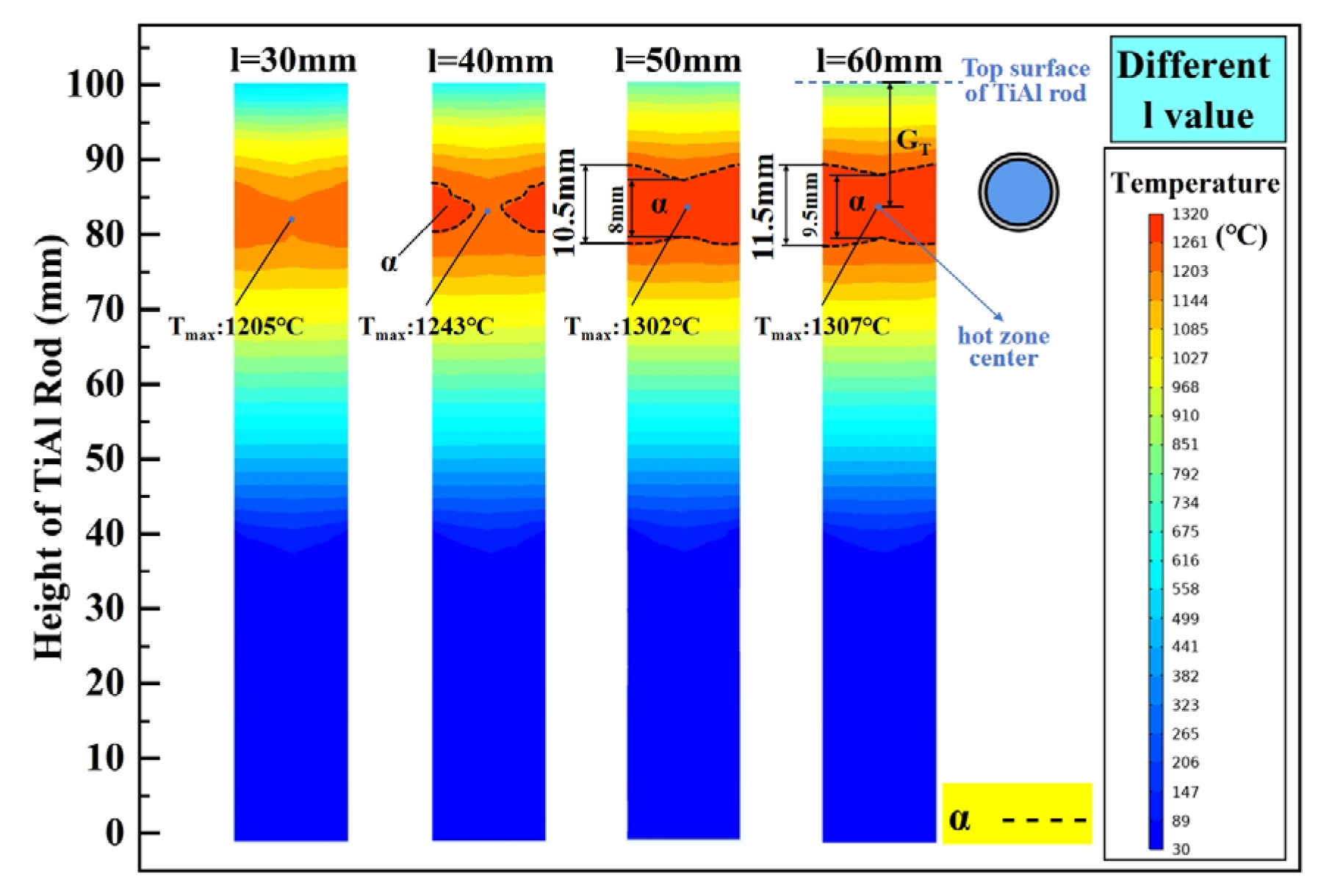
4.1. Effects of Structural Parameters
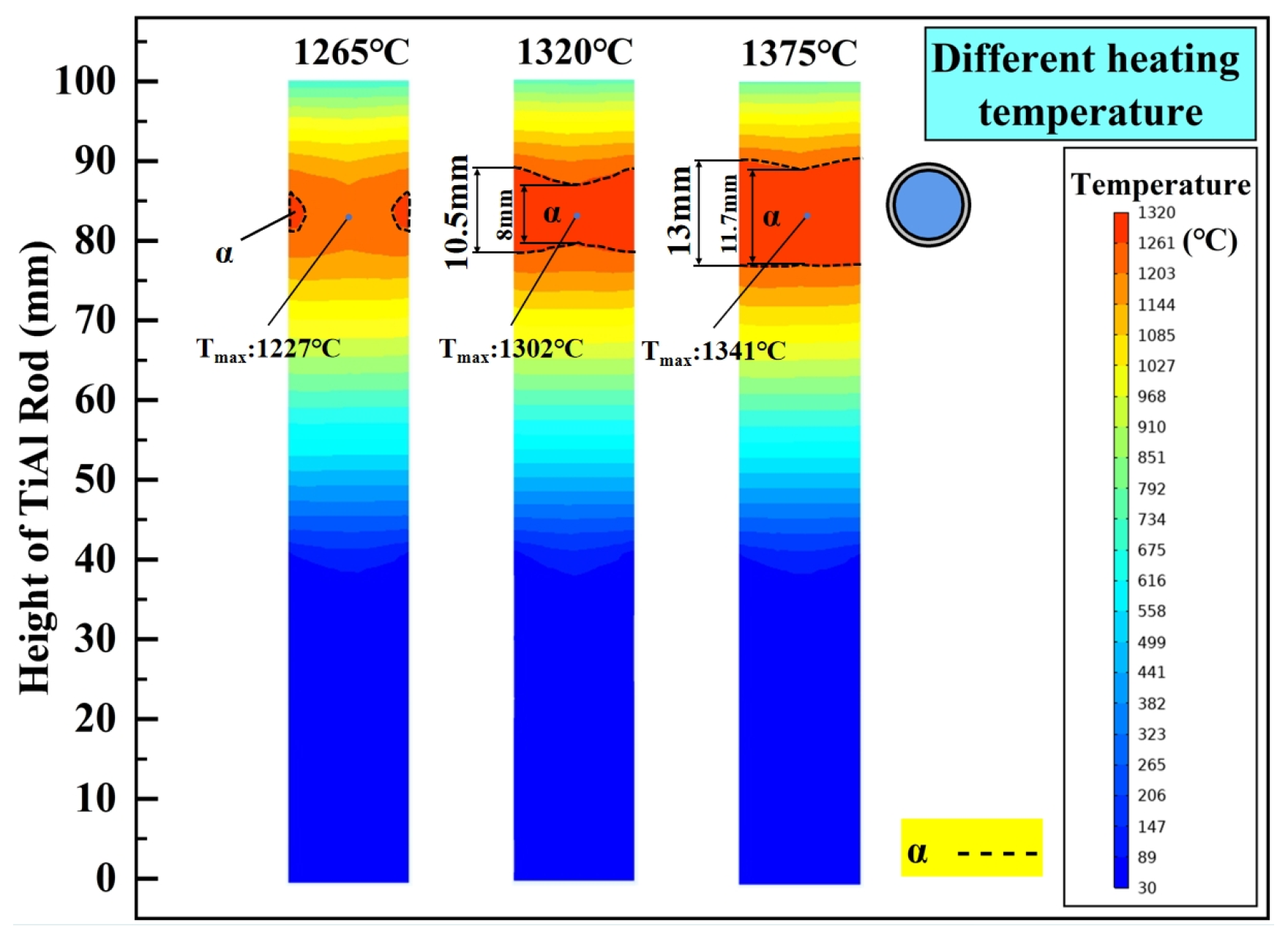
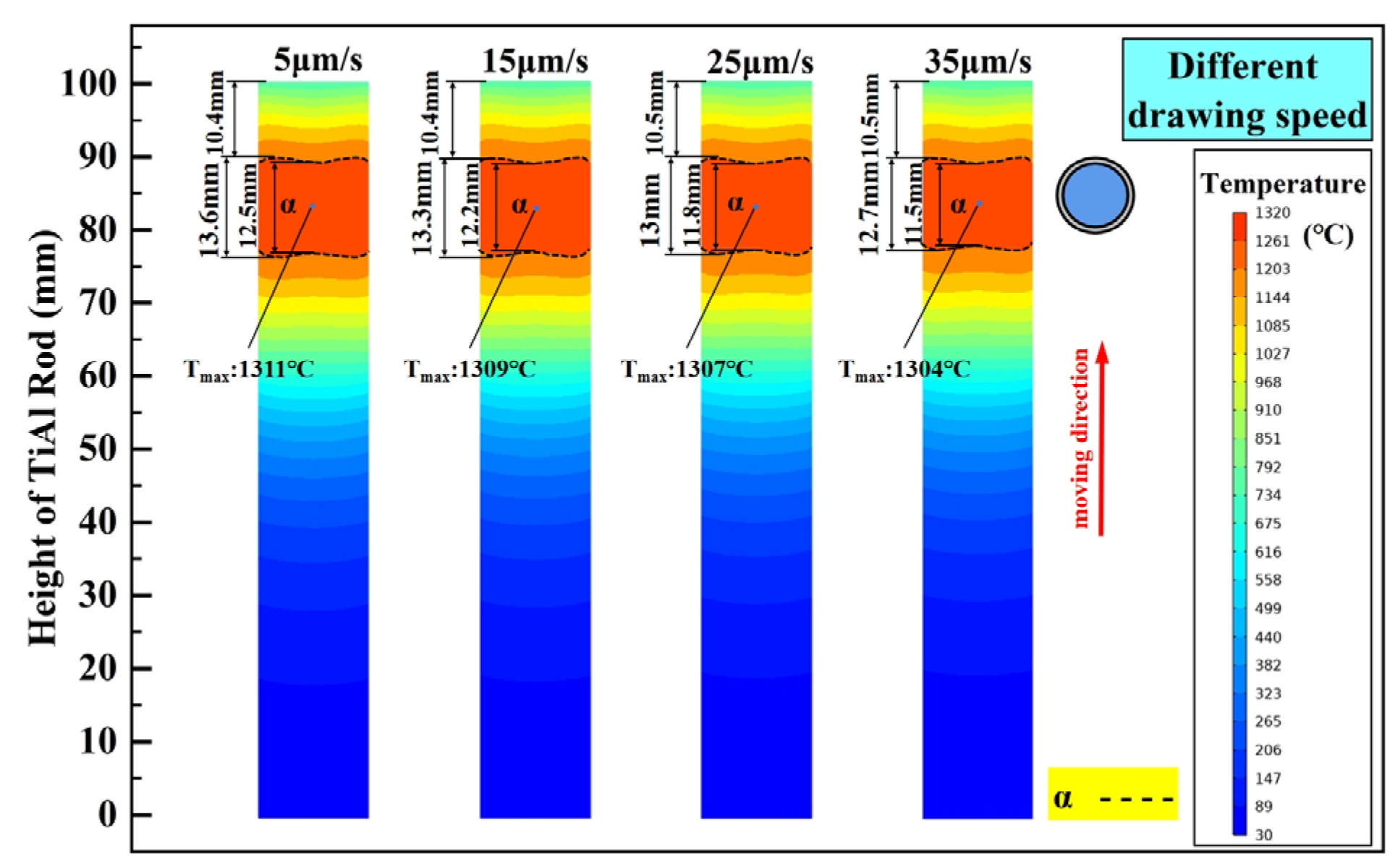
4.2. Effects of Process Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krstić, J.; Jovanović, J.; Gajević, S.; Miladinović, S.; Vaxevanidis, N.; Kiss, I.; Stojanović, B. Application of Metal Matrix Nanocomposites in Engineering. Adv. Eng. Lett. 2024, 3, 180–190. [Google Scholar] [CrossRef]
- Fan, J.; Wei, Z.; Li, Y.; Wang, Y.; Wu, S.; Zhou, X.; Liu, J.; Guo, J. Lamellae Orientation Control and Mechanical Properties of Directionally Solidified Binary Ti-49Al Alloy in Oxide Ceramics Crucible. Int. J. Metalcast. 2022, 16, 622–633. [Google Scholar] [CrossRef]
- Kim, Y.W. Strength and Ductility in TiAl Alloys. Intermetallics 1998, 6, 623–628. [Google Scholar] [CrossRef]
- Chen, G.; Peng, Y.; Zheng, G.; Qi, Z.; Wang, M.; Yu, H.; Dong, C.; Liu, C.T. Polysynthetic Twinned TiAl Single Crystals for High-Temperature Applications. Nat. Mater. 2016, 15, 876–881. [Google Scholar] [CrossRef]
- Chen, G. Research status and development of intermetallic compound structural materials. Mater. Rev. 2000, 9, 1–5. [Google Scholar]
- Bewlay, B.P.; Nag, S.; Suzuki, A.; Weimer, M.J. TiAl Alloys in Commercial Aircraft Engines. Mater. High Temp. 2016, 33, 549–559. [Google Scholar] [CrossRef]
- Duan, B.; Yang, Y.; He, S.; Feng, Q.; Mao, L.; Zhang, X.; Jiao, L.; Lu, X.; Chen, G.; Li, C. History and Development of γ-TiAl Alloys and the Effect of Alloying Elements on Their Phase Transformations. J. Alloys Compd. 2022, 909, 164811. [Google Scholar] [CrossRef]
- Li, Y.; Tu, K.; Chen, C. Tensile Properties of -Oriented Nanotwinned Cu with Different Columnar Grain Structures. Materials 2020, 13, 1310. [Google Scholar] [CrossRef]
- Fan, J.; Li, X.; Su, Y.; Guo, J.; Fu, H. Effect of Growth Rate on Microstructure Parameters and Microhardness in Directionally Solidified Ti–49Al Alloy. Mater. Des. 2012, 34, 552–558. [Google Scholar] [CrossRef]
- Yue, X.; Shen, J.; Xiong, Y.; Li, Q.; Zheng, S. Microstructure and Mechanical Properties of As-Cast and Directionally Solidified Large Size Ti–45Al–8Nb Alloys by Electromagnetic Confinement. Mater. Sci. Eng. A 2021, 825, 141938. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Guo, J.; Ding, H.; Su, Y. Experimental and Numerical Investigation on Mass Transfer Induced by Electromagnetic Field in Cold Crucible Used for Directional Solidification. Int. J. Heat Mass Transf. 2017, 114, 297–306. [Google Scholar] [CrossRef]
- Liu, H.; Ding, X.; Zong, X.; Huang, H.; Nan, H.; Liang, Y.; Lin, J. Review on Progress of Lamellar Orientation Control in Directionally Solidified TiAl Alloys. Materials 2023, 16, 4829. [Google Scholar] [CrossRef] [PubMed]
- Cui, N.; Wu, Q.; Wang, J.; Lv, B.; Kong, F. The Directional Solidification, Microstructural Characterization and Deformation Behavior of β-Solidifying TiAl Alloy. Materials 2019, 12, 1203. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zeng, L.; Ding, H.; Chen, R.; Guo, J.; Fu, H. Microstructures and Mechanical Properties of Directionally Solidified C-Containing γ-TiAl Alloys via Electromagnetic Cold Crucible. Intermetallics 2019, 113, 106587. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, H.; Tang, X.; Ma, L.; Zhang, H.; Gong, S. Interactions between γ-TiAl Melt and Y2O3 Ceramic Material during Directional Solidification Process. Trans. Nonferrous Met. Soc. China 2011, 21, 2415–2420. [Google Scholar] [CrossRef]
- Lapin, J.; Gabalcová, Z. Solidification Behaviour of TiAl-Based Alloys Studied by Directional Solidification Technique. Intermetallics 2011, 19, 797–804. [Google Scholar] [CrossRef]
- Zupan, M.; Hemker, K.J. Tension and Compression Testing of Single-Crystalline Gamma Ti-55.5 Pct Al. Metall. Mater. Trans. A 1998, 29, 65–71. [Google Scholar] [CrossRef]
- Liu, R.; Teng, C.; Cui, Y.; Xu, D.; Xian, Q.; Yang, R. Directional solidification of Ti-43Al-3Si alloys in an optical floating zone furnace. J. Acta Met. Sin. 2013, 48, 235–239. [Google Scholar] [CrossRef]
- Yang, J.; Chen, R.; Su, Y.; Ding, H.; Guo, J.; Fu, H. Optimization of Electromagnetic Energy in Cold Crucible Used for Directional Solidification of TiAl Alloy. Energy 2018, 161, 143–155. [Google Scholar] [CrossRef]
- Baker, I.; Li, J. Directional Annealing of Cold-Rolled Copper Single Crystals. Acta Mater. 2002, 50, 805–813. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, X.; Fang, H.; Tan, Y.; Cui, H.; Chen, R. Columnar Grains Formation and Mechanical Properties Improvement of Ti44Al Alloy by Cyclic Directional Heat Treatment. J. Mater. Res. Technol. 2020, 9, 16355–16366. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, X.; Fang, H.; Chen, R.; Tan, Y.; Su, Y.; Guo, J. Microstructure Evolution of Ti44Al Alloy during Directional Induction Heat Treatment and Its Effect on Mechanical Properties. Mat. Sci. Eng. A 2020, 772, 138701. [Google Scholar] [CrossRef]
- Chen, R.; Liu, Y.; Xue, X.; Fang, H.; Tan, Y.; Cui, H. Optimizing Microstructure and Mechanical Properties of Directionally Solidified Ti44Al6Nb1Cr2V Alloy by Directional Heat Treatment. Mater. Charact. 2021, 179, 111354. [Google Scholar] [CrossRef]
- Chen, R.; Liu, Y.; Xue, X.; Fang, H.; Tan, Y.; Cui, H. Study on Improving Microstructure and Mechanical Properties of Directionally Solidified Ti44Al6Nb1Cr Alloy by Cyclic DHT. Mat. Sci. Eng. A 2021, 809, 140912. [Google Scholar] [CrossRef]
- Ukai, S.; Taya, K.; Nakamura, K.; Aghamiri, M.S.; Oono, N.; Hayashi, S.; Okuda, T. Directional Recrystallization by Zone Annealing in a Ni-Based ODS Superalloy. J. Alloys Compd. 2018, 744, 204–210. [Google Scholar]
- Gao, K.; Qin, X.; Wang, Z.; Chen, H.; Zhu, S.; Liu, Y.; Song, Y. Numerical and Experimental Analysis of 3D Spot Induction Hardening of AISI 1045 Steel. J. Mater. Process. Technol. 2014, 214, 2425–2433. [Google Scholar] [CrossRef]
- Ding, C.; Huang, M.; Zhong, G.; Ming, L.; Huang, X. A Design of Crucible Susceptor for the Seeds Preservation during a Seeded Directional Solidification Process. J. Cryst. Growth 2014, 387, 73–80. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhao, X.; Yang, J.; Zhou, L.; Jin, N.; Liu, Y.; Chen, R. Numerical and Experimental Study of Directional Annealing to Prepare Columnar Grains of TiAl Alloy. Mater. Today Commun. 2024, 38, 108467. [Google Scholar] [CrossRef]
- Jang, B.Y.; Soo Kim, J.; Soo Ahn, Y. Induction Melting Process Using Segmented Graphite Crucible for Silicon Melting. Sol. Energy Mater. Sol. Cells 2011, 95, 101–106. [Google Scholar] [CrossRef]
- Liang, H. Numerical Simulation Study on Electromagnetic Induction Heating of Titanium Aluminide Alloys. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Han, Y.; Wen, H.; Yu, E. Study on Electromagnetic Heating Process of Heavy-Duty Sprockets with Circular Coils and Profile Coils. Appl. Therm. Eng. 2016, 100, 861–868. [Google Scholar] [CrossRef]
- Wen, H.; Han, Y. Study on Mobile Induction Heating Process of Internal Gear Rings for Wind Power Generation. Appl. Therm. Eng. 2017, 112, 507–515. [Google Scholar] [CrossRef]
- Song, B.T. Transient Numerical Simulation on Directional Solidification of Multi-Crystalline Silicon Under Multiphysics Coupling. Master’s Thesis, Nanchang University, Nanchang, China, 2021. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, X.; Chen, R.; Tan, Y.; Su, Y.; Ding, H.; Guo, J. A Novel Method to Prepare Columnar Grains of TiAl Alloys by Controlling Induction Heating. Int. Commun. Heat Mass Transf. 2019, 108, 104315. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, F.; Zhang, L.; Jin, Z.; Cao, G.; Qiu, Z.; Shen, H.; Huang, Y.; Jiang, S.; Sun, J. Break the Superheat Temperature Limitation of Induction Skull Melting Technology. Appl. Therm. Eng. 2023, 220, 119780. [Google Scholar] [CrossRef]
- Cai, H.D. Research on Electromagnetic Induction Self-Healing Heat Transfer Behavior of Steelsand Asphalt Concrete Based on COMSOL. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar] [CrossRef]
- Schuster, J.C.; Palm, M. Reassessment of the Binary Aluminum-Titanium Phase Diagram. J. Phase Equilib. Diff. 2006, 27, 255–277. [Google Scholar] [CrossRef]
- Li, J.; Hao, Q.; Li, S.; Kou, H.; Li, J.; Fu, H. Research on the Non-Linear Temperature Field of Molten Metal Shaped by an Electromagnetic Field in DS Processing. J. Mater. Process. Technol. 2003, 137, 145–150. [Google Scholar]
- Chao, Y.; Ian, B. Directional Recrystallisation Processing: A Review. Int. Mater. Rev. 2021, 66, 256–286. [Google Scholar]
- Yang, J.; Wang, H.; Wang, B.; Hu, R.; Liu, Y.; Luo, X. Numerical and Experimental Study of Electron Beam Floating Zone Melting of Iridium Single Crystal. J. Mater. Process. Technol. 2017, 250, 239–246. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, G.; Bei, H.; Li, F.; Ye, F.; Chen, G.L.; Liu, C.T. Directional Recrystallization and Microstructures of an Fe–6.5wt%Si Alloy. J. Mater. Res. 2009, 24, 2654–2660. [Google Scholar] [CrossRef]
- Zhang, Z.-W.; Chen, G.-L.; Chen, G. Microstructural Evolution of Commercial Pure Iron during Directional Annealing. Mat. Sci. Eng. A 2006, 422, 241–251. [Google Scholar] [CrossRef]
- Wei, C.; Li, S. Effect of Temperature Gradient on Grain Growth Behavior from Phase Field Simulations. Acta Phys. Sin. 2011, 60, 100701. [Google Scholar] [CrossRef]
- Holm, E.A.; Zacharopoulos, N.; Srolovitz, D.J. Nonuniform and Directional Grain Growth Caused by Grain Boundary Mobility Variations. Acta Mater. 1998, 46, 953–964. [Google Scholar] [CrossRef]
- Zhang, Z.W. The Studies on Directional Recrystallization and Its Kinetics. Ph.D. Dissertation, Nanjing University of Science and Technology, Nanjing, China, 2008. [Google Scholar]
- Baker, I.; Iliescu, B.; Li, J.; Frost, H.J. Experiments and Simulations of Directionally Annealed ODS MA 754. Mat. Sci. Eng. A 2008, 492, 353–363. [Google Scholar] [CrossRef]
- Sha, W.; Bhadeshia, H.K.D.H. Directional Recrystallization in Mechanically Alloyed Oxide Dispersion-Strengthened Metals by Annealing in a Moving Temperature Gradient. J. Mater. Sci. 1995, 30, 1439–1444. [Google Scholar] [CrossRef]
- Vallejos, J.M.; Malarría, J.A. Growing Fe-Mn-Al-Ni Single Crystals by Combining Directional Annealing and Thermal Cycling. J. Mater. Process. Technol. 2020, 275, 116317. [Google Scholar] [CrossRef]

| Material Parameter | Copper | Graphite | TiAl Alloy | Asbestos | Ga-In | Units |
|---|---|---|---|---|---|---|
| Relative permeability | 1 | 1 | 1 | 1 | 1 | - |
| Thermal conductivity | 400 | 105 × (T/300)−0.3 × exp(−3.5 × 10−4 (T − 300)) | 21.7959 + 8.1633 × 10−3T | 0.12 | 16.5 | W/(m·K) |
| Density | 8960 | 1950 | 3850 | 1000 | 6350 | kg/m3 |
| Heat capacity at constant pressure (Cp) | 385 | 710 | 1040 | 800 | 306.6 | J/(kg·K) |
| Electrical resistivity | 1.67 × 10−8 | 6.29 × 10−6 | 6.6588 × 10−7 + 0.79 × 10−9T − 8.16 × 10−13T2 + 5.72 × 10−12T3 | - | 9.39 × 10−6 | Ω·m |
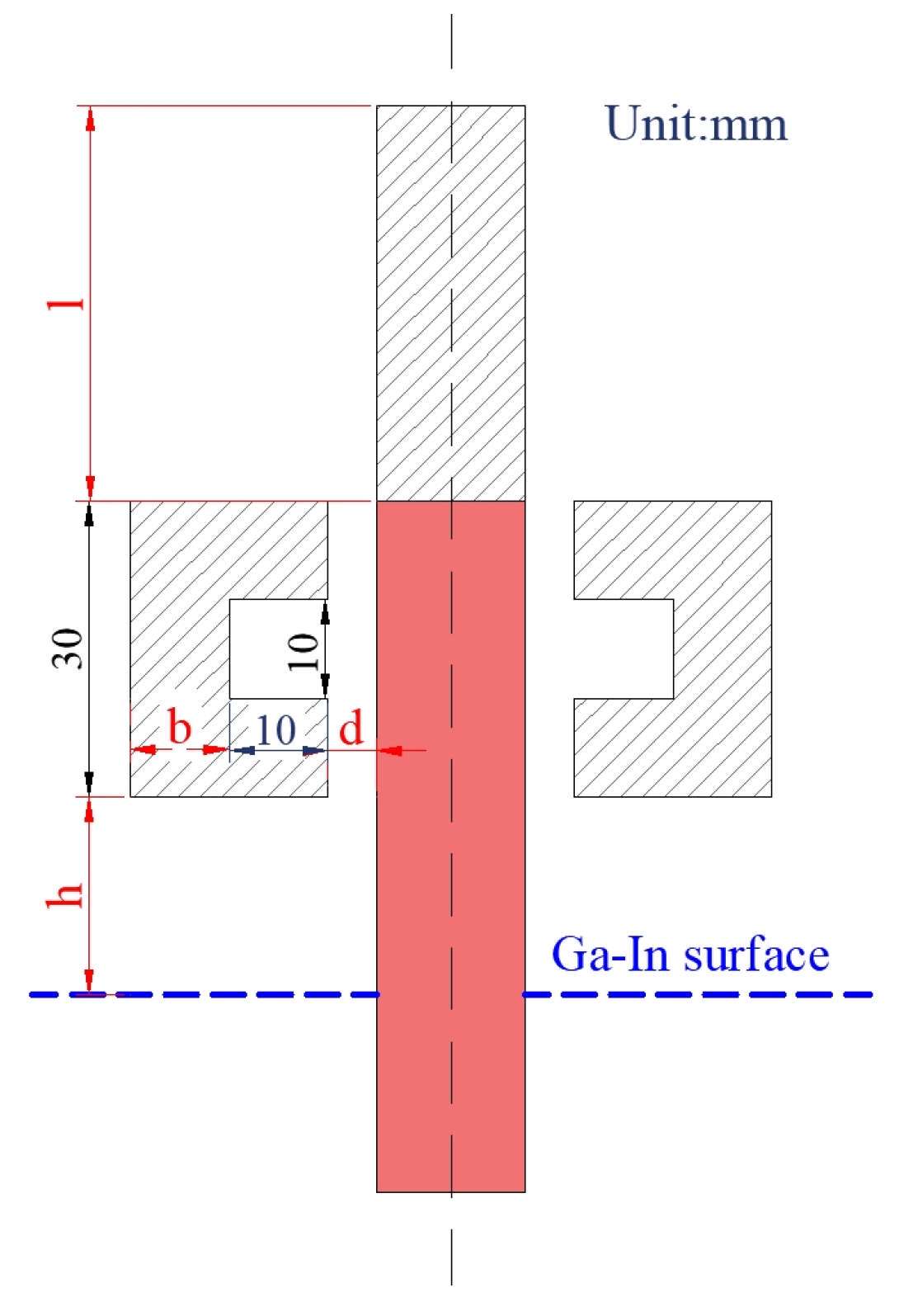
| Parameters | b | h | l | d |
|---|---|---|---|---|
| Effect of b | 10, 20, 30 | 30 | 50 | 5 |
| Effect of d | 10 | 30 | 50 | 3, 5, 7 |
| Effect of l | 10 | 30 | 30, 40, 50, 60 | 5 |
| Effect of h | 10 | 30, 40, 50, 60 | 50 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Hu, Y.; Xu, J.; Hu, Z.; Liu, Y.; Hua, L. Numerical Simulation of Temperature Field Distribution During Directional Annealing of TiAl Alloy with Different Parameters. Materials 2025, 18, 1537. https://doi.org/10.3390/ma18071537
Huang F, Hu Y, Xu J, Hu Z, Liu Y, Hua L. Numerical Simulation of Temperature Field Distribution During Directional Annealing of TiAl Alloy with Different Parameters. Materials. 2025; 18(7):1537. https://doi.org/10.3390/ma18071537
Chicago/Turabian StyleHuang, Feng, Yeyu Hu, Jiaguo Xu, Zhili Hu, Yanxiong Liu, and Lin Hua. 2025. "Numerical Simulation of Temperature Field Distribution During Directional Annealing of TiAl Alloy with Different Parameters" Materials 18, no. 7: 1537. https://doi.org/10.3390/ma18071537
APA StyleHuang, F., Hu, Y., Xu, J., Hu, Z., Liu, Y., & Hua, L. (2025). Numerical Simulation of Temperature Field Distribution During Directional Annealing of TiAl Alloy with Different Parameters. Materials, 18(7), 1537. https://doi.org/10.3390/ma18071537






