Mechanical Analysis of HPFRCC Precast Composite Column
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Mechanical Properties of Materials
2.3. Test Equipment and Loading
3. Results
3.1. Failure Process and Failure Pattern
- For specimen RC-P-01 (Figure 3f), vertical cracks began from the upper column at the load of 449.82 kN. And the cracks appeared and developed vertically and obliquely with the increase in the load. Longitudinal cracks appeared in the lower part of the specimen when the load reached 2550 kN. When the load reached 3204.43 kN, the cracks formed an oblique penetration from the upper to the lower part, and the concrete of the shell began to fall off. At last, the longitudinal crack width of the specimen expanded, the concrete shell at the edges and corners began to peel off in large quantities, the crushing phenomenon occurred at the A side of the specimen, and the reinforced bars were exposed.
- For specimen FC-P-01 (Figure 3a), the specimen showed no surface phenomenon at the beginning. Vertical micro-cracks occurred from the upper of the column at the load of 999.67 kN. The crack in a vertical direction on the right side in the face A developed to the middle part, and then the transverse crack ran through the cross-section at the load of 2640.17 kN. When the peak load was achieved, on face A, the middle part of the specimens was cracked laterally and slightly convex, and the transverse cracks connected with the vertical cracks on both sides of the left and right sides, forming an “H” shape. When the test stopped, the specimen still showed better integrity.
- Compared with FC-P-01, RC-P-01, and RC-C-1, it can be seen that the failure state of RC-C-1 was the most serious, the column body showed obvious brittle failure, and there were four large damages at the corners, resulting in large fragments falling and exposing the stirrup. RC-P-01 was also a brittle failure, but compared with RC-C-1, RC-P-01 has only two damages at the corners and fewer cracks in the column body. Compared with RC-C-1 and RC-P-01, specimen FC-P-01 was in the form of ductile destruction, and only cracks appeared at the edges and corners, and the precast shell maintained good integrity (Figure 3a,f,i).
- Compared with FC-P-01 (ρv was 1.05%), FC-P-02 (ρv was 1.48%), and FC-P-03 (ρv was 0.74%), the damage state of the HPFRCC composite column was more serious with the decrease in the volume stirrup rate. The outer shell of FC-P-03 even appeared to break (Figure 3c). The damage degree in the middle of the precast shell was reduced after increasing the volume stirrup ratio, and the cracks in a vertical direction at the corners of specimens were less. The ductility of composite columns made of reinforced HPFRCC shell was improved, and the development of cracks was also limited, most of which were slender and dense cracks. The overall integrity of FC-P-02 showed the best performance among the three (Figure 3b). Compared with RC-P-01 (ρv was 1.05%), RC-P-02 (ρv was 1.48%), and RC-P-03 (ρv was 0.74%), through the phenomenon analysis, with the increase in the ρv, the damage degree of the RC composite column was decreased, and the three columns all showed crushing phenomena at the column foot (Figure 3f–h). Both RC-P-03 and RC-P-01 had large spalling of the outer shell. The outer shell of specimen RC-P-02 was broken at the corner of the column foot, but there was no spalling. Moreover, the width and depth of vertical cracks of the RC composite column decreased with the increase in the stirrup ratio and increasing the volume stirrup ratio could reduce the possibility that the outer shell of the specimen fell at the cross of cracks. In addition, increasing the ρv improved the restraint effect of the precast shell, which was equivalent to improving the deformation ability of the columns.
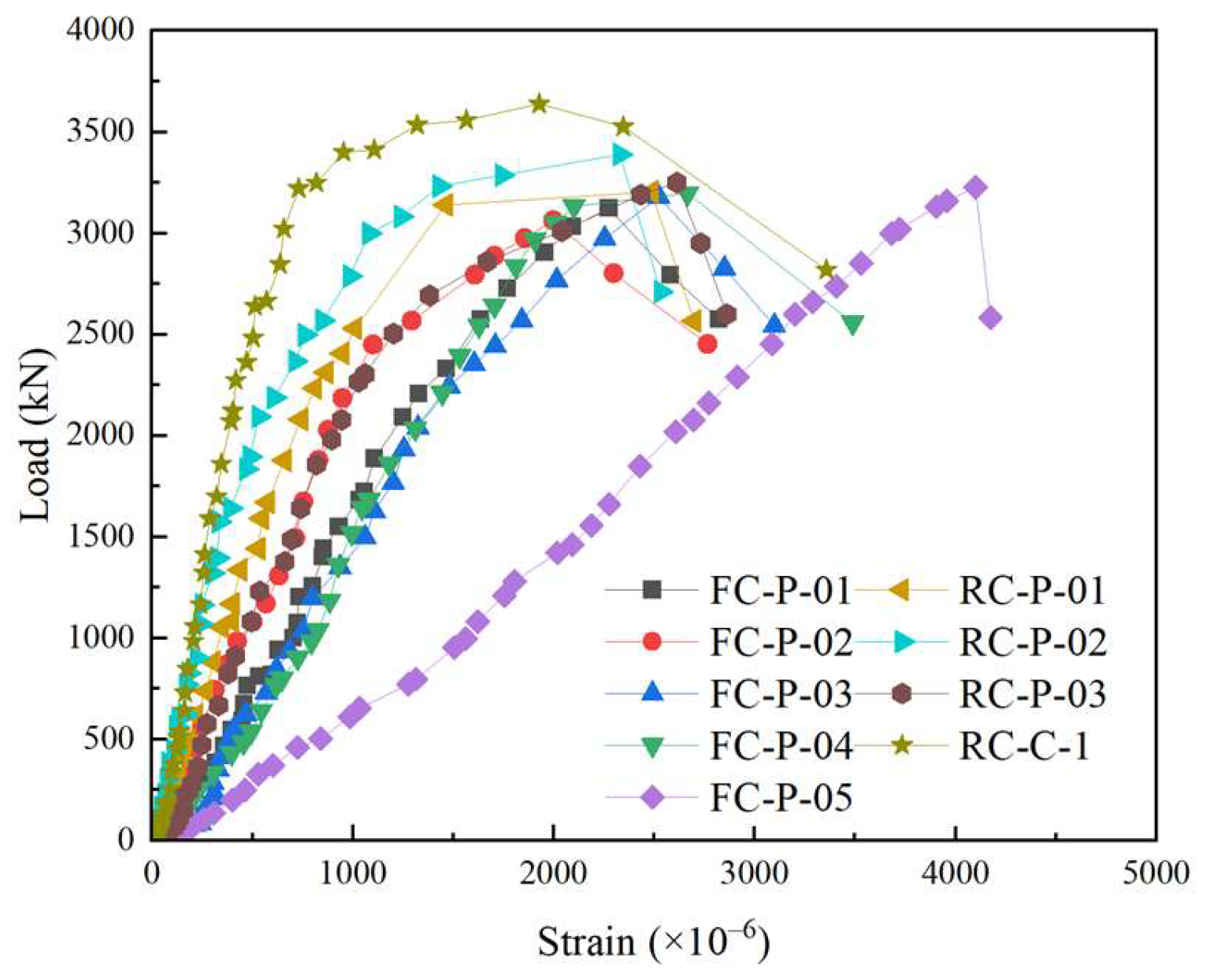
3.2. Load−Deformation Curves
- Compared with specimen RC-P-01, RC-P-02, and RC-P-03, the compressive strain at the yielding point of specimen FC-P-01, FC-P-02, and FC-P-03 increased by 11.25%, 12.49%, and 11.17%, the compressive strain at the peak load point of specimen FC-P-01, FC-P-02, and FC-P-03 increased by 19.43%, 10.86%, and 2.58%.
- Based on Table 6, compared to FC-P-01, the yielding load of FC-P-04 and FC-P-05 increased by 1.54% and 4.10%; the maximum load of FC-P-04 and FC-P-05 increased by 0.73% and 1.40%. The larger the reinforcement ratio of longitudinal reinforcement was, the larger the yield load and peak load of the composite column under axial compression was.
- As seen from Table 6, compared with FC-P-03, the yielding load of FC-P-01 and FC-P-02 increased by 2.42%, 13.09%. The stain at the yielding point of FC-P-01 and FC-P-02 increased by 11.32%, 35.25%. The stain at the maximum load point of FC-P-01 and FC-P-02 increased by 31.75%, 41.31%. The factor of ρv significantly influenced the compressive strain at the characteristic point of the composite column in the axial compression test. Increasing the ρv of the specimens was helpful to its deformation performance. Moreover, the stirrup provided transverse constraint to the composite column, limited its transverse deformation, and was helpful in improving its own compressive bearing capacity.
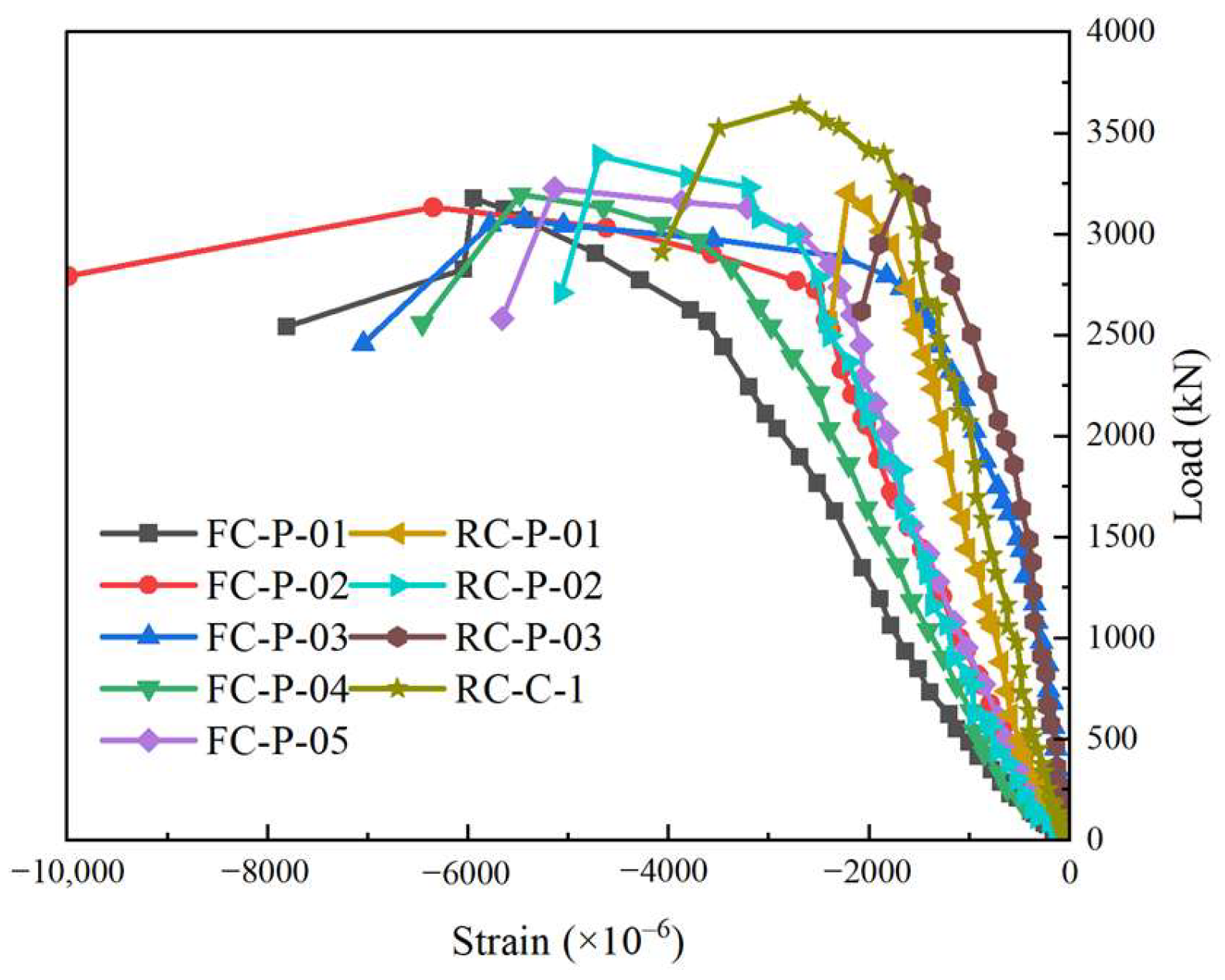
3.3. Load−Strain Curves
3.3.1. Stirrup Strain
- Initially, in the elastic phase, the strain was linearly related to the axial load. When the load was close to 60–80% of the peak load, the stiffness decreased, the increase rate of the stress also decreased and presented a curve shape. The descending speed of HPFRCC specimens was slower than that of RC specimens. In this stage, the bearing capacity gradually decreased until the specimen failed.
- For the RC-P-01 column and FC-P-01 column, at the initial loading stage of the specimen, the variation trend of the stress–strain curve was roughly similar, with linear growth. In the early loading stage, the stirrup strain grew slowly. And after reaching 80% of the maximum load, the stirrup strain growing rate was rapid. During the test, after the stage of peak load, the specimen RC-P-01 declined faster than the specimen FC-P-01.
- Compared with RC-P-01, RC-P-02, and RC-P-03, the stirrup strain at the peak load point of FC-P-01, FC-P-02, and FC-P-03 reduced by 8.54%, 14.22%, and 3.52%, respectively. As the HPFRCC material had better tensile capacity, the precast shell made of HPFRCC provided additional restraint, thus improving the restraint effect.
3.3.2. Longitudinal Reinforced Bars Strain
3.4. Calculation Model of Axial Compression Capacity of HPFRCC Composite Column
3.4.1. Material Stress–Strain Relationship
- (1)
- Stress–Strain Relationship of Concrete
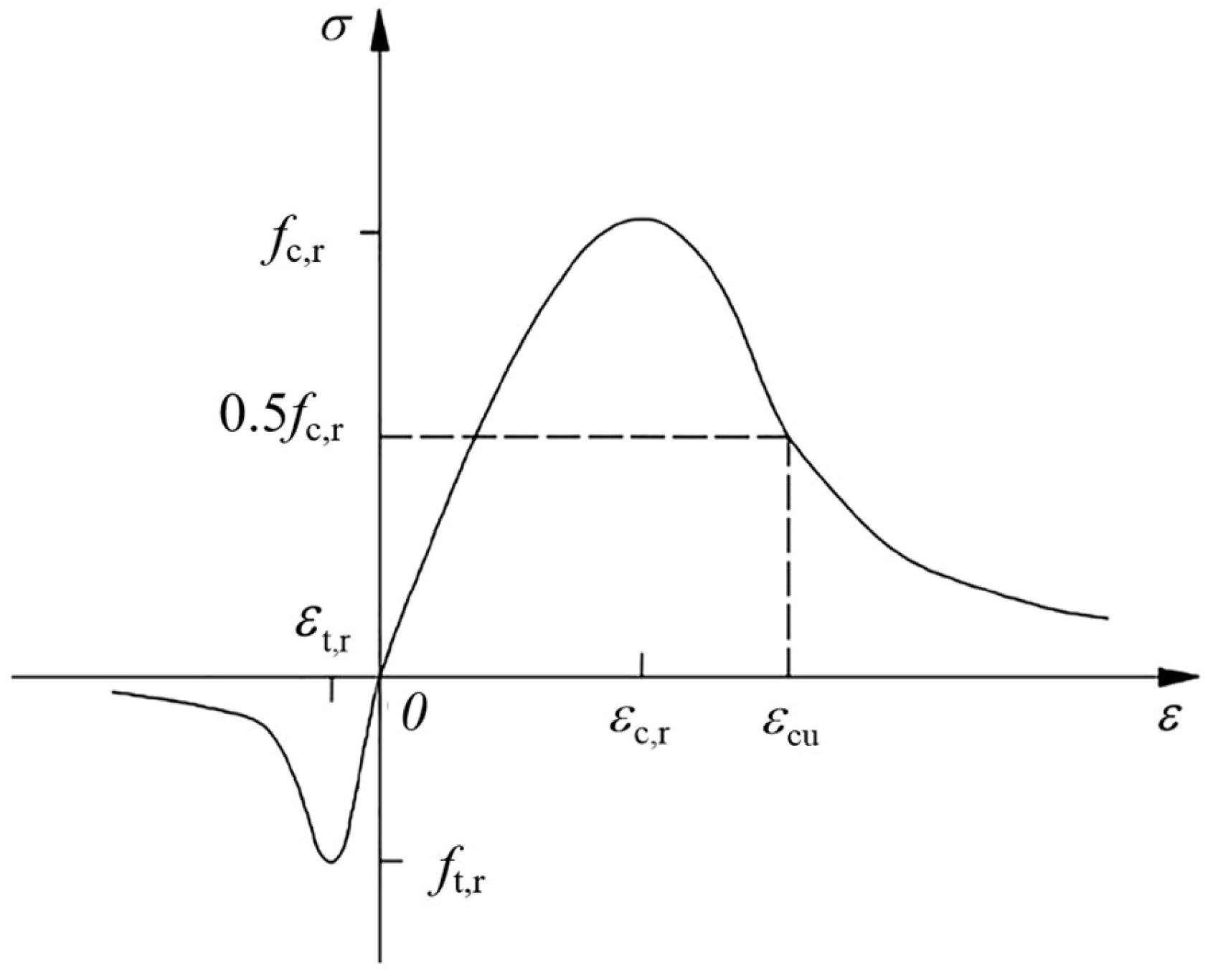
- (2)
- Constitutive model of reinforcement
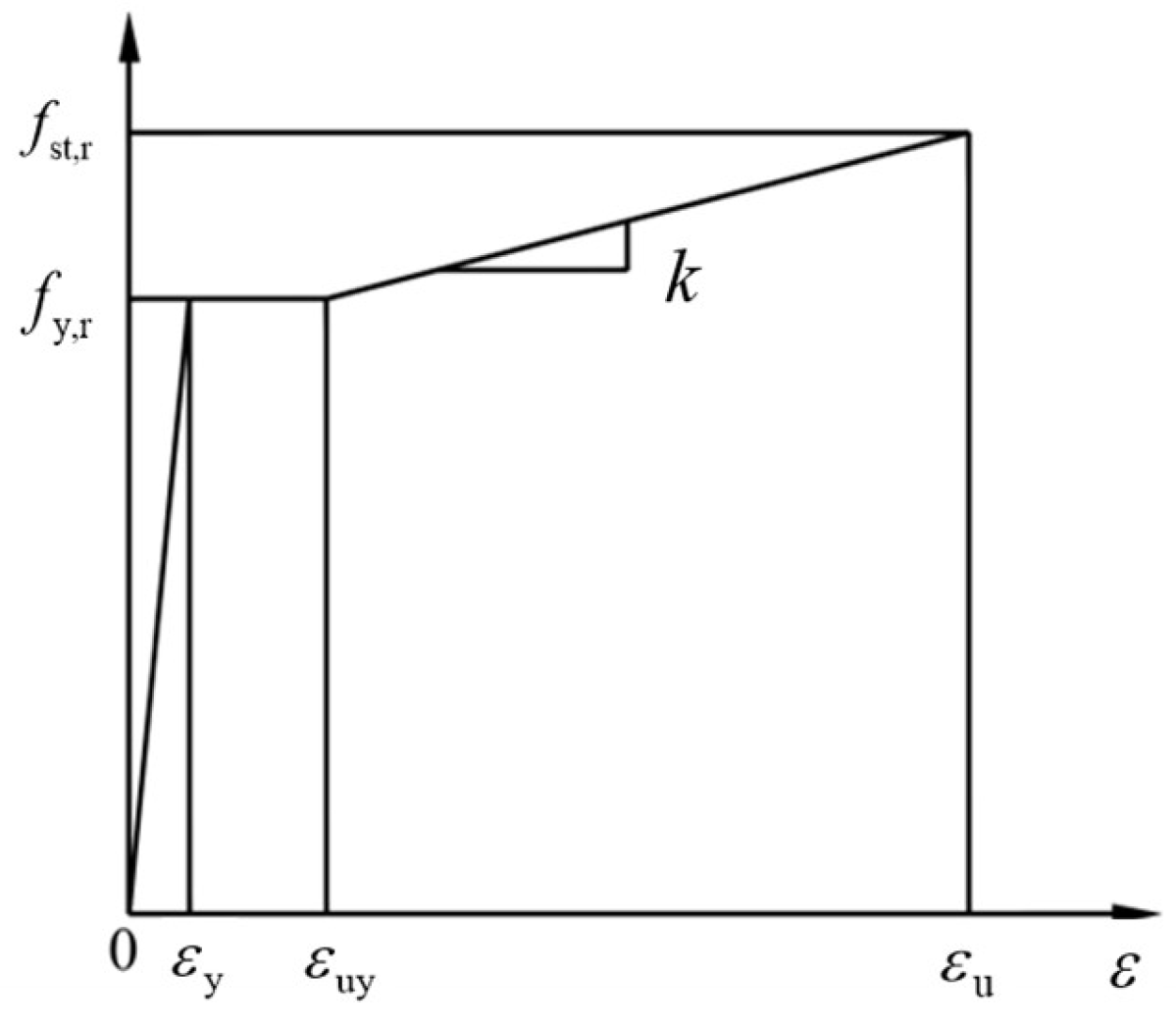
- (3)
- Constitutive model of HPFRCC
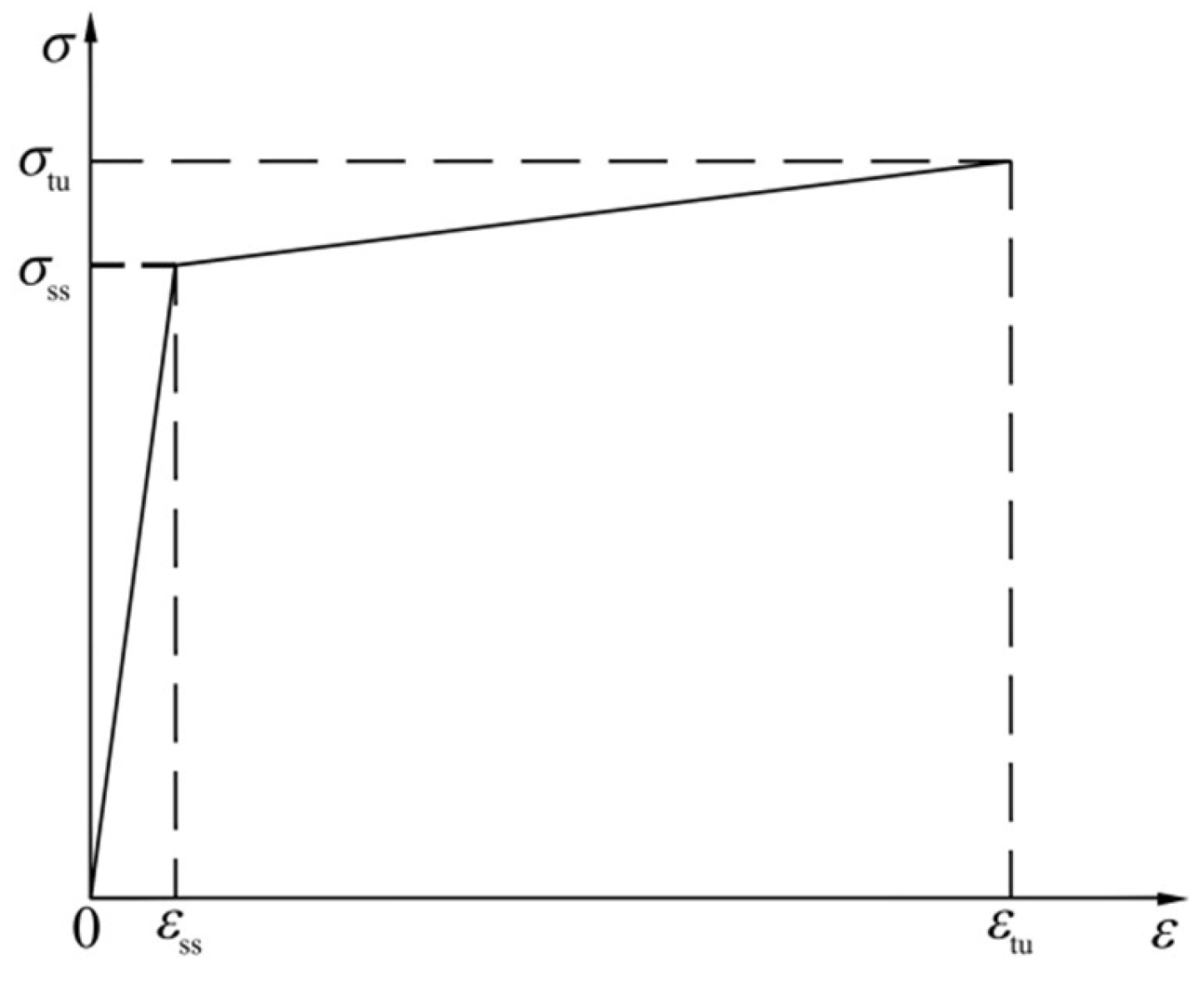
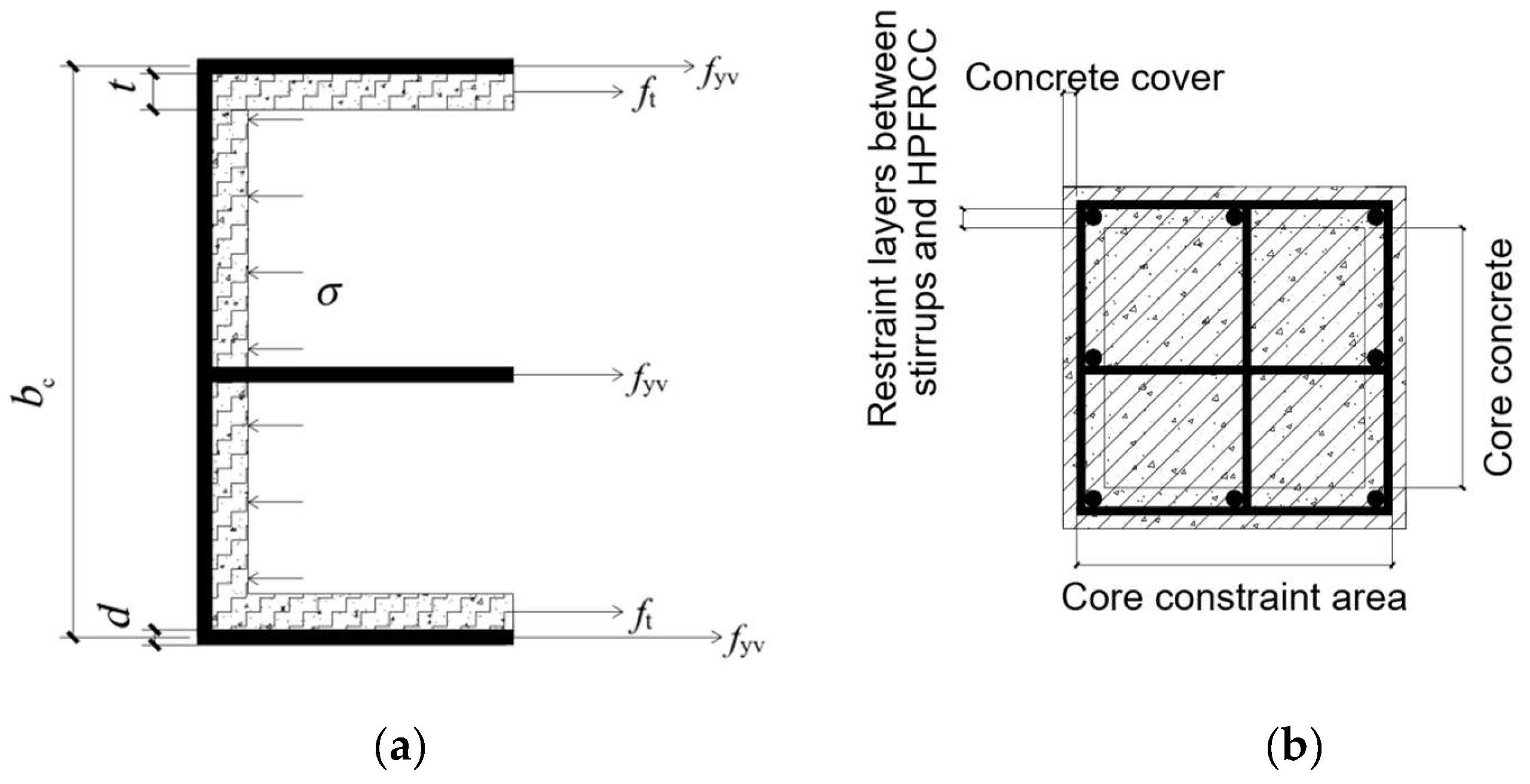
3.4.2. Constraint Coefficient
3.4.3. Peak Stress Calculated Model
3.4.4. Bearing Capacity Calculated Model
4. Discussions
4.1. Analysis of Experimental Results
- The results demonstrate that the incorporation of HPFRCC materials enhances the deformation performance, structural integrity, and load-bearing capacity of composite columns compared with RC composite columns. Through comparisons between RC-P-01 and FC-P-01, RC-P-02 and FC-P-03, and RC-P-03 and FC-P-03, it is evident that the HPFRCC material plays a critical role in improving the ductility and overall behavior of the composite columns. Unlike RC columns, which exhibited severe issues such as the detachment of the precast shell and the formation of large-scale cracks, the HPFRCC composite columns maintained their structural integrity even after failure, exhibiting a more ductile failure mode. During the testing process, the HPFRCC material exhibited strain-hardening behavior when the prefabricated shell cracked. The fibers within the HPFRCC acted as bridges at the crack locations, effectively transferring stress and controlling further crack propagation. This mechanism not only minimized the development of localized large cracks but also prevented the formation of long and wide cracks, which were commonly observed in the RC composite columns. Instead, the HPFRCC composite columns developed a dense network of fine cracks on their surfaces, allowing them to maintain overall integrity post-failure.
- Once peak stress was reached, the RC composite columns experienced a rapid drop in reinforcement bar stress and a significant reduction in deformation resistance, but the HPFRCC composite columns achieved a larger strain at the peak load point. Moreover, when the HPFRCC specimens reached their peak stress, they showed a larger deformation capacity, as evidenced by the gradual decline in the stress–strain curve after peak stress. This behavior highlights the superior energy absorption and ductility, which are critical for structures subjected to high stress or seismic loads.
- The HPFRCC shell provides enhanced confinement of the post-cast concrete, delaying the yielding of longitudinal bars and stirrup. This delay contributed to the improved deformation performance and load-bearing capacity of the composite columns. This constraint is due to the strain-hardening properties of the HPFRCC material, which restrain lateral expansion and distribute stress effectively. The material’s exceptional tensile deformation performance also allowed the precast shell to withstand greater circumferential expansion, maintaining structural integrity under large deformation. These properties make the HPFRCC composite column ideal for seismic-resistant structures. In the future, it is necessary to conduct further research on the seismic performance of HPFRCC composite columns and provide a basis for its application in engineering structures.
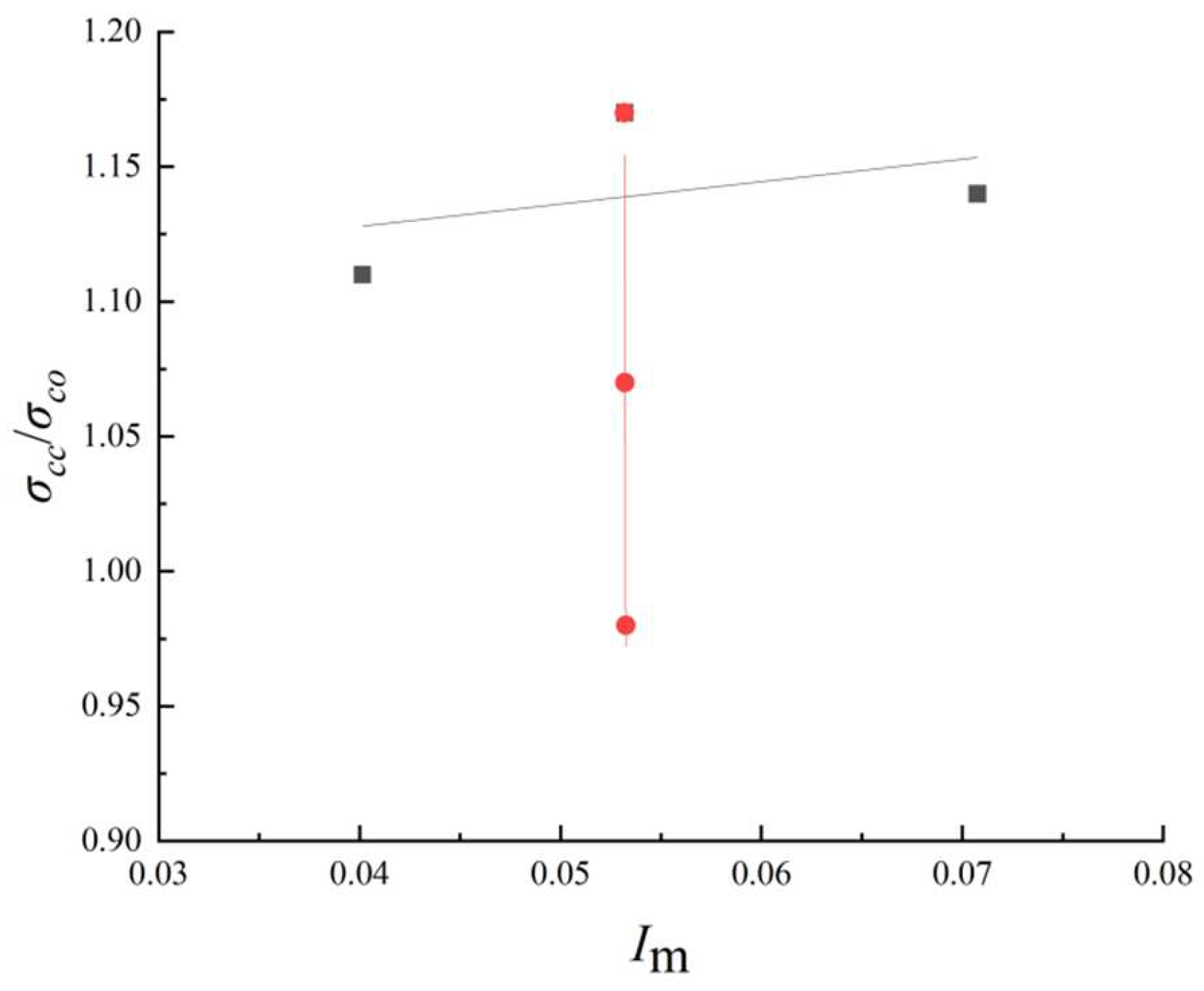
4.2. Evaluation of Peak Stress Calculated Model
4.3. Assessment of Bearing Capacity Calculated Model
5. Conclusions
- HPFRCC prefabricated composite column showed good axial compression performance. Using HPFRCC material as a prefabricated shell can significantly enhance the column deformability. The compressive strain at the yielding point of the HPFRCC specimens was 11.59% higher than the average value of the RC specimens, and the average value of the peak compressive strain was 10.92%. The HPFRCC shell could provide an additional restraint effect to the specimen. The damage degree of the column decreased to a certain extent, avoiding brittle failure. Then, the deformability and integrity of the columns were enhanced.
- According to the analysis of the experimental results, the factor ρv played a great influence on the deformability of the column. Compared with FC-P-01 (ρv was 1.05%), FC-P-02 (ρv was 1.48%) and FC-P-03 (ρv was 0.74%), based on FC-P-01, the compressive strain at the yielding point of the specimen FC-P-02 increased by 21.63%. The compressive strain at the yielding point of the specimen FC-P-03 decreased by 11.20%.
- Increasing the ρt of longitudinal reinforced bars could enhance the axial compressive capacity. Among HPFRCC specimens, based on the FC-P-01 specimen, the maximum load of the FC-P-04 specimen increased by 0.57%, while that of FC-P-05 increased by 1.49%.
- Based on theoretical analysis, the peak stress model, peak strain model, and bearing capacity calculation model of HPFRCC assembled monolithic composite column was established. The average value of NH/Nt is 0.999, and the sample variance is 0.0022. The established peak stress model, peak strain model, and theoretical calculation formula of bearing capacity of HPFRCC assembled monolithic composite column were feasible.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, Y.Y.; Feng, Y.; Yang, G.L.; Xue, Y.T. Summary of wholly precast concrete frame. Earthq. Resist. Eng. Retrofit. 2020, 42, 96–105. [Google Scholar] [CrossRef]
- Park, H.; Lee, H.; Choi, I.; Kim, S.; Park, S. Concrete-Filled Steel Tube Columns Encased with Thin Precast Concrete. J. Struct. Eng. 2015, 141, 04015056. [Google Scholar] [CrossRef]
- Francesco, M.; Alessio, C.; Maria, A.A. A Study on FRP-Confined Concrete in Presence of Different Pre-load Levels. In Proceedings of the 9th International Conference on Fibre-Reinforced Polymer (FRP) Composites in Civil Engineering (CICE 2018), Paris, France, 17–19 July 2018. [Google Scholar]
- Lu, T.T.; Jin, H.W.; Liang, X.W. Research on the Mechanical Properties and Calculation Model of the Joint of Beam-Column Subassembly. Chin. Q. Mech. 2023, 44, 696–708. [Google Scholar] [CrossRef]
- Lu, T.T.; Liang, X.W. Effect of HPFRCC on Seismic Performance of Beam-Column-Slab Subassembly. KSCE J. Civ. Eng. 2020, 24, 3785–3796. [Google Scholar] [CrossRef]
- Li, X.; Pan, J.L.; Cai, J.M. Seismic performance of precast RC and RC/ECC composite columns with grouted sleeve connections. Eng. Struct. 2019, 188, 104–110. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, Y.F.; Xun, Y.; Wu, F.H. Tensile strength test of Interface between Ribbed Concrete Permanent Form and Concrete. Build. Sci. 2015, 31, 78–82. [Google Scholar] [CrossRef]
- Cheng, T.; Li, N.J.; Chen, G.M.; Li, Z.B.; Xiong, Y. Experimental study on axial compressive mechanical properties of concrete-filled steel tube with ECC layer reinforced by textile. J. Xi’an Univ. Archit. Technol. (Nat. Sci. Ed.) 2022, 54, 202–210. [Google Scholar] [CrossRef]
- Liang, X.W.; Shi, J.C.; Yu, J.; Li, L. Seismic behavior of reinforced concrete columns with permanent template of ultra-high performance concrete. China Earthq. Eng. J. 2020, 42, 579–588, 606. [Google Scholar] [CrossRef]
- Huang, J.; Wang, P.; Shi, Q.X.; Rong, C.; Tao, Y. Flexural behavior and numerical simulation of reinforced concrete beams with a UHPC stay-in-place formwork. Structures 2024, 69, 107254. [Google Scholar] [CrossRef]
- Pan, Z.F.; Zhu, Y.Z.; Qiao, Z.; Meng, S. Seismic behavior of composite columns with steel reinforced ECC permanent formwork and infilled concrete. Eng. Struct. 2020, 212, 110541. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Li, Y.; Liu, Z.J. Study on mechanical performance and constitutive equation of high toughness PVA-FRCC under uniaxial compression. J. Build. Mater. 2014, 17, 606–612. [Google Scholar] [CrossRef]
- Li, H.D. Experimental Research on Ultra-High Toughness Cementitious Composites. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Li, V.C.; Lepech, M. General Design Assumptions for Engineered Cementitious Composites. In Proceedings of the International Workshop on HPFRCC in Structural Applications, Honolulu, HI, USA, 23–26 May 2005; Available online: https://hdl.handle.net/2027.42/84789 (accessed on 16 June 2011).
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1998, 114, 1804–1826. [Google Scholar]
- Deng, Z.C.; Yao, J.S. Axial compression behavior of ultra-high performance concrete columns confined by high-strength stirrups. Acta Mater. Compos. Sin. 2020, 37, 2590–2601. [Google Scholar] [CrossRef]
- Chang, Y.F.; Shi, J.P.; Hou, Y.P.; Lu, T.T. Experimental study on the axial compressive capacity of ultra-high performance concrete stub columns confined with stirrups. Acta Mater. Compos. Sin. 2022, 39, 3451–3461. [Google Scholar] [CrossRef]
- Légeron, F.; Paulture, P. Uniaxial confinement model for normal- and high-strength concrete columns. J. Struct. Eng. ASCE 2003, 129, 241–252. [Google Scholar] [CrossRef]
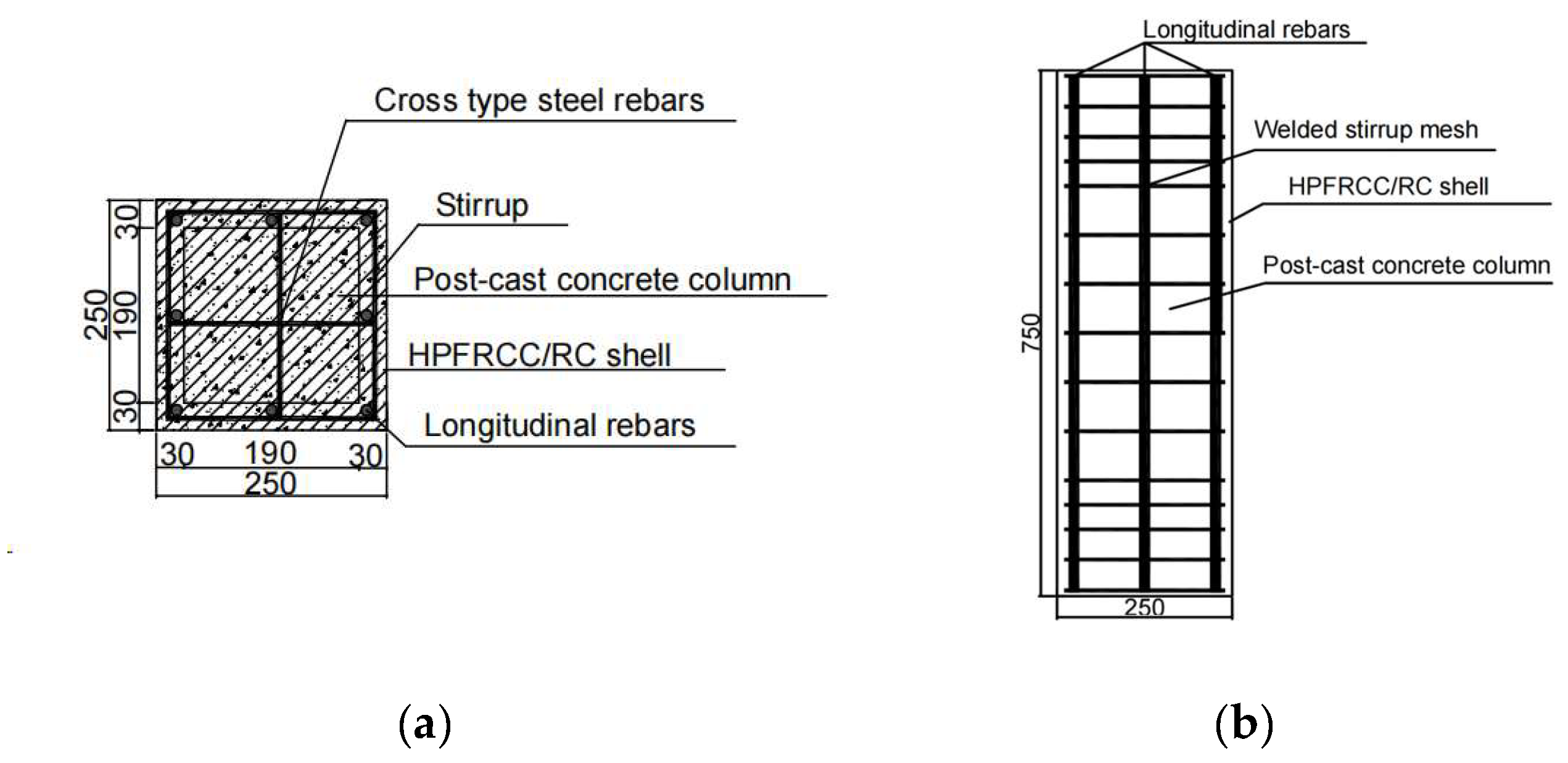




| Test Piece | Column Length (mm) | Cross-Section (mm × mm) | Stirrup Spacing (mm) | Column Reinforcement | |
|---|---|---|---|---|---|
| Longitudinal Bars | Stirrups | ||||
| FC-P-01 | 750 | 250 × 250 | 70 | 8 12 12 | ϕ 6@70 |
| FC-P-02 | 750 | 250 × 250 | 50 | 8 12 12 | ϕ 6@50 |
| FC-P-03 | 750 | 250 × 250 | 100 | 8 12 12 | ϕ 6@100 |
| FC-P-04 | 750 | 250 × 250 | 70 | 8 14 14 | ϕ 6@70 |
| FC-P-05 | 750 | 250 × 250 | 70 | 8 16 16 | ϕ 6@70 |
| RC-P-01 | 750 | 250 × 250 | 70 | 8 12 12 | ϕ 6@70 |
| RC-P-02 | 750 | 250 × 250 | 50 | 8 12 12 | ϕ 6@50 |
| RC-P-03 | 750 | 250 × 250 | 100 | 8 12 12 | ϕ 6@100 |
| RC-C-1 | 750 | 250 × 250 | 70 | 8 12 12 | ϕ 6@70 |
| Cement (g/L) | Fly Ash (g/L) | Quartz Sand (g/L) | PVA Fiber (g/L) | Water Reducer (g/L) | Water (g/L) |
|---|---|---|---|---|---|
| 630 | 630 | 406 | 20 | 15 | 436 |
| Fiber Name | Length (mm) | Diameter (µm) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Elongation (%) |
|---|---|---|---|---|---|
| PVA | 12 | 40 | 1560 | 41 | 6.5 |
| Material Type | Cube Compressive Strength fcu (MPa) | Prismatic Compressive Strength fc (MPa) | Tensile Strength ft (MPa) |
|---|---|---|---|
| HPFRCC | 49.9 | 43.2 | 5.2 |
| RC | 47.2 | 38.2 | 3.4 |
| Types of Rebar | Diameter of Rebar (mm) | Yield Strength (MPa) | Ultimate Strength (MPa) |
|---|---|---|---|
| HPB300 | 6 | 355 | 506 |
| HRB400 | 12 | 463 | 642 |
| HRB400 | 14 | 442 | 614 |
| HRB400 | 16 | 532 | 698 |
| Number | Yielding Point | Maximum Load Point | ||
|---|---|---|---|---|
| Load (kN) | Deformation (10−6) | Load (kN) | Deformation (10−6) | |
| FC-P-01 | 2630.52 | 7780.28 | 3182.55 | 9519.45 |
| FC-P-02 | 2904.47 | 9452.34 | 3143.63 | 10,208.67 |
| FC-P-03 | 2568.13 | 6988.56 | 3074.38 | 7224.52 |
| FC-P-04 | 2670.92 | 7416.34 | 3197.91 | 8962.67 |
| FC-P-05 | 2738.34 | 7280.75 | 3227.32 | 8465.33 |
| RC-P-01 | 2711.88 | 6993.33 | 3204.43 | 7970.67 |
| RC-P-02 | 2869.62 | 8402.61 | 3399.28 | 9208.76 |
| RC-P-03 | 2632.45 | 6286.47 | 3260.43 | 7042.87 |
| RC-C-1 | 2989.32 | 7954.67 | 3649.28 | 10,058.67 |
| Number | Peak Loads (kN) | Stirrup Strain (10−6) | Yield Load (kN) |
|---|---|---|---|
| FC-P-01 | 3182.55 | 2274.07 | 2630.52 |
| FC-P-02 | 3143.63 | 1997.58 | 2914.47 |
| FC-P-03 | 3074.38 | 2522.86 | 2568.13 |
| FC-P-04 | 3197.91 | 2666.80 | 2670.92 |
| FC-P-05 | 3227.32 | 4099.93 | 2738.34 |
| RC-P-01 | 3204.43 | 2486.48 | 2711.88 |
| RC-P-02 | 3399.28 | 2328.51 | 2869.62 |
| RC-P-03 | 3260.43 | 2614.36 | 2632.45 |
| RC-C-1 | 3649.28 | 1927.56 | 2989.32 |
| Test Piece Number | σco (MPa) | σcc (MPa) | σcc/σco |
|---|---|---|---|
| FC-P-01 | 38.2 | 44.90 | 1.18 |
| FC-P-02 | 38.2 | 43.84 | 1.15 |
| FC-P-03 | 38.2 | 42.71 | 1.12 |
| FC-P-04 | 38.2 | 42.30 | 1.11 |
| FC-P-05 | 38.2 | 37.35 | 0.98 |
| RC-P-01 | 38.2 | 45.53 | 1.19 |
| RC-P-02 | 38.2 | 49.22 | 1.29 |
| RC-P-03 | 38.2 | 46.59 | 1.22 |
| RC-C-1 | 38.2 | 53.94 | 1.41 |
| Test Piece Number | σcc(m) (MPa) | σtest (MPa) | σcc(m)/σtest |
|---|---|---|---|
| FC-P-01 | 48.730 | 50.877 | 0.958 |
| FC-P-02 | 52.206 | 50.141 | 1.041 |
| FC-P-03 | 46.146 | 49.187 | 0.938 |
| FC-P-04 | 48.735 | 51.166 | 0.952 |
| FC-P-05 | 48.744 | 51.653 | 0.944 |
| Test Piece Number | N (kN) | NH/Nt | |
|---|---|---|---|
| Calculated Value (NH) | Test Value (Nt) | ||
| FC-P-01 | 3045.17 | 3182.55 | 0.96 |
| FC-P-02 | 3106.61 | 3143.63 | 0.99 |
| FC-P-03 | 2999.48 | 3074.24 | 0.98 |
| FC-P-04 | 3170.60 | 3197.91 | 0.99 |
| FC-P-05 | 3481.99 | 3227.32 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, T.; Wang, B.; Jin, H.; Wen, Y. Mechanical Analysis of HPFRCC Precast Composite Column. Materials 2025, 18, 1567. https://doi.org/10.3390/ma18071567
Lu T, Wang B, Jin H, Wen Y. Mechanical Analysis of HPFRCC Precast Composite Column. Materials. 2025; 18(7):1567. https://doi.org/10.3390/ma18071567
Chicago/Turabian StyleLu, Tingting, Bin Wang, Haowei Jin, and Yuxiang Wen. 2025. "Mechanical Analysis of HPFRCC Precast Composite Column" Materials 18, no. 7: 1567. https://doi.org/10.3390/ma18071567
APA StyleLu, T., Wang, B., Jin, H., & Wen, Y. (2025). Mechanical Analysis of HPFRCC Precast Composite Column. Materials, 18(7), 1567. https://doi.org/10.3390/ma18071567






