Application of Voronoi Tessellation to the Additive Manufacturing of Thermal Barriers of Irregular Porous Materials—Experimental Determination of Thermal Properties
Abstract
:1. Introduction
1.1. Parametric Design
1.2. Design of Cellular Composites That Have a Complex Core Geometry–Voronoi Diagram
2. Materials and Methods
2.1. Materials: Irregular Porous Structure Design
2.2. Experimental Section
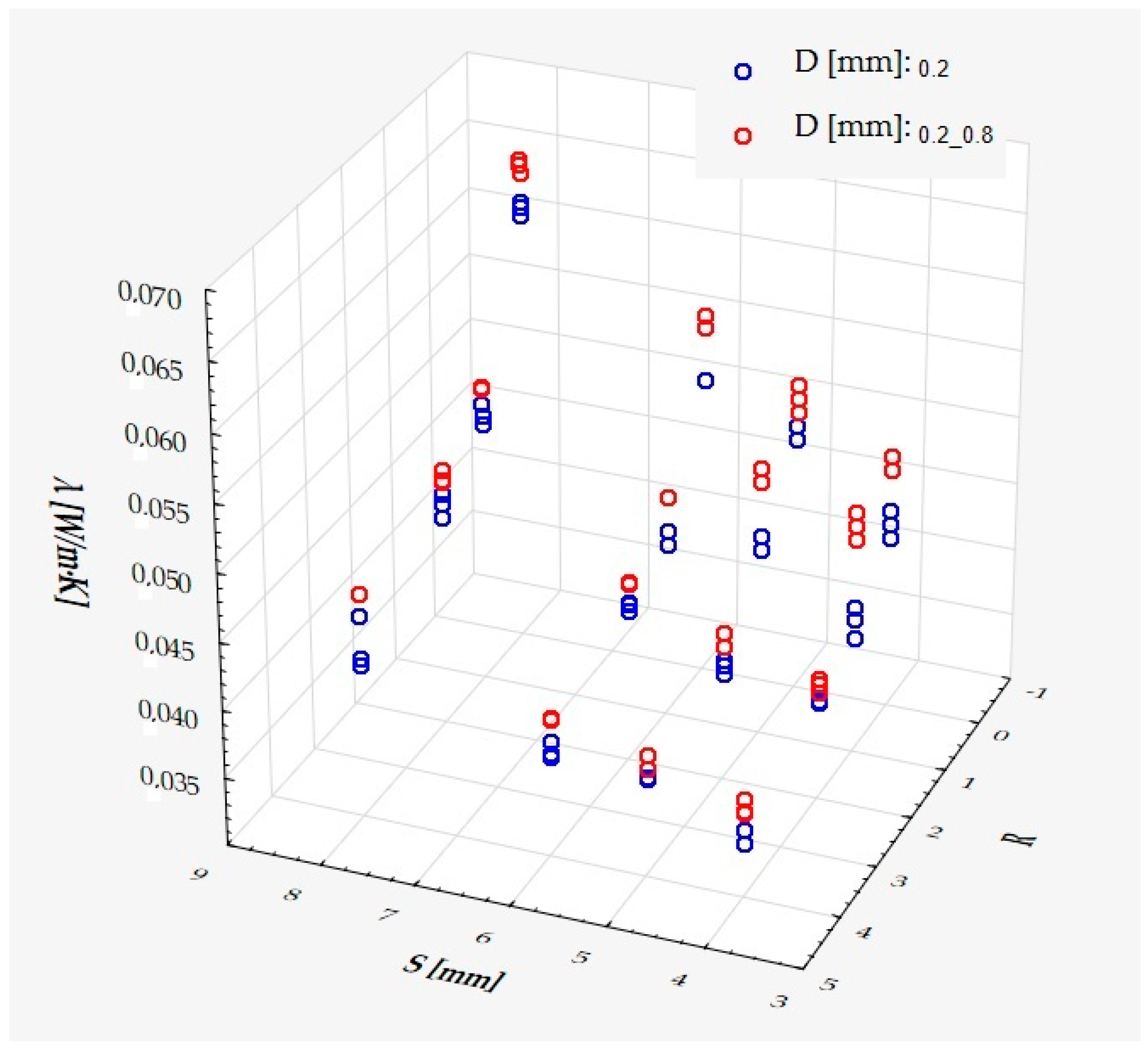
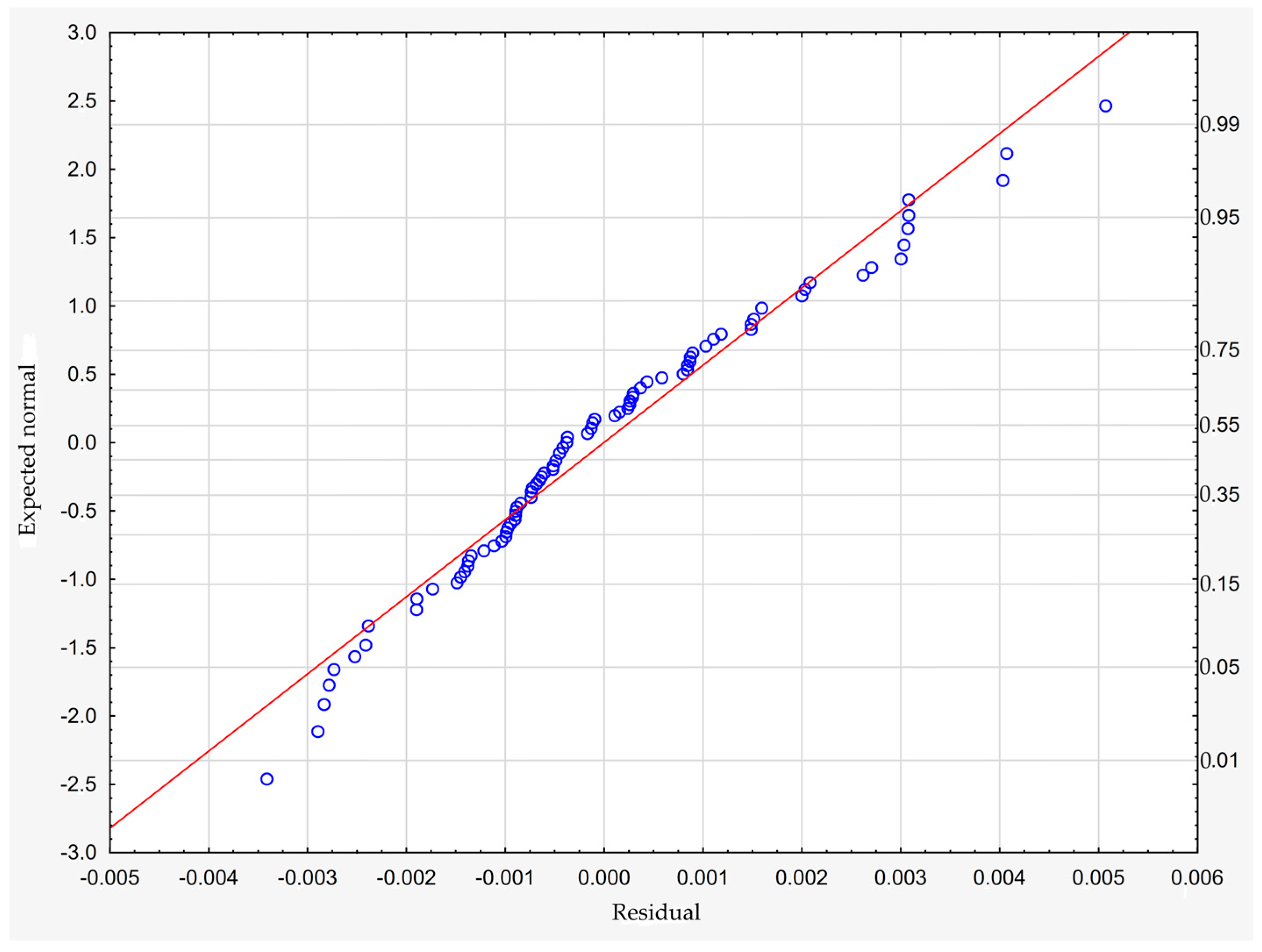
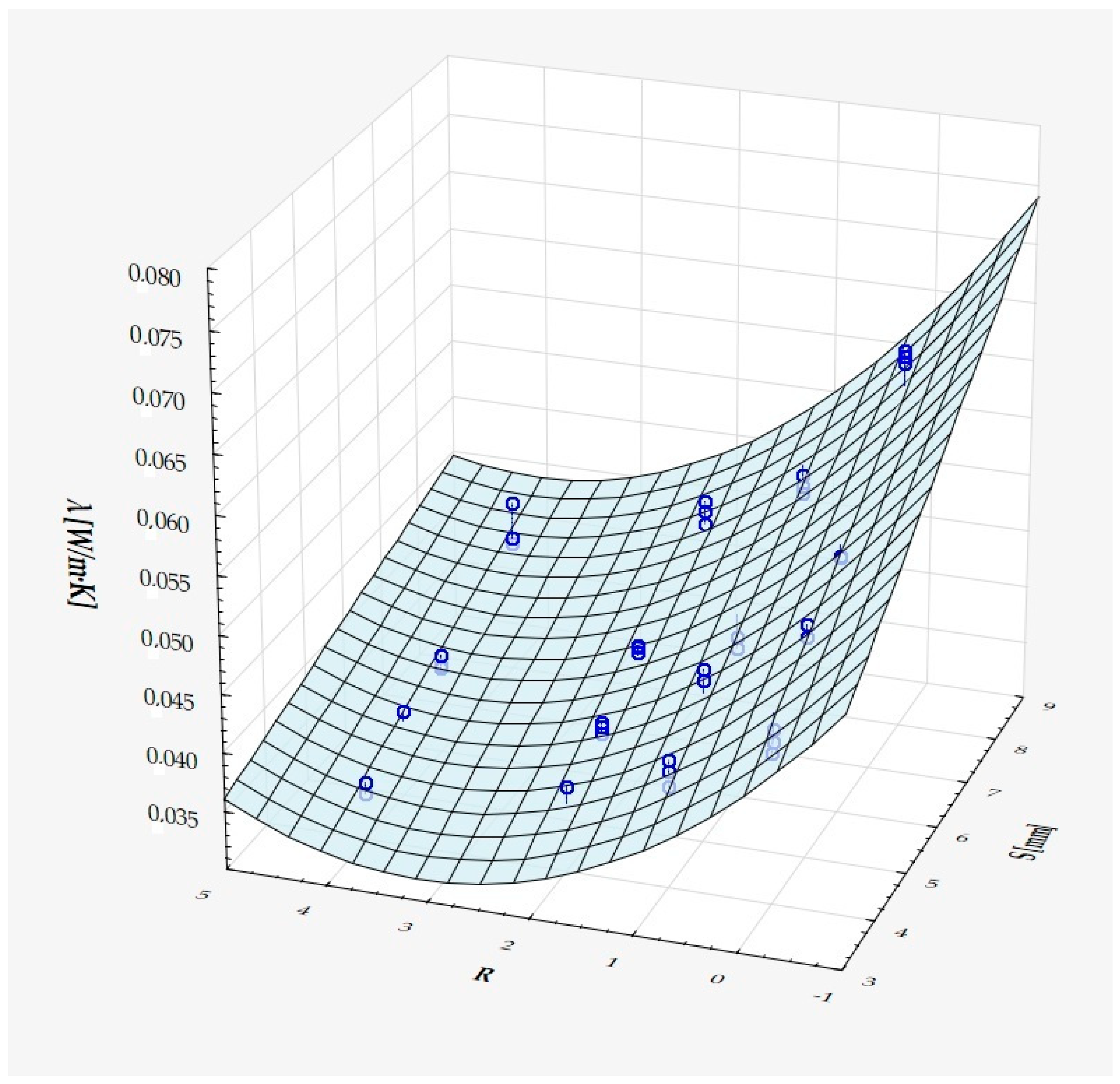
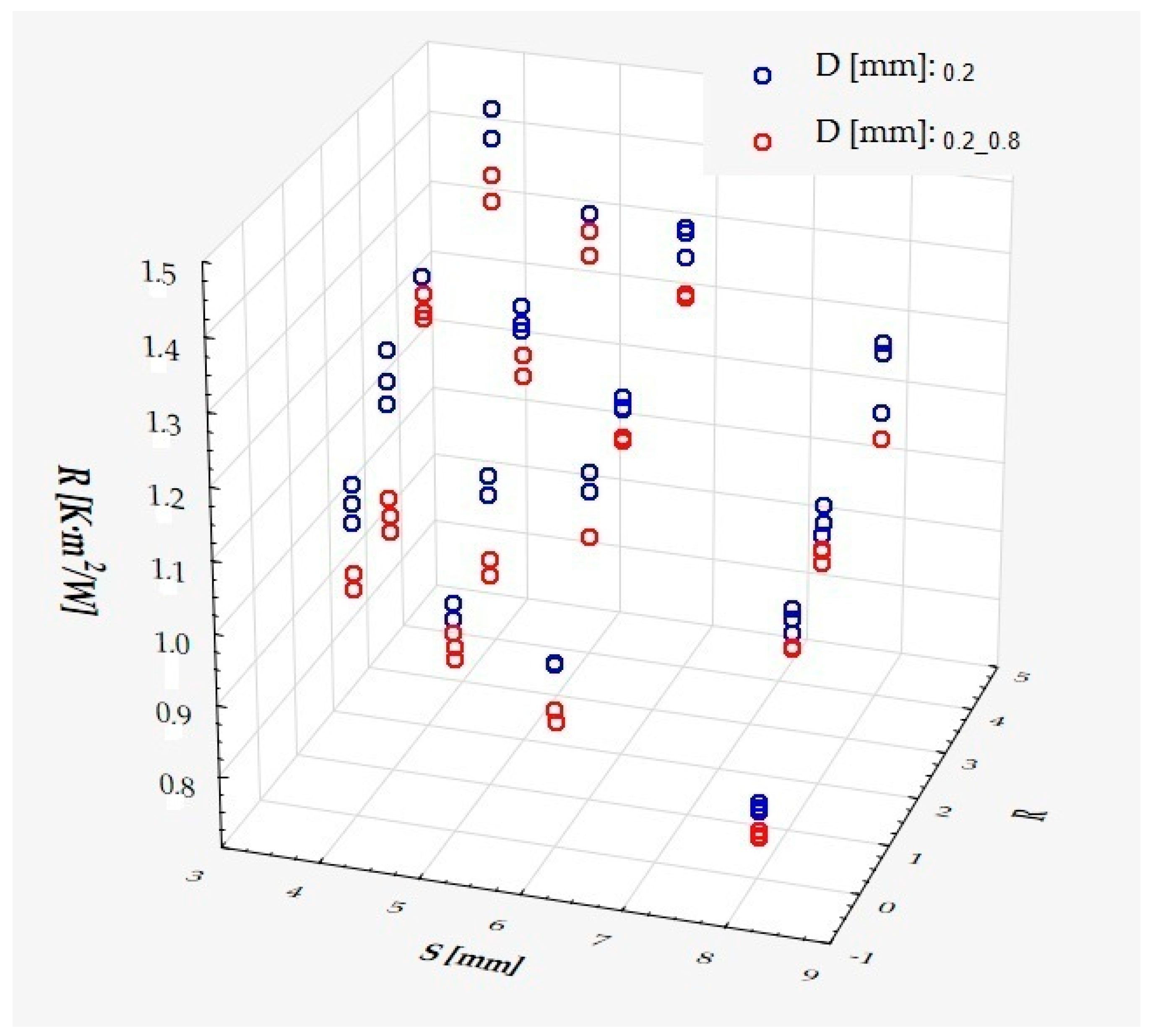
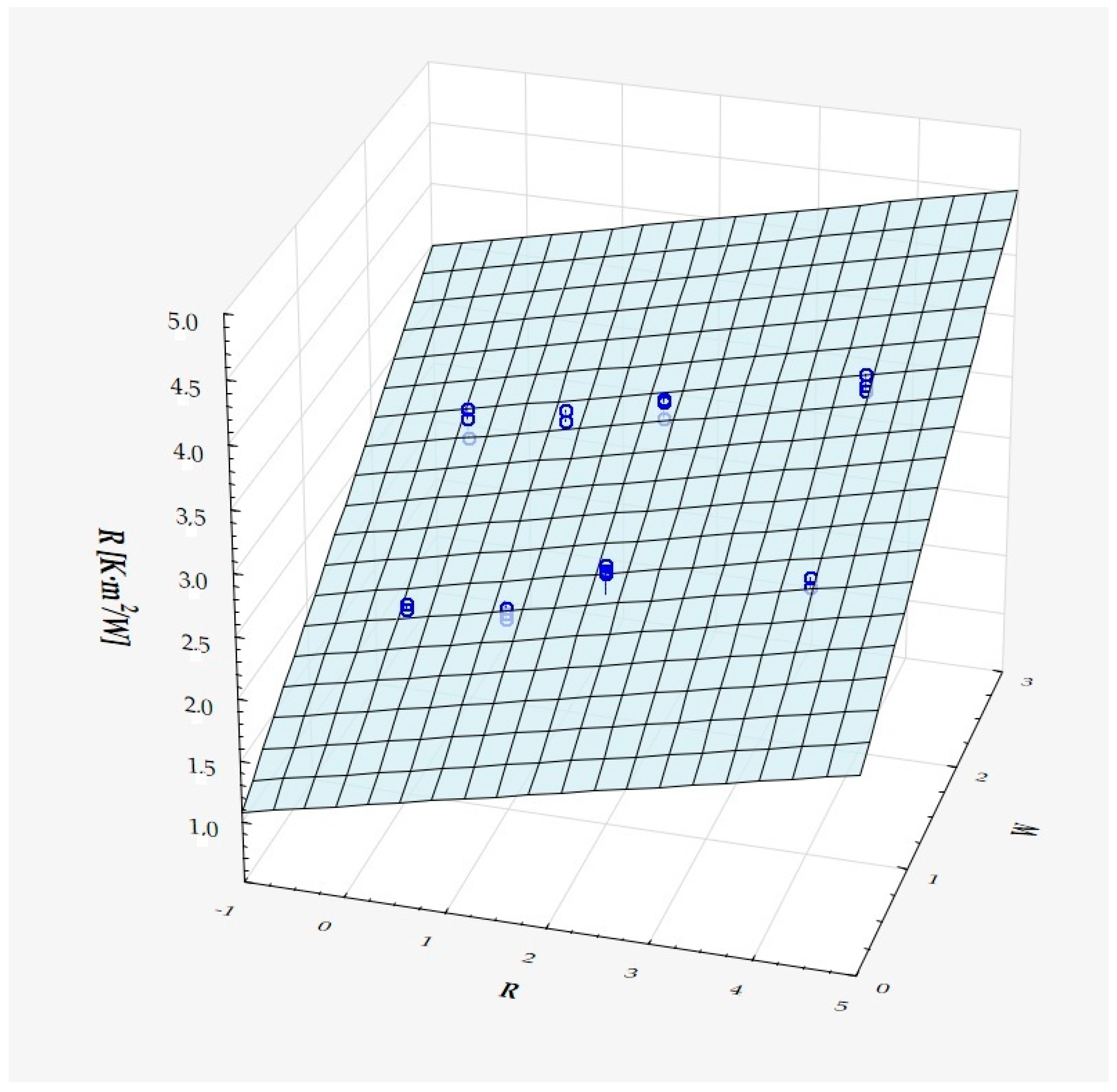
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, F.; Wu, S.; Sun, Y. Hollow-Structured Materials for Thermal Insulation. Adv. Mater. 2019, 31, 1801001. [Google Scholar] [CrossRef]
- Santoni, A.; Bonfiglio, P.; Fausti, P.; Marescotti, C.; Mazzanti, V.; Mollica, F.; Pompoli, F. Improving the Sound Absorption Performance of Sustainable Thermal Insulation Materials: Natural Hemp Fibres. Appl. Acoust. 2019, 150, 279–289. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R.; Rab, S. Role of Additive Manufacturing Applications towards Environmental Sustainability. Adv. Ind. Eng. Polym. Res. 2021, 4, 312–322. [Google Scholar] [CrossRef]
- Kafle, A.; Luis, E.; Silwal, R.; Pan, H.M.; Shrestha, P.L.; Bastola, A.K. 3D/4D Printing of Polymers: Fused Deposition Modelling (FDM), Selective Laser Sintering (SLS), and Stereolithography (SLA). Polymers 2021, 13, 3101. [Google Scholar] [CrossRef]
- Gide, K.M.; Islam, S.; Bagheri, Z.S. Polymer-Based Materials Built with Additive Manufacturing Methods for Orthopedic Applications: A Review. J. Compos. Sci. 2022, 6, 262. [Google Scholar] [CrossRef]
- Sharma, V.; Bhandari, K.; Barua, R. Sustainable Cooling, Layer by Layer, Shaping Magnetic Regenerators via Additive Manufacturing. J. Compos. Sci. 2025, 9, 114. [Google Scholar] [CrossRef]
- Sudamrao Getme, A.; Patel, B. A Review: Bio-Fiber’s as Reinforcement in Composites of Polylactic Acid (PLA). Mater. Today Proc. 2020, 26, 2116–2122. [Google Scholar] [CrossRef]
- Jafferson, J.M.; Sabareesh, M.C.; Sidharth, B.S. 3D Printed Fabrics Using Generative and Material Driven Design. Mater. Today Proc. 2021, 46, 1319–1327. [Google Scholar] [CrossRef]
- Sabbatini, B.; Cambriani, A.; Cespi, M.; Palmieri, G.F.; Perinelli, D.R.; Bonacucina, G. An Overview of Natural Polymers as Reinforcing Agents for 3D Printing. ChemEngineering 2021, 5, 78. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Ishak, M.R.; Mohammad Taha, M.; Mustapha, F.; Leman, Z. A Review of Natural Fiber-Based Filaments for 3D Printing: Filament Fabrication and Characterization. Materials 2023, 16, 4052. [Google Scholar] [CrossRef]
- Delgado Camacho, D.; Clayton, P.; O’Brien, W.J.; Seepersad, C.; Juenger, M.; Ferron, R.; Salamone, S. Applications of Additive Manufacturing in the Construction Industry—A Forward-Looking Review. Autom. Constr. 2018, 89, 110–119. [Google Scholar] [CrossRef]
- Parandoush, P.; Lin, D. A Review on Additive Manufacturing of Polymer-Fiber Composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Zakari, A.; Khan, I.; Tan, D.; Alvarado, R.; Dagar, V. Energy Efficiency and Sustainable Development Goals (SDGs). Energy 2022, 239, 122365. [Google Scholar] [CrossRef]
- Islam, S.; Bhat, G.; Sikdar, P. Thermal and Acoustic Performance Evaluation of 3D-Printable PLA Materials. J. Build. Eng. 2023, 67, 105979. [Google Scholar] [CrossRef]
- de Rubeis, T. 3D-Printed Blocks: Thermal Performance Analysis and Opportunities for Insulating Materials. Sustainability 2022, 14, 1077. [Google Scholar] [CrossRef]
- de Rubeis, T.; Ciccozzi, A.; Paoletti, D.; Ambrosini, D. 3D Printing for Energy Optimization of Building Envelope—Experimental Results. Heliyon 2024, 10, e31107. [Google Scholar] [CrossRef]
- de Rubeis, T.; Ciccozzi, A.; Giusti, L.; Ambrosini, D. The 3D Printing Potential for Heat Flow Optimization: Influence of Block Geometries on Heat Transfer Processes. Sustainability 2022, 14, 15830. [Google Scholar] [CrossRef]
- Grabowska, B.; Kasperski, J. The Thermal Conductivity of 3D Printed Plastic Insulation Materials—The Effect of Optimizing the Regular Structure of Closures. Materials 2020, 13, 4400. [Google Scholar] [CrossRef]
- Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Design and Statistical Analysis of Irregular Porous Scaffolds for Orthopedic Reconstruction Based on Voronoi Tessellation and Fabricated via Selective Laser Melting (SLM). Mater. Chem. Phys. 2020, 239, 121968. [Google Scholar] [CrossRef]
- Sawei, Q.; Xinna, Z.; Qingxian, H.; Renjun, D.; Yan, J.; Yuebo, H. Research Progress on Simulation Modeling of Metal Foams. Rare Met. Mater. Eng. 2015, 44, 2670–2676. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Jia, P. Performance of Forced Convection Heat Transfer in Porous Media Based on Gibson–Ashby Constitutive Model. Heat Transf. Eng. 2011, 32, 1093–1098. [Google Scholar] [CrossRef]
- Chiappini, D. Numerical Simulation of Natural Convection in Open-Cells Metal Foams. Int. J. Heat Mass Transf. 2018, 117, 527–537. [Google Scholar] [CrossRef]
- Zafari, M.; Panjepour, M.; Meratian, M.; Emami, M.D. CFD simulation of forced convective heat transfer by tetrakaidecahedron model in metal foams. J. Porous Media 2016, 19, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Xia, X.; Li, X.; Sun, C. Discrete vs. Continuum-Scale Simulation of Coupled Radiation and Convection inside Rectangular Channel Filled with Metal Foam. Int. J. Therm. Sci. 2018, 132, 219–233. [Google Scholar] [CrossRef]
- Suleiman, A.S.; Dukhan, N. Forced Convection inside Metal Foam: Simulation over a Long Domain and Analytical Validation. Int. J. Therm. Sci. 2014, 86, 104–114. [Google Scholar] [CrossRef]
- Cunsolo, S.; Iasiello, M.; Oliviero, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Lord Kelvin and Weaire–Phelan Foam Models: Heat Transfer and Pressure Drop. J. Heat Transf. 2016, 138, 022601. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Wang, H.; Qin, H.; Wen, D.; Zhou, W. Investigation of Transport Property of Fibrous Media: 3D Virtual Modeling and Permeability Calculation. Eng. Comput. 2017, 33, 997–1005. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, Q.; Liu, J.; Zhao, Y.; Zhou, W.; Deng, D. 3D Stochastic Modeling, Simulation and Analysis of Effective Thermal Conductivity in Fibrous Media. Powder Technol. 2017, 320, 397–404. [Google Scholar] [CrossRef]
- Sadeghi, E.; Bahrami, M.; Djilali, N. Analytic Determination of the Effective Thermal Conductivity of PEM Fuel Cell Gas Diffusion Layers. J. Power Sources 2008, 179, 200–208. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X.; Shen, J.; Becker, J.; Wiegmann, A. Estimating Effective Thermal Conductivity in Carbon Paper Diffusion Media. Chem. Eng. Sci. 2010, 65, 3994–4006. [Google Scholar] [CrossRef]
- Qiu, Q. Effect of Internal Defects on the Thermal Conductivity of Fiber-Reinforced Polymer (FRP): A Numerical Study Based on Micro-CT Based Computational Modeling. Mater. Today Commun. 2023, 36, 106446. [Google Scholar] [CrossRef]
- Suntharalingam, T.; Gatheeshgar, P.; Upasiri, I.; Poologanathan, K.; Nagaratnam, B.; Rajanayagam, H.; Navaratnam, S. Numerical Study of Fire and Energy Performance of Innovative Light-Weight 3D Printed Concrete Wall Configurations in Modular Building System. Sustainability 2021, 13, 2314. [Google Scholar] [CrossRef]
- Giubilini, A.; Colucci, G.; De Trane, G.; Lupone, F.; Badini, C.; Minetola, P.; Bondioli, F.; Messori, M. Novel 3D Printable Bio-Based and Biodegradable Poly(3-Hydroxybutyrate-Co-3-Hydroxyhexanoate) Microspheres for Selective Laser Sintering Applications. Mater. Today Sustain. 2023, 22, 100379. [Google Scholar] [CrossRef]
- Casini, M. Advanced Digital Design Tools and Methods. In Construction 4.0; Elsevier: Amsterdam, The Netherlands, 2022; pp. 263–334. [Google Scholar]
- Ghanavati, R.; Naffakh-Moosavy, H. Additive Manufacturing of Functionally Graded Metallic Materials: A Review of Experimental and Numerical Studies. J. Mater. Res. Technol. 2021, 13, 1628–1664. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Mitra, I.; Goodman, S.B.; Kumar, M.; Bose, S. Improving Biocompatibility for next Generation of Metallic Implants. Prog. Mater. Sci. 2023, 133, 101053. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-Weighting in Aerospace Component and System Design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Hao, C.; Sui, Y.; Yuan, Y.; Li, P.; Jin, H.; Jiang, A. Composition Optimization Design and High Temperature Mechanical Properties of Cast Heat-Resistant Aluminum Alloy via Machine Learning. Mater. Des. 2025, 250, 113587. [Google Scholar] [CrossRef]
- Sun, B.; Yan, X.; Liu, P.; Xia, Y.; Lu, L. Parametric Plate Lattices: Modeling and Optimization of Plate Lattices with Superior Mechanical Properties. Addit. Manuf. 2023, 72, 103626. [Google Scholar] [CrossRef]
- Souza Almeida, L.; Rios, P.R. Insights on the Use of Genetic Algorithm to Tessellate Voronoi Structures in Materials Science. J. Mater. Res. Technol. 2025, 34, 449–462. [Google Scholar] [CrossRef]
- Caetano, I.; Santos, L.; Leitão, A. Computational Design in Architecture: Defining Parametric, Generative, and Algorithmic Design. Front. Archit. Res. 2020, 9, 287–300. [Google Scholar] [CrossRef]
- Drezner, T.; Drezner, Z. Voronoi Diagrams with Overlapping Regions. OR Spectr. 2013, 35, 543–561. [Google Scholar] [CrossRef]
- Arvizu Alonso, A.K.; Armendáriz Mireles, E.N.; Calles Arriaga, C.A.; Rocha Rangel, E. Control of the Properties of the Voronoi Tessellation Technique and Biomimetic Patterns: A Review. Designs 2024, 8, 93. [Google Scholar] [CrossRef]
- Xu, T.; Li, M. Topological and Statistical Properties of a Constrained Voronoi Tessellation. Philos. Mag. 2009, 89, 349–374. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, B.; Wei, G.; Liu, G.; Liu, J. Parametric design, mechanical properties and permeability of biomedical porous scaffolds based on typical structure units. J. Mech. Med. Biol. 2022, 22, 2240063. [Google Scholar] [CrossRef]
- González, S.G.; Vlad, M.D.; López, J.L.; Aguado, E.F. Novel Bio-Inspired 3D Porous Scaffold Intended for Bone-Tissue Engineering: Design and in Silico Characterisation of Histomorphometric, Mechanical and Mass-Transport Properties. Mater. Des. 2023, 225, 111467. [Google Scholar] [CrossRef]
- Herath, B.; Suresh, S.; Downing, D.; Cometta, S.; Tino, R.; Castro, N.J.; Leary, M.; Schmutz, B.; Wille, M.-L.; Hutmacher, D.W. Mechanical and Geometrical Study of 3D Printed Voronoi Scaffold Design for Large Bone Defects. Mater. Des. 2021, 212, 110224. [Google Scholar] [CrossRef]
- Armendáriz-Mireles, E.N.; Raudi-Butrón, F.D.; Olvera-Carreño, M.A.; Rocha-Rangel, E. Design of Bio-Inspired Irregular Porous Structure Applied to Intelligent Mobility Products. Nexo Rev. Cient. 2023, 36, 110–121. [Google Scholar] [CrossRef]
- Chao, L.; Jiao, C.; Liang, H.; Xie, D.; Shen, L.; Liu, Z. Analysis of Mechanical Properties and Permeability of Trabecular-Like Porous Scaffold by Additive Manufacturing. Front. Bioeng. Biotechnol. 2021, 9, 779854. [Google Scholar] [CrossRef]
- Castro, A.P.G.; Ruben, R.B.; Gonçalves, S.B.; Pinheiro, J.; Guedes, J.M.; Fernandes, P.R. Numerical and Experimental Evaluation of TPMS Gyroid Scaffolds for Bone Tissue Engineering. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 567–573. [Google Scholar] [CrossRef]
- Lei, H.-Y.; Li, J.-R.; Xu, Z.-J.; Wang, Q.-H. Parametric Design of Voronoi-Based Lattice Porous Structures. Mater. Des. 2020, 191, 108607. [Google Scholar] [CrossRef]
- EN ISO 9869-1:2014; Thermal Insulation—Building Elements—In Situ Measurement of Thermal Resistance and Thermal Transmittance. Part 1: Heat Flow Meter Method; International Organization for Standardization: Geneva, Switzerland, 2014.
- Bachman, D. Grasshopper: Visual Scripting for Rhinoceros 3D; Industrial Press, Inc.: New York, NY, USA, 2017. [Google Scholar]
- Anwajler, B. Modern Insulation Materials for Sustainability Based on Natural Fibers: Experimental Characterization of Thermal Properties. Fibers 2024, 12, 76. [Google Scholar] [CrossRef]
- Anwajler, B. The Thermal Properties of a Prototype Insulation with a Gyroid Structure—Optimization of the Structure of a Cellular Composite Made Using SLS Printing Technology. Materials 2022, 15, 1352. [Google Scholar] [CrossRef] [PubMed]
- Anwajler, B.; Szulc, P. The Impact of 3D Printing Technology on the Improvement of External Wall Thermal Efficiency—An Experimental Study. J. Compos. Sci. 2024, 8, 389. [Google Scholar] [CrossRef]
- Anwajler, B.; Szkudlarek, M. Właściwości Cieplne Materiałów o Strukturze TPMS Wykonanych w Technologii Druku Addytywnego SLS. Rynek Energii 2023, 1, 11–20. [Google Scholar]
- Anwajler, B.; Szołomicki, J.; Noszczyk, P. Application of a Gyroid Structure for Thermal Insulation in Building Construction. Materials 2024, 17, 6301. [Google Scholar] [CrossRef]
- Anwajler, B.; Szołomicki, J.; Noszczyk, P.; Baryś, M. The Potential of 3D Printing in Thermal Insulating Composite Materials—Experimental Determination of the Impact of the Geometry on Thermal Resistance. Materials 2024, 17, 1202. [Google Scholar] [CrossRef]
- Anwajler, B.; Zielińska, S.; Witek-Krowiak, A. Innovative Cellular Insulation Barrier on the Basis of Voronoi Tessellation—Influence of Internal Structure Optimization on Thermal Performance. Materials 2024, 17, 1578. [Google Scholar] [CrossRef]









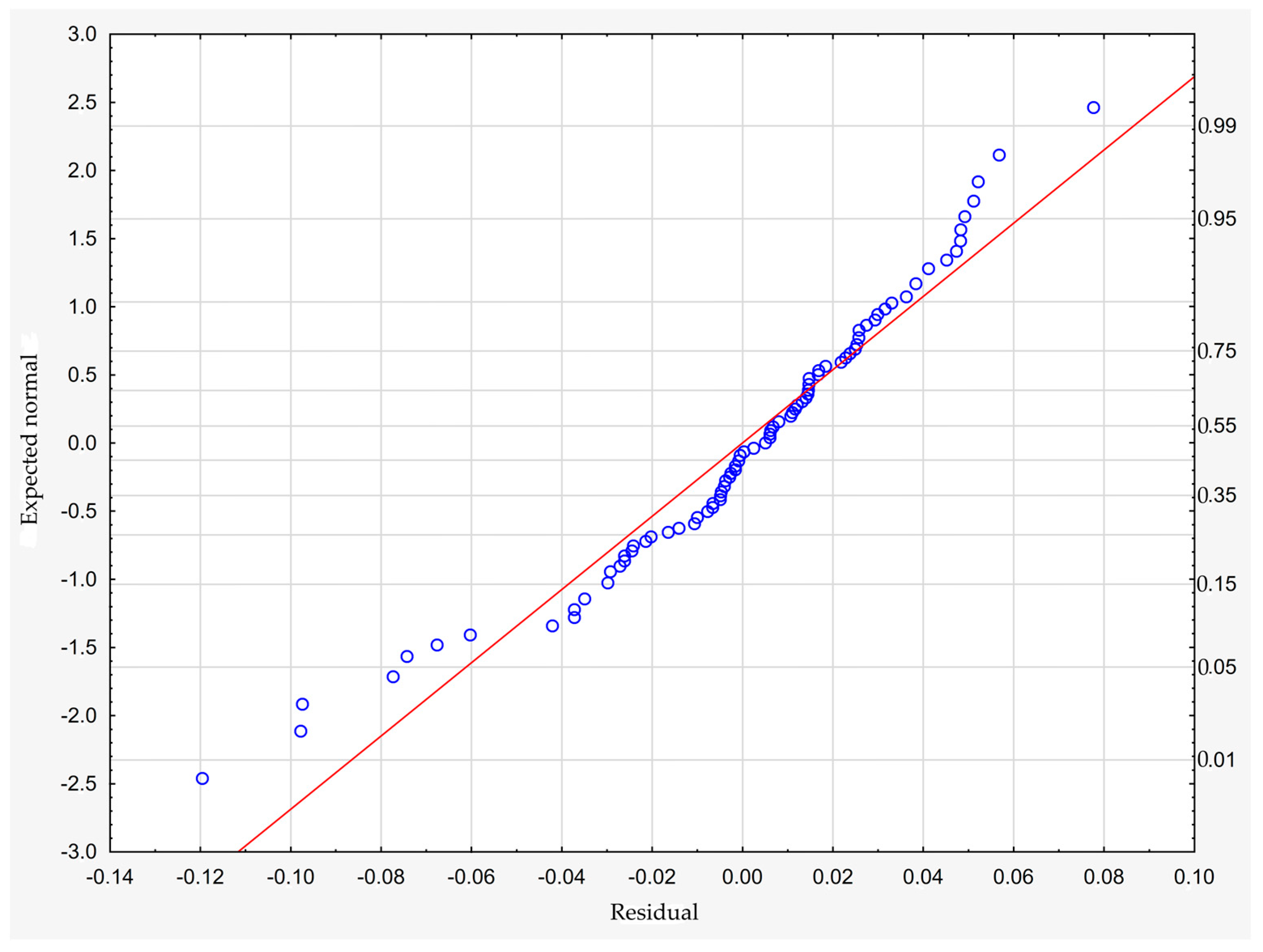
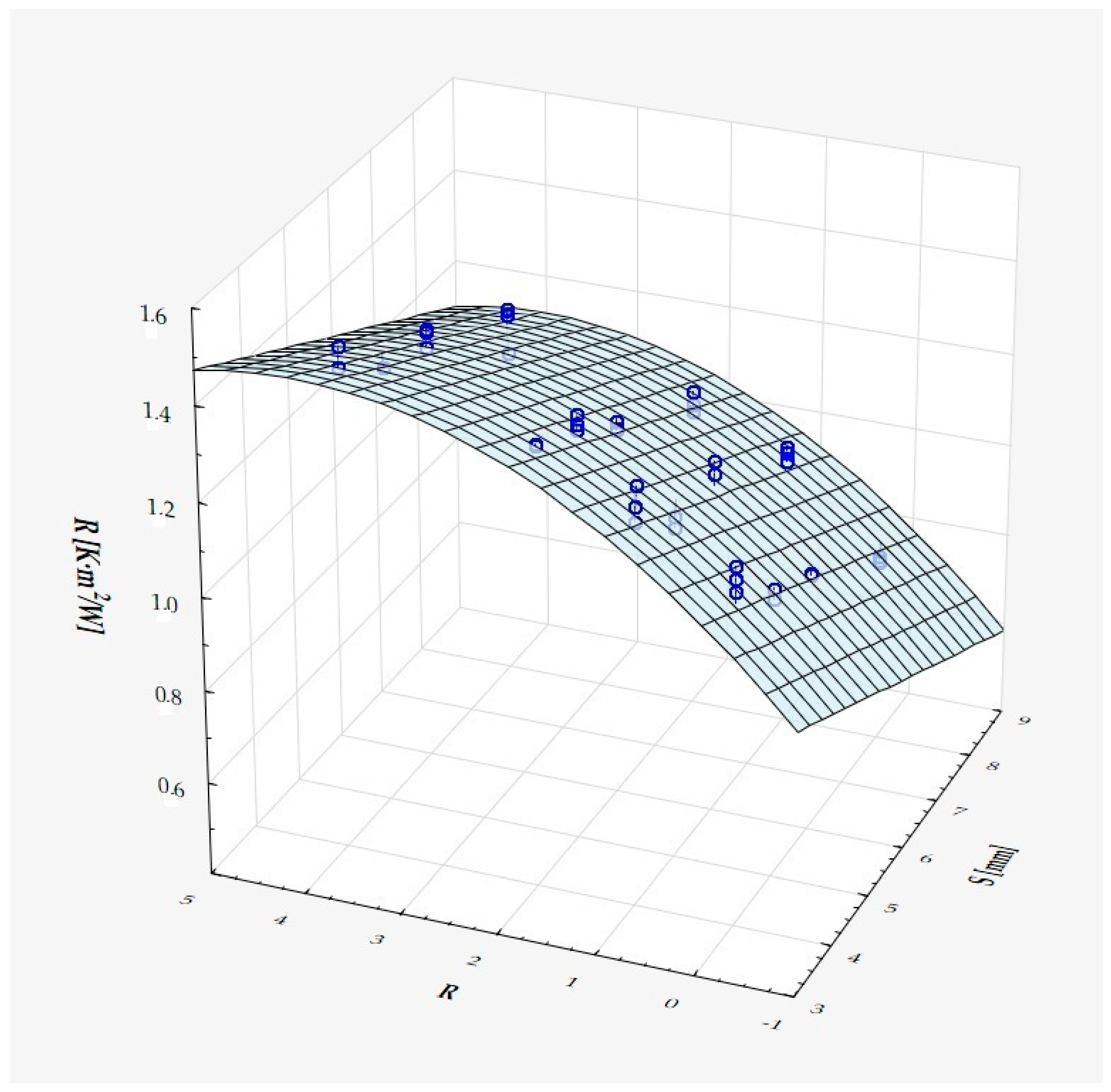
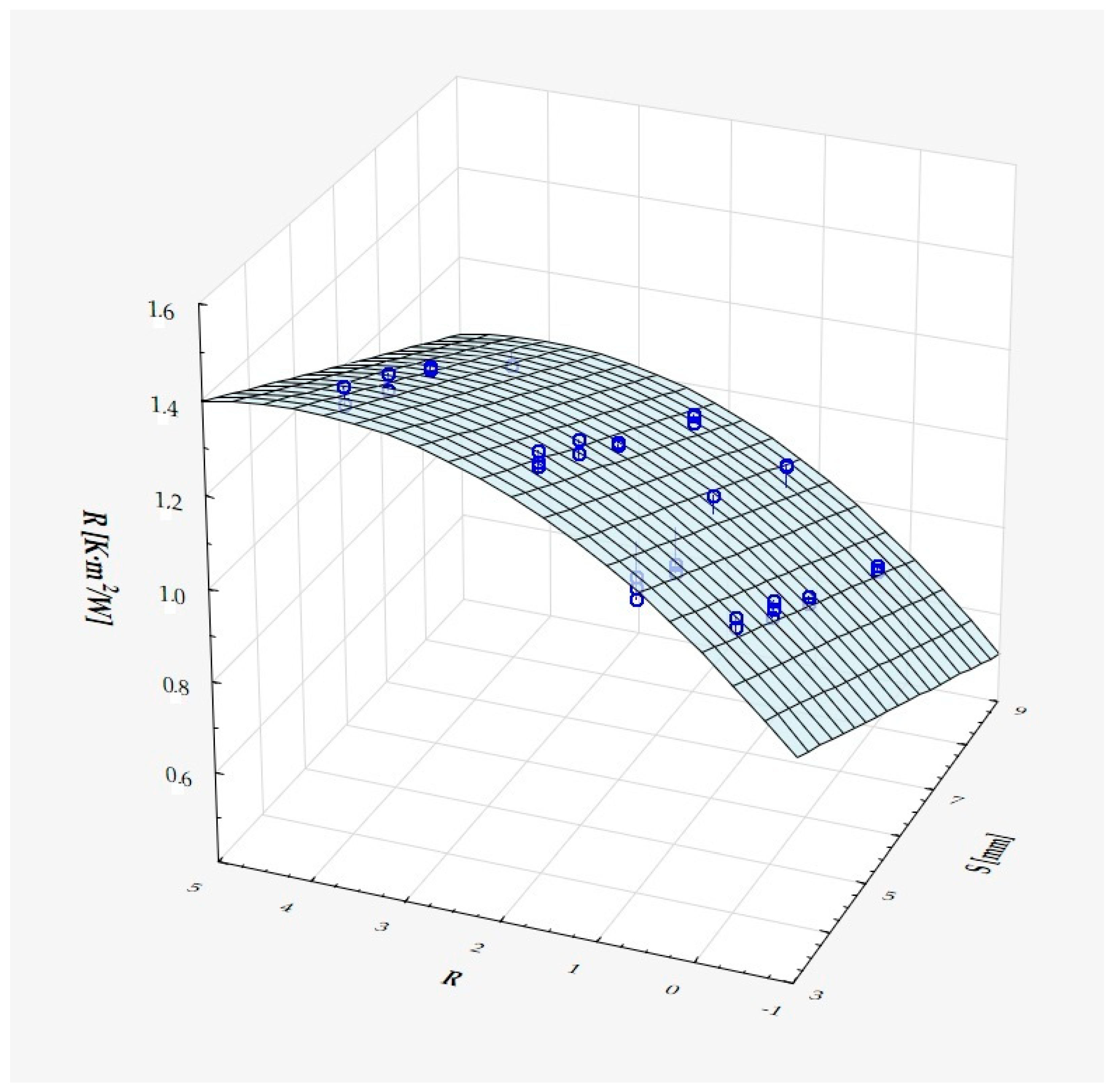
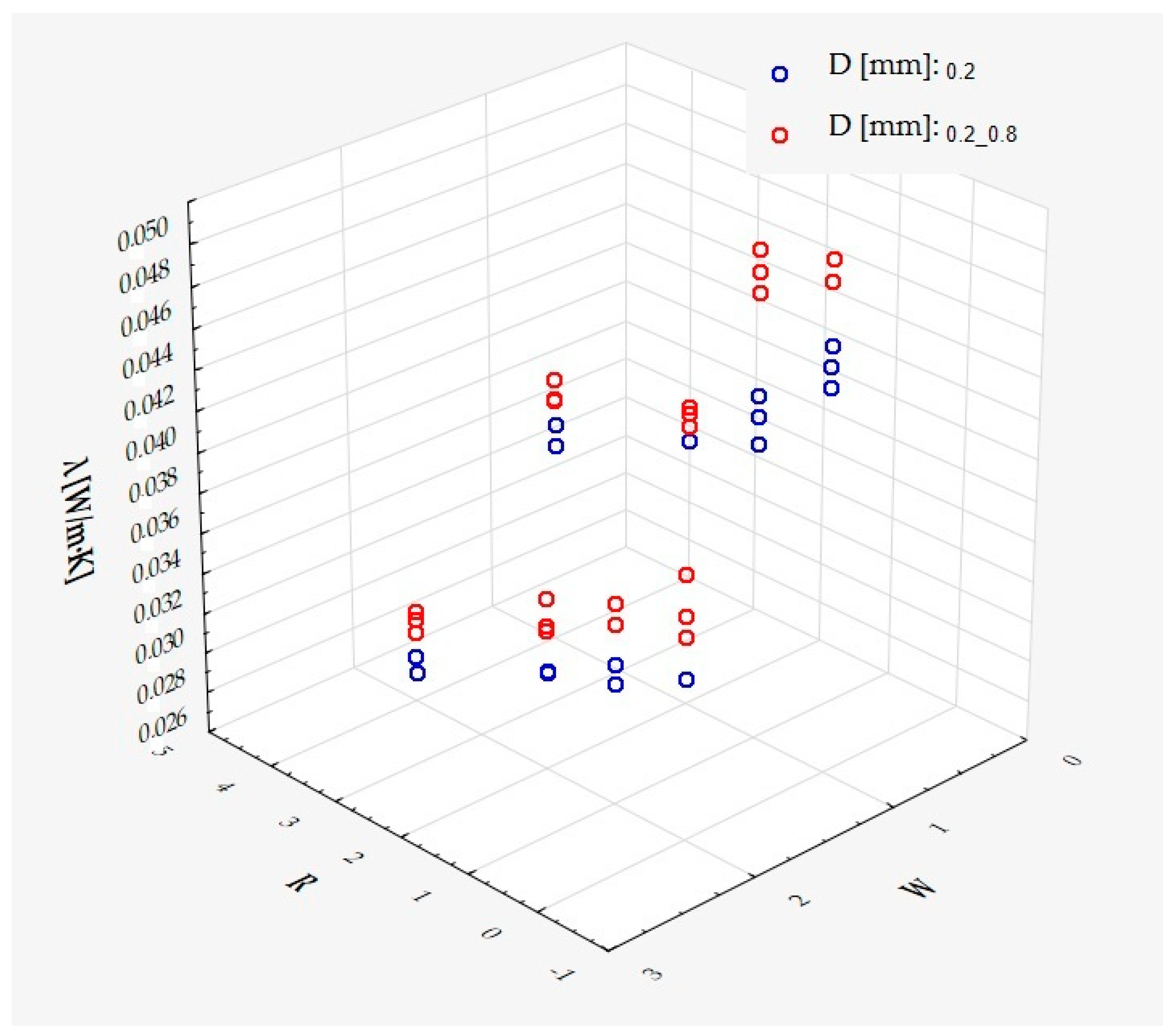
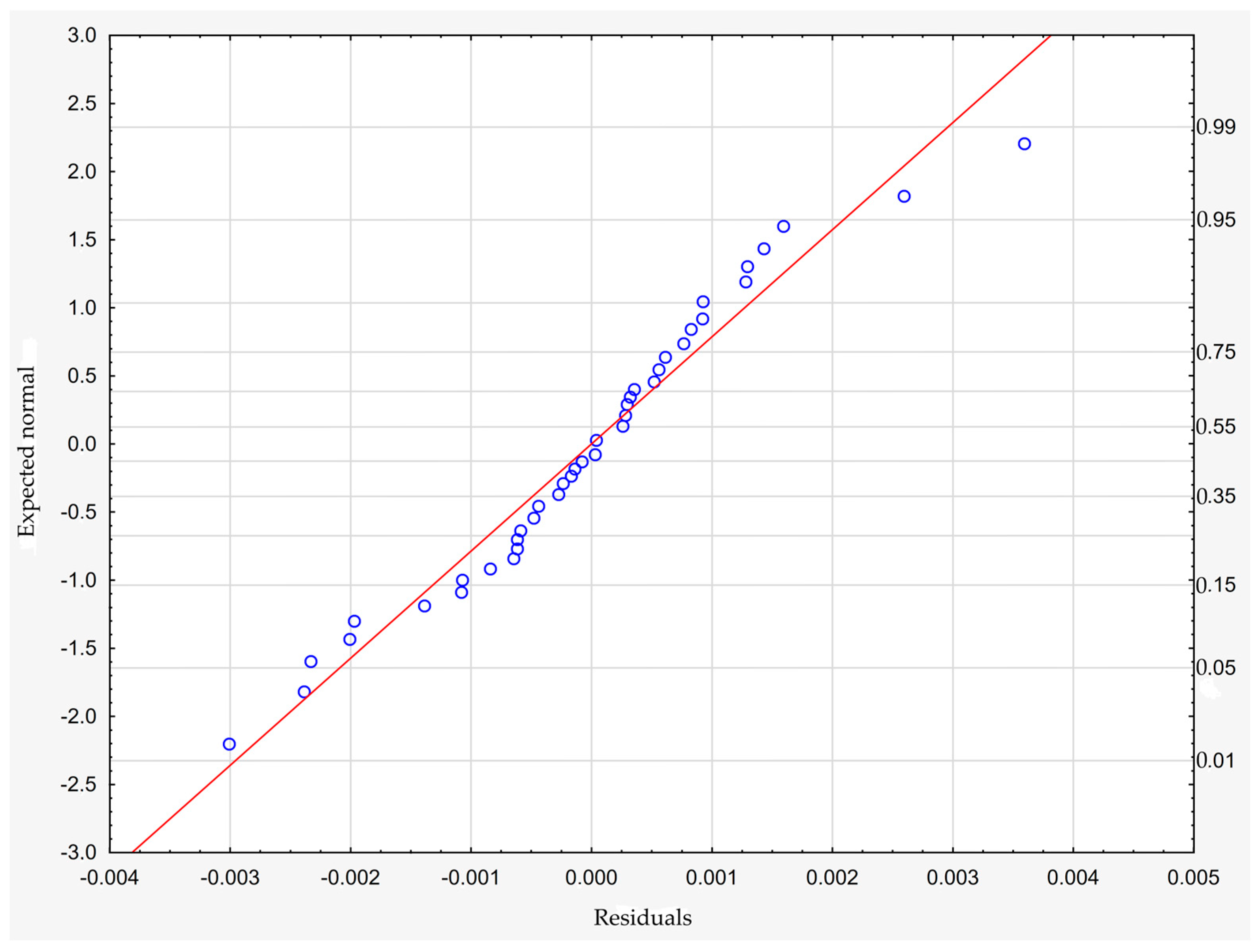
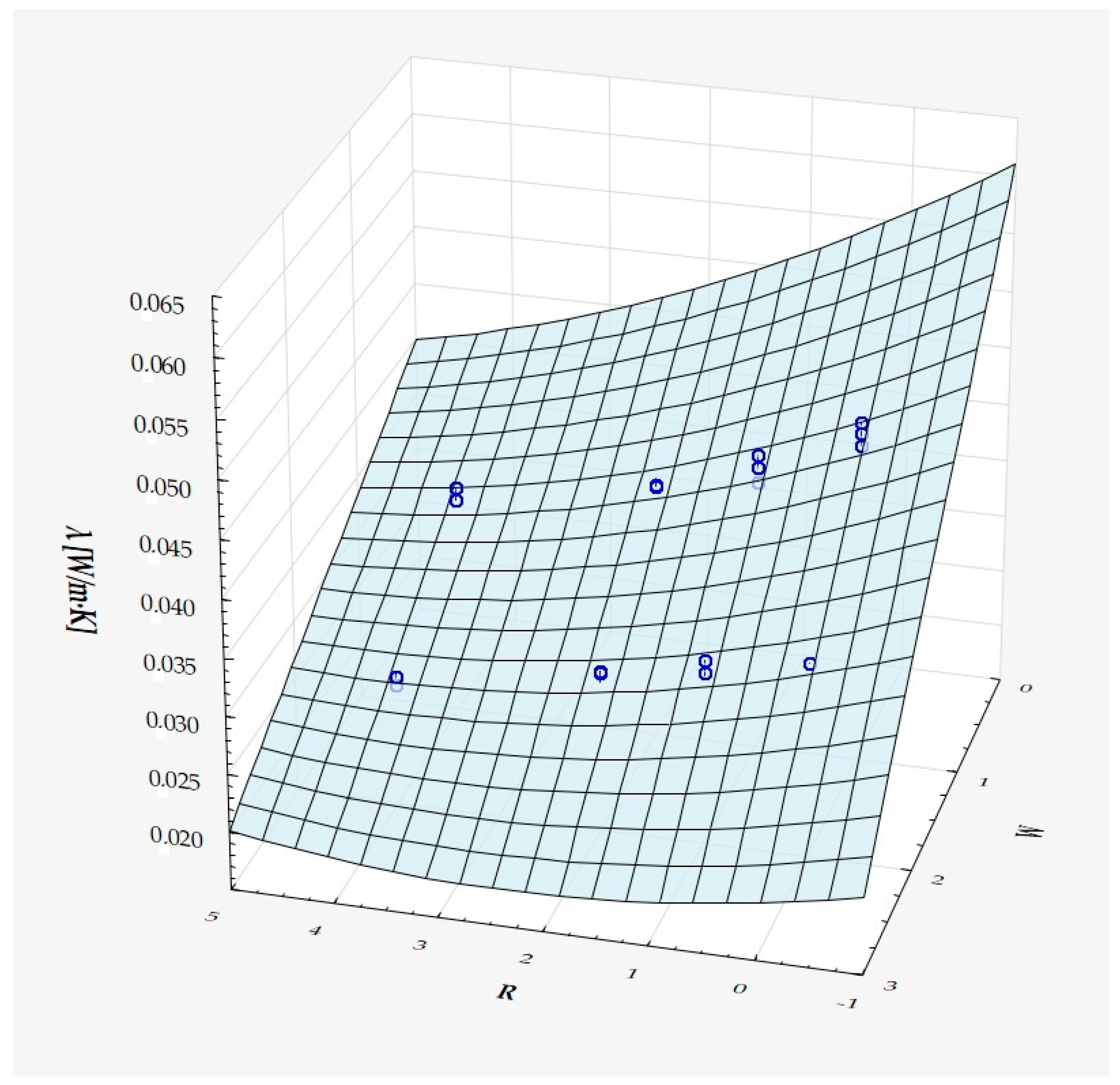

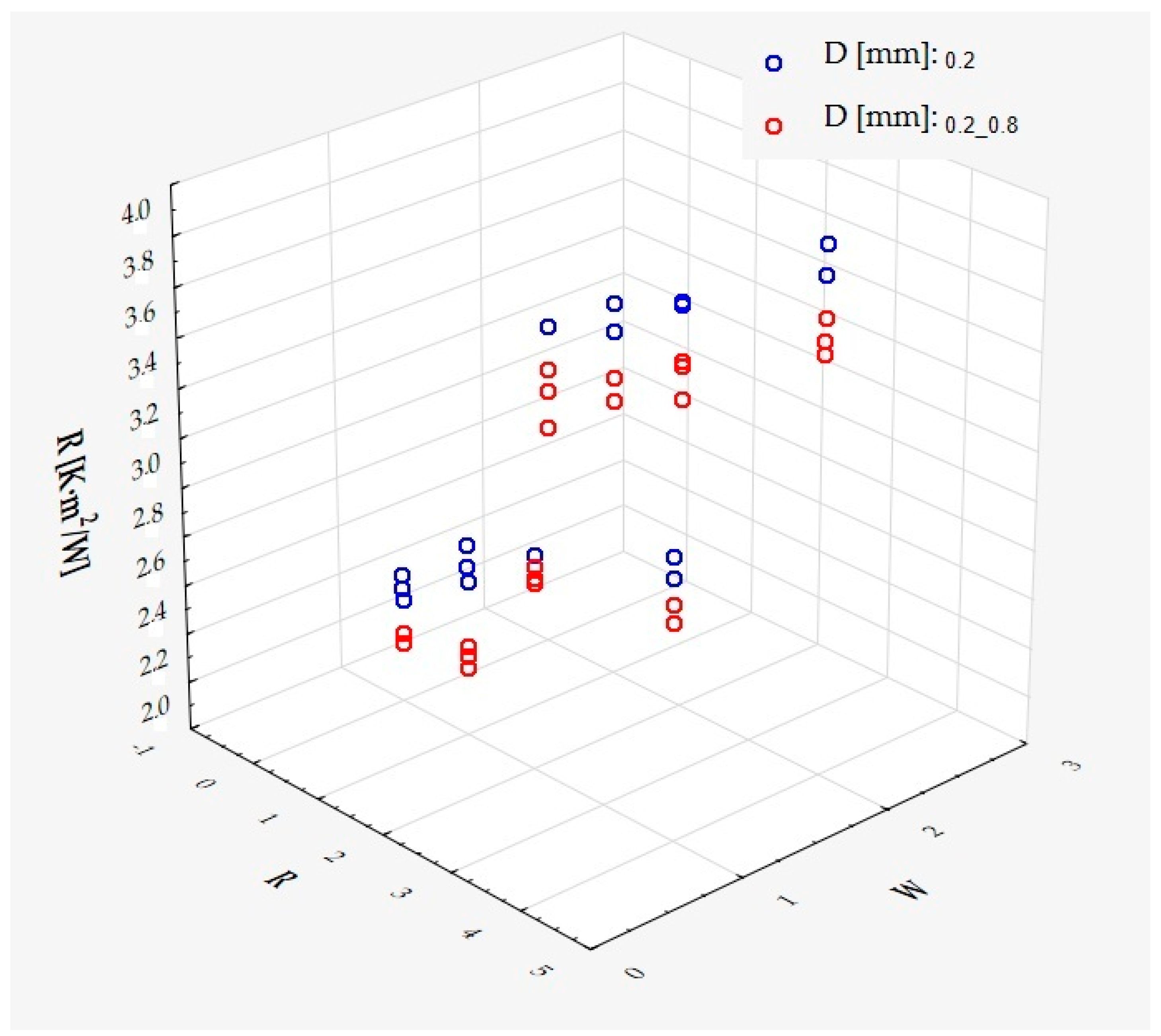

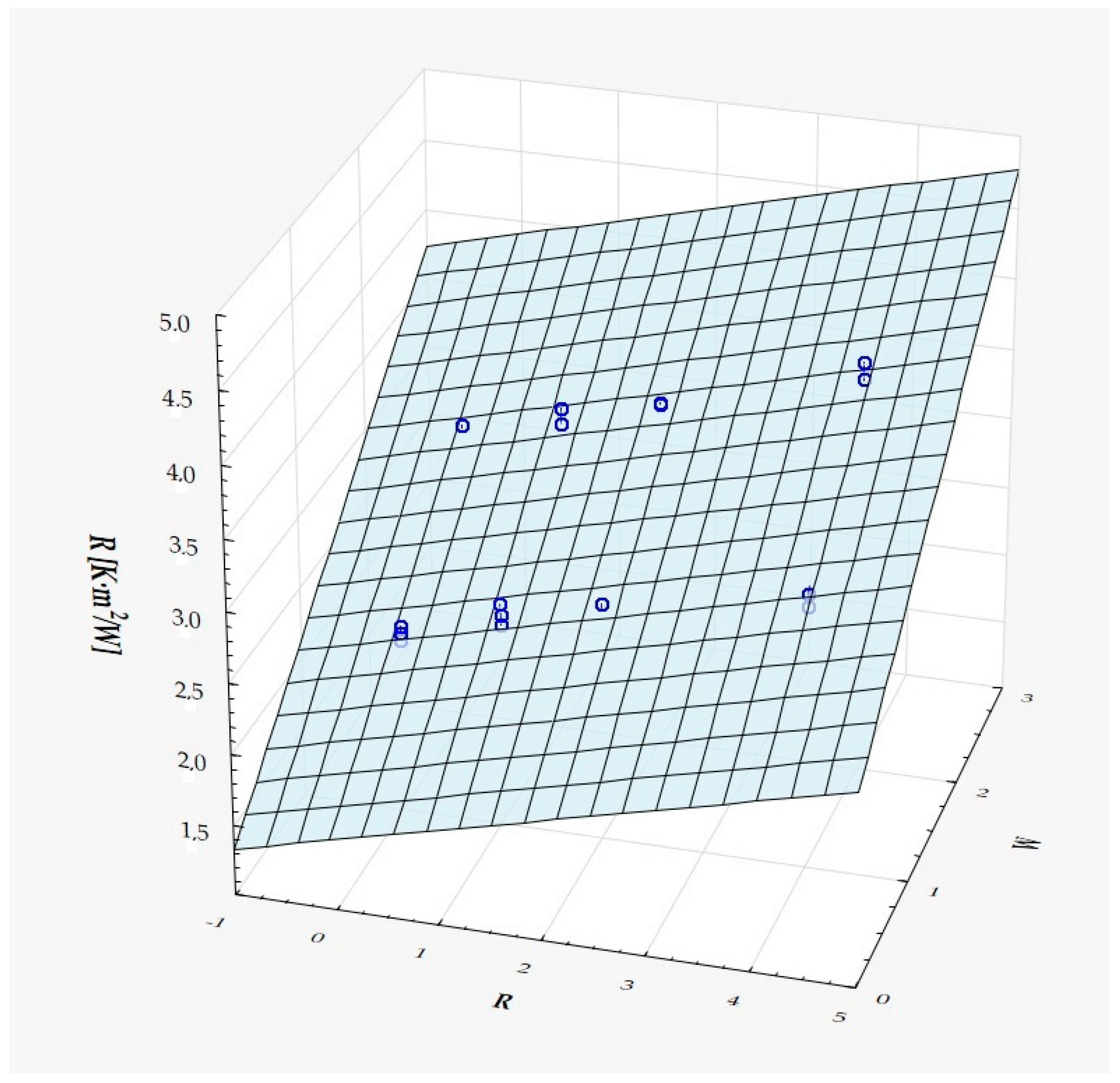
| M | Me | Min | Max | SD | Sk | K | |
|---|---|---|---|---|---|---|---|
| λ, W/(m·K) | 0.045 | 0.044 | 0.034 | 0.066 | 0.0073 | 0.901 | 0.673 |
| M | Me | Min | Max | SD | Sk | K | |
|---|---|---|---|---|---|---|---|
| R, (m2·K)/W | 1.127 | 1.125 | 0.757 | 1.471 | 0.167 | −0.178 | −0.575 |
| M | Me | Min | Max | SD | Sk | K | |
|---|---|---|---|---|---|---|---|
| λ, W/(m·K) | 0.036 | 0.035 | 0.026 | 0.049 | 0.007 | 0.542 | −0.529 |
| M | Me | Min | Max | SD | Sk | K | |
|---|---|---|---|---|---|---|---|
| R, (m2·K)/W | 2.88 | 2.86 | 2.04 | 3.92 | 0.50 | 0.10 | −0.72 |
| Symbol That Identifies the Input Factors and Their Interactions | SS | df | MS | F | p |
|---|---|---|---|---|---|
| λ, W/(m·K) | |||||
| Absolute term | 1 | 0.1979 | 0.197997 | 422,809.7 | 0.000 |
| S | 3 | 0.0016 | 0.000520 | 1111.3 | 0.000 |
| D | 1 | 0.000221 | 0.000221 | 472.1 | 0.000 |
| R | 3 | 0.002895 | 0.000965 | 2060.7 | 0.000 |
| S*D | 3 | 0.000004 | 0.000001 | 3.1 | 0.034 |
| S*R | 9 | 0.00024 | 0.000027 | 57.6 | 0.000 |
| D*R | 3 | 0.000023 | 0.000008 | 16.5 | 0.000 |
| S*D*R | 9 | 0.00003 | 0.000003 | 6.8 | 0.000 |
| Error | 64 | 0.00003 | 0.000 | ||
| General | 95 | 0.005 | |||
| R, (m2·K)/W | |||||
| Absolute term | 1 | 121.9009 | 121.90 | 371,490.6 | 0.000 |
| S | 3 | 0.8331 | 0.278 | 846.2 | 0.000 |
| D | 1 | 0.1340 | 0.134 | 408.5 | 0.000 |
| R | 3 | 1.5610 | 0.52 | 1585.7 | 0.000 |
| S*D | 3 | 0.0084 | 0.003 | 8.5 | 0.000 |
| S*R | 9 | 0.0533 | 0.006 | 18.0 | 0.000 |
| D*R | 3 | 0.0086 | 0.003 | 8.7 | 0.000 |
| S*D*R | 9 | 0.0179 | 0.002 | 6.1 | 0.000 |
| Error | 64 | 0.0210 | 0.0003 | ||
| General | 95 | 2.6373 | |||
| Symbol That Identifies the Input Factors and Their Interactions | SS | df | MS | F | p |
|---|---|---|---|---|---|
| λ, W/(m·K) | |||||
| Absolute term | 1 | 0.061408 | 0.061408 | 110,436.1 | 0.000 |
| D | 1 | 0.000128 | 0.000128 | 229.7 | 0.000 |
| R | 3 | 0.000520 | 0.000173 | 311.5 | 0.000 |
| W | 1 | 0.001227 | 0.001227 | 2206.2 | 0.000 |
| D*R | 3 | 0.000021 | 0.000007 | 12.7 | 0.000 |
| D*W | 1 | 0.000003 | 0.000003 | 5.5 | 0.025 |
| R*W | 3 | 0.000050 | 0.000017 | 30.2 | 0.000 |
| D*R*W | 3 | 0.000013 | 0.000004 | 7.5 | 0.000 |
| Error | 32 | 0.000018 | 0.000001 | ||
| General | 47 | 0.001979 | |||
| R, (m2·K)/W | |||||
| Absolute term | 1 | 399.1361 | 399.1361 | 117,304.8 | 0.000000 |
| D | 1 | 0.7508 | 0.7508 | 220.7 | 0.000000 |
| R | 3 | 3.1676 | 1.0559 | 310.3 | 0.000000 |
| W | 1 | 7.7174 | 7.7174 | 2268.1 | 0.000000 |
| D*R | 3 | 0.0386 | 0.0129 | 3.8 | 0.019845 |
| D*W | 1 | 0.0183 | 0.0183 | 5.4 | 0.026964 |
| R*W | 3 | 0.0785 | 0.0262 | 7.7 | 0.000525 |
| D*R*W | 3 | 0.0323 | 0.0108 | 3.2 | 0.037636 |
| Error | 32 | 0.1089 | 0.0034 | ||
| General | 47 | 11.9125 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwajler, B. Application of Voronoi Tessellation to the Additive Manufacturing of Thermal Barriers of Irregular Porous Materials—Experimental Determination of Thermal Properties. Materials 2025, 18, 1873. https://doi.org/10.3390/ma18081873
Anwajler B. Application of Voronoi Tessellation to the Additive Manufacturing of Thermal Barriers of Irregular Porous Materials—Experimental Determination of Thermal Properties. Materials. 2025; 18(8):1873. https://doi.org/10.3390/ma18081873
Chicago/Turabian StyleAnwajler, Beata. 2025. "Application of Voronoi Tessellation to the Additive Manufacturing of Thermal Barriers of Irregular Porous Materials—Experimental Determination of Thermal Properties" Materials 18, no. 8: 1873. https://doi.org/10.3390/ma18081873
APA StyleAnwajler, B. (2025). Application of Voronoi Tessellation to the Additive Manufacturing of Thermal Barriers of Irregular Porous Materials—Experimental Determination of Thermal Properties. Materials, 18(8), 1873. https://doi.org/10.3390/ma18081873






