Analysis of the Damage and Failure Mechanism of Q345 Steel Plate with Initial Defect Under Different Temperature Conditions by Peridynamics
Abstract
1. Introduction
2. Basic Theory
2.1. Thermophysical and Thermodynamic Properties
- (1)
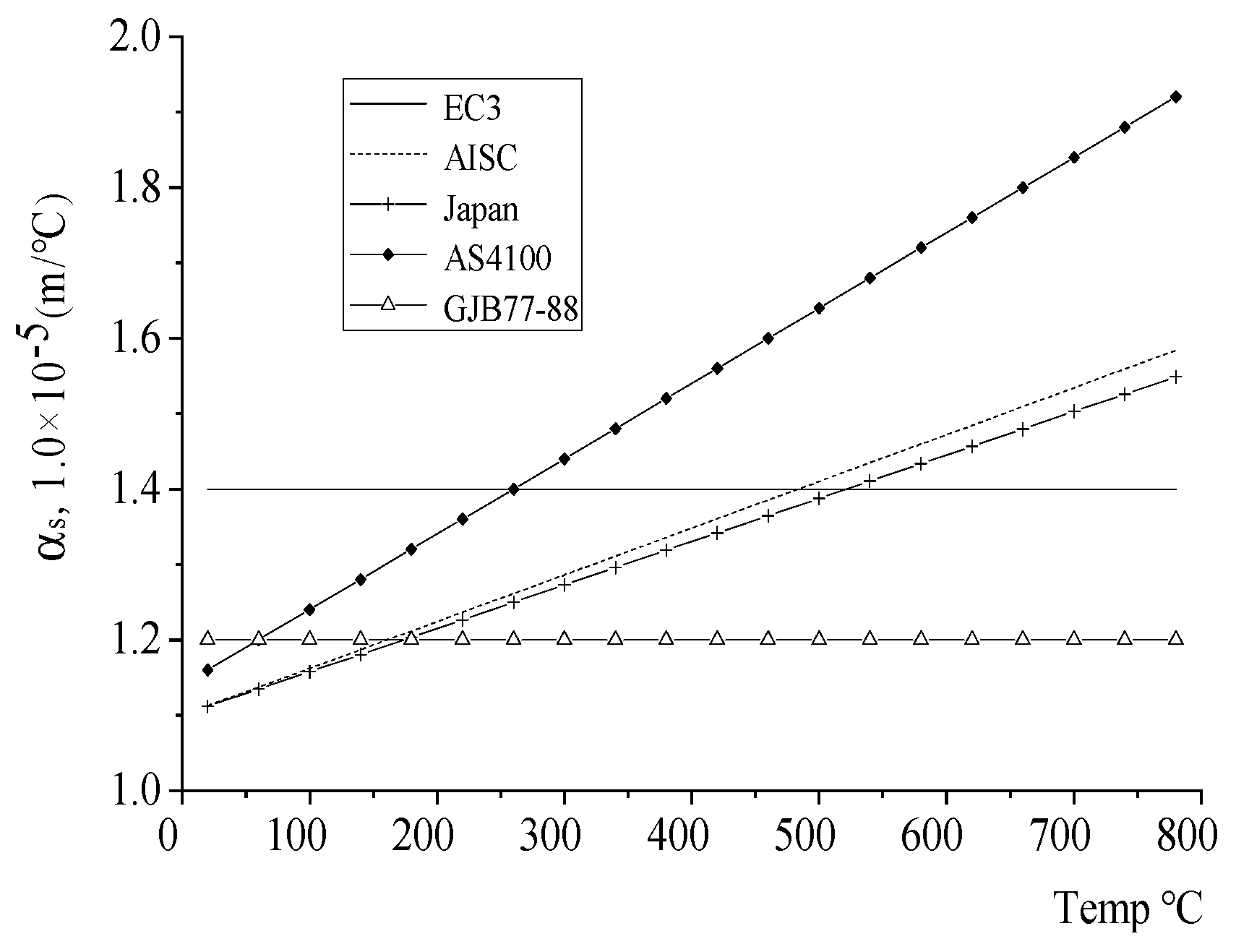
- Thermal expansion coefficient
- (2)
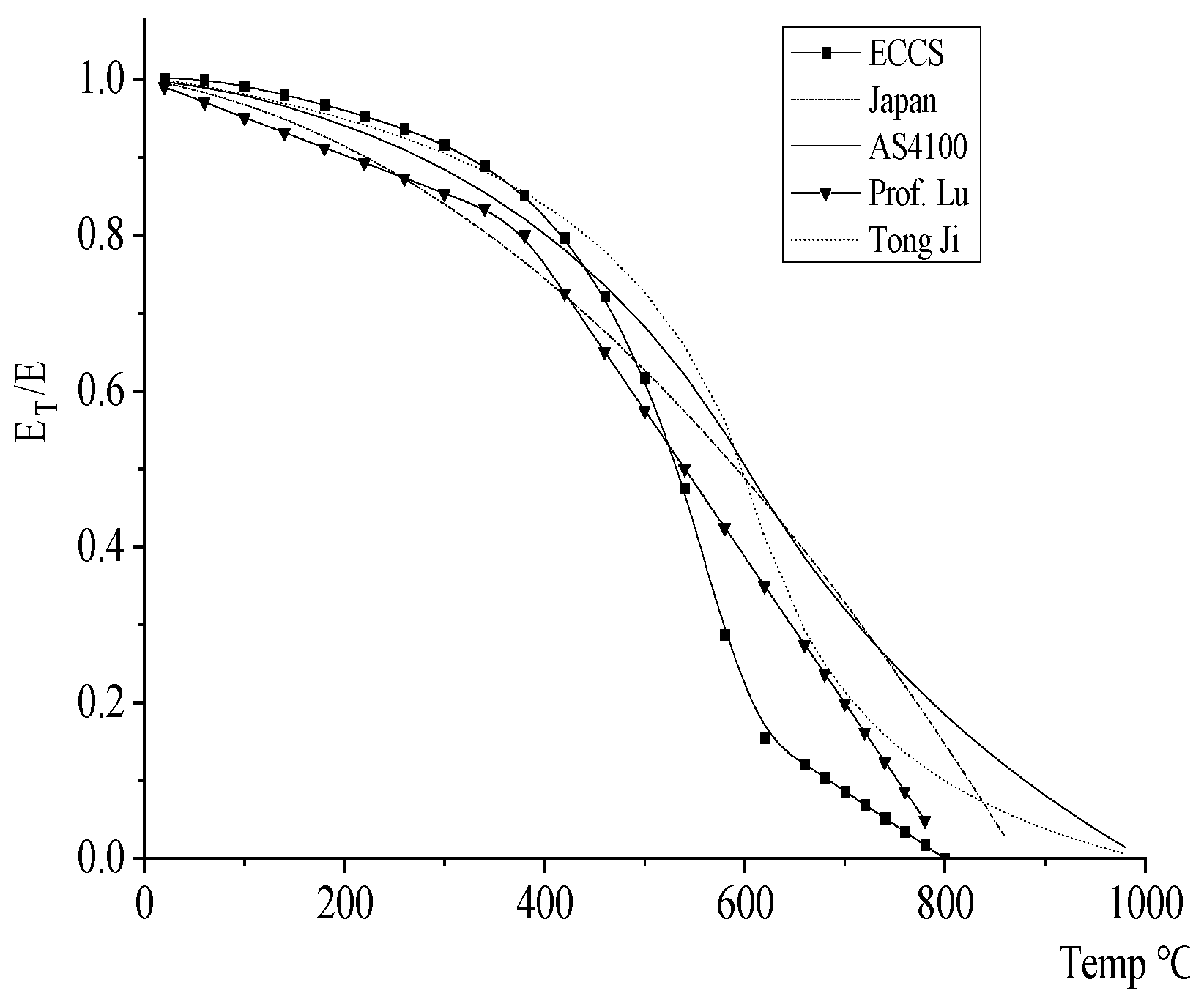
- Elastic mode reduction coefficient
- (3)
- Density
- (4)
- Poisson’s ratio
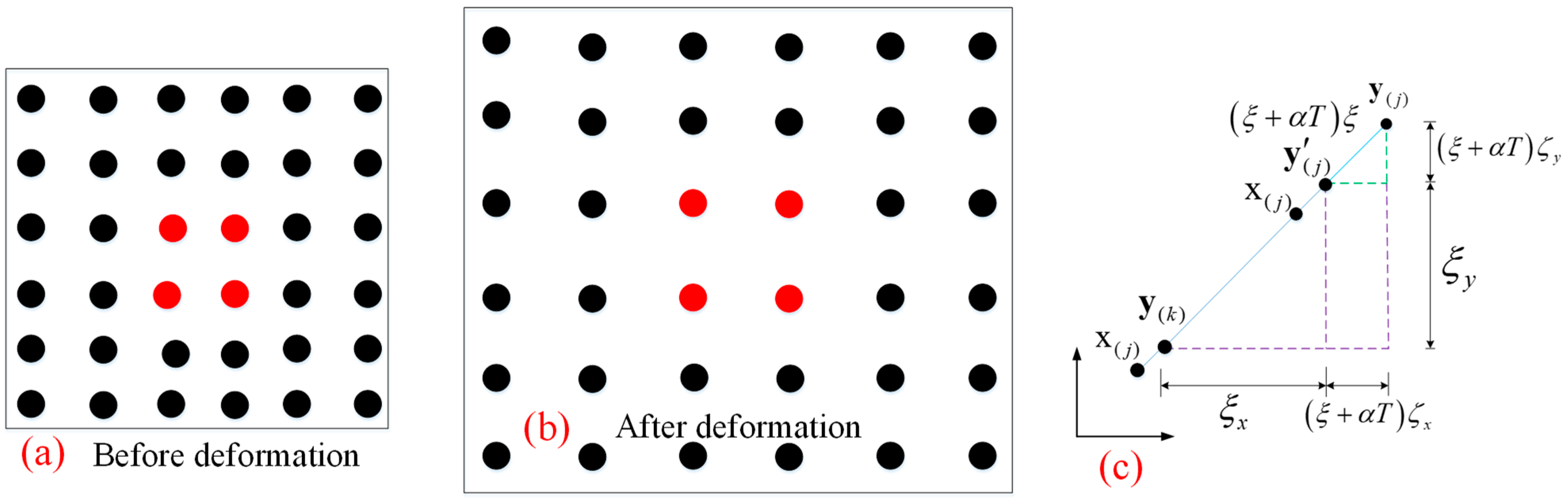
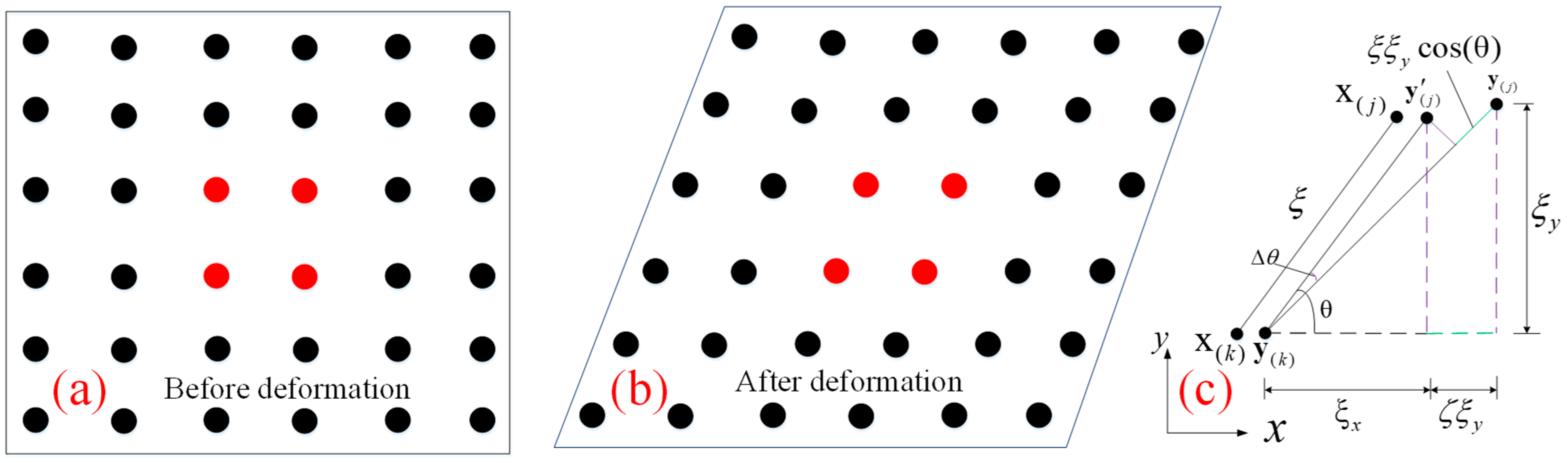
2.2. Basic Theory of PD
2.3. Elastic Crack Propagation Model
3. Damage and Failure Mechanism of Q345 Steel Plates with Bilateral Crack and Bolt Holes Under Temperature
3.1. Analysis of the Influence of Bilateral Cracks on Crack Propagation Path
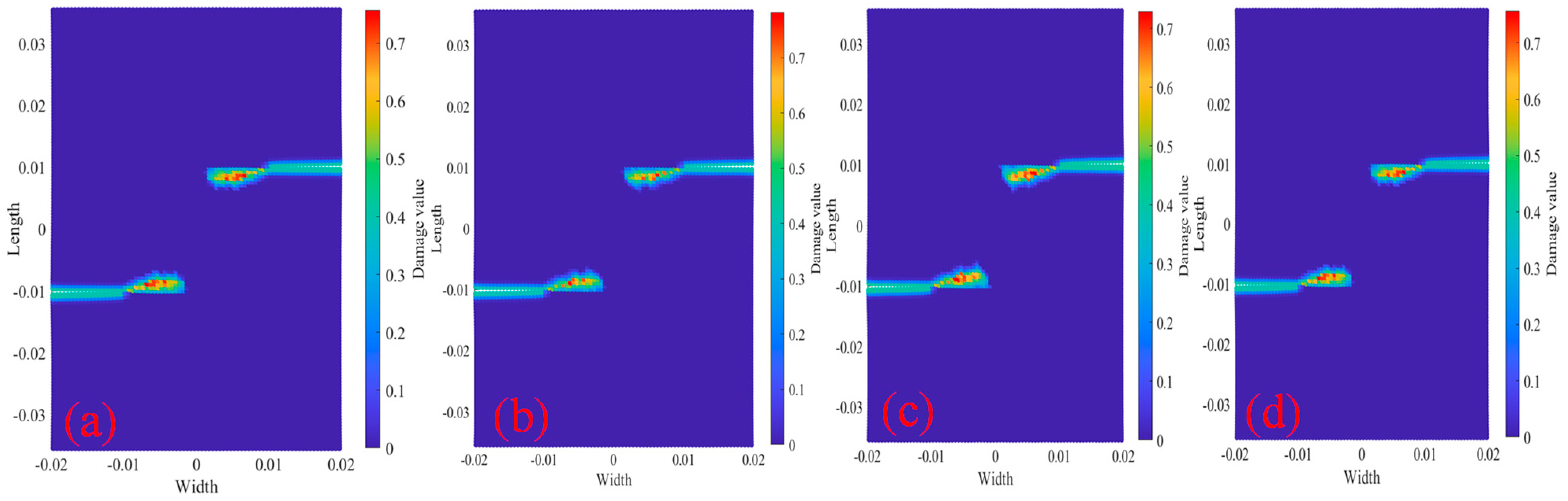
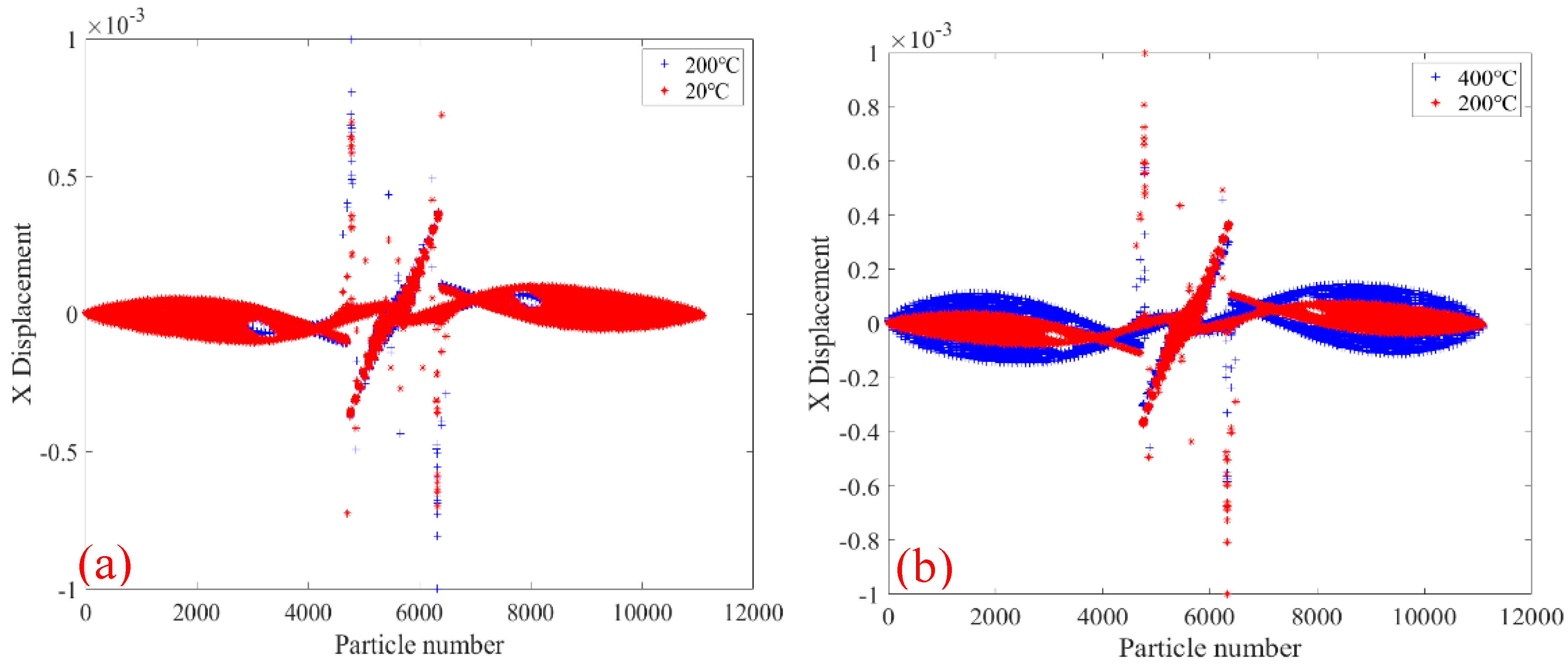
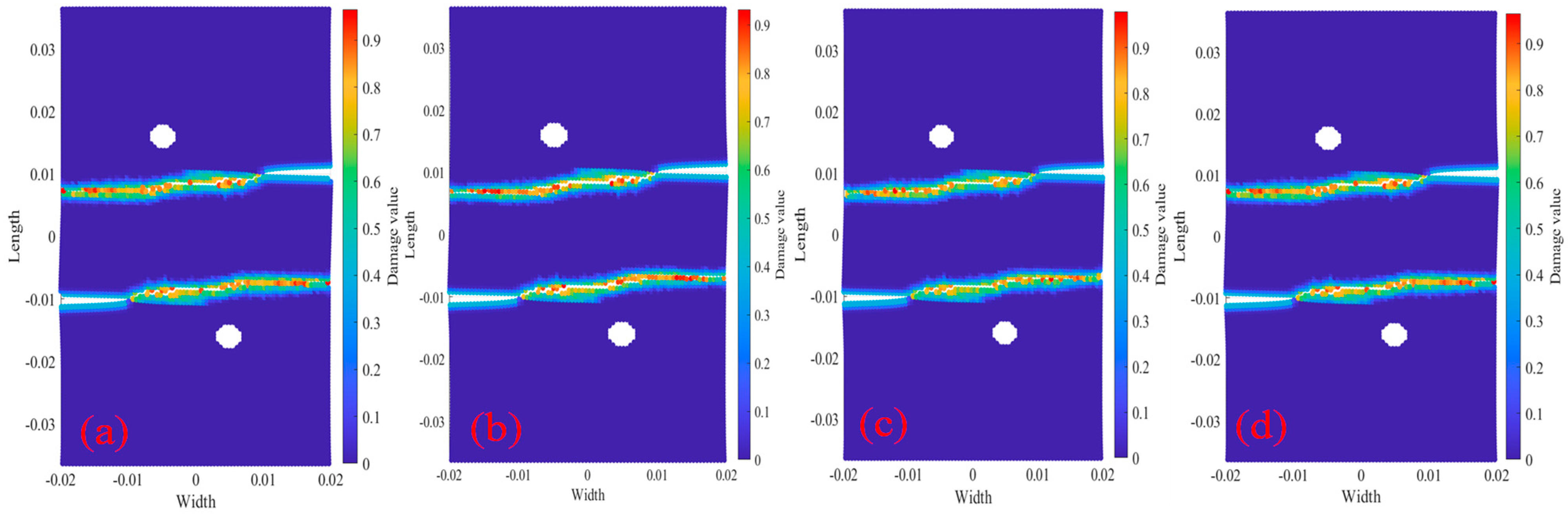
3.2. The Relationship Between Temperature and Crack Pacing on the Crack Paths
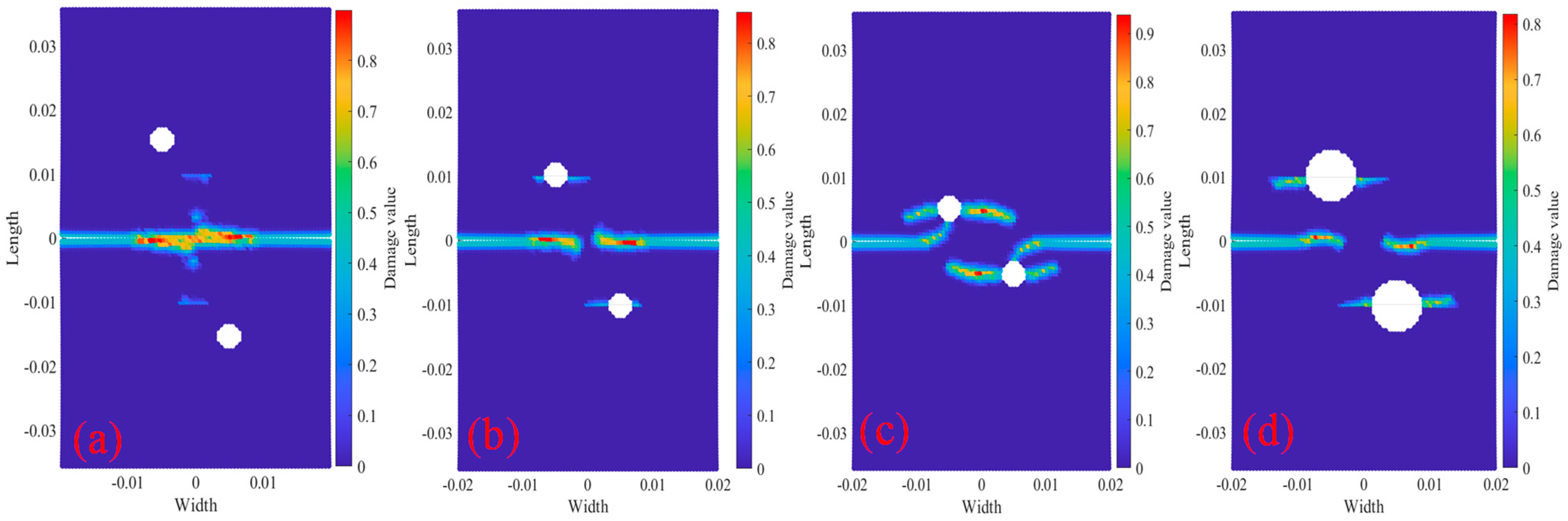
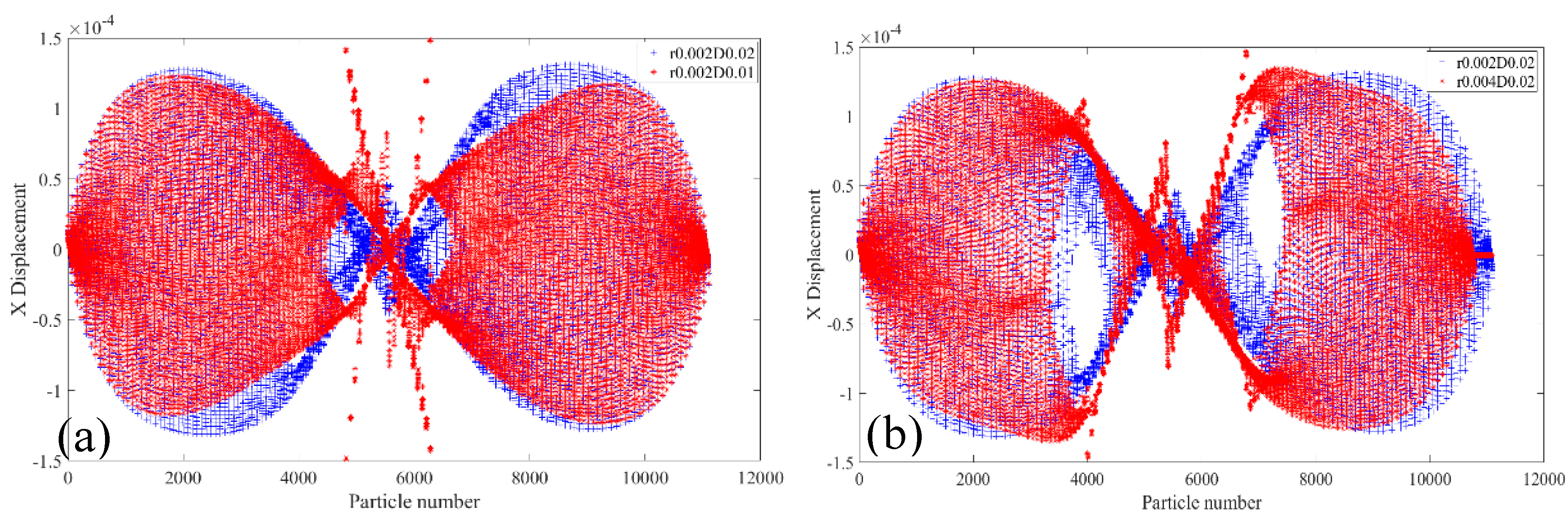
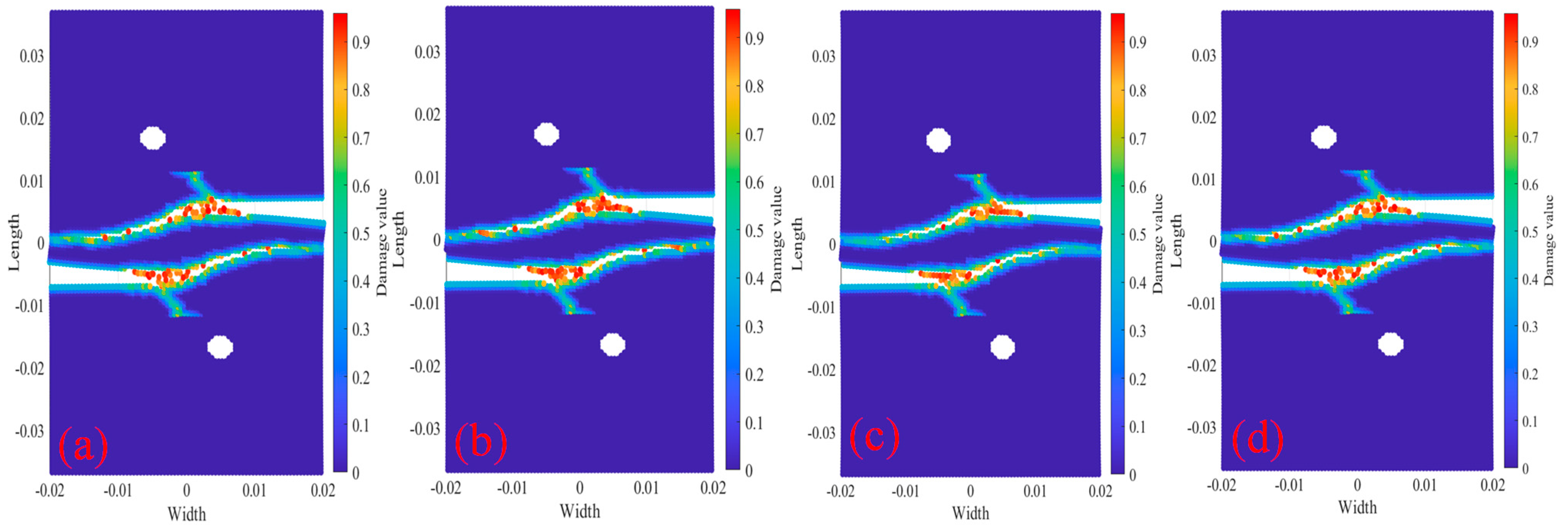
3.3. The Relationship Between Temperature and Bolt Holes on the Crack Paths
4. Conclusions
- At room temperature 20 °C, the tests with bilateral crack longitudinal spacing of 0 mm, 10 mm, and 20 mm, showed crack propagation forming into a horizontal crack, a 45° oblique crack and two horizontal penetration cracks. It shows that the longitudinal crack spacing has a great influence on the crack propagation path.
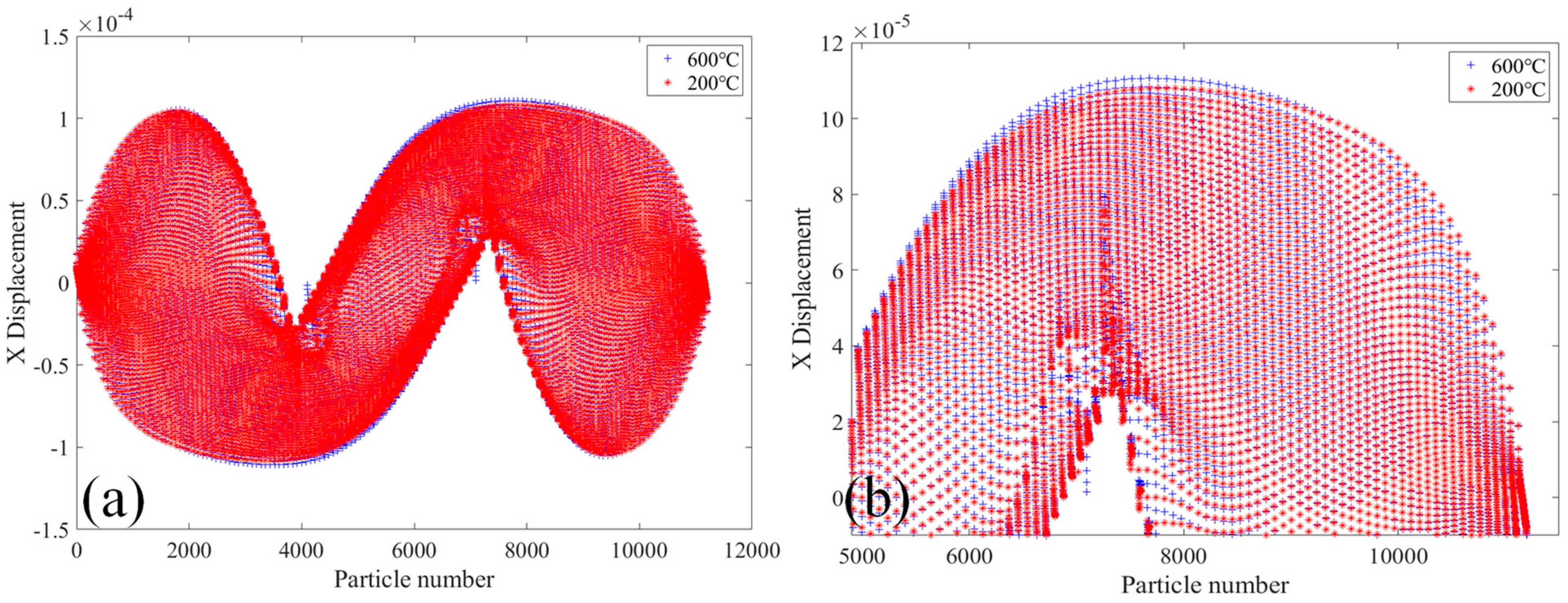
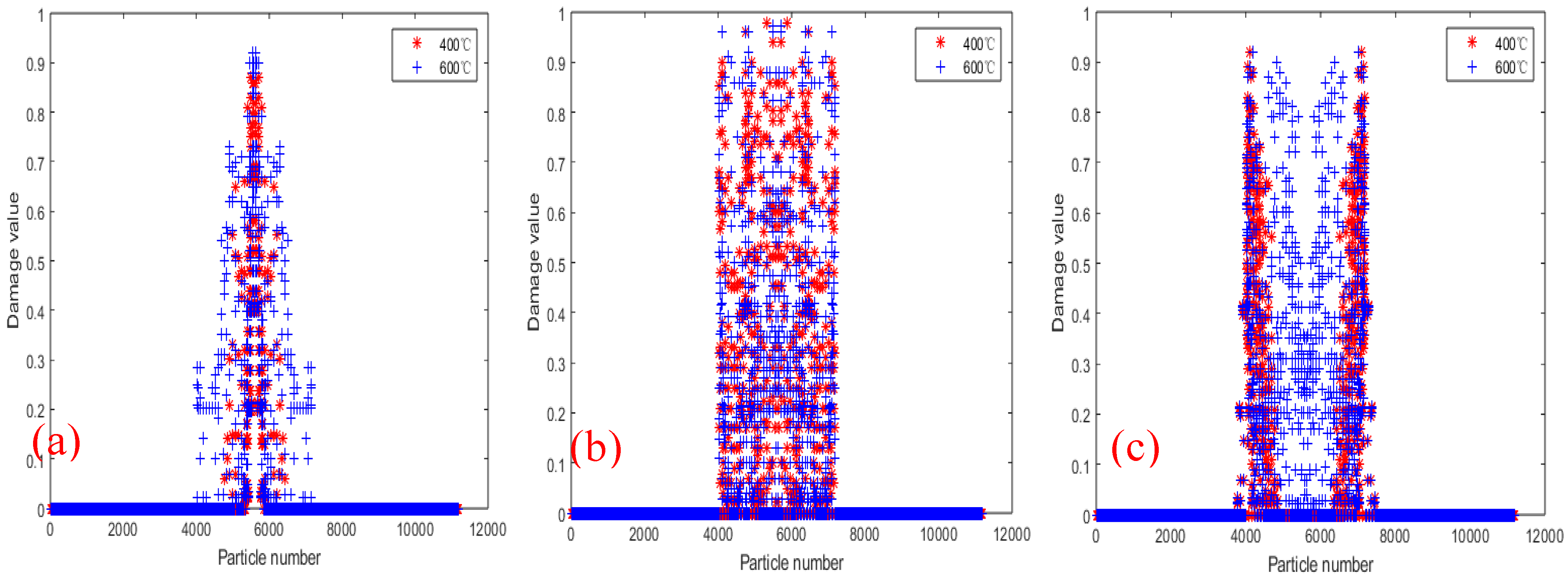
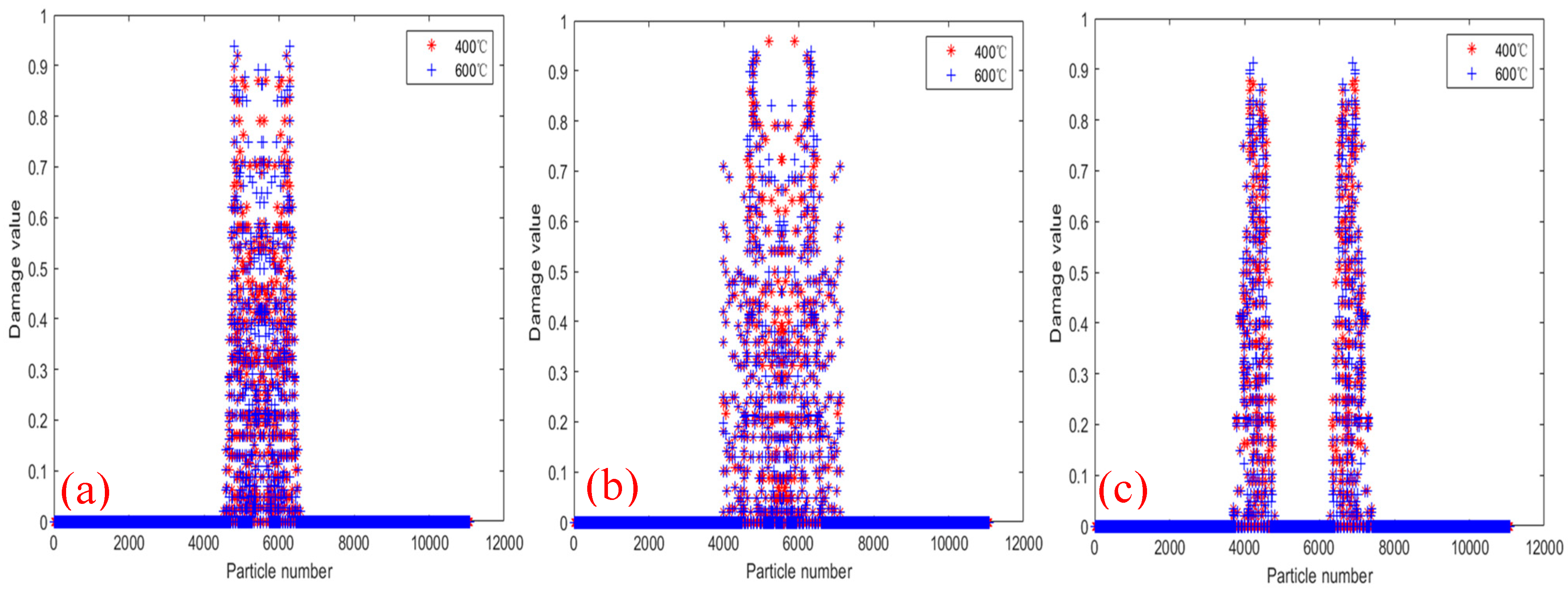
- The damage and crack propagation path of the same tests under different temperatures are basically the same, but the particle damage rate is different. It can be seen that the temperature has relatively little influence on the crack propagation path, but has a greater influence on the material damage rate, and the higher the temperature is, the faster the damage rate will be.
- Under the same initial crack conditions and different bolt holes, the damage, PD particle displacement in X- or Y-direction and crack growth path of the specimen changed greatly. The results show that the location and radius of bolt hole have great influence on the damage, PD particle displacement and crack propagation path.
- Through the results of temperature and bolt holes on the crack propagation rate and path of the tests, it can be concluded that a reasonable bolt hole radius and position are very important to the bearing capacity of steel structures.
- As the temperature increases, the material properties of the steel are reduced, resulting in a decrease in the bearing capacity of the steel structure. Therefore, under the action of load, the higher the temperature, the larger the damage value of the specimen, and the damage parts will also be greatly different. At the same time, the displacement values in the X-direction and the Y-direction change faster under high temperature than under normal temperature. Therefore, steel structure buildings need to take fire protection measures to delay the heating rate of the structure under the action of temperature, and to improve the bearing capacity and the safety performance of the structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
Nomenclature
| PD parameters at room temperature [Dimensionless quantity] | |
| PD parameters at high temperature [Dimensionless quantity] | |
| Coefficient of thermal expansion of steel [Dimensionless quantity] | |
| Body load vectors at particle [N/m3] | |
| Two-dimensional material property matrix [GPa] | |
| Elastic modulus of steel at normal temperature and high temperature [GPa] | |
| Bulk modulus [GPa] | |
| The time of the fire burns [s] | |
| The temperature varies with the fire [°C] | |
| Internal temperature of steel structure [°C] | |
| The sum of the kinetic energy of the object, or temperature load [J, °C] | |
| Shear modulu [GPa] | |
| The displacement vector of particle i [m/s] | |
| The acceleration of particle [m/s2] | |
| The sum of the potential energy of the object [J] | |
| Poisson’s ratio of steel [Dimensionless quantity] | |
| The volume of particle j [m3] | |
| Micro-potential energy depends on the state of material points within the family of material point and [J/m3] | |
| The strain energy density of particle [J/m3] | |
| Particle or Displacement in x direction [m] | |
| The deformed coordinate of particle [m] | |
| The radius of the particle force [m] | |
| Density of steel [kg/m3] | |
| Positive strain [Dimensionless quantity] | |
| , | The stress and strain of the object [MPa] |
| Expansion term [Dimensionless quantity] | |
| PD | Peridynamics |
References
- Li, G.; Wang, Y.; Chen, S.; Sun, F. State-of-the-art on research of high strength structural steels and key issues of using high strength steels in seismic structures. J. Build. Struct. 2013, 34, 1–13. [Google Scholar]
- Gu, J. Mechanical Behaviors Study on the Pyramid Space Truss in Non-Uniform Temperature Istributions. Master’s Thesis, Nanjing Tech University, Nanjing, China, 2013. [Google Scholar]
- Liu, Y.; Xie, Y.; Long, G. Progress of research on self-compacting concrete. J. Chin. Ceram. Soc. 2007, 35, 671–678. [Google Scholar]
- Zhou, H. Study on Fire Resistance of Saddle Cable Net Structure. Master’s Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Li, G.; Han, L.; Lou, G.; Jiang, S. Fire Resistance Design of Steel Structure and Steel-Concrete Composite Structure; China Architecture and Architecture Press: Beijing, China, 2006; pp. 149–157. [Google Scholar]
- Yang, N.; Bai, F. Damage Analysis and Evaluation of Light Steel Structures Exposed to Wind Hazards. Appl. Sci. 2017, 7, 239. [Google Scholar] [CrossRef]
- Mittelman, B.; Rom, N.; Yosibash, Z. Predicting failure initiation at V-notch tips in an AISI 4340 alloy by a continuum damage model. Eng. Fract. Mech. 2024, 302, 110067. [Google Scholar] [CrossRef]
- Yang, D. Fier Performance of Square and Rectangular Tubed-Reinforced-Concrete Columns with End Restraints. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Yang, D.; Liu, F.; Huang, S.; Yang, H. Fire performance of eccentrically-loaded square and rectangular tubed-reinforced-concrete columns. Structures 2021, 33, 1053–1076. [Google Scholar] [CrossRef]
- Mostafaei, H. Hybrid fire testing for assessing performance of structures in fire-Methodology. Fire Saf. J. 2013, 58, 170–179. [Google Scholar] [CrossRef]
- Mostafaei, H. Hybrid fire testing for assessing performance of structures in fire-Application. Fire Saf. J. 2013, 56, 30–38. [Google Scholar] [CrossRef]
- Wang, Y. Study on Fire Resistance of New Tensioned Space Structure. Master’s Thesis, Shanghai Tongji University, Shanghai, China, 2013. [Google Scholar]
- Xue, S.; Qiu, L.; Feng, M. Advances on fireresistance behaviour of space structures. Prog. Steel Build. Struct. 2009, 11, 29–36. [Google Scholar]
- Zhang, X. Experimental Study on High Temperature Drawing of Prestressed Steel Cable with Hot Cast Anchor. Master’s Thesis, Nanjing Tech University, Nanjing, China, 2019. [Google Scholar]
- Shi, J.; Zhao, J. A study of systems methodology for whole structural fire resistance of complex spatial steel buildings. China Civ. Eng. J. 2008, 41, 51–62. [Google Scholar]
- Wang, W.; Xia, Y. Design parameters and reliability analysis of 0345 steel axial loading member under high temperature. J. Chongqing Univ. 2018, 41, 31–41. [Google Scholar]
- Chen, W.; Ye, J.; Jin, L. Influence of test procedure parameters on high-temperature material properties of 0345 cold-formed steel. J. Build. Struct. 2022, 43, 151–159. [Google Scholar]
- Scullion, T.; Ali, F.; Nadjai, A. Finite element numerical evaluation of elliptical hollow section steel columns in fire. Thin-Walled Struct. 2012, 55, 22–36. [Google Scholar] [CrossRef]
- Ye, Z.N.; Hsu, S.C. Predicting real-time deformation of structure in fire using machine learning with CFD and FEM. Autom. Constr. 2022, 143, 104574. [Google Scholar] [CrossRef]
- Yan, X.; Gernay, T. Numerical modeling of localized fire exposures on structures using FDS-FEM and simple models. Eng. Struct. 2021, 246, 112997. [Google Scholar] [CrossRef]
- Liu, S.R.; Xiong, Y.K.; Zhao, J.F.; Liu, B.; Wu, W.; Zhang, X. Nonlocal crystal plasticity and damage modeling of dual-heterostructured steel for strengthening and failure analysis. Int. J. Plast. 2025, 187, 104270. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Wang, B.; Oterkus, S.; Oterkus, E. Determination of horizon size in state-based peridynamics. Contin. Mech. Thermodyn. 2023, 35, 705–728. [Google Scholar] [CrossRef]
- Liu, R.; Xue, Y.; Li, S. A three-dimensional (3D) micro-potential-based peridynamics model for deformation and fracture in solid materials. Eng. Fract. Mech. 2023, 282, 109180. [Google Scholar] [CrossRef]
- Postek, E.; Sadowski, T.; Guhathakurta, J. Steel Ball Impact on SiC/AlSi12 Interpenetrated Composite by Peridynamics. Materials 2025, 18, 290. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Gu, Q.; Chang, R.J.; Zhang, N.; Li, H. Peridynamic modeling of RC beam-column joints under cyclic loading. Sturctures 2025, 73, 108305. [Google Scholar] [CrossRef]
- Wang, G.; Lu, D.; Gao, Y.; Xie, Z.; Du, X. Viscoelastic peridynamic method for the interface in the reinforced concrete. Eng. Fract. Mech. 2025, 315, 110817. [Google Scholar] [CrossRef]
- Zhang, N.; Chang, R.J.; Li, Y.B.; Sun, B.; Gu, Q. Parametric studies of ultra-high performance fiber-reinforced concrete components based on an efficient peridynamic modeling approach. Stuructures 2025, 74, 108542. [Google Scholar] [CrossRef]
- Zhao, J.; Li, T.; Dou, X. Analysis of the center parallel double-crack propagation with initial casting defects by peridynamics. J. Harbin Eng. Univ. 2018, 39, 1612–1616. [Google Scholar]
- Anbarlooie, B.; Hosseini-Toudeshky, H. Damage mechanisms analyses in DP steels using SEM images, FEM, and nonlocal peridynamics methods. Mech. Adv. Mater. Sturctures 2025, 32, 1549–1563. [Google Scholar] [CrossRef]
- Zhao, J.; Ying, W.; Liu, Y.; Yonggang, L.; Jigang, Y.; Yun, L. Study on damage and failure mechanism of steel structure affected by temperature. Curr. Trends Civ. Struct. Eng. 2024, 10, 1–14. [Google Scholar]
- Zhao, J.; Zong, G.; Sun, R.; Zhu, J. Research on damage and failure mechanism of concrete and steel structures caused by temperature. Sylwan 2024, 168, 10–31. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, H.; Zhang, X. Damage and Crack Propagation Mechanism of Q345 Specimen Based on Peridynamics with Temperature and Bolt Holes. Buildings 2024, 14, 3220. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, H.; Ehsan, N. Fracture mechanics analysis of steel bolted joints using a 3D global model based on peridynamics theory. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 135. [Google Scholar]
- ISO 834-11:2014; Fire Resistance Tests—Elements of Building Construction. International Organization for Standardization: Geneva, Switzerland, 2014.
- Zhao, J.; Gao, H.; Guo, X. A numerical study of crack propagation with variable temperature in steel structures using peridynamic constitutive model. Int. Ournal Hydromechatron. 2021, 4, 116–141. [Google Scholar] [CrossRef]




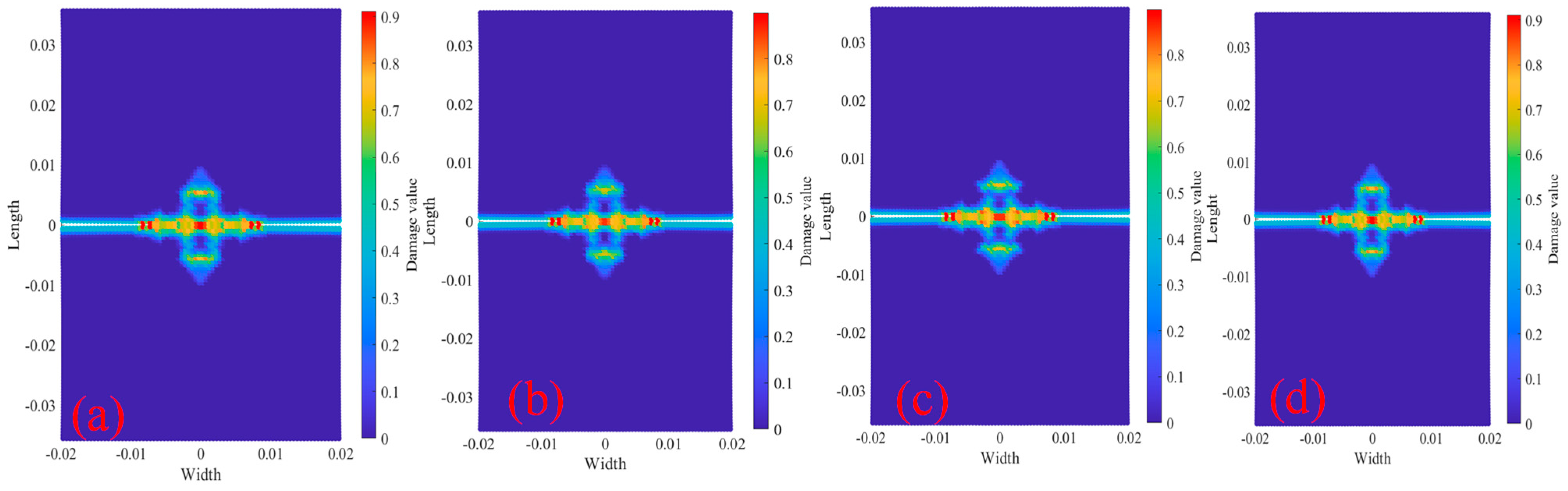
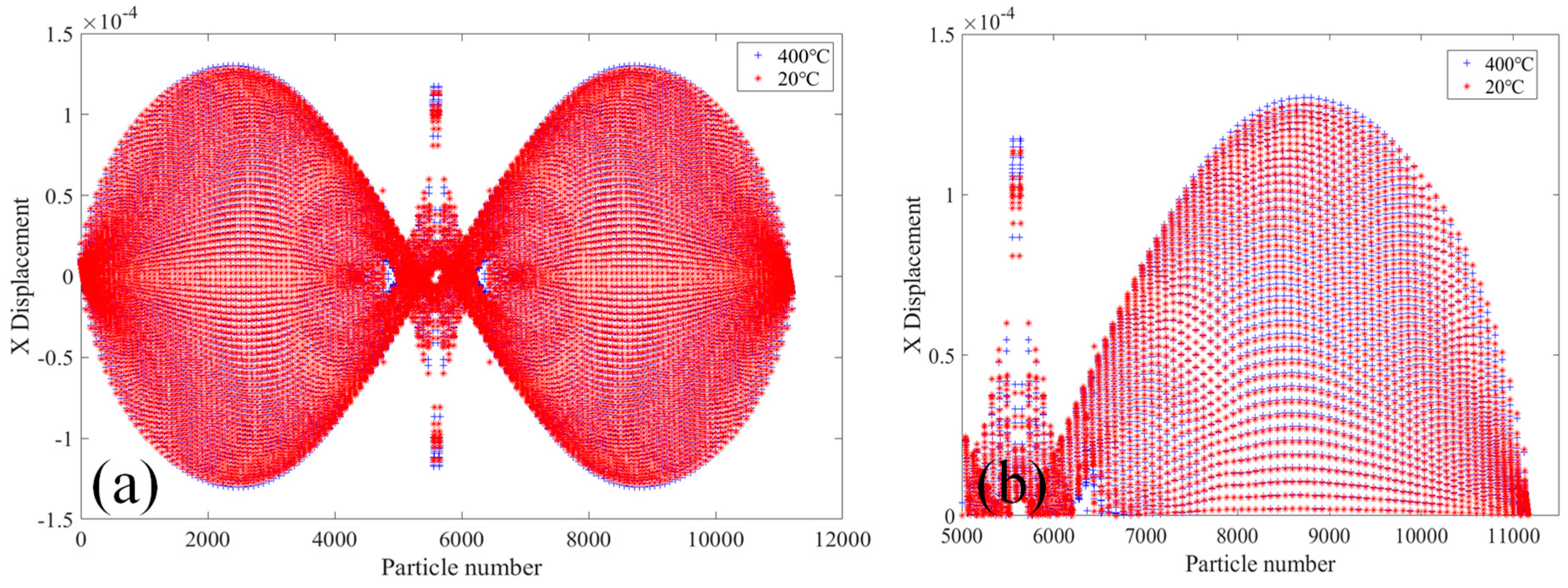


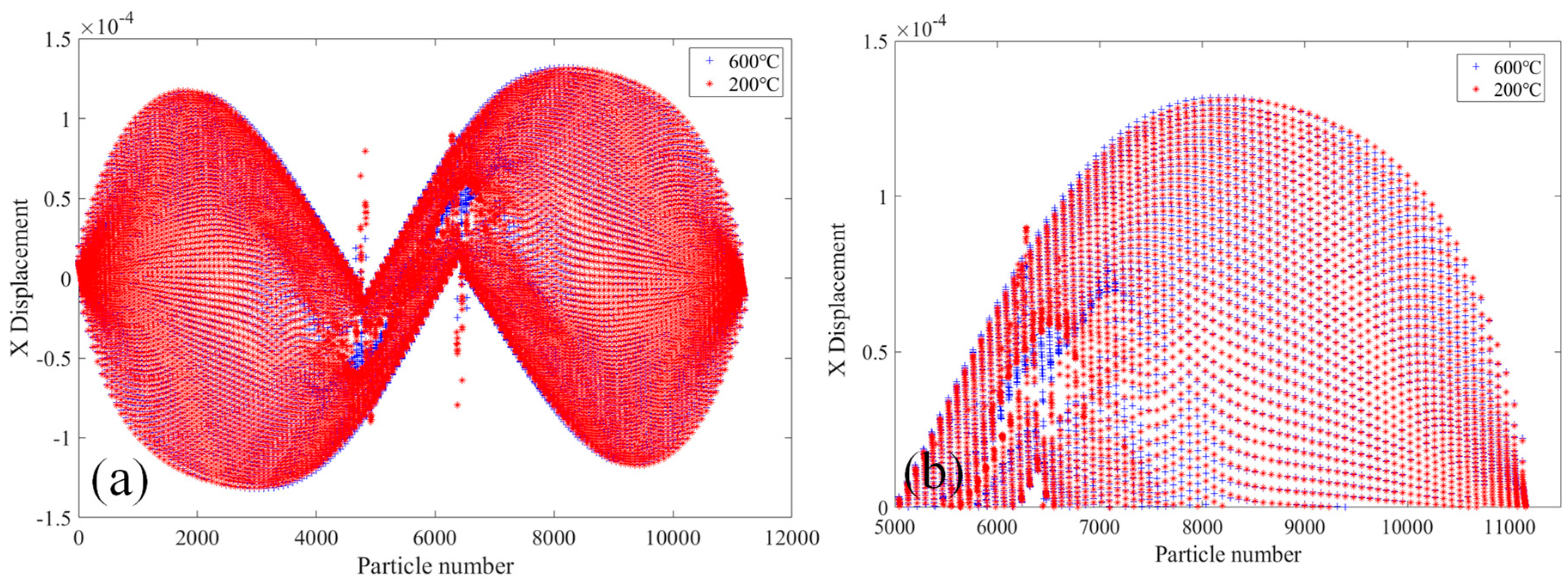
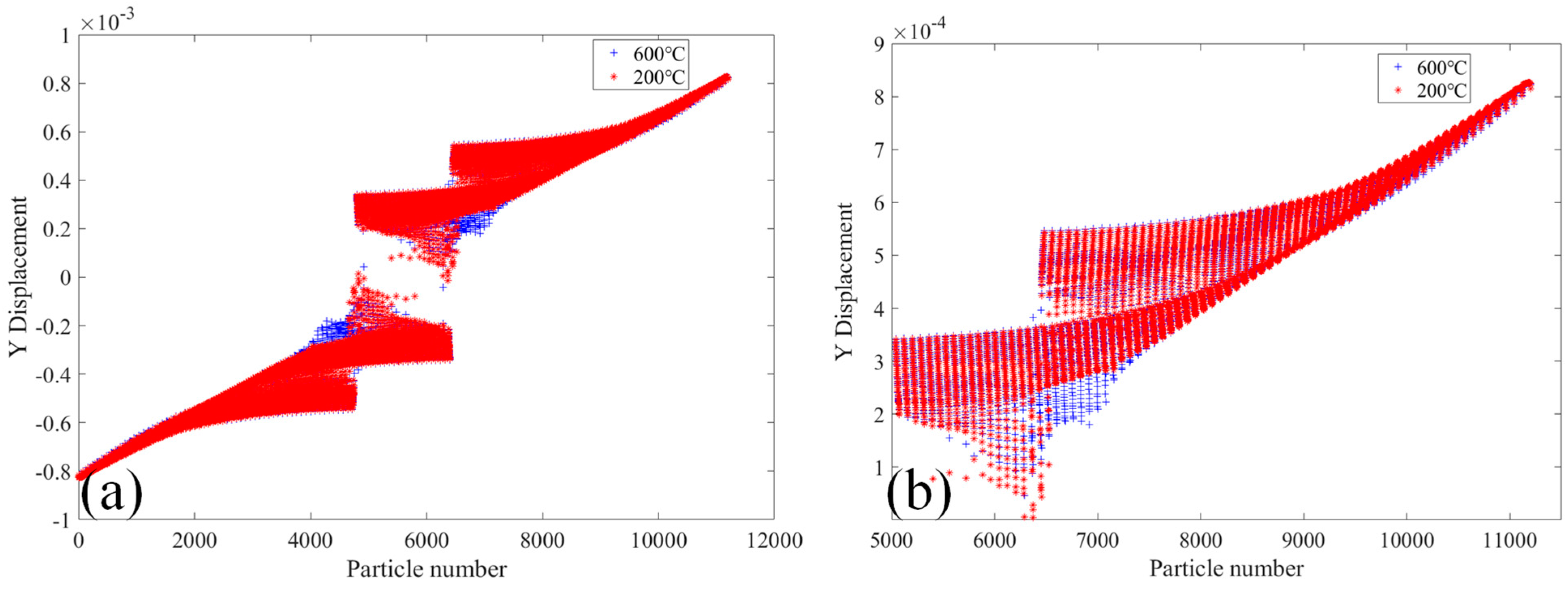

| Crack Length (mm) | Crack Spacing and Specimens No. | |||
|---|---|---|---|---|
| 10 (left) | 10 (right) | 0 (2000×) | 10 (2010×) | 20 (2020×) |
| Crack Length and Longitudinal Spacing | Bolt Hole Radius(r) and Longitudinal Spacing(D) | Specimen No. | ||
|---|---|---|---|---|
| L and R Lengths | Spacing | Bolt Hole Radius | Spacing | |
| 10, 10 | 0 | R = 2 | D = 10 | 2000R2D10 |
| 10, 10 | 0 | R = 2 | D = 20 | 2000R2D20 |
| 10, 10 | 0 | R = 2 | D = 30 | 2000R2D30 |
| 10, 10 | 0 | R = 4 | D = 20 | 2000R4D10 |
| 10, 10 | 10 | R = 2 | D = 30 | 2010R2D30 |
| 10, 10 | 20 | R = 2 | D = 30 | 2020R2D30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, W.; Zhao, J.; Zhou, H.; Zhu, Y.; Yang, Y.; Hu, X. Analysis of the Damage and Failure Mechanism of Q345 Steel Plate with Initial Defect Under Different Temperature Conditions by Peridynamics. Materials 2025, 18, 1886. https://doi.org/10.3390/ma18081886
Ying W, Zhao J, Zhou H, Zhu Y, Yang Y, Hu X. Analysis of the Damage and Failure Mechanism of Q345 Steel Plate with Initial Defect Under Different Temperature Conditions by Peridynamics. Materials. 2025; 18(8):1886. https://doi.org/10.3390/ma18081886
Chicago/Turabian StyleYing, Wudang, Jinhai Zhao, Heipie Zhou, Yuchen Zhu, Yuquan Yang, and Xinzan Hu. 2025. "Analysis of the Damage and Failure Mechanism of Q345 Steel Plate with Initial Defect Under Different Temperature Conditions by Peridynamics" Materials 18, no. 8: 1886. https://doi.org/10.3390/ma18081886
APA StyleYing, W., Zhao, J., Zhou, H., Zhu, Y., Yang, Y., & Hu, X. (2025). Analysis of the Damage and Failure Mechanism of Q345 Steel Plate with Initial Defect Under Different Temperature Conditions by Peridynamics. Materials, 18(8), 1886. https://doi.org/10.3390/ma18081886









