Prediction of Excitation Energies for Conjugated Oligomers and Polymers from Time-Dependent Density Functional Theory
Abstract
:1. Introduction
2. Time-dependent Density Functional Theory
2.1. TDDFT linear response theory
2.2. Adiabatic approximation for the time-dependent XC potential
3. Excitation Energies of Atoms and Small Molecules
3.1. Atoms
3.2. Small molecules
4. Absorption Spectra of Blue-Light Emitting Oligoquinolines
4.1. B1PPQ and BtBPQ
4.2. B2PPQ and BDBPQ
4.3. BPYPQ and B3PPQ
5. Excitation Energies of Conjugated Polymers
6. Conclusion
Acknowledgements
References
- Tonzola, C.J.; Kulkarni, A.P.; Gifford, M.; Kaminsky, W.; Jenekhe, S.A. Blue-light-emitting oligoquinolines: Synthesis, properties, and high-efficiency blue-light-emitting diodes. Adv. Func. Mater. 2007, 17, 863–874. [Google Scholar] [CrossRef]
- Gong, X.; Wang, S.; Moses, D.; Bazan, G.C.; Heeger, A.J. Multilayer polymer light-emitting diodes: White-light emission with high efficiency. Adv. Mat. 2005, 17, 2053–2058. [Google Scholar] [CrossRef]
- May, P. Polymer electronics - fact or fantasy? Phys. World 1995, 8, 52–57. [Google Scholar]
- Forrest, S.R. The path to ubiquitous and low-cost organic electronic appliances on plastic. Nature 2004, 428, 911–918. [Google Scholar] [CrossRef] [PubMed]
- Kraft, A.; Grimsdale, A.C.; Holmes, A.B. Electroluminescent conjugated polymers - seeing polymers in a new light. Angew. Chem. Int. Ed. 1998, 37, 402–428. [Google Scholar] [CrossRef]
- Mitschke, U.; Bauerle, P.J. The electroluminescence of organic materials. J. Mater. Chem. 2000, 10, 1471–1507. [Google Scholar] [CrossRef]
- Kim, D.Y.; Cho, H.N.; Kim, C.Y. Blue light emitting polymers. Prog. Polym. Sci. 2000, 25, 1089–1139. [Google Scholar] [CrossRef]
- Kulkarni, A.P.; Tonzola, C.J.; Babel, A.; Jenekhe, S.A. Electron transport materials for organic light-emitting diodes. Chem. Mater. 2004, 16, 4556–4573. [Google Scholar] [CrossRef]
- Heeger, A.J.; Heeger, D.J.; Langan, J.; Yang, Y. Image enhancement with polymer grid triode arrays. Science 1995, 270, 1642–1644. [Google Scholar] [CrossRef]
- Sirringhaus, H.; Kawase, T.; Friend, R.H.; Shimoda, T.; Inbasekaran, M.; Wu, W.; Woo, E.P. High-resolution inkjet printing of all-polymer transistor circuits. Science 2000, 290, 2123–2126. [Google Scholar] [CrossRef] [PubMed]
- Menard, E.; Meitl, M.; Sun, Y.; Park, J.-U.; Shir, D.-L.; Nam, Y.S.; Jeon, S.; Rogers, J. Micro- and Nanopatterning techniques for organic electronic and optoelectronic systems. Chem. Rev. 2007, 107, 1117–1160. [Google Scholar] [CrossRef] [PubMed]
- Kraft, A.; Grimsdale, A.C.; Holmes, A.B. Electroluminescent Conjugated Polymers - Seeing polymers in a new light. Angew. Chem. Int. Ed. 1998, 37, 402–428. [Google Scholar] [CrossRef]
- Jüstel, T.; Nikol, H.; Ronda, C. New developments in the field of luminescent materials for lighting and displays. Angew. Chem. Int. Ed. 1998, 37, 3084–3103. [Google Scholar] [CrossRef]
- Mitschke, U.; Bäuerle, P. The electroluminescence of organic materials. J. Mater. Chem. 2000, 10, 1471. [Google Scholar] [CrossRef]
- Kim, D.Y.; Cho, H.N.; Kim, C.Y. Blue Light Emitting Polymers. In Progress in Polymer Science; Elsevier: New York, NY, USA, 2000; pp. 1089–1139. [Google Scholar]
- Steuerman, D.W.; Garcia, A.; Dante, M.; Yang, R.; Löfvander, J.P.; Nguyen, T.-Q. Imaging the interfaces of conjugated polymer optoelectronic devices. Adv. Mater. 2008, 20, 528–534. [Google Scholar] [CrossRef]
- Chang, Y.L.; Palacios, R.E.; Chen, J.T.; Stevenson, K.J.; Guo, S.; Lackowski, W.M.; Barbara, P.F. Electrogenerated chemiluminescence of soliton waves in conjugated polymers. J. Am. Chem. Soc. 2009, 131, 14166–14167. [Google Scholar] [CrossRef] [PubMed]
- Palacios, R.E.; Fan, F.-R.F.; Grey, J.K.; Suk, J.; Bard, A.J.; Barbara, P.F. Charging and discharging of single conjugated-polymer nanoparticles. Nat. Mater. 2007, 6, 680–685. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Drori, T.; Vardeny, Z.V. Polarization memory decay spectroscopy of photoexcitations in π-onjugated polymers: Evidence for excimers. Phys. Rev. B 2008, 77, 195304. [Google Scholar] [CrossRef]
- Spano, F.C. Excitons in congugated oligomer aggregates, films, and crystals. Ann. Rev. Phys. Chem. 2006, 57, 217–243. [Google Scholar] [CrossRef] [PubMed]
- Bredas, J.-L.; Cornil, J.; Heeger, A.J. The exciton binding energy in luminescent conjugated polymers. Adv. Mater. 1996, 8, 447–452. [Google Scholar] [CrossRef]
- Bredas, J.-L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-transfer and energy-transfer processes in π-conjugated oligomers and polymers: A molecular picture. Chem. Rev. 2004, 104, 4971–5004. [Google Scholar] [CrossRef] [PubMed]
- Yaron, D. Equation-of-motion calculations on an isolated chain of polyacetylene. Mol. Cryst. Liq. Cryst. 1994, 256, 631–636. [Google Scholar] [CrossRef]
- Moore, E.; Yaron, D. Models of coulomb screening and exciton binding in conjugated polymers. Synth. Met. 1997, 85, 1023–1024. [Google Scholar] [CrossRef]
- Sun, X.; Shuai, Z.; Liu, J.; Fu, R.; Li, X.S.; Lin, D.L.; George, T.F. Polymer a Mott or a Peierls insulator? Synth. Met. 1991, 43, 3549–3552. [Google Scholar] [CrossRef]
- Shuai, Z.; Bredas, J.L. Coupled-cluster approach for studying the electronic and nonlinear optical properties of conjugated molecules. Phys. Rev. B 2000, 62, 15452–15460. [Google Scholar] [CrossRef]
- Spano, F.C. Modeling disorder in polymer aggregates: The optical spectroscopy of regioregular poly(3-hexylthiophene) thin films. J. Chem. Phys. 2005, 122, 234701. [Google Scholar] [CrossRef] [PubMed]
- Dobson, J.F.; Dinte, B.P.; Wang, J. Density Functional Theory: Recent Progress and New Directions; Dobson, J.F., Vignale, G., Das, M.P., Eds.; Plenum: New York, NY, USA, 1998. [Google Scholar]
- Tao, J.; Perdew, J.P.; Ruzsinszky, A. Long-range van der Waals attraction and alkali-metal lattice constants. Phys. Rev. B submitted for publication. 2010. [Google Scholar] [CrossRef]
- Yang, P.; Batista, E.R.; Tretiak, S.; Saxena, A.; Martin, R.L.; Smith, D.L. Effect of intramolecular disorder and intermolecular electronic interactions on the electronic structure of poly-p-phenylene vinylene. Phys. Rev. B 2007, 76, 241201. [Google Scholar] [CrossRef]
- Kilina, S.; Batista, E.R.; Yang, P.; Tretiak, S.; Saxena, A.; Martin, R.L.; Smith, D.L. Electronic structure of amorphous polyfluorene aggregates. ACS Nano 2008, 2, 1381–1388. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.F.; Skaf, M.S.; Yang, C.-Y.; Rossky, P.J.; Bagchi, B.; Hu, D.; Yu, J.; Barbara, P.F. Structural and electronic characterization of chemical and conformational defects in conjugated polymers. J. Phys. Chem. B 2001, 105, 6103–6107. [Google Scholar] [CrossRef]
- Scholes, G.D.; Rumbles, G. Excitons in nanoscale systems. Nat. Mater. 2006, 5, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Scholes, G.D. Insights into excitons confined to nanoscale systems: Electronâhole interaction, binding energy and photodissociation. ACS Nano 2008, 2, 523–537. [Google Scholar] [CrossRef] [PubMed]
- Sterpone, F.; Rossky, P.J. Molecular modeling and simulation of conjugated polymer oligomers: Ground and excited state chain dynamics of PPV in the gas phase. J. Phys. Chem. B 2008, 112, 4983–4993. [Google Scholar] [CrossRef] [PubMed]
- Granstrom, M.; Petritsch, K.; Arias, A.C.; Lux, A.; Andersson, M.R.; Friend, R.H. Laminated fabrication of polymeric photovoltaic diodes. Nature (London) 1998, 395, 257–260. [Google Scholar]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer photovoltaic cells: Enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef]
- Sirringhaus, H.; Brown, P.J.; Friend, R.H.; Nielsen, M.M.; Bechgaard, K.; Langeveld-Voss, B.M.W.; Spiering, A.J.H.; Janssen, R.A.J.; Meijer, E.W.; Herwig, P.; de Leeuw, D.M. Two-dimensional charge transport in self-organized, high-mobility conjugated polymers. Nature (London) 1999, 401, 685–688. [Google Scholar] [CrossRef]
- Nightingale, M.P.; Umrigar, C.J. Quantum Monte Carlo Methods in Physics and Chemistry. In Proceedings of the NATO Advanced Study Institute on Quantum Monte Carlo Methods in Physics and Chemistry, NATO Science Series C; Kluwer Academic: Norwell, MA, USA, 1998; Volume 525. [Google Scholar]
- Schaefer, H.F. Methods of Electronic Structure Theory; Springer: Berlin, Germany, 1977. [Google Scholar]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: density-functional versus many-body Greens-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. First-principles theory of quasiparticles: Calculation of band gaps in semiconductors and insulators. Phys. Rev. Lett. 1985, 55, 1418–1421. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Tao, J.; Tretiak, S.; Zhu, J.-X. Performance of a nonempirical metaâgeneralized gradient approximation density functional for excitation energies. J. Chem. Phys. 2008, 128, 084110. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Tretiak, S.; Zhu, J.-X. Absorption spectra of blue-light emitting oligoquinolines from time-dependent density functional theory. J. Phys. Chem. 2008, 112, 13701–13710. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Tretiak, S. Optical absorptions of new blue-light emitting oligoquinolines bearing pyrenyl and triphenyl endgroups investigated with time-dependent density functional theory. J. Chem. Theory Comput. 2009, 5, 866–872. [Google Scholar] [CrossRef] [PubMed]
- Singlet-triplet transition is forbidden for small molecules, because it violates the selection rule of quantum mechanics for electronic transition.
- Tao, J.; Tretiak, S.; Zhu, J.-X. Prediction of excitation energies for conjugated polymers using time-dependent density functional theory. Phys. Rev. B 2009, 80, 235110. [Google Scholar] [CrossRef]
- Giuliani, G.F.; Vignale, G. Quantum Theory of the Electron Liquid; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Time-Dependent Density Functional Theory. In Lecture Notes in Physics; Marques, M.A.L.; Ullrich, C.A.; Nogueira, F.; Rubio, A.; Burke, K.; Gross, E.K.U. (Eds.) Springer: Berlin, Germany, 2006; Volume 706.
- Casida, M.E. Recent Advances in Density Functional Methods; Chong, D.P., Ed.; World Scientific: Singapore, 1995; p. 155. [Google Scholar]
- Petersilka, M.; Gossmann, U.J.; Gross, E.K.U. Excitation energies from time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 1212–1215. [Google Scholar] [CrossRef] [PubMed]
- Stratmann, R.E.; Scuseria, G.E. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys. 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
- Zangwill, A.; Soven, P. Resonant photoemission in barium and cerium. Phys. Rev. Lett. 1980, 45, 204–207. [Google Scholar] [CrossRef]
- Vignale, G.; Kohn, W. Current-dependent exchange-correlation potential for dynamical linear response theory. Phys. Rev. Lett. 1996, 77, 2037–2040. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G.; Ullrich, C.A.; Conti, S. Time-dependent density functional theory beyond the adiabatic local density approximation. Phys. Rev. Lett. 1997, 79, 4878–4881. [Google Scholar] [CrossRef]
- Tokatly, I.V. Time-dependent deformation functional theory. Phys. Rev. B 2007, 75, 125105. [Google Scholar] [CrossRef]
- Tao, J.; Vignale, G. Time-dependent density-functional theory beyond the local-density approximation. Phys. Rev. Lett. 2006, 97, 036403. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Vignale, G.; Tokatly, I.V. Time-dependent density functional theory: Derivation of gradient-corrected dynamical exchange-correlational potentials. Phys. Rev. B 2007, 76, 195126. [Google Scholar] [CrossRef]
- D’Agosta, R.; Vignale, G. Relaxation in time-dependent current-density-functional theory. Phys. Rev. Lett. 2006, 96, 016405. [Google Scholar] [CrossRef] [PubMed]
- Ullirich, C.A. Time-dependent density-functional theory beyond the adiabatic approximation: Insights from a two-electron model system. J. Chem. Phys. 2006, 125, 234108. [Google Scholar] [CrossRef] [PubMed]
- Tozer, D.J.; Handy, N.C. On the determination of excitation energies using density functional theory. Phys. Chem. Chem. Phys. 2000, 2, 2117–2121. [Google Scholar] [CrossRef]
- Tozer, D.J.; Amos, R.D.; Handy, N.C.; Roos, B.O.; Serrano-Andres, L. Does density functional theory contribute to the understanding of excited states of unsaturated organic compounds? Mol. Phys. 1999, 97, 859–868. [Google Scholar] [CrossRef]
- Dreuw, A.; Weisman, J.L.; Head-Gordan, M. Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange. J. Chem. Phys. 2003, 119, 2943–2946. [Google Scholar] [CrossRef]
- Tozer, D.J. Relationship between long-range charge-transfer excitation energy error and integer discontinuity in KohnâSham theory. J. Chem. Phys. 2003, 119, 12697–12699. [Google Scholar] [CrossRef] [Green Version]
- Maitra, N.T. Undoing static correlation: Long-range charge transfer in time-dependent density-functional theory. J. Chem. Phys. 2005, 122, 234104. [Google Scholar] [CrossRef] [PubMed]
- van Gisbergen, S.J.A.; Kootstra, F.; Schipper, P.R.T.; Gritsenko, O.V.; Snijders, J.G.; Baerends, E.J. Density-functional-theory response-property calculations with accurate exchange-correlation potentials. Phys. Rev. A 1998, 57, 2556–2571. [Google Scholar] [CrossRef]
- Bauernschmit, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Tozer, D.J.; Handy, N.C. Improving virtual KohnâSham orbitals and eigenvalues: Application to excitation energies and static polarizabilities. J. Chem. Phys. 1998, 109, 10180–10189. [Google Scholar] [CrossRef]
- Adamo, C.; Scuseria, G.E.; Barone, V. Accurate excitation energies from time-dependent density functional theory: Assessing the PBE0 model. J. Chem. Phys. 1999, 111, 2889–2899. [Google Scholar] [CrossRef]
- Schipper, P.R.T.; Gritsenko, O.V.; van Gisbergen, S.J.A.; Baerends, E.J. Molecular calculations of excitation energies and hyper...polarizabilities with a statistical average of orbital model exchange-correlation potentials. J. Chem. Phys. 2000, 112, 1344–1352. [Google Scholar] [CrossRef]
- Sala, F.D.; Górling, A. Excitation energies of molecules by time-dependent density functional theory based on effective exact exchange Kohn-Sham potentials. Int. J. Quantum Chem. 2003, 91, 131–138. [Google Scholar] [CrossRef]
- Jacquemin, D.; Bouhy, M.; Perpète, E.A. Excitation spectra of nitro-diphenylaniline: Accurate time-dependent density functional theory predictions for charge-transfer dyes. J. Chem. Phys. 2006, 124, 204321. [Google Scholar] [CrossRef] [PubMed]
- Tretiak, S. Triplet absorption in carbon nanotubes: a TD-DFT study. Nano Lett. 2007, 7, 2201–2206. [Google Scholar] [CrossRef] [PubMed]
- Adams, R.D.; Captain, B.; Hall, M.B.; Trufan, E.; Yang, X.Z. The synthesis, characterization and electronic structures of a novel series of 2-dimensional trimetallic cluster complexes, Ru3(CO)9(u−Sn Ph2)3[Pt(PBut3)]x, x = 0 − 3. J. Am. Chem. Soc. 2007, 129, 12328. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Schmidt, K. Jacobs ladder of Density Functional Approximations for the Exchange-correlation Energy. In Density Functional Theory and Its Application to Materials; Van Doren, V., Van Alsenoy, C., Geerlings, P., Eds.; AIP, Melville: New York, NY, USA, 2001; pp. 1–20. [Google Scholar]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical metaâgeneralized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Tao, J.; Staroverov, V.N.; Scuseria, G.E. Meta-generalized gradient approximation: Explanation of a realistic nonempirical density functional. J. Chem. Phys. 2004, 120, 6898–6911. [Google Scholar] [CrossRef] [PubMed]
- Langreth, D.C.; J.P. Perdew, J.P. The exchange-correlation energy of a metallic surface. Solid State Commun. 1975, 17, 1425–1429. [Google Scholar] [CrossRef]
- Perdew, J.P.; Tao, J. When does static correlation scale to the high-density limit as exchange does? J. Mol. Struct. (Theochem) 2010, 943, 19–22. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of HartreeâFock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Neumann, R.; Nobes, R.H.; Handy, N.C. Exchange functionals and potentials. Mol. Phys. 1996, 87, 1–36. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew Burke Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Tao, J.; Gao, X.; Vignale, G.; Tokatly, I.V. Linear continuum mechanics for quantum many-body systems. Phys. Rev. Lett. 2009, 103, 086401. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Tao, J.; Vignale, G.; Tokatly, I.V. Continuum mechanics for quantum many-body systems: The linear response regime. Phys. Rev. B 2010. submitted. [Google Scholar] [CrossRef]
- van Faassen, M.; de Boeij, P.L.; van Leeuwen, R.; Berger, A.J.; Snijders, J.G. Ultranonlocality in time-dependent current-density-functional theory: Application to conjugated polymers. Phys. Rev. Lett. 2002, 88, 186401. [Google Scholar] [CrossRef] [PubMed]
- van Faassen, M.; de Boeij, P.L.; van Leeuwen, R.; Berger, A.J.; Snijders, J.G. Application of time-dependent current-density-functional theory to nonlocal exchange-correlation effects in polymers. J. Chem. Phys. 2003, 118, 1044–1053. [Google Scholar] [CrossRef]
- van Faassen, M.; de Boeij, P.L. Excitation energies for a benchmark set of molecules obtained within time-dependent current-density functional theory using the VignaleâKohn functional. J. Chem. Phys. 2004, 120, 8353–8363. [Google Scholar] [CrossRef] [PubMed]
- Ullrich, C.A.; Burke, K. Excitation energies from time-dependent density-functional theory beyond the adiabatic approximation. J. Chem. Phys. 2004, 121, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A.; Stratmann, R.E.; Burant, J.C.; et al. Gaussian; Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Moore, C.E. Atomic Energy Levels as Derived from the Analyses of Optical Spectra; U.S. National Bureau of Standards: Washington, DC, USA, 1971; Volume I-II. [Google Scholar]
- Nielsen, E.S.; Jørgensen, P.; Oddershede, J. Transition moments and dynamic polarizabilities in a second order polarization propagator approach. J. Chem. Phys. 1980, 73, 6238–6246. [Google Scholar] [CrossRef]
- Ben-Shlomo, S.B.; Kaldor, U. N2 excitations below 15 eV by the multireference coupled-cluster method. J. Chem. Phys. 1990, 92, 3680–3682. [Google Scholar] [CrossRef]
- Kaldor, U. The open-shell coupled-cluster method: Excitation energies and ionization potentials of H2O. J. Chem. Phys. 1987, 87, 467–471. [Google Scholar] [CrossRef]
- Morgan, L.A. Electron impact excitation of water. J. Phys. B: At. Mol. Opt. Phys. 1998, 31, 5003–5011. [Google Scholar] [CrossRef]
- Foresman, J.B.; Head-Gordan, M.; Pople, J.A. Toward a systematic molecular orbital theory for excited states. J. Phys. Chem. 1992, 96, 135–149. [Google Scholar] [CrossRef]
- Hadad, C.M.; Foresman, J.B.; Wiberg, K.B. Excited states of carbonyl compounds. I. Formaldehyde and acetaldehyde. J. Phys. Chem. 1993, 97, 4293–4312. [Google Scholar] [CrossRef]
- Packer, M.J.; Dalskov, E.K.; Enevoldsen, T.; Jensen, H.J.A.; Oddershede, J. A new implementation of the second-order polarization propagator approximation (SOPPA): The excitation spectra of benzene and naphthalene. J. Chem. Phys. 1996, 105, 5886–5900. [Google Scholar] [CrossRef]
- Lorentzon, J.; Fülscher, M.P.; Ross, B.O. A theoretical study of the electronic spectra of pyridine and phosphabenzene. Theor. Chim. Acta 1995, 92, 67–81. [Google Scholar] [CrossRef]
- Perdew, J.P.; Staroverov, V.N.; Tao, J.; Scuseria, G.E. Density functional with full exact exchange, balanced nonlocality of correlation, and constraint satisfaction. Phys. Rev. A 2008, 78, 052513. [Google Scholar] [CrossRef]
- Jacquemina, D.; Perpète, E.A.; Vydrov, O.A.; Scuseria, G.E.; Adamo, C. Assessment of long-range corrected functionals performance for n → π* transitions in organic dyes. J. Chem. Phys. 2007, 127, 094102. [Google Scholar] [CrossRef] [PubMed]
- Hancock, J.M.; Gifford, A.P.; Tonzola, C.J.; Jenekhe, S.A. High efficiency electroluminescence from new blue-emitting oligoquinolines bearing pyrenyl or triphenyl endgroups. J. Phys. Chem. C 2007, 111, 6875–6882. [Google Scholar] [CrossRef]
- Wohlgenannt, M.; Vardeny, Z.V. Photophysics properties of blue-emitting polymers. Synth. Met. 2001, 125, 55–63. [Google Scholar]
- Tretiak, S.; Igumenshchev, K.; Chernyak, V. Exciton sizes of conducting polymers predicted by time-dependent density functional theory. Phys. Rev. B 2005, 71, 033201. [Google Scholar] [CrossRef]
- Sherwood, G.A.; Cheng, R.; Smith, T.M.; Werner, J.H.; Shreve, A.P.; Peteanu, L.A.; Wildeman, J. Aggregation effects on the emission spectra and dynamics of model oligomers of MEH-PPV. J. Phys. Chem. 2009, 113, 18851. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Martin, R.L. Natural transition orbitals. J. Chem. Phys. 2003, 118, 4775–4777. [Google Scholar] [CrossRef]
- Hong, J.W.; Woo, H.Y.; Liu, B.; Bazan, G.C. Solvatochromism Of distyrylbenzene pairs bound together by [2.2]paracyclophane: Evidence for a polarizable “through-space” delocalized state. J. Am. Chem. Soc. 2005, 127, 7435–7443. [Google Scholar] [CrossRef] [PubMed]
- Chicanne, C.; David, T.; Quidant, R.; Weeber, J.C.; Lacroute, Y.; Bourillot, E.; Dereux, A.; Colas des Francs, G.; Girard, C. conformational dynamics of photoexcited conjugated molecules. Phys. Rev. Lett. 2002, 89, 097402. [Google Scholar] [CrossRef] [PubMed]
- Kasha, M. Characterization of electronic transitions in complex molecules. Discuss. Faraday Soc. 1950, 9, 14–19. [Google Scholar] [CrossRef]
- Wilson, J.S.; Dhoot, A.S.; Seeley, A.J.A.B.; Khan, M.S.; Köhler, A.; Friend, R.H. Spin-dependent exciton formation in π-conjugated compounds. Nature 2001, 413, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Corocpeanu, V.; Brédas, J.L. Exciton dissociation and charge-recombination processes in pentacene-C60 solar cells: A theoretical insight into the impact of interface geometry. J. Am. Chem. Soc. 2009, 131, 15777–15783. [Google Scholar] [CrossRef] [PubMed]
- Monkman, A.P.; Burrows, H.D.; Hartwell, L.J.; Horsburgh, L.E.; Hamblett, I.; Navaratnam, S. Triplet energies of π-conjugated polymers. Phys. Rev. Lett. 2001, 86, 1358–1361. [Google Scholar] [CrossRef] [PubMed]Burrows, H.D.; Seixas de Melo, J.; Serpa, C.; Arnaut, L.G.; Miguel, M.; da, G.; Monkman, A.P.; Hamblett, I.; Navaratnam, S. Triplet state dynamics on isolated conjugated polymer chains. Chem. Phys. 2002, 285, 3–11. [Google Scholar] [Green Version]
- Romanovskii, Yu.V.; Gerhard, A.; Schweitzer, B.; Scherf, U.; Personov, R.I.; Bässler, H. Phosphorescence of π-conjugated oligomers and polymers. Phys. Rev. Lett. 2000, 84, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
- Tretiak, S.; Mukamel, S. Density matrix analysis and simulation of electronic excitations in conjugated and aggregated molecule. Chem. Rev. 2002, 102, 3171–3212. [Google Scholar] [CrossRef] [PubMed]
- S. Tretiak, S.; Chernyak, V.; Mukamel, S. Localized electronic excitations in phenylacetylene dendrimers. J. Phys. Chem. B 1998, 102, 3310–3315. [Google Scholar] [CrossRef]
- Wu, C.; Malinin, S.V.; Tretiak, S.; Chernyak, V.Y. Exciton scattering and localization in branched dendrimeric structures. Nature Phys. 2006, 2, 631–635. [Google Scholar] [CrossRef]
- Kopelman, R.; Shortreed, M.; Shi, Z.-Y.; Tan, W.; Xu, Z.; Moore, J.S.; Bar-Haim, A.; Klafter, J. Spectroscopic evidence for excitonic localization in fractal antenna supermolecules. Phys. Rev. Lett. 1997, 78, 1239–1242. [Google Scholar] [CrossRef]
- Gierschner, J.; Cornil, J.; Egelhaaf, H.J. Optical bandgaps of π-conjugated organic materials at the polymer limit: Experiment and theory. Adv. Mater. 2007, 19, 173–191. [Google Scholar] [CrossRef]
- Perun, S.; Tatchen, J.; Marian, C.M. Singlet and triplet excited states and intersystem crossing in free-base porphyrin: TDDFT and DFT/MRCI study. ChemPhysChem 2008, 9, 282–292. [Google Scholar] [CrossRef] [PubMed]
- Wohlgenannt, M.; Tandon, K.; Mazumdar, S.; Ramesesha, S.; Vardeny, Z.V. Formation cross-sections of singlet and triplet excitons in π-conjugated polymers. Nature 2001, 409, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Walters, K.A.; Ley, K.D.; Shanze, K.S. Triplet state photophysics in an aryleneethynylene π-conjugated polymer. Chem. Commun. 1998, 10, 1115–1116. [Google Scholar] [CrossRef]
- Reindl, S.; Penzkofer, A. Higher excited-state triplet-singlet intersystem crossing of some organic dyes. Chem. Phys. 1996, 211, 431–439. [Google Scholar] [CrossRef]
- Parker, C.A. Photoluminescence of Solutions; Elsevier: Amsterdam, The Netherlands, 1968. [Google Scholar]
- Birks, J.B. Photophysics of Aromatic Molecules; Wiley-Interscience: London, UK, 1970. [Google Scholar]
- Burrows, H.D.; Seixas de Melo, J.; Serpa, C.; Arnaut, L.G.; Monkman, A.P.; Hamblett, I.; Navaratnam, S. S1 → T1 intersystem crossing in pi-conjugated organic polymers. J. Chem. Phys. 2001, 115, 9601–9606. [Google Scholar] [CrossRef]
- Brédas, J.L.; Cornil, J.; Beljonne, D.; dos Santos, D.A.; Shuai, Z. Excited-state electronic structure of conjugated oligomers and polymers: A quantum-chemical approach to optical phenomena. Acc. Chem. Res. 1999, 32, 267–276. [Google Scholar] [CrossRef]
- Barbara, P.F.; Chang, W.S.; Link, S.; Scholes, G.D.; Yethiraj, A. Structure and dynamics of conjugated polymers in liquid crystalline solvents. Annu. Rev. Phys. Chem. 2007, 58, 565–584. [Google Scholar] [CrossRef] [PubMed]
- Schindler, F.; Lupton, J.M.; Feldmann, J.; Scherf, U. A universal picture of chromophores in π-conjugated polymers derived from single molecule spectroscopy. Proc. Natl. Acad. Sci. USA 2004, 101, 14695–14700. [Google Scholar] [CrossRef] [PubMed]
- Grey, J.K.; Kim, D.Y.; Norris, B.C.; Miller, W.L.; Barbara, P.F. Size-dependent spectroscopic properties of conjugated polymer nanoparticles. J. Phys. Chem. B 2006, 110, 25568–25572. [Google Scholar] [CrossRef] [PubMed]
- Igumenshchev, K.; Tretiak, S.; Chernyak, V. Excitonic effects in a time-dependent density functional theory. J. Chem. Phys. 2007, 127, 114902. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, B.J. Conjugated polymers as molecular materials: How chain conformation and film morphology influence energy transfer and interchain interactions. Ann. Rev. Phys. Chem. 2003, 54, 141–172. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, B.J.; Nguyen, T.-Q.; Wu, J.; Tolbert, S.H. Interchain and intrachain exciton transport in conjugated polymers: Ultrafast studies of energy migration in aligned MEH-PPV/mesoporous silica composites. Synth. Met. 2001, 116, 35–40. [Google Scholar] [CrossRef]
- Belletête, M.; Leclerc, M.; Durocher, G. Potentialities of semiempirical calculations (AMPAC and INDO/S) in determining the conformation and electronic properties of 2,2’-bithiophene: A new joint experimental and theoretical approach. J. Phys. Chem. 1994, 98, 9450–9456. [Google Scholar]
- Caruso, M.M.; Davis, D.A.; Shen, Q.; Odom, S.A.; Sottos, N.R.; White, S.R.; Moore, J.S. Mechanically-induced chemical changes in polymeric materials. Chem. Rev. 2009, 109, 5755–5798. [Google Scholar] [CrossRef] [PubMed]
- Grozema, F.C.; van Duijnen, P.Th.; Berlin, Y.A.; Ratner, M.A.; Siebbeles, L.D.A. Intramolecular charge transport along isolated chains of conjugated polymers: Effect of torsional disorder and polymerization defects. J. Phys. Chem. B 2002, 106, 7791–7795. [Google Scholar] [CrossRef]
- Rühle, V.; Kirkpatrick, J.; Kremer, K.; Andrienko, D. Coarse-grained modelling of polypyrrole morphologies. Phys. Stat. Sol. (b) 2008, 245, 844–848. [Google Scholar] [CrossRef]
- Wohlgenannt, M.; Jiang, X.M.; Vardeny, Z.V. Confined and delocalized polarons in π-conjugated oligomers and polymers: A study of the effective conjugation length. Phys. Rev. B 2004, 69, 241204. [Google Scholar] [CrossRef]






| Atom | Transition | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| He | 1s → 2s | 19.59 | 19.73 | 20.27 | 20.58 | 20.62 | 20.50 | 20.62 |
| 1s → 2s | 22.99 | 23.41 | 24.04 | 24.23 | 24.05 | 23.95 | 21.22 | |
| Li | 2s → 2p | 1.98 | 1.98 | 1.99 | 1.97 | 1.95 | 1.98 | 1.85 |
| 2s → 3s | 3.12 | 3.09 | 3.09 | 3.13 | 3.23 | 3.16 | 3.37 | |
| Be | 2s → 2p | 4.84 | 4.91 | 5.06 | 5.05 | 4.94 | 4.88 | 5.28 |
| 2s → 3s | 6.11 | 6.12 | 6.29 | 6.35 | 6.32 | 6.21 | 6.78 | |
| Ne | 2p → 3s | 17.45 | 17.21 | 17.55 | 17.94 | 18.27 | 17.88 | 16.62 |
| 2p → 3p | 19.82 | 19.46 | 19.74 | 20.16 | 20.59 | 20.11 | 18.38 | |
| Na | 3s → 3p | 2.25 | 2.12 | 2.02 | 2.02 | 2.08 | 2.23 | 2.10 |
| 3s → 4s | 3.05 | 2.91 | 2.87 | 2.90 | 3.02 | 3.02 | 3.19 | |
| Mg | 3s → 3p | 4.24 | 4.18 | 4.18 | 4.19 | 4.20 | 4.23 | 4.35 |
| 3s → 4s | 5.02 | 4.93 | 5.01 | 5.06 | 5.08 | 5.00 | 5.39 | |
| Ar | 3p → 4s | 11.32 | 11.27 | 11.59 | 11.81 | 11.90 | 11.56 | 11.55 |
| 3p → 4p | 12.68 | 12.50 | 12.74 | 13.00 | 13.22 | 12.89 | 12.91 | |
| K | 4s → 4p | 1.70 | 1.50 | 1.36 | 1.36 | 1.45 | 1.64 | 1.61 |
| 4s → 5s | 2.52 | 2.35 | 2.28 | 2.30 | 2.42 | 2.43 | 2.61 | |
| Ca | 4s → 3d | 1.88 | 1.88 | 1.87 | 2.02 | 2.24 | 2.16 | 2.71 |
| 4s → 4p | 3.09 | 2.98 | 2.90 | 2.90 | 2.96 | 3.03 | 2.93 | |
| Zn | 4s → 4p | 5.80 | 5.67 | 5.59 | 5.52 | 5.51 | 5.65 | 5.80 |
| 2s → 5s | 6.38 | 6.12 | 6.10 | 6.12 | 6.20 | 6.22 | 6.92 | |
| Kr | 4p → 5s | 9.52 | 9.43 | 9.72 | 9.92 | 10.01 | 9.69 | 9.92 |
| 4p → 5s | 10.84 | 10.64 | 10.85 | 11.10 | 11.30 | 10.98 | 11.30 | |
| m.e. | -0.06 | -0.14 | -0.02 | 0.12 | 0.19 | 0.09 | … | |
| m.a.e. | 0.47 | 0.51 | 0.49 | 0.50 | 0.50 | 0.47 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3Π | 5.98 | 5.68 | 5.75 | 5.78 | 5.77 | 5.89 | 6.32 |
| 3Σ+ | 8.45 | 7.97 | 7.88 | 7.88 | 7.96 | 8.03 | 8.51 |
| 1Π | 8.19 | 8.19 | 8.40 | 8.50 | 8.49 | 8.47 | 8.51 |
| 3Δ | 9.21 | 8.59 | 8.53 | 8.59 | 8.70 | 8.71 | 9.36 |
| 3Σ− | 9.90 | 9.31 | 9.64 | 9.92 | 9.89 | 9.80 | 9.88 |
| 1Σ− | 9.94 | 9.79 | 10.05 | 10.15 | 9.89 | 9.86 | 9.88 |
| 1Δ | 9.90 | 9.72 | 9.96 | 10.01 | 10.29 | 10.26 | 10.23 |
| 3Σ+ | 9.55 | 9.72 | 9.96 | 10.01 | 10.05 | 9.92 | 10.40 |
| 3Σ+ | 10.48 | 10.21 | 10.60 | 10.86 | 10.94 | 10.85 | 11.30 |
| 1Σ+ | 10.73 | 10.62 | 10.89 | 11.15 | 11.31 | 11.32 | 11.40 |
| m.e. | -0.35 | -0.60 | -0.41 | -0.30 | -0.25 | -0.28 | … |
| m.a.e. | 0.36 | 0.60 | 0.45 | 0.36 | 0.27 | 0.28 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 7.96 | 7.42 | 7.22 | 7.12 | 7.14 | 7.25 | 7.75 | |
| 3Πg | 7.62 | 7.34 | 7.43 | 7.54 | 7.64 | 7.68 | 8.04 |
| 3Δu | 8.90 | 8.19 | 8.05 | 8.01 | 8.06 | 8.12 | 8.88 |
| 1Πg | 9.11 | 9.04 | 9.23 | 9.37 | 9.43 | 9.37 | 9.31 |
| 9.73 | 9.58 | 9.82 | 9.79 | 9.53 | 9.47 | 9.67 | |
| 8.73 | 9.58 | 9.82 | 9.79 | 9.53 | 9.47 | 9.92 | |
| 1Δu | 10.28 | 9.98 | 9.95 | 9.98 | 10.05 | 10.86 | 10.27 |
| 3Πu | 10.39 | 10.37 | 10.65 | 10.79 | 10.79 | 10.68 | 11.19 |
| m.e. | -0.29 | -0.44 | -0.36 | -0.33 | -0.36 | -0.27 | … |
| m.a.e. | 0.36 | 0.44 | 0.40 | 0.38 | 0.39 | 0.43 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3B1 | 6.30 | 6.06 | 6.30 | 6.59 | 6.80 | 6.56 | 7.14 |
| 1B1 | 6.60 | 6.44 | 6.65 | 6.96 | 7.24 | 6.96 | 7.49 |
| 3A2 | 7.99 | 7.72 | 7.90 | 8.24 | 8.57 | 8.31 | 9.1 |
| 1A2 | 8.08 | 7.88 | 8.05 | 8.39 | 8.77 | 8.47 | 9.2 |
| 3A1 | 8.26 | 8.10 | 8.36 | 8.64 | 8.84 | 8.58 | 9.35 |
| 1A1 | 8.67 | 8.62 | 8.86 | 9.15 | 9.43 | 9.10 | 9.73 |
| 3B2 | 9.94 | 9.75 | 9.95 | 10.26 | 10.55 | 10.28 | 9.93 |
| 1B2 | 10.14 | 10.04 | 10.23 | 10.57 | 10.93 | 10.59 | 10.0 |
| m.e. | -0.75 | -0.92 | -0.71 | -0.39 | -0.10 | -0.39 | … |
| m.a.e. | 0.78 | 0.93 | 0.77 | 0.62 | 0.49 | 0.62 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3A2 | 3.15 | 3.09 | 3.26 | 3.30 | 3.22 | 3.26 | 3.5 |
| 1A2 | 3.75 | 3.82 | 4.06 | 4.12 | 4.02 | 3.99 | 4.1 |
| 3A1 | 6.37 | 5.75 | 5.57 | 5.46 | 5.43 | 5.58 | 6.0 |
| 3B2 | 5.89 | 5.68 | 5.95 | 6.27 | 6.53 | 6.38 | 7.09 |
| 1B2 | 5.99 | 5.89 | 6.11 | 6.45 | 6.77 | 6.53 | 7.13 |
| 3B2 | 7.10 | 6.91 | 7.17 | 7.44 | 7.62 | 7.46 | 7.92 |
| 1B2 | 7.18 | 7.07 | 7.29 | 7.58 | 7.82 | 7.61 | 7.98 |
| 3A1 | 6.86 | 6.63 | 6.87 | 7.21 | 7.50 | 7.35 | 8.11 |
| 1A1 | 6.95 | 6.82 | 7.01 | 7.36 | 7.72 | 7.47 | 8.14 |
| 1B1 | 8.86 | 8.82 | 9.01 | 9.15 | 9.22 | 9.09 | 9.0 |
| m.e. | -0.69 | -0.87 | -0.69 | -0.49 | -0.31 | -0.43 | … |
| m.a.e. | 0.77 | 0.87 | 0.69 | 0.52 | 0.36 | 0.44 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3A2 | 3.70 | 3.59 | 3.69 | 3.73 | 3.81 | 3.81 | 4.18 |
| 1A2 | 4.22 | 4.21 | 4.37 | 4.41 | 4.49 | 4.44 | 4.43 |
| 3A1 | 6.13 | 5.70 | 5.97 | 5.96 | 5.60 | 5.70 | 5.88 |
| 3A2 | 6.28 | 6.11 | 6.27 | 6.26 | 6.01 | 5.75 | 6.26 |
| 1B2 | 5.09 | 5.00 | 5.22 | 5.22 | 6.08 | 5.80 | 6.36 |
| 1A2 | 6.30 | 6.14 | 6.30 | 6.30 | 7.18 | 6.92 | 7.36 |
| 1A1 | 6.08 | 5.92 | 6.08 | 6.08 | 7.02 | 6.72 | 7.41 |
| 1B1 | 6.51 | 6.36 | 6.53 | 6.52 | 7.37 | 7.12 | 7.49 |
| m.e. | -0.63 | -0.79 | -0.62 | -0.61 | -0.23 | -0.39 | … |
| m.a.e. | 0.70 | 0.79 | 0.64 | 0.53 | 0.24 | 0.39 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3B1u | 4.81 | 4.26 | 4.12 | 4.02 | 3.97 | 4.17 | 4.36 |
| 3B3u | 6.75 | 6.45 | 6.58 | 6.74 | 6.86 | 6.65 | 6.98 |
| 1B3u | 6.82 | 6.58 | 6.67 | 6.84 | 7.01 | 6.75 | 7.15 |
| 1B1u | 7.58 | 7.44 | 7.53 | 7.59 | 7.61 | 7.48 | 7.66 |
| 3B1g | 6.95 | 6.99 | 7.17 | 7.34 | 7.39 | 7.27 | 7.79 |
| 3B2g | 7.34 | 7.02 | 7.12 | 7.31 | 7.52 | 7.26 | 7.79 |
| 1B1g | 7.36 | 7.16 | 7.25 | 7.43 | 7.60 | 7.34 | 7.83 |
| 1B2g | 7.41 | 7.13 | 7.21 | 7.40 | 7.64 | 7.34 | 8.0 |
| 3Ag | 8.39 | 8.03 | 8.20 | 8.33 | 8.37 | 8.25 | 8.15 |
| 1Ag | 8.71 | 8.48 | 8.56 | 8.70 | 8.85 | 8.63 | 8.29 |
| m.e. | -0.22 | -0.47 | -0.37 | -0.25 | -0.12 | -0.29 | … |
| m.a.e. | 0.41 | 0.50 | 0.42 | 0.35 | 0.27 | 0.37 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3B1u | 4.47 | 3.98 | 3.84 | 3.73 | 3.68 | 3.84 | 3.94 |
| 3E1u | 4.82 | 4.61 | 4.67 | 4.70 | 4.75 | 4.72 | 4.76 |
| 1B2u | 5.33 | 5.22 | 5.32 | 5.42 | 5.52 | 5.41 | 4.90 |
| 3B2u | 5.05 | 4.89 | 4.98 | 5.06 | 5.12 | 5.07 | 5.60 |
| 1B1u | 6.07 | 5.94 | 6.00 | 6.09 | 6.18 | 6.05 | 6.20 |
| 1E1g | 6.12 | 5.89 | 5.99 | 6.18 | 6.38 | 6.11 | 6.33 |
| 3E1g | 6.09 | 5.84 | 5.95 | 6.14 | 6.32 | 6.07 | 6.34 |
| 1A2u | 6.70 | 6.43 | 6.50 | 6.69 | 6.90 | 6.62 | 6.93 |
| 1E2u | 6.71 | 6.44 | 6.50 | 6.70 | 6.95 | 6.65 | 6.95 |
| 3E1u | 6.66 | 6.37 | 6.45 | 6.63 | 6.82 | 6.57 | 6.98 |
| m.e. | -0.09 | -0.33 | -0.27 | -0.16 | -0.03 | -0.18 | … |
| m.a.e. | 0.30 | 0.40 | 0.36 | 0.26 | 0.17 | 0.28 | … |
| Symmetry | LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | Expta |
| 3B1 | 3.69 | 3.68 | 3.84 | 3.99 | 3.81 | 3.97 | 4.1 |
| 3A1 | 4.59 | 4.11 | 3.97 | 3.86 | 4.08 | 4.05 | 4.1 |
| 1B1 | 4.22 | 4.33 | 4.55 | 4.74 | 4.86 | 4.76 | 4.59 |
| 3B2 | 4.62 | 4.41 | 4.44 | 4.49 | 4.54 | 4.52 | 4.84 |
| 3A1 | 5.04 | 4.78 | 4.81 | 4.86 | 4.92 | 4.88 | 4.84 |
| 1B2 | 5.46 | 5.33 | 5.41 | 5.53 | 5.63 | 5.52 | 4.99 |
| 3A2 | 4.19 | 4.30 | 4.57 | 4.83 | 5.03 | 4.93 | 5.40 |
| 1A2 | 4.29 | 4.43 | 4.71 | 4.99 | 5.20 | 5.07 | 5.43 |
| 3B2 | 5.45 | 5.40 | 5.65 | 6.06 | 5.72 | 5.64 | 6.02* |
| 1A1 | 6.03 | 5.97 | 6.18 | 6.31 | 6.41 | 6.23 | 6.38 |
| m.e. | -0.31 | -0.40 | -0.26 | -0.08 | -0.05 | -0.11 | … |
| m.a.e. | 0.54 | 0.47 | 0.34 | 0.25 | 0.25 | 0.26 | … |
| LSDA | PBE | TPSS | TPSSh | PBE0 | B3LYP | |
| m.a.r.e. (%) | 7.3 | 8.3 | 7.1 | 5.7 | 4.4 | 5.3 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.70 | 0.745 | 3.37 | 0.197 | 3.49 | 0.121 | 2.26 | 0.708 | 2.66 | 0.948 | 3.38 | 0.122 | 3.50 | 0.194 | 2.67 | 1.052 |
| TPSS | 2.81 | 0.747 | 3.50 | 0.187 | 3.60 | 0.124 | 2.18 | 0.838 | 2.78 | 0.938 | 3.50 | 0.155 | 3.61 | 0.231 | 2.19 | 1.231 |
| TPSSh | 3.12 | 0.916 | 3.90 | 0.205 | 4.15 | 0.919 | 2.23 | 0.865 | 3.08 | 1.137 | 3.89 | 0.174 | 4.09 | 1.144 | 2.24 | 1.261 |
| B3LYP | 3.33 | 1.040 | 4.37 | 0.623 | 4.40 | 0.422 | 2.35 | 0.901 | 3.28 | 1.288 | 4.20 | 0.650 | 4.31 | 0.856 | 2.37 | 1.300 |
| PBE0 | 3.45 | 1.112 | 4.41 | 0.786 | 4.54 | 0.744 | 2.27 | 0.902 | 3.40 | 1.359 | 4.38 | 1.279 | 4.50 | 0.464 | 2.29 | 1.305 |
| Expt | 3.48 | 4.43 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.64 | 0.896 | 3.33 | 0.316 | 3.61 | 0.3685 | 2.24 | 0.699 | 2.61 | 1.095 | 3.34 | 0.535 | 3.59 | 0.485 | 2.25 | 1.010 |
| TPSS | 2.77 | 0.868 | 3.47 | 0.458 | 3.73 | 0.339 | 2.18 | 0.844 | 2.74 | 1.058 | 3.47 | 0.536 | 3.69 | 0.207 | 2.19 | 1.220 |
| TPSSh | 3.08 | 1.093 | 3.87 | 0.427 | 4.10 | 0.627 | 2.23 | 0.872 | 3.04 | 1.300 | 3.88 | 0.337 | 4.06 | 0.815 | 2.24 | 1.248 |
| B3LYP | 3.29 | 1.255 | 4.17 | 0.764 | 4.36 | 0.753 | 2.35 | 0.916 | 3.25 | 1.473 | 4.16 | 0.931 | 4.32 | 0.704 | 2.36 | 1.300 |
| PBE0 | 3.41 | 1.346 | 4.36 | 1.160 | 4.56 | 0.415 | 2.27 | 0.909 | 3.37 | 1.575 | 4.33 | 1.431 | 4.53 | 0.299 | 2.28 | 1.286 |
| Expt | 3.44 | 4.35 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.48 | 1.168 | 3.04 | 0.235 | 3.19 | 0.306 | 2.14 | 0.708 | 2.44 | 1.403 | 3.03 | 0.404 | 3.20 | 0.277 | 2.14 | 1.025 |
| TPSS | 2.62 | 1.135 | 3.19 | 0.366 | 3.35 | 0.261 | 2.11 | 0.828 | 2.59 | 1.332 | 3.17 | 0.590 | 3.62 | 0.193 | 2.12 | 1.227 |
| TPSSh | 2.95 | 1.446 | 3.73 | 0.336 | 4.05 | 0.607 | 2.18 | 0.847 | 2.91 | 1.695 | 3.75 | 0.442 | 4.01 | 0.863 | 2.19 | 1.244 |
| B3LYP | 3.18 | 1.690 | 4.01 | 0.692 | 4.32 | 0.876 | 2.31 | 0.908 | 3.14 | 1.952 | 3.98 | 0.851 | 4.29 | 0.885 | 2.32 | 1.308 |
| PBE0 | 3.31 | 1.812 | 4.18 | 1.155 | 4.52 | 0.808 | 2.23 | 0.889 | 3.26 | 2.082 | 4.18 | 0.753 | 4.49 | 0.688 | 2.25 | 1.287 |
| Expt | 3.39 | 4.22 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.63 | 0.683 | 2.70 | 0.173 | 3.26 | 0.149 | 2.25 | 0.772 | 2.61 | 0.896 | 2.70 | 0.140 | 3.31 | 0.131 | 2.26 | 1.092 |
| TPSS | 2.76 | 0.797 | 3.36 | 0.120 | 3.46 | 0.246 | 2.18 | 0.891 | 2.74 | 0.957 | 3.37 | 0.143 | 3.44 | 0.266 | 2.19 | 1.231 |
| TPSSh | 3.08 | 1.069 | 3.85 | 0.217 | 3.91 | 0.138 | 2.22 | 0.922 | 3.05 | 1.236 | 3.57 | 0.131 | 3.86 | 0.284 | 2.23 | 1.262 |
| B3LYP | 3.31 | 1.227 | 4.14 | 0.446 | 4.27 | 0.153 | 2.36 | 1.014 | 3.28 | 1.400 | 3.83 | 0.171 | 4.13 | 0.436 | 2.37 | 1.361 |
| PBE0 | 3.42 | 1.321 | 4.31 | 0.644 | 4.45 | 0.270 | 2.27 | 0.982 | 3.39 | 1.501 | 4.29 | 0.842 | 4.44 | 0.407 | 2.28 | 1.335 |
| Expt | 3.45 | 4.40 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.10 | 0.558 | 2.48 | 0.358 | 3.06 | 0.286 | 1.90 | 1.031 | 2.08 | 0.714 | 2.47 | 0.499 | 3.03 | 0.384 | 1.90 | 1.645 |
| TPSS | 2.21 | 0.473 | 2.58 | 0.392 | 3.17 | 0.334 | 1.85 | 1.112 | 2.19 | 0.610 | 2.56 | 0.536 | 3.15 | 0.400 | 1.86 | 1.761 |
| TPSSh | 2.61 | 0.852 | 3.16 | 0.506 | 3.48 | 0.271 | 1.88 | 1.138 | 2.58 | 1.081 | 3.14 | 0.503 | 3.45 | 0.314 | 1.89 | 1.784 |
| B3LYP | 2.89 | 1.275 | 3.44 | 0.501 | 3.64 | 0.092 | 1.98 | 1.122 | 2.85 | 1.998 | 3.42 | 0.513 | 3.61 | 0.122 | 1.98 | 1.744 |
| PBE0 | 3.04 | 1.516 | 3.62 | 0.448 | 3.79 | 0.071 | 1.88 | 1.190 | 3.00 | 1.817 | 3.60 | 0.479 | 4.09 | 0.096 | 1.89 | 1.839 |
| Expt | 3.26 | 3.60 | 4.34 |
| gas | gas | gas | gas | gas | gas | gas | gas | sol | sol | sol | sol | sol | sol | sol | sol | |
| LSDA | 2.34 | 1.235 | 2.78 | 0.598 | 3.27 | 0.575 | 2.09 | 1.137 | 2.31 | 1.421 | 2.75 | 0.721 | 3.26 | 0.593 | 2.09 | 1.457 |
| TPSS | 2.49 | 1.209 | 2.93 | 0.425 | 3.42 | 0.503 | 2.079 | 1.234 | 2.46 | 1.378 | 2.89 | 0.430 | 3.42 | 0.391 | 2.09 | 1.602 |
| TPSSh | 2.86 | 1.779 | 3.42 | 0.502 | 3.95 | 1.047 | 2.16 | 1.267 | 2.83 | 1.998 | 3.74 | 0.772 | 3.92 | 0.856 | 2.18 | 1.636 |
| B3LYP | 3.12 | 2.197 | 3.86 | 0.542 | 4.09 | 0.923 | 2.29 | 1.265 | 3.08 | 2.429 | 3.81 | 0.498 | 4.06 | 0.642 | 2.30 | 1.632 |
| PBE0 | 3.27 | 2.373 | 4.02 | 0.957 | 4.30 | 0.962 | 2.23 | 1.306 | 3.23 | 2.609 | 4.02 | 0.842 | 4.28 | 1.099 | 2.24 | 1.676 |
| Expt | 3.32 | 4.04 |
| Excited state | Electron | Hole |
| |1〉 ΔE = 3.45 eV f = 1.112 W = 97.4% | 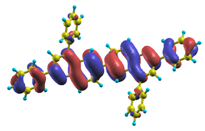 | 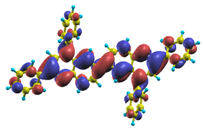 |
| |8〉 ΔE = 4.41 eV f = 0.786 W = 53.5% | 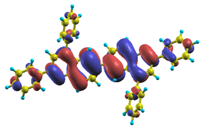 | 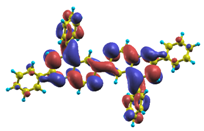 |
| |9〉 ΔE = 4.54 eV f = 0.744 W = 81.8% |  |  |
| Excited state | Electron | Hole |
| |1〉 ΔE = 3.41 eV f = 1.346 W = 97.2% | 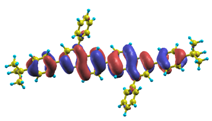 |  |
| |8〉 ΔE = 4.36 eV f = 1.160 W = 58.7% | 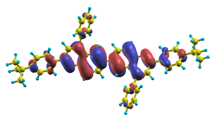 | 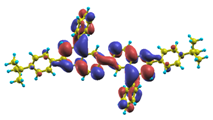 |
| |11〉 ΔE = 4.56 eV f = 0.415 W = 82.5% | 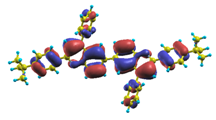 | 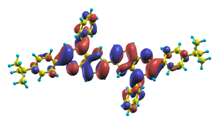 |
| S0 − S1 | |||||||||||||
| Polymer | Expta | LSDA | TPSS | TPSSh | B3LYP | PBE0 | Expta | LSDA | TPSS | TPSSh | B3LYP | PBE0 | |
| P3OT(28) | 2.8-3.8 | 0.99 | 0.99 | 1.35 | 1.59 | 1.76 | 1.7-2.2 | 0.90 | 0.80 | 0.88 | 0.96 | 0.95 | |
| PBOPT(32) | 2.52 | 1.49 | 1.55 | 1.96 | 2.26 | 2.39 | 1.60 | 1.37 | 1.31 | 1.42 | 1.57 | 1.54 | |
| MEHPPV(16) | 2.48 | 1.14 | 1.27 | 1.66 | 1.94 | 2.07 | 1.30 | 1.04 | 1.08 | 1.18 | 1.31 | 1.24 | |
| PFO(36) | 3.22 | 2.30 | 2.45 | 2.89 | 3.13 | 3.30 | 2.30 | 2.22 | 2.23 | 2.34 | 2.45 | 2.43 | |
| DHOPPV(16) | 2.58 | 1.14 | 1.27 | 1.67 | 1.95 | 2.07 | 1.50 | 1.04 | 1.08 | 1.18 | 1.32 | 1.24 | |
| PPY(24) | 3.4-3.9 | 1.82 | 2.10 | 2.61 | 2.87 | 3.03 | 2.4-2.5 | 1.82 | 1.99 | 2.11 | 2.23 | 2.20 | |
| CN-MEHPPV(16) | 2.72 | 1.10 | 1.34 | 1.84 | 2.16 | 2.27 | N/A | 1.06 | 1.22 | 1.34 | 1.48 | 1.43 | |
| PANi(20) | 2.00 | 2.34 | 2.53 | 3.05 | 3.30 | 3.44 | < 0.9 | 2.31 | 2.43 | 2.63 | 2.75 | 2.73 | |
| Polymer | Expt | PBE0 | Energy |
| P3OTa | ∼ 24 ° | ∼ 0 ° | redshift |
| PBOPT | ∼ 35 ° | ∼ 40 ° | On experiment |
| MEHPPVb | ∼ 30 ° | ∼ 1 ° | redshift |
| PFOc | ∼ 40 ° | ∼ 38 ° | On experiment |
| DHOPPV | ∼ 30 ° | ∼ 0 ° | redshift |
| PPYd | ≳ 0 ° | ∼ 0 − 1 ° | slightly redshift |
| CN-MEHPPV | ∼ 30 ° | ∼ 0 ° | redshift |
| PANi | ∼ 0 ° | ∼ 18 − 26 ° | too blueshift |
| S0 − S1 | |||||||||||||
| Polymer | Expta | LSDA | TPSS | TPSSh | B3LYP | PBE0 | Expta | LSDA | TPSS | TPSSh | B3LYP | PBE0 | |
| P3OT(28) | 2.8-3.8 | 0.97 | 0.97 | 1.32 | 1.56 | 1.73 | 1.7-2.2 | 0.89 | 0.80 | 0.87 | 0.95 | 0.94 | |
| PBOPT(32) | 2.52 | 1.60 | |||||||||||
| MEHPPV(16) | 2.48 | 1.12 | 1.25 | 1.64 | 1.91 | 2.04 | 1.30 | 1.03 | 1.07 | 1.18 | 1.32 | 1.25 | |
| PFO(36) | 3.22 | 2.30 | 2.45 | 2.88 | 3.12 | 3.29 | 2.30 | 2.22 | 2.24 | 2.35 | 2.46 | 2.43 | |
| DHOPPV(16) | 2.58 | 1.12 | 1.25 | 1.64 | 1.92 | 2.04 | 1.50 | 1.03 | 1.07 | 1.18 | 1.32 | 1.25 | |
| PPY(24) | 3.4-3.9 | 2.08 | 2.16 | 2.61 | 2.85 | 3.01 | 2.4-2.5 | 2.02 | 1.99 | 2.11 | 2.23 | 2.20 | |
| CN-MEHPPV(16) | 2.72 | 1.10 | 1.32 | 1.80 | 2.10 | 2.21 | N/A | 1.05 | 1.21 | 1.34 | 1.48 | 1.43 | |
| PANi(20) | 2.00 | 2.33 | 2.53 | 3.03 | 3.27 | 3.41 | < 0.9 | 2.30 | 2.42 | 2.62 | 2.75 | 2.73 | |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Tao, J.; Tretiak, S.; Zhu, J.-X. Prediction of Excitation Energies for Conjugated Oligomers and Polymers from Time-Dependent Density Functional Theory. Materials 2010, 3, 3430-3467. https://doi.org/10.3390/ma3053430
Tao J, Tretiak S, Zhu J-X. Prediction of Excitation Energies for Conjugated Oligomers and Polymers from Time-Dependent Density Functional Theory. Materials. 2010; 3(5):3430-3467. https://doi.org/10.3390/ma3053430
Chicago/Turabian StyleTao, Jianmin, Sergei Tretiak, and Jian-Xin Zhu. 2010. "Prediction of Excitation Energies for Conjugated Oligomers and Polymers from Time-Dependent Density Functional Theory" Materials 3, no. 5: 3430-3467. https://doi.org/10.3390/ma3053430
APA StyleTao, J., Tretiak, S., & Zhu, J.-X. (2010). Prediction of Excitation Energies for Conjugated Oligomers and Polymers from Time-Dependent Density Functional Theory. Materials, 3(5), 3430-3467. https://doi.org/10.3390/ma3053430




