Monitoring the Cure State of Thermosetting Resins by Ultrasound
Abstract
:1. Introduction
2. Basis of Ultrasonic Wave Propagation in Polymers
3. Contact Ultrasonic Cure Monitoring
3.1. Experimental Set-Up for Contact Ultrasonic Cure Monitoring
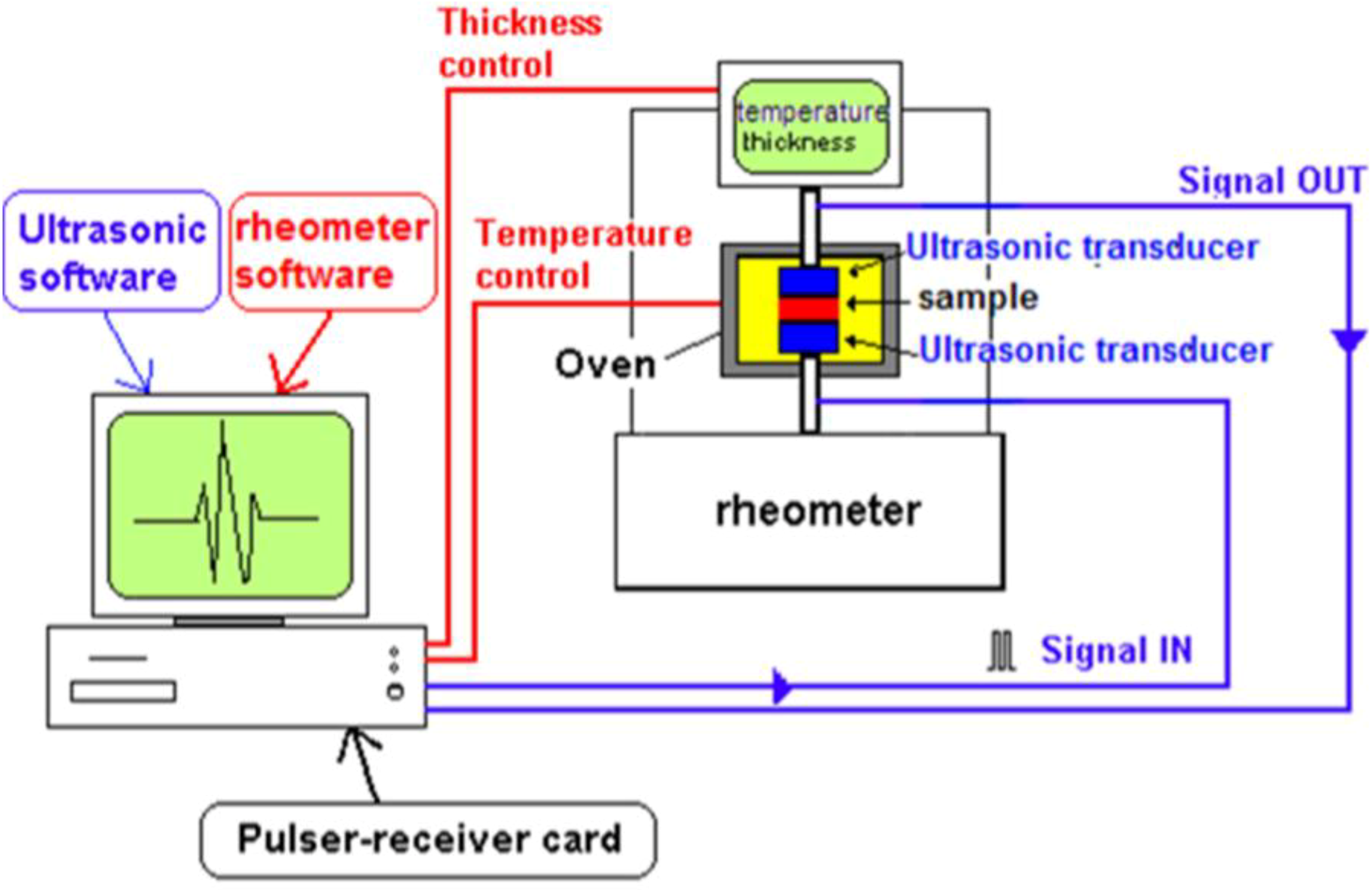
3.2. Results Obtained by Contact Ultrasonic Cure Monitoring
3.2.1. Phase Transformations During Cure: Gelation and Vitrification




3.2.2. Ultrasonic Degree of Conversion and Sensitivity to Vitrification

3.2.3. Determination of Elastic Properties after Gelation


3.2.4. Post-Cure Monitoring

4. Air-Coupled Ultrasonic Cure Monitoring
4.1. Experimental Set-Up for Air-Coupled Ultrasonic Cure Monitoring

4.2. Results Obtained by Air-Coupled Ultrasonic Cure Monitoring

5. Conclusions
Conflicts of Interest
References
- Lionetto, F.; Mascia, L.; Frigione, M. Evolution of transient states and properties of an epoxy–silica hybrid cured at ambient temperature. Eur. Polym. J. 2013, 49, 1298–1313. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Freuli, F.; Maffezzoli, A. The aspect ratio of epoxy matrix nanocomposites reinforced with graphene stacks. Polym. Eng. Sci. 2013, 53, 531–539. [Google Scholar]
- Manfredi, L.B.; Puglia, D.; Kenny, J.M.; Vazquez, A. Structure-properties relationship in resol/montmorillonite nanocomposites. J. Appl. Polym. Sci. 2007, 104, 3082–3089. [Google Scholar]
- Aggelis, D.G.; Paipetis, A.S. Monitoring of resin curing and hardening by ultrasound. Constr. Build. Mater. 2012, 26, 755–760. [Google Scholar] [CrossRef]
- Simitzis, J.; Triantou, D.; Soulis, S.; Tsangaris, G.; Zoumpoulakis, L.; Manolopoulos, E. Influence of backbone rigidity on the curing and the dielectric relaxations of unsaturated polyesters. J. Appl. Polym. Sci. 2011, 120, 1984–1993. [Google Scholar]
- Esposito Corcione, C.; Frigione, M. Characterization of nanocomposites by thermal analysis. Materials 2012, 5, 2960–2980. [Google Scholar]
- Stark, W.; Goering, H.; Michel, U.; Bayerl, H. Online monitoring of thermoset postcuring by dynamic mechanical thermal analysis DMTA. Polym. Test. 2009, 28, 561–566. [Google Scholar]
- Lionetto, F.; Maffezzoli, A. Relaxations during the postcure of unsaturated polyester networks by ultrasonic wave propagation, dynamic mechanical analysis and dielectric analysis. J. Polym. Sci. Polym. Phys. 2005, 43, 596–602. [Google Scholar] [CrossRef]
- Maistros, G.M.; Partridge, I.K. Monitoring autoclave cure in commercial carbon fibre/epoxy composites. Compos. Part B Eng. 1998, 29, 245–250. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Maffezzoli, A. Transport properties of graphite/epoxy composites: Thermal, permeability and dielectric characterization. Polym. Test. 2013, 32, 880–888. [Google Scholar] [CrossRef]
- Nikolic, G.; Zlatkovic, S.; Cakic, M.; Cakic, S.; Lacnjevac, C.; Rajic, Z. Fast fourier transform IR characterization of epoxy GY systems crosslinked with aliphatic and cycloaliphatic EH polyamine adducts. Sensors 2010, 10, 684–696. [Google Scholar] [CrossRef] [PubMed]
- Dessipri, E.; Minopoulou, E.; Chryssikos, G.D.; Gionis, V.; Paipetis, A.; Panayiotou, C. Use of FT-NIR spectroscopy for on-line monitoring of formal dehyde-based resin synthesis. Eur. Polym. J. 2003, 39, 1533–1540. [Google Scholar] [CrossRef]
- Alig, I.; Lellinger, D.; Agarwal, S.; Oehler, H. Monitoring of photopolymerization kinetics and network formation bycombined real-time near-infrared spectroscopy and ultrasonic reflectometry. React. Funct. Polym. 2013, 73, 316–322. [Google Scholar] [CrossRef]
- Merad, L.; Cochez, M.; Margueron, S.; Jauchem, F.; Ferriol, M.; Benyoucef, B.; Bourson, P. In situ monitoring of the curing of epoxy resins by Raman spectroscopy. Polym. Test. 2009, 28, 42–45. [Google Scholar]
- Schubel, P.J.; Crossley, R.J.; Boateng, E.K.G.; Hutchinson, J.R. Review of structural health and cure monitoring techniques for large wind turbine blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Lionetto, F.; Montagna, F.; Maffezzoli, A. Ultrasonic dynamic mechanical analysis of polymers. Appl. Rheol. 2005, 15, 326–335. [Google Scholar]
- Maffezzoli, A.; Quarta, E.; Luprano, V.A.M.; Montagna, G.; Nicolais, L. Cure monitoring of epoxy matrices for composites by ultrasonic wave propagation. J. Appl. Polym. Sci. 1999, 73, 1969–1977. [Google Scholar]
- Lionetto, F.; Rizzo, R.; Luprano, V.A.M.; Maffezzoli, A. Phase transformations during the cure of unsaturated polyester resins. Mater. Sci. Eng. A Struct. 2004, 370, 284–287. [Google Scholar] [CrossRef]
- Challis, R.E.; Blarel, F.; Unwin, M.E.; Paul, J.; Guo, X. Models of ultrasonic wave propagation in epoxy materials. IEEE T. Ultrason. Ferr. 2009, 56, 1225–1237. [Google Scholar]
- Mason, W.P.; Baker, W.O.; McSkimin, H.J.; Heiss, J.H. Measurement of shear elasticity and viscosity of liquids at ultrasonic frequencies. Phys. Rev. 1949, 75, 936–946. [Google Scholar] [CrossRef]
- Alig, I.; Tadjbakhsch, S.; Zosel, A. Comparison of ultrasonic shear wave and dynamic-mechanical measurements in acrylic-type copolymers. J. Polym. Sci. Polym. Phys. 1998, 36, 1703–1711. [Google Scholar]
- Challis, R.E.; Unwin, M.E.; Chadwick, D.L.; Freemantle, R.J.; Partridge, I.K.; Dare, D.J.; Karkanas, P.I. Following network formation in an epoxy/amine system by ultrasound, dielectric, and nuclear magnetic resonance measurements: A comparative study. J. Appl. Polym. Sci. 2003, 88, 1665–1675. [Google Scholar] [CrossRef]
- Ávila-Orta, C.; Espinoza-González, C.; Martínez-Colunga, G.; Bueno-Baqués, D.; Maffezzoli, A.; Lionetto, F. An overview of progress and current challenges in ultrasonic treatment of polymer melts. Adv. Polym. Techn. 2013, 32, E582–E602. [Google Scholar] [CrossRef]
- Krautkramer, J.; Krautkramer, H. Ultrasonic Testing of Materials; Springler-Verlag: Berlin, Germany, 1977. [Google Scholar]
- Van Krevelen, D.W. Properties of Polymers; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Lairez, D.; Adam, M.; Emery, J.R.; Durand, D. Rheological behavior of an epoxy/amine system near the gel point. Macromolecules 1992, 25, 286–289. [Google Scholar] [CrossRef]
- Fonseca, G.E.; Dubé, M.A.; Penlidis, A. A critical overview of sensors for monitoring polymerizations. Macromol. React. Eng. 2009, 3, 327–373. [Google Scholar]
- Perepechko, I. Acoustic Methods of Investigating Polymers; Mir Publishers: Moscow, Russia, 1975. [Google Scholar]
- Lionetto, F.; Maffezzoli, A. Polymer characterization by ultrasonic wave propagation. Adv. Polym. Tech. 2008, 27, 63–73. [Google Scholar] [CrossRef]
- Lionetto, F.; Maffezzoli, A.; Ottenhof, M.A.; Farhat, I.A.; Mitchell, J.R. Ultrasonic investigation of wheat starch retrogradation. J. Food Eng. 2006, 75, 258–266. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Pindinelli, C.; Montagna, G.; Luprano, V.A.M.; Maffezzoli, A. Network development during epoxy curing: Experimental ultrasonic data and theoretical predictions. Macromol. Symp. 2002, 180, 73–88. [Google Scholar] [CrossRef]
- Lionetto, F.; Montagna, F.; Maffezzoli, A. Ultrasonic transducers for cure monitoring: Design, modelling and validation. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
- Lionetto, F.; Sannino, A.; Maffezzoli, A. Ultrasonic monitoring of the network formation in superabsorbent cellulose based hydrogels. Polymer 2005, 46, 1796–1803. [Google Scholar] [CrossRef]
- Snijkers, F.; Vlassopoulos, D. Cone-partitioned-plate geometry for the ARES rheometer with temperature control. J. Rheol. 2011, 55, 1167–1186. [Google Scholar] [CrossRef]
- Enns, J.B.; Gillham, J. K. Time–temperature–transformation (TTT) cure diagram: Modeling the cure behavior of thermosets. J. Appl. Polym. Sci. 1983, 28, 2567–2591. [Google Scholar] [CrossRef]
- Lionetto, F.; Coluccia, G.; D’Antona, P.; Maffezzoli, A. Gelation of waxy crude oils by ultrasonic and dynamic mechanical analysis. Rheol. Acta 2007, 46, 601–609. [Google Scholar] [CrossRef]
- Van Assche, G.; Verdonck, E.; Van Mele, B. TMDSC and dynamic rheometry, gelation, vitrification and autoacceleration in the cure of an unsaturated polyester resin. J. Therm. Anal. Calorim. 2000, 59, 305–318. [Google Scholar] [CrossRef]
- Ellis, B. Chemistry and Technology of Epoxy Resins; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Matsukawa, M.; Nagai, I. Ultrasonic characterization of a polymerizing epoxy resin with imbalanced stoichiometry. J. Acoust. Soc. Am. 1996, 99, 2110–2115. [Google Scholar] [CrossRef]
- Babayevsky, P. G.; Gillham, J. K. Epoxy thermosetting systems: dynamic mechanical analysis of the reactions of aromatic diamines with the diglycidyl ether of bisphenol A. J. Appl. Polym. Sci. 1973, 17, 2067–2088. [Google Scholar] [CrossRef]
- Maffezzoli, A.; Trivisano, A.; Opalicki, M.; Mijovic, J.; Kenny, J.M. Correlation between dielectric and chemorheological properties during cure of epoxy-based composites. J. Mater. Sci. 1994, 29, 800–808. [Google Scholar] [CrossRef]
- Samet, N.; Maréchal, P.; Duflo, H. Ultrasonic characterization of a fluid layer using a broadband transducer. Ultrasonics 2012, 52, 427–434. [Google Scholar] [CrossRef] [PubMed]
- Samet, N.; Maréchal, P.; Duflo, H. Ultrasound monitoring of bubble size and velocity in a fluid model. NDTE Int. 2011, 44, 621–627. [Google Scholar] [CrossRef]
- Lionetto, F.; Tarzia, A.; Coluccia, M.; Maffezzoli, A. Air-coupled ultrasonic cure monitoring of unsaturated polyester resins. Macromol. Symp. 2007, 247, 50–58. [Google Scholar] [CrossRef]
- Yang, H.; Lee, L.J. Comparison of unsaturated polyester and vinylester resins in low temperature polymerization. J. Appl. Polym. Sci. 2001, 79, 1230–1242. [Google Scholar] [CrossRef]
- De La Caba, K.; Guerrero, P.; Eceiza, A.; Mondragon, I. Kinetic and rheological studies of two unsaturated polyester resins cured at different temperatures. Eur. Polym. J. 1997, 33, 19–23. [Google Scholar] [CrossRef]
- Winter, H.H. Can the gel point of a cross-linking polymer be detected by the G′-G″ crossover? Polym. Eng. Sci. 1987, 27, 1698–1702. [Google Scholar] [CrossRef]
- Odian, G. Principles of Polymerization; J. Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Yousefi, A.; Lafleur, P.G.; Gauvin, R. Kinetic studies of thermoset cure reactions: A review. Polym. Compos. 1997, 18, 157–168. [Google Scholar] [CrossRef]
- Monti, M.; Puglia, D.; Natali, M.; Torre, L.; Kenny, J.M. Effect of carbon nanofibers on the cure kinetics of unsaturated polyester resin: Thermal and chemorheological modeling. Compos. Sci. Technol. 2011, 71, 1507–1516. [Google Scholar]
- Chiacchiarelli, L.M.; Puri, I.; Puglia, D.; Kenny, J.M.; Torre, L. Cure kinetics of a highly reactive silica–polyurethane nanocomposite. Thermochim. Acta 2012, 549, 172–178. [Google Scholar] [CrossRef]
- Rivero, G.; Pettarin, V.; Vázquez, A.; Manfredi, L.B. Curing kinetics of a furan resin and its nanocomposites. Thermochim. Acta 2011, 516, 79–87. [Google Scholar] [CrossRef]
- Miller, D.R.; Macosko, C.V. A new derivation of postgel properties of network polymers. Macromolecules 1976, 9, 206–210. [Google Scholar] [CrossRef]
- Macosko, C.W.; Miller, D.R. A new derivation of average molecular weights of nonlinear polymers. Macromolecules 1976, 9, 199–205. [Google Scholar] [CrossRef]
- Nielsen, L.E.; Landel, R.F. Mechanical Properties of Polymers and Composites; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Lionetto, F.; Sannino, A.; Mensitieri, G.; Maffezzoli, A. Evaluation of the degree of crosslinking of cellulose-based superabsorbent hydrogels: a comparison between different techniques. Macromol. Symp. 2003, 200, 199–207. [Google Scholar] [CrossRef]
- Greco, A.; Gennaro, R.; Rizzo, M. Glass transition and cooperative rearranging regions in amorphous thermoplastic nanocomposites. Polym. Int. 2012, 61, 1326–1333. [Google Scholar] [CrossRef]
- Greco, A.; Rizzo, M.; Maffezzoli, M. Effect of the addition of organically modified nanofiller on the relaxation behavior of a thermoplastic amorphous matrix. Thermoch. Acta 2012, 543, 226–231. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Sci. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Senturia, S.D.; Sheppard, N.F. Dielectric analysis of thermoset cure. Adv. Polym. Sci. 1986, 80, 1–47. [Google Scholar]
- Lionetto, F.; Frigione, M. Mechanical and natural durability properties of wood treated with a novel organic preservative/consolidant product. Mater. Design 2009, 30, 3303–3307. [Google Scholar] [CrossRef]
- Lionetto, F.; del Sole, R.; Cannoletta, D.; Vasapollo, G.; Maffezzoli, A. Monitoring wood degradation during weathering by cellulose crystallinity. Materials 2012, 5, 1910–1922. [Google Scholar] [CrossRef]
- Bhardwaj, M.C. Non-destructive evaluation: Introduction of non-contact ultrasound. In Encyclopedia of Smart Materials; Schwartz, M., Ed.; John Wiley & Sons: New York, NY, USA, 2002; pp. 690–714. [Google Scholar]
- Blomme, E.; Bulcaen, D.; Declercq, F. Recent observations with air-coupled NDE in the frequency range of 650 kHz to 1.2 MHz. Ultrasonics 2002, 40, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Dixon, S.; Jacques, D.; Palmer, S.B. The measurement of shear and compression waves in curing epoxy adhesives using ultrasonic reflection and transmission techniques simultaneously. Meas. Sci. Technol. 2004, 15, 939–947. [Google Scholar] [CrossRef]
- Budzik, M.K.; Mascaro, B.; Jumel, J.; Castaings, M.; Shanahan, M.E.R. Monitoring of crosslinking of a DGEBA-PAMAM adhesive in composite/aluminium bonded joint using mechanical and ultra-sound techniques. Int. J. Adhes. Adhes. 2012, 35, 120–128. [Google Scholar] [CrossRef]
- Lionetto, F.; Tarzia, A.; Maffezzoli, A. Air-coupled ultrasound: A novel technique for monitoring the curing of thermosetting matrices. Ultrason. Ferrelectr. Freq. Control IEEE Trans. 2007, 54, 1437–1444. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lionetto, F.; Maffezzoli, A. Monitoring the Cure State of Thermosetting Resins by Ultrasound. Materials 2013, 6, 3783-3804. https://doi.org/10.3390/ma6093783
Lionetto F, Maffezzoli A. Monitoring the Cure State of Thermosetting Resins by Ultrasound. Materials. 2013; 6(9):3783-3804. https://doi.org/10.3390/ma6093783
Chicago/Turabian StyleLionetto, Francesca, and Alfonso Maffezzoli. 2013. "Monitoring the Cure State of Thermosetting Resins by Ultrasound" Materials 6, no. 9: 3783-3804. https://doi.org/10.3390/ma6093783
APA StyleLionetto, F., & Maffezzoli, A. (2013). Monitoring the Cure State of Thermosetting Resins by Ultrasound. Materials, 6(9), 3783-3804. https://doi.org/10.3390/ma6093783





