Theoretical Methods of Domain Structures in Ultrathin Ferroelectric Films: A Review
Abstract
:1. Introduction
2. Fundamentals of Ultrathin Ferroelectric Films (UFFs)
2.1. Polarization and Its Modern Theory
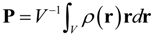
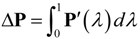
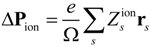
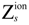 the charge of the nucleus located at the position rs. Based on the first order adiabatic perturbation theory, the electron contribution can be deduced as:
the charge of the nucleus located at the position rs. Based on the first order adiabatic perturbation theory, the electron contribution can be deduced as:
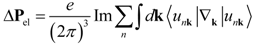
2.2. Ferroelectric Phase Transition
2.2.1. Phenomenological Theory of Ferroelectric Phase Transition: Landau Theory
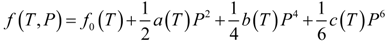
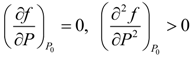
2.2.2. Microscopic Theory of Ferroelectric Phase Transition
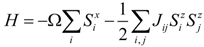
2.3. Domain Formation
2.3.1. The Formation of 180° Domain Pattern: Role of Depolarization Field

2.3.2. Elastic Compatible Domain Pattern
2.3.3. Domain Structures in Ultrathin Ferroelectric Films
2.4. Finite Size Effects
2.4.1. Polarization Relaxation near Surfaces/Interfaces

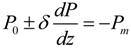

2.4.2. Interfacial Electrostatics
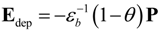
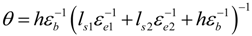 under the assumption of homogeneous polarization state. Here h is the thickness of the film. ɛe1, ɛe2 and ls1, ls2 are the dielectric constants and screening lengths of electrodes 1 and 2, respectively. ɛb is the background dielectric constants. The depolarization field is dependent on the screening ability of the electrodes and the thickness of the ferroelectric thin films. In UFFs, the question how effectively the strong depolarization field can be screened is central to the critical thickness for ferroelectricity [123,146,147,148,149]. The screening effect of the electrodes has also been reported to play vital roles in the formation of ferroelectric domains [127,150,151].
under the assumption of homogeneous polarization state. Here h is the thickness of the film. ɛe1, ɛe2 and ls1, ls2 are the dielectric constants and screening lengths of electrodes 1 and 2, respectively. ɛb is the background dielectric constants. The depolarization field is dependent on the screening ability of the electrodes and the thickness of the ferroelectric thin films. In UFFs, the question how effectively the strong depolarization field can be screened is central to the critical thickness for ferroelectricity [123,146,147,148,149]. The screening effect of the electrodes has also been reported to play vital roles in the formation of ferroelectric domains [127,150,151]. 
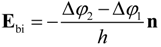
3. Simulation Methodologies
3.1. First-Principles Calculations

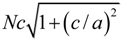 , a, and
, a, and 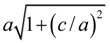 in the x, y, and z directions, respectively. Furthermore, Lubk et al. [174] studied the 71°, 109° and 180° domain walls in BiFeO3. Recently, Shimada et al. [175] adopted first-principles calculations to elucidate the stability of 180° domain wall in ultrathin PbTiO3 films. The characteristics of such a domain wall in PbTiO3/SrTiO3 superlattices have also been investigated by Aguado-Puente and Junquera [176].
in the x, y, and z directions, respectively. Furthermore, Lubk et al. [174] studied the 71°, 109° and 180° domain walls in BiFeO3. Recently, Shimada et al. [175] adopted first-principles calculations to elucidate the stability of 180° domain wall in ultrathin PbTiO3 films. The characteristics of such a domain wall in PbTiO3/SrTiO3 superlattices have also been investigated by Aguado-Puente and Junquera [176]. 
3.2. Molecular Dynamics Simulation
3.2.1. Potential Models for Ferroelectrics
3.2.2. Techniques of Calculating Interatomic Forces
3.2.3. Molecular Dynamics in Various Ensembles
3.3. Monte Carlo Simulation
3.4. Effective Hamiltonian Method
3.4.1. Construction of the Effective Hamiltonian
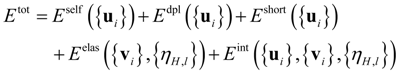
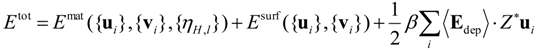
3.4.2. Numerical Implement
3.5. Phase Field Method
3.5.1. Free Energy
3.5.2. Evolution Equation
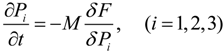
3.5.3. Numerical Methods of Calculating Electromechanical Fields
3.6. Multiscale Simulation
4. Results of Domain Structures in UFFs
4.1. Effects of Surface, Interface, and Electrostatic Boundary Conditions
4.1.1. Stability of Ferroelectricity and Polarization in UFFs
4.1.2. Domain Morphology and Evolution in UFFs

4.2. Effects of Strain

4.2.1. The Role of Misfit Strain


 at T = 75 °C and e0 = 0.0; (d) phase
at T = 75 °C and e0 = 0.0; (d) phase  at T = 50 °C and e0 = 0.2%; (e) phase
at T = 50 °C and e0 = 0.2%; (e) phase 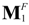 +
+ 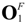 at T = −25 °C and e0 = 0.1%; (f) phase
at T = −25 °C and e0 = 0.1%; (f) phase 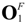 +
+ 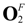 at T = 25°C and e0 = 0.25%; (g) phase
at T = 25°C and e0 = 0.25%; (g) phase 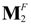 at T = −100 °C and e0 = 0.1%. (Reprinted with permission from [302]. Copyright 2006, AIP Publishing LLC.)
at T = −100 °C and e0 = 0.1%. (Reprinted with permission from [302]. Copyright 2006, AIP Publishing LLC.)
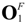 at T = 75 °C and e0 = 0.0; (d) phase
at T = 75 °C and e0 = 0.0; (d) phase 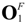 at T = 50 °C and e0 = 0.2%; (e) phase
at T = 50 °C and e0 = 0.2%; (e) phase 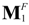 +
+ 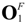 at T = −25 °C and e0 = 0.1%; (f) phase
at T = −25 °C and e0 = 0.1%; (f) phase 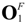 +
+ 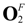 at T = 25°C and e0 = 0.25%; (g) phase
at T = 25°C and e0 = 0.25%; (g) phase 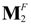 at T = −100 °C and e0 = 0.1%. (Reprinted with permission from [302]. Copyright 2006, AIP Publishing LLC.)
at T = −100 °C and e0 = 0.1%. (Reprinted with permission from [302]. Copyright 2006, AIP Publishing LLC.)


4.2.2. The Role of Misfit Dislocations
4.2.3. Manipulating Domain Structures in UFFs by External Mechanical Loads

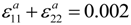 and (c)
and (c) 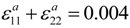 . Phase diagrams of equilibrium domain pattern in cell under (d) uniaxial strain and € biaxial strain. (f) and (g) the average polarization of the equilibrium domain patterns in z-direction, i.e., <P3>, in the initial cylindrical domain region, for the two loading cases (Reprint with permission from [330]).
. Phase diagrams of equilibrium domain pattern in cell under (d) uniaxial strain and € biaxial strain. (f) and (g) the average polarization of the equilibrium domain patterns in z-direction, i.e., <P3>, in the initial cylindrical domain region, for the two loading cases (Reprint with permission from [330]).
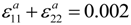 and (c)
and (c) 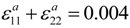 . Phase diagrams of equilibrium domain pattern in cell under (d) uniaxial strain and € biaxial strain. (f) and (g) the average polarization of the equilibrium domain patterns in z-direction, i.e., <P3>, in the initial cylindrical domain region, for the two loading cases (Reprint with permission from [330]).
. Phase diagrams of equilibrium domain pattern in cell under (d) uniaxial strain and € biaxial strain. (f) and (g) the average polarization of the equilibrium domain patterns in z-direction, i.e., <P3>, in the initial cylindrical domain region, for the two loading cases (Reprint with permission from [330]).
4.3. Effect of External Electrical Loads
4.3.1. Manipulating Domain Structures in UFFs by Homogeneous Electric Field

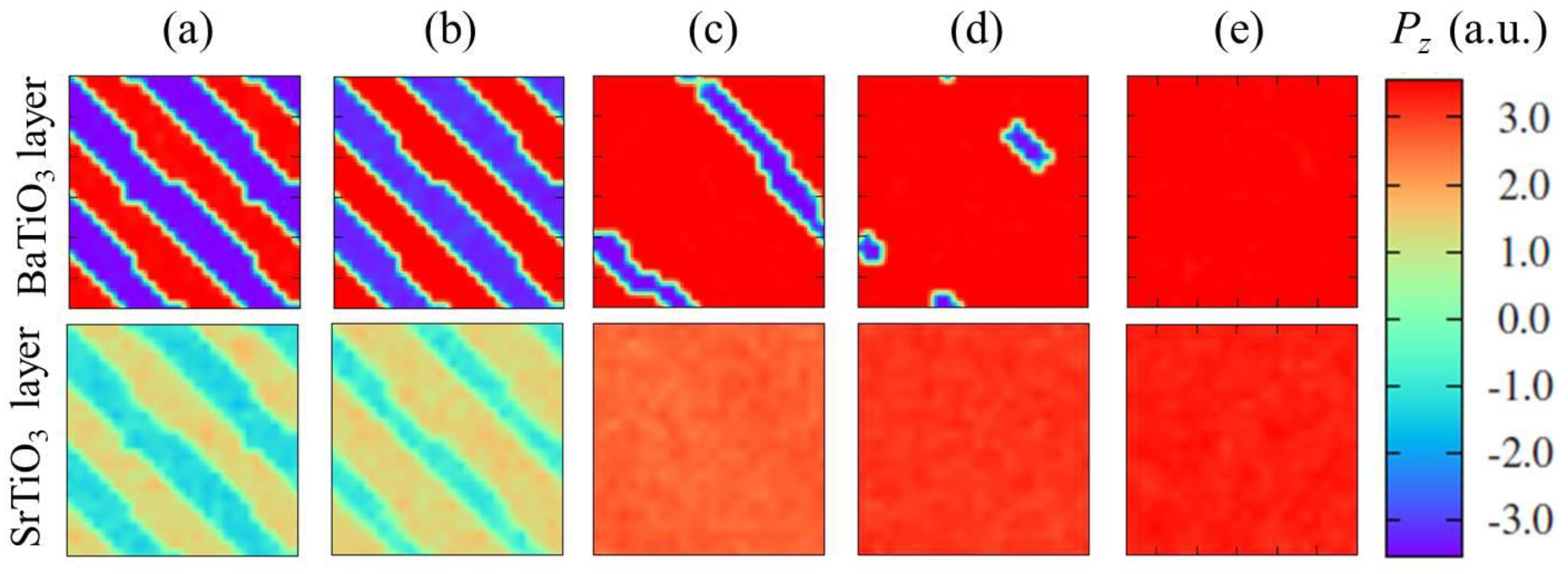
4.3.2. Manipulating Domain Structures in UFFs by Inhomogeneous Electric Field
4.4. Ferroelectric Domain Wall and Its Dynamics
4.4.1. Domain Wall Energy and Configuration


4.4.2. Dynamics of Domain Walls UFFs

4.5. Some Other Effects Related to Domain Structure in UFFs
5. Conclusions and Outlook
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Oxford University Press: New York, NY, USA, 2001; pp. 8–15. [Google Scholar]
- Sidorkin, A.S. Domain Structure in Ferroelectrics and Related Materials; Cambridge International Science Publishing: Great Abington, Cambridge, UK, 2006. [Google Scholar]
- Auciello, O.; Scott, J.F.; Ramesh, R. The physics of ferroelectric memories. Phys. Today 1998, 51, 22–27. [Google Scholar]
- Muralt, P. Ferroelectric thin films for micro-sensors and actuators: A review. J. Micromech. Microeng. 2000, 10, 136–146. [Google Scholar]
- Zhang, Q.; Whatmore, R.W. Improved ferroelectric and pyroelectric properties in Mn-doped lead zirconate titanate thin films. J. Appl. Phys. 2003, 94, 5228–5233. [Google Scholar]
- Wessels, B.W. Ferroelectric epitaxial thin films for integrated optics. Annu. Rev. Mater. Res. 2007, 37, 659–679. [Google Scholar]
- Tagantsev, A.; Cross, L.E.; Fousek, J. Domains in Ferroic Crystals and Thin Films; Springer: New York, NY, USA, 2010. [Google Scholar]
- Landau, L.; Lifshits, E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Zeitsch. Der Sow. 1935, 8, 153–169. [Google Scholar]
- Kittel, C. Theory of the structure of ferromagnetic domains in films and small particles. Phys. Rev. 1946, 70, 965–971. [Google Scholar]
- Mitsui, T.; Furuichi, J. Domain structure of rochelle salt and KH2PO4. Phys. Rev. 1953, 90, 193–202. [Google Scholar]
- Roitburd, A.L. Equilibrium structure of epitaxial layers. Phys. Stat. Sol. A 1976, 37, 329–339. [Google Scholar]
- Roytburd, A.L. Thermodynamics of polydomain heterostructures. I. Effect of macrostresses. J. Appl. Phys. 1998, 83, 228–238. [Google Scholar]
- Roytburd, A.L. Thermodynamics of polydomain heterostructures. II. Effect of microstresses. J. Appl. Phys. 1998, 83, 239–245. [Google Scholar]
- Roytburd, A.L. Thermodynamics of polydomain heterostructures. III. Domain stability map. J. Appl. Phys. 1998, 83, 4714–4723. [Google Scholar]
- Roytburd, A.L.; Alpay, S.P.; Bendersky, L.A.; Nagarajan, V.; Ramesh, R. Three-domain architecture of stress-free epitaxial ferroelectric films. J. Appl. Phys. 2001, 89, 553–556. [Google Scholar]
- Roytburd, A.L.; Roytburd, V; Slutsker, J. Domain structures in continuously graded ferroelectric films. Appl. Phys. Lett. 2009, 94, 152904:1–152904:3. [Google Scholar]
- Pertsev, N.A.; Zembilgotov, A.G.; Tagantsev, A.K. Effect of mechanical boundary conditions on phase diagrams of epitaxial ferroelectric thin films. Phys. Rev. Lett. 1998, 80, 1988–1991. [Google Scholar]
- Pertsev, N.A.; Zembilgotov, A.G.; Tagantsev, A.K. Equilibrium states and phase transitions in epitaxial ferroelectric thin films. Ferroelectrics. 1999, 223, 79–90. [Google Scholar]
- Tagantsev, A.K.; Pertsev, N.A.; Muralt, P.; Setter, N. Strain-induced diffuse dielectric anomaly and critical point in perovskite ferroelectric thin films. Phys. Rev. B. 2001, 65, 012104:1–012104:4. [Google Scholar]
- Pertsev, N.A.; Kukhar, V.G.; Kohlstedt, H.; Waser, R. Phase diagrams and properties of single-domain epitaxial Pb(Zr1-xTix)O3 thin films. Phys. Rev. B. 2003, 67, 054107:1–054107:10. [Google Scholar]
- Pertsev, N.A.; Tagantsev, A.K.; Setter, N. Phase transitions and strain-induced ferroelectricity in SrTiO3 epitaxial thin films. Phys. Rev. B 2000, 61, R825–R829. [Google Scholar]
- Pertsev, N.A.; Koukhar, V.G. Polarization instability in polydomain ferroelectric epitaxial thin films and the formation of heterophase structures. Phys. Rev. Lett. 2000, 84, 3722–3725. [Google Scholar]
- Emelyanov, A.Y.; Pertsev, N.A.; Kholkin, A.L. Effect of external stress on ferroelectricity in epitaxial thin films. Phys. Rev. B 2002, 66, 214108:1–214108:8. [Google Scholar]
- Rabe, K.M.; Scott, J.F.; Dawber, M. Physics of thin-film ferroelectric oxides. Rev. Mod. Phys. 2005, 77, 1083–1130. [Google Scholar]
- Kornev, I.; Fu, H.; Bellaiche, L. Properties of ferroelectric ultrathin films from first principles. In Frontiers of Ferroelectricity: A Special Issue of the Journal of Materials Science; Lang, S.B., Chan, H.L.W., Eds.; Springer: New York, NY, USA, 2007; pp. 137–145. [Google Scholar]
- Rabe, K.M. Theoretical investigations of epitaxial strain effects in ferroelectric oxide thin films and superlattices. Curr. Opin. Solid State Mater. Sci. 2005, 9, 122–127. [Google Scholar]
- Chen, L.Q. Phase-field method of phase transitions/domain structures in ferroelectric thin films: A review. J. Am. Ceram. Soc. 2008, 91, 1835–1844. [Google Scholar]
- Resta, R. Theory of the electric polarization in crystals. Ferroelectrics 1992, 136, 51–55. [Google Scholar]
- Vanderbilt, D.; King-Smith, R.D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651–1654. [Google Scholar]
- Shapere, A.; Wilczek, F. Geometric Phases in Physics; World Scientific: Singapore, 1989. [Google Scholar]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747–2750. [Google Scholar]
- Posternak, M.; Baldereschi, A.; Resta, R. Towards a quantum theory of polarization in ferroelectrics: The case of KNbO3. Phys. Rev. Lett. 1993, 70, 1010–1013. [Google Scholar]
- King-Smith, R.D.; Vanderbilt, D. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 1993, 48, 4442–4455. [Google Scholar]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar]
- Resta, R. Modern theory of polarization in ferroelectrics. Ferroelectrics 1994, 151, 49–58. [Google Scholar]
- Resta, R.; Vanderbilt, D. Theory of polarization: A modern approach. In Physics of Ferroelectrics: A Modern Perspective; Rabe, K.M., Ahn, C.H., Triscone, J.M., Eds.; Springer: Berlin, German, 2007; pp. 31–68. [Google Scholar]
- Raffaele, R. Manifestations of Berry’s phase in molecules and condensed matter. J. Phys. Condens. Matter 2000, 12, R107–R143. [Google Scholar]
- Landau, L.D. Theory of phase transformations. I. Zh. Eksp. Teor. Fiz. 1937, 7, 19–32. [Google Scholar]
- Landau, L.D. Theory of phase transformations. II. Zh. Eksp. Teor. Fiz. 1937, 7, 627–632. [Google Scholar]
- Devonshire, A.F. XCVI. Theory of barium titanate. Philos. Mag. Ser. 7 1949, 40, 1040–1063. [Google Scholar]
- Devonshire, A.F. CIX. Theory of barium titanate—Part II. Philos. Mag. Ser. 7 1951, 42, 1065–1079. [Google Scholar]
- Cochran, W. Crystal stability and the theory of ferroelectricity. Phys. Rev. Lett. 1959, 3, 412–414. [Google Scholar]
- Cochran, W. Crystal stability and the theory of ferroelectricity. Adv. Phys. 1960, 9, 387–423. [Google Scholar]
- Cochran, W. Crystal stability and the theory of ferroelectricity part II. Piezoelectric crystals. Adv. Phys. 1961, 10, 401–420. [Google Scholar]
- Anderson, P.W. Qualitative considerations on the statistics of the phase transition in BaTiO3-type ferroelectrics. In Fizika Dielektrikov; Skanavi, G.I., Ed.; Akad. Nauk SSR: Mascow, Russia, 1960; pp. 290–294. [Google Scholar]
- De Gennes, P.G. Collective motions of hydrogen bonds. Solid State Commun. 1963, 1, 132–137. [Google Scholar]
- Blinc, R.; Žekš, B. Soft Modes in Ferroelectrics and Antiferroelectrics; North-Holland Publishing Company: New York, NY, USA, 1974. [Google Scholar]
- Wang, C.L.; Zhong, W.L.; Zhang, P.L. The Curie temperature of ultra-thin ferroelectric films. J. Phys. Condens. Matter 1992, 3, 4743–4749. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Elsevier Science: Singapore, 1996; pp. 446–516. [Google Scholar]
- Ginzburg, V.L.; Levanyuk, A.P.; Sobyanin, A.A. Comments on the region of applicability of the landau theory for structural phase transitions. Ferroelectrics 1987, 73, 171–182. [Google Scholar]
- Benhouria, Y.; Essaoudi, I.; Ainane, A.; Oubelkacem, A.; Saber, M.; Dujardin, F. Pyroelectric, dielectric properties and hysteresis loops of a ferroelectric bilayer system described by the transverse Ising model with long-range interactions. Phys. Scr. 2012, 86, 045704:1–045704:8. [Google Scholar]
- Kittel, C. Theory of antiferroelectric crystals. Phys. Rev. 1951, 82, 729–732. [Google Scholar]
- Devonshire, A.F. Theory of ferroelectrics. Adv. Phys. 1954, 3, 85–130. [Google Scholar]
- Fatuzzo, E.; Merz, W.J. Ferroelectricity; North-Holland: Amsterdam, the Netherlands, 1967. [Google Scholar]
- Müser, H.E.; Petersson, J. Thermodynamic theory of relaxation phenomena. Fortschr. Phys. 1971, 19, 559–612. [Google Scholar]
- Strukov, B.A.; Levanyuk, A.P. Ferroelectric Phenomena in Crystals; Springer: Berlin, German, 1998; pp. 119–134. [Google Scholar]
- Alpay, S.P.; Misirlioglu, I.B.; Nagarajan, V. Comment on “Simulation of interface dislocations effect on polarization distribution of ferroelectric thin films”. Appl. Phys. Lett. 2007, 90, 236101:1–236101:2. [Google Scholar]
- Misirlioglu, I.B.; Akcay, G.; Zhong, S.; Alpay, S.P. Interface effects in ferroelectric bilayers and heterostructures. J. Appl. Phys. 2007, 101, 036107:1–036107:3. [Google Scholar]
- Woo, C.H.; Zheng, Y. Depolarization in modeling nano-scale ferroelectrics using the Landau free energy functional. Appl. Phys. A 2008, 91, 59–63. [Google Scholar]
- Zheng, Y.; Woo, C.H. Thermodynamic modeling of critical properties of ferroelectric superlattices in nano-scale. Appl. Phys. A 2009, 97, 617–626. [Google Scholar]
- Tagantsev, A.K. Landau expansion for ferroelectrics: Which variable to use? Ferroelectrics 2008, 375, 19–27. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Weak ferroelectrics. Ferroelectrics 1988, 79, 57–60. [Google Scholar]
- Comes, R.; Lambert, M.; Guinier, A. The chain structure of BaTiO3 and KNbO3. Solid State Commun. 1968, 6, 715–719. [Google Scholar]
- Itoh, K.; Zeng, L.Z.; Nakamura, E.; Mishima, N. Crystal structure of BaTiO3 in the cubic phase. Ferroelectrics 1985, 63, 29–37. [Google Scholar]
- Chen, J.; Fan, C.; Li, Q.; Feng, D. Transmission electron microscope studies of paraferroelectric phase transitions in BaTiO3 and KNbO3. J. Phys. C Solid State Phys. 1988, 21, 2255–2266. [Google Scholar]
- Nelmes, R.J.; Piltz, R.O.; Kuhs, W.F.; Tun, Z.; Restori, R. Order-disorder behaviour in the transition of PbTiO3. Ferroelectrics 1990, 108, 165–170. [Google Scholar]
- Fontana, M.D.; Idrissi, H.; Kugel, G.E.; Wojcik, K. Raman spectrum in PbTiO3 re-examined: Dynamics of the soft phonon and the central peak. J. Phys. Condens. Matter 1991, 3, 8695–8705. [Google Scholar]
- Gillis, N.S.; Koehler, T.R. Phase transitions in a model of interacting anharmonic oscillators. Phys. Rev. B 1973, 7, 4980–4999. [Google Scholar]
- Aubry, S. A unified approach to the interpretation of displacive and order-disorder systems. I. Thermodynamical aspect. J. Chem. Phys. 1975, 62, 3217–3229. [Google Scholar]
- Stamenkovic, S.; Plakida, N.M.; Aksienov, V.L.; Siklos, T. On a possible unified theory of ferroelectricity. Ferroelectrics 1976, 14, 655–659. [Google Scholar]
- Bersuker, I.B.; Vekhter, B.G. The vibronic theory of ferroelectricity. Ferroelectrics 1978, 19, 137–150. [Google Scholar]
- Krakauer, H.; Cohen, R.E. Lattice dynamics and origin of ferroelectricity in BaTiO3: Linearized-augmented-plane-wave total-energy calculations. Phys. Rev. B 1990, 42, 6416–6423. [Google Scholar]
- Cohen, R.E.; Krakauer, H. Electronic structure studies of the differences in ferroelectric behavior of BaTiO3 and PbTiO3. Ferroelectrics 1992, 136, 65–83. [Google Scholar]
- Cohen, R.E. Origin of ferroelectricity in perovskite oxides. Nature 1992, 358, 136–138. [Google Scholar]
- Raffaele, R. Ab initio simulation of the properties of ferroelectric materials. Model. Simul. Mater. Sci. Eng. 2003, 11, R69–R96. [Google Scholar]
- Scott, B.A.; Burns, G. Lattice modes in ferroelectric perovskites: PbTiO3. Phys. Rev. B 1973, 7, 3088–3101. [Google Scholar]
- Tinkham, M.; Barker, A.S. Far-Infrared ferroelectric vibration mode in SrTiO3. Phys. Rev. 1962, 125, 1527–1530. [Google Scholar]
- Cowley, R.A. Temperature dependence of a transverse optic mode in strontium titanate. Phys. Rev. Lett. 1962, 9, 159–161. [Google Scholar]
- Blinc, R. The soft mode concept and the history of ferroelectricity. Ferroelectrics 1987, 74, 301–303. [Google Scholar]
- Cowley, R.A. Soft modes and structural phase transitions. Integr. Ferroelectr. 2012, 133, 109–117. [Google Scholar]
- Zhong, W.L.; Zhang, P.L.; Wang, Y.G. Surface effects and size effects on ferroelectrics with a first-order phase transition. Phys. Rev. B 1996, 53, 11439–11443. [Google Scholar]
- Wang, X.S.; Wang, C.L.; Zhong, W.L. First-order phase transition in ferroelectric superlattice described by the transverse Ising model. Solid State Commun. 2002, 122, 311–315. [Google Scholar]
- Stinchcombe, R.B. Ising model in a transverse field: I. Basic theory. J. Phys. C Solid State Phys. 1973, 6, 2459–2483. [Google Scholar]
- Lage, E.J.S.; Stinchcombe, R.B. The bond-diluted problem in the transverse Ising model. J. Phys. C Solid State Phys. 1979, 12, 1319–1329. [Google Scholar]
- Qu, B.D.; Zhang, P.L.; Wang, Y.G.; Zhong, W.L. Thickness dependence of the dielectric susceptibility of ferroelectric thin films. Phys. Rev. B 1994, 50, 12375–12380. [Google Scholar]
- Wang, Y.G.; Zhong, W.L.; Zhang, P.L. Ferroelectric films described by transverse ising model with long-range interactions. Solid State Commun. 1997, 101, 807–810. [Google Scholar]
- Xin, Y.; Wang, C.L.; Zhong, W.L.; Zhang, P.L. Pyroelectric properties of ferroelectric superlattice on transverse Ising model. Solid State Commun. 1999, 110, 265–269. [Google Scholar]
- Sy, H.K. Surface modification in ferroelectric transitions. J. Phys. Condens. Matter 1993, 5, 1213–1220. [Google Scholar]
- Oubelkacem, A.; Esssaoudi, I.; Ainane, A.; Saber, M.; Dujardin, F.; Gonzalez, J. The effects of surface transition layers on the phase diagrams and the pyroelectric properties of ferroelectric thin films. Phys. Stat. Sol. B 2009, 246, 1723–1730. [Google Scholar]
- Arlt, G. Twinning in ferroelectric and ferroelastic ceramics: Stress relif. J. Mater. Sci. 1990, 25, 2655–2666. [Google Scholar]
- Fesenko, E.G.; Gavrilyatchenko, V.G.; Semenchev, A.F. Domain structure of multiaxial ferroelectric crystals. Ferroelectrics 1989, 100, 195–207. [Google Scholar]
- Lee, K.S.; Choi, J.H.; Lee, J.Y.; Baik, S. Domain formation in epitaxial Pb(Zr, Ti)O3 thin films. J. Appl. Phys. 2001, 90, 4095–4102. [Google Scholar]
- Kobayashi, S.; Ikuhara, Y.; Yamamoto, T. Labyrinth-type domain structure of heteroepitaxial SrMnO2.5 film. Appl. Phys. Lett. 2013, 102, 231911:1–231911:5. [Google Scholar]
- Kighelman, Z.; Damjanovic, D.; Cantoni, M.; Setter, N. Properties of ferroelectric PbTiO3 thin films. J. Appl. Phys. 2002, 91, 1495–1501. [Google Scholar]
- Chae, S.C.; Horibe, Y.; Jeong, D.Y.; Lee, N.; Iida, K.; Tanimura, M.; Cheong, S.-W. Evolution of the domain topology in a ferroelectric. Phys. Rev. Lett. 2013, 110, 167601:1–167601:5. [Google Scholar]
- Rodriguez, B.J.; Gao, X.S.; Liu, L.F.; Lee, W.; Naumov, I.I.; Bratkovsky, A.M.; Hesse, D.; Alexe, M. Vortex polarization states in nanoscale ferroelectric arrays. Nano. Lett. 2009, 9, 1127–1131. [Google Scholar]
- Cheong, S.-W.; Mostovoy, A.M. Multiferroics: a magnetic twist for ferroelectrictiy. Nature 2007, 6, 13–20. [Google Scholar]
- Fousek, J.; Janovec, V. The orientation of domain walls in twinned ferroelectric crystals. J. Appl. Phys. 1969, 40, 135–142. [Google Scholar]
- Sapriel, J. Domain-wall orientations in ferroelastics. Phys. Rev. B 1975, 12, 5128–5140. [Google Scholar]
- Janovec, V. A symmetry approach to domain structures. Ferroelectrics 1976, 12, 43–53. [Google Scholar]
- Hooton, J.A.; Merz, W.J. Etch patterns and ferroelectric domains in BaTiO3 single crystals. Phys. Rev. 1955, 98, 409–413. [Google Scholar]
- Shu, Y.C.; Bhattacharya, K. Domain patterns and macroscopic behaviour of ferroelectric materials. Philo. Maga. B 2001, 81, 2021–2054. [Google Scholar]
- Pompe, W.; Gong, X.; Suo, Z.; Speck, J.S. Elastic energy release due to domain formation in the strained epitaxy of ferroelectric and ferroelastic films. J. Appl. Phys. 1993, 74, 6012–6019. [Google Scholar]
- Speck, J. S.; Pompe, W. Domain configurations due to multiple misfit relaxation mechanisms in epitaxial ferroelectric thin films. I. Theory. J. Appl. Phys. 1994, 76, 466–476. [Google Scholar]
- Speck, J. S.; Daykin, A.C.; Seifert, A.; Romanov, A.E.; Pompe, W. Domain configurations due to multiple misfit relaxation mechanisms in epitaxial ferroelectric thin films. III. Interfacial defects and domain misorientations. J. Appl. Phys. 1995, 78, 1696–1706. [Google Scholar]
- Pertsev, N.A.; Zembilgotov, A.G. Energetics and geometry of 90° domain structures in epitaxial ferroelectric and ferroelastic films. J. Appl. Phys. 1995, 78, 6170–6180. [Google Scholar]
- Pertsev, N.A.; Zembilgotov, A.G. Domain populations in epitaxial ferroelectric thin films: Theoretical calculations and comparison with experiment. J. Appl. Phys. 1996, 80, 6401–6406. [Google Scholar]
- Choi, K.J.; Biegalski, M.; Li, Y.L.; Sharan, A.; Schubert, J.; Uecker, R.; Reiche, P.; Chen, Y.B.; Pan, X.Q.; Gopalan, V.; et al. Enhancement of ferroelectricity in strained BaTiO3 thin films. Science 2004, 306, 1005–1009. [Google Scholar]
- Haeni, J.H.; Irvin, P.; Chang, W.; Uecker, R.; Reiche, P.; Li, Y.L.; Choudhury, S.; Tian, W.; Hawley, M.E.; Craigo, B.; et al. Room-temperature ferroelectricity in strained SrTiO3. Science 2004, 430, 758–761. [Google Scholar]
- Schlom, D.G.; Chen, L.-Q.; Eom, C.-B.; Rabe, K.M.; Streiffer, S.K.; Triscone, J.-M. Strain tuning of ferroelectric thin films. Annu. Rev. Mater. Res. 2007, 37, 589–626. [Google Scholar]
- Zembilgotov, A.G.; Pertsev, N.A.; Böttger, U.; Waser, R. Effect of anisotropic in-plane strains on phase states and dielectric properties of epitaxial ferroelectric thin films. Appl. Phys. Lett. 2005, 86, 052903:1–052903:3. [Google Scholar]
- Wang, J.; Zhang, T.-Y. Effect of nonequally biaxial misfit strains on the phase diagram and dielectric properties of epitaxial ferroelectric thin films. Appl. Phys. Lett. 2005, 86, 192905:1–192905:3. [Google Scholar]
- Qiu, J.H.; Jiang, Q. Effect of external mechanical loading on the phase diagrams and dielectric properties in epitaxial ferroelectric thin films with anisotropic in-plane misfit strians. J. Appl. Phys. 2007, 101, 034110:1–034110:7. [Google Scholar]
- Alpay, S.P.; Misirlioglu, I.B.; Nagarajan, V.; Ramesh, R. Can interface dislocations degrade ferroelectric properties? Appl. Phys. Lett. 2004, 85, 2044–2046. [Google Scholar]
- Balzar, D.; Ramakrishnan, P.A.; Spagnol, P.; Mani, S.; Hermann, A.M.; Matin, M.A. Influence of strains and defects on ferroelectric and dielectric properties of thin-film barium-strontium titanates. Jpn. J. Appl. Phys. 2002, 41, 6628–6632. [Google Scholar] [CrossRef]
- Balzar, D.; Ramakrishnan, P.A.; Hermann, A.M. Defect-related lattice strain and the transition temperature in ferroelectric thin films. Phys. Rev. B 2004, 70, 092103:1–092103:4. [Google Scholar]
- Kopal, A.; Mokrýa, P.; Fousek, J.; Bahníka, T. Displacements of 180° domain walls in electroded ferroelectric single crystals: The effect of surface layers on restoring force. Ferroelectrics 1999, 223, 127–134. [Google Scholar]
- Bratkovsky, A.M.; Levanyuk, A.P. Abrupt appearance of the domain pattern and fatigue of thin ferroelectric films. Phys. Rev. Lett. 2000, 84, 3177–3180. [Google Scholar]
- Streiffer, S.K.; Eastman, J.A.; Fong, D.D.; Thompson, C.; Munkholm, A.; Ramana Murty, M.V.; Auciello, O.; Bai, G.R.; Stephenson, G.B. Observation of nanoscale 180° stripe domains in ferroelectric PbTiO3 thin films. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.-Y. Influence of depolarizing field on polarization states in epitaxial ferroelectric thin films with nonequally biaxial misfit strains. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Urtiev, F.A.; Kukhar, V.G.; Pertsev, N.A. Phase diagrams of single-domain ferroelectric-dielectric superlattices. Appl. Phys. Lett. 2007, 90, 252910:1–252910:3. [Google Scholar]
- Gerra, G.; Tagantsev, A.K.; Setter, N. Ferroelectricity in asymmetric metal-ferroelectric-metal heterostructures: A combined first-principles-phenomenological approach. Phys. Rev. Lett. 2007, 98, 207601:1–207601:4. [Google Scholar]
- Tagantsev, A.K.; Gerra, G.; Setter, N. Short-range and long-range contributions to the size effect in metal-ferroelectric-metal heterostructures. Phys. Rev. B 2008, 77, 174111:1–174111:9. [Google Scholar]
- Ma, D.C.; Zheng, Y.; Woo, C.H. Surface and size effects on phase diagrams of ferroelectric thin films. Appl. Phys. Lett. 2009, 95, 262901:1–262901:3. [Google Scholar]
- Zheng, Y.; Cai, M.Q.; Woo, C.H. Critical properties of symmetric nanoscale metal-ferroelectric-metal capacitors. Acta. Mater. 2010, 58, 3050–3058. [Google Scholar]
- Zheng, Y.; Chen, W.J.; Luo, X.; Wang, B.; Woo, C.H. Critical properties of nanoscale asymmetric ferroelectric tunnel junctions or capacitors. Acta. Mater. 2012, 60, 1857–1870. [Google Scholar]
- Chen, W.J.; Zheng, Y.; Wang, B. Electrodes controlling phase diagrams of symmetric ferroelectric tunneling junctions or capacitors. Appl. Phys. Lett. 2011, 98, 222902:1–222902:3. [Google Scholar]
- Chen, W.J.; Zheng, Y.; Wang, B.; Ma, D.C.; Wu, C.M. Misfit strain-temperature phase diagrams and domain stability of asymmetric ferroelectric capacitors: Thermodynamic calculation and phase-field simulation. J. Appl. Phys. 2014, 115, 094101:1–094101:10. [Google Scholar]
- De Gennes, P.G. Superconductivity of Metals and Alloys; Westview Press: Boulder, CO, USA, 1999. [Google Scholar]
- Guyon, E.; Mitescu, C.D. Comparative study of size effects in solid and liquid films. Thin Solid Films 1972, 12, 355–366. [Google Scholar]
- Mills, D.L. Surface effects in magnetic crystals near the ordering temperature. Phys. Rev. B 1971, 3, 3887–3895. [Google Scholar]
- Kretschmer, R.; Binder, K. Surface effects on phase transitions in ferroelectrics and dipolar magnets. Phys. Rev. B 1979, 20, 1065–1076. [Google Scholar]
- Okuyama, M.; Ishibashi, Y. Ferroelectric Thin Films: Basic Properties and Device Physics for Memory Applications; Springer: Berlin, German, 2005; p. 5. [Google Scholar]
- Tilley, D.R.; Žekš, B. Landau theory of phase transitions in thick films. Solid State Commun. 1984, 49, 823–828. [Google Scholar]
- Li, S.; Eastman, J.A.; Li, Z.; Foster, C.M.; Newnham, R.E.; Cross, L.E. Size effects in nanostructured ferroelectrics. Phys. Lett. A 1996, 212, 341–346. [Google Scholar]
- Glinchuk, M.D.; Morozovskaya, A.N. Effect of surface tension and depolarization field on ferroelectric nanomaterial properties. Phys. Stat. Sol. B 2003, 238, 81–91. [Google Scholar]
- Glinchuk, M.D.; Morozovska, A.N. The internal electric field originating from the mismatch effect and its influence on ferroelectric thin film properties. J. Phys. Condens. Matter 2004, 16, 3517–3531. [Google Scholar]
- Duan, C.; Sabirianov, R.F.; Mei, W.; Jaswal, S.S.; Tsymbal, E.Y. Interface effect on ferroelectricity at the nanoscale. Nano. Lett. 2006, 6, 483–487. [Google Scholar]
- Stachiotti, M.G.; Tinte, S. Surface effects and ferroelectric phase transitions in BaTiO3 ultrathin films. Phys. Rev. B 2001, 64, 235403:1–235403:7. [Google Scholar]
- Sepliarsky, M.; Stachiotti, M.G.; Migoni, R.L. Surface reconstruction and ferroelectricity in PbTiO3 thin films. Phys. Rev. B 2005, 72, 014110:1–014110:6. [Google Scholar]
- Almahmoud, E.; Navtsenya, Y.; Kornev, I.; Fu, H.; Bellaiche, L. Properties of Pb(Zr,Ti)O3 ultrathin films under stress-free and open-circuit electrical boundary conditions. Phys. Rev. B 2004, 70, 220102:1–220102:4. [Google Scholar]
- Ghosez, P.; Rabe, K.M. Microscopic model of ferroelectricity in stress-free PbTiO3 ultrathin films. Appl. Phys. Lett. 2000, 76, 2767–2769. [Google Scholar]
- Dawber, M.; Chandra, P.; Littlewood, P.B.; Scott, J.F. Depolarization corrections to the coercive field in thin-film ferroelectrics. J. Phys. Condens. Matter 2003, 15, L393:1–L393:6. [Google Scholar] [CrossRef]
- Dawber, M.; Stucki, N.; Lichtensteiger, C.; Gariglio, S.; Triscone, J.-M. New phenomena at the interfaces of very thin ferroelectric oxides. J. Phys. Condens. Matter 2008, 20, 264015:1–264015:6. [Google Scholar]
- Mehta, R.R.; Silverman, B.D.; Jacobs, J.T. Depolarization fields in thin ferroelectric films. J. Appl. Phys. 1973, 44, 3379–3385. [Google Scholar]
- Junquera, J.; Ghosez, P. Critical thickness for ferroelectricity in perovskite ultrathin films. Nature 2003, 422, 506–509. [Google Scholar]
- Sai, N.; Kolpak, A.M.; Rappe, A.M. Ferroelectricity in ultrathin perovskite films. Phys. Rev. B 2005, 72, 020101:1–020101:4. [Google Scholar]
- Umeno, Y.; Meyer, B.; Elsässer, C.; Gumbsch, P. Ab initio study of the critical thickness for ferroelectricity in ultrathin Pt/PbTiO3/Pt films. Phys. Rev. B 2006, 74, 060101:1–060101:4. [Google Scholar]
- Al-Saidi, W.A.; Rappe, A.M. Density functional study of PbTiO3 nanocapacitors with Pt and Au electrodes. Phys. Rev. B 2010, 82, 155304:1–155304:7. [Google Scholar]
- Li, Y.L.; Hu, S.Y.; Liu, Z.K.; Chen, L.Q. Effect of electrical boundary conditions on ferroelectric domain structures in thin films. Appl. Phys. Lett. 2002, 81, 427–429. [Google Scholar]
- Kornev, I.; Fu, H.; Bellaiche, L. Ultrathin films of ferroelectric solid solutions under a residual depolarizing field. Phys. Rev. Lett. 2004, 93, 196104:1–196104:4. [Google Scholar]
- Chen, W.J.; Zheng, Y.; Luo, X.; Wang, B.; Woo, C.H. Ab initio study on the size effect of symmetric and asymmetric ferroelectric tunnel junctions: A comprehensive picture with regard to the details of electrode/ferroelectric interfaces. J. Appl. Phys. 2013, 114, 064105:1–064105:14. [Google Scholar]
- Sághi-szabó, G.; Cohen, R.E. Long-range order effects in Pb(Zr1/2Ti1/2)O3. Ferroelectrics 1997, 194, 287–298. [Google Scholar]
- Wang, Y.X.; Zhong, W.L.; Wang, C.L.; Zhang, P.L.; Peng, Y.P. Electronic structure of NaNO2 in the ferroelectric phase. Solid State Commun. 1999, 112, 495–498. [Google Scholar]
- Cohen, R.E.; Inbar, I. Comparison of the electronic structures and energetics of ferroelectric LiNbO3 and LiTaO3. Phys. Rev. B 1996, 53, 1193–1204. [Google Scholar]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar]
- Cora, F.; Catlow, C.R.A. QM investigations on perovskite-structured transition metal oxides: Bulk, surfaces and interfaces. Faraday Discuss. 1999, 114, 421–442. [Google Scholar]
- Yaschenko, E.; Resca, L.; Resta, R.; Fu, L. Hartree-Fock studies of surface properties of BaTiO3. Phys. Rev. B 1999, 60, 2697–2703. [Google Scholar]
- Cohen, R.E. Periodic slab LAPW computations for ferroelectric BaTiO3. J. Phys. Chem. Solids 1996, 57, 1393–1396. [Google Scholar]
- Cohen, R.E. Surface effects in ferroelectrics: Periodic slab computations for BaTiO3. Ferroelectrics 1997, 194, 323–342. [Google Scholar]
- Vanderbilt, D.; Padilla, J. Ab initio study of BaTiO3 surfaces. Phys. Rev. B 1997, 56, 1625–1631. [Google Scholar]
- Padilla, J.; Vanderbilt, D. Ab initio study of SrTiO3 surfaces. Surf. Sci. 1998, 418, 64–70. [Google Scholar]
- Bengtsson, L. Dipole correction for surface supercell calculations. Phys. Rev. B 1999, 59, 12301–12304. [Google Scholar]
- Meyer, B.; Vanderbilt, D. Ab initio study of BaTiO3 and PbTiO3 surfaces in external electric fields. Phys. Rev. B 2001, 63, 205426:1–205426:10. [Google Scholar]
- Neaton, J.B.; Rabe, K.M. Theory of polarization enhancement in epitaxial BaTiO3/SrTiO3 superlattices. Appl. Phys. Lett. 2003, 82, 1586–1588. [Google Scholar]
- Sepliarsky, M.; Phillpot, S.R.; Stachiotti, M.G.; Migoni, R.L. Ferroelectric phase transitions and dynamical behavior in KNbO3/KTaO3 superlattices by molecular-dynamics simulation. J. Appl. Phys. 2002, 91, 3165–3171. [Google Scholar]
- Sepliarsky, M.; Phillpot, S.R.; Wolf, D.; Stachiotti, M.G.; Migoni, R.L. Ferroelectric properties of KNbO3/KTaO3 superlattices by atomic-level simulation. J. Appl. Phys. 2001, 90, 4509–4519. [Google Scholar]
- Kolpak, A.M.; Sai, N.; Rappe, A.M. Short-circuit boundary conditions in ferroelectric PbTiO3 thin films. Phys. Rev. B 2006, 74, 054112:1–054112:5. [Google Scholar]
- Souza, I.; Íñiguez, J.; Vanderbilt, D. First-principles approach to insulators in finite electric fields. Phys. Rev. Lett. 2002, 89, 117602:1–117602:4. [Google Scholar]
- Diéguez, O.; Vanderbilt, D. First-principles calculations for insulators at constant polarization. Phys. Rev. Lett. 2006, 96, 056401:1–056401:4. [Google Scholar]
- Stengel, M.; Spaldin, N.A.; Vanderbilt, D. Electric displacement as the fundamental variable in electronic-structure calculations. 2009, 5, 304–308. [Google Scholar]
- Pöykkö, S.; Chadi, D.J. Ab initio study of 180° domain wall energy and structure in PbTiO3. Appl. Phys. Lett. 1999, 75, 2830–2832. [Google Scholar]
- Meyer, B.; Vanderbilt, D. Ab initio study of ferroelectric domain walls in PbTiO3. Phys. Rev. B 2002, 65, 104111:1–104111:11. [Google Scholar]
- Lubk, A.; Gemming, S.; Spaldin, N.A. First-principles study of ferroelectric domain walls in multiferroic bismuth ferrite. Phys. Rev. B 2009, 80, 104110:1–104110:8. [Google Scholar]
- Shimada, T.; Tomoda, S.; Kitamura, T. Ab initio study of ferroelectric closure domains in ultrathin PbTiO3 films. Phys. Rev. B 2010, 81, 144116:1–144116:6. [Google Scholar]
- Aguado-Puente, P.; Junquera, J. Structural and energetic properties of domains in PbTiO3/SrTiO3 superlattices from first principles. Phys. Rev. B 2012, 85, 184105:1–184105:8. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: New York, NY, USA, 1989; pp. 71–108. [Google Scholar]
- Overhauser, A.W.; Dick, B.G. Theory of the dielectric constants of alkali halide crystals. Phys. Rev. 1958, 112, 90–103. [Google Scholar]
- Sepliarsky, M.; Asthagiri, A.; Phillpot, S.R.; Stachiotti, M.G.; Migoni, R.L. Atomic-level simulation of ferroelectricity in oxide materials. Curr. Opin. Solid State Mater. Sci. 2005, 9, 107–113. [Google Scholar]
- Stachiotti, M.G.; Sepliarsky, M.; Migoni, R.L.; Rodriguez, C.O. Modelling and microscopic dynamics of KNbO3 from first-principles. In Proceedings of the AIP Conference, Williamsburg, VA, USA, 1–4 February 1998.
- Tinte, S; Stachiotti, M.G.; Sepliarsky, M.; Migoni, R.L.; Rodriguez, C.O. Atomistic modelling of BaTiO3 based on first-principles calculations. J. Phys. Condens. Matter 1999, 11, 9679–9690. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Phillpot, S.R.; Wolf, D.; Stachiotti, M.G.; Migoni, R.L. Atomic-level simulation of ferroelectricity in perovskite solid solutions. Appl. Phys. Lett. 2000, 76, 3986–3988. [Google Scholar]
- Tinte, S; Stachiotti, M.G.; Phillpot, S.R.; Sepliarsky, M.; Wolf, D.; Migoni, R.L. Ferroelectric properties of BaxSr1−xTiO3 solid solutions obtained by molecular dynamics simulation. J. Phys. Condens. Matter 2004, 16, 3495–3506. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Cohen, R.E. Development of a shell model potential for molecular dynamics for PbTiO3 by fitting first principles results. In Proceedings of the AIP Conference, Washington, DC, USA, 3–6 February 2002.
- Asthagiri, A.; Wu, Z.; Choudhury, N.; Cohen, R.E. Advances in first-principles studies of transducer materials. Ferroelectrics 2006, 333, 69–78. [Google Scholar]
- M, S.A.R.E. First-principles based atomistic modeling of phase stability in PMN–xPT. J. Phys. Condens. Matter 2011, 23, 435902:1–435902:11. [Google Scholar]
- Goddard, W.A.; Zhang, Q.; Uludogan, M.; Strachan, A.; Cagin, T. The ReaxFF polarizable reactive force fields for molecular dynamics simulation of ferroelectrics. In Proceedings of the AIP Conference, Washington, DC, USA, 3–6 February 2002.
- Phillpot, S.R.; Sinnott, S.B.; Asthagiri, A. Atomic-level simulation of ferroelectricity in oxides: Current status and opportunities. Annu. Rev. Mater. Res. 2007, 37, 239–270. [Google Scholar]
- Vielma, J.M.; Schneider, G. Shell model of BaTiO3 derived from ab-initio total energy calculations. J. Appl. Phys. 2013, 114, 174108:1–174108:4. [Google Scholar]
- Grinberg, I.; Cooper, V.R.; Rappe, A.M. Relationship between local structure and phase transitions of a disordered solid solution. Nature 2002, 419, 909–911. [Google Scholar]
- Shin, Y.; Cooper, V.R.; Grinberg, I.; Rappe, A.M. Development of a bond-valence molecular-dynamics model for complex oxides. Phys. Rev. B 2005, 71, 054104:1–054104:4. [Google Scholar]
- Brown, I.D. Recent developments in the methods and applications of the bond valence model. Chem. Rev. 2009, 109, 6858–6919. [Google Scholar]
- Shin, Y.H.; Son, J.Y.; Lee, B.J.; Grinberg, I.; Rappe, A.M. Order–disorder character of PbTiO3. J. Phys.: Condens. Matter 2008, 20, 015224:1–015224:5. [Google Scholar]
- Liu, S.; Grinberg, I.; Takenaka, H.; Rappe, A.M. Reinterpretation of the bond-valence model with bond-order formalism: An improved bond-valence-based interatomic potential for PbTiO3. Phys. Rev. B 2013, 88, 104102:1–104102:7. [Google Scholar]
- Grinberg, I.; Shin, Y.; Rappe, A.M. Molecular dynamics study of dielectric response in a relaxor ferroelectric. Phys. Rev. Lett. 2009, 103, 197601:1–197601:4. [Google Scholar]
- Grinberg, I.; Tekenaka, H.; Shin, Y.; Rappe, A.M. Prediction of dielectric dispersion for lead based perovskites and study of local dielectric response in 0.75Pb(Mg1/3Nb2/3)O3–0.25PbTiO3. J. Adv. Dielect. 2012, 2, 1241009:1–1241009:6. [Google Scholar]
- Takenaka, H.; Grinberg, I.; Rappe, A.M. Anisotropic local correlations and dynamics in a relaxor ferroelectric. Phys. Rev. Lett. 2013, 110, 147602:1–147602:5. [Google Scholar]
- Costa, S.C.; Pizani, P.S.; Rino, J.P.; Borges, D.S. Structural phase transition and dynamical properties of PbTiO3 simulated by molecular dynamics. J. Phys. Condens. Matter 2005, 17, 5771–5783. [Google Scholar]
- Placeres-Jiménez, R; Goncalves, L.G.V.; Rino, J.P.; Fraygola, B.; Nascimento, W.J.; Eiras, J.A. Low-temperature elastic anomalies in CaTiO3: Dynamical characterization. J. Phys. Condens. Matter 2012, 24, 475401:1–475401:11. [Google Scholar]
- Verlet, L. Computer experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Thompson, S.M. Use of neighbour lists in molecular dynamics. CCP5 Newsletter 1983, 8, 20–28. [Google Scholar]
- O’Shea, S.F. Neighbour list again. CCP5 Newlett. 1983, 9, 41–45. [Google Scholar]
- Hockney, R.W.; Goel, S.P.; Eastwood, J.W. Quiet high-resolution computer models of a plasma. J. Comput. Phys. 1974, 14, 148–158. [Google Scholar]
- Auerbach, D.J.; Paul, W.; Bakker, A.F.; Lutz, C.; Rudge, W.E.; Abraham, F.F. A special purpose parallel computer for molecular dynamics: Motivation, design, implementation, and application. J. Phys. Chem. 1987, 91, 4881–4890. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier Science: Amsterdam, The Netherlands, 2001; pp. 545–558. [Google Scholar]
- Ewald, P.P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. Berlin 1921, 369, 253–287. [Google Scholar]
- Eastwood, J.W.; Hockney, R.W. Shaping the force law in two-dimensional particle-mesh models. J. Comput. Phys. 1974, 16, 342–359. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1997, 135, 280–292. [Google Scholar]
- Lee, K.E.S.A. Implementing the fast multipole method in three dimensions. J. Stat. Phys. 1991, 63, 1223–1235. [Google Scholar]
- Ding, H.Q.; Karasawa, N.; Goddard, W.A. Atomic level simulations on a million particles: The cell multipole method for Coulomb and London nonbond interactions. J. Chem. Phys. 1992, 97, 4309–4315. [Google Scholar]
- Hautman, J.; Klein, M.L. An Ewald summation method for planar surfaces and interfaces. Mol. Phys. 1992, 75, 379–395. [Google Scholar]
- Barker, J.A.; Watts, R.O. Monte Carlo studies of the dielectric properties of water-like models. Mol. Phys. 1973, 26, 789–798. [Google Scholar]
- Wolf, D.; Keblinski, P.; Phillpot, S.R.; Eggebrecht, J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r−1 summation. J. Chem. Phys. 1999, 110, 8254–8282. [Google Scholar]
- Fennell, C.J.; Gezelter, J.D. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J. Chem. Phys. 2006, 124, 234104:1–234104:12. [Google Scholar]
- Sang, Y.; Liu, B.; Fang, D. The size and strain effects on the electric-field-induced domain evolution and hysteresis loop in ferroelectric BaTiO3 nanofilms. Comp. Mater. Sci. 2008, 44, 404–410. [Google Scholar]
- Woodcock, L.V. Isothermal molecular dynamics calculations for liquid salts. Chem. Phys. Lett. 1971, 10, 257–261. [Google Scholar]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar]
- Parrinello, M.; Rahman, A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar]
- Rahman, A.; Parrinello, M. Crystal structure and pair potentials: A molecular-dynamics study. Phys. Rev. Lett. 1980, 45, 1196–1199. [Google Scholar]
- Bond, S.D.; Leimkuhler, B.J.; Laird, B.B. The Nose-Poincaré method for constant temperature molecular dynamics. J. Comput. Phys. 1999, 151, 114–134. [Google Scholar]
- Sturgeon, J.B.; Laird, B.B. Symplectic algorithm for constant-pressure molecular dynamics using a Nosé-Poincaré thermostat. J. Chem. Phys. 2000, 112, 3474–3482. [Google Scholar]
- Kouser, S.; Nishimatsu, T.; Waghmare, U.V. Ferroelectric domains and diffuse transitions in ultrathin films of PbTiO3: Effects of strain and electrodes. Phys. Rev. B 2013, 88, 064102:1–064102:6. [Google Scholar]
- Nishimatsu, T.; Waghmare, U.V.; Kawazoe, Y.; Vanderbilt, D. Fast molecular-dynamics simulation for ferroelectric thin-film capacitors using a first-principles effective Hamiltonian. Phys. Rev. B 2008, 78, 104104:1–104104:11. [Google Scholar]
- Paul, J.; Nishimatsu, T.; Kawazoe, Y.; Waghmare, U.V. Ferroelectric phase transitions in ultrathin films of BaTiO3. Phys. Rev. Lett. 2007, 99, 077601:1–077601:4. [Google Scholar]
- Abel, M.; Siems, R. Domain walls in 3d ferroelectrics: Static properties. Ferroelectrics 1992, 126, 275–280. [Google Scholar]
- Beale, P.D.; Duiker, H.M. Grain-size effects in ferroelectric switching. Phys. Rev. B 1990, 41, 490–495. [Google Scholar]
- Liu, J.M.; Wu, Z.C.; Cao, G.H.; Liu, X.H.; Liu, Z.G. A Monte-Carlo approach of remanence enhancement effect in ferroelectric Potts lattice. Ferroelectrics 2001, 252, 145–153. [Google Scholar]
- Liu, J.M.; Liu, Z.G. A Monte-Carlo approach of domain switching in ferroelectric Potts lattice under external electric field. Mater. Lett. 1998, 36, 17–23. [Google Scholar]
- Wu, F.Y. The Potts model. Rev. Mod. Phys. 1982, 54, 235–268. [Google Scholar]
- Cao, H.; Lo, V.C.; Chung, W.W.Y. Investigation of electromechanical properties in ferroelectric thin films using Monte Carlo simulation. J. Appl. Phys. 2006, 99, 24101–24103. [Google Scholar]
- Li, K.T.; Lo, V.C. Simulation of oxygen vacancy induced phenomena in ferroelectric thin films. J. Appl. Phys. 2005, 97, 034107:1–034107:8. [Google Scholar]
- Potter, B.G.; Tikare, V.; Tuttle, B.A. Monte Carlo simulation of ferroelectric domain structure and applied field response in two dimensions. J. Appl. Phys. 2000, 87, 4415–4424. [Google Scholar]
- Potter, B.G.; Tuttle, B.A.; Tikare, V. Monte Carlo simulation of ferroelectric domain structure: Electrostatic and elastic strain energy contributions. In Proceedings of the AIP Conference, Aspen, CO, USA, 13–20 February 2000.
- Schorn, P.J.; Böttger, U.; Waser, R. Monte Carlo simulations of imprint behavior in ferroelectrics. Appl. Phys. Lett. 2005, 87, 242902:1–242902:3. [Google Scholar]
- Wu, Y.; Yao, D.; Li, Z. Monte-Carlo simulation of the switching behavior in ferroelectrics with dipolar defects. Solid State Commun. 2002, 122, 395–400. [Google Scholar]
- Bolten, D.; Böttger, U.; Waser, R. Influence of defects on the properties of a 2D ferroelectric: A Monte-Carlo simulation study. Jpn. J. Appl. Phys. 2002, 41, 7202–7210. [Google Scholar]
- Liu, J.M.; Wang, X.; Chan, H.L.W.; Choy, C.L. Monte Carlo simulation of the dielectric susceptibility of Ginzburg-Landau mode relaxors. Phys. Rev. B 2004, 69, 094114:1–094114:6. [Google Scholar]
- Wang, X.; Liu, J.M.; Chan, H.L.W.; Choy, C.L. Monte Carlo simulation on dielectric and ferroelectric behaviors of relaxor ferroelectrics. J. Appl. Phys. 2004, 95, 4282–4290. [Google Scholar]
- Liu, J.M.; Wang, X.; Chan, H.L.W.; Choy, C.L. Monte-Carlo simulation on the dipole alignment in ferroelectric square lattice. Mater. Sci. Eng. B 2004, 113, 67–72. [Google Scholar]
- Li, B.L.; Liu, X.P.; Fang, F.; Zhu, J.L.; Liu, J.M. Monte Carlo simulation of ferroelectric domain growth. Phys. Rev. B 2006, 73, 014107:1–014107:7. [Google Scholar]
- Xue, F.; Gao, X.S.; Liu, J.M. Monte Carlo simulation on the size effect in ferroelectric nanostructures. J. Appl. Phys. 2009, 106, 114103:1–114103:6. [Google Scholar]
- Rabe, K.M.; Waghmare, U.V. Localized basis for effective lattice Hamiltonians: Lattice Wannier functions. Phys. Rev. B 1995, 52, 13236–13246. [Google Scholar]
- Rabe, K.M.; Waghmare, U.V. Ferroelectric phase transitions: A first-principles approach. Ferroelectrics 1995, 164, 15–32. [Google Scholar]
- Rabe, K.M.; Waghmare, U.V. Ferroelectric phase transitions from first principles. J. Phys. Chem. Solids 1996, 57, 1397–1403. [Google Scholar]
- Waghmare, U.V.; Rabe, K.M. Ab initio statistical mechanics of the ferroelectric phase transition in PbTiO3. Phys. Rev. B 1996, 55, 6161–6173. [Google Scholar]
- Zhong, W.; Vanderbilt, D.; Rabe, K.M. First-principles theory of ferroelectric phase transitions for perovskites: The case of BaTiO3. Phys. Rev. B 1995, 52, 6301–6312. [Google Scholar]
- Akbarzadeh, A.; Kornev, I.; Malibert, C.; Bellaiche, L.; Kiat, J. Combined theoretical and experimental study of the low-temperature properties of BaZrO3. Phys. Rev. B 2005, 72, 205104:1–205104:8. [Google Scholar]
- Krakauer, H.; Yu, R.; Wang, C.; Rabe, K.M.; Waghmare, U.V. Dynamic local distortions in KNbO3. J. Phys. Condens. Matter 1999, 11, 3779–3787. [Google Scholar]
- Akbarzadeh, A.R.; Bellaiche, L.; Leung, K.; Íñiguez, J.; Vanderbilt, D. Atomistic simulations of the incipient ferroelectric KTaO3. Phys. Rev. B 2004, 70, 054103:1–054103:5. [Google Scholar]
- Bellaiche, L.; Garcia, A.; Vanderbilt, D. Finite-temperature properties of Pb(Zr1-xTix)O3 alloys from first principles. Phys. Rev. Lett. 2000, 84, 5427–5430. [Google Scholar]
- Walizer, L.; Lisenkov, S.; Bellaiche, L. Finite-temperature properties of (Ba,Sr)TiO3 systems from atomistic simulations. Phys. Rev. B 2006, 73, 144105:1–144105:6. [Google Scholar]
- Akbarzadeh, A.R.; Prosandeev, S.; Walter, E.J.; Al-Barakaty, A.; Bellaiche, L. Finite-temperature properties of Ba(Zr,Ti)O3 relaxors from first principles. Phys. Rev. Lett. 2012, 108, 257601:1–257601:5. [Google Scholar]
- Kornev, I.A.; Bellaiche, L.; Janolin, P.E.; Dkhil, B.; Suard, E. Phase diagram of Pb(Zr,Ti)O3 solid solutions from first principles. Phys. Rev. Lett. 2006, 97, 157601:1–157601:4. [Google Scholar]
- Naumov, I.I.; Fu, H. A new method for determining dipole-dipole energy in 1D and 2D systems. arXiv:cond-mat/0505497 2005, 0505497:1–0505497:4. [Google Scholar]
- Ponomareva, I.; Naumov, I.; Kornev, I.; Fu, H.; Bellaiche, L. Atomistic treatment of depolarizing energy and field in ferroelectric nanostructures. Phys. Rev. B 2005, 72, 140102:1–140102:4. [Google Scholar]
- Almahmoud, E.; Kornev, I.; Bellaiche, L. Dependence of Curie temperature on the thickness of an ultrathin ferroelectric film. Phys. Rev. B 2010, 81, 064105:1–064105:5. [Google Scholar]
- Prosandeev, S.; Bellaiche, L. Influence of crystallographic steps on properties of ferroelectric ultrathin films: An ab initio study. Appl. Phys. Lett. 2007, 91, 072901:1–072901:3. [Google Scholar]
- Prosandeev, S.; Bellaiche, L. Order parameter in complex dipolar structures: Microscopic modeling. Phys. Rev. B 2008, 77, 060101:1–060101:4. [Google Scholar]
- Íñiguez, J.; Vanderbilt, D. First-principles study of the temperature-pressure phase diagram of BaTiO3. Phys. Rev. Lett. 2002, 89, 115503:1–115503:4. [Google Scholar]
- Waghmare, U.V.; Cockayne, E.J.; Burton, B.P. Ferroelectric phase transitions in nano-scale chemically ordered PbSc0.5Nb0.5O3 using a first-principles model Hamiltonian. Ferroelectrics 2003, 291, 187–196. [Google Scholar] [CrossRef]
- Chen, L.Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar]
- Cahn, J.W. On spinodal decomposition. Acta. metallurgica 1961, 9, 795–801. [Google Scholar]
- Chen, L.Q.; Shin, J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 1998, 108, 147–158. [Google Scholar]
- Li, Y.L.; Hu, S.Y.; Liu, Z.K.; Chen, L.Q. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films. Acta Mater. 2002, 50, 395–411. [Google Scholar]
- Wang, J.; Zhang, T. Size effects in epitaxial ferroelectric islands and thin films. Phys. Rev. B 2006, 73, 144107:1–144107:11. [Google Scholar]
- Chen, W.J.; Zheng, Y.; Wang, B. Vortex domain structure in ferroelectric nanoplatelets and control of its transformation by mechanical load. Sci. Rep. 2012, 2, 796:1–796:8. [Google Scholar]
- Li, Y.L.; Hu, S.Y.; Liu, Z.K.; Chen, L.Q. Phase-field model of domain structures in ferroelectric thin films. Appl. Phys. Lett. 2001, 78, 3878–3880. [Google Scholar]
- Li, Y.L. Ferroelectric domain structures in SrBi2Nb2O9 epitaxial thin films: Electron microscopy and phase-field simulations. J. Appl. Phys. 2004, 95, 6332–6340. [Google Scholar]
- Naumov, I.I.; Bellaiche, L.; Fu, H. Unusual phase transitions in ferroelectric nanodisks and nanorods. 2004, 432, 737–740. [Google Scholar]
- Pöykkö, S.; Chadi, D.J. Ab initio study of dipolar defects and 180º domain walls in PbTiO3. J. Phys. Chem. Solids. 2000, 61, 291–294. [Google Scholar]
- He, L.; Vanderbilt, D. First-principles study of oxygen-vacancy pinning of domain walls in PbTiO3. Phys. Rev. B 2003, 68, 134103:1–134103:7. [Google Scholar]
- Lisenkov, S.; Ponomareva, I.; Bellaiche, L. Unusual static and dynamical characteristics of domain evolution in ferroelectric superlattices. Phys. Rev. B 2009, 79, 024101:1–024101:6. [Google Scholar]
- Zhang, Q.; Herchig, R.; Ponomareva, I. Nanodynamics of ferroelectric ultrathin films. Phys. Rev. Lett. 2011, 107, 177601:1–177601:5. [Google Scholar]
- Ponomareva, I.; Bellaiche, L. Nature of dynamical coupling between polarization and strain in nanoscale ferroelectrics from first principles. Phys. Rev. Lett. 2008, 101, 197602:1–197602:4. [Google Scholar]
- Cross, L.E.; Pohanka, R.C. Ferroelectricity in bismuth oxide type layer structure compounds. Mater. Res. Bull. 1971, 6, 939–949. [Google Scholar]
- Haun, M.J.; Furman, E.; Jang, S.J.; McKinstry, H.A.; Cross, L.E. Thermodynamic theory of PbTiO3. J. Appl. Phys. 1987, 62, 3331–3338. [Google Scholar]
- Wang, Y.L.; Tagantsev, A.K.; Damjanovic, D.; Setter, N.; Yarmarkin, V.K.; Sokolov, A.I. Anharmonicity of BaTiO3 single crystals. Phys. Rev. B 2006, 73, 132103:1–132103:4. [Google Scholar]
- Völker, B.; Landis, C.M.; Kamlah, M. Multiscale modeling for ferroelectric materials: Identification of the phase-field model’s free energy for PZT from atomistic simulations. Smart Mater. Struct. 2012, 21, 035025:1–035025:14. [Google Scholar]
- Völker, B.; Marton, P.; Elsässer, C.; Kamlah, M. Multiscale modeling for ferroelectric materials: A transition from the atomic level to phase-field modeling. Continuum Mech. Therm. 2011, 23, 435–451. [Google Scholar]
- Kumar, A.; Waghmare, U.V. First-principles free energies and Ginzburg-Landau theory of domains and ferroelectric phase transitions in BaTiO3. Phys. Rev. B 2010, 82, 054117:1–054117:10. [Google Scholar]
- Umeno, Y.; Albina, J.M.; Meyer, B.; Elsässer, C. Ab initio calculations of ferroelectric instability in PbTiO3 capacitors with symmetric and asymmetric electrode layers. Phys. Rev. B 2009, 80, 205122:1–205122:8. [Google Scholar]
- Stengel, M.; Vanderbilt, D.; Spaldin, N.A. Enhancement of ferroelectricity at metal-oxide interfaces. Nature mater. 2009, 8, 392–397. [Google Scholar]
- Stengel, M.; Vanderbilt, D.; Spaldin, N.A. First-principles modeling of ferroelectric capacitors via constrained displacement field calculations. Phys. Rev. B 2009, 80, 224110:1–224110:23. [Google Scholar]
- Fong, D.D.; Kolpak, A.M.; Eastman, J.A.; Streiffer, S.K.; Fuoss, P.H.; Stephenson, G.B.; Thompson, C.; Kim, D.M.; Choi, K.J.; Eom, C.B. Stabilization of monodomain polarization in ultrathin PbTiO3 films. Phys. Rev. Lett. 2006, 96, 127601:1–127601:4. [Google Scholar]
- Wang, R.V.; Fong, D.D.; Jiang, F.; Highland, M.J.; Fuoss, P.H.; Thompson, C.; Kolpak, A.M.; Eastman, J.A.; Streiffer, S.K.; Rappe, A.M. Reversible chemical switching of a ferroelectric film. Phys. Rev. Lett. 2009, 102, 047601:1–047601:4. [Google Scholar]
- Shin, J.; Nascimento, V.B.; Geneste, G.; Rundgren, J.; Plummer, E.W.; Dkhil, B.; Kalinin, S.V.; Baddorf, A.P. Atomistic screening mechanism of ferroelectric surfaces: An in situ study of the polar phase in ultrathin BaTiO3 films exposed to H2O. Nano. Lett. 2009, 9, 3720–3725. [Google Scholar]
- Stephenson, G.B.; Highland, M.J. Equilibrium and stability of polarization in ultrathin ferroelectric films with ionic surface compensation. Phys. Rev. B 2011, 84, 064107:1–064107:15. [Google Scholar]
- Highland, M.J.; Fister, T.T.; Fong, D.D.; Fuoss, P.H.; Thompson, C.; Eastman, J.A.; Streiffer, S.K.; Stephenson, G.B. Equilibrium polarization of ultrathin PbTiO3 with surface compensation controlled by oxygen partial pressure. Phys. Rev. Lett. 2011, 107, 187602:1–187602:5. [Google Scholar]
- Stachiotti, M.G. Ferroelectricity in BaTiO3 nanoscopic structures. Appl. Phys. Lett. 2004, 84, 251–253. [Google Scholar]
- Ma, D.C.; Zheng, Y.; Wang, B.; Woo, C.H. Domain structures of ferroelectric thin film controlled by oxidizing atmosphere. Appl. Phys. Lett. 2011, 99, 142908:1–142908:3. [Google Scholar]
- Ma, D.C.; Zheng, Y.; Wang, B.; Woo, C.H. A strain-driven morphotropic phase boundary in BiFeO3. Science 2009, 326, 977–980. [Google Scholar]
- Diéguez, O.; Tinte, S.; Antons, A.; Bungaro, C.; Neaton, J.B.; Rabe, K.M.; Vanderbilt, D. Ab initio study of the phase diagram of epitaxial BaTiO3. Phys. Rev. B 2004, 69, 212101:1–212101:4. [Google Scholar]
- Bungaro, C.; Rabe, K.M. Epitaxially strained [001]−(PbTiO3)1(PbZrO3)1 superlattice and PbTiO3 from first principles. Phys. Rev. B 2004, 69, 184101:1–184101:8. [Google Scholar]
- Antons, A.; Neaton, J.B.; Rabe, K.M.; Vanderbilt, D. Tunability of the dielectric response of epitaxially strained SrTiO3 from first principles. Phys. Rev. B 2005, 71, 024102:1–024102:11. [Google Scholar]
- Li, Y.L.; Chen, L.Q. Temperature-strain phase diagram for BaTiO3 thin films. Appl. Phys. Lett. 2006, 88, 072905:1–072905:3. [Google Scholar]
- Lai, B.-K.; Kornev, I.A.; Bellaiche, L.; Salamo, G.J. Phase diagrams of epitaxial BaTiO3 ultrathin films from first principles. Appl. Phys. Lett. 2005, 86, 132904:1–132904:3. [Google Scholar]
- Yu, J.; Wu, Z.; Liu, Z.; Yan, Q.; Wu, J.; Duan, W. Phase diagrams of ferroelectric BaTiO3 ultrathin films under open-circuit conditions. J. Phys.: Condens. Matter 2008, 20, 135203:1–135203:6. [Google Scholar]
- Gui, Z.; Prosandeev, S.; Bellaiche, L. Properties of epitaxial (110) BaTiO3 films from first principles. Phys. Rev. B 2011, 84, 214112:1–214112:5. [Google Scholar]
- Li, Y.L.; Choudhury, S.; Haeni, J.H.; Biegalski, M.D.; Vasudevarao, A.; Sharan, A.; Ma, H.Z.; Levy, J.; Gopalan, V.; Trolier-McKinstry, S.; et al. Phase transitions and domain structures in strained pseudocubic (100) SrTiO3 thin films. Phys. Rev. B 2006, 73, 184112:1–184112:3. [Google Scholar]
- Bin-Omran, S. The influence of strain on the polarization of epitaxial (Ba0.70Sr0.30)TiO3 ultrathin film obtained from first principles. J. Phys. Condens. Matter. 2010, 22, 275901:1–275901:6. [Google Scholar]
- Li, Y.L.; Choudhury, S.; Haeni, J.H.; Biegalski, M.D.; Vasudevarao, A.; Sharan, A.; Ma, H.Z.; Levy, J.; Gopalan, V.; Trolier-McKinstry, S.; et al. Phase diagrams and dielectric response of epitaxial (Ba0.70Sr0.30)TiO3 ultrathin film: A first-principles study. Physica. B 2012, 407, 3627–3631. [Google Scholar] [CrossRef]
- Li, Y.L.; Choudhury, S.; Liu, Z.K.; Chen, L.Q. Effect of external mechanical constraints on the phase diagram of epitaxial PbZr1-xTixO3 thin films-thermodynamic calculations and phase-field simulations. Appl. Phys. Lett. 2003, 83, 1608–1610. [Google Scholar]
- Choudhury, S.; Li, Y.; Chen, L. A phase diagram for epitaxial PbZr1-xTixO3 thin films at the bulk morphotropic boundary composition. J. Am. Ceram. Soc. 2005, 88, 1669–1672. [Google Scholar]
- Li, Y.L.; Hu, S.Y.; Chen, L.Q. Ferroelectric domain morphologies of (001) PbZr1-xTixO3 epitaxial thin films. J. Appl. Phys. 2005, 97, 034112:1–034112:7. [Google Scholar]
- Sichuga, D.; Ponomareva, I.; Bellaiche, L. Phase diagrams of epitaxial Pb(Zr,Ti)O3 ultrathin films from first principles. Phys. Rev. B 2009, 80, 134116:1–134116:6. [Google Scholar]
- Sichuga, D.; Bellaiche, L. Epitaxial Pb(Zr,Ti)O3 ultrathin films under open-circuit electrical boundary conditions. Phys. Rev. Lett. 2011, 106, 196102:1–196102:4. [Google Scholar]
- Sheng, J.; Zhang, J.X.; Li, Y.L.; Choudhury, S.; Jia, Q.X.; Liu, Z.K.; Chen, L.Q. Domain stability of PbTiO3 thin films under anisotropic misfit strains: Phase-field simulations. J. Appl. Phys. 2008, 104, 054105:1–054105:4. [Google Scholar]
- Sheng, J.; Zhang, J.X.; Li, Y.L.; Choudhury, S.; Jia, Q.X.; Liu, Z.K.; Chen, L.Q. Misfit strain–misfit strain diagram of epitaxial BaTiO3 thin films: Thermodynamic calculations and phase-field simulations. Appl. Phys. Lett. 2008, 93, 232904:1–232904:3. [Google Scholar]
- Chu, M.W.; Szafraniak, I.; Scholz, R.; Harnagea, C.; Hesse, D.; Alexe, M.; Gosele, U. Impact of misfit dislocations on the polarization instability of epitaxial nanostructured ferroelectric perovskites. Nature Mater. 2004, 3, 87–90. [Google Scholar]
- Morozovska, A.N.; Eliseev, E.A.; Svechnikov, S.V.; Krutov, A.D.; Shur, V.Y.; Borisevich, A.Y.; Maksymovych, P.; Kalinin, S.V. Finite size and intrinsic field effect on the polar-active properties of ferroelectric-semiconductor heterostructures. Phys. Rev. B 2010, 81, 205308:1–205308:15. [Google Scholar]
- Zhu, Z.-X.; Li, J.-F.; Liu, Y.; Li, J. Shifting of the morphotropic phase boundary and superior piezoelectric response in Nb-doped Pb(Zr,Ti)O3 epitaxial thin films. Acta. Mater. 2009, 57, 4288–4295. [Google Scholar]
- Liu, Y.Y.; Zhu, Z.X.; Li, J.F.; Li, J.Y. Misfit strain modulated phase structures of epitaxial Pb(Zr1-xTix)O3 thin films: The effect of substrate and film thickness. Mech. Mater. 2010, 42, 816–826. [Google Scholar]
- Hu, S.Y.; Li, Y.L.; Chen, L.Q. Effect of interfacial dislocations on ferroelectric phase stability and domain morphology in a thin film—A phase-field model. J. Appl. Phys. 2003, 94, 2542–2547. [Google Scholar]
- Zheng, Y.; Wang, B.; Woo, C.H. Simulation of interface dislocations effect on polarization distribution of ferroelectric thin films. Appl. Phys. Lett. 2006, 88, 092903:1–092903:3. [Google Scholar]
- Zheng, Y.; Wang, B.; Woo, C.H. Critical thickness for dislocation generation during ferroelectric transition in thin film on a compliant substrate. Appl. Phys. Lett. 2006, 89, 083115:1–083115:3. [Google Scholar]
- Zheng, Y.; Wang, B.; Woo, C.H. Effects of interface dislocations on properties of ferroelectric thin films. J. Mech. Phys. Solids 2007, 55, 1661–1676. [Google Scholar]
- Li, Y.L.; Hu, S.Y.; Choudhury, S.; Baskes, M.I.; Saxena, A.; Lookman, T.; Jia, Q.X.; Schlom, D.G.; Chen, L.Q. Influence of interfacial dislocations on hysteresis loops of ferroelectric films. J. Appl. Phys. 2008, 104, 104110:1–104110:6. [Google Scholar]
- Misirlioglu, I.B.; Vasiliev, A.L.; Alpay, S.P.; Aindow, M.; Ramesh, R. Defect microstructures in epitaxial PbZr0.2Ti0.8O3 films grown on (001) SrTiO3 by pulsed laser deposition. J. Mater. Sci. 2006, 41, 697–707. [Google Scholar] [CrossRef]
- Zavala, G.; Fendler, J.H.; Trolier-Mckinstry, S. Characterization of ferroelectric lead zirconate titanate films by scanning force microscopy. J. Appl. Phys. 1997, 81, 7480–7491. [Google Scholar]
- Kholkin, A.L.; Shvartsman, V.V.; Emelyanov, A.Y.; Poyato, R.; Calzada, M.L.; Pardo, L. Stress-induced suppression of piezoelectric properties in PbTiO3: La thin films via scanning force microscopy. Appl. Phys. Lett. 2003, 82, 2127–2129. [Google Scholar]
- Gaillard, Y.; Macías, A.H.; Muñoz-Saldaña, J.; Anglada, M.; Trápaga, G. Nanoindentation of BaTiO3: Dislocation nucleation and mechanical twinning. J. Phys. D Appl. Phys. 2009, 42, 085502:1–085502:8. [Google Scholar]
- H., Lu; Bark, C.-W.; de los Ojos, D.E.; Alcala, J.; Eom, C.B.; Catalan, G.; Gruverman, A. Mechanical writing of ferroelectric polarization. Science 2012, 336, 59–61. [Google Scholar]
- Chen, W.J.; Zheng, Y.; Xiong, W.M.; Feng, X.; Wang, B.; Wang, Y. Effect of mechanical loads on stability of nanodomains in ferroelectric ultrathin films: Towards flexible erasing of the non-volatile memories. Sci. Rep. 2014, 4, 5339:1–5339:10. [Google Scholar]
- Lai, B.; Ponomareva, I.; Naumov, I.I.; Kornev, I.; Fu, H.; Bellaiche, L.; Salamo, G.J. Electric-field-induced domain evolution in ferroelectric ultrathin films. Phys. Rev. Lett. 2006, 96, 137602:1–137602:4. [Google Scholar]
- Lai, B.; Ponomareva, I.; Kornev, I.A.; Bellaiche, L.; Salamo, G.J. Domain evolution of BaTiO3 ultrathin films under an electric field: A first-principles study. Phys. Rev. B 2007, 75, 085412:1–085412:7. [Google Scholar]
- Sichuga, D.; Bellaiche, L. Domain evolution in epitaxial (001) Pb(Zr,Ti)O3 ultrathin films under an electric field applied along the [111] direction. Phys. Rev. B 2012, 85, 214111:1–214111:11. [Google Scholar]
- Artemev, A.; Geddes, B.; Slutsker, J.; Roytburd, A. Thermodynamic analysis and phase field modeling of domain structures in bilayer ferroelectric thin films. J. Appl. Phys. 2008, 103, 074104:1–074104:10. [Google Scholar]
- Morozovska, A.N.; Eliseev, E.A. Screening and size effects on the nanodomain tailoring in ferroelectrics semiconductors. Phys. Rev. B 2006, 73, 104440:1–104440:9. [Google Scholar]
- Li, D.; Bonnell, D.A. Ferroelectric domains: Fundamental concepts and applicaitons. Annu. Rev. Mater. Res. 2008, 38, 351–368. [Google Scholar]
- Morozovska, A.N.; Kalinin, S.V.; Eliseev, E.A.; Gopalan, V.; Svechnikov, S.V. Interaction of a 180° ferroelectric domain wall with a biased scanning probe microscopy tip: Effective wall geometry and thermodynamics in Ginzburg-Landau-Devonshire theory. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Balke, N.; Choudhury, S.; Jesse, S.; Huijben, M.; Chu, Y.H.; Baddorf, A.P.; Chen, L.; Ramesh, R.; Kalinin, S.V. Deterministic control of ferroelastic switching in multiferroic materials. Nature Nanotechnol. 2009, 4, 868–875. [Google Scholar]
- Vasudevan, R.K.; Chen, Y.; Tai, H.; Balke, N.; Wu, P.; Bhattacharya, S.; Chen, L.; Chu, Y.; Lin, I.; Kalinin, S.V. Exploring topological defects in epitaxial BiFeO3 thin films. ACS Nano. 2011, 5, 879–887. [Google Scholar]
- Gao, P.; Britson, J.; Jokisaari, J.R.; Nelson, C.T.; Baek, S.; Wang, Y.; Eom, C.; Chen, L.; Pan, X. Atomic-scale mechanisms of ferroelastic domain-wall-mediated ferroelectric switching. Nat. commun. 2013, 4. [Google Scholar] [CrossRef]
- Morozovska, A.N. Domain wall conduction in ferroelectrics. Ferroelectrics 2012, 438, 3–19. [Google Scholar]
- Geng, Y.; Lee, N.; Choi, Y.J.; Cheong, S.-W.; Wu, W. Collective magnetism at multiferroic vortex domain walls. Nano. Lett. 2012, 12, 6055–6059. [Google Scholar]
- Yang, S.Y.; Seidel, J.; Byrnes, S.J.; Shafer, P.; Yang, C.-H.; Rossell, M.D.; Yu, P.; Chu, Y.-H.; Scott, J.F.; Ager, J.W.; et al. Above-bandgap voltages from ferroelectric photovoltaic devices. Nature Nanotechnol. 2010, 5, 143–147. [Google Scholar]
- Choi, T.; Lee, S.; Choi, Y.J.; Kiryukhin, V.; Cheong, S.-W. Switchable Ferroelectric Diode and Photovoltaic Effect in BiFeO3. Science 2009, 324, 63–66. [Google Scholar]
- Pintilie, L.; Stancu, V.; Vasile, E.; Pintilie, I. About the complex relation between short-circuit photocurrent, imprint and polarization in ferroelectric thin films. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Qin, M.; Yao, K.; Liang, Y.C. Photovoltaic characteristics in polycrystalline and epitaxial (Pb0.97La0.03) (Zr0.52Ti0.48 )O3 ferroelectric thin films sandwiched between different top and bottom electrodes. J. Appl. Phys. 2009, 105. [Google Scholar] [CrossRef]
- Zhirnov, V.A. A contribution to the theory of domain walls in ferroelectrics. Zh. Eksp. Teor. Fiz. 1958, 5, 1175–1180. [Google Scholar]
- Bulaevskii, L.N. Thermodynamic theory of domain walls in ferroelectric materials with the perovskite structure. Fiz. Tverd. Tela. St. Petersburg 1963, 5, 3183. [Google Scholar]
- Cao, W.; Cross, L.E. Theory of tetragonal twin structures in ferroelectric perovskites with a first-order phase transition. Phys. Rev. B 1991, 44, 5–12. [Google Scholar]
- Ishibashi, Y.; Salje, E. A theory of ferroelectric 90 degree domain wall. J. Phys. Soc. Jpn. 2002, 71, 2800–2803. [Google Scholar]
- Huang, X.R.; Jiang, S.S.; Hu, X.B.; Liu, W.J. Theory of twinning structures in the orthorhombic phase of ferroelectric perovskites. J. Phys. Condens. Matter 2002, 9, 4467–4482. [Google Scholar]
- Hlinka, J.; Marton, P. Phenomenological model of a 90° domain wall in BaTiO3-type ferroelectrics. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Marton, P.; Rychetsky, I.; Hlinka, J. Domain walls of ferroelectric BaTiO3 within the Ginzburg-Landau-Devonshire phenomenological model. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Stepkova, V.; Marton, P.; Hlinka, J. Sress-induced phase transition in ferroelectric domain walls of BaTiO3. J. Phys.: Condens. Matter 2012, 24, 212201:1–212201:4. [Google Scholar]
- Lee, D.; Behera, R.K.; Wu, P.; Xu, H.; Sinnott, S.B.; Phillpot, S.R.; Chen, L.Q.; Gopalan, V. Mixed Bloch-Néel-Ising character of 180° ferroelectric domain walls. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Padilla, J.; Zhong, W; Vanderbilt, D. First-principles investigation of 180° domain walls in BaTiO3. Phys. Rev. B 1996, 53. [Google Scholar] [CrossRef]
- Diéguez, O.; Aguado-Puente, P.; Junquera, J.; Íñiguez, J. Domain walls in a perovskite oxide with two primary structural order parameters: First-principles study of BiFeO3. Phys. Rev. B 2013, 87, 024102:1–024102:11. [Google Scholar]
- Ren, W.; Yang, Y.; Diéguez, O.; Íñiguez, J.; Choudhury, N.; Bellaiche, L. Ferroelectric Domains in Multiferroic BiFeO3 Films under Epitaxial Strains. Phys. Rev. Lett. 2013, 110, 187601:1–187601:5. [Google Scholar]
- Catalan, G.; Lubk, A.; Vlooswijk, A.H.G.; Snoeck, E.; Magen, C.; Janssens, A.; Rispens, G.; Rijnders, G.; Blank, D.H.A.; Noheda, B. Flexoelectric rotation of polarization in ferroelectric thin films. 2011, 10, 963–967. [Google Scholar] [Green Version]
- Lee, D.; Yoon, A.; Jang, S.Y.; Yoon, J.G.; Chung, J.S.; Kim, M.; Scott, J.F.; Noh, T.W. Giant flexoelectric effect in ferroelectric epitaxial thin films. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef]
- Catalan, G.; Noheda, B.; McAneney, J.; Sinnamon, L.J.; Gregg, J.M. Strain gradients in epitaxial ferroelectrics. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar]
- Nguyen, T.D.; Mao, S.; Yeh, Y.-W.; Purohit, P.K.; McAlpine, M.C. Nanoscale Flexoelectricity. Adv. Mater. 2013, 25, 946–974. [Google Scholar]
- Chen, H.T.; Soh, A.K.; Ni, Y. Phase field modeling of flexoelectric effects in ferroelectric epitaxial thin films. Acta. Mech. 2014, 225, 1323–1333. [Google Scholar]
- Jiawang, H.A.G.C. The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 2010, 22. [Google Scholar] [CrossRef]
- Resta, R. Towards a bulk theory of flexoelectricity. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Ponomareva, I.; Tagantsev, A.K.; Bellaiche, L. Finite-temperature flexoelectricity in ferroelectric thin films from first principles. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
- Hong, J.; Vanderbilt, D. First-principles theory of frozen-ion flexoelectricity. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
- Prosandeev, S.; Lisenkov, S.; Bellaiche, L. Kittel law in BiFeO3 ultrathin films: A first-principles-based study. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, J.; Chen, W.; Wang, B.; Zheng, Y. Theoretical Methods of Domain Structures in Ultrathin Ferroelectric Films: A Review. Materials 2014, 7, 6502-6568. https://doi.org/10.3390/ma7096502
Liu J, Chen W, Wang B, Zheng Y. Theoretical Methods of Domain Structures in Ultrathin Ferroelectric Films: A Review. Materials. 2014; 7(9):6502-6568. https://doi.org/10.3390/ma7096502
Chicago/Turabian StyleLiu, Jianyi, Weijin Chen, Biao Wang, and Yue Zheng. 2014. "Theoretical Methods of Domain Structures in Ultrathin Ferroelectric Films: A Review" Materials 7, no. 9: 6502-6568. https://doi.org/10.3390/ma7096502
APA StyleLiu, J., Chen, W., Wang, B., & Zheng, Y. (2014). Theoretical Methods of Domain Structures in Ultrathin Ferroelectric Films: A Review. Materials, 7(9), 6502-6568. https://doi.org/10.3390/ma7096502



