Numerical Characterization of Piezoceramics Using Resonance Curves
Abstract
:1. Introduction

2. Piezoelectric Materials and Constitutive Equations
| Tensor Number | Tensor Letter | IEEE Index | ANSYS Index |
|---|---|---|---|
| 11 | xx | 1 | 1 |
| 22 | yy | 2 | 2 |
| 33 | zz | 3 | 3 |
| 23 = 32 | yz = zy | 4 | 5 |
| 13 = 31 | xz = zx | 5 | 6 |
| 12 = 21 | xy = yx | 6 | 4 |
3. One-Dimensional Electromechanical Modeling and Impedance Characterization
3.1. One-Dimensional Modeling

3.2. Electrical Modeling





3.3. Electromechanical Model

4. Finite Element Method in Piezoelectric Materials



5. Finite Element Method (FEM) Optimization Techniques
- Initial conditions: Nonlinear optimization algorithms usually require an initial guess for the material constants.
- FEM computation: The numerical data is obtained from a FEM simulation.
- Objective function: The optimization problem is defined to minimize an objective function.
- Optimization algorithm: Using the value of the objective function the next set of parameters is determined.
- Exit criteria: Usually, the exit criterion is a threshold in the value of the objective function. Alternatively, the number of simulation steps or the difference between two consecutive values in the objective function can be used.

5.1. Problem Statement
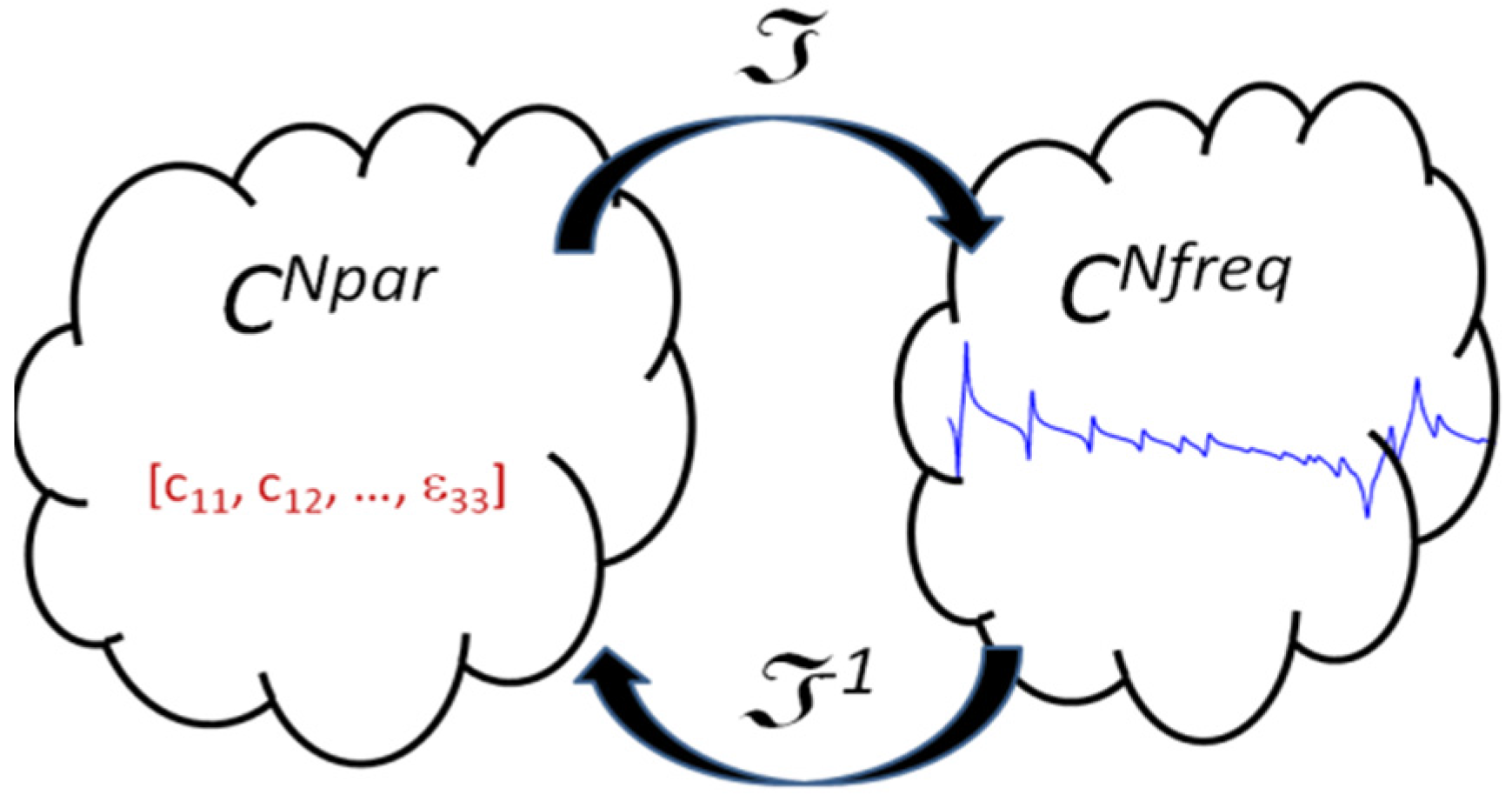
5.2. Determination of the Initial Conditions




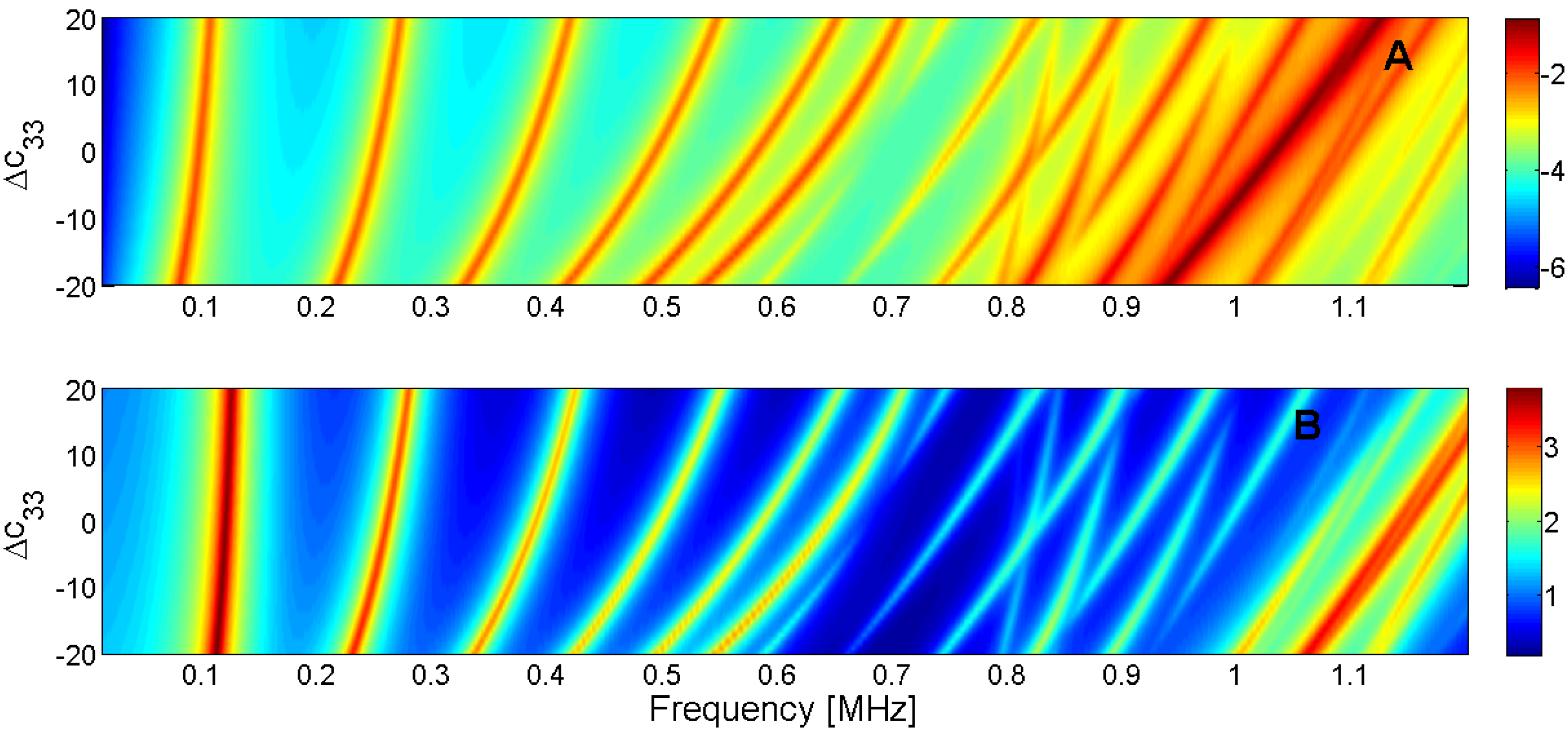
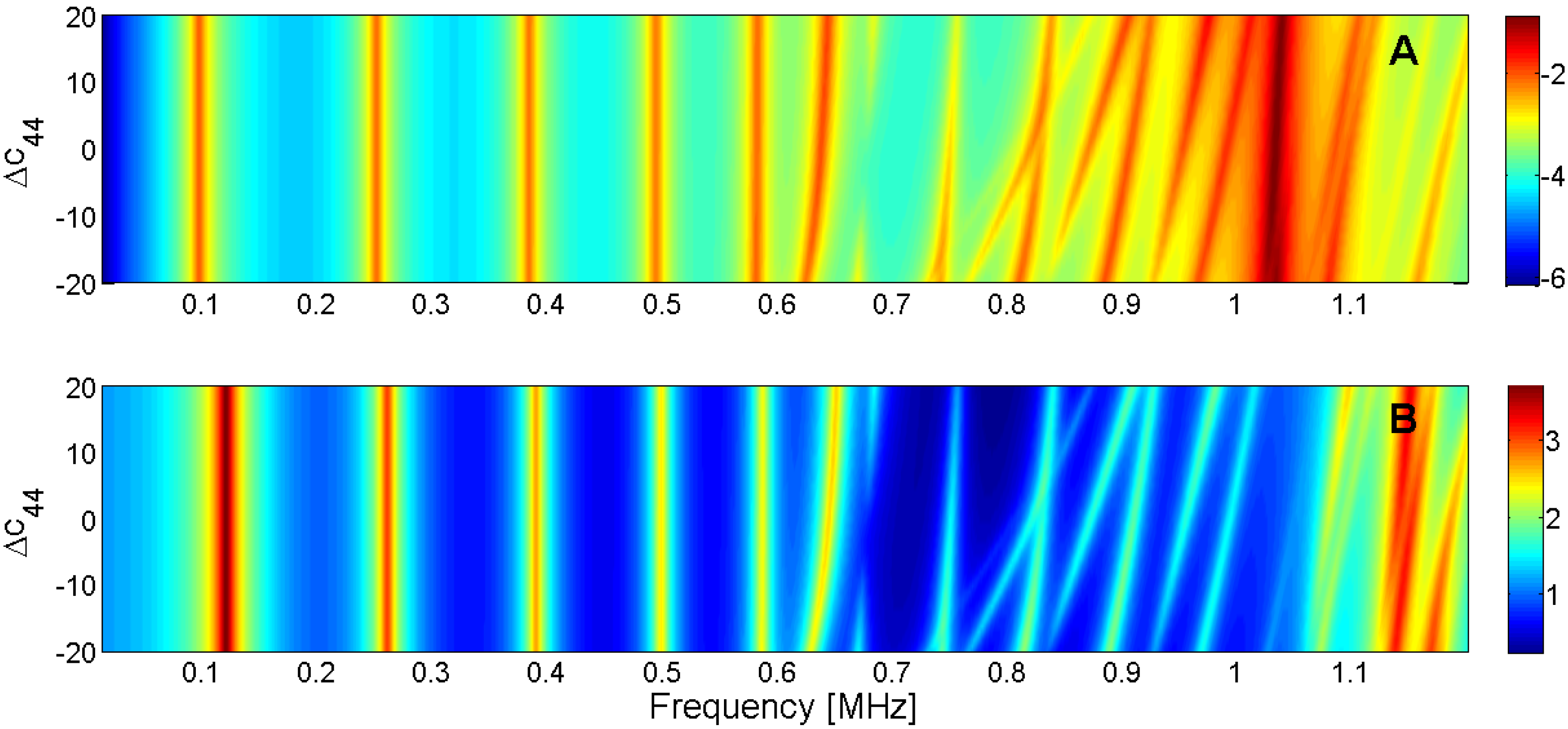




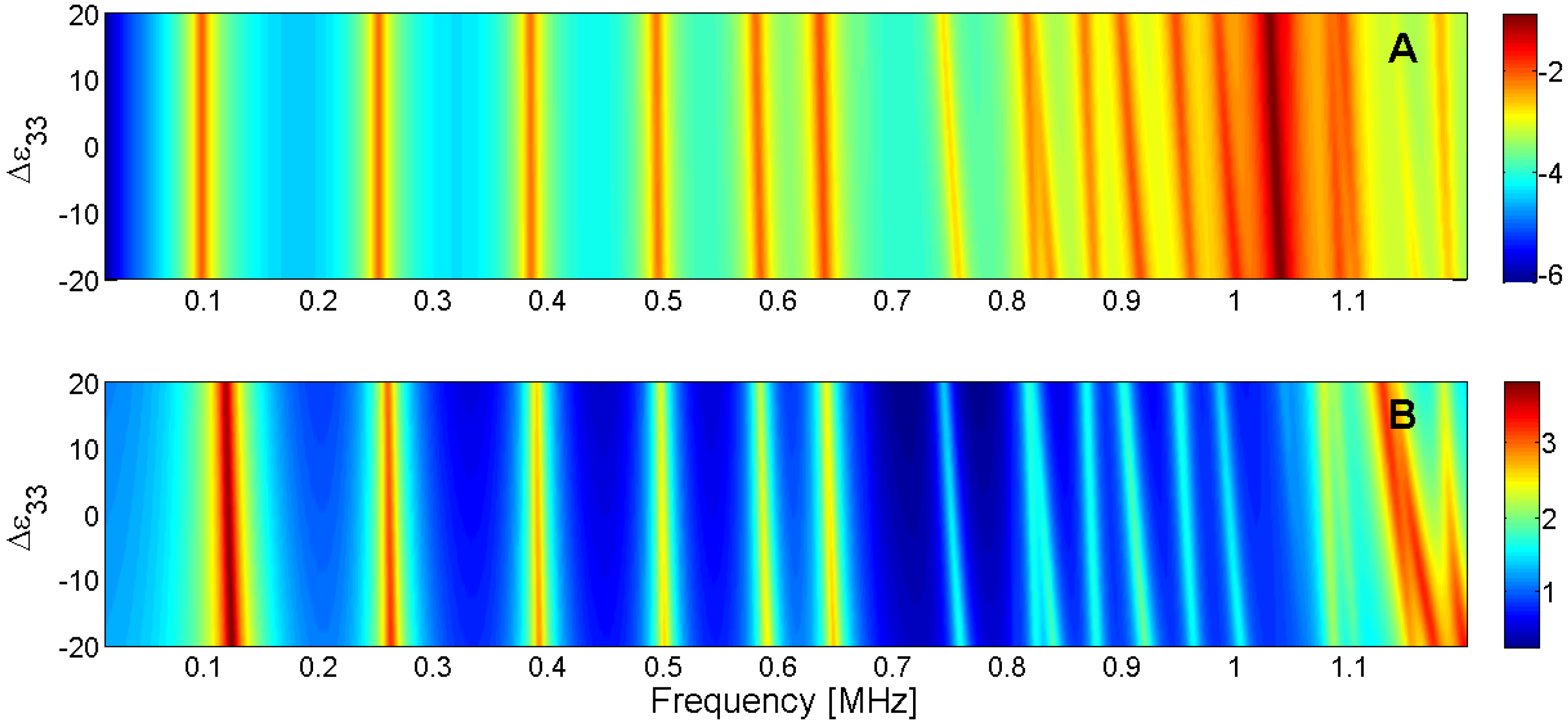


| Parameter | Radial Mode | Edge Mode | Coupled Mode | Thickness Mode |
|---|---|---|---|---|
| c11 | High, +slope | High, +slope | High, +slope | No influence |
| c12 | Low, +slope | No influence | No Influence | No influence |
| c13 | High, −slope | High, −slope | High, −slope | No influence |
| c33 | High, +slope | High, +slope | High, +slope | High, +slope |
| c44 | No influence | High, +slope | High, +slope | Low, +slope |
| e13 | Low, +slope | Low, +slope | Low, +slope | No influence |
| e15 | No influence | No influence | High, ±slope | No influence |
| e33 | Low, +slope | Low, −slope | Low, +slope | High, +slope |
| ε11 | No influence | No influence | Low, −slope | No influence |
| ε33 | Low, −slope | Low, −slope | Low, −slope | High, −slope |

5.3. Optimization Algorithm
6. Validation Methods
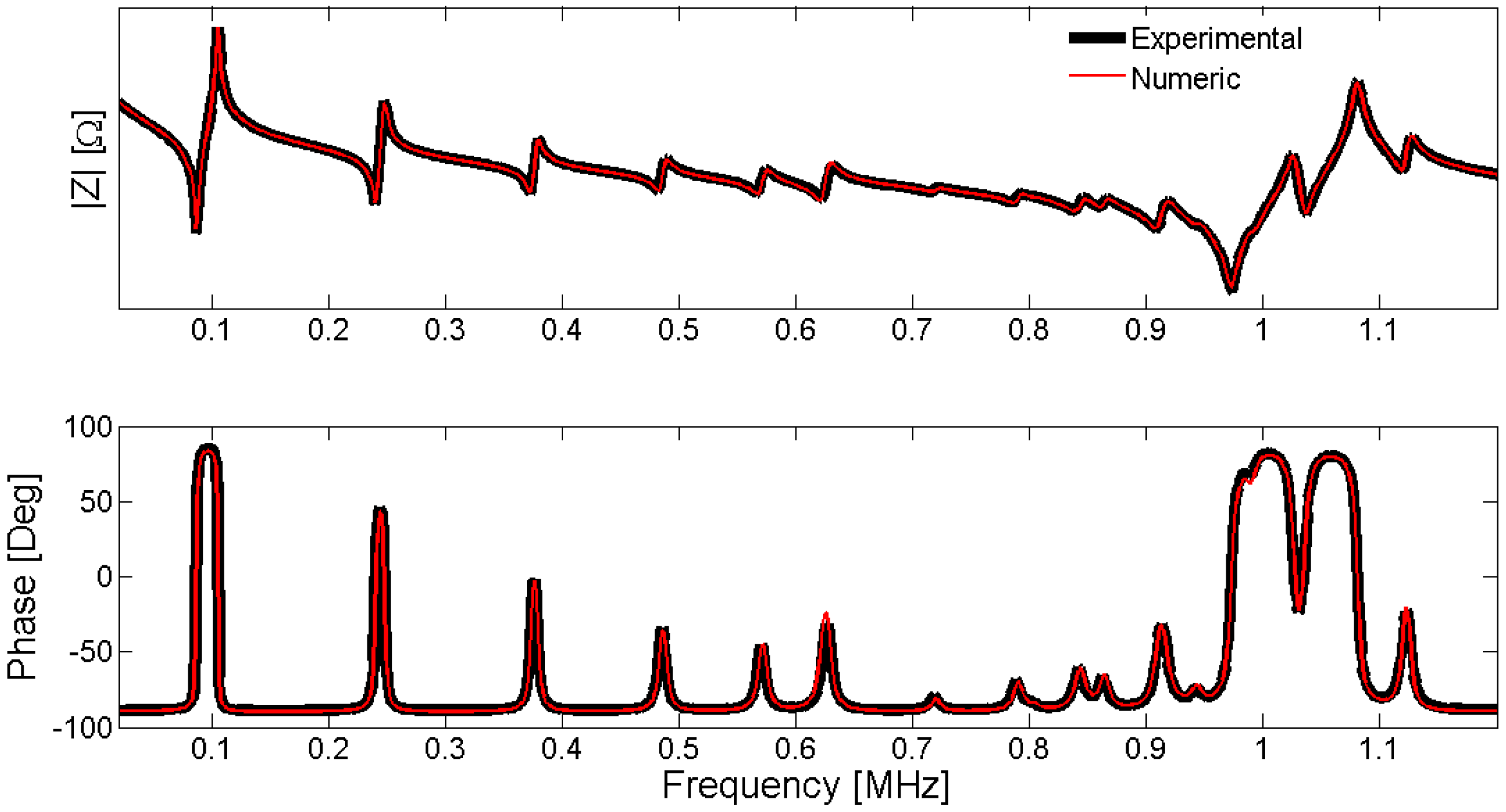


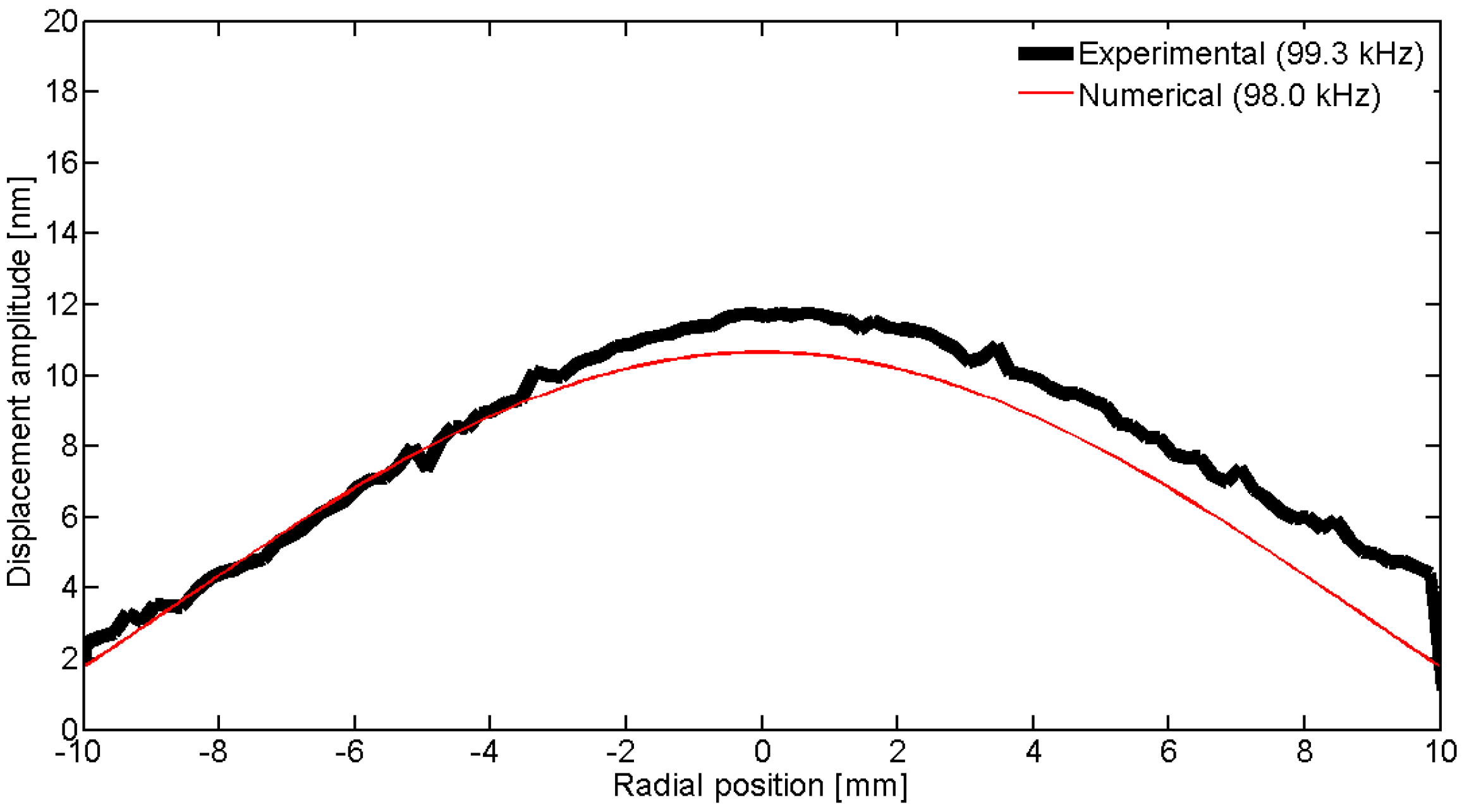





7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferroperm Piezoceramics. High Quality Components and Materials for the Electronic Industry. Available online: http://www.ferroperm-piezo.com/files/files/Ferroperm%20Catalogue.pdf (accessed on 21 December 2015).
- Allik, H.; Hughes, T.J.R. Finite element method for piezoelectric vibration. Int. J. Numer. Meth. Eng. 1970, 2, 151–157. [Google Scholar] [CrossRef]
- Kagawa, Y.; Yamabuchi, T. Finite element approach for a piezoelectric circular rod. IEEE Trans. Sonics Ultrason. 1976, 23, 379–385. [Google Scholar] [CrossRef]
- Lerch, R. Simulation of piezoelectric devices by two- and three-dimensional finite elements. IEEE Trans. Ultrason. Ferr. 1990, 37, 233–247. [Google Scholar] [CrossRef] [PubMed]
- Kunkel, H.A.; Locke, S.; Pikeroen, B. Finite-element analysis of vibrational modes in piezoelectric ceramic disks. IEEE Trans. Ultrason. Ferr. 1990, 37, 316–328. [Google Scholar] [CrossRef] [PubMed]
- Kaltenbacher, M.; Kaltenbacher, B.; Nicolai, M.; Schönecker, A. Models and an efficient finite element scheme for the simulation of piezoelectric materials. In Proceedings of the 19th International Conference on Computer Methods in Mechanics (CMM-2011), Warsaw, Poland, 9–12 May 2011.
- Benjeddou, A. Advances in piezoelectric finite element modeling of adaptive structural elements: A survey. Comput. Struct. 2000, 76, 347–363. [Google Scholar] [CrossRef]
- Kaltenbacher, B.; Kaltenbacher, M.; Lerch, R.; Simkovics, R. Identification of material tensors for piezoceramic materials. In Proceedings of the 2000 IEEE Ultrasonics Symposium, San Juan, Puerto Rico, 22–25 October 2000.
- Kybartas, D.; Lukoševičius, A. Determination of piezoceramics parameters by the use of mode interaction and fitting of impedance characteristics. Ultragarsas 2002, 45, 22–28. [Google Scholar]
- Joo, H.W.; Lee, C.H.; Rho, J.S.; Jung, H.K. Identification of material constants for piezoelectric transformers by three-dimensional, finite-element method and a design-sensitivity method. IEEE Trans. Ultrason. Ferr. 2003, 50, 965–971. [Google Scholar] [CrossRef]
- Joo, H.W.; Lee, C.H.; Jung, H.K. Identification of the piezoelectric material coefficients using the finite element method with an asymptotic waveform evaluation. Ultrasonics 2004, 43, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Friswell, M.I.; Mottershead, J.E. Solid Mechanics and Its Applications 38. In Finite Element Model Updating in Structural Dynamics; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Kaltenbacher, B.; Lahmer, T.; Mohr, M.; Kaltenbacher, M. PDE based determination of piezoelectric material tensors. Eur. J. Appl. Math. 2006, 17, 383–416. [Google Scholar] [CrossRef]
- Lahmer, T.; Kaltenbacher, M.; Kaltenbacher, B.; Lerch, R.; Leder, E. FEM-based determination of real and complex elastic, dielectric, and piezoelectric moduli in piezoceramic materials. IEEE Trans. Ultrason. Ferr. 2008, 55, 465–475. [Google Scholar]
- Rupitsch, S.J.; Lerch, R. Inverse method to estimate material parameters for piezoceramic disc actuators. Appl. Phys. A Mater. 2009, 97, 735–740. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex-method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Silva, E.C.N.; Buiochi, F.; Adamowski, J.C. Characterization of piezoelectric materials by using an optimization algorithm. In Proceedings of the International Congress on Ultrasonics, Vienna, Austria, 9–13 April 2007.
- Perez, N.; Andrade, M.A.B.; Buiochi, F.; Adamowski, J.C. Identification of elastic, dielectric, and piezoelectric constants in piezoceramic disks. IEEE Trans. Ultrason. Ferr. 2010, 57, 2772–2783. [Google Scholar] [CrossRef] [PubMed]
- Perez, N.; Carbonari, R.C.; Andrade, M.A.B.; Buiochi, F.; Adamowski, J.C. A FEM-based method to determine the complex material properties of piezoelectric disks. Ultrasonics 2014, 54, 1631–1641. [Google Scholar] [CrossRef] [PubMed]
- Perez, N.; Buiochi, F.; Andrade, M.A.B.; Adamowski, J.C. Numerical characterization of soft piezoelectric ceramics. In Proceedings of the International Congress on Ultrasonics, Gdańsk, Poland, 5–8 September 2011.
- Perez, N.; Andrade, M.A.B.; Carbonari, R.C.; Buiochi, F.; Adamowski, J.C. Identification of piezoelectric complex parameters in rings for power ultrasound applications. IOP Conf. Ser. Mater. Sci. Eng. 2012, 42. [Google Scholar] [CrossRef]
- Perez, N.; Andrade, M.A.B.; Carbonari, R.C.; Adamowski, J.C.; Buiochi, F. Accurate determination of piezoelectric ceramic constants using a broadband approach. Proc. Meet. Acoust. 2013, 19. [Google Scholar] [CrossRef]
- Perez, N.; Carbonari, R.C.; Andrade, M.A.B.; Buiochi, F.; Adamowski, J.C. Sensitivity analysis and identification of damping parameters in the finite element modeling of piezoelectric ceramic disks. Adv. Mater. Res. 2014, 975, 288–293. [Google Scholar]
- Unverzagt, C.; Rautenberg, J.; Henning, B.; Kulshreshtha, K. Modified electrode shape for the improved determination of piezoelectric material parameters. In Proceedings of the 2013 International Congress on Ultrasonics, Singapore, 2–5 May 2013.
- Kulshreshtha, K.; Jurgelucks, B.; Bause, F.; Rautenberg, J.; Unverzagt, C. Increasing the sensitivity of electrical impedance to piezoelectric material parameters with non-uniform electrical excitation. J. Sens. Sens. Syst. 2015, 4, 217–227. [Google Scholar] [CrossRef]
- Lahmer, T.; Kaltenbacher, B.; Schulz, V. Optimal measurement selection for piezoelectric material tensor identification. Inverse Probl. Sci. Eng. 2008, 16, 369–387. [Google Scholar] [CrossRef]
- Li, S.; Zheng, L.; Jiang, W.; Sahul, R.; Gopalan, V.; Cao, W. Characterization of full set material constants of piezoelectric materials based on ultrasonic method and inverse impedance spectroscopy using only one sample. J. Appl. Phys. 2013, 114, 104505. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zheng, L.; Cao, W. Determination of full set material constants of [011]c poled 0.72Pb(Mg1/3Nb2/3)O3-0.28PbTiO3 single crystal from one sample. Appl. Phys. Lett. 2014, 105, 012901. [Google Scholar] [CrossRef] [PubMed]
- Jonsson, U.G.; Andersson, B.M.; Lindahl, O.A. A FEM-based method using harmonic overtones to determine the effective elastic, dielectric, and piezoelectric parameters of freely vibrating thick piezoelectric disks. IEEE Trans. Ultrason. Ferr. 2013, 60, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Buiochi, F.; Kiyono, C.Y.; Peréz, N.; Adamowski, J.C.; Silva, E.C.N. Efficient algorithm using a broadband approach to determine the complex constants of piezoelectric ceramics. Phys. Proced. 2015, 70, 143–146. [Google Scholar] [CrossRef]
- Kiyono, C.Y.; Peréz, N.; Silva, E.C.N. Determination of full piezoelectric complex parameters using gradient-based optimization algorithm. Smart Mater. Struct. 2015. to be published. [Google Scholar] [CrossRef]
- Rupitsch, S.J.; Ilg, J. Complete characterization of piezoceramic materials by means of two block-shaped test samples. IEEE Trans. Ultrason. Ferr. 2015, 62, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Cao, W. Temperature dependence of self-consistent full matrix material constants of lead zirconate titanate ceramics. Appl. Phys. Lett. 2015, 106, 052902. [Google Scholar] [CrossRef] [PubMed]
- Linder, C. A complex variable solution based analysis of electric displacement saturation for a cracked piezoelectric material. J. Appl. Mech. 2014, 81, 091006. [Google Scholar] [CrossRef]
- Linder, C.; Zhang, X. Three-dimensional finite elements with embedded strong discontinuities to model failure in electromechanical coupled materials. Comp. Meth. Appl. Mech. Eng. 2014, 273, 143–160. [Google Scholar] [CrossRef]
- Linder, C. An analysis of the exponential electric displacement saturation model in fracturing piezoelectric ceramics. Tech. Mech. 2012, 32, 53–69. [Google Scholar]
- Linder, C.; Miehe, C. Effect of electric displacement saturation on the hysteretic behavior of ferroelectric ceramics and the initiation and propagation of cracks in piezoelectric ceramics. J. Mech. Phys. Solids 2012, 60, 882–903. [Google Scholar] [CrossRef]
- Curie, J.; Curie, P. Développement, par pression, de l'électricité polaire dans les cristaux hémièdres à faces inclinées. Comptes Rendus 1880, 91, 294–295. [Google Scholar]
- Cady, W.G. The piezo-electric resonator. Radio Eng. Proc. Inst. 1922, 10, 83–114. [Google Scholar] [CrossRef]
- Jaffe, B.; Cook, W.R., Jr.; Jaffe, H. Piezoelectric Ceramics; Academic Press: Waltham, MA, USA, 1971. [Google Scholar]
- Meeker, T.R. Publication and proposed revision of ANSI/IEEE standard 176-1987 ANSI/IEEE Standard on piezoelectricity. IEEE Trans. Ultrason. Ferr. 1996, 43, 717–772. [Google Scholar]
- Theory and Reference for the Mechanical APDL and Mechanical Applications. Available online: http://orange.engr.ucdavis.edu/Documentation12.0/120/ans_thry.pdf (accessed on 14 January 2016).
- Uchino, K.; Hirose, S. Loss mechanisms in piezoelectrics: How to measure different losses separately. IEEE Trans. Ultrason. Ferr. 2001, 48, 307–321. [Google Scholar] [CrossRef]
- Ballato, A.; Kelly, J.; Ballato, J.; Safari, A. Dissipation in ceramic resonators and transducers. In Proceedings of the 1996 IEEE International Freauency Control Symposium, Honolulu, HI, USA, 5–7 June 1996.
- Nader, G.; Silva, E.C.N.; Adamowski, J.C. Effective damping value of piezoelectric transducer determined by experimental techniques and numerical analysis. Available online: http://www.abcm.org.br/symposium-series/SSM_Vol1/Section_II_Control_Systems/SSM_II_14.pdf (accessed on 21 December 2015).
- Holland, R. Representation of dielectric, elastic, and piezoelectric losses by complex coefficients. IEEE Trans. Son. Ultrason. 1967, 14, 18–20. [Google Scholar] [CrossRef]
- Kino, G.S. Acoustic Waves: Devices, Imaging, and Analog Signal Processing; Prentice-Hall: New York, NY, USA, 1987; pp. 27–84. [Google Scholar]
- Dyke, K.V. The piezo-electric resonator and its equivalent network. Proc. Inst. Radio Eng. 1928, 16, 742–764. [Google Scholar]
- Dye, D.W. The piezo-electric quartz resonator and its equivalent electrical circuit. Proc. Phys. Soc. London 1925, 38, 399–458. [Google Scholar] [CrossRef]
- Mason, W.P. Electromechanical Transducers and Wave Filters, 2nd ed.; D. Van Nostrand Company Inc.: Princeton, NJ, USA, 1948. [Google Scholar]
- Ballato, A. Equivalent Circuits for Resonators and Transducers Driven Piezoelectrically. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a231520.pdf (accessed on 21 December 2015).
- Kaltenbacher, M. Numerical Simulation of Mechatronic Sensors and Actuators; Springer: Berlin, Germany, 2004. [Google Scholar]
- Zheng, C.; Khan, H.; Hung, KC. Modeling of Material Damping Properties in ANSYS. Available online: http://easc.ansys.com/staticassets/ANSYS/staticassets/resourcelibrary/confpaper/2002-Int-ANSYS-Conf-197.PDF (accessed on 21 December 2015).
- Heinonen, E.; Juuti, J.; Leppävuori, S. Characterization and modelling of 3D piezoelectric ceramic structures with ATILA software. J. Eur. Ceram. Soc. 2005, 25, 2467–2470. [Google Scholar] [CrossRef]
- Desilets, C.; Wojcik, G.; Nikodym, L.; Mesterton, K. Analyses and measurements of acoustically matched, air-coupled tonpilz transducers. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Lake Tahoe, NV, USA, 17–20 October 1999.
- Piezoelectric Ceramics, Electro Ceramics Solutions. Available online: http://www.morganadvancedmaterials.com/sites/default/files/documents/r6001_piezo_brochureweb.pdf (accessed on 14 January 2016).
- Sherrit, S.; Wiederick, H.D.; Mukherjee, B.K.; Sayer, M. An accurate equivalent circuit for the unloaded piezoelectric vibrator in the thickness mode. J. Phys. D Appl. Phys. 1997, 30, 2354–2363. [Google Scholar] [CrossRef]
- Mukherjee, B.; Yang, G.; Sherritt, S. The use of complex material constants to model losses in piezoelectric. J. Acoust. Soc. Am. 1999, 106. [Google Scholar] [CrossRef]
- Sherrit, S.; Masys, T.J.; Wiederick, H.D.; Mukherjee, B.K. Determination of the reduced matrix of the piezoelectric, dielectric, and elastic material constants for a piezoelectric material with C∞ symmetry. IEEE Trans. Ultrason. Ferr. 2011, 58, 1714–1720. [Google Scholar] [CrossRef] [PubMed]
- Alemany, C.; Pardo, L.; Jimnez, B.; Carmona, F.; Mendiola, J. Automatic iterative evaluation of complex material constants in piezoelectric ceramics. J. Phys. D Appl. Phys. 1994, 27, 148–155. [Google Scholar] [CrossRef]
- Alemany, C.; Gonzalez, A.; Pardo, L.; Jimenez, B.; Carmona, F.; Mendiola, J. Automatic determination of complex constants of piezoelectric lossy materials in radial mode. J. Phys. D Appl. Phys. 1995, 28, 945–956. [Google Scholar] [CrossRef]
- Pardo, L.; Brebøl, K. Properties of Ferro-Piezoelectric Ceramic Materials in the Linear Range: Determination from Impedance Measurements at Resonance. In Springer Series in Materials Science; Springer: Dordrecht, The Netherland, 2011; pp. 2162–2169. [Google Scholar]
- Lin, Y.C.; Ma, C.C. Experimental measurement and numerical analysis on resonant characteristics of piezoelectric disks with partial electrode designs. IEEE Trans. Ultrason. Ferr. 2004, 51, 937–947. [Google Scholar]
- Wang, H.; Cao, W. Determination of full set material constants of piezoceramics from phase velocities. J. Appl. Phys. 2002, 92, 4578–4583. [Google Scholar] [CrossRef]
- Fialka, J.; Benes, P. Comparison of methods of piezoelectric coefficient measurement. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, N.; Buiochi, F.; Brizzotti Andrade, M.A.; Adamowski, J.C. Numerical Characterization of Piezoceramics Using Resonance Curves. Materials 2016, 9, 71. https://doi.org/10.3390/ma9020071
Pérez N, Buiochi F, Brizzotti Andrade MA, Adamowski JC. Numerical Characterization of Piezoceramics Using Resonance Curves. Materials. 2016; 9(2):71. https://doi.org/10.3390/ma9020071
Chicago/Turabian StylePérez, Nicolás, Flávio Buiochi, Marco Aurélio Brizzotti Andrade, and Julio Cezar Adamowski. 2016. "Numerical Characterization of Piezoceramics Using Resonance Curves" Materials 9, no. 2: 71. https://doi.org/10.3390/ma9020071
APA StylePérez, N., Buiochi, F., Brizzotti Andrade, M. A., & Adamowski, J. C. (2016). Numerical Characterization of Piezoceramics Using Resonance Curves. Materials, 9(2), 71. https://doi.org/10.3390/ma9020071







