Abstract
Functional Near InfraRed Spectroscopy (fNIRS) connectivity analysis is often performed using the measured oxy-haemoglobin (HbO2) signal, while the deoxy-haemoglobin (HHb) is largely ignored. The in-common information of the connectivity networks of both HbO2 and HHb is not regularly reported, or worse, assumed to be similar. Here we describe a methodology that allows the estimation of the symmetry between the functional connectivity (FC) networks of HbO2 and HHb and propose a differential symmetry index (DSI) indicative of the in-common physiological information. Our hypothesis is that the symmetry between FC networks associated with HbO2 and HHb is above what should be expected from random networks. FC analysis was done in fNIRS data collected from six freely-moving healthy volunteers over 16 locations on the prefrontal cortex during a real-world task in an out-of-the-lab environment. In addition, systemic data including breathing rate (BR) and heart rate (HR) were also synchronously collected and used within the FC analysis. FC networks for HbO2 and HHb were established independently using a Bayesian networks analysis. The DSI between both haemoglobin (Hb) networks with and without systemic influence was calculated. The relationship between the symmetry of HbO2 and HHb networks, including the segregational and integrational characteristics of the networks (modularity and global efficiency respectively) were further described. Consideration of systemic information increases the path lengths of the connectivity networks by 3%. Sparse networks exhibited higher asymmetry than dense networks. Importantly, our experimental connectivity networks symmetry between HbO2 and HHb departs from random (t-test: t(509) = 26.39, p < 0.0001). The DSI distribution suggests a threshold of 0.2 to decide whether both HbO2 and HHb FC networks ought to be studied. For sparse FC networks, analysis of both haemoglobin species is strongly recommended. Our DSI can provide a quantifiable guideline for deciding whether to proceed with single or both Hb networks in FC analysis.
1. Introduction
Diffuse near-infrared light can be used to interrogate brain haemodynamics and oxygenation non-invasively [1,2]. By measuring the light attenuation changes of the reflected light from the head, functional near infrared spectroscopy (fNIRS) quantifies the relative changes in the brain tissue concentrations of oxygenated (Δ[HbO2]) and deoxygenated (Δ[HHb]) haemoglobin in response to neuronal activation in the cerebral cortex. The bivariate nature of the paired haemoglobin reconstruction conveys rich information about the brain haemodynamics and oxygenation but increases the complexity of the analysis.
Brain connectivity expresses patterns of co-activity among brain regions and it is often investigated following two major types of relations, (i) associative or simply functional connectivity (FC); (ii) causal referred to as effective connectivity [3,4]. It is accepted that fNIRS is sensitive to the haemodynamic response subsequent to the neuronal activity. Ignoring the transient inverse response phase, the neuronal activity is inferred from the concomitant increase in HbO2 and decrease in HHb [1,5], consistent with our current understanding of the neurovascular coupling [6,7]. Most approaches for the analysis of connectivity yield a graph’s binary adjacency matrix characterizing the connectivity network. These approaches have two inherent shortcomings: (i) the binarization depends on a threshold that severely affects the graph density with important implications for interpretation [8]; (ii) a step to decide which haemoglobin (Hb) signal is to be used for subsequent analysis or whether analysing both Hb species is needed. Many researchers have studied different aspects of FC with fNIRS [9,10,11,12,13,14,15]; however, the analysis of connectivity maps is often done only using the fNIRS HbO2 time courses. It is important to understand whether during the analysis both Hb species time courses are relevant, or if either provide analogous information and hence univariate analysis of connectivity may sufficient. In fNIRS connectivity analysis, an important decision is to opt for one of the haemoglobin species to generate the connectivity network of interest, whether the HbO2 or HHb. A part of the scientific community favours the connectivity networks derived from the HbO2 signal due to its higher signal-to-noise (SNR) ratio. Another part favours an analysis based on the HHb signal arguing its higher specificity to activity and higher robustness to physiological contaminations [16]. The rest of the community opts either for considering two univariate analysis or a true bivariate analysis [17].
A critical evaluation has not yet been performed on whether the connectivity network revealed by either haemoglobin species are equivalent - and thus a univariate analysis is enough—or not—and thus bivariate analysis should be employed considering both Hb species. This issue has not been investigated yet, as it might not be well understood what kind of information on brain connectivity is shared between the two Hb connectivity networks and how to quantify such information. Considering that HbO2 and HHb often exhibit highly anticorrelated patterns during brain activation, one might expect a strong match between the connectivity graphs generated from either signal. However, this is not always the case. For instance, classical reconstruction methods based on inverting the modified Beer-Lambert law introduce cross-talk between the two signals species [6], further artifactually supporting the univariate argument of equivalent results. In addition, these fNIRS haemodynamic signals have notable differences in their contribution from factors such as systemic physiology [18,19,20]. When two brain regions are co-active, this may conceal any substantial differences in the HbO2 and HHb network structures. Differences in structural connections of FC networks can be described quantitatively by simple enough methods such as the Jaccard index (Ji). Nevertheless, the Ji is sensitive to the density of links in each network, which can lead to suggest two networks to be symmetric only because the number of connections is high. The FC analysis with fNIRS has mostly focused on describing and understanding the cortical connections within the normal healthy brain. However, when the connectivity analysis is expanded to the diseased brain, there can be various pathological conditions that involve the alteration of neurovascular coupling mechanisms (e.g., Alzheimer’s disease or stroke) and thus differences in the dynamics and in the connectivity networks of HbO2 and HHb might occur. In addition, having now the capacity to monitor functional brain activity on freely moving people in the real-world through wearable fNIRS systems, bigger changes in systemic physiology might occur. Current investigations have expanded the research on more complex realistic settings which consider, for example, inter-personal interactions [21,22]. Therefore, the analysis of data recorded in such ecologically-valid settings might require further consideration of which haemoglobin signal is the best indicator of FC due to differences in systemic interferences between the signals.
The amount of in-common information between HbO2 and HHb species has been estimated mainly as a complementary instead of a guiding task for the connectivity analysis. Correlations between the BOLD signal and the haemoglobin species hinted a latent incongruence between HbO2 and HHb responses [23] with Strangman et al. [24] suggesting to address the issue prior the analysis. Wolf et al. [25] found different symmetric patterns across brain areas; for instance, while in the visual cortex the HbO2 and HHb exhibited symmetry, in the motor cortex such symmetry was not found. These asymmetries may also occur across frequency bands [26]. More importantly, such asymmetry may substantially alter the FC analysis itself, for instance using during a independent component analysis (ICA) when analysing resting state connectivity [12] as ICA-based analysis is capable of removing certain types of noise and artefacts [27]. Despite these early studies, more studies are needed regarding the understanding of the asymmetry/symmetry between Hb species. There are very few studies that investigated the symmetry of Hb species prior to the FC analysis and none has studied the symmetry directly from the Hb connectivity networks. However, in the context of FC networks, we emphasise that any symmetry analysis metric should take into account the structural features of these networks. In this paper, our goal is to quantify differences (if any) between the FC networks retrieved from the analysis based on each Hb species, both at baseline and during task-evoked responses, in order to understand how these two Hb derived networks are related. To achieve this, we describe a new metric for the quantification of the symmetry between the FC networks of HbO2 versus the HHb. In addition, we introduce FC analysis between fNIRS signals and systemic variables, allowing for the first time an analysis approach that takes into consideration systemic driven fNIRS changes. We derived a set of connectivity networks for both haemoglobin species complicated functional study in freely moving participants in an ecological situation. We select an out-of-lab situation due to the induced walk-related systemic changes whereby the observed response would be affected and therefore also the expected symmetry values. In this sense, we hypothesize that in healthy subjects during certain brain functional experiments these non-neuronal confounding factors disproportionately affect the structure of the connectivity networks causing a decrease in their symmetry. Finally, we propose a novel index to quantify the extent of symmetry between Hb-derived connectivity networks; and further suggest a threshold which can aid in the decision of opting for one Hb signal over the other or either keeping both. The decision of opting for one signal over the other or either keeping both has important implications for interpretation. The analysis based on incomplete brain networks information could lead to deceptive inference. For instance, as the different Hb species FC networks depart from symmetry, their associated connectivity graph will consequently be dissimilar. Reducing connectivity analysis to a single Hb species under disparate responses will pose a greater risk for misinterpretation. Also, it can be argued that upon showing symmetry or asymmetry, this may justify univariate analysis saving otherwise mandatory bivariate FC connectivity analysis and to draw wrong conclusions when e.g., predicting whether a person is a healthy control or a patient [28,29].
2. Materials and Methods
2.1. Experimental Protocol
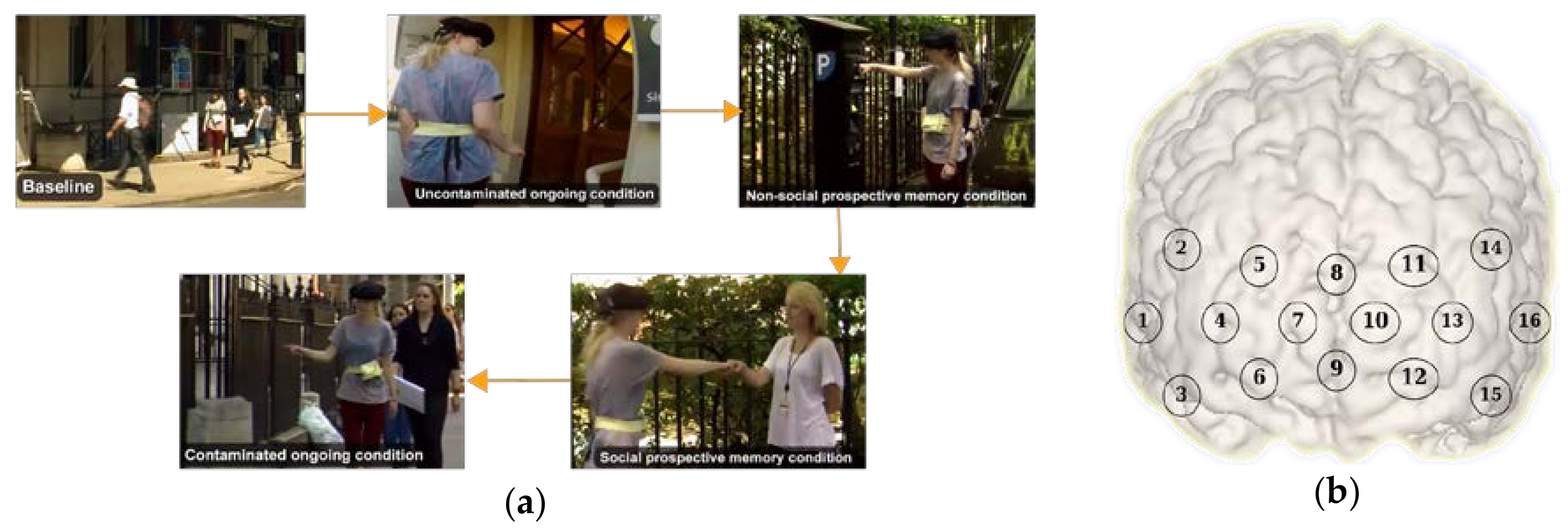
For this research, we used data from a study originally presented in [30]. In brief, the study investigated the role of prefrontal cortex during a prospective memory task in an ecological setting. Prospective memory is defined as the ability to remember to carry out delayed intentions [31]. During prospective memory tasks, 6 participants were asked to respond to an infrequent cue e.g., a familiar face (social) or a parking meter (non-social), while performing another demanding task within the experimental area (counting certain items such as the number of signs containing the word “Queen” or the number of unobstructed stairways, or the number of doorbells, etc.) known as the ongoing (OG) task. The protocol included: (i) two Rest conditions (i.e., counting the number of Os on a piece of paper while the participant is standing stationary, and walking a short distance doing nothing else); (ii) a Baseline (BL) condition (i.e., the experimenter showing the experimental area to the participant); (iii) two OG-only conditions (i.e., walking around the streets counting certain items without knowledge of any other instruction) were included one before and one after the prospective memory tasks. The first OG task is defined as ‘uncontaminated’ as participants do not have the representation of the delayed intention in their mind and have not encountered the prospective memory cues yet. The second OG task is called ‘contaminated’ (OGc) as participants have already performed the prospective memory task and the representation of pre-formed intentions can remain; (iv) a social and non-social prospective memory condition. The prospective memory tasks consisted in a social (SocPM; performing the OG task while responding to social cues, e.g., fist bumping an experimenter) and non-social (NonSocPM; performing the OG task while responding to non-social cues, e.g., fist bump parking meters). The Rest conditions were repeated in opposite order at the end of the experimental session. The tasks were carried out at self-pace. Figure 1a shows the different activities during the conditions.
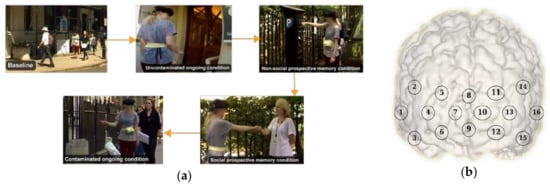
Figure 1.
(a) Examples of the baseline, ongoing, social prospective memory, non-social prospective memory, and ongoing contaminated conditions during the experiment; (b) functional near infrared spectroscopy (fNIRS) channels distribution.
2.2. Data Acquisition and Processing
Changes in prefrontal cortex haemoglobin responses were monitored by using a Wearable Optical Topography (WOT, Hitachi High-technologies Corporation, Tokyo, Japan) fNIRS system on 6 freely moving healthy adults. The fNIRS system integrates 6 light sources (705 nm and 830 nm) and 6 detectors arranged in an alternating geometry and creating 16 measurements channels (Figure 1b), with an inter-optode separation of 3 cm. The WOT system operates at a sampling frequency of 5 Hz. The headset covers the dorsolateral and rostral prefrontal cortex (Figure 1b). The changes in heart rate and breathing rate were simultaneously recorded using a wearable monitoring belt (Bioharness, Zephyr Technology, Annapolis, MD, USA). Heart rate and breathing rate were sampled at 250 Hz and 25 Hz respectively, and internally averaged by the device to provide output data at 1 Hz. Three cameras were used to record the entire experimental session and to recover the start and end of each condition. All the recordings were synchronised.
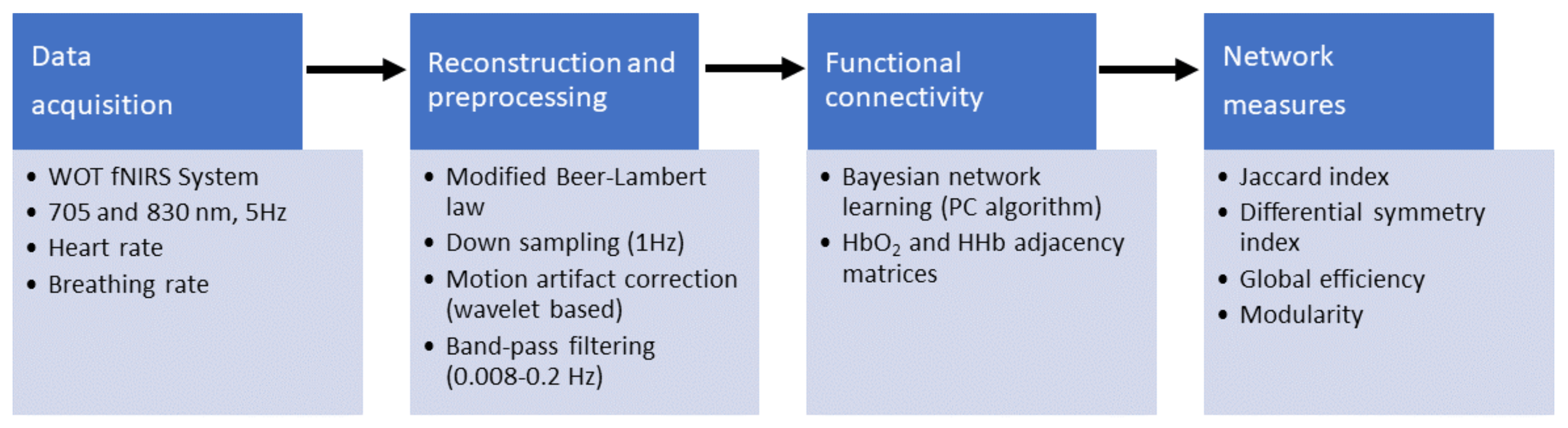
Relative changes in HbO2 and HHb from an arbitrary zero baseline at the beginning of the measurement period were calculated by the fNIRS system processing unit [32]. Using the modified Beer-Lambert law the concentration values were calculated and expressed in molar concentrations (mmol/L) multiplied by the path length (mm) as they are not corrected for the optical path length. The processing included down-sampling to 1 Hz, and motion artifacts identification and correction was performed through a wavelet-based method [33]. Physiological noise reduction was achieved by using a band-pass filter (3rd order Butterworth band-pass filter, 0.008–0.2 Hz) to remove slow trends and physiological noise (e.g., respiration). The general pipeline is shown in Figure 2.
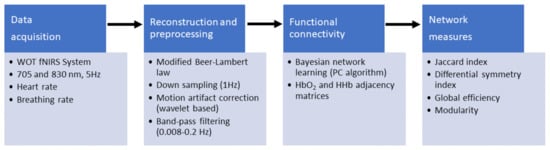
Figure 2.
Preprocessing flowchart. fNIRS measurements were acquired by using a wearable optical topography fNIRS system. Then, the haemoglobin (Hb) signals were reconstructed and preprocessed, and the systemic information was added. A set of connectivity networks were determined by the PC [34] algorithm by using the implementation in pcalg R package [35]. Finally, the symmetry between functional connectivity networks and global efficiency and modularity across networks were computed.
2.3. Functional Connectivity Analysis
Often, brain connectivity investigations are aimed to draw inferences from a cohort of participants at group-level. For a group-level analysis, three typical approaches are: (i) an averaged representation typically called virtual-typical-subject (VTS) [36,37,38]; (ii) the individual-structure (IC); (iii) the common-structure (CS). The VTS representation uses an averaged-data version of the cohort, whereby a model is learned. The IS approach considers a single model for each subject, and, after a sort of model marginalization generates a single model with coinciding patterns among them. For the CS approach a unique model is learned (as in VTS). However, the set of individual parameters are preserved for each subject. Our aim is to analyse how the contribution derived from systemic factors affects the asymmetry between HbO2 and HHb connectivity networks. In order to articulate our results (see Section 3), we opt for a group-level analysis by using a VTS representation.
Connectivity networks were generated for each Hb signal and each condition using a Bayesian network (BN) [39]. Bayesian networks were previously used for the investigation of brain connectivity in studies such as [36,37,38,40,41,42,43,44,45]. Formally, a BN is a pair <G(V, E), θ> for encoding the structure or skeleton G(V, E) and the parametrization of the network θ. The structure G(V, E) is a directed acyclic graph conformed to a set of nodes (V) and links between them (E). For our purpose, the sets V and E represent the set of brain regions (channels measurements) and the functional associations between them, respectively. The BNs framework determines the connectivity between pairs of observed nodes (fNIRS channels measurements) by examining the probabilistic independence relationships between them. Statistical independence tests are carried out so that the links in a connectivity network can be established. There are many algorithms described in the literature for automatically learning of the structure G which either consider the directionality of the links or not. In our case, we have used the PC algorithm [34] (PC stands for the initials of its creators Peter Spirtes and Clark Glymour) as we are dealing with functional connectivity (FC), and thus we only need the discovery of statistical associations between fNIRS channels regardless of the direction. Hence, we only considered the first phase of the PC algorithm that recovers the skeleton (undirected graph) of the BN.
In order to do so, each processed fNIRS time series was split according to experimental conditions into blocks for baseline (BS), ongoing (OG), social prospective memory (SocPM), non-social prospective memory (NonSocPM), and ongoing contaminated (OGc). The block-splitting task was done using the start and end timestamps obtained from the analysis of video recordings. We then obtained an averaged block for every condition according to the VTS group-level analysis. Four connectivity networks are retrieved for every condition corresponding to the two-haemoglobin species (HbO2, HHb) and the inclusion or not of systemic information—heart rate (HR) and breathing rate (BR)—as nodes in the network.
To contextualise our findings with relevant features of the recovered FC networks, we computed the global efficiency (GE) and modularity (MOD), which are summary measures of functional integration and functional segregation in complex networks analysis, respectively. GE measures how efficiently information is exchanged over the network [46]. GE values are in the [0, 1] range. Since GE is defined as the average of the inverse shortest distance between nodes, disconnected nodes have infinity distance, producing then 0 efficiency. On the contrary, connected nodes by one-edge path have 1 efficiency, and the global efficiency is the average of such efficiencies for all pair of nodes. MOD estimates the extent of community structure of a network, where the community structure is an arrangement of the network in which groups of nodes exhibit high intra-group connections and low inter-group connections [47]. The MOD values are in the [0, 1] range, where 0 means that the number of intra-group edges is no better than a random division, and values approaching 1 indicating strong community structure. However, in practice values typically fall in the range [0.3, 0.7] and higher values are rare [48]. For this work, we apply a group-level analysis by obtaining a set of FC networks for the VTS representation, furthermore we obtained the summary measures GE and MOD to characterise patterns of such networks.
2.4. Quantification of Network Symmetry
Networks similarity was quantified in terms of the symmetry between the connectivity matrices (graph adjacency matrices) between networks, compared using the Jaccard index (Ji) [49]. The Ji of two connectivity matrices A and B is defined as:
where |•| indicates the cardinality of the set. The Ji yields values in the range between 0 and 1, ranging from totally dissimilar to fully identical connectivity matrices, respectively. The Ji is a convenient metric to study the symmetry of functional networks because it ignores absent connections between graph nodes. Nevertheless, the symmetry is affected by the networks density. In general, comparing two densely connected networks, functional networks will result in a large Ji, whilst comparing two sparse networks will likely result in a low Ji. This is further discussed in Section 3.1. This is a mathematical artefact with no relation to physiology which should be discounted before interpreting symmetry. To separate the mathematical effect of the Ji index from the pure physiological effect, we propose a differential symmetry index (DSI) which discounts baseline Ji values expected for random networks.
Let be the network density for the HbO2 and HHb networks respectively. A graph density is calculated according to Equation (2):
with ℓ being the number of links, n the number of nodes, and X represents one of the Hb species. Let be the chosen symmetry function (Ji in our case). Then the DSI is presented in Equation (3).
where is the expected baseline symmetry. The expected baseline symmetry can be obtained from an analytical model describing the symmetry values produced by random connectivity networks. can be approximated by multiple linear regression, radial basis functions approximation or interpolation methods. We choose a bilinear interpolation because of its computational simplicity. Using bilinear interpolation, is approximated according to Equation (4):
where the model coefficients are found by solving the linear system in Equation (5).
where, are the connection densities of the m-th FC network from oxy-haemoglobin (HbO2) and deoxy-haemoglobin (HHb), respectively. Note that the DSI represents the residuals of a symmetry model for random networks discounting the mathematical baseline and leaving what is assumed to be the physiological contribution. The DSI has been implemented in Matlab 2017b and can be downloaded at https://github.com/multimodalspectroscopy/DSI.git.
The proposed DSI quantifies the similarity with respect to the structure between connectivity networks and has been constructed without knowledge of the active channels. The DSI can be applied regardless the experimental design, as it does not rely on specific assumptions regarding the origin of the FC networks neither the chosen paradigm (block-design or event-related).
3. Results
3.1. Network Symmetry Analysis
Understanding brain networks must be done with respect to random networks. For this reason, we simulated synthetic random networks as follows: pairs of random networks representative of the Hb species were generated starting with one random link (ℓ1 = ℓ2 = 1) each one. Because our experimental dataset has 16 channels we fixed the random networks size to sixteen nodes (n = 16). Henceforth, we continue increasing their density by randomly adding one link at time until both networks are fully connected (ℓ1 = ℓ2 = L with L = (n × (n − 1))/2). For each pair of edges cardinality <ℓ1, ℓ2> we repeated the process 50 times. Then, the connection densities and their associated Ji were calculated for every scenario. Finally, the mean Ji across the 50 repetitions was calculated.
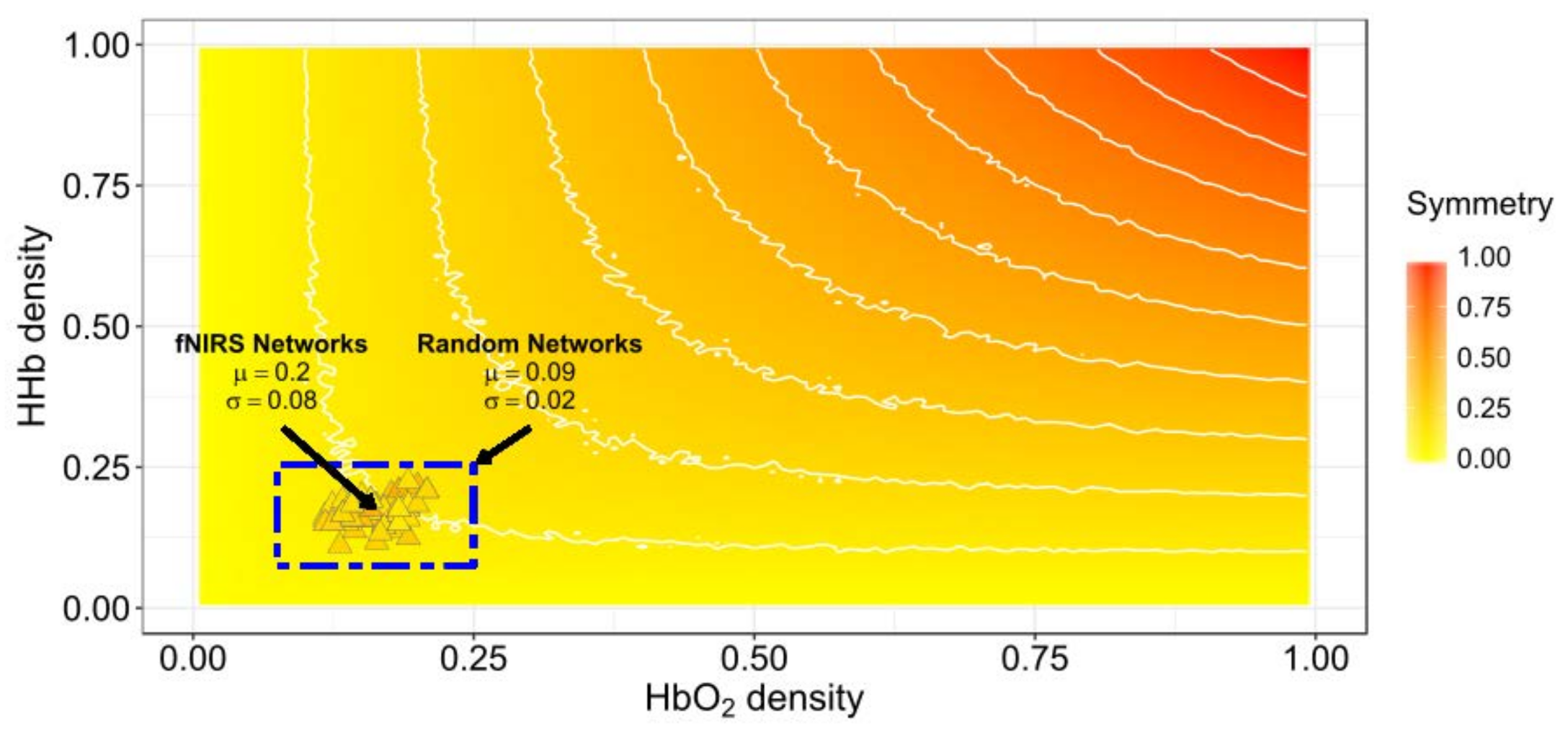
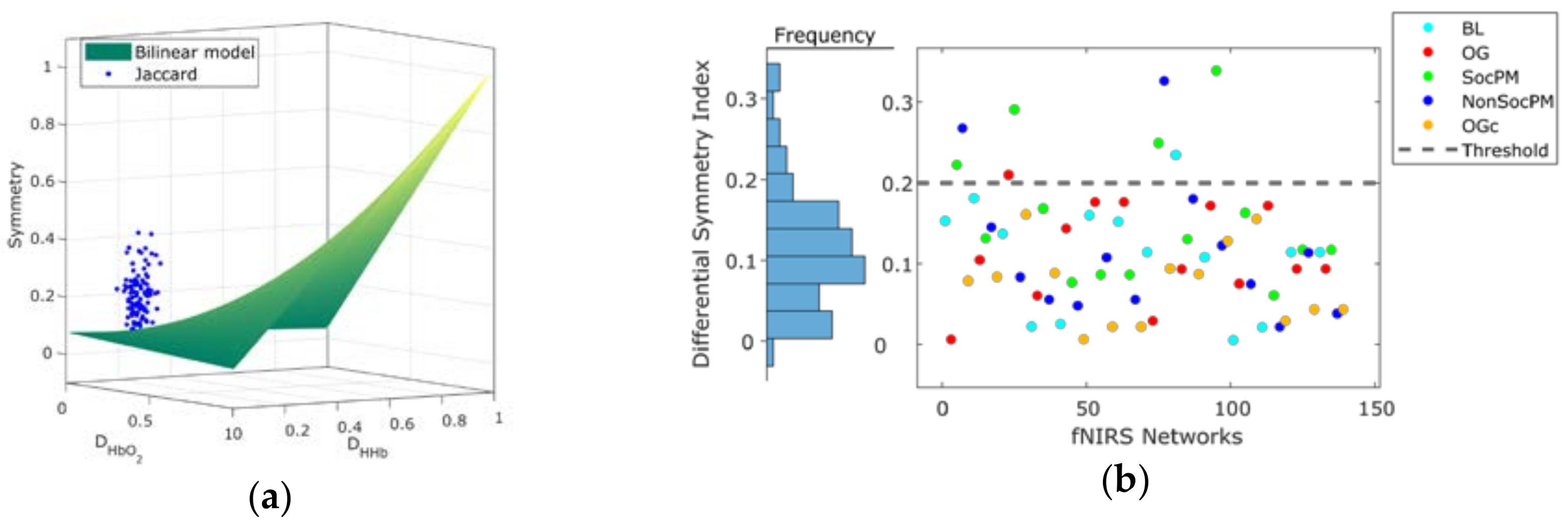
Figure 3 shows the relationship between the density of networks and their average random Ji symmetry. Also, the symmetries between the HbO2 and HHb experimental networks retrieved from the six participants with systemic information is projected over the expected symmetry space in Figure 3. The experimental functional connectivity (FC) networks exhibit low densities but with comparatively higher symmetry than would be expected from random behaviour. Then, we can expect small absolute changes in both symmetry and density values when systemic variables are added. The symmetry of experimental FC networks (M = 0.2, SD = 0.07) significantly differ from the symmetry of the random networks pairs (M = 0.09, SD = 0.02) (t-test: t(509) = 26.39, p < 0.0001 assuming equal variances; C.I. 95% for the Difference (0.11,0.13)) (see Figure 3 blue rectangle).
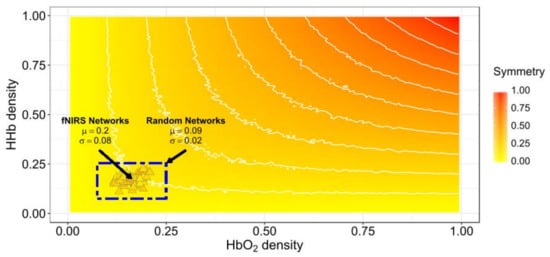
Figure 3.
Jaccard symmetry response from experimental and random connectivity networks pairs varying density. The x-axis represents HbO2 density and the y-axis represents HHb density. Color encodes the extent of symmetry. The background symmetry field corresponds to values expected for random synthetic networks from disconnected to complete connected ([0−1]) in both networks. Triangles correspond to experimental functional connectivity (FC) networks pairs from the six-subjects across conditions. High-density networks are those with a large number of connections (ℓ ≈ L). The results for high symmetry values are observed only for high-density random networks pairs but not for our experimental fNIRS FC networks pairs.
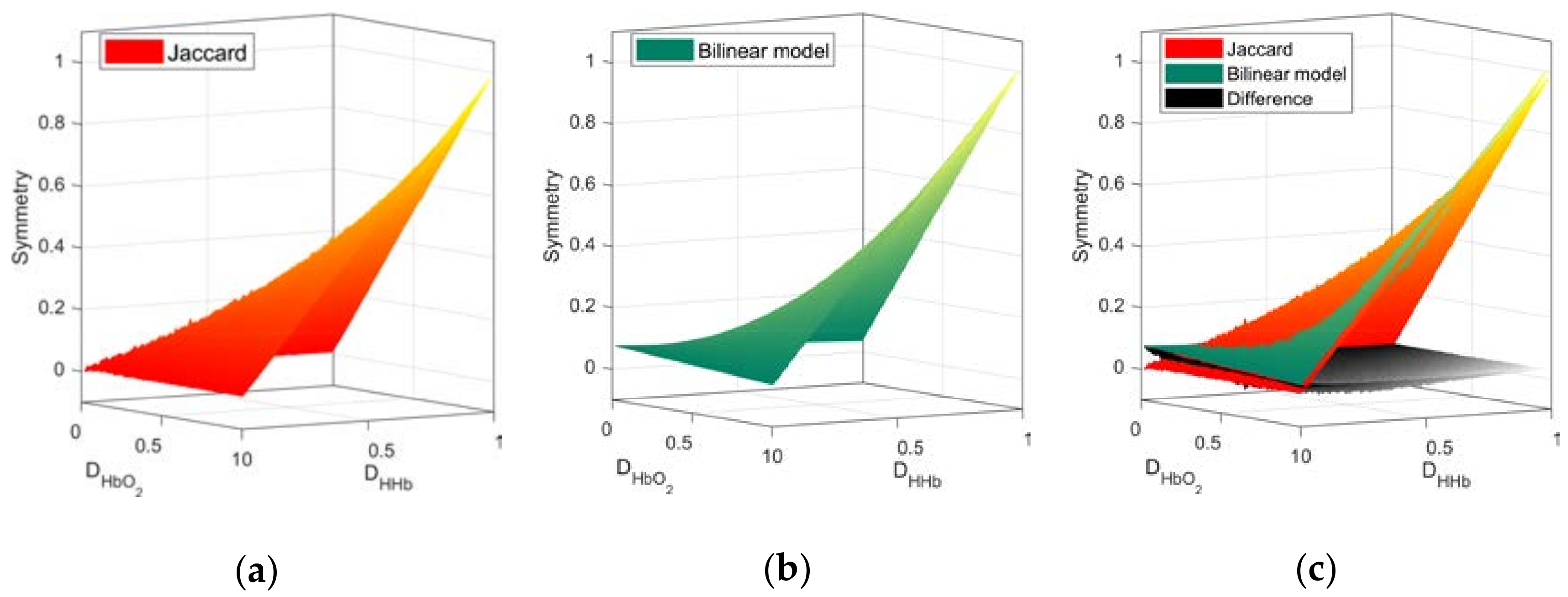
Focusing on the symmetry values due to physiological changes, we apply the DSI to the FC networks derived from Hb species as per Equation (3). First, from the Ji values of the random FC networks pairs, the a coefficients of the bilinear interpolation in Equation (4) to approximate were computed (a = (0.0768, −0.0484, −0.0485, 1.0512)). The mean Ji based symmetry from pairs of random networks and the approximated bilinear model are presented in Figure 4.
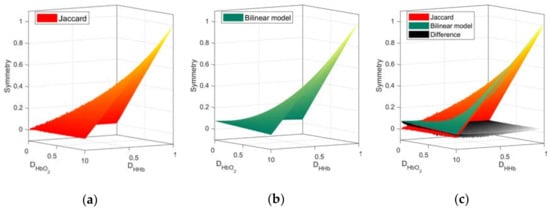
Figure 4.
Symmetry space from random networks. Surfaces obtained from the Ji values (a) and the approximation from the bilinear model (b). The graphical comparison and the differences between both surfaces (c). Higher order interpolation models can yield a better approximation with increasing degree of complexity.
Figure 5a shows the separation of the Ji based networks symmetry between the experimental and the expected baseline random values described by the bilinear model. Figure 5b shows the DSI values for fNIRS network. The distribution of the DSI values (residual differences between observed symmetry and the expected baseline counterpart) suggests that most fNIRS FC networks exhibit symmetry below DSI < 0.2. This suggests an empirical threshold for deciding when to proceed with connectivity analysis across both Hb; networks pairs with DSI < 0.2 could be considered as asymmetric, and the FC analysis including the two Hb-derived networks is encouraged.
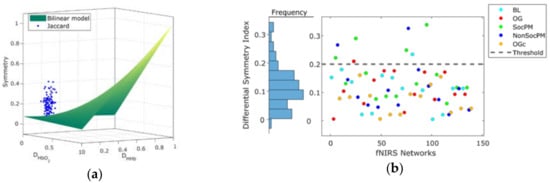
Figure 5.
(a) Projection of the symmetry values of fNIRS FC networks obtained by Jaccard index (blue dots) over the random baseline approximated by a bilinear model (green surface); (b) differential symmetry index (DSI) values grouped by condition and its distribution (left margin histogram). A threshold (grey dashed line) derived from the distribution of DSI values is also shown.
3.2. Integrational Analysis of Connectivity
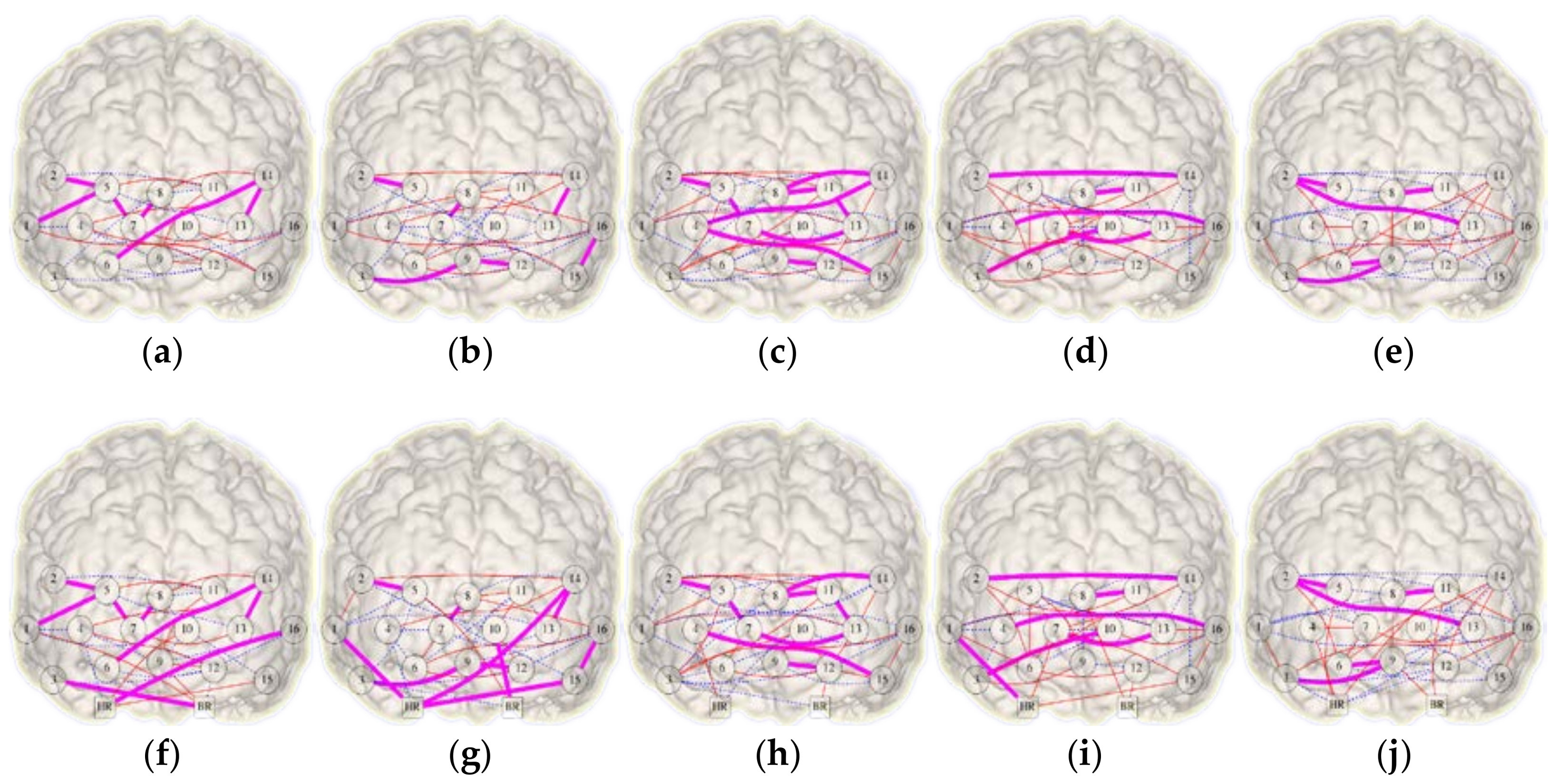
The networks in Figure 6 shows the links existing in the corresponding pair of HbO2 and HHb networks for each condition. Also, Figure 6 depicts the FC networks obtained with and without the systemic factors (heart rate and breathing rate). Regarding in-common links, the inclusion of systemic variables increases the number of such relations during BL, OG, and NonSocPM conditions by 4, 8, and 2 increments respectively. The OGc condition remains unchanged and SocPM condition diminished in 2 links. More connections were found in the PM blocks (Figure 6c,d,h,i) in respect to the OG blocks (Figure 6b,g,e,j). These connections are more observed between the two hemispheres and, some of them, at the left and right lateral prefrontal cortex (PFC). Also, Figure 6b,g shows a set of connections between the close channels 13–14, 15–16, 2–5, 7–8, 9–12 within the same region. On the other hand, connections between corresponding channels (Ch. 2–14, 4–16, 3–10, 7–13) in the two lateral PFC were also found (Figure 6d,i). This could be caused by a higher involvement of lateral PFC, which has been observed in prospective memory tasks and a major involvement of medial PFC is related to OG activities [31]. Table 1 summarises the changes in density and symmetry values from the combined networks presented in Figure 6. The five FC networks exhibits an increase in density of 2%, 3%, 2%, 2% and 5% for BL, OG, SocPM, NonSocPM, and OGc conditions respectively. In terms of Jaccard symmetry, BL, OG, and NonSocPM conditions showed increasing values of 4%, 8%, and 1% respectively while the SocPM and OGc conditions decreased by 4% and 3% respectively. Unlike random networks, fNIRS FC networks tends to have absolute low values of symmetry. Thus, the addition of the systemic information produced small changes in both symmetry and density.
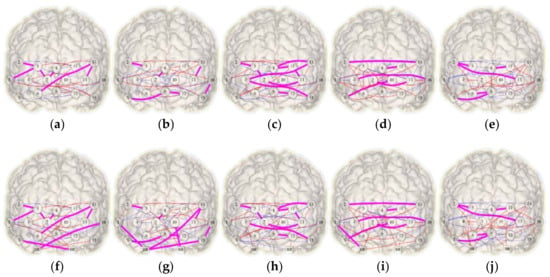
Figure 6.
Combined HbO2-HHb functional connectivity networks recovered from a virtual-typical-subject. Top (a–e) and bottom (f–j) rows show the networks without and with systemic variables information respectively. From left to right, columns representing the conditions: baseline (a,f), ongoing (b,g), social prospective memory (c,h), non-social prospective memory (d,i), and ongoing contaminated (e,j). Functional links determined from HbO2 and HHb are shown in solid red and dashed blue respectively and in-common links in bold magenta.

Table 1.
Density, Jaccard and DSI symmetry changes with/without systemic information from the virtual-typical-subject. Experimental connectivity networks from baseline, ongoing, social prospective memory, non-social prospective memory, and ongoing contaminated conditions.
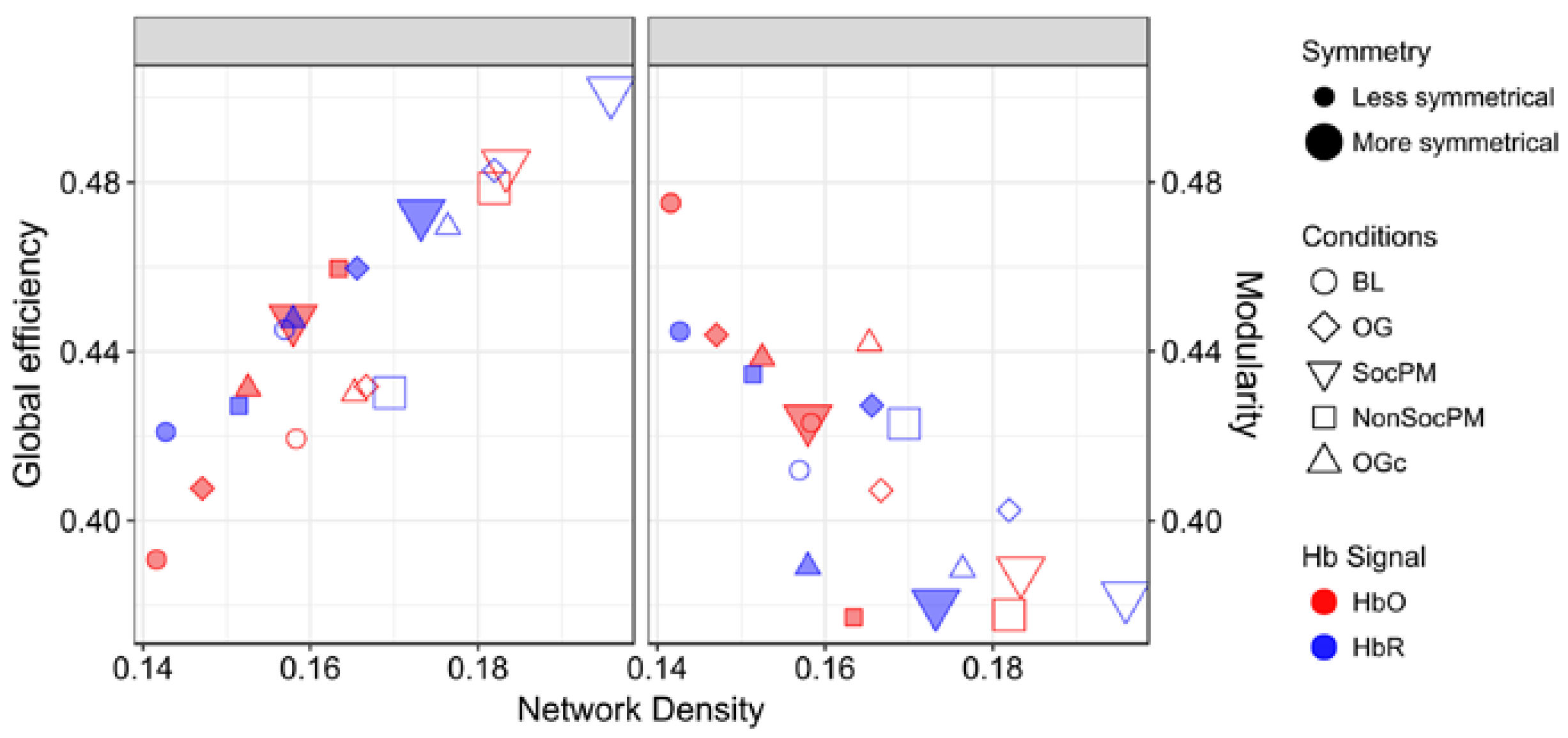
Finally, Figure 7 presents the GE and MOD with respect to density. In general, a contrapositive behaviour for SocPM and BL networks was observed (greater values of GE and smaller values of MOD). This trend is somewhat expected; fully connected networks have maximum GE and minimal modularity, and in the opposite extreme, strictly modular networks have little efficiency. More specifically for GE, a positive trend is observed and roughly the BL-OG-OGc-NonSocPM-SocPM order can be recognised. On the other hand, for MOD results a negative trend can be seen with almost the opposite order. Also, more than the half of the HbO2 networks were found to be over the mean MOD value.
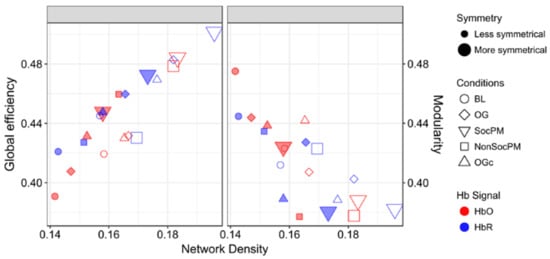
Figure 7.
Measures of integration (global efficiency) and segregation (modularity) in functional networks. The size, shape, colour and padding of markers encode the amount of symmetry, experimental condition, Hb signal and the inclusion or exclusion of systemic data, respectively.
4. Discussion
We have developed and presented a new method that allows the quantification of the symmetry between the FC network maps of HbO2 and HHb. This novel approach is based on the DSI and the Jaccard index; and can help in improving the interpretation of functional connectivity (FC) analyses with fNIRS. In addition, we have demonstrated for the first time how systemic data can be integrated within the HbO2 and HHb FC networks to disentangle spurious relation between brain regions. Considering that the brain networks are dynamically produced, we can expect some variations in their structures across subjects, or even longitudinally within the same person [10,15]. The DSI is able to separate the symmetric response of the FC networks between HbO2 and HHb derived from physiology by removing the mathematical contribution of the Jaccard index. This provides us with a new tool to decide whether HbO2 or HHb networks individually would lead to a better representation of the functional paths, or if both signals must be used to assess FC.
4.1. Symmetry between HbO2 and HHb Connectivity Networks
The analysis of random networks suggested a relation between density and the symmetry in FC networks (see Figure 3). In particular, we showed that the networks derived from fNIRS recordings exhibit symmetry values between HbO2 and HHb above its random counterpart. In synthetic random networks, the symmetry value is higher when the connectivity density in both networks increases. This is consistent with the experimental observation that, for highly dense diffuse optical tomography spatial configurations, both HbO2 and HHb networks include a high number of functional links [11]. Such higher channels density is often associated with a higher number of links i.e., denser networks (ℓ ≈ L). In this case, the decision of choosing one of the two Hb species is not crucial, as we expect high symmetries between them. In case of low channel density data sets, we cannot ignore the differences in the symmetry between HbO2 and HHb FC networks. Most of the current fNIRS technologies are still spatially low channel density devices [2], hence likely to be accompanied with a less dense-connectivity graph. Therefore, the symmetry between HbO2 and HHb FC networks must be investigated and taken into consideration to draw more correct neuroscientific conclusions based on fNIRS-derived FC measures. Regarding the fNIRS networks presented here, the social and non-social prospective memory (SocPM and NonSocPM) conditions achieved more symmetric responses (Figure 6 bigger markers) between the HbO2 and HHb FC networks. In this sense, this could be related the prospective memory task itself. In fact, prospective memory involves the integration of several executive functions (e.g., planning, retrospective/working memory, cognitive flexibility and inhibitory control, attentional monitoring, etc. [50]) and requires the conscious interruption of the OG task to fulfill the delayed intention, thus being more complex than only the OG task or the rest conditions. Our data suggests that the memory-related tasks within our current functional protocol produced higher symmetric FC networks between the Hb species compared to the other tasks. In addition, the walking-related tasks were found to produce more asymmetrical FC networks between the Hb species. These results refer to the particular prospective memory protocol described here. Additional work is needed to further expand and investigate the proposed DSI method with additional functional paradigms, different experimental designs and brain regions.
The frontal cortex is highly interconnected, both between cytoarchitectonic subdivisions within the frontal lobes, and also between these subregions and regions elsewhere. Indeed, this interconnectivity has been argued to be the main reason why neuronal density within PFC is so low compared to other regions of the brain: it means that more space is available for white matter connections (for review see [51]). The white matter connections within frontal cortex and with non-frontal regions are usefully given by [52,53,54]. However, the structural connections are only one way of considering connectivity. A further approach is to consider the functional connectivity as considered here. For fMRI, this has been conducted for a range of tasks (e.g., [55]). While broadly speaking, as one might expect, cortical regions that have direct white matter connections tend to show greater coactivations, the cognitive functions that the frontal cortex are performing are sometimes determined by the regions with which they are co-active. Thus for instance, for a range of types of mental activity (e.g., mentalising, multitasking, working memory), medial rostral PFC coactivates with posterior cingulate, during performance of episodic memory tasks, it is lateral rostral PFC that coactivates with posterior cingulate [55]. Therefore, decoding the functional organisation of the frontal cortex depends critically upon understanding the differential patterns of connections between tasks, not just the coactivations across them or the structural connections between them. With this in mind, it is important to consider these changes in patterns of activation in the context of naturalistic settings. This is because it has been known for a long time that the frontal lobes respond to degrees of novelty, technical difficulty (and danger) and also control voluntary and spontaneous/self-generated behaviour (e.g., [56]). Thus, removing the participant from the natural setting in which a mental process would normally be used in order to study differential patterns of coactivation risks (as in a typical lab experiment) seriously compromises the ecological or construct validity of the task. (“Ecological validity” refers to the degree to which results found in experimental lab settings relate to results in the “real life” situations one wishes to understand, and the term “construct validity” refers to the degree to which one is measuring the mental process or system that one intends to measure. See [57] for explanation.)
An exciting possibility arising from the results here would be to create maps of predicted coactivations between FC subregions based on our anatomical knowledge and discover, for specified cognitive tasks, the perturbation from them. For instance, FC follows broadly the same principles of activation in other brain regions, which is that there is a tendency towards contralateral coactivations. Indeed, for participants carrying out prospective memory tasks (as here, but in a lab), it is common to see bilateral rostral PFC activation when the participant is maintaining an intention [58]. Other subregions can show negatively correlated activity. For instance, the fronto-marginal tract connects medial and lateral regions of the frontal pole, and during maintenance of an intention it is common to see significant activation increases in the lateral frontal pole accompanied by significant decreases in the medial frontal pole (BA 10). For performance of the ongoing task only (i.e., where there is no intention maintenance), this pattern is reversed [58]. But this is not true of every task, and deviations from these kinds of pattern almost certainly have functional significance for understanding mind-brain relations. Yet cognitive neuroscientists do not currently understand them well. However, they may hold an important key to understanding plasticity in the brain, relevant to, for example, functional recovery from brain injury. So, it is of high importance that we discover the underlying principles. In this way, establishing the relation between structural connectivity and functional connectivity and how these are attenuated by task and physiological factors is a key aim for the cognitive neuroscience community, and the methods demonstrated here offer a new way of approaching this while maintaining a gold standard for ecological and construct validity.
The DSI has been constructed without knowledge of the active channels, but it can also be constrained to the functional active channels. In principle, given that the DSI aims to eliminate the bias due to the artificial contribution of the comparison function e.g., Ji, over some particular feature e.g., the density of the network; it seems plausible to think that the abstract construct could be adjusted to work with other objects encoding information about haemodynamics other than the connectivity networks. For instance, a promising use of DSI could include the assessment of similarity between HbO2 and HHb activation maps, or on a different example, the DSI could evaluate the (dis-)similarity among HbO2 or HHb activation maps longitudinally acquired for a subject. However, different comparison functions and different features would combine to generate different bias, which is what our second term of the DSI removes. Further work is necessary to allow the development of a more generally applied second term.
4.2. Inclusion of Systemic Data in fNIRS Functional Connectivity Analysis
The contribution of non-neuronal physiological changes to the fNIRS signal have been widely investigated over the past years. Previous studies [10,29,59,60] have found that excluding the impact of systemic confounders leads to discrepancies in the connectivity maps. On the other hand, taking physiological interferences into consideration will likely increase the number of the overall connections. Consequently, this can reduce (in average) the length of functional paths between two any nodes. However, not accounting for them might lead to a misleading interpretation due to the appearance of spurious associations. This risk can be reduced by simultaneously measuring physiological data alongside fNIRS, performing digital filtering as a preprocessing step, or including systemic confounders when modelling the fNIRS signal reconstruction, processing and analysis to compute relative changes in Hb species [19,61,62,63]. However, to date, only few researchers have considered the inclusion of physiological measurements when dealing with fNIRS FC analysis [10,60,64]. Here, we investigated the possibility of including systemic data (heart rate and breathing rate) in the FC analysis in order to obtain a more accurate representation of the symmetry between FC networks. In general, we found structural variations within FC networks and we observed changes in HbO2 and HHb connectivity density and symmetry when systemic data were included. Based on our group-level results presented in Figure 7, we showed that the addition of systemic information tends to change both integrational and segregational characteristic measures of the networks.
Concerning the integration, a decrease in the global efficiency was observed in four out of five networks corresponding to the baseline, social prospective memory, non-social prospective memory, and ongoing contaminated conditions, in both Hb-derived networks. By contrast, only during the ongoing task the HbO2 network seems to increase the global efficiency. This could be caused by the inclusion of confounding variables that removes spurious relationships and generate a re-route of the functional paths between regions, resulting in a larger one. On the other hand, the segregational measure, the modularity, presents the opposite pattern in respect to the global efficiency. The modularity of both Hb networks increases when non-neuronal signals are taken into account. The inclusion of physiological variables is performed by considering them as nodes. These systemic nodes become mediators between channel nodes, creating new paths and producing a reorganization of groups of nodes (community structure). Here, we found that the 80% of the functional networks are above 0.3 modularity, a value from which a network is considered to have a significant community structure.
The experimental results presented here are preliminary and are based on data from a small sample size. Although the statistical results shown here are strong, we will further validate the proposed method on bigger data sets. In addition, we have included the contribution of only heart and breathing rate and evaluated their effect on 16 fNIRS channels recorded on the prefrontal cortex during a prospective memory task. In our future studies, we will enrich our investigations with a wider set of physiological variables (e.g., galvanic skin response, blood pressure). It would also be interesting to investigate how the symmetry between HbO2 and HHb connectivity networks varies in case of different cognitive tasks and task designs (e.g., block, event-related, continuous), and across different brain regions, and with less/more dense channels configurations.
5. Conclusions
In this work, we have tackled the problem of quantifying the in-common information expressed from HbO2 and HHb functional connectivity (FC) networks. This is achieved by our proposed Differential Symmetry Index or DSI.
We found that performing a symmetry analysis between the HbO2 and HHb FC networks can help in deciding if it is more appropriate to use one Hb signal (either HbO2 or HHb) or both when computing FC. This becomes particularly relevant when we deal with fNIRS experiments with low-density FC networks or with naturally sparse functional networks—as in typical commercially-available fNIRS devices. Simultaneously, it is possible to infer that having high-density data makes such contrast likely redundant as a high symmetry between HbO2 and HHb networks may be expected. From a data set including six healthy subjects performing a series of cognitive tasks in an ecological environment while walking, we recovered the task-related FC networks. We found that the FC networks of HbO2 and HHb retrieved from the social and non-social prospective memory tasks are more symmetric than the networks from the other tasks. Furthermore, we investigated the segregational and integrational impact on the networks when including walk-related breathing rate and heart rate systemic factors. By including these non-neuronal factors, the information expressed by the functional networks was elucidated. A set of spurious associations vanished (conjectured from the increase in path length and a decrease in global efficiency), and the distribution of functional links changed (inferred from the change in modularity). In summary, the resulting symmetry values were significantly different from the expected ones as shown by the random networks analysis. Therefore, the FC analysis must include a subsequent integration-segregation measures analysis and the addition of a symmetry analysis between HbO2 and HHb FC networks is highly recommended. The DSI distribution suggested that values over 0.2 indicate that Hb networks are symmetric.
Author Contributions
S.M.-H., I.T., F.O.-E. and L.E.S. conceived the idea of this work and conducted the definition of the mathematical model. P.P. defined the experimental design and carried out the experiment. A.H. and P.B. contributed and strength the interpretation of the findings. S.M.-H. and P.P. wrote and prepared the Matlab codes to be available online. All authors contributed to the redaction of the manuscript.
Acknowledgments
Research funded by EU Marie curie FP7-PEOPLE-2012-IRSES-316337 and CONACYT CB-2014-01-237251. I.T. and P.P. are supported by the Wellcome Trust (104580/Z/14/Z).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Villringer, A.; Chance, B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997, 20, 435–442. [Google Scholar] [CrossRef]
- Yücel, M.A.; Selb, J.J.; Huppert, T.J.; Franceschini, M.A.; Boas, D.A. Functional near infrared spectroscopy: Enabling routine functional brain imaging. Curr. Opin. Biomed. Eng. 2017, 4, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Functional and effective connectivity in neuroimaging: A synthesis. Hum. Brain Mapp. 1994, 2, 56–78. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and Effective Connectivity: A Review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Leff, D.R.; Orihuela-Espina, F.; Elwell, C.; Athanasiou, T.; Delpy, D.; Darzi, A.W.; Yang, G.-Z. Assessment of the Cerebral Cortex during Motor Task Behaviours in Adults: A Systematic Review of Functional Near Infrared Spectroscopy (fNIRS) Studies. Neuroimage 2011, 54, 2922–2936. [Google Scholar] [CrossRef] [PubMed]
- Villringer, A.; Dirnagl, U. Coupling of brain activity and cerebral blood flow: Basis of functional neuroimaging. Cerebrovasc. Brain Metab. Rev. 1995, 7, 240–276. [Google Scholar] [PubMed]
- Raichle, M.E.; Mintun, M.A. Brain Work and Brain Imaging. Annu. Rev. Neurosci. 2006, 29, 449–476. [Google Scholar] [CrossRef] [PubMed]
- Van Wijk, B.C.M.; Stam, C.J.; Daffertshofer, A. Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE 2010, 5, e13701. [Google Scholar] [CrossRef] [PubMed]
- Toronov, V.Y.; Zhang, X.; Webb, A.G. A spatial and temporal comparison of hemodynamic signals measured using optical and functional magnetic resonance imaging during activation in the human primary visual cortex. Neuroimage 2007, 34, 1136–1148. [Google Scholar] [CrossRef] [PubMed]
- Mesquita, R.C.; Franceschini, M.A.; Boas, D.A. Resting state functional connectivity of the whole head with near-infrared spectroscopy. Biomed. Opt. Express 2010, 1, 324–336. [Google Scholar] [CrossRef] [PubMed]
- White, B.R.; Snyder, A.Z.; Cohen, A.L.; Petersen, S.E.; Raichle, M.E.; Schlaggar, B.L.; Culver, J.P. Resting-state functional connectivity in the human brain revealed with diffuse optical tomography. Neuroimage 2009, 47, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Y.J.; Lu, C.M.; Ma, S.Y.; Zang, Y.F.; Zhu, C.Z. Functional connectivity as revealed by independent component analysis of resting-state fNIRS measurements. Neuroimage 2010, 51, 1150–1161. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Duan, L.; Zhang, Y.-J.; Lu, C.-M.; Liu, H.; Zhu, C.-Z. Test–retest assessment of independent component analysis-derived resting-state functional connectivity based on functional near-infrared spectroscopy. Neuroimage 2011, 55, 607–615. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.-M.; Zhang, Y.-J.; Biswal, B.B.; Zang, Y.-F.; Peng, D.-L.; Zhu, C.-Z. Use of fNIRS to assess resting state functional connectivity. J. Neurosci. Methods 2010, 186, 242–249. [Google Scholar] [CrossRef] [PubMed]
- Novi, S.L.; Rodrigues, R.B.M.L.; Mesquita, R.C. Resting state connectivity patterns with near-infrared spectroscopy data of the whole head. Biomed. Opt. Express 2016, 7, 2524–2537. [Google Scholar] [CrossRef] [PubMed]
- Tachtsidis, I.; Scholkmann, F. Publisher’s note: False positives and false negatives in functional near-infrared spectroscopy: Issues, challenges, and the way forward. Neurophotonics 2016, 3, 39801. [Google Scholar] [CrossRef] [PubMed]
- Orihuela-Espina, F.; Leff, D.R.; James, D.R.C.; Darzi, A.W.; Yang, G.-Z.Z. Quality control and assurance in functional near infrared spectroscopy (fNIRS) experimentation. Phys. Med. Biol. 2010, 55, 3701–3724. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, M.; Scholkmann, F.; Wolf, U.; Wolf, M.; Elwell, C.; Tachtsidis, I. Modelling confounding effects from extracerebral contamination and systemic factors on functional near-infrared spectroscopy. Neuroimage 2016, 143, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Kirilina, E.; Jelzow, A.; Heine, A.; Niessing, M.; Wabnitz, H.; Brühl, R.; Ittermann, B.; Jacobs, A.M.; Tachtsidis, I. The physiological origin of task-evoked systemic artefacts in functional near infrared spectroscopy. Neuroimage 2012, 61, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Hocke, L.M.; Fan, X.; Janes, A.C.; Frederick, B. deB Can apparent resting state connectivity arise from systemic fluctuations? Front. Hum. Neurosci. 2015, 9, 285. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Holper, L.; Wolf, U.; Wolf, M. A new methodical approach in neuroscience: Assessing inter-personal brain coupling using functional near-infrared imaging (fNIRI) hyperscanning. Front. Hum. Neurosci. 2013, 7, 813. [Google Scholar] [CrossRef] [PubMed]
- Crivelli, D.; Balconi, M. Near-Infrared Spectroscopy Applied to Complex Systems and Human Hyperscanning Networking. Appl. Sci. 2017, 7, 922. [Google Scholar] [CrossRef]
- Uludag, K.; Steinbrink, J.; Villringer, A.; Obrig, H. Separability and cross-talk: Optimizing dual wavelength combinations for near-infrared spectroscopy of the adult head. Neuroimage 2004, 22, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Strangman, G.; Culver, J.P.; Thompson, J.H.; Boas, D.A. A quantitative comparison of simultaneous BOLD fMRI and NIRS recordings during functional brain activation. Neuroimage 2002, 17, 719–731. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.; Wolf, U.; Toronov, V.; Michalos, A.; Paunescu, L.A.; Choi, J.H.; Gratton, E. Different time evolution of oxyhemoglobin and deoxyhemoglobin concentration changes in the visual and motor cortices during functional stimulation: A near-infrared spectroscopy study. Neuroimage 2002, 16, 704–712. [Google Scholar] [CrossRef] [PubMed]
- Sasai, S.; Homae, F.; Watanabe, H.; Taga, G. Frequency-specific functional connectivity in the brain during resting state revealed by NIRS. Neuroimage 2011, 56, 252–257. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Diamond, S.G.; Franceschini, M.A.; Boas, D. A HomER: A review of time-series analysis methods for near-infrared spectroscopy of the brain. Appl. Opt. 2009, 48, D280–D298. [Google Scholar] [CrossRef] [PubMed]
- Craddock, R.C.; Holtzheimer, P.E.; Hu, X.P.; Mayberg, H.S. Disease state prediction from resting state functional connectivity. Magn. Reson. Med. 2009, 62, 1619–1628. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Wang, L.; Liu, Y.; Hu, D. Discriminative analysis of resting-state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI. Neuroimage 2010, 49, 3110–3121. [Google Scholar] [CrossRef] [PubMed]
- Pinti, P.; Aichelburg, C.; Lind, F.; Power, S.; Swingler, E.; Merla, A.; Hamilton, A.; Gilbert, S.; Burgess, P.; Tachtsidis, I. Using Fiberless, Wearable fNIRS to Monitor Brain Activity in Real-world Cognitive Tasks. J. Vis. Exp. 2015, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Scott, S.K.; Frith, C.D. The role of the rostral frontal cortex (area 10) in prospective memory: A lateral versus medial dissociation. Neuropsychologia 2003, 41, 906–918. [Google Scholar] [CrossRef]
- Atsumori, H.; Kiguchi, M.; Obata, A.; Sato, H.; Katura, T.; Funane, T.; Maki, A. Development of wearable optical topography system for mapping the prefrontal cortex activation. Rev. Sci. Instrum. 2009, 80, 43704. [Google Scholar] [CrossRef] [PubMed]
- Molavi, B.; Dumont, G.A. Wavelet-based motion artifact removal for functional near-infrared spectroscopy. Physiol. Meas. 2012, 33, 259. [Google Scholar] [CrossRef] [PubMed]
- Spirtes, P.; Glymour, C.; Scheines, R.; Burr, T. Causation, Prediction, and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2000; Volume 45, ISBN 0262194406. [Google Scholar]
- Kalisch, M.; Machler, M.; Colombo, D.; Maathuis, M.H.; Buhlmann, P.; Mächler, M.; Colombo, D.; Maathuis, M.H. Causal Inference Using Graphical Models with the R Package pcalg. J. Stat. Softw. 2012, 47, 26. [Google Scholar] [CrossRef]
- Tong, W.; Xia, W.; Xuyun, W.; Li, Y. Group-analysis of Resting-state fMRI Based on Bayesian Network: A Comparison of Three Virtual-typical-subject Methods. Neurosci. Biomed. Eng. 2015, 2, 92–98. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.J.; Palmer, S.J.; McKeown, M.J. Dynamic Bayesian network modeling of fMRI: A comparison of group-analysis methods. Neuroimage 2008, 41, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Ide, J.S.; Zhang, S.; Li, C.R. Bayesian network models in brain functional connectivity analysis. Int. J. Approx. Reason. 2014, 55, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Sucar, L.E. Probabilistic Graphical Models: Principles and Applications; Advances in Computer Vision and Pattern Recognition; Springer: London, UK, 2015; ISBN 9781447166993. [Google Scholar]
- Montero-Hernandez, S.A.; Orihuela-Espina, F.; Herrera-Vega, J.; Sucar, L.E. Causal Probabilistic Graphical Models for Decoding Effective Connectivity in Functional Near InfraRed Spectroscopy. In Twenty-Ninth International Florida Artificial Intelligence Research Society Conference Causal; AAAI Press: Palo Alto, CA, USA, 2016; pp. 686–689. [Google Scholar]
- Waldorp, L.; Christoffels, I.; van de Ven, V. Effective connectivity of fMRI data using ancestral graph theory: Dealing with missing regions. Neuroimage 2011, 54, 2695–2705. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yu, X.; Yao, L.; Li, R. Bayesian network analysis revealed the connectivity difference of the default mode network from the resting-state to task-state. Front. Comput. Neurosci. 2014, 8, 118. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, J.D.; Hanson, S.J.; Hanson, C.; Halchenko, Y.O.; Poldrack, R.A.; Glymour, C. Six problems for causal inference from fMRI. Neuroimage 2010, 49, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Rajapakse, J.C. Learning functional structure from fMR images. Neuroimage 2006, 31, 1601–1613. [Google Scholar] [CrossRef] [PubMed]
- Rajapakse, J.C.; Zhou, J. Learning effective brain connectivity with dynamic Bayesian networks. Neuroimage 2007, 37, 749–760. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2004, 69, 66133. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 26113. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Varmuza, K. A comparative analysis of the Tanimoto index and graph edit distance for measuring the topological similarity of trees. Appl. Math. Comput. 2015, 259, 242–250. [Google Scholar] [CrossRef]
- Landsiedel, J.; Williams, D.M.; Abbot-Smith, K. A Meta-Analysis and Critical Review of Prospective Memory in Autism Spectrum Disorder. J. Autism Dev. Disord. 2017, 47, 646–666. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Wu, H.-C. Rostral Prefrontal Cortex (Brodmann Area 10): Metacognition in the Brain. In Principles of Frontal Lobe Function; Stuss, D.T., Knight, R.T., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 524–534. [Google Scholar]
- Rojkova, K.; Volle, E.; Urbanski, M.; Humbert, F.; Dell’Acqua, F.; Thiebaut de Schotten, M. Atlasing the frontal lobe connections and their variability due to age and education: A spherical deconvolution tractography study. Brain Struct. Funct. 2016, 221, 1751–1766. [Google Scholar] [CrossRef] [PubMed]
- Thiebaut de Schotten, M.; Dell’Acqua, F.; Valabregue, R. Monkey to human comparative anatomy of the frontal lobe association tracts. Cortex 2012, 48, 82–96. [Google Scholar] [CrossRef] [PubMed]
- Catani, M.; Howard, R.J.; Pajevic, S.; Jones, D.K. Virtual in Vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 2002, 17, 77–94. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, S.J.; Gonen-Yaacovi, G.; Benoit, R.G.; Volle, E.; Burgess, P.W. Distinct functional connectivity associated with lateral versus medial rostral prefrontal cortex: A meta-analysis. Neuroimage 2010, 53, 1359–1367. [Google Scholar] [CrossRef] [PubMed]
- Shallice, T.; Burgess, P. The Domain of Supervisory Processes and Temporal Organization of Behaviour. Philos. Trans. R. Soc. B Biol. Sci. 1996, 351, 1405–1412. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Alderman, N.; Forbes, C.; Costello, A.; Coates, L.M.A.; Dawson, D.R.; Anderson, N.D.; Gilbert, S.J.; Dumontheil, I.; Channon, S. The case for the development and use of “ecologically valid” measures of executive function in experimental and clinical neuropsychology. J. Int. Neuropsychol. Soc. 2006, 12, 194–209. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Gonen-Yaacovi, G.; Volle, E. Functional neuroimaging studies of prospective memory: What have we learnt so far? Neuropsychologia 2011, 49, 2246–2257. [Google Scholar] [CrossRef] [PubMed]
- Carbonell, F.; Bellec, P.; Shmuel, A. Quantification of the impact of a confounding variable on functional connectivity confirms anti-correlated networks in the resting-state. Neuroimage 2014, 86, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Ramb, R.; Eichler, M.; Ing, A.; Thiel, M.; Weiller, C.; Grebogi, C.; Schwarzbauer, C.; Timmer, J.; Schelter, B. The impact of latent confounders in directed network analysis in neuroscience. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20110612. [Google Scholar] [CrossRef] [PubMed]
- Obrig, H.; Neufang, M.; Wenzel, R.; Kohl, M.; Steinbrink, J.; Einhäupl, K.; Villringer, A. Spontaneous low frequency oscillations of cerebral hemodynamics and metabolism in Human Adults. Neuroimage 2000, 12, 623–639. [Google Scholar] [CrossRef] [PubMed]
- Habermehl, C.; Steinbrink, J.; Müller, K.-R.; Haufe, S. Optimizing the regularization for image reconstruction of cerebral diffuse optical tomography. J. Biomed. Opt. 2014, 19, 96006. [Google Scholar] [CrossRef] [PubMed]
- Kirlilna, E.; Yu, N.; Jelzow, A.; Wabnitz, H.; Jacobs, A.M.; Tachtsidis, I. Identifying and quantifying main components of physiological noise in functional near infrared spectroscopy on the prefrontal cortex. Front. Hum. Neurosci. 2013, 7, 864. [Google Scholar] [CrossRef] [PubMed]
- Toronov, V.; Franceschini, M.A.; Filiaci, M.; Fantini, S.; Wolf, M.; Michalos, A.; Gratton, E. Near-infrared study of fluctuations in cerebral hemodynamics during rest and motor stimulation: Temporal analysis and spatial mapping. Med. Phys. 2000, 27, 801–815. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).