Linking Scheduling Criteria to Shop Floor Performance in Permutation Flowshops
Abstract
:1. Introduction
- Some widely employed scheduling criteria have been subject of criticism due to their apparent lack of applicability to real-world situations (see, e.g., the early comments in [4] on Johnson’s famous paper, or [5] and [1] on the lack of real-life application of makespan minimisation algorithms), which suggest a poor alignment of these criteria with the companies’ goals.
- Some justifications for using specific scheduling criteria are given without a formal proof. For instance, it is usual in the scheduling literature to mention that minimising the completion time in a flowshop leads to minimising work-in-process, whereas this statement—as we discuss in Section 2.2—is not correct from a theoretical point of view.
- Some scheduling criteria employed in manufacturing have been borrowed from other areas. For instance, the minimisation of the completion time variance is taken from the computer scheduling context; therefore their potential advantages on manufacturing have to be tested.
- There are different formulations for some scheduling criteria intuitively linked to shop floor performance: While machine idle time minimisation can be seen, at least approximately, as related to increasing the utilisation of the system, there are alternative, non-equivalent, manners to formulate idle time. Therefore, it remains an open question to know which formulation is actually better in terms of effectively increasing the utilisation of the system.
- Finally, since it is customary that different, conflicting goals have to be balanced in the shop floor (such as balancing work in process, and throughput), it would be interesting to know the contribution of the different scheduling criteria to shop floor performance in order to properly balance them.
- There are several scheduling criteria (most notably the completion time variance and one definition of idle time) which are poorly related with any of the indicators considered for shop floor performance.
- Makespan minimisation is heavily oriented towards increasing throughput, but it yields poor results in terms of average completion time and work-in-process. This confines its suitability to manufacturing scenarios with very high utilisation costs as compared to those associated with cycle time and inventory.
- Minimisation of one definition of idle times results in sequences with only a marginal worsening in terms of throughput, but a substantial improvement in terms of cycle time and inventory. Therefore, this criterion emerges as an interesting one when the alignment with shop floor performance is sought.
- Minimisation of completion times also provides quite balanced schedules in terms of shop floor performance measures; note that it does not lead to the minimisation of WIP, as recurrently stated in the literature.
2. Background and Related Work
2.1. Scheduling Criteria
- The idle time, as well as the head and tail, of every single machine, i.e., the time before the first job is started on a machine and the time after the last job is finished on a machine, but the whole schedule has started on the first machine and has not been finished yet on the last machine, can be included into the idle time or not. In a static environment, including all heads and tails means that idle time minimisation is equivalent to minimisation of makespan (see, e.g., in [4]). This case would not have to be considered further.
- Excluding heads and tails would give an idle time within the schedule, implicitly assuming that the machines could be used for other tasks/jobs outside the current problem before and after the current schedule passes/has passed the machine. This definition of idle time is also known as “core idle time” (see, e.g., in [10,11,12]) and it has been used by [13] and by [14] in the context of a multicriteria problem. We denote this definition of idle time as .
- Including machine heads in the idle time computation whereas the tails are not included means that the machines are reserved for the schedule before the first job of the schedule arrives but are released for other jobs outside the schedule as soon as the last job has left the current machine. In the following, we denote this definition as . This definition is first encountered in [15] and in [16] and it has been used recently as a secondary criterion for the development of tie-breaking rules for makespan minimisation algorithms (see, e.g., [17,18]).
2.2. Shop Floor Performance Measures
3. Computational Experience
- Build a number of scheduling instances of different sizes and with different mechanisms for generating the processing times. The procedure to build these test-beds is described in Section 3.1.
- For each one of these instances, find the sequences optimising each one of the scheduling criteria under consideration. For small-sized instances, the optimal solutions can be found, while for the biggest instances, a good solution found by a heuristic approach is employed. The procedure for this step is described in Section 3.2.
- Analyse the so-obtained results. This is carried out in Section 4.
3.1. Testbed Setting
- Set the upper and lower bounds of processing times, and , respectively, and a factor controlling the correlation of the processing times.
- Obtain the value by drawing a uniform sample from the interval , where .
- For each machine j, obtain , where is sampled from the interval and is uniformly sampled from the interval .
- For each job i, a real value is uniformly sampled from the interval . Then, the processing times are obtained in the following manner: , where is a ’noise factor’ obtained by uniformly sampling from the interval .
- are ensured to be within the upper and lower bounds, i.e. if , then . Analogously, if , then .
- LC (Medium Correlation): Processing times are drawn according to the procedure described above and .
- MC (Medium Correlation): Processing times are drawn according to the procedure described above and .
- HC (High Correlation): Processing times are drawn according to the procedure described above and .
- NC (No Correlation): Processing times are drawn from a uniform distribution [1,99]. This represents the “classical” noncorrelated assumption in many scheduling papers.
3.2. Optimisation of Scheduling Criteria
- The neighbourhood definition includes the sum of the general pairwise interchange and insertion neighbourhoods. Both neighbourhood definitions are widely used in the literature.
- The size of the tabu list L has been set to the maximum value between the number of jobs and the number of machines, i.e., . As the size of the list is used to avoid getting trapped into local optima, the idea is keeping a list size related to the size of the neighbourhood.
- As stopping criterion, the algorithm terminates after a number of iterations without improvement. This number has been set as the minimum of . This ensures a large minimum number of iterations, while increasing this number of iterations with the problem size.
4. Computational Results
4.1. Dominance Relationships among Scheduling Criteria
- Regarding Table 1, it is clear that makespan outperforms the total completion time regarding throughput, and that the total completion time outperforms the makespan regarding average cycle time. These results are known from theory and, although they could have been omitted, we include them for symmetry. The table also shows that completion time outperforms makespan with respect to work in process, a result that cannot be theoretically predicted. This results is obtained for all instance sizes and different methods to generate the processing times. As a consequence, if shop floor performance is measured using primarily one indicator, would be the most aligned objective with respect to throughput, whereas would be the most aligned with respect to cycle time and work in process.
- From Table 2, it can be seen that makespan outperforms with respect to throughput, and, in general, with respect to (with the exception of small problem instances for certain processing times’ generation). Finally, regarding work in process, in general, makespan outperforms if , whereas the opposite occurs if .
- Table 3 and Table 4 show an interesting result: despite the problem size and/or the distribution of the processing times, makespan outperforms both and for all three shop floor performance measures considered. This result reveals that the minimisation of or are poorly linked to shop floor performance, as least compared to makespan minimisation.
- Table 5 show that, regardless the generation of processing times and/or the problem size, completion time performs worse than for makespan, whereas it outperforms it in terms of average cycle time and work in process.
- Table 6 show that, with few exception cases, the completion time outperforms for all three SF indicators.
- In Table 7, a peculiar pattern can be observed: while it can be that dominates with respect to the three SF indicators, this is not the case for the random processing times, as in this case the makespan values obtained by are higher than those observed for the total completion time.
- In Table 8 and Table 9 it can be seen that outperforms both and for all instance sizes and all generation of the processing times. Regarding considering the heads or not in the idle time function, this result makes clear that idle time minimisation including the heads is better with respect to all shop floor performance measures considered.
- Finally, in Table 10 it can be seen that the relative performance of and with respect to the indicators depends on the type of testbed and on the problem instance size. However, in view of the scarce alignment of both scheduling criteria with any SF already detected in Table 3, Table 4, Table 8 and Table 9, these results do not seem relevant for the purpose of our analysis.
- If a trade-off between two shop floor performance measures is sought, for each pair of indicators it is possible to represent the set of efficient scheduling criteria in a multi-objective manner, i.e., criteria for which no other criterion in the set obtains better results with respect to both two indicators considered. This set is represented in Table 11, and it can be seen that completion time minimisation is the only efficient criterion to minimise both and . In contrast, if is involved in the trade-off, a better value for (and worse for and ) can be obtained by minimising , and a further better value for (at the expenses of worsening and ) would be obtained by minimising .
4.2. Ranking of Scheduling Criteria
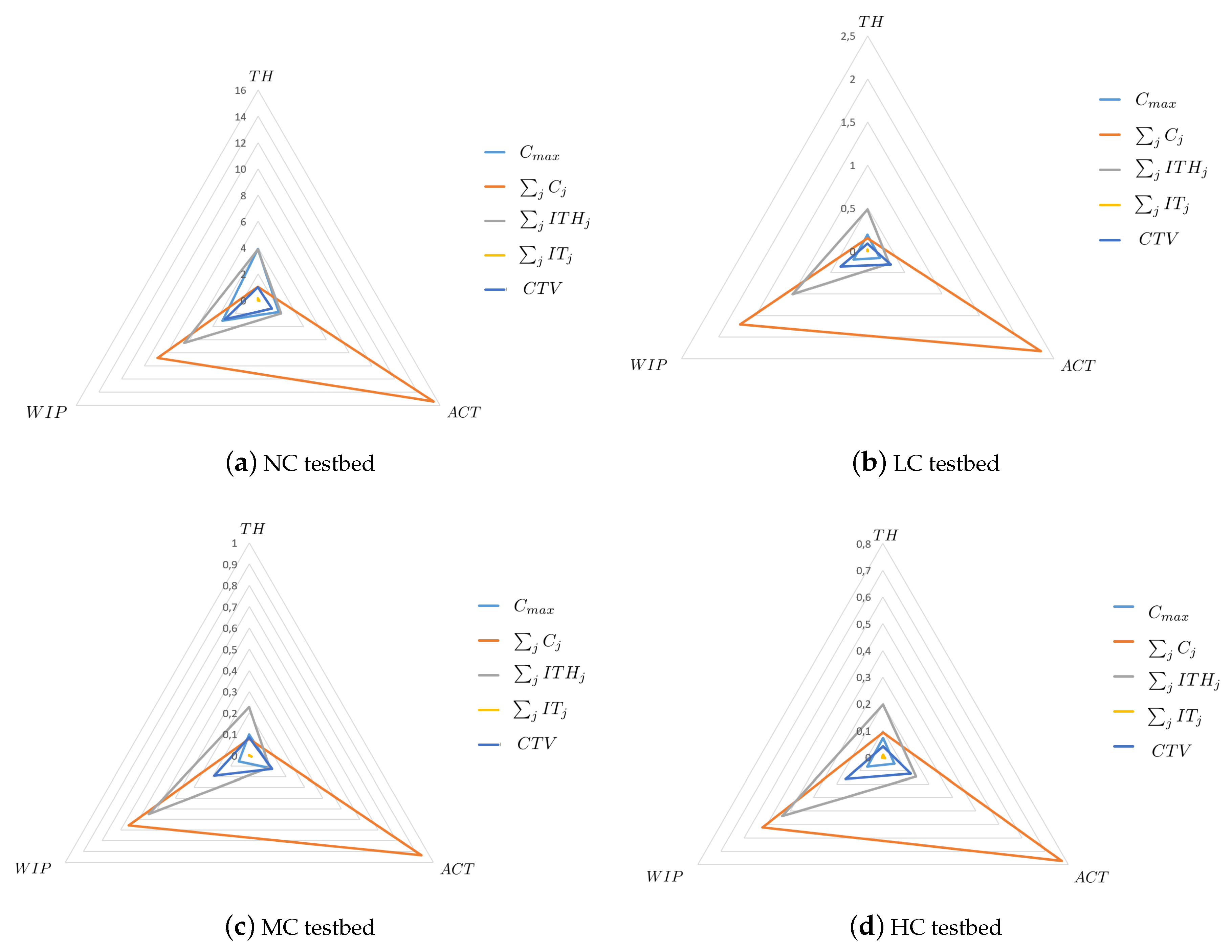
- emerges as an interesting criterion as its performance is only marginally worse than with respect to —particularly in the NC testbed, see Figure 2a, but it obtains better values regarding and . Similarly, although it performs worse than for and , it performs better in terms of throughput.
- The differences in ARD for throughput are, in general, smaller than those for and . For the correlated test-beds (LC to HC), the differences never reach 1%. This speaks for the little difference between minimising any of the scheduling measures if throughput maximisation is sought. The highest differences are encountered for the random test-bed (~6%).
- The differences in all measures for structured instances are smaller than for random test-bed. For instance, whereas makespan ranks first for TH (theoretically predictable), the maximum ARD for a given problem size in the random test-bed is 6.04%, whereas this is reduced to 0.52% for LC, and to 0.16% for HC. Analogously, the maximum differences between the completion time (ranking first for ) and the next criterion raise up to 23.84% for the random test-bed while dropping to 1.27% for HC. This means that the structured problems are easier than random problems because the distribution of the processing times flattens the objective functions, at least with respect to the considered shop floor performance measures.
5. Conclusions and Further Research
- Roughly speaking, we could divide the considered scheduling criteria into two big categories: those tightly related to any (some) shop floor performance measure, and those poorly related to SF performance. Among the later, we may classify and . Nevertheless, this is not meant to say that these criteria are not useful. However, from a shop floor performance perspective, it may be interesting to investigate whether these scheduling criteria relate to other performance measures. Perhaps extending the analysis to a due date scenario might yield some positive answer.
- Makespan matches (as theoretical predicted) throughput maximisation better than any other considered criteria. However, it turns out that differences between its minimisation and the minimisation of other criteria with respect to throughput are very small. Additionally, given the relatively poor performance of makespan with respect to , one might ask whether makespan minimisation pays off for many manufacturing scenarios in terms of shop floor performance as compared, e.g., to completion time or minimisation. A positive answer seems to be confined to these scenarios where costs associated to cycle time are almost irrelevant as compared to costs related to machine utilisation. The fact that this situation is not common in many manufacturing scenarios may lead to the lack of practical descriptions on the application of this criteria already discussed by [4].
- Completion time minimisation matches extremely well both work in process and average cycle time minimisation (the latter being theoretical predictable), better than any other criteria. In addition, the rest of the scheduling criteria perform much worse. Therefore, completion time minimisation emerges as a major criterion when it comes to increase shop floor performance. This empirical reasoning indicates the interest of the research on completion time minimisation rather than on other criteria, at least within the flowshop scheduling context.
- The minimisation of idle time (including the heads) performs better than completion time with respect to throughput. However, its performance is substantially worse than completion time regarding and . Hence, it seems an interesting criterion when throughput maximisation is the most important performance measure but work-in-process costs are not completely irrelevant.
- With respect to the influence of the test-bed design on the results, there are noticeable differences between the overall results obtained in the correlated test-beds (LC-HC), and those obtained from the random test-bed. In general, the introduction of structured processing times seems to reduce the differences between the scheduling criteria. At a first glance, this means that random processing times make it difficult to achieve a good shop floor performance by the application of a specific scheduling criterion. It is widely know that random problems produce difficult instances in the sense that there were high differences between bad and good schedules (with respect to a given scheduling criterion), at least for the makespan criterion. In view of the results of the experiments, we can also assert that these also translate into shop floor performance measures.
- emerges as an interesting scheduling criterion, with virtues in between makespan and completion time. For most of the problem settings, it compares to makespan in terms of cycle time, and it outperforms total completion time in terms of throughput. In view of these results, perhaps it is interesting devoting more efforts to flowshop minimisation with this criterion, which so far has been used only as a secondary tie-breaking rule. Interestingly, the results in this paper might suggest that its excellent performance in terms of tie-breaking rule is motivated by its alignment with shop floor performance.
- While it is possible to perfectly match the shop floor objectives of throughput and average cycle time with scheduling criteria (makespan and completion time, respectively), cannot be linked to a scheduling criterion in a straightforward manner. Although the minimisation of completion time achieves the best results for minimisation among the tested criteria, “true” work-in-process optimization is not the same as completion time minimisation. Here, the quotient between total completion time and makespan emerges as a “combined” scheduling criteria which may be worth of research as it matches an important shop floor performance measure such as work-in-process minimisation.
- The results of the present study are limited by the shop layout (i.e., the permutation flowshop) and the scheduling criteria (i.e., not due date-related criteria) considered. Therefore, an obvious extension of this study is to analyse other environments and scheduling measures. Particularly, the inclusion of due date related criteria could provide some additional insights on the linkage between these and the shop floor performance measures, as well as between the due date and non-due date scheduling criteria.
Author Contributions
Funding
Conflicts of Interest
References
- Hopp, W.; Spearman, M. Factory Physics. Foundations of Manufacturing Management, 3rd ed.; Irwin: New York, NY, USA, 2008. [Google Scholar]
- Framinan, J.; Leisten, R.; Ruiz, R. Manufacturing Scheduling Systems: An Integrated View on Models, Methods and Tools; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–400. [Google Scholar]
- Aytug, H.; Lawley, M.A.; McKay, K.; Mohan, S.; Uzsoy, R. Executing production schedules in the face of uncertainties: A review and some future directions. Eur. J. Oper. Res. 2005, 161, 86–110. [Google Scholar] [CrossRef]
- Conway, R.; Maxwell, W.L.; Miller, L.W. Theory of Scheduling; Dover: Mineola, NY, USA, 1967. [Google Scholar]
- Dudek, R.A.; Panwalkar, S.S.; Smith, M.L. The Lessons of Flowshop Scheduling Research. Oper. Res. 1992, 40, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Viagas, V.; Ruiz, R.; Framinan, J. A new vision of approximate methods for the permutation flowshop to minimise makespan: State-of-the-art and computational evaluation. Eur. J. Oper. Res. 2017, 257, 707–721. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J. A beam-search-based constructive heuristic for the PFSP to minimise total flowtime. Comput. Oper. Res. 2017, 81, 167–177. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J. A new set of high-performing heuristics to minimise flowtime in permutation flowshops. Comput. Oper. Res. 2015, 53, 68–80. [Google Scholar] [CrossRef]
- Framinan, J.; Leisten, R.; Rajendran, C. Different initial sequences for the heuristic of Nawaz, Enscore and Ham to minimize makespan, idletime or flowtime in the static permutation flowshop sequencing problem. Int. J. Prod. Res. 2003, 41, 121–148. [Google Scholar] [CrossRef]
- Benkel, K.; Jørnsten, K.; Leisten, R. Variability aspects in flowshop scheduling systems. In Proceedings of the 2015 International Conference on Industrial Engineering and Systems Management (IESM), Seville, Spain, 21–23 October 2015; pp. 118–127. [Google Scholar]
- Maassen, K.; Perez-Gonzalez, P.; Framinan, J.M. Relationship between common objective functions, idle time and waiting time in permutation flowshop scheduling. In Proceedings of the 29th European Conference on Operational Research (EURO 2018), Valencia, Spain, 8–11 July 2018. [Google Scholar]
- Maassen, K.; Perez-Gonzalez, P. Diversity of processing times in permutation flow shop scheduling problems. In Proceedings of the 66th Operations Research Conference, Dresden, Germany, 3–6 September 2019. [Google Scholar]
- Liao, C.J.; Tseng, C.T.; Luarn, P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 2007, 34, 3099–3111. [Google Scholar] [CrossRef]
- Liu, W.; Jin, Y.; Price, M. A new Nawaz-Enscore-Ham-based heuristic for permutation flow-shop problems with bicriteria of makespan and machine idle time. Eng. Optim. 2016, 48, 1808–1822. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, J.; Rajendran, C. Scheduling in flowshop and cellular manufacturing systems with multiple objectives-a genetic algorithmic approach. Prod. Plan. Control 1996, 7, 374–382. [Google Scholar] [CrossRef]
- Ho, J.; Chang, Y.L. A new heuristic for the n-job, M-machine flow-shop problem. Eur. J. Oper. Res. 1991, 52, 194–202. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J. On insertion tie-breaking rules in heuristics for the permutation flowshop scheduling problem. Comput. Oper. Res. 2014, 45, 60–67. [Google Scholar] [CrossRef]
- Fernandez-Viagas, V.; Framinan, J. A best-of-breed iterated greedy for the permutation flowshop scheduling problem with makespan objective. Comput. Oper. Res. 2019, 112, 104767. [Google Scholar] [CrossRef]
- King, J.; Spachis, A. Heuristics for flow-shop scheduling. Int. J. Prod. Res. 1980, 18, 345–357. [Google Scholar] [CrossRef]
- Merten, A.; Muller, M. Variance minimization in single machine sequencing problems. Manag. Sci. 1972, 18, 518–528. [Google Scholar] [CrossRef]
- Kanet, J.J. Minimizing variation of flow time in single machine systems. Manag. Sci. 1981, 27, 1453–1464. [Google Scholar] [CrossRef]
- Baker, K.R.; Scudder, G.D. Sequencing with earliness and tardiness penalties. A review. Oper. Res. 1990, 38, 22–36. [Google Scholar] [CrossRef]
- Gupta, M.; Gupta, Y.; Bector, C. Minimizing the flow-time variance in single-machine systems. J. Oper. Res. Soc. 1990, 41, 767–779. [Google Scholar] [CrossRef]
- Cai, X.; Cheng, T. Multi-machine scheduling with variance minimization. Discret. Appl. Math. 1998, 84, 55–70. [Google Scholar] [CrossRef] [Green Version]
- Cai, X. V-shape property for job sequences that minimize the expected completion time variance. Eur. J. Oper. Res. 1996, 91, 118–123. [Google Scholar] [CrossRef]
- Marangos, C.; Govande, V.; Srinivasan, G.; Zimmers, E., Jr. Algorithms to minimize completion time variance in a two machine flowshop. Comput. Ind. Eng. 1998, 35, 101–104. [Google Scholar] [CrossRef]
- Gowrishankar, K.; Rajendran, C.; Srinivasan, G. Flow shop scheduling algorithms for minimizing the completion time variance and the sum of squares of completion time deviations from a common due date. Eur. J. Oper. Res. 2001, 132, 643–665. [Google Scholar] [CrossRef]
- Leisten, R.; Rajendran, C. Variability of completion time differences in permutation flow shop scheduling. Comput. Oper. Res. 2015, 54, 155–167. [Google Scholar] [CrossRef]
- Ganesan, V.; Sivakumar, A.; Srinivasan, G. Hierarchical minimization of completion time variance and makespan in jobshops. Comput. Oper. Res. 2006, 33, 1345–1367. [Google Scholar] [CrossRef]
- Gajpal, Y.; Rajendran, C. An ant-colony optimization algorithm for minimizing the completion-time variance of jobs in flowshops. Int. J. Prod. Econ. 2006, 101, 259–272. [Google Scholar] [CrossRef]
- Krishnaraj, J.; Pugazhendhi, S.; Rajendran, C.; Thiagarajan, S. A modified ant-colony optimisation algorithm to minimise the completion time variance of jobs in flowshops. Int. J. Prod. Res. 2012, 50, 5698–5706. [Google Scholar] [CrossRef]
- Krishnaraj, J.; Pugazhendhi, S.; Rajendran, C.; Thiagarajan, S. Simulated annealing algorithms to minimise the completion time variance of jobs in permutation flowshops. Int. J. Ind. Syst. Eng. 2019, 31, 425–451. [Google Scholar] [CrossRef]
- Goldratt, E. The Haystack Syndrome: Shifting Information out of the Data Ocean; North River Press: Croton-on-Hudson, NY, USA, 1996. [Google Scholar]
- Nahmias, S. Production and Operations Analysis; Irwin: Homewood, IL, USA, 1993. [Google Scholar]
- Wiendahl, H.P. Load-Oriented Manufacturing Control; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Li, W.; Dai, H.; Zhang, D. The Relationship between Maximum Completion Time and Total Completion Time in Flowshop Production. Procedia Manuf. 2015, 1, 146–156. [Google Scholar] [CrossRef] [Green Version]
- Land, M. Parameters and sensitivity in workload control. Int. J. Prod. Econ. 2006, 104, 625–638. [Google Scholar] [CrossRef]
- Thürer, M.; Stevenson, M.; Land, M.; Fredendall, L. On the combined effect of due date setting, order release, and output control: An assessment by simulation. Int. J. Prod. Res. 2019, 57, 1741–1755. [Google Scholar] [CrossRef] [Green Version]
- Land, M. Workload in Job Shop, Grasping the Tap. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2004. [Google Scholar]
- Wiendahl, H.P.; Glassner, J.; Petermann, D. Application of load-oriented manufacturing control in industry. Prod. Plan. Control 1992, 3, 118–129. [Google Scholar] [CrossRef]
- Grewal, N.S.; Bruska, A.C.; Wulf, T.M.; Robinson, J.K. Integrating targeted cycle-time reduction into the capital planning process. In Proceedings of the 1998 Winter Simulation Conference, Washington, DC, USA, 13–16 December 1998; Volume 2, pp. 1005–1010. [Google Scholar]
- Leachman, R.; Kang, J.; Lin, V. SLIM: Short cycle time and low inventory in manufacturing at Samsung electronics. Interfaces 2002, 32, 61–77. [Google Scholar] [CrossRef] [Green Version]
- Sandell, R.; Srinivasan, K. Evaluation of lot release policies for semiconductor manufacturing systems. In Proceedings of the 1996 Winter Simulation Conference, Coronado, CA, USA, 8–11 December 1996; pp. 1014–1022. [Google Scholar]
- Abedini, A.; Li, W.; Badurdeen, F.; Jawahir, I. Sustainable production through balancing trade-offs among three metrics in flow shop scheduling. Procedia CIRP 2019, 80, 209–214. [Google Scholar] [CrossRef]
- Bestwick, P.F.; Hastings, N. New bound for machine scheduling. Oper. Res. Q. 1976, 27, 479–487. [Google Scholar] [CrossRef]
- Lahiri, S.; Rajendran, C.; Narendran, T. Evaluation of heuristics for scheduling in a flowshop: A case study. Prod. Plan. Control 1993, 4, 153–158. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for Basic Scheduling Problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Vallada, E.; Ruiz, R.; Framinan, J. New hard benchmark for flowshop scheduling problems minimising makespan. Eur. J. Oper. Res. 2015, 240, 666–677. [Google Scholar] [CrossRef] [Green Version]
- Demirkol, E.; Mehta, S.; Uzsoy, R. Benchmarks for shop scheduling problems. Eur. J. Oper. Res. 1998, 109, 137–141. [Google Scholar] [CrossRef]
- Campbell, H.G.; Dudek, R.A.; Smith, M.L. A Heuristic Algorithm for the n Job, m Machine Sequencing Problem. Manag. Sci. 1970, 16, B-630–B-637. [Google Scholar] [CrossRef] [Green Version]
- Dannenbring, D.G. An evaluation of flowshop sequencing heuristics. Manag. Sci. 1977, 23, 1174–1182. [Google Scholar] [CrossRef]
- Amar, A.D.; Gupta, J. Simulated versus real life data in testing the efficiency of scheduling algorithms. IIE Trans. 1986, 18, 16–25. [Google Scholar] [CrossRef]
- Panwalkar, S.S.; Dudek, R.; Smith, M.L. Sequencing research and the industrial scheduling problem. In Symposium on the Theory of Scheduling and Its Applications; Springer: Berlin/Heidelberg, Germany, 1973; pp. 29–38. [Google Scholar]
- Rinnooy Kan, A. Machine Scheduling Problems; Martinus Nijhoff: The Hague, The Netherlands, 1976. [Google Scholar]
- Lageweg, B.; Lenstra, J.; Rinnooy Kan, A. A general bounding scheme for the permutation flow-shop problem. Oper. Res. 1978, 26, 53–67. [Google Scholar] [CrossRef]
- Reeves, C. A genetic algorithm for flowshop sequencing. Comput. Oper. Res. 1995, 22, 5–13. [Google Scholar] [CrossRef]
- Watson, J.P.; Barbulescu, L.; Whitley, L.; Howe, A. Contrasting structured and random permutation flow-shop scheduling problems: Search-space topology and algorithm perfomance. INFORMS J. Comput. 2002, 14, 98–123. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Pegden, C.; Enscore, E. A survey and evaluation of static flowshop scheduling heuristics. Int. J. Prod. Res. 1984, 22, 127–141. [Google Scholar] [CrossRef]
- Hoos, H.H.; Stützle, T. Stochastic Local Search: Foundations and Applications; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]

| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 5 | 10 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 10 | 5 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 10 | 10 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 20 | 10 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 20 | 20 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 20 | 50 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 50 | 10 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 50 | 20 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 50 | 50 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 100 | 97.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 85.9 | 0.0 | 100 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | ||||
| 10 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 100 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 74.9 | 0.0 | 100 | 100.0 | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | 100.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.16 | 100.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 100.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 100.0 | 0.0 | 0 | 97.9 | 0.0 | 0.0 | 7.4 | 0.0 | 0.0 | 100.0 | ||||
| 20 | 50 | 0.0 | 0.0 | 100.0 | 0.0 | 0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 18.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 0.0 | 0.0 | 100.0 | 0.0 | 0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | ||||
| 0.0 | 0.0 | 46.1 | 0.0 | 40.0 | 71.3 | 0.0 | 0.0 | 40.8 | 0.0 | 0.0 | 70.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 10 | 10 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 10 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 20 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 99.8 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 95.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 96.9 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 94.6 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 98.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 29.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 49.1 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 97.4 | 0.0 | 0.0 | ||||
| 5 | 10 | 99.9 | 0.0 | 0.0 | 27.5 | 0.0 | 0.0 | 93.6 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 99.4 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 30.0 | 0.0 | 0.0 | 2.8 | 0.0 | 0.0 | 9.4 | 0.0 | 0.0 | 79.7 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 99.8 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 95.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 96.9 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 94.6 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 98.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 29.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 49.1 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 5 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 10 | 5 | 100.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 99.8 | 0.0 | 0.0 | ||||
| 10 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 20 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 20 | 50 | 95.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 96.9 | 0.0 | 0.0 | ||||
| 50 | 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 94.6 | 0.0 | 0.0 | ||||
| 50 | 20 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | ||||
| 50 | 50 | 98.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||||
| 29.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 49.1 | 0.0 | 0.0 | ||||||
| LC | MC | HC | NC | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | TH | ACT | WIP | ||||
| 5 | 5 | 100.0 | 100.0 | 100.0 | 100.00 | 100.0 | 67.97 | 7.29 | 0.03 | 0.00 | 100.0 | 100.0 | 100.0 | ||||
| 5 | 10 | 100.0 | 100.0 | 0.0 | 100.0 | 100.00 | 0.00 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 0.0 | ||||
| 10 | 5 | 0.0 | 99.96 | 100.0 | 6.96 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 7.94 | 100.0 | 100.0 | ||||
| 10 | 10 | 100.0 | 100.0 | 100.0 | 100.0 | 100.00 | 98.09 | 100.00 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | ||||
| 20 | 10 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 20 | 20 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | ||||
| 20 | 50 | 100.0 | 100.0 | 64.3 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | ||||
| 50 | 10 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 8.4 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 50 | 20 | 1.1 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | ||||
| 50 | 50 | 0.0 | 1.2 | 100.0 | 100.0 | 100.0 | 100.0 | 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | ||||
| 70.1 | 89.0 | 86.4 | 100.0 | 100.0 | 100.0 | 63.6 | 100.0 | 88.9 | 66.7 | 100.0 | 80.0 | ||||||
| SF Indicators | Efficient Scheduling Criteria | |
|---|---|---|
| , , | ||
| , , |
| 5 | 5 | 2.10 | 3.68 | 6.03 | 0.00 | 0.42 | 0.55 | 13.44 | 4.39 | 0.00 | 0.96 | 2.52 | 6.34 | 9.24 | 0.00 | 4.74 | ||
| (1) | (4) | (2) | (5) | (3) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 5 | 10 | 2.79 | 1.89 | 1.48 | 0.00 | 1.50 | 2.33 | 9.88 | 1.24 | 0.64 | 0.00 | 1.51 | 5.85 | 5.38 | 0.00 | 2.66 | ||
| (1) | (4) | (2) | (5) | (3) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 5 | 1.82 | 0.00 | 8.51 | 0.13 | 0.37 | 4.98 | 18.48 | 0.54 | 0.00 | 1.43 | 1.24 | 10.03 | 12.90 | 0.00 | 1.00 | ||
| (1) | (5) | (2) | (3) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 10 | 5.13 | 1.30 | 2.66 | 0.00 | 2.36 | 2.17 | 13.59 | 2.71 | 0.00 | 0.88 | 2.26 | 7.20 | 6.87 | 0.00 | 4.37 | ||
| (1) | (4) | (2) | (5) | (3) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 10 | 3.77 | 0.00 | 5.21 | 0.45 | 2.17 | 2.51 | 19.88 | 0.97 | 0.00 | 3.47 | 2.68 | 11.21 | 8.72 | 0.00 | 2.21 | ||
| (1) | (5) | (2) | (3) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 20 | 5.71 | 0.67 | 1.93 | 0.00 | 1.92 | 1.53 | 14.62 | 1.01 | 0.00 | 1.36 | 4.47 | 7.21 | 4.14 | 0.00 | 3.83 | ||
| (1) | (4) | (2) | (5) | (3) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 50 | 4.79 | 0.00 | 3.27 | 0.13 | 0.02 | 0.28 | 10.66 | 1.83 | 0.30 | 0.00 | 2.84 | 5.20 | 2.36 | 0.00 | 2.90 | ||
| (1) | (5) | (3) | (4) | (2) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 10 | 1.70 | 1.87 | 5.61 | 0.11 | 0.00 | 1.95 | 23.84 | 2.92 | 0.00 | 4.02 | 3.75 | 18.67 | 9.11 | 0.00 | 2.03 | ||
| (1) | (4) | (2) | (3) | (5) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 20 | 5.11 | 0.45 | 3.49 | 0.66 | 0.00 | 0.53 | 17.96 | 3.41 | 0.00 | 0.18 | 5.56 | 10.31 | 4.26 | 0.00 | 2.37 | ||
| (1) | (4) | (2) | (3) | (5) | (2) | (1) | (4) | (5) | (3) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 50 | 6.04 | 0.57 | 0.53 | 0.00 | 1.27 | 1.12 | 11.93 | 1.21 | 0.00 | 0.03 | 4.50 | 6.12 | 1.75 | 0.00 | 2.96 | ||
| (1) | (4) | (2) | (5) | (3) | (4) | (1) | (2) | (5) | (3) | (2) | (1) | (3) | (5) | (4) | ||||
| 3.90 | 1.04 | 3.87 | 0.15 | 1.00 | 1.80 | 15.43 | 2.02 | 0.09 | 1.23 | 3.13 | 8.81 | 6.47 | 0.00 | 2.91 | ||||
| 5 | 5 | 0.08 | 0.06 | 0.33 | 0.00 | 0.15 | 0.05 | 0.83 | 0.32 | 0.00 | 0.05 | 0.14 | 0.42 | 0.71 | 0.00 | 0.20 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 5 | 10 | 0.08 | 0.09 | 0.13 | 0.00 | 0.03 | 0.07 | 0.45 | 0.00 | 0.02 | 0.00 | 0.08 | 0.22 | 0.22 | 0.00 | 0.09 | ||
| (1) | (4) | (2) | (5) | (3) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 5 | 0.03 | 0.00 | 0.31 | 0.05 | 0.04 | 0.03 | 1.08 | 0.39 | 0.00 | 0.10 | 0.06 | 0.66 | 0.74 | 0.00 | 0.05 | ||
| (1) | (5) | (2) | (4) | (3) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 10 | 0.15 | 0.15 | 0.32 | 0.00 | 0.16 | 0.31 | 1.00 | 0.00 | 0.00 | 0.27 | 0.15 | 0.55 | 0.77 | 0.00 | 0.42 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 10 | 0.09 | 0.14 | 0.29 | 0.00 | 0.07 | 0.19 | 1.33 | 0.44 | 0.00 | 0.21 | 0.27 | 0.96 | 0.87 | 0.00 | 0.28 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 20 | 0.34 | 0.26 | 0.83 | 0.00 | 0.14 | 0.25 | 2.54 | 0.05 | 0.00 | 0.63 | 0.29 | 1.46 | 1.39 | 0.00 | 0.74 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 50 | 0.29 | 0.00 | 0.39 | 0.02 | 0.02 | 0.05 | 0.89 | 0.19 | 0.00 | 0.00 | 0.10 | 0.38 | 0.63 | 0.00 | 0.03 | ||
| (1) | (5) | (2) | (4) | (3) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 10 | 0.24 | 0.30 | 0.88 | 0.00 | 0.24 | 0.26 | 10.83 | 0.98 | 0.00 | 1.26 | 0.49 | 9.72 | 2.06 | 0.00 | 1.64 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 20 | 0.07 | 0.08 | 0.13 | 0.01 | 0.00 | 0.07 | 0.94 | 0.20 | 0.00 | 0.14 | 0.13 | 0.74 | 0.42 | 0.00 | 0.14 | ||
| (1) | (3) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 50 | 0.52 | 0.42 | 1.20 | 0.06 | 0.00 | 0.33 | 3.37 | 0.31 | 0.00 | 0.42 | 0.21 | 1.97 | 2.24 | 0.05 | 0.00 | ||
| (1) | (4) | (2) | (3) | (5) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (4) | (5) | ||||
| 0.19 | 0.15 | 0.48 | 0.01 | 0.09 | 0.16 | 2.33 | 0.29 | 0.00 | 0.31 | 0.19 | 1.71 | 1.01 | 0.01 | 0.36 | ||||
| 5 | 5 | 0.06 | 0.07 | 0.19 | 0.00 | 0.11 | 0.20 | 0.52 | 0.01 | 0.00 | 0.00 | 0.05 | 0.28 | 0.48 | 0.00 | 0.10 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 5 | 10 | 0.16 | 0.01 | 0.39 | 0.00 | 0.24 | 0.08 | 0.79 | 0.10 | 0.11 | 0.00 | 0.05 | 0.35 | 0.74 | 0.00 | 0.12 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 5 | 0.03 | 0.05 | 0.21 | 0.01 | 0.00 | 0.02 | 0.86 | 0.17 | 0.00 | 0.19 | 0.04 | 0.60 | 0.44 | 0.00 | 0.18 | ||
| (1) | (3) | (2) | (4) | (5) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 10 | 0.17 | 0.15 | 0.27 | 0.00 | 0.17 | 0.39 | 0.80 | 0.09 | 0.00 | 0.02 | 0.08 | 0.46 | 0.91 | 0.00 | 0.18 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 10 | 0.07 | 0.07 | 0.16 | 0.00 | 0.06 | 0.23 | 0.99 | 0.04 | 0.00 | 0.14 | 0.02 | 0.81 | 0.51 | 0.00 | 0.20 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 20 | 0.09 | 0.08 | 0.22 | 0.00 | 0.07 | 0.08 | 0.77 | 0.01 | 0.00 | 0.20 | 0.08 | 0.47 | 0.39 | 0.00 | 0.26 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 50 | 0.18 | 0.06 | 0.44 | 0.00 | 0.06 | 0.07 | 0.87 | 0.12 | 0.00 | 0.04 | 0.05 | 0.38 | 0.69 | 0.00 | 0.09 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 10 | 0.05 | 0.10 | 0.13 | 0.00 | 0.04 | 0.01 | 2.05 | 0.31 | 0.00 | 0.30 | 0.06 | 1.88 | 0.53 | 0.00 | 0.36 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 20 | 0.09 | 0.11 | 0.10 | 0.00 | 0.05 | 0.02 | 1.12 | 0.21 | 0.00 | 0.25 | 0.11 | 0.94 | 0.43 | 0.00 | 0.29 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 50 | 0.09 | 0.07 | 0.16 | 0.00 | 0.04 | 0.09 | 0.58 | 0.05 | 0.00 | 0.09 | 0.04 | 0.39 | 0.35 | 0.00 | 0.13 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 0.10 | 0.08 | 0.23 | 0.00 | 0.08 | 0.12 | 0.94 | 0.11 | 0.01 | 0.12 | 0.06 | 0.66 | 0.55 | 0.00 | 0.19 | ||||
| 5 | 5 | 0.05 | 0.08 | 0.26 | 0.01 | 0.00 | 0.07 | 0.59 | 0.16 | 0.05 | 0.00 | 0.11 | 0.29 | 0.48 | 0.04 | 0.00 | ||
| (1) | (3) | (2) | (4) | (5) | (2) | (1) | (3) | (4) | (5) | (2) | (1) | (3) | (4) | (5) | ||||
| 5 | 10 | 0.16 | 0.24 | 0.20 | 0.00 | 0.02 | 0.12 | 0.52 | 0.02 | 0.03 | 0.00 | 0.12 | 0.18 | 0.38 | 0.00 | 0.16 | ||
| (1) | (4) | (2) | (5) | (3) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 5 | 0.01 | 0.06 | 0.35 | 0.05 | 0.00 | 0.03 | 0.99 | 0.33 | 0.00 | 0.14 | 0.03 | 0.67 | 0.66 | 0.00 | 0.12 | ||
| (1) | (3) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 10 | 10 | 0.08 | 0.14 | 0.20 | 0.00 | 0.09 | 0.01 | 0.61 | 0.22 | 0.00 | 0.13 | 0.09 | 0.31 | 0.56 | 0.00 | 0.22 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 10 | 0.07 | 0.08 | 0.17 | 0.00 | 0.08 | 0.02 | 0.97 | 0.26 | 0.00 | 0.24 | 0.07 | 0.72 | 0.50 | 0.00 | 0.28 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 20 | 0.11 | 0.07 | 0.18 | 0.00 | 0.12 | 0.00 | 0.70 | 0.11 | 0.00 | 0.19 | 0.11 | 0.42 | 0.35 | 0.00 | 0.30 | ||
| (1) | (3) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 20 | 50 | 0.11 | 0.11 | 0.20 | 0.00 | 0.05 | 0.01 | 0.43 | 0.07 | 0.00 | 0.07 | 0.03 | 0.20 | 0.37 | 0.00 | 0.12 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 10 | 0.02 | 0.03 | 0.12 | 0.00 | 0.00 | 0.03 | 1.27 | 0.21 | 0.00 | 0.13 | 0.06 | 1.14 | 0.37 | 0.00 | 0.14 | ||
| (1) | (3) | (2) | (4) | (5) | (2) | (1) | (3) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 20 | 0.05 | 0.06 | 0.11 | 0.00 | 0.04 | 0.14 | 0.98 | 0.01 | 0.00 | 0.16 | 0.04 | 0.83 | 0.32 | 0.00 | 0.19 | ||
| (1) | (3) | (2) | (5) | (4) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 50 | 50 | 0.07 | 0.06 | 0.19 | 0.03 | 0.00 | 0.05 | 0.67 | 0.04 | 0.00 | 0.13 | 0.02 | 0.45 | 0.37 | 0.00 | 0.09 | ||
| (1) | (3) | (2) | (4) | (5) | (3) | (1) | (2) | (5) | (4) | (2) | (1) | (3) | (5) | (4) | ||||
| 0.07 | 0.09 | 0.20 | 0.01 | 0.04 | 0.05 | 0.77 | 0.14 | 0.01 | 0.12 | 0.07 | 0.52 | 0.44 | 0.00 | 0.16 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Framinan, J.M.; Leisten, R. Linking Scheduling Criteria to Shop Floor Performance in Permutation Flowshops. Algorithms 2019, 12, 263. https://doi.org/10.3390/a12120263
Framinan JM, Leisten R. Linking Scheduling Criteria to Shop Floor Performance in Permutation Flowshops. Algorithms. 2019; 12(12):263. https://doi.org/10.3390/a12120263
Chicago/Turabian StyleFraminan, Jose M., and Rainer Leisten. 2019. "Linking Scheduling Criteria to Shop Floor Performance in Permutation Flowshops" Algorithms 12, no. 12: 263. https://doi.org/10.3390/a12120263
APA StyleFraminan, J. M., & Leisten, R. (2019). Linking Scheduling Criteria to Shop Floor Performance in Permutation Flowshops. Algorithms, 12(12), 263. https://doi.org/10.3390/a12120263





