Image Error Concealment Based on Deep Neural Network
Abstract
:1. Introduction
2. Problem Formulation
3. Our Proposal
3.1. Design of AE-P Neural Network
3.2. Training Data Collection
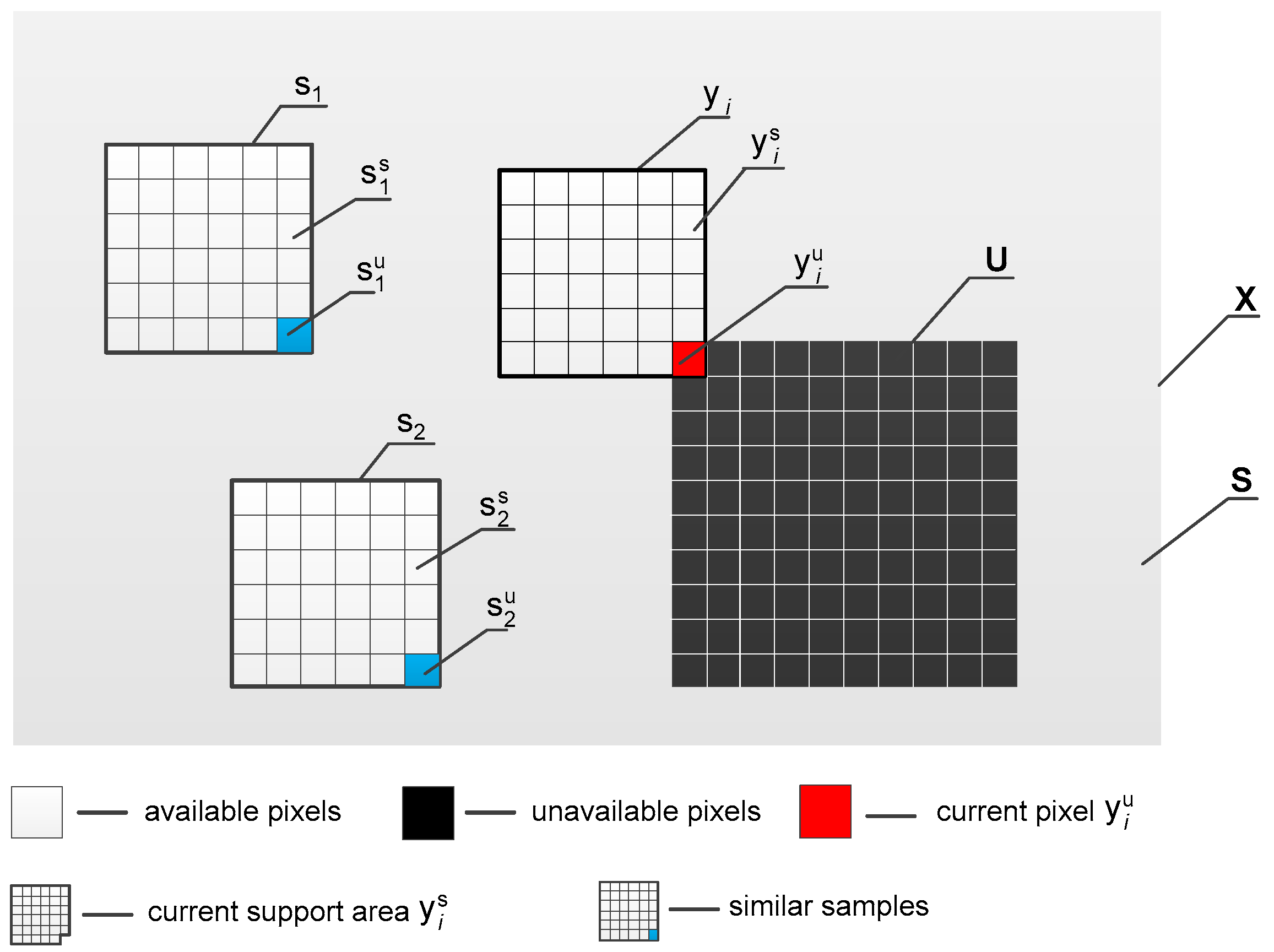
3.3. Similar Data Collection
3.4. Prediction Error Correct
3.5. Adaptive Scan Order
4. Experiments
4.1. Comparative Studies
4.2. Objective and Subjective Performance Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Xiang, X.; Zhao, D.; Ma, S.; Gao, W. Packet video error concealment with auto regressive model. IEEE Trans. Circuits Syst. Video Technol. 2012, 1, 12–27. [Google Scholar] [CrossRef]
- Zhai, G.; Yang, X.; Lin, W.; Zhang, W. Bayesian error concealment with DCT pyramid for images. IEEE Trans. Circuits Syst. Video Technol. 2010, 9, 1224–1232. [Google Scholar] [CrossRef]
- Hsia, S.C. An edge-oriented spatial interpolation for consecutive block error concealment. IEEE Signal Process. Lett. 2004, 1, 577–580. [Google Scholar] [CrossRef]
- Sun, H.; Kwok, W. Concealment of damaged block transform coded images using projections onto convex sets. IEEE Trans. Image Process. 1995, 4, 470–477. [Google Scholar] [CrossRef] [PubMed]
- Zeng, W.; Liu, B. Geometric-structure-based error concealment with novel applications in block-based low-bit-rate coding. IEEE Trans. Circuits Syst. Video Technol. 1999, 1, 648–665. [Google Scholar] [CrossRef]
- Li, X.; Orchard, M.T. Novel sequential error-concealment techniques using orientation adaptive interpolation. IEEE Trans. Circuits Syst. Video Technol. 2002, 10, 857–864. [Google Scholar]
- Koloda, J.; Sánchez, V.; Peinado, A.M. Spatial Error Concealment Based on Edge Visual Clearness for Image/Video Communication. Circuits Syst. Signal Process. 2013, 4, 815–824. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, G.; Yang, X.; Yang, B.; Chen, L. Spatial error concealment with an adaptive linear predictor. IEEE Trans. Circuits Syst. Video Technol. 2015, 3, 353–366. [Google Scholar]
- Koloda, J.; Ostergaard, J.; Jensen, S.H.; Sánchez, V.; Peinado, A.M. Sequential error concealment for video/images by sparse linear prediction. IEEE Trans. Multimed. 2013, 6, 957–969. [Google Scholar] [CrossRef]
- Koloda, J.; Peinado, A.M.; Sánchez, V. Kernel-based MMSE multimedia signal reconstruction and its application to spatial error concealment. IEEE Trans. Multimed. 2014, 10, 1729–1738. [Google Scholar] [CrossRef]
- Park, J.; Park, D.C.; Marks, R.J.; El-Sharkawi, M.A. Recovery of image blocks using the method of alternating projections. IEEE Trans. Image Process. 2005, 4, 461–474. [Google Scholar] [CrossRef]
- Koloda, J.; Seiler, J.; Peinado, A.M.; Kaup, A. Scalable kernel-based minimum mean square error estimator for accelerated image error concealment. IEEE Trans. Broadcast. 2017, 11, 59–70. [Google Scholar] [CrossRef]
- Akbari, A.; Trocan, M.; Granard, B. Joint-domin dictionary learning-based error concealment using common space mapping. In Proceedings of the 2017 22nd International Conference on Digital Signal Processing-DSP, London, UK, 23–25 August 2017; pp. 1–5. [Google Scholar]
- Ding, D.; Ram, S.; Rodríguez, J.J. Image inpainting using nonlocal texture matching and nonlinear filtering. IEEE Trans. Image Process. 2019, 4, 1705–1719. [Google Scholar] [CrossRef]
- Alilou, V.K.; Yaghmaee, F. Application of GRNN neural network in non-texture image inpainting and restoration. Pattern Recognit. Lett. 2015, 9, 24–31. [Google Scholar] [CrossRef]
- Lam, W.M.; Reibman, A.R.; Liu, B. Recovery of lost or erroneously received motion vectors. In Proceedings of the 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing-ICASSP, Minneapolis, MN, USA, 27–30 April 1993; Volume 5, pp. 417–420. [Google Scholar]
- Zhang, J.; Arnold, J.F.; Frater, M.R. A cell-loss concealment technique for MPEG-2 coded video. IEEE Trans. Circuits Syst. Video Technol. 2000, 6, 659–665. [Google Scholar] [CrossRef]
- Wu, J.; Liu, X.; Yoo, K.Y. A temporal error concealment method for H.264/AVC using motion vector recovery. IEEE Trans. Consum. Electron. 2008, 11, 1880–1885. [Google Scholar] [CrossRef]
- Qian, X.; Liu, G.; Wang, W. Recovering connected error region based on adaptive error concealment order determination. IEEE Trans. Multimed. 2009, 6, 683–695. [Google Scholar] [CrossRef]
- Shao, S.C.; Chen, J.H. A novel error concealment approach based on general regression neural network. In Proceedings of the 2011 International Conference on Consumer Electrics, Communication and Networks-CECNet, XianNing, China, 16–18 April 2011; pp. 4679–4682. [Google Scholar]
- Sankisa, A.; Punjabi, A.; Katsaggelos, A.K. Video error concealment using deep neural networks. In Proceedings of the IEEE International Conference on Image Processing-ICIP, Athens, Greece, 7–10 October 2018; pp. 380–384. [Google Scholar]
- Ghuge, A.D.; Rajani, P.K.; Khaparde, A. Video error concealment using moment Invariance. In Proceedings of the 2017 International Conference on Computing, Communication, Control and Automation-ICCUBEA, Pune, India, 17–18 August 2017; pp. 1–5. [Google Scholar]
- Zhang, Y.; Xiang, X.; Ma, S.; Zhao, D.; Gao, W. Auto regressive model and weighted least squares based packet video error concealment. In Proceedings of the 2010 Data Compression Conference-DCC, Snowbird, UT, USA, 24–26 March 2010; pp. 455–464. [Google Scholar]
- Agrafiotis, D.; Bull, D.R.; Canagarajah, C.N. Enhanced error concealment with mode selection. IEEE Trans. Circuits Syst. Video Technol. 2006, 8, 960–973. [Google Scholar] [CrossRef]
- Kung, W.-Y.; Kim, C.-S.; Kuo, C.-C.J. Spatial and temporal error concealment techniques for video transmission over noisy channels. IEEE Trans. Circuits Syst. Video Technol. 2006, 7, 789–803. [Google Scholar] [CrossRef]
- Ma, M.; Au, O.C.; Chan, S.-H.G.; Sun, M.-T. Edge-directed error concealment. IEEE Trans. Circuits Syst. Video Technol. 2010, 3, 382–395. [Google Scholar]
- Shirani, S.; Kossentini, F.; Ward, R. An Adaptive Markov Random Field Based Error Concealment Method for Video Communication in an Error Prone Environment. In Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing-ICASSP, Phoenix, AZ, USA, 15–19 March 1999; Volume 6, pp. 3117–3120. [Google Scholar]
- Koloda, J.; Peinado, A.M.; Sánchez, V. On the application of multivariate kernel density estimation to image error concealment. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing-ICASSP, Vancouver, BC, Canada, 26–31 May 2013; pp. 1330–1334. [Google Scholar]
- Liu, X.; Zhai, D.; Zhou, J.; Wang, S. Sparsity-Based image error concealment via adaptive dual dictionary learning and regularization. IEEE Trans. Image Process. 2017, 2, 782–796. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 7, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Varsa, V.; Hannuksela, M.M.; Wang, Y.-K. Non-Normative Error Concealment Algorithms. In Proceedings of the 14th ITU-T VCEG Meeting Document: VCEG-N62, Santa Barbara, CA, USA, 21–24 September 2001. [Google Scholar]
- Rongfu, Z.; Yuanhua, Z.; Xiaodong, H. Content-adaptive spatial error concealment for video communication. IEEE Trans. Consum. Electron. 2004, 2, 335–341. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 4, 600–612. [Google Scholar] [CrossRef]
- Janko. Available online: http://dtstc.ugr.es/~jkoloda/download.html (accessed on 1 March 2019).




















| Layer | Number of Neurons | |
|---|---|---|
| AE | Prediction | |
| FC 1 | 49 | |
| FC 2 | 45 | |
| FC 3 | 40 | |
| FC 4 | 35 | |
| FC 5 | 30 | |
| FC 6 | 25 | |
| FC 7 | 30 | 20 |
| FC 8 | 35 | 15 |
| FC 9 | 40 | 10 |
| FC 10 | 45 | 5 |
| FC 11 | 49 | 1 |
| Images | Metrics | Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| POCS | OAI | AVC | CAD | MRF | VC | SLP | KMMSE | Ours | ||
| Baboon | PSNR | 24.58 | 26.10 | 25.27 | 24.36 | 26.13 | 25.95 | 24.60 | 26.24 | 26.54 |
| SSIM | 0.8381 | 0.8678 | 0.8477 | 0.8472 | 0.861 | 0.8596 | 0.8573 | 0.8676 | 0.8703 | |
| Barbara | PSNR | 24.31 | 28.18 | 26.60 | 26.67 | 27.21 | 27.29 | 28.56 | 29.18 | 29.75 |
| SSIM | 0.8417 | 0.9149 | 0.8801 | 0.8877 | 0.8935 | 0.8926 | 0.9254 | 0.9264 | 0.9311 | |
| Boat | PSNR | 26.50 | 27.53 | 27.29 | 26.07 | 27.10 | 27.12 | 26.44 | 27.49 | 27.65 |
| SSIM | 0.8723 | 0.8964 | 0.8893 | 0.8815 | 0.7781 | 0.8913 | 0.8893 | 0.8938 | 0.8958 | |
| Butterfly | PSNR | 20.56 | 25.10 | 21.91 | 23.07 | 23.72 | 24.19 | 24.21 | 24.46 | 26.34 |
| SSIM | 0.8599 | 0.9251 | 0.8755 | 0.9221 | 0.9090 | 0.9280 | 0.9426 | 0.9440 | 0.9474 | |
| Columbia | PSNR | 23.76 | 26.46 | 25.07 | 25.84 | 25.45 | 27.46 | 26.36 | 26.94 | 28.02 |
| SSIM | 0.8859 | 0.9338 | 0.9229 | 0.9272 | 0.9160 | 0.9288 | 0.9404 | 0.9395 | 0.9429 | |
| Cornfield | PSNR | 26.69 | 28.97 | 28.88 | 26.62 | 28.50 | 28.97 | 28.36 | 29.19 | 30.42 |
| SSIM | 0.8954 | 0.9318 | 0.9269 | 0.9201 | 0.9027 | 0.9303 | 0.9326 | 0.9371 | 0.9422 | |
| Couple | PSNR | 25.08 | 27.87 | 27.44 | 26.10 | 27.42 | 27.56 | 27.13 | 27.84 | 28.04 |
| SSIM | 0.8590 | 0.9071 | 0.8932 | 0.8841 | 0.8915 | 0.8980 | 0.9010 | 0.9044 | 0.9073 | |
| Goldhill | PSNR | 26.40 | 28.50 | 28.24 | 25.06 | 27.95 | 28.38 | 28.21 | 28.78 | 28.82 |
| SSIM | 0.8612 | 0.8975 | 0.8877 | 0.8624 | 0.8856 | 0.8909 | 0.8948 | 0.8978 | 0.8997 | |
| Hat | PSNR | 27.28 | 31.63 | 28.72 | 29.74 | 30.35 | 31.04 | 31.20 | 31.82 | 32.56 |
| SSIM | 0.8994 | 0.9501 | 0.9315 | 0.9431 | 0.9442 | 0.9427 | 0.9522 | 0.9576 | 0.9636 | |
| Man | PSNR | 23.14 | 26.35 | 24.83 | 24.30 | 25.46 | 25.72 | 24.06 | 25.68 | 25.54 |
| SSIM | 0.8350 | 0.8843 | 0.8613 | 0.847 | 0.8748 | 0.8727 | 0.8758 | 0.8845 | 0.8799 | |
| Peppers | PSNR | 24.29 | 29.93 | 27.37 | 27.92 | 28.46 | 28.85 | 29.08 | 29.50 | 29.98 |
| SSIM | 0.8584 | 0.9293 | 0.9062 | 0.9098 | 0.9229 | 0.9164 | 0.9294 | 0.9300 | 0.9306 | |
| Cameraman | PSNR | 23.89 | 27.55 | 26.29 | 26.96 | 26.84 | 26.83 | 26.31 | 27.37 | 27.88 |
| SSIM | 0.8858 | 0.9402 | 0.9290 | 0.9332 | 0.9298 | 0.9327 | 0.9464 | 0.9482 | 0.9484 | |
| Tower | PSNR | 23.68 | 26.78 | 26.13 | 25.36 | 25.17 | 26.53 | 25.71 | 26.50 | 27.15 |
| SSIM | 0.8801 | 0.9197 | 0.9089 | 0.9093 | 0.9080 | 0.9175 | 0.9191 | 0.9262 | 0.9279 | |
| Average | PSNR | 24.63 | 27.77 | 26.46 | 26.01 | 26.90 | 27.38 | 26.94 | 27.77 | 28.36 |
| SSIM | 0.8671 | 0.9152 | 0.8969 | 0.8981 | 0.8936 | 0.9078 | 0.9159 | 0.9198 | 0.9221 | |
| Images | Metrics | Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| POCS | OAI | AVC | CAD | MRF | VC | SLP | KMMSE | Ours | ||
| Baboon | PSNR | 21.38 | 22.77 | 22.27 | 19.81 | 22.94 | 21.76 | 21.26 | 22.92 | 22.95 |
| SSIM | 0.6719 | 0.7305 | 0.6981 | 0.6554 | 0.7202 | 0.6872 | 0.7013 | 0.7228 | 0.7208 | |
| Barbara | PSNR | 21.32 | 25.19 | 23.36 | 22.16 | 24.23 | 22.65 | 25.36 | 26.59 | 26.53 |
| SSIM | 0.6993 | 0.8407 | 0.7693 | 0.772 | 0.8019 | 0.7531 | 0.8520 | 0.8620 | 0.8593 | |
| Boat | PSNR | 23.89 | 24.14 | 24.83 | 22.59 | 24.80 | 23.32 | 23.46 | 24.53 | 24.93 |
| SSIM | 0.7427 | 0.7942 | 0.7892 | 0.7613 | 0.7781 | 0.7376 | 0.7716 | 0.7833 | 0.7951 | |
| Butterfly | PSNR | 18.11 | 21.11 | 18.91 | 19.42 | 20.61 | 19.97 | 20.24 | 21.10 | 22.77 |
| SSIM | 0.7062 | 0.8429 | 0.7556 | 0.7925 | 0.8260 | 0.7809 | 0.8623 | 0.8693 | 0.8814 | |
| Columbia | PSNR | 21.66 | 24.17 | 22.91 | 23.74 | 23.48 | 24.12 | 23.35 | 24.23 | 25.05 |
| SSIM | 0.7722 | 0.8679 | 0.8454 | 0.8537 | 0.8280 | 0.8172 | 0.8600 | 0.8665 | 0.8655 | |
| Cornfield | PSNR | 23.84 | 24.88 | 25.31 | 23.07 | 25.12 | 24.35 | 24.13 | 25.27 | 25.66 |
| SSIM | 0.7927 | 0.8624 | 0.8563 | 0.8172 | 0.8393 | 0.7859 | 0.8492 | 0.8617 | 0.8651 | |
| Couple | PSNR | 21.95 | 24.62 | 23.96 | 22.17 | 23.55 | 22.94 | 22.56 | 23.54 | 24.76 |
| SSIM | 0.7191 | 0.8118 | 0.782 | 0.773 | 0.7747 | 0.7510 | 0.7748 | 0.7886 | 0.7940 | |
| Goldhill | PSNR | 23.61 | 25.37 | 25.44 | 23.50 | 25.24 | 24.69 | 24.75 | 25.43 | 25.62 |
| SSIM | 0.7321 | 0.7995 | 0.7818 | 0.7489 | 0.7785 | 0.7594 | 0.7822 | 0.7908 | 0.7920 | |
| Hat | PSNR | 24.52 | 28.40 | 26.27 | 24.18 | 27.57 | 25.17 | 27.31 | 27.73 | 28.62 |
| SSIM | 0.7947 | 0.8913 | 0.8606 | 0.8128 | 0.8844 | 0.7931 | 0.8954 | 0.8998 | 0.9010 | |
| Man | PSNR | 19.77 | 22.14 | 21.77 | 17.17 | 22.13 | 21.60 | 21.02 | 22.06 | 22.49 |
| SSIM | 0.6668 | 0.7501 | 0.72 | 0.6701 | 0.7390 | 0.7085 | 0.7310 | 0.7461 | 0.7542 | |
| Peppers | PSNR | 20.88 | 25.73 | 23.16 | 19.71 | 24.14 | 23.18 | 23.52 | 24.14 | 25.76 |
| SSIM | 0.7209 | 0.8516 | 0.8055 | 0.7696 | 0.8319 | 0.7770 | 0.8371 | 0.8434 | 0.8530 | |
| Cameraman | PSNR | 20.42 | 24.06 | 22.41 | 20.42 | 22.62 | 22.51 | 22.63 | 23.16 | 23.74 |
| SSIM | 0.7654 | 0.8704 | 0.8417 | 0.8333 | 0.8475 | 0.7941 | 0.8753 | 0.8757 | 0.8747 | |
| Tower | PSNR | 20.37 | 23.47 | 22.78 | 21.04 | 22.04 | 22.55 | 22.47 | 23.35 | 23.96 |
| SSIM | 0.7499 | 0.8339 | 0.8106 | 0.7826 | 0.8030 | 0.7704 | 0.8311 | 0.8407 | 0.8354 | |
| Average | PSNR | 21.67 | 24.31 | 23.34 | 21.46 | 23.73 | 22.99 | 23.24 | 24.16 | 24.83 |
| SSIM | 0.7334 | 0.8267 | 0.7935 | 0.7725 | 0.8040 | 0.7627 | 0.8172 | 0.8270 | 0.8301 | |
| Images | Metrics | Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| POCS | OAI | AVC | CAD | MRF | VC | SLP | KMMSE | Ours | ||
| Baboon | PSNR | 22.93 | 23.72 | 23.81 | 20.44 | 24.38 | 18.93 | 22.76 | 24.20 | 24.47 |
| SSIM | 0.7852 | 0.8142 | 0.7986 | 0.7801 | 0.8125 | 0.7837 | 0.8049 | 0.8146 | 0.8163 | |
| Barbara | PSNR | 22.92 | 25.80 | 25.07 | 21.62 | 25.85 | 19.91 | 26.76 | 27.77 | 27.77 |
| SSIM | 0.7995 | 0.8747 | 0.8445 | 0.8327 | 0.8621 | 0.8235 | 0.8959 | 0.8997 | 0.9033 | |
| Boat | PSNR | 25.37 | 26.08 | 26.44 | 21.85 | 26.38 | 18.01 | 25.11 | 26.17 | 26.64 |
| SSIM | 0.8336 | 0.8611 | 0.8601 | 0.825 | 0.8590 | 0.8089 | 0.8564 | 0.8635 | 0.8637 | |
| Butterfly | PSNR | 19.27 | 21.96 | 19.93 | 18.49 | 21.58 | 17.93 | 21.54 | 22.05 | 23.03 |
| SSIM | 0.8031 | 0.8754 | 0.827 | 0.8484 | 0.8739 | 0.8422 | 0.9038 | 0.9008 | 0.9111 | |
| Columbia | PSNR | 22.26 | 23.77 | 22.86 | 22.59 | 23.10 | 21.80 | 23.79 | 24.25 | 24.54 |
| SSIM | 0.8463 | 0.8898 | 0.8875 | 0.8806 | 0.8757 | 0.8537 | 0.8990 | 0.9063 | 0.9077 | |
| Cornfield | PSNR | 25.23 | 25.04 | 26.33 | 21.32 | 26.05 | 19.42 | 25.51 | 26.48 | 25.87 |
| SSIM | 0.8555 | 0.8869 | 0.8948 | 0.8591 | 0.8785 | 0.8263 | 0.8930 | 0.9004 | 0.8963 | |
| Couple | PSNR | 23.60 | 25.45 | 25.66 | 22.06 | 25.42 | 19.77 | 24.15 | 25.31 | 26.40 |
| SSIM | 0.8125 | 0.8571 | 0.8544 | 0.8281 | 0.8505 | 0.8214 | 0.8520 | 0.8574 | 0.8656 | |
| Goldhill | PSNR | 25.16 | 26.61 | 27.13 | 22.70 | 27.12 | 20.81 | 26.76 | 27.51 | 27.31 |
| SSIM | 0.8177 | 0.8546 | 0.8498 | 0.8069 | 0.8460 | 0.8102 | 0.8574 | 0.8608 | 0.8552 | |
| Hat | PSNR | 26.18 | 27.83 | 26.98 | 21.36 | 28.42 | 19.5802 | 27.50 | 29.15 | 29.28 |
| SSIM | 0.8763 | 0.9076 | 0.9081 | 0.8661 | 0.9278 | 0.8344 | 0.9294 | 0.9386 | 0.9346 | |
| Man | PSNR | 21.39 | 23.17 | 22.36 | 20.49 | 22.77 | 21.2781 | 21.71 | 22.76 | 23.48 |
| SSIM | 0.7783 | 0.8308 | 0.8125 | 0.7793 | 0.8249 | 0.8096 | 0.8211 | 0.8315 | 0.8346 | |
| Peppers | PSNR | 21.66 | 25.41 | 23.28 | 21.35 | 24.05 | 20.09 | 24.75 | 25.06 | 25.67 |
| SSIM | 0.8163 | 0.8772 | 0.8542 | 0.836 | 0.8733 | 0.8284 | 0.8892 | 0.8925 | 0.8955 | |
| Cameraman | PSNR | 22.71 | 25.68 | 24.95 | 21.51 | 25.77 | 19.27 | 25.36 | 25.79 | 26.61 |
| SSIM | 0.8452 | 0.8971 | 0.8952 | 0.8796 | 0.8974 | 0.8361 | 0.9128 | 0.9142 | 0.9164 | |
| Tower | PSNR | 22.22 | 23.99 | 24.35 | 21.81 | 23.44 | 19.84 | 24.85 | 25.44 | 25.01 |
| SSIM | 0.8276 | 0.8704 | 0.869 | 0.854 | 0.8626 | 0.8321 | 0.8854 | 0.8918 | 0.8834 | |
| Average | PSNR | 23.15 | 24.96 | 24.55 | 21.35 | 24.95 | 19.74 | 24.66 | 25.53 | 25.85 |
| SSIM | 0.8229 | 0.8690 | 0.8581 | 0.8366 | 0.8649 | 0.8239 | 0.8769 | 0.8825 | 0.8834 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Huang, R.; Han, F.; Wang, Z. Image Error Concealment Based on Deep Neural Network. Algorithms 2019, 12, 82. https://doi.org/10.3390/a12040082
Zhang Z, Huang R, Han F, Wang Z. Image Error Concealment Based on Deep Neural Network. Algorithms. 2019; 12(4):82. https://doi.org/10.3390/a12040082
Chicago/Turabian StyleZhang, Zhiqiang, Rong Huang, Fang Han, and Zhijie Wang. 2019. "Image Error Concealment Based on Deep Neural Network" Algorithms 12, no. 4: 82. https://doi.org/10.3390/a12040082
APA StyleZhang, Z., Huang, R., Han, F., & Wang, Z. (2019). Image Error Concealment Based on Deep Neural Network. Algorithms, 12(4), 82. https://doi.org/10.3390/a12040082




