Deep Learning with a Recurrent Network Structure in the Sequence Modeling of Imbalanced Data for ECG-Rhythm Classifier
Abstract
:1. Introduction
2. Materials and Methods
2.1. ECG Raw Data
2.2. ECG Segmentation
2.3. Sequence Modeling Classifier
2.3.1. Recurrent Neural Network
2.3.2. Long Short-Term Memory
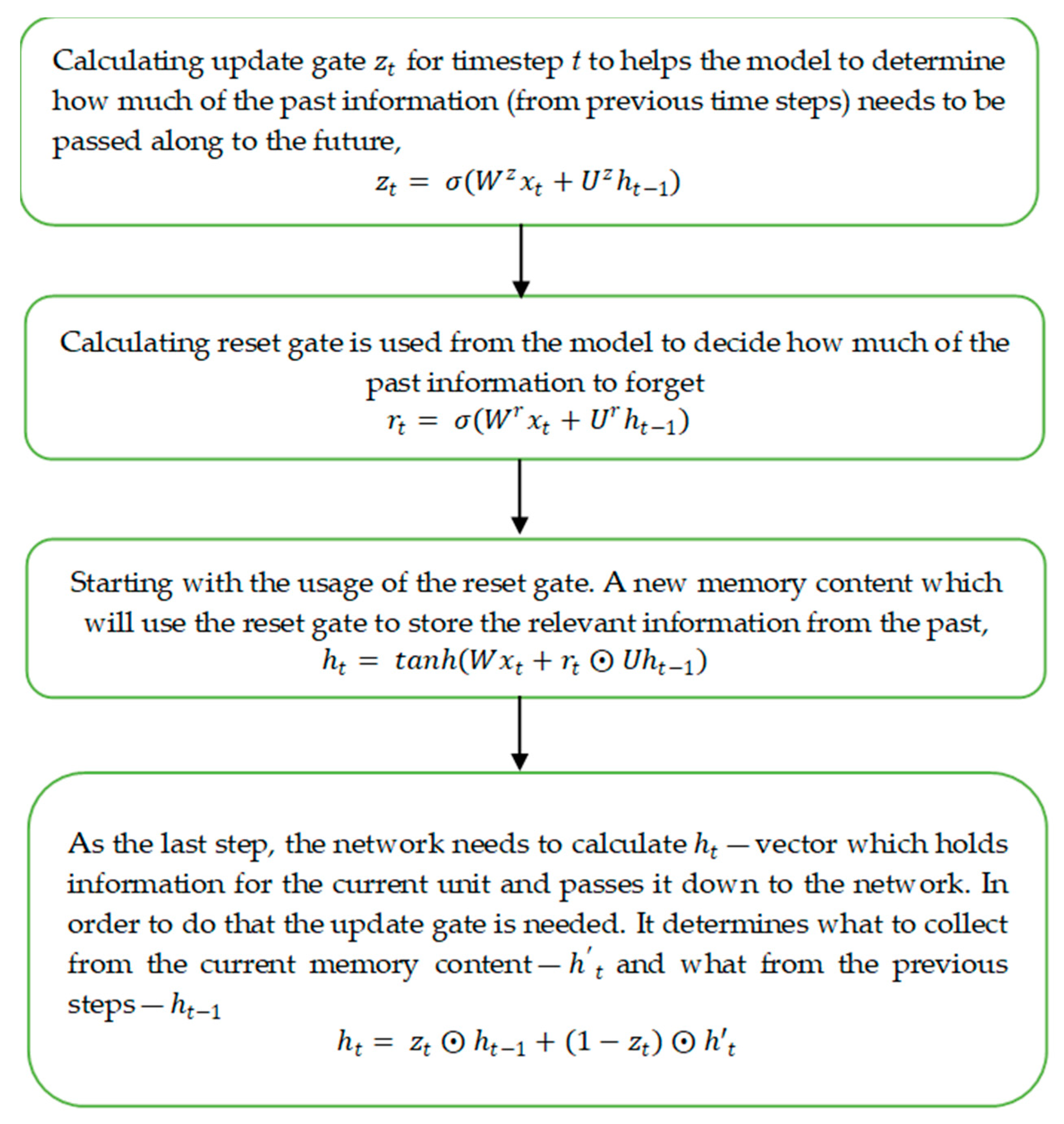
2.3.3. Gated Recurrent Unit
3. Evaluation Performance
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goldberger, A.L.; Goldberger, Z.D.; Shvilkin, A. Clinical Electrocardiography: A Simplified Approach E-Book; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Nurmaini, S.; Gani, A. Cardiac Arrhythmias Classification Using Deep Neural Networks and Principal Component Analysis Algorithm. Int. J. Adv. Soft Comput. Appl. 2018, 10, 14–32. [Google Scholar]
- Caesarendra, W.; Ismail, R.; Kurniawan, D.; Karwiky, G.; Ahmad, C. Suddent cardiac death predictor based on spatial QRS-T angle feature and support vector machine case study for cardiac disease detection in Indonesia. In Proceedings of the 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 4–8 December 2016; pp. 186–192. [Google Scholar]
- Pławiak, P. Novel genetic ensembles of classifiers applied to myocardium dysfunction recognition based on ECG signals. Swarm Evol. Comput. 2018, 39, 192–208. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Tan, R.S. Deep convolutional neural network for the automated diagnosis of congestive heart failure using ECG signals. Appl. Intell. 2018, 1–12. [Google Scholar] [CrossRef]
- Steinhubl, S.R.; Waalen, J.; Edwards, A.M.; Ariniello, L.M.; Mehta, R.R.; Ebner, G.S.; Carter, C.; Baca-Motes, K.; Felicione, E.; Sarich, T.; et al. Effect of a home-based wearable continuous ECG monitoring patch on detection of undiagnosed atrial fibrillation: The mSToPS randomized clinical trial. JAMA 2018, 320, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.G. Rapid ECG Interpretation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Fleming, J.S. Interpreting the Electrocardiogram; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zimetbaum, P.J.; Josephson, M.E. Use of the electrocardiogram in acute myocardial infarction. N. Engl. J. Med. 2003, 348, 933–940. [Google Scholar] [CrossRef]
- Gaziano, T.; Reddy, K.S.; Paccaud, F.; Horton, S.; Chaturvedi, V. Cardiovascular disease. In Disease Control Priorities in Developing Countries, 2nd ed.; The International Bank for Reconstruction and Development/The World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Thygesen, K.; Alpert, J.S.; White, H.D. Universal definition of myocardial infarction. J. Am. Coll. Cardiol. 2007, 50, 2173–2195. [Google Scholar] [CrossRef]
- Lui, H.W.; Chow, K.L. Multiclass classification of myocardial infarction with convolutional and recurrent neural networks for portable ECG devices. Inform. Med. Unlocked 2018, 13, 26–33. [Google Scholar] [CrossRef]
- Strodthoff, N.; Strodthoff, C. Detecting and interpreting myocardial infarctions using fully convolutional neural networks. arXiv 2018, arXiv:1806.07385. [Google Scholar] [CrossRef]
- Goto, S.; Kimura, M.; Katsumata, Y.; Goto, S.; Kamatani, T.; Ichihara, G.; Ko, S.; Sasaki, J.; Fukuda, K.; Sano, M. Artificial intelligence to predict needs for urgent revascularization from 12-leads electrocardiography in emergency patients. PLoS ONE 2019, 14, e0210103. [Google Scholar] [CrossRef]
- Mawri, S.; Michaels, A.; Gibbs, J.; Shah, S.; Rao, S.; Kugelmass, A.; Lingam, N.; Arida, M.; Jacobsen, G.; Rowlandson, I.; et al. The comparison of physician to computer interpreted electrocardiograms on ST-elevation myocardial infarction door-to-balloon times. Crit. Pathw. Cardiol. 2016, 15, 22–25. [Google Scholar] [CrossRef]
- Banerjee, S.; Mitra, M. Application of cross wavelet transform for ECG pattern analysis and classification. IEEE Trans. Instrum. Meas. 2014, 63, 326–333. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Jia, H.; Deng, Y.; Li, P.; Qiu, X.; Tao, Y. Research and Realization of ECG Classification based on Gated Recurrent Unit. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2189–2193. [Google Scholar]
- Koutnik, J.; Greff, K.; Gomez, F.; Schmidhuber, J. A clockwork rnn. arXiv 2014, arXiv:1402.3511. [Google Scholar]
- Le, Q.V.; Jaitly, N.; Hinton, G.E. A simple way to initialize recurrent networks of rectified linear units. arXiv 2015, arXiv:1504.00941. [Google Scholar]
- Krueger, D.; Maharaj, T.; Kramár, J.; Pezeshki, M.; Ballas, N.; Ke, N.R.; Goyal, A.; Bengio, Y.; Courville, A.; Pal, C. Zoneout: Regularizing rnns by randomly preserving hidden activations. arXiv 2016, arXiv:1606.01305. [Google Scholar]
- Campos, V.; Jou, B.; Giró-i-Nieto, X.; Torres, J.; Chang, S.-F. Skip rnn: Learning to skip state updates in recurrent neural networks. arXiv 2017, arXiv:1708.06834. [Google Scholar]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Wiatowski, T.; Bölcskei, H. A mathematical theory of deep convolutional neural networks for feature extraction. IEEE Trans. Inf. Theory 2018, 64, 1845–1866. [Google Scholar] [CrossRef]
- Faust, O.; Shenfield, A.; Kareem, M.; San, T.R.; Fujita, H.; Acharya, U.R. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals. Comput. Biol. Med. 2018, 102, 327–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bullinaria, J.A. Recurrent Neural Networks. 2015. Available online: http://www.cs.bham.ac.uk/~jxb/INC/l12.pdf (accessed on 18 February 2019).
- Singh, S.; Pandey, S.K.; Pawar, U.; Janghel, R.R. Classification of ECG Arrhythmia using Recurrent Neural Networks. Procedia Comput. Sci. 2018, 132, 1290–1297. [Google Scholar] [CrossRef]
- Darmawahyuni, A. Coronary Heart Disease Interpretation Based on Deep Neural Network. Comput. Eng. Appl. J. 2019, 8, 1–12. [Google Scholar] [CrossRef]






| Classifier | Hidden State Model |
|---|---|
| RNN | |
| LSTM | |
| GRU |
| Diagnostic | MI | Healthy Control | Total |
|---|---|---|---|
| MI | True Positive (TP) | False Positive (FP) | All Positive Test (T+) |
| Healthy Control | False Negative (FN) | True Negative (TN) | All Negative Test (T−) |
| Total | Total of MI | Total of Healthy Control | Total Sample |
| Training: Testing (%) | Sequence Model Classifier | Performance Metrics (%) | |||||
|---|---|---|---|---|---|---|---|
| Sensitivity | Specificity | Precision | F1-score | BACC | MCC | ||
| 90:10 | Vanilla RNN | 85.81 | 87.92 | 89.56 | 84.97 | 88.14 | 89.85 |
| LSTM | 98.49 | 97.97 | 95.67 | 96.32 | 97.56 | 95.32 | |
| GRU | 87.07 | 98.10 | 94.89 | 94.08 | 98.73 | 93.78 | |
| 80:20 | Vanilla RNN | 86.86 | 87.28 | 88.37 | 82.40 | 81.66 | 89.64 |
| LSTM | 92.47 | 97.62 | 90.11 | 88.57 | 89.81 | 79.62 | |
| GRU | 87.17 | 88.49 | 90.60 | 86.69 | 88.90 | 87.90 | |
| 70:30 | Vanilla RNN | 81.88 | 90.78 | 60.46 | 63.60 | 75.00 | 67.08 |
| LSTM | 88.18 | 93.61 | 71.51 | 82.55 | 83.33 | 78.78 | |
| GRU | 92.59 | 93.60 | 71.51 | 82.27 | 83.33 | 78.78 | |
| 60:40 | Vanilla RNN | 67.09 | 91.12 | 60.46 | 69.56 | 75.00 | 67.08 |
| LSTM | 97.61 | 92.16 | 65.11 | 74.91 | 75.00 | 67.08 | |
| GRU | 96.85 | 93.79 | 72.67 | 81.43 | 83.33 | 78.78 | |
| 50:50 | Vanilla RNN | 31.44 | 88.70 | 64.53 | 42.28 | 73.14 | 54.71 |
| LSTM | 88.14 | 93.00 | 69.18 | 77.52 | 83.33 | 78.78 | |
| GRU | 51.02 | 87.80 | 43.41 | 46.91 | 67.06 | 48.50 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darmawahyuni, A.; Nurmaini, S.; Sukemi; Caesarendra, W.; Bhayyu, V.; Rachmatullah, M.N.; Firdaus. Deep Learning with a Recurrent Network Structure in the Sequence Modeling of Imbalanced Data for ECG-Rhythm Classifier. Algorithms 2019, 12, 118. https://doi.org/10.3390/a12060118
Darmawahyuni A, Nurmaini S, Sukemi, Caesarendra W, Bhayyu V, Rachmatullah MN, Firdaus. Deep Learning with a Recurrent Network Structure in the Sequence Modeling of Imbalanced Data for ECG-Rhythm Classifier. Algorithms. 2019; 12(6):118. https://doi.org/10.3390/a12060118
Chicago/Turabian StyleDarmawahyuni, Annisa, Siti Nurmaini, Sukemi, Wahyu Caesarendra, Vicko Bhayyu, M Naufal Rachmatullah, and Firdaus. 2019. "Deep Learning with a Recurrent Network Structure in the Sequence Modeling of Imbalanced Data for ECG-Rhythm Classifier" Algorithms 12, no. 6: 118. https://doi.org/10.3390/a12060118
APA StyleDarmawahyuni, A., Nurmaini, S., Sukemi, Caesarendra, W., Bhayyu, V., Rachmatullah, M. N., & Firdaus. (2019). Deep Learning with a Recurrent Network Structure in the Sequence Modeling of Imbalanced Data for ECG-Rhythm Classifier. Algorithms, 12(6), 118. https://doi.org/10.3390/a12060118








