A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks
Abstract
:1. Introduction
2. Model Assumptions
2.1. Network Model
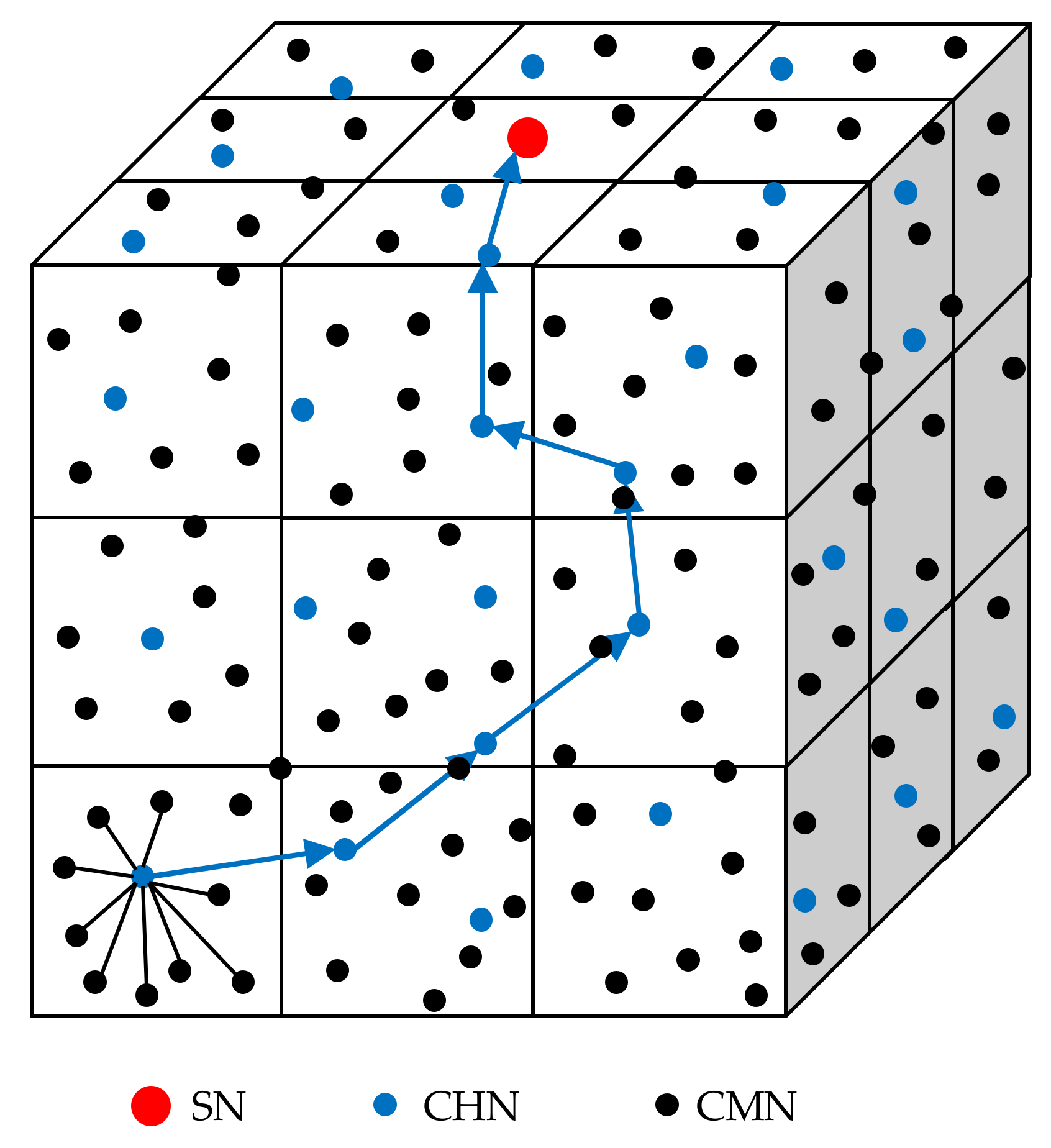
- The 3D underwater network is evenly divided into small cubes and each cube is regarded as a cluster.
- Two types of nodes are considered in the network: the ordinary underwater acoustic sensor nodes and the SN. The underwater acoustic sensor nodes are static after random deployment.
- The single SN is always the destination node and is located at the center of the surface of the monitoring area, which has a continuous energy supply. However, the energy of the ordinary sensor nodes is restrained and they do not have an energy supply.
- All nodes (except the SN) have the same initial energy and every node has a unique ID.
- The locations of the SN and sensor nodes after placement can be obtained by localization algorithms [54], and the distance between two nodes can be calculated.
- The sending power can be controlled by nodes according to different distances to the receiving nodes.
- In every small cube, sensor nodes run for CHN. One of them will become the CHN and the others become CMNs. CMNs collect data and send them to the CHN by a single hop. After receiving the data from the CMNs, the CHN processes the data and then transmits them to the SN in one data packet by multiple hops. The relay nodes on multi-hop paths are other CHNs. If some CHNs are near the SN, they can directly forward data to the SN by a single hop.
2.2. Energy Consumption Model
3. The Improved Strategy of the ACO Algorithm
3.1. Overview of ACO
3.2. The Improved Evaporation Parameter
3.3. The Heuristic Information
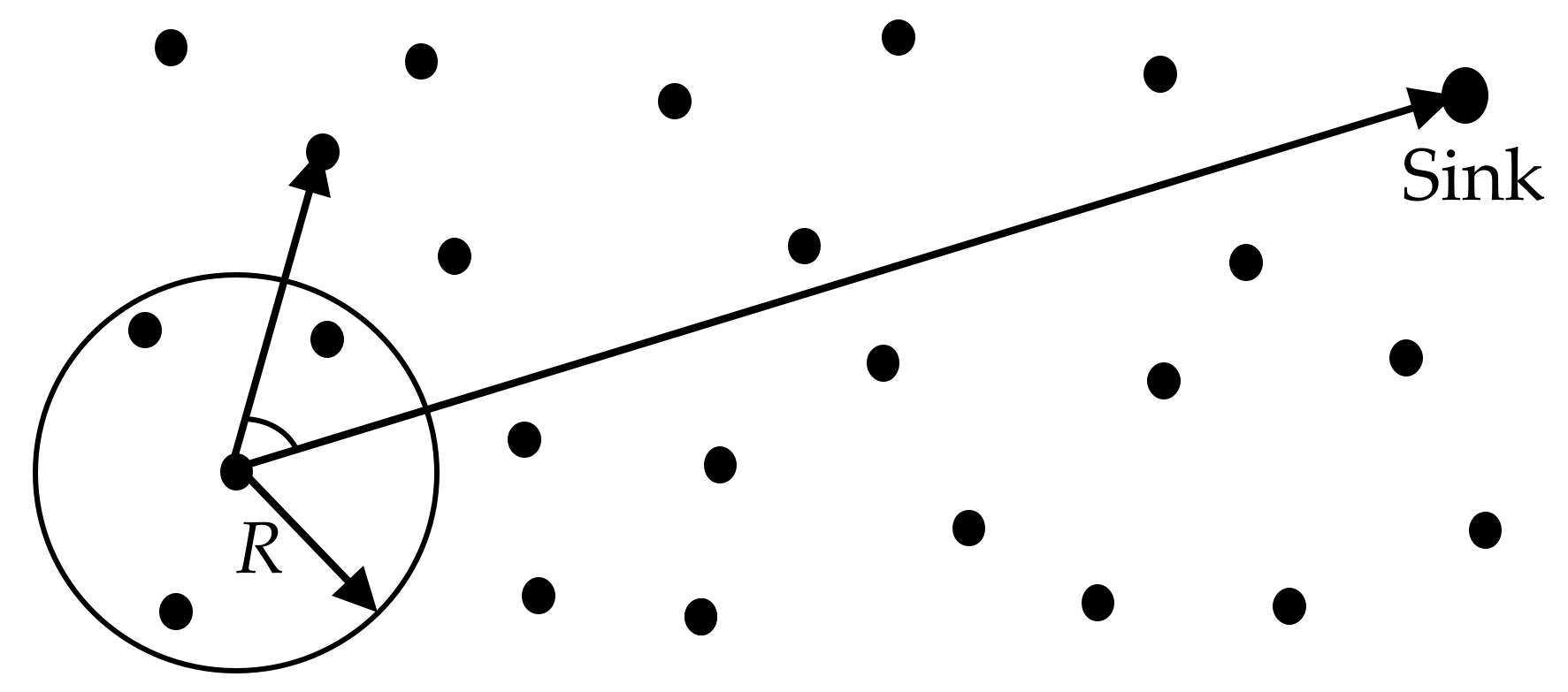
3.4. The Proposal of Ant Searching Scope
4. Clustering Routing Algorithm Design
4.1. Cluster Head Selection Phase
4.2. Data Transmission Phase
5. Simulation Results and Analyses
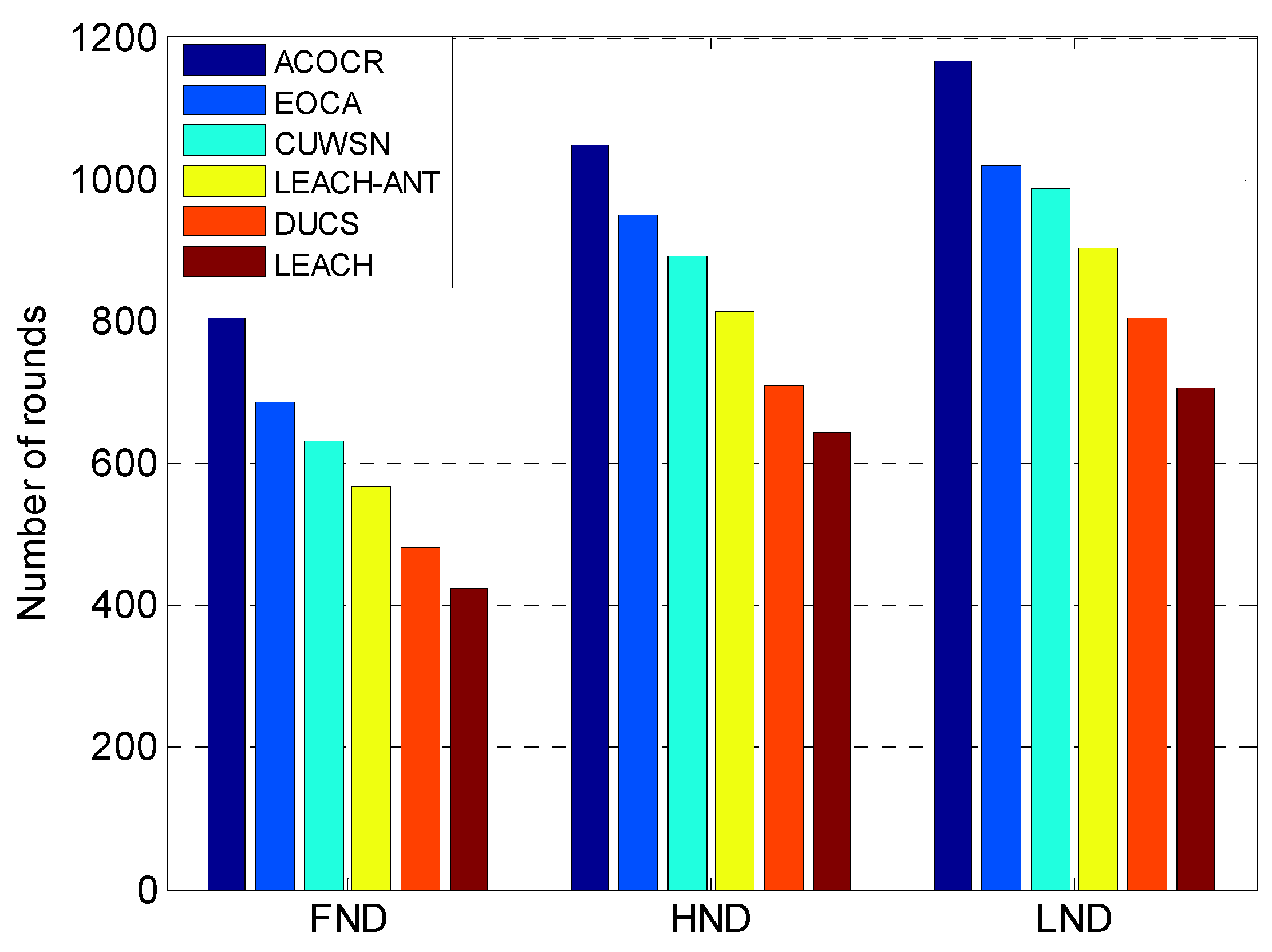
5.1. Comparison and Analysis of the Number of Surviving Nodes
5.2. Comparison and Analysis of the Energy Consumption of the Network
5.3. Comparison and Analysis of the Packet Loss Ratio
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Harb, H.; Makhoul, A.; Couturier, R. An enhanced k-means and ANOVA-based clustering approach for similarity aggregation in underwater wireless sensor networks. IEEE Sens. J. 2015, 15, 5483–5493. [Google Scholar] [CrossRef] [Green Version]
- Jouhari, M.; Ibrahimi, K.; Tembine, H.; Ben-Othman, J. Underwater wireless sensor networks: A survey on enabling technologies, localization protocols, and internet of underwater things. IEEE Access 2019, 7, 96879–96899. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Ekman, T.; Dong, H. Energy detection for MIMO decision fusion in underwater sensor networks. IEEE Sens. J. 2015, 15, 1630–1640. [Google Scholar] [CrossRef]
- Yahya, A.; Islam, S.U.; Zahid, M.; Ahmed, G.; Raza, M.; Pervaiz, H.; Yang, F. Cooperative routing for energy efficient underwater wireless sensor networks. IEEE Access 2019, 7, 141888–141899. [Google Scholar] [CrossRef]
- Bouabdallah, F.; Zidi, C.; Boutaba, R. Joint routing and energy management in underwater acoustic sensor networks. IEEE Trans. Netw. Serv. Manag. 2017, 14, 456–471. [Google Scholar] [CrossRef]
- Zhou, Z.; Peng, Z.; Cui, J.; Jiang, Z. Handling triple hidden terminal problems for multichannel MAC in long-delay underwater sensor networks. IEEE Trans. Mob. Comput. 2012, 11, 139–154. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, H.; Hu, Y.; Kung, S. Cross-layer network lifetime maximization in underwater wireless sensor networks. IEEE Syst. J. 2020, 14, 220–231. [Google Scholar] [CrossRef]
- Wang, K.; Gao, H.; Xu, X.; Jiang, J.; Yue, D. An energy-efficient reliable data transmission scheme for complex environmental monitoring in underwater acoustic sensor networks. IEEE Sens. J. 2016, 16, 4051–4062. [Google Scholar] [CrossRef]
- Wang, Z.; Han, G.; Qin, H.; Zhang, S.; Sui, Y. An energy-aware and void-avoidable routing protocol for underwater sensor networks. IEEE Access 2018, 6, 7792–7801. [Google Scholar] [CrossRef]
- Xing, G.; Chen, Y.; He, L.; Su, W.; Hou, R.; Li, W.; Zhang, C.; Chen, X. Energy consumption in relay underwater acoustic sensor networks for NDN. IEEE Access 2019, 7, 42694–42702. [Google Scholar] [CrossRef]
- Yu, W.; Chen, Y.; Wan, L.; Zhang, X.; Zhu, P.; Xu, X. An energy optimization clustering scheme for multi-hop underwater acoustic cooperative sensor networks. IEEE Access 2020, 8, 89171–89184. [Google Scholar] [CrossRef]
- Ahmed, G.; Zhao, X.; Fareed, M.M.S.; Fareed, M.Z. An energy-efficient redundant transmission control clustering approach for underwater acoustic networks. Sensors 2019, 19, 4241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Fang, S.; Zhang, Y. The Study on Clustering Algorithm of the Underwater Acoustic Sensor Networks. In Proceedings of the 14th International Conference on Mechatronics and Machine Vision in Practice, Xiamen, China, 4–6 December 2007; pp. 78–81. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, M.; Han, G.; Qian, Y.; Shu, L. Cellular clustering-based interference-aware data transmission protocol for underwater acoustic sensor networks. IEEE Trans. Veh. Technol. 2020, 69, 3217–3230. [Google Scholar] [CrossRef]
- Dang, H.; Wu, H. Clustering and cluster-based routing protocol for delay-tolerant mobile networks. IEEE Trans. Wirel. Commun. 2010, 9, 1874–1881. [Google Scholar] [CrossRef]
- Hou, R.; He, L.; Hu, S.; Luo, J. Energy-balanced unequal layering clustering in underwater acoustic sensor networks. IEEE Access 2018, 6, 39685–39691. [Google Scholar] [CrossRef]
- Oudani, H.; Laassiri, J.; Krit, S.; Maimouni, L.E. Comparative Study and Simulation of Flat and Hierarchical Routing Protocols for Wireless Sensor Network. In Proceedings of the 2016 International Conference on Engineering & MIS (ICEMIS), Agadir, Morocco, 22–24 September 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000; pp. 3005–3014. [Google Scholar] [CrossRef]
- Domingo, M.C. A distributed energy-aware routing protocol for underwater wireless sensor networks. Wirel. Pers. Commun. 2011, 57, 607–627. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Yue, Z.; Lv, L. Clustering routing algorithm and simulation of internet of things perception layer based on energy balance. IEEE Access 2019, 7, 145667–145676. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Wang, X.; Zhang, Z. Hybrid multihop partition-based clustering routing protocol for WSNs. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Wan, Z.; Liu, S.; Ni, W.; Xu, Z. An energy-efficient multi-level adaptive clustering routing algorithm for underwater wireless sensor networks. Clust. Comput. 2019, 22, 14651–14660. [Google Scholar] [CrossRef]
- Bhattacharjya, K.; Alam, S.; De, D. CUWSN: Energy efficient routing protocol selection for cluster based underwater wireless sensor network. Microsyst. Technol. 2019. [Google Scholar] [CrossRef]
- Ayaz, M.; Baig, I.; Abdullah, A.; Faye, I. A survey on routing techniques in underwater wireless sensor networks. J. Netw. Comput. Appl. 2011, 34, 1908–1927. [Google Scholar] [CrossRef]
- Wang, P.; Li, C.; Zheng, J. Distributed Minimum-Cost Clustering Protocol for Underwater Sensor Networks (UWSNs). In Proceedings of the IEEE International Conference on Communications (ICC ’07), Glasgow, UK, 24–28 June 2007; pp. 3510–3515. [Google Scholar] [CrossRef]
- Ayaz, M.; Abdullah, A.; Jung, L.T. Temporary Cluster Based Routing for Underwater Wireless Sensor Networks. In Proceedings of the International Symposium in Information Technology-Engineering Technology (ITSim), Lumpur, Malaysia, 15–17 June 2010; pp. 1009–1014. [Google Scholar] [CrossRef]
- Anupama, K.R.; Sasidharan, A.; Vadlamani, S. A Location-Based Clustering Algorithm for Data Gathering in 3D Underwater Wireless Sensor Networks. In Proceedings of the International Symposium on Telecommunications, (IST), Tehran, Iran, 27–28 August 2008; pp. 343–348. [Google Scholar] [CrossRef]
- Seah, W.K.G.; Tan, H.P. Multipath Virtual Sink Architecture for Wireless Sensor Networks in Harsh Environments. In Proceedings of the First International Conference on Integrated Internet Ad hoc and Sensor Networks, Nice, France, 30–31 May 2006. [Google Scholar] [CrossRef]
- Lee, U.; Wang, P.; Noh, Y.; Vieira, L.F.M.; Gerla, M.; Cui, J. Pressure Routing for Underwater Sensor Networks. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, J.; Han, G.; Zhang, X.; Feng, Y. A cluster sleep-wake scheduling algorithm based on 3D topology control in underwater sensor networks. Sensors 2019, 19, 156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rakotomamonjy, A.; Koco, S.; Ralaivola, L. Greedy methods, randomization approaches, and multiarm bandit algorithms for efficient sparsity-constrained optimization. IEEE Trans. Neural Netw. Learn. Syst. 2019, 28, 2789–2802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, J.; Zhao, X.; Zhang, X.; Zhao, D.; Li, H. Task allocation for multi-agent systems based on distributed many-objective evolutionary algorithm and greedy algorithm. IEEE Access 2020, 8, 19306–19318. [Google Scholar] [CrossRef]
- Saito, Y.; Nonomura, T.; Nankai, K.; Yamada, K.; Asai, K.; Sasaki, Y.; Tsubakino, D. Data-driven vector-measurement-sensor selection based on greedy algorithm. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Lee, D.C. Proof of a modified Dijkstra’s algorithm for computing shortest bundle delay in networks with deterministically time-varying links. IEEE Commun. Lett. 2006, 10, 734–736. [Google Scholar] [CrossRef]
- Gnana Swathika, O.V.; Hemamalini, S. Prims-aided Dijkstra algorithm for adaptive protection in microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1279–1286. [Google Scholar] [CrossRef]
- Luo, M.; Hou, X.; Yang, J. Surface optimal path planning using an extended Dijkstra algorithm. IEEE Access 2020, 8, 147827–147838. [Google Scholar] [CrossRef]
- Xia, P.; Xia, Z.; Hongyi, Y.; Chao, Z. Study on Routing Protocol for WSNs Based on the Improved Prim Algorithm. In Proceedings of the 2009 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G.C. Greedy randomized adaptive search procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef] [Green Version]
- Jovanovic, R.; Stefan, V. The fixed set search applied to the power dominating set problem. Expert Syst. 2020. [Google Scholar] [CrossRef]
- Arnaout, J.P. A worm optimization algorithm to minimize the makespan on unrelated parallel machines with sequence-dependent setup times. Ann. Oper. Res. 2020, 285, 273–293. [Google Scholar] [CrossRef] [Green Version]
- Krishnaswamy, V.; Manvi, S.S. Fuzzy and PSO based clustering scheme in underwater acoustic sensor networks using energy and distance parameters. Wirel. Pers. Commun. 2019, 108, 1529–1546. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, X.; Yu, Z. A novel hybrid ant colony optimization for a multicast routing problem. Algorithms 2019, 12, 18. [Google Scholar] [CrossRef] [Green Version]
- Liu, X. Routing protocols based on ant colony optimization in wireless sensor networks: A survey. IEEE Access 2017, 5, 26303–26317. [Google Scholar] [CrossRef]
- Stodola, P. Using metaheuristics on the multi-depot vehicle routing problem with modified optimization criterion. Algorithms 2018, 11, 74. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.; Wang, X.; Huang, M. Ant colony optimization-inspired ICN routing with content concentration and similarity relation. IEEE Commun. Lett. 2017, 21, 1313–1316. [Google Scholar] [CrossRef]
- Li, X.; Keegan, B.; Mtenzi, F.; Weise, T.; Tan, M. Energy-efficient load balancing ant based routing algorithm for wireless sensor networks. IEEE Access 2019, 7, 113182–113196. [Google Scholar] [CrossRef]
- Agarwal, T.; Kumar, D.; Prakash, N.R. Prolonging Network Lifetime Using Ant Colony Optimization Algorithm on Leach Protocol for Wireless Sensor Networks. In Proceedings of the 2nd International Conference on Networks and Communications, Chennai, India, 23–25 July 2010; pp. 634–641. [Google Scholar] [CrossRef]
- Okdem, S.; Karaboga, D. Routing in Wireless Sensor Networks Using Ant Colony Optimization. In Proceedings of the First NASA/ESA Conference on Adaptive Hardware and Systems (AHS’06), Istanbul, Turkey, 15–18 June 2006; pp. 401–404. [Google Scholar] [CrossRef]
- Camilo, T.; Carreto, C.; Silva, J.S.; Boavida, F. An Energy-Efficient Ant-Based Routing Algorithm for Wireless Sensor Networks. In Proceedings of the 5th International Workshop on Ant Colony Optimization and Swarm Intelligence, Brussels, Belgium, 4–7 September 2006; pp. 49–59. [Google Scholar]
- Shan, Y. Study on Submarine Path Planning Based on Modified Ant Colony Optimization Algorithm. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 288–292. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, G.; Zeng, Q.; Song, G.; Li, C.; Duan, H. Routing clustering protocol for 3d wireless sensor networks based on fragile collection ant colony algorithm. IEEE Access 2020, 8, 58874–58888. [Google Scholar] [CrossRef]
- Sun, Y.; Dong, W.; Chen, Y. An improved routing algorithm based on ant colony optimization in wireless sensor networks. IEEE Commun. Lett. 2017, 21, 1317–1320. [Google Scholar] [CrossRef]
- Liu, X. A transmission scheme for wireless sensor networks using ant colony optimization with unconventional characteristics. IEEE Commun. Lett. 2014, 18, 1214–1217. [Google Scholar] [CrossRef]
- Han, G.; Jiang, J.; Shu, L.; Xu, Y.; Wang, F. Localization algorithms of underwater wireless sensor networks: A survey. Sensors 2012, 12, 2026–2061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sozer, E.M.; Stojanovic, M.; Proakis, J.G. Underwater acoustic networks. IEEE J. Ocean. Eng. 2000, 25, 72–83. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Stützle, T.; Hoos, H.H. MAX–MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Jovanovic, R.; Tuba, M. An ant colony optimization algorithm with improved pheromone correction strategy for the minimum weight vertex cover problem. Appl. Soft Comput. J. 2011, 11, 5360–5366. [Google Scholar] [CrossRef]





| Source Node ID | SN ID | Hop Count | Taboo List | Packet Length | Packet Type |
| Algorithms | Packet Loss Ratio |
|---|---|
| ant colony optimization clustering routing (ACOCR) | 12.8% |
| energy optimization clustering algorithm (EOCA) | 14.9% |
| cluster-based underwater wireless sensor network (CUWSN) | 15.8% |
| low-energy adaptive clustering hierarchy based on ant colony (LEACH-ANT) | 17.1% |
| distributed underwater clustering scheme (DUCS) | 18.8% |
| low-energy adaptive clustering hierarchy (LEACH) | 20.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Huang, H. A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks. Algorithms 2020, 13, 250. https://doi.org/10.3390/a13100250
Xiao X, Huang H. A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks. Algorithms. 2020; 13(10):250. https://doi.org/10.3390/a13100250
Chicago/Turabian StyleXiao, Xingxing, and Haining Huang. 2020. "A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks" Algorithms 13, no. 10: 250. https://doi.org/10.3390/a13100250
APA StyleXiao, X., & Huang, H. (2020). A Clustering Routing Algorithm Based on Improved Ant Colony Optimization Algorithms for Underwater Wireless Sensor Networks. Algorithms, 13(10), 250. https://doi.org/10.3390/a13100250





