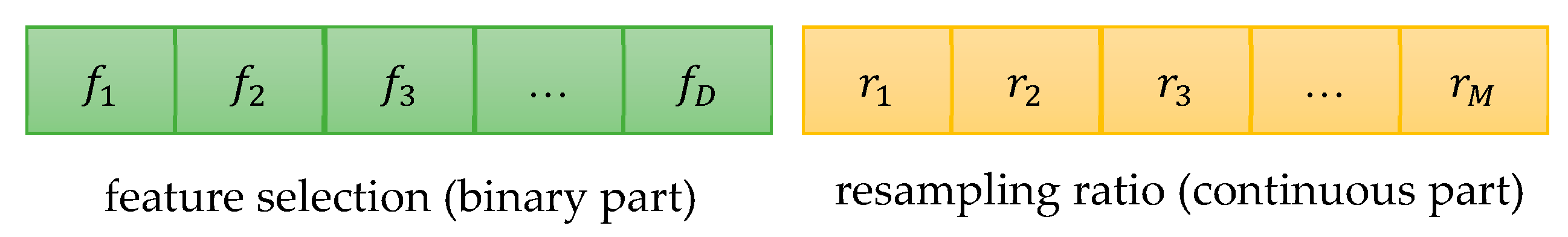A Weighted Ensemble Learning Algorithm Based on Diversity Using a Novel Particle Swarm Optimization Approach

Abstract

In ensemble learning, accuracy and diversity are the main factors affecting its performance. In previous studies, diversity was regarded only as a regularization term, which does not sufficiently indicate that diversity should implicitly be treated as an accuracy factor. In this study, a two-stage weighted ensemble learning method using the particle swarm optimization (PSO) algorithm is proposed to balance the diversity and accuracy in ensemble learning. The first stage is to enhance the diversity of the individual learner, which can be achieved by manipulating the datasets and the input features via a mixed-binary PSO algorithm to search for a set of individual learners with appropriate diversity. The purpose of the second stage is to improve the accuracy of the ensemble classifier using a weighted ensemble method that considers both diversity and accuracy. The set of weighted classifier ensembles is obtained by optimization via the PSO algorithm. The experimental results on 30 UCI datasets demonstrate that the proposed algorithm outperforms other state-of-the-art baselines.

1. Introduction

Ensemble learning combines multiple individual learners to improve the generalization performance of an individual learner [1,2]. It is an important and popular branch of machine learning and is widely used in attack detection [3,4,5], fraud recognition [6,7], image recognition [8,9], biomedicine [10,11], intelligent manufacturing [12,13], time series analysis [14,15] and other fields. Ensemble learning usually involves multiple weak classifiers, such as decision trees [16], support vector machines [17], neural networks [18] and k-nearest neighbors [19], to form a strong classifier, multiple strong classifiers [20] or even a combination of multiple machine learners to complete the learning task. Currently, ensemble learning is regarded as the best way to solve machine learning problems [21].

Classic ensemble learning algorithms include bagging and boosting [22,23]. The basic idea of bagging is that the original dataset is first repeatedly replaced with uniform random sampling to obtain sample subsets; then, different individual learners are trained on these subsets, which are finally integrated by voting. The basic idea of boosting is to select a subset from the sample set as a training set according to a uniform distribution, then run a weak classifier multiple times to give a larger distribution weight to the samples that failed to train, and finally integrate the set by weighting. Bagging and boosting are the most elegant and widely utilized ensemble strategies, Livieris et al. [24] develop two ensemble prediction models that use these strategies for combining the predictions of multiple weight-constrained neural network classifiers. Based on bagging and boosting design philosophy, the current popular ensemble learning algorithms mainly include AdaBoost [25], random forest (RF) [26], gradient boosting decision tree (GBDT) [27], and extremely randomized trees (ERTs) [28].

To obtain good ensemble effects, individual learners should be accurate and diverse [23]. Theoretical and experimental studies have shown that combining a set of accurate and complementary learners can improve the generalization ability of ensemble learning. The diversity between learners is an important factor affecting the generalization performance of ensemble systems. Most existing classical ensemble learning algorithms implicitly use the diversity between learners. To enhance the diversity, Rokach [29] proposes a variety of methods, such as manipulating the inducer, manipulating the training sample, changing the target attribute representation and partitioning the search space. For example, the DECORATE algorithm [30] adds artificial data to the training dataset to train the classifier to increase the diversity of the training data and reduce the classification error.

Although the diversity of learners is necessary for improving the ensemble effect, maximizing diversity does not result in the best generalization performance. The experimental results also show that no strong correlation exists between the accuracy of the learners and diversity. An increase in diversity actually reduces the overall accuracy [31], as its improvement comes with the cost of reducing the accuracy of each individual classifier [32]. Compared with the overall diversity, the accuracy of an individual learner is the main factor of the success of ensemble learning [33]. Liu et al. [34] introduce the diversity factor as a regular term for ensemble learning to avoid overfitting. Therefore, to improve the overall ensemble learning performance, a balance between the diversity and accuracy of the learners must be established. Under the premise of considering accuracy and diversity, Zhang et al. [35] propose a classifier selection method based on a genetic algorithm. They integrated unsupervised clustering with a fuzzy assignment process to make full use of data patterns to improve the ensemble performance. Mao et al. [36] propose a transformation ensemble learning framework in which the combination of multiple base learners is converted into a linear transformation of all these base learners and which constructs an optimization objective function for balancing accuracy and diversity. The alternating direction multiplier method is used to solve this problem. This method effectively improves the performance of ensemble learning.

In previous studies [35,36], when the ensemble learning model was built, although the objective function includes accuracy and diversity factors, the diversity factor is used as a regularization term to avoid overfitting. Nevertheless, the diversity factor considers only the prediction results of the classifier. The diversity does not express the accuracy factor that the diversity should imply, nor does it reflect how to produce an individual learner with moderate diversity. The weighted ensemble strategy is to assign a weight to the individual learner so that it can properly represent the ensemble. It has been demonstrated to be highly efficient in many real-world fields, such as biochemistry [37], medical diagnosis [38] and statistical modeling [39]. In the past two decades, there has been an unprecedented development in the field of computational intelligence. Evolutionary computing and swarm intelligence have proved effective in many applications because of their flexible methods and few assumptions based on objective functions, such as deep learning [40] and multiobjective optimization [41,42,43]. Particle swarm optimization (PSO) is one among many such techniques and has been widely used in continuous/discrete function with complex structures optimization problems [44].

In this paper, a novel weighted ensemble learning algorithm based on diversity (WELAD) is proposed to balance the accuracy and diversity in ensemble learning. The method is divided into two stages: the first stage follows the principle of moderate diversity of individual learners to generate diversified individual learners by manipulating training samples and input features, and the diversity measure adopts the disagreement equation of the pairwise measure. This method includes the accuracy factor of the ensemble classifier and uses this value as the fitness function value of the PSO algorithm [45] to control the iterative search process, after which a set of ensemble classifiers with appropriate accuracy and adequate diversity is obtained. In the second stage, the weighted ensemble of the classifiers is used. In the ensemble process, the optimization objective function considers both the accuracy and diversity simultaneously for ensemble learning. The diversity factor at this stage is used as a regularization term to prevent overfitting. The diversity measurement method at this stage considers only the dissimilarity in the prediction results of the ensemble classifiers. Then, the PSO algorithm is used to optimize the weight values of a set of classifiers, and finally, a weighted ensemble classifier with good generalization performance is obtained. The major distinction between the WELAD design philosophy and previous studies is in the use of ensemble classifiers with appropriate diversity as an important factor when constructing ensemble learning models. Therefore, in the first stage, when the PSO algorithm is used to search for appropriate diversified individual classifiers, the fitness function of the PSO algorithm takes into account the accuracy of the individual learner and deliberately generates the individual learner to improve the performance of the ensemble classifier.

The rest of this paper is organized as follows: Section 2 provides the relevant theoretical background for this study, including introductions to the strategies for combining ensemble classifiers, the diversity measure and the PSO algorithm. In Section 3, we describe the proposed WELAD approach using a two-stage PSO algorithm. We present our experimental results in Section 4 and analyze the proposed method and the current and classic ensemble learning algorithms. Finally, in Section 5, we provide conclusions, summarize this study and suggest future research directions.

2. Related Work

2.1. Notations and definitions

For convenience of description, the following notations and definitions are shown in Table 1.

Table 1. Notations and definitions.

Notations	Description
$h_l$	The lth classifier (L = size of ensemble classifier)
$\mathit{h}$	Ensemble classifier, $\mathit{h}=\left\{h_l\right\},l=1,2,\dots ,L$
$D$	The number of dimensions (features) of dataset
$N$	The number of samples of dataset
$C$	The categories of dataset
$h_i\left(x\right)$	The predicted output of classifier $h_i$ on sample $x$
$\mathit{w}$	The weight vector of an ensemble classifier
$.\ast$	The multiplication operation of the corresponding elements in the same dimension vector
$\oplus$	The XOR operation
$H_1\left(x\right)$	The prediction output of ensemble learning by the majority voting method
$H_2\left(x,\mathit{w}\right)$	The prediction output of ensemble learning by the weighted voting method
$Di{v}_1\left(\mathit{h}\right)$	Diversity measures based on consideration of accuracy
$Di{v}_2\left(\mathit{h},\mathit{w}\right)$	Diversity measures based on avoiding overfitting
$K$	The number of subsets on a dataset using K-fold cross-validation method
$M$	The number of clusters on a dataset using K-means clustering method

2.2. Combining Strategies of Classifiers

Given an ensemble learning system that contains $L$ classifiers and the dataset ${\rm X}=\left\{x_n\right\},n=1,2,\dots ,N,{\rm X}\in {ℝ}^{D\times N}$, that includes $C$ categories $\left\{c_1,c_2,\dots ,c_C\right\}$. For classification problems, if the prediction output of $h_i$ for sample $x$ is represented by a one-hot coding, then the prediction output can be expressed as a $C$-dimensional vector $\left(h_i^1\left(x\right),h_i^2\left(x\right),\dots ,h_i^C\left(x\right)\right)$, where $h_i^j\left(x\right)\in \left\{0,1\right\}$ denotes the output of $h_i$ on the class label $c_j$. If $h_i$ predicts the sample $x$ as the class $c_j$, set $h_i^j\left(x\right)=1$; otherwise, $h_i^j\left(x\right)=0$.

A common classifier combination strategy is the relative majority voting method. The prediction output of ensemble learning $H_1\left(x\right)$ can be obtained as follows:

$$H_1\left(x\right)=c_{\arg \underset{j}{\max }{\displaystyle \sum }_{i=1}^L{h}_i^j\left(x\right)}$$

(1)

Another classifier combination strategy is the weighted voting method. The prediction output of ensemble learning $H_2\left(x,\mathit{w}\right)$ can be obtained as follows:

$$H_2\left(x,\mathit{w}\right)=c_{\arg \underset{j}{\max }{\displaystyle \sum }_{i=1}^L{w}_i{h}_i^j\left(x\right)}$$

(2)

where $\mathit{w}=\left(w_1,w_2,\dots ,w_L\right), {\displaystyle \sum }_{i=1}^L{w}_i=1,w_i\in \left[0,1\right]$.

2.3. Classifier Diversity Metrics

However, many methods exist for measuring the diversity between learners. Kuncheva and Whitaker [46] collected more than 10 different measurement methods from different fields and different perspectives, but none has yet been generally recognized by scholars. According to the needs of optimizing the ensemble learner in two stages, this paper uses the following two different measurement methods.

2.3.1. Individual Learner Diversity Measurement Method

Set the category label $\left\{y_n\right\},n=1,2,\dots ,N$ of the sample ${\rm X}$, the vector ${\mathit{q}}_i$ denotes whether the prediction result of the $i$th classifier on sample ${\rm X}$ is correct. The value of each element can be obtained by Equation (3), and the pairwise diversity metric between classifiers $h_i$ and $h_j$ can be calculated by Equation (4).

$${\mathit{q}}_i\left(x_n\right)=\{\begin{array}{cc}1,& h_i\left(x_n\right)=y_n\\ 0,& h_i\left(x_n\right)\ne y_n\end{array}$$

(3)

$$di{s}_1\left(h_i,h_j\right)=\frac{1}{N}{\mathit{q}}_i.\ast {\left({\mathit{q}}_i\oplus {\mathit{q}}_j\right)}_1, i\ne j$$

(4)

Equation (4) indicates that under the premise of correct classification by one classifier, i.e., the ratio of the sum of the number of misclassified samples to the total number of samples in another classifier, this diversity measurement includes an accuracy factor. For the ensemble classifier with $L$ classifiers, the diversity measure considering accuracy in the first stage of this paper can be calculated by Equation (5) which represents the average of the sum of the diversity values of the paired classifiers.

$$Di{v}_1\left(\mathit{h}\right)=\frac{2}{L\left(L-1\right)}{\displaystyle \sum }_{i=1}^L{\displaystyle \sum }_{j\ne i}di{s}_1\left(h_i,h_j\right)$$

(5)

2.3.2. Weighted Ensemble Process Diversity Measurement Method

Unlike the first stage, in the second stage of the classifier weighted ensemble, the diversity between classifiers is mainly used as a regularization term to prevent overfitting of the ensemble classifier. It does not consider the correctness of the classifiers and considers only the diversity in the prediction results between the classifiers. Similar to Mao et al. [33], the weighted diversity metric between classifiers $h_i$ and $h_j$ can be defined as Equation (6), and the weighted diversity metric of the ensemble classifier can be defined as Equation (7).

$$di{s}_2\left(h_i,h_j\right)=\frac{1}{N}\Vert w_i{\mathit{q}}_i-w_j{\mathit{q}}_j{\Vert }^2, i\ne j$$

(6)

$$Di{v}_2\left(\mathit{h},\mathit{w}\right)={{\displaystyle \sum }}_{i=1}^L{{\displaystyle \sum }}_{j\ne i}di{s}_2\left(h_i,h_j\right)$$

(7)

Following [36], Equation (7) can be transformed into Equation (8):

$$Di{v}_2\left(\mathit{h},\mathit{w}\right)=\frac{1}{N}{\mathit{w}}^T\mathit{D}\mathit{w}$$

(8)

where $\mathit{D}$ denotes the diversity matrix between classifiers $h_i$ and $h_j$ and each element $d_{ij}$ can be obtained by Equation (9):

$$d_{ij}=\{\begin{array}{ll}\Vert {\mathit{q}}_i\oplus {\mathit{q}}_j\Vert {}_1,& \mathrm{if} i\ne j\\ 0,& \mathrm{otherwise}\end{array}$$

(9)

2.4. PSO Algorithm

The PSO algorithm was initially developed by Eberhart and Kennedy [45]. It is inspired by the intelligent behavior of birds in search of food. As a swarm intelligence optimization algorithm, PSO has many advantages, such as stability, a short time convergence, few parameters to adjust and ease of implementation. PSO has been successfully applied to the combination optimization of various engineering problem areas, such as data mining [47], artificial neural network training [48], vehicle path planning [49], medical diagnosis [50,51] and system and engineering design [52].

2.4.1. Basic PSO Solution Process

In the PSO algorithm, each particle is represented as a potential solution, and several particles form a swarm. Let ${ℝ}^D$ denote the D-dimensional problem space. In the tth generation, the position and velocity of the ith particle are expressed as ${\mathit{x}}_i^t=\left(x_{i1},x_{i2},\dots ,x_{iD}\right)\in {ℝ}^D$ and ${\mathit{v}}_i^t=\left(v_{i1},v_{i2},\dots ,v_{iD}\right)\in {ℝ}^D$. Let $\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t$ be the individual best position of this particle and $\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t$ be the swarm best position. In the (t + 1)th generation, the velocity and position of the particle are updated as follows:

$${\mathit{v}}_i^{t+1}\left(j\right)=\omega \ast {\mathit{v}}_i^t\left(j\right)+c_1\ast r_1\ast \left(\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t\left(j\right)-x_{ij}^t\right)+c_2\ast r_2\ast \left(\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t\left(j\right)-x_{ij}^t\right),j=1,2,\dots D$$

(10)

$${\mathit{x}}_i^{t+1}={\mathit{v}}_i^{t+1}+{\mathit{x}}_i^t$$

(11)

where c₁ is the social learning factor, c₂ is the cognition learning factor, c₁ and c₂ determine the magnitude of the random force in the direction of particles with the previous best-visited position and the best particle, $r_1$ and $r_2$ are two independent uniform random numbers between [0,1], and $\omega$ is the inertia weight used to control the balance between exploration and exploitation. A large $\omega$ is useful for jumping out of the local optimal solution and improves the global search ability. In contrast, a small $\omega$ is suitable for algorithm convergence and enhancing the local search ability. Since inertia weight is one of the essential parameters in PSO, in this study, a dynamic inertia weight [53] is used to improve PSO performance through a linearly decreasing mechanism, as shown in Equation (12). This scenario requires emphasizing the particle’s exploration ability in the early period and the particle’s exploitation ability in the later period.

$$\omega ={\omega }_{max}-\frac{t\ast \left({\omega }_{max}-{\omega }_{min}\right)}{T_{max}}$$

(12)

where ${\omega }_{max}$ and ${\omega }_{min}$ are the bounds on the inertia weight, $t$ is the number of iterations, and $T_{max}$ is the maximum number of iterations. Generally, ${\omega }_{max}=0.9$ and ${\omega }_{min}=0.4$ are fixed values.

In addition, a maximum velocity ${\mathit{v}}_{\mathit{m}\mathit{a}\mathit{x}}$ serves as a constraint to control the positions of swarms within the solution search space.

2.4.2. PSO Algorithm for Binary Optimization

The original PSO algorithm is able to optimize only continuous problems and cannot be used directly for optimization in binary spaces. Therefore, an early binary version of PSO (BPSO) was proposed in 1997 [54]. In BPSO, first, the velocity of the particle is converted into a binary probability of 1 by the sigmoid function, as shown in Equation (13).

$$sig\left(v_i^{t+1}\right)=\frac{1}{1+\exp \left(-{\mathit{v}}_i^{t+1}\right)}$$

(13)

Then, the current binary bit state of the particle’s position is changed by determining the random values:

$${\mathit{x}}_i^{t+1}=\{\begin{array}{ll}1,& \mathrm{if} rand()\le sig\left({\mathit{v}}_i^{t+1}\right)\\ 0,& \mathrm{otherwise}\end{array}$$

(14)

where $rand()$ is a function that generates a number in the interval (0, 1) using a uniform distribution. ${\mathit{v}}_{max}$ was set to prevent $sig\left({\mathit{v}}_i^t\right)$ from being too close to 0 or 1.

Although the early version of BPSO was successfully applied to many combinatorial optimization problems, BPSO does have some issues, such as the velocity formula of BPSO being exactly the same as that of PSO, which might not be suitable since, in a binary space [55], the three most important components, i.e., momentum, the cognitive component (defined as pbest) and the social component (defined as gbest), may have different meanings in a binary space. Thus, some new velocity and momentum concepts must be determined.

2.4.3. Mixed PSO Algorithm

In the first stage of this study, in the process of generating a set of individual classifiers with moderate diversity, the characteristics of the dataset are selected as discrete values of {0, 1}. The resampling ratio of the sub-dataset is [0,1] continuous values; hence, this stage involves discrete and continuous mixed space optimization problems. Therefore, we designed a mixed PSO algorithm (MPSO), and the design search space was divided into a continuous domain and a binary domain, which correspond to the continuous and binary components of the design variable vector, respectively [56].

The position code of a particle consists of two parts: continuous and binary, as shown in Figure 1, where $f_d\in \left\{0,1\right\},d=1,2,\dots ,D,r_m\in \left[0,1\right],m=1,2,\dots ,M$.

Figure 1. The particle position code in MPSO.

The MPSO solution process is divided into two steps: a continuous search step and a binary search step. The continuous search step uses the conventional PSO method, and the binary search step is implemented as the primary search strategy and uses a “stickiness” momentum mechanism in BPSO. The term “stickiness” was proposed by Nguyen et al. [55,57]. Since applying the speed concept of PSO directly to BPSO is not appropriate, the main idea of "stickiness" is that a particle moves by flipping its position entry in BPSO. When the bit has just flipped, it should keep its new value for a while and then decrease it in successive iterations.

In the binary search step, a $\mathit{c}\mathit{u}\mathit{r}\mathit{L}\mathit{i}\mathit{f}{\mathit{e}}_j^t\left(j=1,2,\dots ,D\right)$ vector is used to record the number of iterations of the jth bit of the particle binary position since the bit has only recently been flipped. If the bit has just been flipped or initialized, then $\mathit{c}\mathit{u}\mathit{r}\mathit{L}\mathit{i}\mathit{f}{\mathit{e}}_j^t$ should be 1; after a number of iterations, if the bit does not flip, $\mathit{c}\mathit{u}\mathit{r}\mathit{L}\mathit{i}\mathit{f}{\mathit{e}}_j^t$ increases by 1. The stickiness of the jth bit can be calculated as follows:

$$\mathit{S}\mathit{t}{\mathit{k}}_j^t=\frac{\mathit{c}\mathit{u}\mathit{r}\mathit{L}\mathit{i}\mathit{f}{\mathit{e}}_j^t}{\alpha \ast T_{max}}$$

(15)

$$\mathit{S}\mathit{t}\mathit{i}\mathit{c}\mathit{k}\mathit{n}\mathit{e}\mathit{s}{\mathit{s}}_i^t\left(j\right)=\{\begin{array}{ll}1-\mathit{S}\mathit{t}{\mathit{k}}_j^t,& \mathrm{if} \mathit{S}\mathit{t}{\mathit{k}}_j^t\le 1\\ 0,& \mathrm{otherwise}\end{array}$$

(16)

where $\mathsf{\alpha }\in \left(0,1\right)$ in Equation (15) is the scale factor of the number of iterations (in this study, $\mathsf{\alpha }=0.2$). If a bit is not flipped, as the number of iterations increases, the bit’s stickiness property decreases.

For each bit of the particle’s binary position, the flipping probability is as given in Equation (17):

$$\mathit{P}\mathit{r}\mathit{o}{\mathit{b}}_i^{t+1}\left(j\right)={\beta }_m\ast \left(1-\mathit{S}\mathit{t}\mathit{i}\mathit{c}\mathit{k}\mathit{n}\mathit{e}\mathit{s}{\mathit{s}}_i^t\left(j\right)\right)+{\beta }_p\ast \left|\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t\left(j\right)-x_{ij}^t\right|+{\beta }_g\ast \left|\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t\left(j\right)-x_{ij}^t\right|,{\beta }_m+{\beta }_p+{\beta }_g=1,j=1,2,\dots ,D$$

(17)

where ${\beta }_m$, ${\beta }_p$ and ${\beta }_g$ are the proportion factors, which represent the contribution of the momentum and the cognitive and social factors to the flipping probability, respectively. In this study, ${\beta }_m=0.25$, ${\beta }_p=0.25$, and ${\beta }_g=0.5$, which means that the global best particle’s position is more important. Based on Equation (17), the new position of a particle can be calculated by Equation (18).

$${\mathit{x}}_i^{t+1}=\{\begin{array}{cc}\hfill 1-{\mathit{x}}_i^t,& \mathrm{if} rand()\le \mathit{P}\mathit{r}\mathit{o}{\mathit{b}}_i^{t+1}\hfill \\ \hfill {\mathit{x}}_i^t,& \mathrm{otherwise}\hfill \end{array}$$

(18)

3. Materials and Methods

3.1. Architecture of the Proposed Methodology

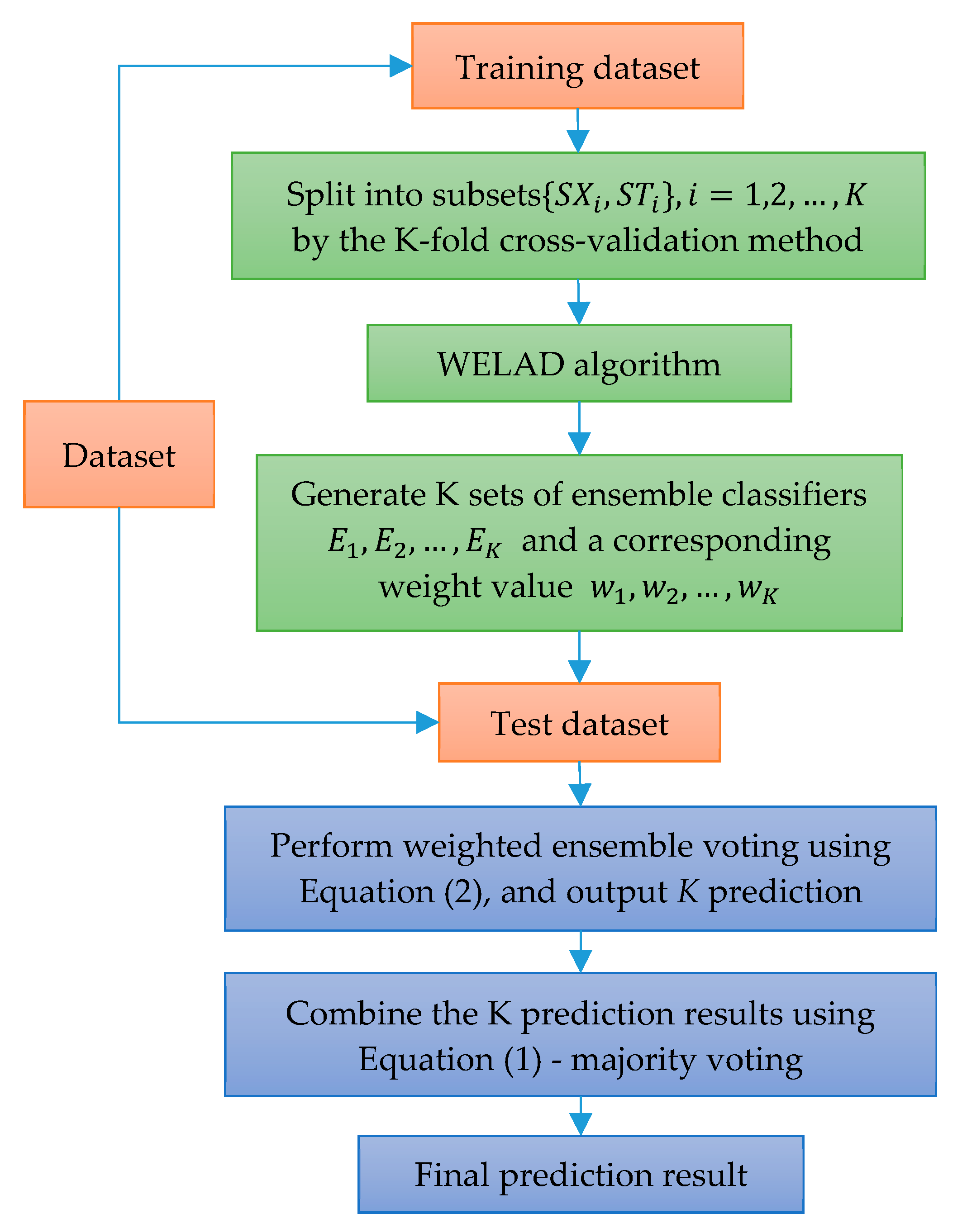
The architecture of this research method is shown in Figure 2. According to the K-fold cross-validation method, the basic idea is to split the training dataset into K subsets, denoted as $\{S{X}_i,S{T}_i\},i=1,2,\dots ,K$, where $S{X}_i$ is used for individual learner diversity training and $S{T}_i$ is used for individual learner weighted ensemble training. With the WELAD (refer to Section 3.2. for the two-stage specific implementation process), K set ensemble classifiers are generated, denoted as ${\mathit{E}}_k=\left\{h_{k1},\dots h_{kl},\dots h_{kL}\right\}, k=1,2,\dots ,K$, and L is the number of ensemble classifiers. Each classifier in each set of ensemble classifiers has a corresponding weight value ${\mathit{w}}_k=\left\{w_{k1},\dots w_{kl},\dots w_{kL}\right\},k=1,2,\dots ,K$. When making predictions on the test dataset, first use the K set of ensemble classifiers to perform weighted ensemble voting, and then output K prediction results. Then, the K prediction results are combined by majority voting to obtain the final prediction result. The idea behind this approach (i.e., K set of ensemble classifiers) is to test the model’s ability to predict new data and avoid overfitting or selection bias and to provide insight. The model will generalize to an independent dataset.

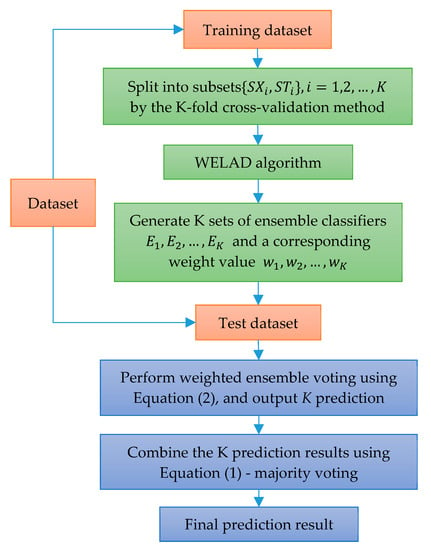
Figure 2. Architecture diagram of the weighted ensemble.

3.2. Description of the WELAD

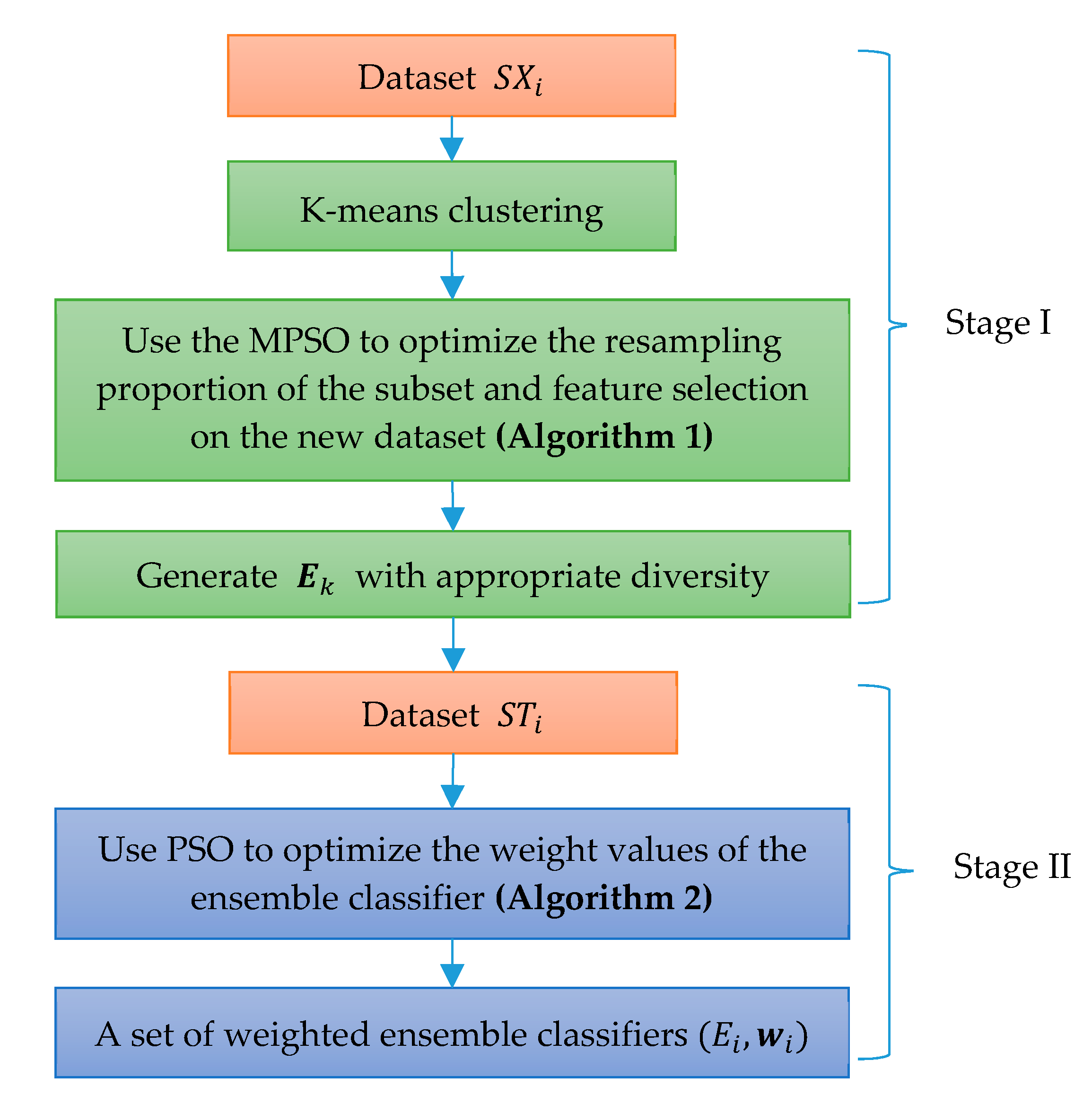
The two-stage implementation of the WELAD is shown in Figure 3. In the first stage, to enhance the diversity of the training set, K-means clustering, resampling and feature selection are performed on the training dataset $S{X}_i$. Using the diversity measurement method, which considers accuracy as the fitness value function of the MPSO algorithm, iterative optimization generates a set of individual learners with appropriate diversity. The second stage involves the weighted ensemble of individual learners. First, a set of individual learners created in the first stage is used to predict the training dataset $S{T}_i$, and then the weight coefficients of the individual learners are optimized by the PSO algorithm. Finally, the weighted ensemble classifier $(E_i,{\mathit{w}}_i)$ is obtained.

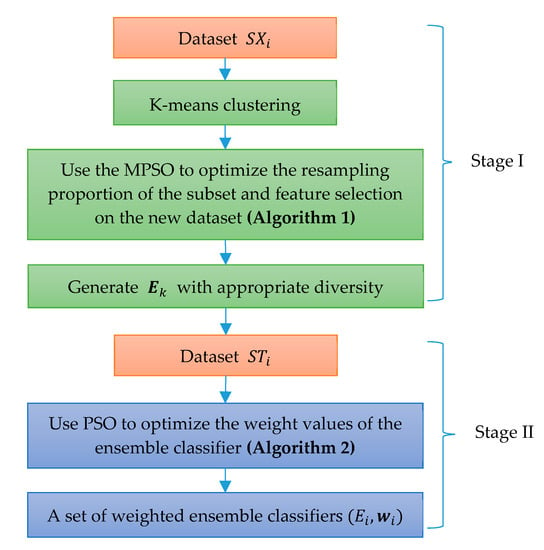
Figure 3. Implementation diagram of the WELAD.

3.2.1. Stage I: Generate the Ensemble Classifier with Appropriate Diversity

The purpose of this stage is to generate a set of ensemble classifiers with appropriate accuracy and adequate diversity by manipulating the training dataset with resampling and select features to create diverse learners. Suppose $D$ features exist in the diversity training dataset; use K-means clustering to form $M$ clusters, and let $\mathit{R}=\left({\mathit{r}}_1,{\mathit{r}}_2,\dots ,{\mathit{r}}_L\right)$ represent the resampling ratio of L classifiers to $M$ sample data clusters matrix, where ${\mathit{r}}_i={\left(r_{i1},r_{i2},\dots ,r_{iM}\right)}^T,i\in \left\{1,2,\dots ,L\right\},{\displaystyle \sum }_{j=1}^M{r}_{ij}=1,r_{ij}\in \left[0,1\right]$. Let $\mathit{F}=\left({\mathit{f}}_1,{\mathit{f}}_2,\dots ,{\mathit{f}}_L\right)$ represent a classifier’s feature selection matrix for the sample, where ${\mathit{f}}_i={\left(f_{i1},f_{i2},\dots ,f_{iD}\right)}^T,i\in \left\{1,2,\dots ,L\right\},{\displaystyle \sum }_{j=1}^D{f}_{ij}>0,f_{ij}\in \left\{0,1\right\}$. For a set of ensemble classifiers with resampling ratios and feature selection parameters, MPSO is used to solve the following problems:

$$\begin{array}{c}max Di{v}_1\left(\mathit{h}\right)\\ s.t. {\displaystyle \sum }_{i=1}^M{r}_{Li}=1,r_{Li}\in \left[0,1\right]\\ {\displaystyle \sum }_{i=1}^F{f}_{Li}>0,f_{Li}\in \left\{0,1\right\}\end{array}$$

(19)

Implement resampling and feature selection on the clustered subsets so that the training samples of each classifier are different. Use MPSO to optimize the sample resampling ratio and feature selection parameters of each classifier (i.e., individual learner). After training, a set of ensemble classifiers $E_i$ with appropriate diversity are obtained. Let $T_{max}$ represent the maximum number of iterations, $SS$ represent the population size of the swarm, and $\{B_1,B_2,\dots ,B_M\}$ represent the subset after clustering; the pseudocode of Algorithm 1 is as follows.

Algorithm1. Using MPSO to optimize the resampling ratio of subset and carry out feature selection

Input:   $M,S{X}_i,\{B_1,B_2,\dots ,B_M\},T_{max},SS,L$ Process: // Initialize a population of particles, ${\mathit{x}}_j^0\left(j=1,2,\dots ,SS\right)$ for $j=1$ to $SS$ do   for l = 1 to L do     Initialize ${\mathit{f}}_l,{\mathit{f}}_l\leftarrow rand\left\{0,1\right\},{\displaystyle \sum }_{j=1}^F{f}_{lj}>0$; // At least one feature is selected     Initialize ${\mathit{r}}_l,{\mathit{r}}_l\leftarrow rand\left(0,1\right),{\mathit{r}}_l\leftarrow {\mathit{r}}_l/{\displaystyle \sum }_{j=1}^M{r}_{lj}$;     Resample $\{B_1,B_2,\dots ,B_M\}$ according to ${\mathit{r}}_l$, and then execute feature selection to generate a new dataset $N{S}_l$;     Use $N{S}_l$ to train the learner $h_l$;     Use learner $h_l$ to conduct the classification prediction on $S{X}_i$, and obtain the category label;   End  ${\mathit{x}}_j^0\leftarrow \left(\mathit{f},\mathit{r}\right)$   Initialize $\mathit{S}\mathit{t}{\mathit{k}}^0$ and calculate $\mathit{S}\mathit{t}\mathit{i}\mathit{c}\mathit{k}\mathit{n}\mathit{e}\mathit{s}{\mathit{s}}_j^0$; end Calculate the diversity measure $Di{v}_1\left(\mathit{h}\right)$ according to Equation (5); Evaluate the fitness of particles, and set $\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^0$ and $\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^0$; for $t=1$ to $T_{max}$ do   for $j=1$ to $SN$ do     Calculate the flipping probability using Equation (17);     Update the binary part of ${\mathit{x}}_j^t$ using Equation (18);     Update the continuous part of ${\mathit{x}}_j^t$ using PSO;     According to ${\mathit{x}}_j^t$, train and evaluate the learners;   end   Calculate the diversity measure $Di{v}_1\left(\mathit{h}\right)$ according to Equation (5);   Evaluate the fitness of particles, and set $\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t$ and $\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t;$ end Output:$\mathit{F},\mathit{R}$

3.2.2. Stage II: Generate the Weighted Ensemble Classifier

The purpose of this stage is to determine the weight values of a set of ensemble classifiers. Given a training dataset used for the weighted ensemble, which has G samples, under the effect of weight $\mathit{w}$, the prediction result of the weighted ensemble classifier for $x_i$ is expressed by Equation (20), and the training error is expressed by Equation (21).

$$\mathit{w}\mathit{q}\left(x_i\right)=\{\begin{array}{c}1, H_2\left(x_i,\mathit{w}\right)=y_i\\ 0, H_2\left(x_i,\mathit{w}\right)\ne y_i\end{array}$$

(20)

$$trainErr\left(\mathit{h},\mathit{w}\right)=\frac{1}{G}{\displaystyle \sum }_{i=1}^G\mathit{w}\mathit{q}\left(x_i\right)$$

(21)

At this stage, the PSO algorithm is used to solve the following problems:

$$\begin{array}{c}min trainErr\left(\mathit{h},\mathit{w}\right)-\lambda Di{v}_2\left(\mathit{h},\mathit{w}\right)\\ s.t. {\displaystyle \sum }_{i=1}^L{w}_i=1,w_i\in \left[0,1\right]\end{array}$$

(22)

where $Di{v}_2\left(\mathit{h},\mathit{w}\right)$ is a regularization term, which is used to prevent overfitting. $\lambda \in \left(0, 1\right)$ is a regularization coefficient, which is used to balance the accuracy and diversity of the ensemble learning.

Algorithm 2 is implemented to assign different weights to the obtained set of classifiers with appropriate diversity. Let the prediction results of the L classifiers in the weighted ensemble training dataset be $\{{\mathit{q}}_1,{\mathit{q}}_2,\dots ,{\mathit{q}}_L\}$; their pseudocodes are as follows.

Algorithm2. Using PSO to optimize the weight parameters of the classifier w

Input:   $\{{\mathit{q}}_1,{\mathit{q}}_2,\dots ,{\mathit{q}}_L\},T_{max},SS,L$ Process: for $j=1$ to $SS$ do   Initialize $\mathit{w},\mathit{w}\leftarrow rand\left(0,1\right),\mathit{w}\leftarrow \mathit{w}/{\displaystyle \sum }_{i=1}^L{w}_i;$   ${\mathit{x}}_j^0\leftarrow \mathit{w};$ end Calculate the diversity measure $Di{v}_2\left(\mathit{h},\mathit{w}\right)$ according to Equation (7); Calculate $trainErr\left(\mathit{h},\mathit{w}\right)$ according to Equation (21); Evaluate the fitness of particles $trainErr\left(\mathit{h},\mathit{w}\right)-\lambda Di{v}_2\left(\mathit{h},\mathit{w}\right)$; Set $\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^0$ and $\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^0$; for $t=1$ to $T_{max}$ do   Update ${\mathit{x}}_j^t$ using Equation (11);   Calculate the diversity measure $Di{v}_2\left(\mathit{h},\mathit{w}\right)$ and $trainErr\left(\mathit{h},\mathit{w}\right)$;   Evaluate the fitness of particles, and set $\mathit{p}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t$ and $\mathit{g}\mathit{b}\mathit{e}\mathit{s}{\mathit{t}}^t$; end Output:$\mathit{w}$

4. Results and Discussion

4.1. Experimental Dataset and Setup

4.1.1. Experimental Dataset

The experiment used 30 UCI public datasets (http://archive.ics.uci.edu/ml/datasets.php) as test datasets to verify the performance of the algorithm. The information regarding the samples, attributes, and categories of each dataset is shown in Table 2.

Table 2. Information on the UCI datasets used in the experiment.

Dataset ID	Dataset Name	Samples	Features	Classes	Computational Complexity
1	abalone	4177	8	5	3.57 × 1010
2	australian	690	14	2	1.09 × 1011
3	balance-scale	625	4	3	2.50 × 107
4	breast_cancer-wis	699	9	2	2.25 × 109
5	breast_cancer	286	9	2	3.77 × 108
6	cervical_cancer	858	32	2	1.01 × 1017
7	cleveland	303	13	5	9.78 × 109
8	crowdsourced-mapping	10,545	28	6	8.36 × 1017
9	dermatology	366	34	6	7.82 × 1016
10	diabetes	768	8	2	1.21 × 109
11	drug_consumption	1885	12	7	1.75 × 1011
12	firm-teacher	10,796	16	4	1.22 × 1014
13	flags	194	29	8	5.86 × 1014
14	frogs_mfccs	7195	22	10	4.78 × 1015
15	haberman	306	3	2	2.25 × 106
16	heart-disease-h	294	13	2	9.21 × 109
17	heart-stalog	270	13	2	7.76 × 109
18	hepatitis	155	19	2	2.39 × 1011
19	indian-liver	583	10	2	3.48 × 109
20	ionosphere	351	34	2	7.20 × 1016
21	lymph	148	18	4	1.03 × 1011
22	mammographic	961	5	2	1.48 × 108
23	primary-tumor	339	17	2	2.56 × 1011
24	segment	2310	19	7	5.32 × 1013
25	seismic-bumps	2584	18	2	3.15 × 1013
26	sonar	208	60	2	2.99 × 1024
27	transfusion	748	4	2	3.58 × 107
28	vehicle	846	18	4	3.38 × 1012
29	waveform	5000	40	3	1.10 × 1021
30	wholesale	440	7	3	1.73 × 108

The computational complexity of the WELAD algorithm is composed of two factors: the decision tree algorithm and the feature selection required to generate the base classifier with diversity. The computational complexity of the decision tree algorithm is $O\left(N^{2}F\right)$. The computational complexity of the feature selection required to generate the base classifier with diversity is $O\left(2^F\right)$, where $F$ is the number of features in the dataset. Hence, the overall computational complexity of the WELAD algorithm for each dataset is $O\left(N^{2}F{2}^F\right)$.

4.1.2. Experimental Setup

In this study, WELAD is defined as the experimental group, and the AdaBoost, Bagging, DECORATE, ERT, GBDT, and RF algorithms are listed as the control group. The performance of the WELAD is verified through experiments. The WELAD is implemented via the Python language, due to the decision tree classifier in the machine learning toolkit scikit-learn (https://scikit-learn.org/stable/) uses classification and regression trees (CART) as default classification algorithm, all algorithms exception the DECORATE in the control group, the base classifier also use CART. Since scikit-learn does not integrate the DECORATE algorithm, we use the WEKA machine learning toolkit (https://www.cs.waikato.ac.nz/ml/weka/) instead, and its base learner uses J48 decision tree.

The parameter values in the two stages of the WELAD are determined by the grid search method, the bounds of $\lambda$ ranges from 0.1 to 0.9 step 0.1, $M\in \left\{3,5,7\right\}$, $SS\in \left\{20,30,50\right\}$, and the final choice is $M=3,\lambda =0.4,SS=30,T_{max}=50$. The number L of base classifier trees of the experimental group and the control group is uniformly set to 30. For the selection of the training dataset splitting parameter K, according to the idea of majority voting ensemble, a larger K value will improve accuracy, but for a dataset with a small number of samples, a larger K value will result in too few samples for training, leading to increase individual errors. In preliminary experiments, we tried to use $K\in \left\{5,7,9\right\}$ and finally chose K = 7.

4.2. Experiment

4.2.1. Experimental Results

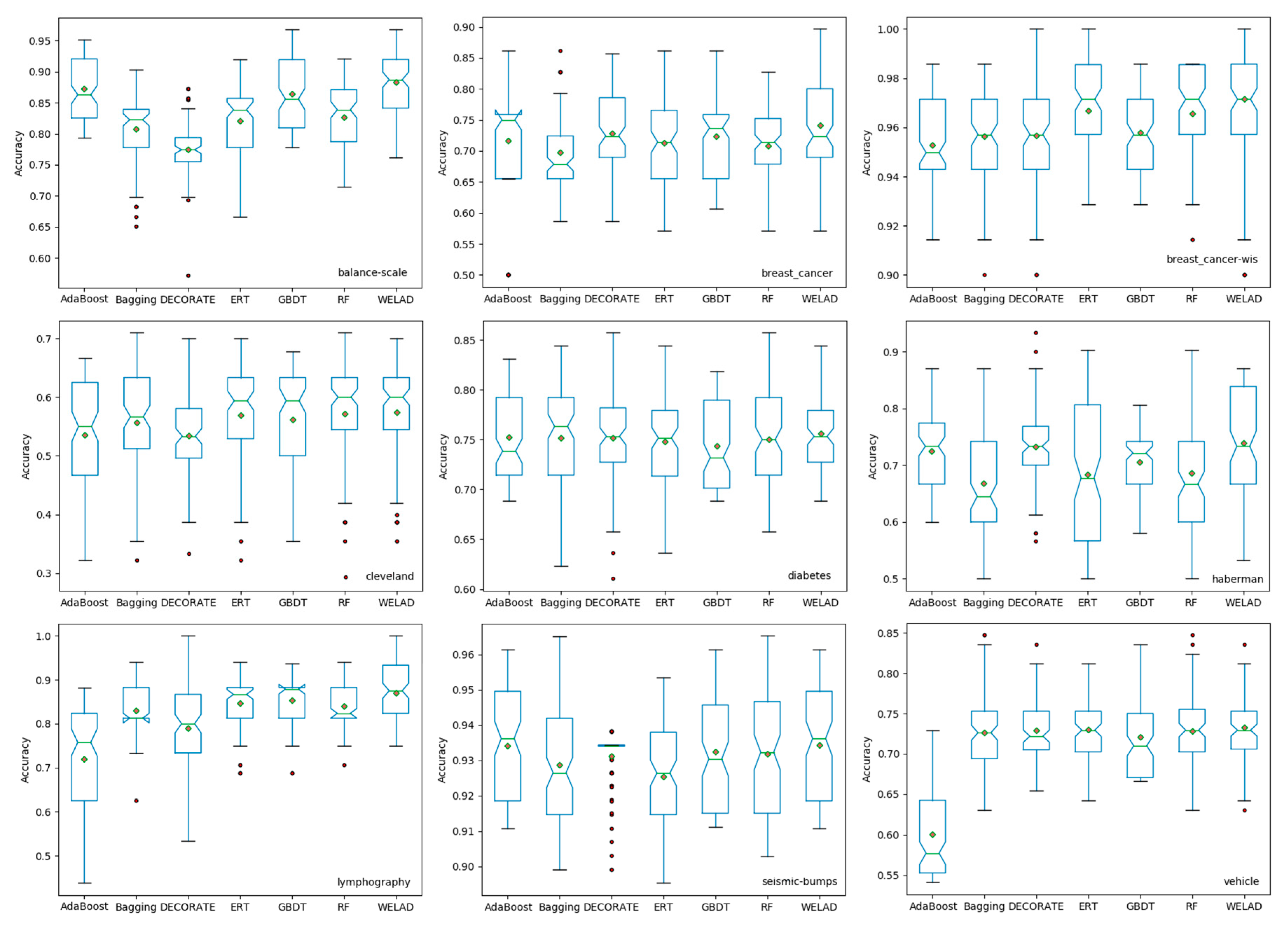
The experiment uses the accuracy as the performance index. To better check the generalization ability of each algorithm and avoid overfitting of the training caused by the cutting of the dataset, which affects the experimental results, the accuracy of each algorithm in the dataset is tested by 10-fold cross-validation repeated ten times (i.e., 10×10 cross-validations), and then the average is taken. The accuracy results of the seven algorithms on the 30 sets UCI datasets are shown in Table 3, and the box plots of the nine selected datasets are shown in Figure 4.

Table 3. Comparison of accuracy on 30 datasets.

Dataset ID	AdaBoost	Bagging	DECORATE	ERT	GBDT	RF	WELAD
1	0.6481	0.6760	0.6831	0.6864	0.6934	0.6906	0.6836
2	0.8681	0.8654	0.8459	0.8603	0.8603	0.8704	0.8674
3	0.8722	0.8080	0.7747	0.8213	0.8642	0.8268	0.8830
4	0.9528	0.9564	0.9568	0.9667	0.9578	0.9655	0.9717
5	0.7165	0.6973	0.7287	0.7128	0.7235	0.7088	0.7412
6	0.9138	0.8925	0.9008	0.9082	0.9068	0.9054	0.9118
7	0.5356	0.5565	0.5347	0.5690	0.5615	0.5714	0.5739
8	0.8337	0.9368	0.9372	0.9503	0.9206	0.9432	0.9398
9	0.5642	0.9708	0.9777	0.9761	0.9702	0.9723	0.9766
10	0.7526	0.7517	0.7517	0.7482	0.7434	0.7499	0.7561
11	0.6757	0.6783	0.6390	0.6859	0.6968	0.6882	0.6938
12	0.7360	0.8044	0.7656	0.8024	0.7808	0.8074	0.7771
13	0.5067	0.6188	0.6248	0.6551	0.6635	0.6522	0.6507
14	0.7792	0.9695	0.9735	0.9832	0.9672	0.9808	0.9788
15	0.7249	0.6676	0.7325	0.6842	0.7055	0.6862	0.7389
16	0.8332	0.7941	0.7879	0.8271	0.8093	0.8177	0.8322
17	0.8000	0.8078	0.8033	0.8048	0.8111	0.8204	0.8163
18	0.6750	0.6489	0.6396	0.6495	0.6192	0.6614	0.6690
19	0.6911	0.6984	0.6836	0.7266	0.7004	0.7062	0.7158
20	0.9230	0.9198	0.9257	0.9410	0.9288	0.9313	0.9344
21	0.7200	0.8303	0.7904	0.8469	0.8531	0.8400	0.8697
22	0.8273	0.7911	0.8246	0.7863	0.8343	0.7951	0.8269
23	0.7609	0.7300	0.7334	0.7368	0.7786	0.7318	0.7624
24	0.7320	0.9762	0.9797	0.9795	0.9749	0.9800	0.9743
25	0.9342	0.9287	0.9312	0.9253	0.9326	0.9319	0.9341
26	0.8362	0.7967	0.8115	0.8482	0.8117	0.8164	0.8225
27	0.7795	0.7410	0.7831	0.7421	0.782	0.7447	0.7784
28	0.6005	0.7264	0.7292	0.7302	0.7206	0.7282	0.7326
29	0.8128	0.8134	0.7796	0.8336	0.8424	0.8288	0.8394
30	0.7182	0.6864	0.6973	0.6873	0.6966	0.6998	0.7168
Mean	0.7575	0.7913	0.7909	0.8025	0.8037	0.8018	0.8123
Standard deviation	0.1134	0.1137	0.1148	0.1128	0.1099	0.1112	0.1084
Best/Worst	4/11	0/8	2/7	5/2	6/2	4/0	9/0

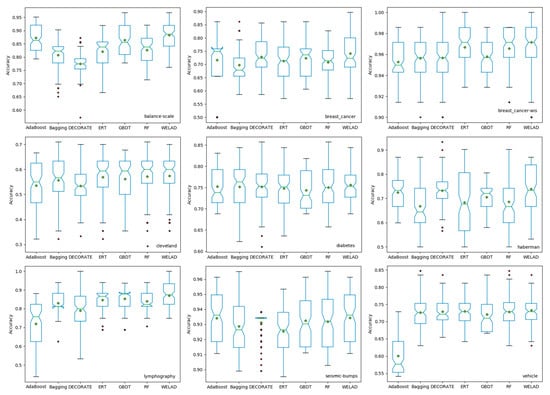
Figure 4. Boxplots of the performances of the compared algorithms on 9 selected datasets.

The bold values in Table 3 indicate the best performance of a line. The WELAD achieved the highest mean accuracy of 0.8123 on the 30 datasets, being superior to the six algorithms of the control group on nine of the sets. The standard deviation of the mean value of the WELAD is also the lowest, showing that the algorithm has good stability. Clearly, ERT, GBDT and RF all achieve good and similar performances. The experimental results also reflect the instability of AdaBoost. However, it reached the highest accuracy on 4 of the 30 datasets. It had the lowest accuracy on 11 datasets, resulting in its mean accuracy being the worst among all algorithms. The box plots of the nine datasets also reflect the advantages of the WELAD.

4.2.2. Statistical Test

To further verify the overall performance of the WELAD, this study conducts a statistical analysis in which we follow the procedure proposed in Demsar [58] and use nonparametric statistical tests for multiple comparisons by combining all the datasets. First, we apply the Friedman test to rank the performances of the seven ensemble learning methods and evaluate whether these ensemble learning methods show statistically significant differences on the 30 datasets. Table 4 shows the Friedman rank comparison table, according to which the ensemble learning algorithms, ranked from best to worst, are WELAD (5.70), RF (4.60), ERT (4.38), GBDT (4.22), AdaBoost (3.47), DECORATE (3.15), and Bagging (2.48). The WELAD method is the best, as expected. RF, ERT, and GBDT are recently developed, well-known approaches that achieve the second-best results. The traditional ensemble learning methods AdaBoost, Bagging, and DECORATE with diverse factors perform relatively poorly.

Table 4. Ranks of the Friedman test.

Dataset ID	AdaBoost	Bagging	DECORATE	ERT	GBDT	RF	WELAD
1	1	2	3	5	7	6	4
2	6	4	1	2	2	7	5
3	6	2	1	3	5	4	7
4	1	2	3	6	4	5	7
5	4	1	6	3	5	2	7
6	7	1	2	5	4	3	6
7	2	3	1	5	4	6	7
8	1	3	4	7	2	6	5
9	1	3	7	5	2	4	6
10	6	4	4	2	1	3	7
11	2	3	1	4	7	5	6
12	1	6	2	5	4	7	3
13	1	2	3	6	7	5	4
14	1	3	4	7	2	6	5
15	5	1	6	2	4	3	7
16	7	2	1	5	3	4	6
17	1	4	2	3	5	7	6
18	7	3	2	4	1	5	6
19	2	3	1	7	4	5	6
20	2	1	3	7	4	5	6
21	1	3	2	5	6	4	7
22	6	2	4	1	7	3	5
23	5	1	3	4	7	2	6
24	1	4	6	5	3	7	2
25	6	2	3	1	5	4	7
26	6	1	2	7	3	4	5
27	5	1	7	2	6	3	4
28	1	3	5	6	2	4	7
29	2	3	1	5	7	4	6
30	7	1	4	2	3	5	6
Mean Rank	3.47	2.48	3.15	4.38	4.22	4.60	5.70

Table 5 reflects the results of the Friedman test and shows whether an overall statistically significant difference exists between the mean ranks of related groups. Based on the Friedman test results in Table 5, a p-value from 0.000 to 0.05 indicates that the differences between the seven ensemble learning algorithms in this study are statistically significant. Then, we apply the nonparametric Wilcoxon signed-rank test to analyze the differences between paired ensemble learning algorithms.

Table 5. Statistics of the Friedman test.

Number (N)	Chi-Square	Degrees of Freedom (df)	Asymp. Sig. (p-Value)
30	43.452	6	0.000

Table 5 shows whether statistically significant differences exist between the WELAD using the Wilcoxon signed-rank test and other ensemble learning methods. As shown in Table 6, the WELAD and the comparison group algorithms are statistically significantly different.

Table 6. Wilcoxon signed-rank test.

	WELAD- AdaBoost	WELAD- Bagging	WELAD- DECORATE	WELAD- ERT	WELAD- GBDT	WELAD- RF
Z	−3.733	−4.350	−4.371	−2.376	−3.304	−3.219
Significance (two-tailed)	0.000	0.000	0.000	0.018	0.002	0.001

In summary, the experimental results on these 30 sets of data show that the WELAD ensemble method proposed in this study has the highest accuracy and the best overall performance.

5. Conclusions

To obtain a good ensemble performance, each individual learner that composes an ensemble classifier is required to have high accuracy and appropriate diversity. To balance the diversity and accuracy in the existing research on ensemble learning, the problem of how to generate individual learners with diversity cannot be fully reflected. In this study, a two-stage weighted ensemble learning method is proposed. When creating individual classifiers and classifiers for integration, the diversity and accuracy are considered at the same time, the corresponding adaptive function of the PSO algorithm is constructed, and the PSO algorithm is used to optimize the target model.

The proposed ensemble learning method is evaluated on 30 UCI datasets, and the experimental results show that the proposed method achieves the highest mean accuracy and the lowest standard deviation of the mean value, which means that the proposed method has better classification performance and stability. In subsequent work, other evolutionary optimization algorithms (i.e., differential evolution [59]) or different swarm intelligence optimization algorithms (i.e., cuckoo search [60] and artificial bee colony [61]) can be used to compare whether their classification performances are different. Another ensemble model called stacking will be used [62]. The method can also be applied to related fields, such as high-tech industry or quality medical services management.