Segment-Based Clustering of Hyperspectral Images Using Tree-Based Data Partitioning Structures

Abstract

Hyperspectral image classification has been increasingly used in the field of remote sensing. In this study, a new clustering framework for large-scale hyperspectral image (HSI) classification is proposed. The proposed four-step classification scheme explores how to effectively use the global spectral information and local spatial structure of hyperspectral data for HSI classification. Initially, multidimensional Watershed is used for pre-segmentation. Region-based hierarchical hyperspectral image segmentation is based on the construction of Binary partition trees (BPT). Each segmented region is modeled while using first-order parametric modelling, which is then followed by a region merging stage using HSI regional spectral properties in order to obtain a BPT representation. The tree is then pruned to obtain a more compact representation. In addition, principal component analysis (PCA) is utilized for HSI feature extraction, so that the extracted features are further incorporated into the BPT. Finally, an efficient variant of k-means clustering algorithm, called filtering algorithm, is deployed on the created BPT structure, producing the final cluster map. The proposed method is tested over eight publicly available hyperspectral scenes with ground truth data and it is further compared with other clustering frameworks. The extensive experimental analysis demonstrates the efficacy of the proposed method.

1. Introduction

Hyperspectral images (HSIs) contain rich spectral information from a large number of densely-spaced contiguous frequency bands. The HSI data that are collected by aircrafts and satellites provide significant information about the spectral characteristics of surfaces and materials of the Earth and they can be used for applications, such as environmental sciences, agriculture, and urban planning [1,2,3]. In the recent years, a growing number of advanced HSI remote sensing classification techniques have reported a high accuracy and efficiency on the state-of-the-art public data sets. HSI classification that is based on supervised methods provides excellent performance on standard data sets, e.g., more than 95% of the overall accuracy [4]. However, the existing supervised methods face challenges in dealing with large-scale hyperspectral image data sets due to their high computational complexity [5] and the “curse of dimensionality”, which results from a large number of spectral dimensions and the scarcity of labelled training examples [6].

Clustering-based techniques do not require prior knowledge and they are commonly used for HSI unsupervised classification, but still face challenges due to high spectral resolution and the presence of complex spatial structures [7]. The optimal selection of spectral bands is one of the major tasks for the HSI classification and feature extraction (FE) is often used as a pre-processing step for HSI classification methods to address the high spectral resolution problem [8]. FE techniques for HSI analysis can be either supervised, such as embedded feature selection with support vector machines (EFS-SVM) [9], linear discriminant analysis (LDA) [10], or unsupervised, including principal component analysis (PCA) [11], mainfold learning [12], and maximum noise factoring (MNF) [13]. There are a number of recent research studies that address the effect of different feature extraction techniques on HSI analysis [14,15,16]. Similar to unsupervised classification, unsupervised feature extraction methods are used in the absence of labeled training data. FE methods, such as PCA and MNF, are widely used unsupervised approaches for dimensionality reduction in HSI images [13]. PCA searches for maximum variance in the data, whereas MNF sorts the components based on the maximum estimated signal-to-noise ratio (SNR) [14]. In [11], PCA transform is applied to the original HSI cube prior to k-means clustering method. In another study, the improved classification accuracy of a spectral angle mapper (SAM) classifier is reported when applying MNF for pre-processing [17]. In addition to linear features, non-linearity is also present in HSI images, due to the nonlinear nature of multipath scattering in the atmosphere [18]. Isometric mapping (ISOMAP) [12], which is an unsupervised manifold learning approach that is based on nonlinear transformation, is applied to improve HSI classification of 1-nearest neighbor classifier. The study presents competitive results in PCA and ISOMAP comparison. A solution for the removal of the noisy or redundant bands as a part of HSI clustering is proposed in [19], where a local band selection approach identifies the effective subset of bands (relevant subspace) that are based on relevancy and redundancy among the spectral bands. The relevancy score of a band to a cluster is obtained using the average Euclidean distance between each cluster member and the cluster centroid along each dimension. Redundancy among the bands is defined by the use of the inter-band distances [19].

Image segmentation is used to incorporate spatial information into the classifiers assigning each image pixel to one class in order to tackle the complex spatial structures in hyperspectral images. Image segmentation, in general, is a process in which an image is partitioned into multiple regions, where pixels within a region have the same label and share the same features [20]. The regions form a segmentation map that can be used as spatial structures for a spectral-spatial classification technique [21]. In recent years, different segment-based clustering HSI classification frameworks [7,19,22] have been proposed. The general idea is to initially obtain a segmentation map, followed by applying clustering on the segments refined in the region merging process rather than directly on the HSI pixels. In [23], an HSI segmentation map is obtained using two partition clustering algorithms, namely projected clustering and correlation clustering. Projected clustering algorithms focus on the identification of subspace clusters, where each pixel is assigned to exactly one subspace cluster [24]. Similarly, correlation clustering forms clusters of pixels that are positively or negatively correlated based on a subset of relevant attributes in a high dimensional space [25]. The resulted cluster map is converted to a segmented map by making use of a connected component labelling (CCL) procedure. This procedure assigns different labels to pixels, which are in the same cluster, but disjoint regions. In a separate stage, pixel-level classification while using support vector machines (SVM) is performed on the input HSI. The segmentation map is combined with the pixel-level classification results by using majority voting, such that, for each segment of the segmentation map, the majority class is found in the pixel-level classification map and all of the pixels within that segment are assigned to that majority class. A similar approach is proposed in [19], where k-means clustering is applied to the hyperspectral image in order to obtain an initial cluster map, which is then converted to a segmented map while using CCL. The segmented map is further refined by using a region merging method in which similar regions in the map are merged by using their shape and spectral properties according to a merging criterion. In the next stage, a projected clustering is performed over segments instead of pixels. Further, the clustering makes use of the local band selection approach for identifying a relevant subset of bands for each cluster. An approach that incorporates local band selection [7] starts by converting the k-means obtained cluster map from the first stage into a segmentation map while using CCL. This map is then converted to cluster map by considering each segment as a cluster. For performing clustering, a different two-step projected clustering is used. In the first step, clusters are merged, depending on their mutual nearest neighbour (MNN) information calculated using the spectral space. The next step identifies the k significant clusters while using an entropy-based criterion and produces the final cluster map by assigning all the remaining clusters to k significant clusters. These techniques commonly use a three-step scheme in order (i) HSI segmentation, (ii) region merging, and finally (iii) projected clustering for the HSI classification problem. It has been observed that segmentation using the k-means algorithm is the initial stage for the aforementioned frameworks. To the best of the authors’ knowledge, no study has been conducted on other segmentation methods for HSI segment-based clustering. Hierarchical segmentation algorithms have proven to be valuable in exploiting the spatial content of HSI images by providing a hierarchy of segmentation stages at different scales [26]. HSI segmentation using the binary partition trees (BPT) proposed in [27] models the HSI data into regions that can be merged to form a binary tree representing the most dissimilar regions.

The proposed framework is a four-stage scheme. The Watershed segmentation technique [28] is used in a pre-segmentation stage for obtaining initial over-segmented segments/regions. In this manner, creating large under-segmented regions is avoided, which can affect the performance and cause inaccurate region merging in the segmentation stage. The segmentation stage that is based on BPT representation [27] models each region by using a first-order parametric model [29]. The modeled regions are then merged in order to construct the BPT that is based on their spectral similarity by using the spectral angle mapper (SAM) [26]. In the subsequent stage, a number of the most dissimilar regions in BPT are selected, forming a meangingful HSI segmentation map. This produces a partitioning with the most distinguishable regions on the map. In a separate stage, PCA is applied to the original set of HSI pixels for feature extraction. As aforementioned, both hierarchical segmentation and dimensionality reduction methods have proven to be advantageous for extracting spatial and spectral information, respectively. In that sense, the contextual information from the segmentation stage and the extracted spectral features from PCA are combined as input of a tree-based partitioning k-means clustering method in order to improve the classification accuracy. The clustering is based on a pruning algorithm—the filtering algorithm [30]. This heuristic method optimizes the time complexity of the standard k-means algorithm from O($n^2$) to O(n) [31]. The idea is to turn the center update of the standard k-means into a tree traversal, which allows for pruning data point-center pairs at an early stage in the clustering process, so as to reduce the number of computations required. In addition to the computation efficiency of the filtering algorithm, the tree-based clustering method is compatible with the tree data structure of the BPT representation. This allows for efficient flow of data throughout the framework.

The rest of this paper is organized, as follows. Section 2 introduces the concepts and describes the implementation of the proposed framework. Section 3 presents the experimental setup and results, including performance analyses, computational complexity, and parameter determination. Section 4 concludes this paper.

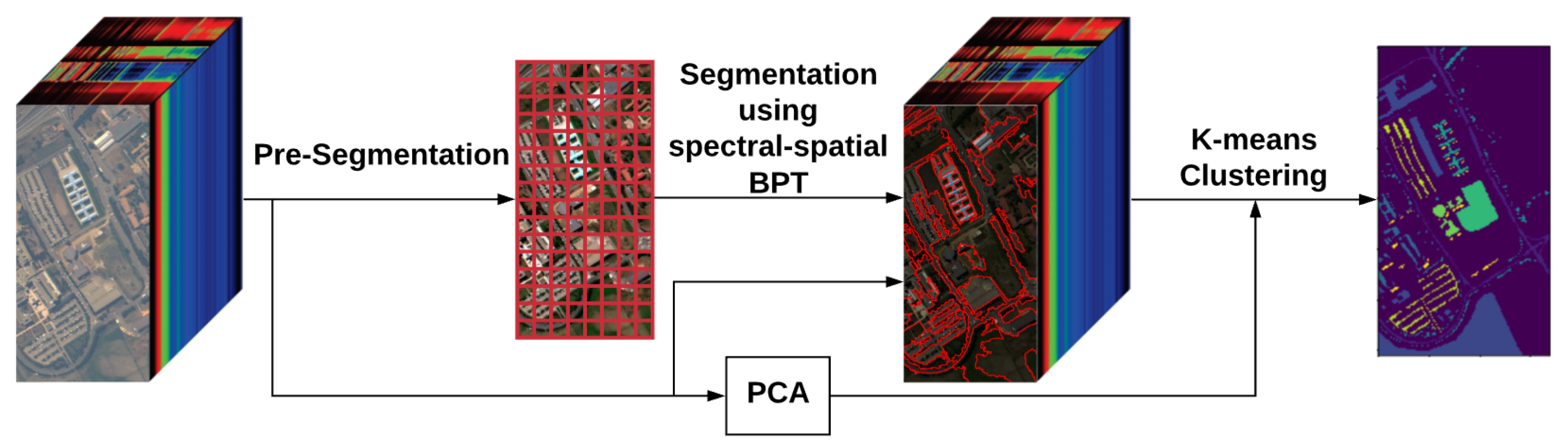
2. Methodology

The proposed Clustering using BPT (CLUS-BPT) framework integrates segmentation, region modelling, PCA, and clustering, as depicted in Figure 1. It starts by obtaining an over-segmented image partition of the input HSI cube prior to forming the segmentation map (spatial discrimination). This initial partition is then used for BPT construction that consists of region modelling and region merging. In the next step, principal component analysis (PCA) is applied to the input HSI cube and the result is combined with the final segmentation map that is produced by BPT. Finally, the filtering algorithm for k-means clustering is applied to the refined segments in order to obtain the cluster map.

2.1. Pre-Segmentation

In the first stage, the CLUS-BPT framework applies the adapted Watershed segmentation algorithm [21] on HSI cube to obtain a segmented map. First, the algorithm assumes an N-band hyperspectral image as a set of N one-band images. The gradients of every spectral band separately results in N gradient images. The images are further combined into one-band gradient image using the supremum operator. A classical Watershed is used onto this map, resulting in each pixel (watershed pixel) containing the label of the region it belongs to. Finally, each pixel is assigned to the neighboring region with the closest median. As an output of this stage, an initial 2D-oversegmented map is obtained. The purpose of this initial spatial partition, rather than using the initial set of pixels, is to reduce the computational time for BPT building [26]. In addition, the Watershed algorithm is used in order to avoid the creation of an under-segmented map in which further region splitting can be challenging. Instead, a produced over-segmented map contains regions that are small and accurate enough to be reconstructed with high accuracy in the BPT building process [26].

2.2. BPT Building

The creation of BPT consists of two stages: region modelling and region merging. The region model $M_{R_i}$ defines how regions are represented and how to model the union of two regions. The CLUS-BPT framework uses the first-order parametric model for region modelling due to its simplicity in definition leading to straightforward merging order process [27]. Given a hyperspectral region R formed by $N_{R_p}$ spectra containing $N_n$ different radiance values, the first-order parametric model $M_R$ is defined as a vector of $N_n$ components, which corresponds to the average of the values of all spectra $p\in R$ in each band ${\lambda }_i$, as follows:

$$M_R\left({\lambda }_i\right)=\frac{1}{N_{R_p}}\sum _{j=1}^{N_{R_p}}{H}_{{\lambda }_i}\left(p_j\right)i\in [1,\cdots ,N_n]$$

(1)

where $H_{{\lambda }_i}\left(p_j\right)$ represents the radiance value in the wavelength ${\lambda }_i$ of the pixel with spatial coordinates $p_j$.

The second stage of BPT construction is the merging criterion $O(M_{R_i},M_{R_j})$, which defines the similarity of neighboring regions as a distance measure between the region models $M_{R_i}$ and $M_{R_j}$ and it determines the order in which regions are to be merged. In [27], different region models with their compatible region merging criterion for BPT construction are described. A merging criterion that is defined as the spectral angle distance $d_{SAD}$ between the average values of any two adjacent regions is defined as:

$$O(M_{R_a},M_{R_b})=d_{SAD}=arccos\left(\frac{R_a^T{R}_b}{\left|\left|R_a\right|\right|\left|\left|R_b\right|\right|}\right).$$

(2)

Given the initial partition of small regions, the distances between each region and its neighbouring regions are computed and sorted. The smallest distance between the current region and neighboring regions indicates the candidate region for merging. Figure 2 depicts the BPT building process, where the leaf nodes correspond to the initial partition of the image. From this initial partition, an iterative bottom-up region merging algorithm is applied by keeping track of the merging steps until only one region remains. The last region that corresponds to the whole image is the root of the tree.

Before the merging stage, small regions in the initial partition may result in a spatially unbalanced tree during BPT construction. Those regions are prioritized to be merged first by determining whether their size is smaller than a given percentage (typically 15%) of the average region size of the initial partition [27].

2.3. BPT Pruning

As a result of the BPT construction phase, a BPT representation of the hyperspectral image that incorporates its spatial and spectral features is obtained. The next step is to process the BPT, such that a partition featuring the $P_R$ most dissimilar regions created during the BPT construction is obtained by extracting a given number of regions $P_R$, hence pruning the tree. There exists several BPT pruning strategies suited for a number of applications such as classification, segmentation, and object detection [32,33,34]. The region-based BPT pruning is chosen in the proposed work. It provides the last $P_R$ regions remaining before the completion of the BPT by traversing the tree in an inverse order to its construction and stopping when the desired number of regions $P_R\ge 0$ is reached. It shows whether the BPT construction is reasonable and balanced, since the last $P_R$ regions are the most dissimilar regions. A well-refined segmentation map of the hyperspectral image is obtained as a result of this stage, as depicted in Figure 1.

2.4. K-Means Clustering

Hyperspectral images have high spectral resolution; hence, a high redundancy is present in the data from the neighboring bands. Consequently, neighboring bands of the image are highly correlated. In addition, the large amount of data present increases the processing complexity and time. In order to effectively remove the correlation among the bands and reduce the size of HSI data, principal component analysis (PCA) is utilized as a pre-processing technique, such that the optimum linear combination of the original bands is produced. The extracted features are then embedded with the segmentation map of the BPT stage before k-means clustering is applied. The embedding approach that is used by CLUS-BPT assigns a set of PCA-reduced pixel values for each region from the segmentation map. For instance, the data structure of a region represented by pruned tree node number 5 ($P_R\left(5\right)$) that is shown in Figure 3 contains the following objects:

• region label: a unique region number,
• bounding box: a rectangular box formed by i and j pixel coordinates of the segmentation map with the size of the box equal to the number of pixels included in the region and
• PCA data values: a vector containing the PCA-reduced values with the pixel coordinates corresponding to the coordinates of the bounding box.

Region label and bounding box data objects are set for each node during BPT construction. In contrast, PCA data values are assigned to the node during the embedding process based on their positions that correspond to the bounding box coordinates of the region on the segmentation map. The segmentation map is a set of boundaries between data points of the values that were obtained by PCA, as depicted in Figure 4. The tree containing the segmentation map embedded with the PCA data values is fed to the clustering stage, which gives labels to the formed regions.

CLUS-BPT performs an efficient k-means clustering algorithm that is specifically designed for a multidimensional binary space partition tree, called kd-tree [30]. The goal of k-means clustering is to find the minimum argument for each cluster group and calculate the distances of each point in a cluster to the centroid of that cluster. The complexity of the algorithm increases linearly with the number of centers, data points, dimensions in a data set, and iterations number. A straightforward implementation of k-means standard algorithm in high-dimensional HSI data sets can be quite slow, due to the cost of computing nearest neighbors [25,30]. The filtering algorithm that is introduced in [30] is applicable for the BPT data structure used throughout the stages of CLUS-BPT. The main idea of the filtering algorithm is to prune (filter) down the search space for the optimal cluster partition, such that the computation burden is reduced. At the initial iteration of clustering, the regions of the segmentation map act as a base for the algorithm to start from. During clustering, these regions are either differentiated or joined by assigning them cluster labels as the tree is traversed.

Algorithm 1 shows a pseudo code for one iteration of the filtering algorithm. Each node $P_R\left(i\right)$ of the BPT tree represents a region and it is associated with the bounding box (C) information from which the number of pixels ($count$) is deduced. A new data vector representing the sum of the associated pixels (the weighted centroid, $wgt\_Cent$) is added to the tree and it is used for updating the cluster centers after each iteration. The actual centroid is computed as $wgt\_Cent/count$. In addition, a set of possible candidate centers U is kept for each node and is propagated down the tree [30]. The set is defined to be a set of center points that can be the nearest neighbor for some pixel within the bounding box of a tree node. It follows that the candidate centers for the root node consist of all k centers. For a tree node $P_R\left(i\right)$, the closest candidate center $u^{*}\in U$ to the midpoint of the bounding box is found during clustering. The closest centre search involves the computation of the Euclidean distances. The remaining $u\in U\setminus \left\{u^{*}\right\}$ is pruned to the following node down the tree if no part of C is closer to u than the closest center $u^{*}$, since it is not the nearest center to the pixels within C. If $P_R\left(i\right)$ is an internal node, its left and right children nodes are examined. The center update occurs if a leaf is reached or only one candidate remains.

Algorithm 1 The filtering algorithm introduced in [30].

function Filter (RootTree $P_R$, CandidateSet U) { U←$P_R.U$ if ($P_R$ is a leaf) {     $u^{*}\leftarrow$ the closest point in U to $P_R.data\_values$     $u^{*}.wgtCent\leftarrow u^{*}.wgtCent+P_R.data\_values$     $u*.count\leftarrow u^{*}.count+1$} else{     $u^{*}\leftarrow$ the closest point in U to C’s midpoint     for all ($u\in U\setminus \left\{u^{*}\right\}$) do       if u.isFarther($u^{*},C)$ then $U\leftarrow U\setminus \left\{u\right\}$     end for     if ($\left|U\right|=1$) {       $u^{*}.wgtCent\leftarrow u^{*}.wgtCent+P_R.wgtCent$       $u*.count\leftarrow u^{*}.count+P_R.count$ }     else{       Filter($P_R.left$, U)       Filter($P_R.right$, U) }   } }

The $isFarther$ function in Algorithm 1 checks whether any point of a bounding box C is closer to u than to $u^{*}$. The function returns true if the sum of squares difference between the candidate u and closest candidate $u^{*}$ is greater than 2× the sum of squares difference between either boundary points (high or low) and the closest candidate center $u^{*}$. On termination of the filtering algorithm, center u is moved to the centroid of its associated points, which is, $u\leftarrow u.wgtCent/u.count$, resulting in the final cluster map.

3. Results and Comparisons

The framework that is shown in Figure 1 has been implemented in MATLAB. The proposed framework performance is evaluated and verified on a number of available standard HSI data sets [35,36] with ground truth:

• Salinas scene—collected by the 224-band AVIRIS (Airborne Visible/Infrared Imaging Spectrometer) sensor over Salinas Valley, California, and it is characterized by high spatial resolution (3.7-m pixels) and resolution 512 lines by 217 samples in the wavelength range 0.4–2.5 μm. Salinas ground truth contains 16 classes.
• Salinas-A is a subscene of Salinas image and it comprises $86\times 83$ pixels that are located within the same scene as Salinas at [samples, lines] = [591–676, 158–240]. It includes vegetables, bare soils, and vineyard fields, and its ground truth contains six classes.
• PaviaC is acquired by the ROSIS (Reflective Optics System Imaging Spectrometer) sensor over the city center of Pavia (referred as PaviaC), central Italy. The data set contains 115 spectral bands covering the wavelength ranging from 0.43 to 0.86 μm, but only 102 effective bands were used for experiments after removing low-SNR and water absorption bands [37]. The original image dimension, $1096\times 715$ with the spatial resolution of 1.3 m, is used in this experiment. The data set consists of nine land cover classes.
• PaviaU is also acquired by the ROSIS senser over University of Pavia. The image is of a size of $610\times 340$ and it has a spatial resolution of 1.3 m. Similar to PaviaC, a total of 115 spectral bands were collected of which 12 spectral bands are removed due to noise and the remaining 103 bands are used for classification [37]. The ground reference image available with the data has nine land cover classes.
• Indian Pines scene was gathered by AVIRIS sensor over the Indian Pines test site in North-western Indiana and consists of $145\times 145$ pixels and 224 spectral reflectance bands in the wavelength range 0.4–2.5 ×${10}^{-6}$ m. The scene contains two-thirds agriculture, and one-third forest or other natural perennial vegetation. There are two major dual lane highways, a rail line, low density housing, other built structures, and smaller roads. The ground truth available is divided into 16 classes.
• Samson scene is an image with $95\times 95$ pixels and 156 spectral channels covering the wavelengths from 401 nm to 889 nm. The spectral resolution is 3.13 nm. There are three target end-members in the data set, including “Rock”, “Tree”, and “Water”.
• Jasper Ridge is one of the most widely used hyperspectral image data sets, with each image of size $100\times 100$ pixels. Each pixel contains at 198 effective channels with the wavelengths ranging from 380 to 2500 nm. The spectral resolution is up to 9.46 nm. There are four end-members latent in this data set, including “Road”, “Dirt”, “Water”, and “Tree”.
• Urban scene consists of images of $307\times 307$ pixels with spatial resolution of 10 m and 210 channels with wavelengths ranging from 400 nm to 2500 nm. There are three versions of the ground truth, which contain four, five, and six end-members, respectively. In this experiment, four end-members are used, including “Asphalt”, “Grass”, “Tree”, and “Roof”.

3.1. Evaluation Metrics

The clustering results of the proposed framework are evaluated by Purity, Normalized Mutual Information (NMI), and overall accuracy (OA) scores. Let C be the set of classes that were obtained from ground reference information and $\omega$ be the set of clusters obtained from a clustering method/framework.

• Purity is an external evaluation criterion of cluster quality. It is the most common metric for clustering results evaluation, defined as:

  $$Purity(\omega ,C)=\frac{1}{n}\sum _i\underset{j}{max}|{\omega }_i\cap C_j|,$$

  (3)

  where n denotes the number of data points in the image. The range of purity metric is $(0,1)$, where 0 and 1 represent the lowest and highest cluster quality.
• NMI is a normalization of the mutual information score (MI), where $MI$ is obtained as:

  $$MI(\omega ,C)=\sum _i\sum _{j}p({\omega }_i\cap C_j){log}_2\frac{p({\omega }_i\cap C_j)}{p\left({\omega }_i\right).p\left(C_j\right)}.$$

  (4)

  $P\left({\omega }_k\right)$, $P\left(C_j\right)$, and $P({\omega }_k\cap C_j)$ are the probabilities of a data point being in cluster ${\omega }_k$, class $C_j$, and in the intersection of ${\omega }_k$ and $C_j$, respectively. The NMI score is defined, as follows:

  $$NMI(\omega ,C)=\frac{MI(\omega ,C)}{max\left[H\right(\omega ),H(C\left)\right]},$$

  (5)

  where $H\left(\omega \right)=-{\sum }_{i}p\left({\omega }_i\right){log}_{2}p\left({\omega }_i\right)$ and $H\left(C\right)=-{\sum }_{j}p\left(C_j\right){log}_{2}p\left(C_j\right)$ are the entropies of $\omega$ and C, respectively. The larger NMI value indicates higher clustering accuracy.
• OA is the number of correctly classified pixels in $\omega$ divided by the total number of pixels.

3.2. Parameter Settings

CLUS-BPT requires the number of pruned regions $N_{P_R}$ and number of clusters k as input user-defined parameters. Experiments are performed by varying both $N_{P_R}$ and k. Initially, NMI values are obtained for the proposed method by setting k equal to the number of classes in an image while varying $N_{P_R}$ from k to $5\times k$ regions, in steps of k for all HSI images except PaviaC, PaviaU, and Urban. In the case of PaviaC and PaviaU, due to the large image spatial size when compared to the other data sets, $N_{P_R}$ is varied from 150 to 400, in steps of 50 regions. Once the optimal values of $N_{P_R}$ for each data set are determined, the experiments are also performed by varying the values of k and fixing $N_{P_R}$ to the values, for which the NMI score is the highest.

The identification of parameter k for a data set is a non-trivial task and, in this study, for all of the hyperspectral images, the accuracy is measured by varying the value of k in steps of 2.

Table 1. Number of clusters for each Hhyperspectral image (HSI) data set and experiment parameter setting.

Data Set	Number of Clusters (k)	Varying k (Steps of 2)
Salinas	16	16 to 26
PaviaU	9	9 to 19
Indian Pines	16	16 to 26
Salinas-A	6	6 to 16
Samson	3	3 to 13
Urban	4	4 to 14
Jasper Ridge	4	4 to 14
PaviaC	9	9 to 19

presents the ranges of k values for each data set. Throughout the experiments, the number of chosen PCA components is set to 1, forming a 2D data structure. It has been verified that the first principal component explains at least 80% of the total variance for any of the 8 HSI data sets.

The experiments are performed under the same environment: Intel(R) Core(TM) i7-5930K CPU, 3.50 GHz, 64 GB memory, Windows 10 OS, and Matlab version R2019a.

3.3. Effect of the Number of Regions

Initially, the influence of the number of regions on the NMI values that were obtained for the proposed method is investigated. Figure 5 illustrates the variation of NMI with respect to the different number of regions ($N_{P_R}$) of the segmentation map. The values of NMI represent the average of 10 runs for each setting. In Figure 5, it can be observed that the images have different values of $N_{P_R}$ at which the NMI is the highest. Salinas-A has the highest value of NMI at the number of regions in the segmentation map equal to the number of clusters ($N_{P_R}=k=6$). A downward trend is observed for PaviaC, Salinas-A, and Indian Pines images as the number of regions increases. For PaviaU, it can be observed in Figure 5a that the quality of clustering increases as the number of segments increases across the segmentation map, whereas for Jasper Ridge and Urban images, at $k=4$, the NMI values tend to converge to a certain value. Once the optimal value of $N_{P_R}$ is set for each image, the NMI values are obtained for a varying number of clusters.

3.4. Effect of Number of Clusters

The comparison with two recent unsupervised clustering methods, segment-based projected clustering using mutual nearest neighbor (PCMNN) [7] and fast spectral clustering (FSC) [6], is performed in order to assess the effectiveness of the CLUS-BPT method. Both of the methods are specifically developed for hyperspectral image classification. PCMNN is a three-stage framework involving segmentation, region merging, and projected clustering. FSC is a spectral clustering method for unsupervised HSI classification with experiments on eight different HSI data sets. Classical spectral clustering is not capable of dealing with large-scale HSI classification. Hence, FSC performs efficient affinity matrix approximation and the effective resolution of eigenvalue decomposition of Laplacian matrix.

Figure 6 and Figure 7 show the NMI scores as a function of increasing k for the data sets. The proposed method scores the highest NMI when k is the original number of clusters for five out of eight images, as shown in Figure 6. However, for PaviaC, the peak NMI value of 0.5806 is achieved for $k=17$. In the case of Salinas and Indian Pines images, CLUS-BPT scores the peak NMI values at $k=26$ and $k=20$ respectively.

Table 2. Evaluation of clustering performance for HSI data sets.

Data Set	Framework
	PCMNN [7]			FSC [6]			CLUS-BPT
	NMI	$\mathbf{OA}(\%)$	k	Purity	NMI	k	Purity	NMI	$\mathbf{OA}(\%)$	k	${\mathit{N}}_{{\mathit{P}}_{\mathit{R}}}$
Salinas	0.8586	82.06	24	0.62	0.72	16	0.7638	0.8882	89.37	26	48
PaviaU	0.5654	57.98	13	0.61	0.57	16	0.6996	0.5806	82.44	17	400
Indian Pines	-	-	-	0.46	0.49	16	0.5758	0.6025	57.75	20	32
Salinas-A	-	-	-	0.85	0.81	6	0.8753	0.8572	91.22	6	6
Samson	-	-	-	0.91	0.75	3	0.6896	0.6698	87.93	3	6
Urban	-	-	-	0.51	0.33	4	0.90	0.3906	79.96	4	128
Jasper Ridge	-	-	-	0.91	0.76	4	0.7652	0.5658	76.73	4	32
PaviaC	-	-	-	-	-	-	0.8412	0.8369	83.97	9	150

reports clustering evaluation scores for all of the compared methods on different hyperspectral image data sets. For the proposed method, the shown NMI, purity, and OA scores correspond to k values, which have achieved the highest NMI value. For PCMNN, NMI, and OA scores are reported on Salinas and PaviaU scenes, whereas purity and NMI scores are available on all data sets except PaviaC for FSC. Overall, CLUS-BPT results in the highest values for almost all accuracy indicators. The ground truth, class color codes, and the classification results of the CLUS-BPT method are presented for comparison in Figure 8 and Figure 9. For Indian Pines and Salinas-A, Table 2 shows that CLUS-BPT results in higher NMI and purity values when compared to the FSC method. CLUS-BPT scores the highest NMI value at $k=20$ and $k=6$ for Indian Pines and Salinas-A, respectively. Figure 8a,b show that CLUS-BPT has misclassified corn-type classes as soybeans or hay-windrowed for Indian Pines. On the other hand, it can be observed that the proposed method is able to detect the Salinas-A scene classes with minor error in Figure 8c,d. The proposed method achieves the highest NMI of $0.8882$ at $k=26$ for Salinas scene, outperforming the other compared techniques. The Salinas cluster map that is shown in Figure 9b reveals that the proposed method identifies all of the 16 classes of Salinas image, except “grapes untrained”, which is assigned to vineyard untrained class, scoring an overall accuracy of 89.37%. In the case of PaviaU, Table 2 shows that CLUS-BPT scores the highest NMI value of $0.5806$ for $k=17$, whereas FSC method scores the lowest, $0.5654$ for $k=13$. In addition, a marked difference in the successful identification of classes is observed between the proposed method ($OA$ = 82.44%) and PCMNN ($OA$ = 57.98%). Figure 9c,d illustrate that some difficulty was faced by CLUS-BPT in identifying the shadows and self-blocking bricks classes of PaviaU.

The FSC method results in a lesser number of miss-classification errors for Samson and Jasper Ridge. However, CLUS-BPT scores 90% purity for Urban image, which means that each cluster $C_i$ in CLUS-BPT result identifies a group of pixels as the same class as the ground truth label. This can be seen in Figure 8g,h, where the only miss-classified class out of the total four is the roof. Cluster label coloring is different for PaviaC ground truth and result, as can be observed in Figure 9e,f, while the accuracy is high, as indicated by the metrics in Table 2. This is because clustering algorithms do not necessarily learn the specific label number; hence, class label numbers of ground truth and cluster results may not match, but may point to the same object on an image.

3.5. Computational Time

Figure 10 lists the computational time on Salinas, PaviaU, Salinas-A, and Indian Pines data sets for the proposed CLUS-BPT method in the presented experimental setup. The computational time is computed as a function of an increasing number of regions $N_{P_R}$ from 50 to 1000, in steps of 50. The number of clusters k matching the highest NMI value is fixed, as indicated in Table 2 for Salinas, PaviaU, Salinas-A, and Indian Pines, respectively.

In Figure 10, it can be observed that the computational time increases along with the increase of the number of regions for Salinas and PaviaU images, while the computational time increases at a lower rate for the same number of regions is observed for Indian Pines and Salinas-A images. This difference is due to having images with high spatial dimensions, such as $512\times 217$ and $610\times 610$ for Salinas and PaviaU, respectively. On the other hand, Salinas-A has spatial image dimensions that are about $7\times$ smaller than Salinas and PaviaU. In addition, Figure 10 shows a near-linear execution time for the Salinas image. It can be concluded that large spatial dimension images lead to a large number of regions being processed and, thus, to the increased computational time. A significant improvement in terms of computational time can be achieved by performing the PCA stage in parallel, since there are no data dependencies between the PCA stage and segmentation stage.

Table 3. Computational time for projected clustering using mutual nearest neighbor (PCMNN), fast spectral clustering (FSC), and clustering using BPT (CLUS-BPT) obtained for the best purity and NMI results for hyperspectral image data sets.

	Framework	PCMNN CT(s) [7]	FSC CT(s) [6]	CLUS-BPT CT(s)
Data Set
Salinas		134.63	1.62	7.48
PaviaU		-	1.34	58.2
Indian Pines		-	0.53	2.72
Salinas-A		-	0.06	1.56
Samson		-	0.10	1.52
Urban		-	0.41	2.15
Jasper Ridge		-	0.11	2.78
PaviaC		-	-	18.26

shows the average times for producing cluster maps in the presented experiments on eight publicly available data sets that are reported in [6]. The displayed values are the average of ten runs. These values are obtained by setting the parameters, as indicated in Table 2. As it can be observed, the CLUS-BPT framework takes more time than FSC to output the best results in almost all of the data sets. PaviaU image experiment achieves the largest timing difference, while the difference in the clustering accuracy between CLUS-BPT and FSC is not substantial. On the other hand, the clustering accuracy difference is significant for Salinas image and, hence, the large timing difference can be justified. The execution time difference between CLUS-BPT and FSC is smaller for the other data sets, including Indian Pines, Salinas-A, Samson, and Jasper. In addition, Table 3 shows that the execution time for PCMNN is higher than FSC and CLUS-BPT for Salinas image.

4. Conclusions

In this paper, we have developed a multistage clustering framework, termed CLUS-BPT, for unsupervised HSI classification. The proposed clustering framework contains the Watershed algorithm as a pre-processing stage, segmentation and feature extractions stages, and final clustering stage. In the first stage, an initial over-segmentation map of the image is obtained. The regions of the obtained segmentation map are then modeled while using first-order parameteric modelling. According to their spatial and spectral features, the regions are merged to form a BPT representation of the HSI cube. Subsequently, PCA is applied to the input HSI cube. Finally, each HSI pixel is clustered to one class by using a filtering algorithm with a feature vector as input containing information that is extracted from the closest neighborhood (spatial information) of the pixel and its transformed spectral value. As future work, other feature extraction techniques can be explored for improving the accuracy. For the publicly available HSI datasets that are used in the analysis, the proposed method results in competitive accuracy when compared to the other state-of-the-art clustering frameworks.