Abstract
The article presents a parallel hardware-oriented algorithm designed to speed up the division of two octonions. The advantage of the proposed algorithm is that the number of real multiplications is halved as compared to the naive method for implementing this operation. In the synthesis of the discussed algorithm, the matrix representation of this operation was used, which allows us to present the division of octonions by means of a vector–matrix product. Taking into account a specific structure of the matrix multiplicand allows for reducing the number of real multiplications necessary for the execution of the octonion division procedure.
1. Introduction
The dynamic development of science and technology of data processing as well as the need to implement more and more complex problems and practical applications require the use of ever more complex mathematical methods and formalisms. Currently, the algebra of hypercomplex numbers [1] is increasingly used for the synthesis, description, and implementation of highly efficient numerical algorithms in the field of digital signals, like in [2,3,4,5] where the analysis of complex signals was extended to multidimensional hypercomplex signals and hypercomplex digital signal processing. Frequency-domain adaptive filters used for the derivation of the most popular algorithms for a wide variety of signals, from real-valued ones to hypercomplex-valued signals are presented in [6]. The use of hypercomplex numbers for image recognition, due to their internal correlation, is a more natural fit for recognition of multicolor patterns than does the use of color vector spaces [7,8]. Similarly, the use of complex numbers with their internal correlation allows for a more complete analysis of the image [9,10], or analyse the various watermarking techniques [11]. Hypercomplex numbers are widely used in robotics, in rotation and moving of robot manipulators [12,13,14], in automation for the analysis of multidimensional spaces [11,15], or in wireless data transmission [16]. Deep neural networks are also a popular area of application for hypercomplex numbers: quaternion valued neural network [17,18] and octonion valued neural network [19,20].
A promising area also seems to be the application of hypercomplex numbers to big data analysis, e.g., in parallel training architecture for large-scale convolutional neural networks [21], in parallel extreme learning machine [22,23,24], in cloud computing service system based on big data [25], in blockchain [26,27], or in IoT [28]. In all of the above cases, the use of octonions in parallel algorithms can provide significant benefits, due to the internal relations of hypercomplex numbers.
When performing the aforementioned hypercomplex-valued algorithms, the most time-consuming macro operations are multiplication and division, since they require several dozen of the nested real multiplications and additions [29,30]. For natural reasons, the intention of developers of highly efficient algorithms for processing hypercomplex data has always been to look for ways to reduce the number of arithmetic operations in these algorithms. This, in particular, refers to the minimization of the number of real multiplications, which from the very beginning of the development of computerization has been the most time-consuming operation in the entire set of data processing operations. As for the operation of multiplying hypercomplex numbers, everything is more or less clear. Quite a lot of efficient algorithms for multiplying hypercomplex numbers have been developed. However, if various hypercomplex numbers have already been invented, then it would be good to have efficient algorithms on hand to perform all the defined mathematical operations on those numbers. Nevertheless, fast algorithms for dividing hypercomplex numbers are practically not described anywhere. The only exception is the fast quaternion division algorithm [31]. To eliminate this disadvantage, the authors proposed an algorithm for the fast division of octonions.
Thus, the purpose of this article is to present the original results of the synthesis of a rationalized algorithm for calculating the quotient of two octonions, which requires fewer real multiplications compared to the direct naive calculation method at the cost of some increase in the number of real additions.
The paper is organized as follows: The next section presents a short background of dividing two octonions. The main chapter, which presents the synthesis of a fast algorithm for octonion division is given in Section 3. Evaluation of computational complexity of proposed algorithm is provided in Section 4. The paper finishes with the concluding remarks in Section 5.
2. Short Background
Consider the problem of dividing two octonions
where
and ; are imaginary units. The division operation (1) can be written as the multiplication of the octonion-dividend a by the conjugate octonion-divisor divided by the square of the norm of the quaternion-divisor R
where
The rules for multiplying the octonion imaginary units are presented in Table 1 [1].

Table 1.
Rules for multiplying the octonion imaginary units.
The operation of division (2) can be rewritten in the matrices-vector form [32,33,34]
where is a scalar matrix
is the identity matrix of order N, is a inverse of the square of the norm of the quaternion-divisor
and are the vector representation of the quotient d and octonion-dividend a, respectively
and is the left real matrix representation of the conjugate octonion-divisor
The direct multiplication of the vector–matrix product in Equation (3) requires 72 multipliers, 63 adders, 8 squarers and one divider of real numbers. The authors proposed some tricks, which reduce the multiplicative complexity of this operation to 38 real multiplications at the price of 56 more real additions.
3. Synthesis of a Fast Algorithm for Octonion Division
Let us multiply by () the first column of the matrix . It is easy to see that this procedure leads to minimising the computational complexity of the final algorithm. This results in the following matrix:
Taking into account the performed manipulations, the operation of dividing one octonion by another octonion can be written as follows:
where
The following notation may be introduced: , and . Then, the division of two octonions can be represented as the following sum:
It is easy to see that the matrix has symmetric Toeplitz-type structure. A matrix with such a structure can be successfully diagonalized using the fast discrete Walsh–Hadamard transform [35]. Let us take a closer look at this thought.
The matrix has a block-symmetric structure:
where
For matrices with such a structure, the following factorization takes place [35]:
where
is Hadamard matrix of order 2, is the null matrix (all of its entries are zero), and symbols “⊗”, “⊕” denote the tensor product and direct sum of two matrices, respectively [31,35,36,37].
The next step is to analyze the structures of matrix and matrix :
As you can see, these matrices also have block-symmetric structures and a similar factorization takes place for them. This means that expression (10) can be rewritten as follows:
where
Now, consider the structures of the matrices , , , and . It is easy to see that also in this case there are block-symmetric matrices. Thus, this is again a similar case. Then, expression (11) can be rewritten as follows:
where
The triple products of matrices on the left and on the right with respect to the diagonal matrix are in fact the factorized representations of the eighth order Hadamard matrices and describe the algorithms for the fast Walsh–Hadamard transform.
It is possible to write:
It is easy to check that the elements of the matrix can also be calculated using the eight-point fast Walsh–Hadamard transform:
Unfortunately, the process of calculating product defies any effort at rationalization. However, since the matrix is a sparse matrix and contains only 22 nonzero entries, the calculation of the entries of the vector requires only 22 real multiplications.
Combining partial computing procedures into a single one:
where , , , , and is a matrix of ones ( every element is equal to one).
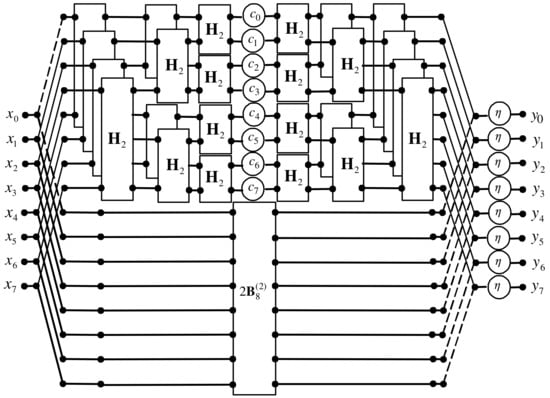
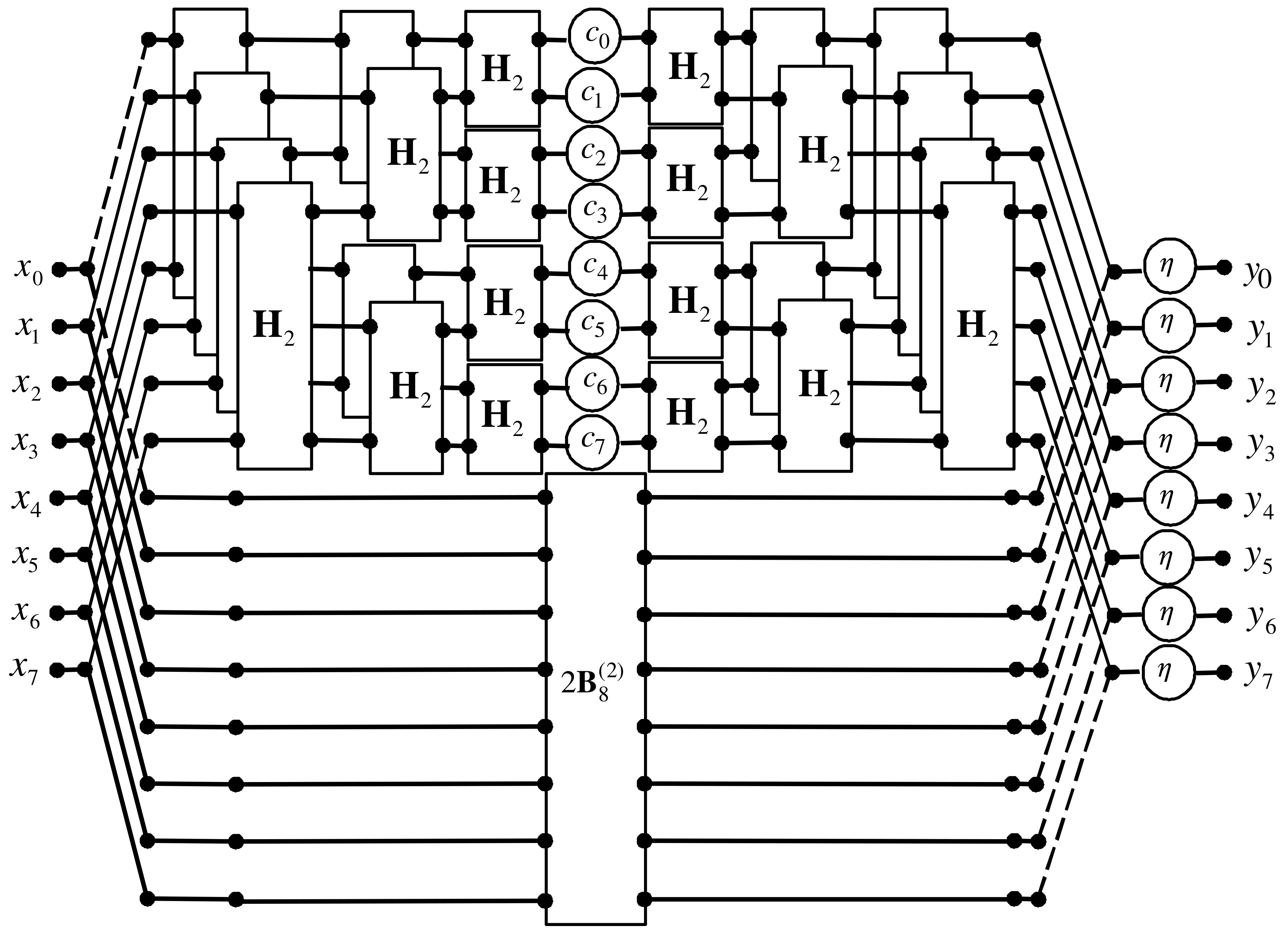
Figure 1.
The signal flow graph of the proposed algorithm.
4. Evaluation of Computational Complexity
The concept of computing the quotient of two octonions discussed in the article is an attempt to rationalize the computation process in terms of minimizing the number of multipliers required for a fully parallel hardware implementation of computations. The number of multiplication operations (multipliers) in the proposed solution is nearly twice as small as the naive method, and it is reduced from 72 to 38, which is a reduction of about 47.2%. This is at the expense of increasing the number of addition operations (adders) from 63 to 133, which is an increase of approximately 106.3%. It is also necessary to use eight three-bit barrel shifters. The number of dividers and squarers remained the same as in the compared method.
It should be noted that in most digital signal processing tasks one of the divided octonions is the so-called "constant", which means that its coefficients are known constant real numbers in advance. This means that the matrix entries can be computed in advance only once and stored in the read-only memory (ROM) of the computational system. Then, the solution proposed in the article becomes even more effective because it requires the same number of operating blocks as in the case of the naive method, among which only 38 blocks (twice less) are multipliers, and 70 adders. The total number of operating blocks necessary for the implementation of the processor system for calculating the obtained quotient in this case is 108 (128 in the case of the implementation of the naive method). In this way, the solution proposed in the article becomes the best in terms of the total number of arithmetic operations or operating blocks (in the case of hardware implementation) necessary to calculate the quotient of octonions.
5. Conclusions
The paper presented a new parallel algorithm for calculating the quotient of two octonions. The use of this algorithm reduces the multiplicative complexity of dividing octonion operation, thus reducing its hardware implementation complexity. The proposed algorithm has a simple, regular, and modular structure suitable for VLSI implementation. It is known that, all other things being equal, a conventional hardwired multiplier is a more complex device than a binary adder and occupies a much larger die area than an adder. Therefore, reducing the number of embedded multipliers is especially important when developing a specialized fully parallel VLSI-based module such as an octonion divider. Minimizing the number of multipliers required also reduces power dissipation and the cost of realization of such a module. Thus, it can be argued that a decrease in the number of embedded multipliers even due to a small increase in the number of adders plays an important role in the hardware implementation of the algorithm.
In addition, it can be seen that the total number of arithmetic operations in the presented algorithm is less than the total number of operations in the compared algorithm. Therefore, the proposed algorithm in some cases may turn out to be better than the naive algorithm even from the point of view of its software implementation on a general-purpose computer. Many applications of presented in the paper algorithm could be proposed. However, these questions are beyond the scope of this study and will be considered in the following articles by the authors.
Author Contributions
Conceptualization, A.C. and J.P.P.; methodology, A.C. and J.P.P.; software, J.P.P.; validation, A.C. and J.P.P.; formal analysis, A.C. and J.P.P.; investigation, A.C. and J.P.P.; resources, A.C.; data curation, J.P.P.; writing—original draft preparation, A.C.; writing—review and editing, J.P.P.; visualization, A.C.; supervision, A.C.; project administration, J.P.P.; funding acquisition, A.C. and J.P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge S.I. Klipkov for helpful clarifications regarding the dividing of octonions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kantor, I.L.; Kantor, I.; Solodovnikov, A. Hypercomplex Numbers: An Elementary Introduction to Algebras; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Alfsmann, D.; Göckler, H.G.; Sangwine, S.J.; Ell, T.A. Hypercomplex algebras in digital signal processing: Benefits and drawbacks. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 1322–1326. [Google Scholar]
- Bulow, T.; Sommer, G. Hypercomplex signals-a novel extension of the analytic signal to the multidimensional case. IEEE Trans. Signal Process. 2001, 49, 2844–2852. [Google Scholar] [CrossRef] [Green Version]
- Sangwine, S.J.; Le Bihan, N. Hypercomplex analytic signals: Extension of the analytic signal concept to complex signals. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 621–624. [Google Scholar]
- Schutte, H.D.; Wenzel, J. Hypercomplex numbers in digital signal processing. In Proceedings of the 1990 IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 1–3 May 1990; pp. 1557–1560. [Google Scholar]
- Comminiello, D.; Scarpiniti, M.; Parisi, R.; Uncini, A. Frequency-domain adaptive filtering: From real to hypercomplex signal processing. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 7745–7749. [Google Scholar]
- Labunets, V.G.; Smetanin, J.G.; Chasovskikh, V.P.; Ostheimer, E. Hypercomplex Algebras as Unified Language for Image Processing and Pattern Recognition Part 1. Cliffordean Models of Multichannel Images. In Advances in Information Technologies, Telecommunication, and Radioelectronics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–19. [Google Scholar]
- Pei, S.C.; Ding, J.J.; Chang, J. Color pattern recognition by quaternion correlation. In Proceedings of the 2001 International Conference on Image Processing (Cat. No. 01CH37205), Thessaloniki, Greece, 7–10 October 2001; Volume 1, pp. 894–897. [Google Scholar]
- Wang, C.; Hao, Q.; Ma, B.; Wu, X.; Li, J.; Xia, Z.; Gao, H. Octonion continuous orthogonal moments and their applications in color stereoscopic image reconstruction and zero-watermarking. Eng. Appl. Artif. Intell. 2021, 106, 104450. [Google Scholar] [CrossRef]
- Sangwine, S.J. Fourier transforms of colour images using quaternion or hypercomplex, numbers. Electron. Lett. 1996, 32, 1979–1980. [Google Scholar] [CrossRef]
- Gao, W.B.; Li, B.Z. The octonion linear canonical transform: Definition and properties. Signal Process. 2021, 188, 108233. [Google Scholar] [CrossRef]
- Cariow, A.; Cariowa, G.; Majorkowska-Mech, D. An Algorithm for Quaternion–Based 3D Rotation. Int. J. Appl. Math. Comput. Sci. 2020, 30, 149–160. [Google Scholar]
- Hu, C.; Meng, M.Q.H.; Mandal, M.; Liu, P.X. Robot rotation decomposition using quaternions. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1158–1163. [Google Scholar]
- Takahashi, K.; Fujita, M.; Hashimoto, M. Remarks on Octonion–valued Neural Networks with Application to Robot Manipulator Control. In Proceedings of the 2021 IEEE International Conference on Mechatronics (ICM), Kashiwa, Japan, 7–9 March 2021; pp. 1–6. [Google Scholar]
- Błaszczyk, Ł. Hypercomplex fourier transforms in the analysis of multidimensional linear time-invariant systems. In Progress in Industrial Mathematics at ECMI 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 575–581. [Google Scholar]
- Seberry, J.; Finlayson, K.; Adams, S.S.; Wysocki, T.A.; Xia, T.; Wysocki, B.J. The theory of quaternion orthogonal designs. IEEE Trans. Signal Process. 2007, 56, 256–265. [Google Scholar] [CrossRef]
- Cariow, A.; Cariowa, G. Fast Algorithms for Quaternion-Valued Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 457–462. [Google Scholar] [CrossRef]
- Saoud, L.S.; Ghorbani, R.; Rahmoune, F. Cognitive quaternion valued neural network and some applications. Neurocomputing 2017, 221, 85–93. [Google Scholar] [CrossRef]
- Popa, C.A. Global exponential stability of octonion-valued neural networks with leakage delay and mixed delays. Neural Netw. 2018, 105, 277–293. [Google Scholar] [CrossRef]
- Wu, J.; Xu, L.; Wu, F.; Kong, Y.; Senhadji, L.; Shu, H. Deep octonion networks. Neurocomputing 2020, 397, 179–191. [Google Scholar] [CrossRef]
- Chen, J.; Li, K.; Bilal, K.; Li, K.; Philip, S.Y.; Zhou, X. A bi-layered parallel training architecture for large-scale convolutional neural networks. IEEE Trans. Parallel Distrib. Syst. 2018, 30, 965–976. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Li, K.; Ouyang, A.; Tang, Z.; Li, K. Gpu-accelerated parallel hierarchical extreme learning machine on flink for big data. IEEE Trans. Syst. Man, Cybern. Syst. 2017, 47, 2740–2753. [Google Scholar] [CrossRef]
- Duan, M.; Li, K.; Liao, X.; Li, K. A parallel multiclassification algorithm for big data using an extreme learning machine. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 2337–2351. [Google Scholar] [CrossRef]
- Jamel, A.A.; Akay, B. A Survey and systematic categorization of parallel K-means and Fuzzy-c-Means algorithms. Comput. Syst. Sci. Eng. 2019, 34, 259–281. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Wang, T.; Sherratt, R.S.; Zhang, J. Big data service architecture: A survey. J. Internet Technol. 2020, 21, 393–405. [Google Scholar]
- Zhang, J.; Zhong, S.; Wang, T.; Chao, H.C.; Wang, J. Blockchain-based systems and applications: A survey. J. Internet Technol. 2020, 21, 1–14. [Google Scholar]
- Deepa, N.; Pham, Q.V.; Nguyen, D.C.; Bhattacharya, S.; Prabadevi, B.; Gadekallu, T.R.; Maddikunta, P.K.R.; Fang, F.; Pathirana, P.N. A survey on blockchain for big data: Approaches, opportunities, and future directions. arXiv 2020, arXiv:2009.00858. [Google Scholar]
- Rani, R.; Pushpalatha, M. Generation of Frequent sensor epochs using efficient Parallel Distributed mining algorithm in large IOT. Comput. Commun. 2019, 148, 107–114. [Google Scholar] [CrossRef]
- Cariow, A.; Cariowa, G. Algorithm for multiplying two octonions. Radioelectron. Commun. Syst. 2012, 55, 464–473. [Google Scholar] [CrossRef]
- Tariov, A.; Tariova, G. Algorithmic aspects of the processor unit organization for Cayley numbers multiplication (In Polish): Aspekty algorytmiczne organizacji jednostki procesorowej do mnożenia liczb Cayleya. Elektron. Konstr. Technol. Zastos. 2010, 51, 104–108. [Google Scholar]
- Cariow, A.; Cariowa, G. An algorithm for dividing quaternions. arXiv 2020, arXiv:2009.00425. [Google Scholar]
- Klipkov, S. Some features of the matrix representations of the octonions. Èlektronic Model. 2019, 41, 19–34. [Google Scholar] [CrossRef]
- Karataş, A.; Halici, S. Vector matrix representation of octonions and their geometry. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2018, 67, 161–167. [Google Scholar]
- Tian, Y. Matrix representations of octonions and their applications. arXiv 2000, arXiv:math/0003166. [Google Scholar] [CrossRef] [Green Version]
- Cariow, A. Strategies for the Synthesis of Fast Algorithms for the Computation of the Matrix-vector Products. J. Signal Process. Theory Appl. 2014, 3, 1–19. [Google Scholar] [CrossRef]
- Granata, J.; Conner, M.; Tolimieri, R. The tensor product: A mathematical programming language for FFTs and other fast DSP operations. IEEE Signal Process. Mag. 1992, 9, 40–48. [Google Scholar] [CrossRef]
- Regalia, P.A.; Sanjit, M.K. Kronecker products, unitary matrices and signal processing applications. SIAM Rev. 1989, 31, 586–613. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).