Optimized Weighted Nearest Neighbours Matching Algorithm for Control Group Selection
Abstract
:1. Introduction
2. Related Work
3. Weighted Nearest Neighbours Control Group Selection with Simulated Annealing (WNNSA)
Conflicting Candidates
| Algorithm 1: Weighted Nearest Neighbours Control Group Selection with Simulated Annealing (WNNSA). |
|
| Algorithm 2: Determination of the minimal size for the reduced environment for the WNNSA algorithm. |
|
4. Study Design
4.1. Dataset for Scenario I
- correction for binary:
- low:
- medium:
- high:
- very high:
4.2. Dataset for Scenario II
4.3. Methodology of the Evaluation
5. Results
5.1. Results of the Scenario I
5.2. Results of the Scenario II
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DDI | Distribution Dissimilarity Index |
| GDI | Global Dissimilarity Index |
| HB | Hansen and Bowers test |
| MMM | Mahalanobis metric matching |
| NN | Nearest neighbour |
| NNI | Nearest Neighbour Index |
| NNM | Nearest neighbour matching |
| OR | Odds ratio |
| PSM | Propensity Score Matching |
| SA | Simulated annealing |
| SM | Stratified matching |
| SMD | Standardized mean difference |
| WNNEM | Weighted Nearest Neighbours Control Group Selection with Error Minimization |
| WNNSA | Weighted Nearest Neighbours Control Group Selection with Simulated Annealing |
References
- Sirois, C. Case-Control Studies. In Encyclopedia of Pharmacy Practice and Clinical Pharmacy; Babar, Z.U.D., Ed.; Elsevier: Oxford, UK, 2019; pp. 356–366. [Google Scholar] [CrossRef]
- Li, L.; Donnell, E.T. Incorporating Bayesian methods into the propensity score matching framework: A no-treatment effect safety analysis. Accid. Anal. Prev. 2020, 145, 105691. [Google Scholar] [CrossRef]
- Li, Q.; Lin, J.; Chi, A.; Davies, S. Practical considerations of utilizing propensity score methods in clinical development using real-world and historical data. Contemp. Clin. Trials 2020, 97, 106123. [Google Scholar] [CrossRef]
- Fang, Y.; He, W.; Wang, H.; Wu, M. Key considerations in the design of real-world studies. Contemp. Clin. Trials 2020, 96, 106091. [Google Scholar] [CrossRef] [PubMed]
- Kondo, Y.; Noda, T.; Sato, Y.; Ueda, M.; Nitta, T.; Aizawa, Y.; Ohe, T.; Kurita, T. Comparison of 2-year Outcomes between Primary and Secondary Prophylactic Use of Defibrillators in Patients with Coronary Artery Disease: A Prospective Propensity Score-Matched Analysis from the Nippon Storm Study. Heart Rhythm O2 2021, 2, 5–11. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Szekér, S.; Vathy-Fogarassy, Á. Weighted nearest neighbours-based control group selection method for observational studies. PLoS ONE 2020, 15, e0236531. [Google Scholar] [CrossRef]
- Wright, R.E. Logistic Regression; American Psychological Association: Washington, DC, USA, 1995. [Google Scholar]
- Rudaś, K.; Jaroszewicz, S. Linear regression for uplift modeling. Data Min. Knowl. Discov. 2018, 32, 1275–1305. [Google Scholar] [CrossRef] [Green Version]
- Baser, O. Too much ado about propensity score models? Comparing methods of propensity score matching. Value Health 2006, 9, 377–385. [Google Scholar] [CrossRef] [Green Version]
- Caliendo, M.; Kopeinig, S. Some Practical Guidance for the Implementation of Propensity Score Matching. J. Econ. Surv. 2008, 22, 31–72. [Google Scholar] [CrossRef] [Green Version]
- Austin, P.C. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar. Behav. Res. 2011, 46, 399–424. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Schnell, P.; Song, C.; Huang, B.; Lu, B. Subgroup causal effect identification and estimation via matching tree. Comput. Stat. Data Anal. 2021, 159, 107188. [Google Scholar] [CrossRef]
- Shi, J.; Qin, G.; Zhu, H.; Zhu, Z. Communication-efficient distributed M-estimation with missing data. Comput. Stat. Data Anal. 2021, 16, 107251. [Google Scholar] [CrossRef]
- Tousi, S.S.; Tabesh, H.; Saki, A.; Tagipour, A.; Tajfard, M. Comparison of Nearest Neighbor and Caliper Algorithms in Outcome Propensity Score Matching to Study the Relationship between Type 2 Diabetes and Coronary Artery Disease. J. Biostat. Epidemiol. 2021, 7, 251–262. [Google Scholar] [CrossRef]
- Austin, P.C. A critical appraisal of propensity-score matching in the medical literature between 1996 and 2003. Stat. Med. 2008, 27, 2037–2049. [Google Scholar] [CrossRef] [PubMed]
- Pell, G.S.; Briellmann, R.S.; Chan, C.H.P.; Pardoe, H.; Abbott, D.F.; Jackson, G.D. Selection of the control group for VBM analysis: Influence of covariates, matching and sample size. Neuroimage 2008, 41, 1324–1335. [Google Scholar] [CrossRef]
- Biondi-Zoccai, G.; Romagnoli, E.; Agostoni, P.; Capodanno, D.; Castagno, D.; D’Ascenzo, F.; Sangiorgi, G.; Modena, M.G. Are propensity scores really superior to standard multivariable analysis? Contemp. Clin. Trials 2011, 32, 731–740. [Google Scholar] [CrossRef] [Green Version]
- Mansournia, M.A.; Jewell, N.P.; Greenland, S. Case–control matching: Effects, misconceptions, and recommendations. Eur. J. Epidemiol. 2018, 33, 5–14. [Google Scholar] [CrossRef] [PubMed]
- King, G.; Nielsen, R. Why propensity scores should not be used for matching. Political Anal. 2019, 27, 435–454. [Google Scholar] [CrossRef] [Green Version]
- Moser, P. Out of Control? Managing Baseline Variability in Experimental Studies with Control Groups. Handb. Exp. Pharmacol. 2019, 257, 101–117. [Google Scholar] [CrossRef] [Green Version]
- Wan, F. Matched or unmatched analyses with propensity-score-matched data? Stat. Med. 2019, 38, 289–300. [Google Scholar] [CrossRef]
- He, Y.; Kim, S.; Kim, M.O.; Saber, W.; Ahn, K.W. Optimal treatment regimes for competing risk data using doubly robust outcome weighted learning with bi-level variable selection. Comput. Stat. Data Anal. 2021, 158, 107167. [Google Scholar] [CrossRef]
- Anderson, D.W.; Kish, L.; Cornell, R.G. On stratification, grouping and matching. Scand. J. Stat. 1980, 7, 61–66. [Google Scholar]
- Austin, P.C. Balance diagnostics for comparing the distribution of baseline covariates between treatment groups in propensity-score matched samples. Stat. Med. 2009, 28, 3083–3107. [Google Scholar] [CrossRef] [Green Version]
- Gosset, W.S. The probable error of a mean. Biometrika 1908, 1–25. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una lgge di distribuzione. Inst. Ital. Attuari Giorn. 1933, 4, 83–91. [Google Scholar]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef] [Green Version]
- MacFarland, T.W.; Yates, J.M. Mann–Whitney U test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Berlin/Heidelberg, Germany, 2016; pp. 103–132. [Google Scholar]
- Szekér, S.; Vathy-Fogarassy, Á. How Can the Similarity of the Case and Control Groups be Measured in Case-Control Studies? In Proceedings of the 2019 IEEE International Work Conference on Bioinspired Intelligence (IWOBI), Budapest, Hungary, 3–5 July 2019; pp. 33–40. [Google Scholar] [CrossRef]
- Bowers, J.; Fredrickson, M.; Hansen, B. RItools: Randomization inference tools. R Package Version 0.1-11. 2010. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Austin, P.C. Comparing paired vs non-paired statistical methods of analyses when making inferences about absolute risk reductions in propensity-score matched samples. Stat. Med. 2011, 30, 1292–1301. [Google Scholar] [CrossRef] [Green Version]
- Rubin, D.B. Matching to remove bias in observational studies. Biometrics 1973, 29, 159–183. [Google Scholar] [CrossRef]
- Rubin, D.B. Bias reduction using Mahalanobis-metric matching. Biometrics 1980, 36, 293–298. [Google Scholar] [CrossRef]



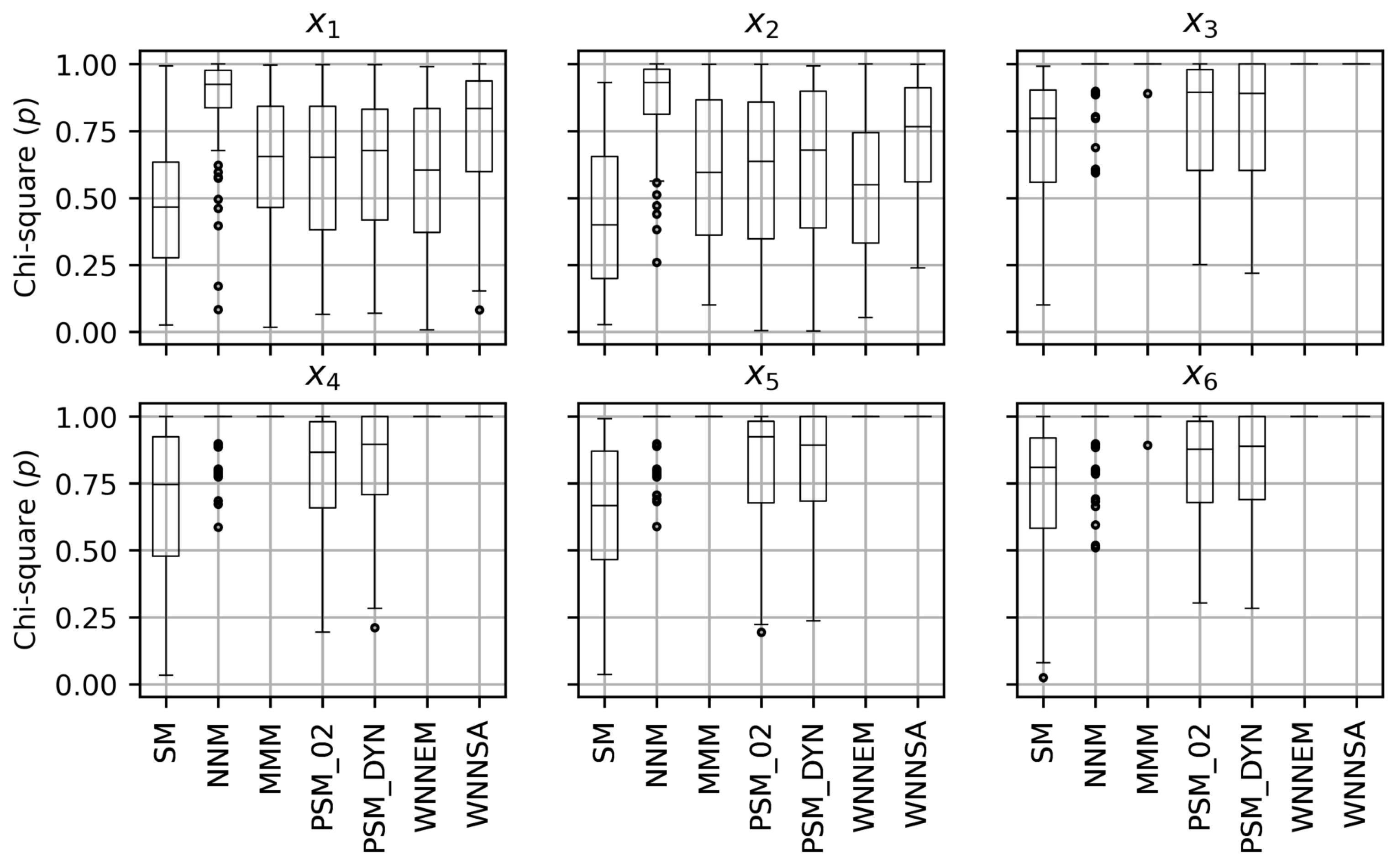
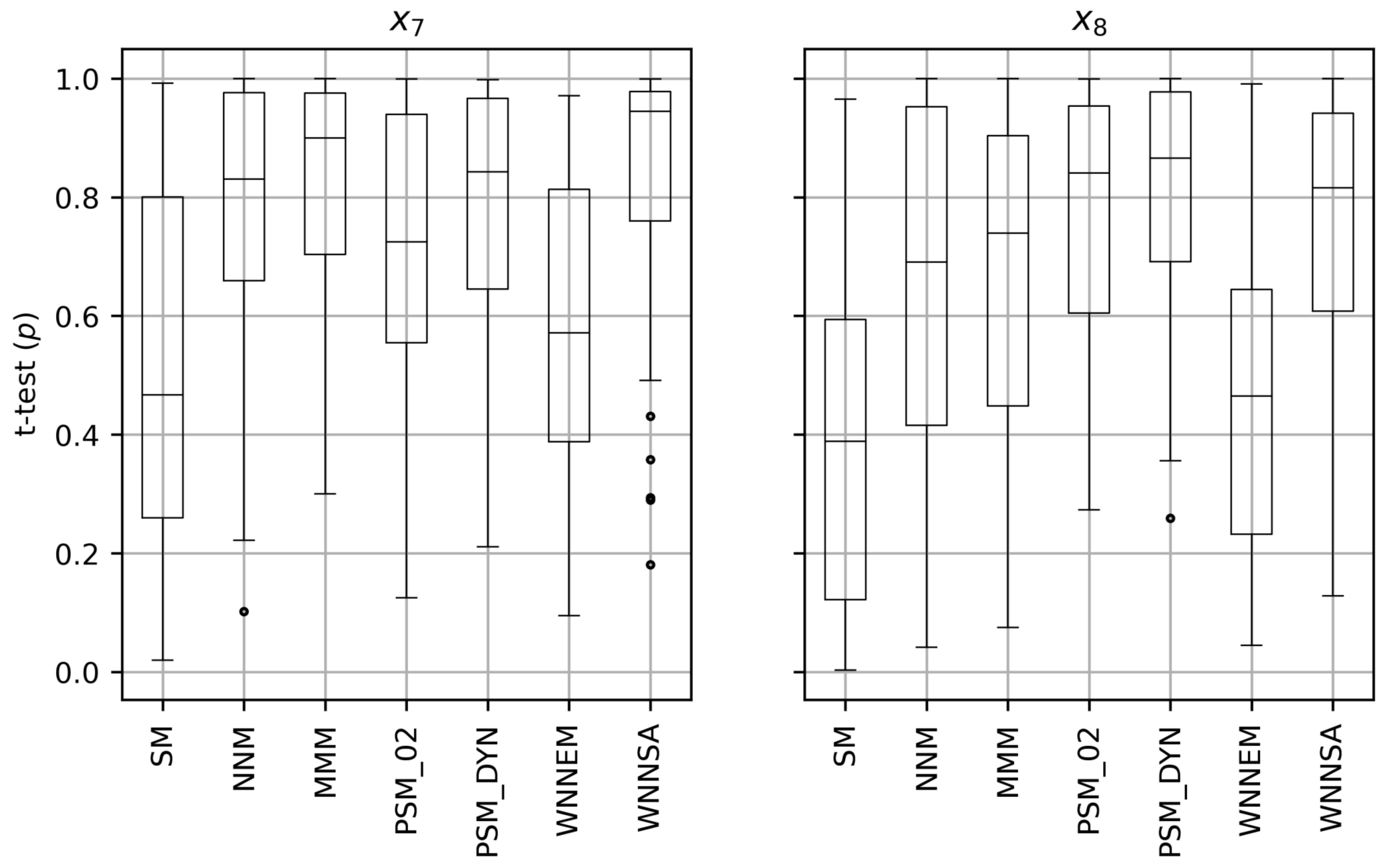

| NNM | MMM | SM | ||||||||||
| HB(p) | 0.583 | 0.976 | 1.000 | 0.347 | 0.960 | 1.000 | 0.512 | 0.873 | 1.000 | |||
| DDI(d) | 0.006 | 0.015 | 0.035 | 0.004 | 0.015 | 0.030 | 0.504 | 0.574 | 0.631 | |||
| NNI(d) | 0.054 | 0.065 | 0.075 | 0.057 | 0.066 | 0.078 | 0.504 | 0.574 | 0.631 | |||
| GDI(d) | 0.062 | 0.075 | 0.095 | 0.059 | 0.076 | 0.097 | 0.504 | 0.574 | 0.631 | |||
| PSM_02 | PSM_DYN | WNNEM | WNNSA | |||||||||
| HB(p) | 0.813 | 0.978 | 1.000 | 0.904 | 0.993 | 1.000 | 0.740 | 0.991 | 1.000 | 0.955 | 0.998 | 1.000 |
| DDI(d) | 0.021 | 0.061 | 0.116 | 0.006 | 0.014 | 0.023 | 0.006 | 0.012 | 0.022 | 0.005 | 0.011 | 0.021 |
| NNI(d) | 0.194 | 0.316 | 0.374 | 0.190 | 0.278 | 0.325 | 0.052 | 0.060 | 0.070 | 0.056 | 0.070 | 0.080 |
| GDI(d) | 0.214 | 0.348 | 0.416 | 0.212 | 0.313 | 0.367 | 0.052 | 0.061 | 0.077 | 0.062 | 0.073 | 0.097 |
| NNM | MMM | SM | ||||||||||
| HB(p) | 0.432 | 0.968 | 1.000 | 0.686 | 0.974 | 1.000 | 0.140 | 0.724 | 0.995 | |||
| DDI(d) | 0.034 | 0.061 | 0.093 | 0.035 | 0.058 | 0.084 | 0.617 | 0.710 | 0.800 | |||
| NNI(d) | 0.300 | 0.325 | 0.362 | 0.289 | 0.305 | 0.331 | 0.718 | 0.789 | 0.858 | |||
| GDI(d) | 0.043 | 0.058 | 0.081 | 0.054 | 0.071 | 0.107 | 0.637 | 0.728 | 0.815 | |||
| PSM_02 | PSM_DYN | WNNEM | WNNSA | |||||||||
| HB(p) | 0.523 | 0.941 | 1.000 | 0.729 | 0.960 | 1.000 | 0.769 | 0.969 | 1.000 | 0.815 | 0.991 | 1.000 |
| DDI(d) | 0.062 | 0.102 | 0.162 | 0.050 | 0.072 | 0.102 | 0.032 | 0.056 | 0.078 | 0.034 | 0.052 | 0.071 |
| NNI(d) | 0.591 | 0.661 | 0.705 | 0.528 | 0.640 | 0.678 | 0.285 | 0.303 | 0.321 | 0.300 | 0.318 | 0.335 |
| GDI(d) | 0.314 | 0.411 | 0.463 | 0.279 | 0.376 | 0.446 | 0.035 | 0.046 | 0.057 | 0.043 | 0.056 | 0.069 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szekér, S.; Vathy-Fogarassy, Á. Optimized Weighted Nearest Neighbours Matching Algorithm for Control Group Selection. Algorithms 2021, 14, 356. https://doi.org/10.3390/a14120356
Szekér S, Vathy-Fogarassy Á. Optimized Weighted Nearest Neighbours Matching Algorithm for Control Group Selection. Algorithms. 2021; 14(12):356. https://doi.org/10.3390/a14120356
Chicago/Turabian StyleSzekér, Szabolcs, and Ágnes Vathy-Fogarassy. 2021. "Optimized Weighted Nearest Neighbours Matching Algorithm for Control Group Selection" Algorithms 14, no. 12: 356. https://doi.org/10.3390/a14120356
APA StyleSzekér, S., & Vathy-Fogarassy, Á. (2021). Optimized Weighted Nearest Neighbours Matching Algorithm for Control Group Selection. Algorithms, 14(12), 356. https://doi.org/10.3390/a14120356








