Particle Swarm Optimization Based on a Novel Evaluation of Diversity

Abstract

In this paper, we propose a particle swarm optimization variant based on a novel evaluation of diversity (PSO-ED). By a novel encoding of the sub-space of the search space and the hash table technique, the diversity of the swarm can be evaluated efficiently without any information compression. This paper proposes a notion of exploration degree based on the diversity of the swarm in the exploration, exploitation, and convergence states to characterize the degree of demand for the dispersion of the swarm. Further, a disturbance update mode is proposed to help the particles jump to the promising regions while reducing the cost of function evaluations for poor particles. The effectiveness of PSO-ED is validated on the CEC2015 test suite by comparison with seven popular PSO variants out of 12 benchmark functions; PSO-ED achieves six best results for both 10-D and 30-D.

1. Introduction

Inspired by the emergent motion of the foraging behavior of a flock of birds in nature, the particle swarm optimization (PSO) was first proposed by Kennedy and Eberhart [1,2] in 1995 to solve the continuous nonlinear optimization problems. Compared with other evolutionary algorithms, the PSO has attracted much attention since it was proposed because of its fewer control parameters and better convergence. Nowadays, PSO has been widely used in many fields, such as communication networks [3,4], medicine engineering [5,6,7], task scheduling [8,9], energy management [10], linguistics studies [11], supply chain management [12] and neural networks [13,14].

Despite its robustness for solving complex optimization problems, rapid convergence may cause the swarm to be easily trapped into some local optima when solving multimodal problems via PSO [15,16,17,18,19,20,21,22]. Therefore, reasonably using the swarm’s exploration ability (global investigation of the search place) and exploitation ability (finer search around a local optimum) is a crucial factor for PSO’s success, especially for complex multimodal problems having a large number of local minima. For this purpose, several PSO variants have been reported. In the following, we shall discuss three main types: PSO with adjusted parameters, PSO with various topology structures, and PSO with hybrid strategies.

PSO with adjusted parameters: It is evident that appropriate control parameters, such as the inertia weight ω and the acceleration coefficients c₁ and c₂, have significant effects on the exploration and exploitation abilities of the swarm. By increasing the value of ω significantly diversity of the swarm increases while increasing the values of c₁ and c₂ accelerates the particles towards the historical optimal position or the optimal position of the whole swarm. Zhan [15] proposed an adaptive particle swarm optimization (APSO) algorithm in 2009, which updated control parameters (ω, c₁ and c₂) adaptively based on the distribution of positions and fitness of the swarm. Zhang et al. [23] proposed an inertia weight adjustment scheme based on Bayesian techniques to enhance the swarm’s exploitation ability. Tanweer et al. [24] proposed a PSO algorithm (SRPSO) that employed a self-regulating inertia weight strategy to the best particle to enhance the exploration ability. Taherkhani [25] proposed an adaptive approach which determines the inertia weight in different dimensions for each particle, based on its performance and distance from its best position.

PSO with various topology structures: PSO with different topology structures, namely: improved fixed topology structures, dynamic topology structures, and multi-swarms, have been shown to be efficient in controlling the exploration and exploitation capabilities [26,27,28].

Kennedy [29] proposed a small-world social network and studied different topologies’ influences on PSO algorithms’ performances. It was found that sparsely connected networks were suitable for complex functions, and densely connected networks were useful for simple functions.

Suganthan [30] first introduced the concept of dynamic topologies for PSO, where sub-swarms (each was a particle initially) were gradually merged as the evolution progressed. Cooren et al. [28] proposed an adaptive PSO called TRIBES, which were multiple sub-swarms with independent topological structures changing over time. Bonyadi et al. [31] presented dynamic topologies by growing the sub-swarms’ sizes, merging the sub-swarms. Zhang [32] proposed DEPSO, which generated a weighted search center based on top-k elite particles to guide the swarm.

Bergh and Engelbrecht [33] divided a d-dimension swarm into k (k < d) sub-swarms and made sub-swarms cooperated by exchanging their information (e.g., the best particle). Blackwell and Branke [34] proposed a multi-swarm PSO for dynamic functions with the optimal values changing over time. Liang’s group [35,36] presented a dynamic multi-swarm PSO with small sub-swarms frequently regrouped using various schedules. Xu et al. [37] hybridized the dynamic multi-swarm PSO with a new cooperative learning strategy in which the worst two particles learned from the two better sub-swarms. Chen et al. [21] proposed a dynamic multi-swarm PSO with a differential learning strategy. It combined the differential mutation into PSO and employed Quasi-Newton method as a local searcher.

PSO with hybrid strategies: To improve the performances of PSO, combining excellent strategies into PSO has been shown to be an effective approach. For example, Mirjalili et al. [38] combined PSO with gravitational search algorithm for efficiently training feedforward neural networks. Zhang et al. [39] combined PSO with a back-propagation algorithm to efficiently train the weights of feedforward neural networks. Nagra et al. [40] developed a hybrid of dynamic multi-swarm PSO with a gravitational search algorithm for improving the performance of PSO. Zhan et al. [41] combined PSO with orthogonal experimental design to discover an excellent exemplar from which the swarm can quickly learn and speed up the searching process. Bonyadi et al. [31] hybridized PSO with a covariance matrix adaptation strategy to improve the solutions in the latter phases of the searching process. Garg [42] combined PSO with genetic algorithms (GA): creating a new population by replacing weak particles with excellent ones via selection, crossover, and mutation operators. Plevris and Papadrakakis [43] combined PSO with a gradient-based quasi-Newton SQP algorithm for optimizing engineering structures. N. Singh and S.B. Singh [44] combined PSO with grey wolf optimizer for improving the convergence rate of the iterations. Raju et al. [45] combined PSO with a bacterial foraging optimization for 3D printing parameters of complicated models. Visalakshi and Sivanandam [46] combined PSO and the simulated annealing algorithm for processing dynamic task scheduling. Kang [47] introduced opposition-based learning (OBL) into PSO to improve the swarm’s performance in noisy environments. Cao et al. [48] embedded the comprehensive learning particle swarm optimizer (CLPSO) with local search (CL) to take advantage of both the exploration ability of CLPSO and the exploitation ability of CL.

Many scholars have conducted intensive research on the theory and applications of the PSO algorithms. However, there are still some shortcomings. For example, the parameter adaptive adjustment strategy cannot truly reflect the evolution of the population, and the particle swarm cannot effectively jump out of local optimal areas. To address these issues, a particle swarm optimization variant based on a novel evaluation of diversity (PSO-ED) is proposed in this paper and the major innovation is listed as follows:

• We propose a novel approach to compute swarm diversity based on the particles’ positions. By a series of encoding operations on the sub-space of the search space and the aid of hash table, the diversity can be determined in $O\left(N_{s}D\right)$ time, and it can reflect the distribution of the swarm without any information compression. Section 3.2.1 details the related techniques.
• We proposed a novel notion of exploration degree based on the diversity in the exploration, exploitation, and convergence states. It reflects the degree of demand for the swarm’s dispersion, and it can be used to realize adaptive update of the inertial weight of the PSO’s velocity function. Section 3.2.3 details the related techniques.
• We proposed a disturbance update mode based on the particles’ fitness. We replace the positions of the poor particles with new positions obtained by disturbing the best position. It saves the cost of function evaluations and improves convergence efficiency. Section 3.5 details the related techniques.

2. Related Work

2.1. Standard PSO

PSO is a population-based stochastic optimization algorithm introduced in 1995 by Kennedy and Eberhart without inertia weight [1,2]. Since the introduction of inertia weight was introduced by Shi and Eberhart [49] in 1998, it has shown its power in controlling the exploration and exploitation processes of evolution (Equations (1) and (2)).

$$v_i^d\left(t+1\right)=\omega v_i^d\left(t\right)+c_1{r}_1\left(P_i^d\left(t\right)-x_i^d\left(t\right)\right)+c_2{r}_2\left(P_g^d\left(t\right)-x_i^d\left(t\right)\right)$$

(1)

$$x_i^d\left(t+1\right)=x_i^d\left(t\right)+v_i^d\left(t+1\right)$$

(2)

When searching in a D-dimensional hyperspace, each particle i has a velocity vector $v_i\left(t\right)=\left[v_i^1\left(t\right),v_i^2\left(t\right),\cdots ,v_i^D\left(t\right)\right]$ and a position vector $x_i\left(t\right)=\left[x_i^1\left(t\right),x_i^2\left(t\right),\cdots ,x_i^D\left(t\right)\right]$ for the t-th iteration. $P_i$ is the historically best position of particle i, and $P_g$ is the position of the globally best particle. Acceleration coefficients c₁ and c₂ are commonly set in the range [0.5, 2.5] ([50,51]). $r_1$ and $r_2$ are two randomly generated values within range [0, 1], ω typically decreases linearly from 0.9 to 0.4 [49].

2.2. Existing Diversity Evaluation Strategies

Diversity, a parameter for evaluating the degree of dispersion in a swarm, is widely used to improve the PSO’s performance by adaptively balancing the swarm’s exploration and exploitation capabilities [17,52,53,54,55]. When diversity is small, the swarm can explore more accurate solutions; on the other hand, it can explore a large space to avoid premature convergence when the diversity is large. Therefore, it is suggested to maintain a large diversity in the early stage of evolution to explore a vast space where the optimal solution may exist, and reduce the swarm’s diversity near the end of the evolution to refine the result locally.

A proper diversity value should reflect the real characteristics of the swarm. If the diversity value is incorrectly evaluated, it may mislead the swarm’s movement. However, measuring the diversity of the swarm is a somewhat challenging problem.

At present, a lot of researchers have proposed different diversity evaluation schemes, which can be divided into two categories: distance-based diversity evaluation schemes [56] and information entropy-based diversity evaluation schemes [57,58,59,60,61,62].

The distance-based diversity evaluation methods can be further divided into two categories: (1) the average distance between each pair of particles in the swarm [63]; (2) the average distance between each particle and geometric center of the particle swarm [64].

The information entropy-based diversity evaluation scheme is developed from the information theory proposed by Shannon in 1948 [65]. After that, many scholars introduced this concept into particle swarm optimization algorithm. For example, Pires [60] proposed an entropy-based index to measure the diversity of the swarm. The basic idea of this method is as follows: (1) evenly dividing the search space into Q subspace; (2) counting the number Z_q of particles in each subspace; (3) calculating the probability in the subspace by Equation (3); (4) evaluating the diversity (the information entropy) by Equation (4).

$$p_q=\frac{Z_q}{N_s}$$

(3)

$$E=-{{\displaystyle \sum }}_{q=1}^Q{p}_{q}lo{g}_n{p}_q$$

(4)

where N_s represents the total number of particles, q represents the q-th subspace, and E represents the information entropy and is taken as the value of diversity.

3. PSO-ED

This section presents the technical details of PSO-ED. Section 3.1 introduces the main idea of PSO-ED; Section 3.2 presents our evaluation strategy of computing the exploration degree; Section 3.3 presents an adaptive update of inertia weight based on the exploration degree; Section 3.4 presents the swarm reinitialization mechanism that helps the swarm escape local traps; Section 3.5 presents two update modes, i.e., normal update mode and disturbance update mode, for saving function evaluations (FEs) on poor-performed particles.

3.1. The Main Idea of PSO-ED

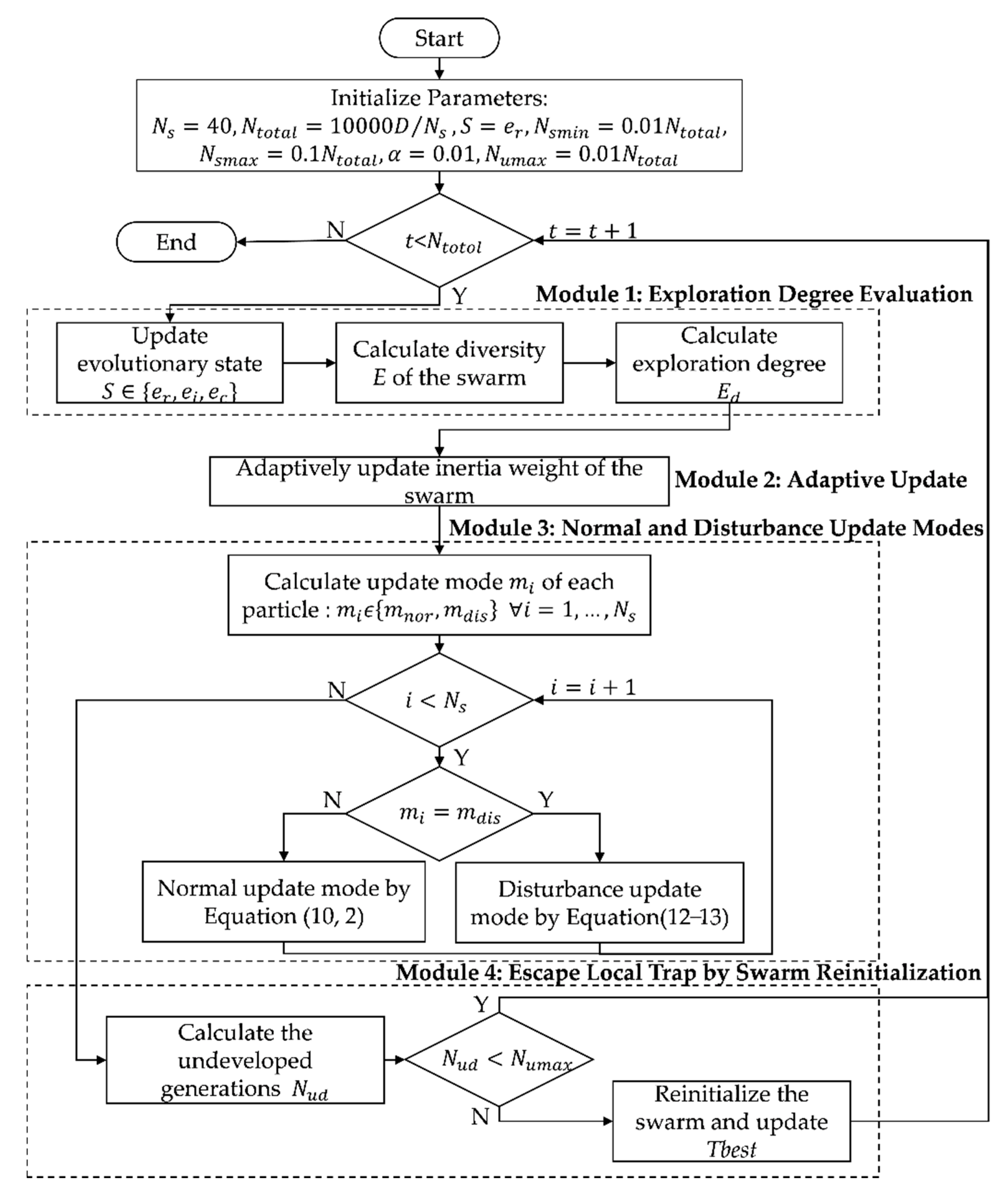
Given a dimension D (D = 10 or 30 for CEC2015), the flowchart of the PSO-ED is shown in Figure 1. PSO-ED has four main modules: exploration degree evaluation, an adaptive update of inertia weight, normal and disturbance update modes, and swarm reinitialization.

As mentioned above, the core problem of particle swarm optimization algorithm is how to balance the exploration and exploitation abilities of the swarm. To address this problem, in Module 1, we develop a technique of exploration degree based on the diversity of the swarm in the exploration, exploitation, and convergence states. In module 2, with the help of exploration degree, we adaptively update the inertial weight of the swarm to ensure that the swarm has a larger exploration degree in the exploration state and a smaller one in the convergence state. In Module 3, we give two update modes (normal and disturbance update modes) for each particle according to its fitness, so as to achieve the global optimum quickly. In Module 4, to help the swarm escape from local traps, a novel swarm reinitialization scheme is proposed.

For ease of description, we summarize the parameters used in the rest of the paper in

Table 1. Nomenclature.

Symbol	Quantity
$t$	The index of the current iteration
$x_i$	The position of particle i, and $x_i\in \left[x_{lb},x_{ub}\right]$ where $x_{lb}$and $x_{ub}$are lower and upper bounds of the position
$v_i$	The velocity of particle i, and $v_i\in \left[-v_{ub},v_{ub}\right]$ where $v_{ub}$ is the upper bound of the velocity
$\mathsf{\omega },c_1,c_2,c_3$	The inertial weight and accelerations for PSO respectively, and $c_3$ is defined in Section 3.4
$P_i, P_g, P_t$	The position of Pbest, Gbest and Tbest, where Tbest denotes the best position over all historical rounds of evolutions
$N_s$	The size of the swarm
$D$	The dimension of the problem space
$N_{total}$	The total number of iterations
$S$	The evolution state of the swarm, and $S ϵ \left\{e_r, e_i, e_c\right\}$ where $e_r, e_i, e_c$ represents the Exploration state, the Exploitation state, and the Convergence state, respectively.
$N_{state}$	The number of generations of state maintenance, and $N_{state}\in \left[N_{smin},N_{smax}\right]$ where $N_{smin}$ and $N_{smax}$ are the minimum and maximum generations of state maintenance
$E_r$	The average evolution rate
$N_{ud}$	The number of undeveloped generations, and $N_{ud}<N_{umax}$ where $N_{uamx}$ is the Maximum consecutive undeveloped generations
$c_i$	The ID of subspace where the i-th particle is located and will be discussed in Section 3.2.1
$E$	The information entropy of swarm position
$E_d$	The exploration degree of the swarm, and $E_d\in \left[E{d}_{lb},E{d}_{ub}\right]$ where $E{d}_{lb}$ and $E{d}_{ub}$ are the lower and upper bounds of the $E_d$
$N_w$	the number of weak particles that require the disturbance update mode
$m_i$	The update mode of particle i, and $m_i\in \left\{m_{nor},m_{dis}\right\}$ where $m_{nor}$ and $m_{dis}$ are the Normal and Disturbance update modes

. The definition of each critical parameter is also given when it first appears in the context.

3.2. Evaluation of the Exploration Degree

3.2.1. A Novel Diversity Evaluation Scheme

As mentioned above, the distance-based diversity is evaluated by computing the distances between particles. The essence of this scheme is space compression, which compresses the D-dimensional space features into one-dimensional space. For example, assume that there are three particles in the three-dimensional space, their positions are p₁ = {1,0,0}, p₂ = {0,1,0} and p₃ = {0,0,1}, then the mutual distance between any two particles is {(p₁, p₂) = 2^0.5, (p₁, p₃) = 2^0.5, (p₂, p₃) = 2^0.5}, which has only one dimension. Observe that the three points are separated by a distance of 2^0.5, but they are regarded as being aggregated together since the information entropy of the distance information is 0 (Equations (3) and (4)). Therefore, the information entropy based on distance cannot reflect the swarm diversity very well. On the other hand, if space is divided into multiple small subspaces, the complexity of traversing all subspaces is fairly high. For example, in the D-dimensional space, if each dimension is divided into K equal parts, then the complexity of traveling all subspaces is ($O\left(K^D\right)$), which is formidable when D is larger than 10.

To calculate the information entropy of the swarm efficiently and evaluate the degree of dispersion of the swarm as accurately as possible, we propose a novel diversity Evaluation scheme. The crucial steps of our approach are as follows:

For each particle in the swarm, compute the index (ID) of the subspace where the particle is located. First of all, each dimension of the search space is divided into K equal parts. Then the ID of a subspace is a string of D numbers, each of which represents the index of the part of the dimension occupied by the subspace. For example, in the 3-dimensional space in Figure 2, the ID of the blue subspace is {2, 3, 1}.

Denote $c_i=\left\{c_i^1,c_i^2,\dots ,c_i^D\right\}$ as the ID of subspace where the i-th particle is located, where $c_i^d$ is obtained from Equation (5):

$$C_i^d=\lceil \frac{x_i^d-x_{lb}}{\left(x_{ub}-x_{lb}\right)/K}\rceil$$

(5)

Build a hash table h by traversing the IDs obtained in the Step (1). h is composed of key-value pairs {key, value}, where key is the ID of the subspace, and value is the number of particles in the subspace. We traverse the IDs of the subspaces obtained by the above steps, if a key c exists in h its value h(c) is increased by 1, else a new key-value pair {c,1} is inserted into h.

Determine the information entropy E of the swarm based on h. Note that the empty subspace without any particle contributes 0 to the calculation of information entropy since the probability p of particles falling into this subspace is 0 by Equations (3) and (4). Therefore, only the subspace corresponding to a key of h can contribute to the information entropy. $p_q$ in Equation (3) represents the probability of falling into the subspace q, and $p_i=h\left(c\right)/N_s$. Therefore, E can be obtained by Equations (3) and (4) based on the keys of h and can be used in evaluating the exploration degree in Equation (8).

The time complexity of the above procedure is analyzed as follows: in step 1, we need to calculate the $c_i^d$ of each particle i in each dimension d, so its time complexity is $O\left(N_{s}D\right)$, where $N_s$ is the size of the swarm, and D is the dimension of the search space; in step 2, inserting a key-value pair into hash table h can be done in O(1) time, the time of traversing the IDs to establish hash table h is $O\left(N_s\right)$; in the last step, because only the key of the hash table h needs to be traversed, and the number of IDs is no more than $N_s$, the time complexity is also $O\left(N_s\right)$. In summary, the running time of the above procedures is $O\left(N_{s}D\right)$, which is significantly smaller than $O\left(N_s{}^D\right)$.

3.2.2. Switch of Evolutionary States

A conventional state transition of PSO simply set the initial state, the middle state and the last state of evolution as Exploration, Exploitation and Convergence, respectively. We are more flexible in switching the evolution states, and we allow multiple state switches during the whole evolution process. The swarm starts with the Exploration state, and its switching circle is Exploration→Exploitation→Convergence→Exploration. The process terminates as the maximum number of FEs is invoked.

As for the conditions of state switches, let $N_{ud}$ be the number of consecutive generations when the result of the swarm evolution has not been improved, if $N_{ud}>$ $N_{umax}$, the state should be switched at this time to enhance the chance of achieving better results (exploration→exploitation, exploitation→convergence) or jumping out of the local trap (convergence→exploration). However, if the state switches too frequently, it may not lead to any promising result while wasting time in state switch. To address this issue, let $N_{state}$ be the number of generations the current state has been maintained, depending on whether when $N_{ud}>N_{umax}$, we constraint $N_{state}$ in a range of generations (i.e., [$N_{smin}$, $N_{smax}$]) to control the switching frequency as follows:

• $N_{state}\le N_{smin}$: No switch
• $N_{smin}<N_{state}\le N_{smax}$: Switch only when $N_{ud}>N_{umax}$
• $N_{smax}<N_{sate}$: Switch

Note that the state S shall be used in the Section 3.2.3 to determine the upper and lower bound of the exploration degree.

Since the swarm may not evolve in every iteration during the evolution process, we use the notion of average evolution rate to judge whether the current iteration has evolved. As shown in Equation (6), the average evolution rate of consecutive K generations is obtained as the total evolution rate of these K generations divided by K. When the evolution rate is less than a user-defined threshold α, we increase $N_{ud}$ by 1, otherwise, we set $N_{ud}$ as 0.

$$Er\left(t\right)= \frac{F\left(t-K\right)-F\left(t\right)}{K\ast F\left(t-K\right)}$$

(6)

where the F(t) is the best result obtained in t-generation.

$$N_{ud}\left(t+1\right)= \{\begin{array}{cc}{N}_{ud}\left(t\right)+1& Er\left(t\right)<\alpha \\ 0& otherwise\end{array}$$

(7)

3.2.3. Exploration Degree

Let $E_d$ denote the exploration degree, which characterizes the degree of demand for the dispersion of the swarm. By trial and error, the relationship of the upper and lower bounds of $E_d$. The three evolutionary states can lead to fairly fine results if set, as shown in Figure 3.

We use the diversity E(t) to determine the exact value of $E_d$. When E(t) is high, it indicates that the swarm may still explore a wider area and the corresponding value of $E_d$ should be larger, and vice versa. To mimic this, we develop a linear function to express the relationship between $E_d$ and E(t) in Equation (8).

$$E_d\left(t\right)=E{d}_{lb}+\left(E{d}_{ub}-E{d}_{lb}\right)E\left(t\right)$$

(8)

In the following, we show how to realize an adaptive update of the inertial weight and, therefore, the balance of the exploration and exploitation by $E_d\left(t\right)$.

3.3. Adaptive Update of Inertia Weight

The inertia weight plays a critical role in balancing the swarm’s exploration and exploitation capabilities, and it also significantly affects the result’s accuracy [23,24,25]. Therefore, we adaptively adjust the swarm’s inertia weight to ensure that the swarm has a larger exploration degree in the exploration stage and a smaller one in the convergence stage. Finally, we use a sigmoid-like mapping that decreases from 0.9 to 0.4 [66,67] to characterize our inertia weight adjustment (Equation (9)). It is evident from this formula that when the exploration degree Ed of the population is large (close to 1.0), the inertia weight ω will also be large (close to 0.9) to ensure that the swarm can continue to explore a wider space. In contrast, when Ed becomes small, the inertia weight is also reduced to enhance the swarm’s convergence ability.

$$\omega \left(t\right)=\frac{1}{1+0.67e^{-2.67E_d\left(t\right)}}\in \left[0.4,0.9\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \forall E_d\left(t\right)\in \left[0,1\right]$$

(9)

3.4. Excape Local Trap by Swarm Reintialization

Note that Module 3 (Normal and Disturbance Update Modes) relies on Tbest, which is equal to Gbest when no reinitialization is conducted, therefore we shall present Module 4 ahead of Module 3 for ease of description. When the swarm falls into the trap of local optimal and cannot rely on its own to jump out, reinitializing the swarm has been proved to be an effective method of addressing this issue [68,69,70].

A crucial issue is how to judge whether the swarm has fallen into a local optimum or not. In this article, we say that the swarm has fallen into a local optimum if the iterations of undeveloped generation of the swarm $N_{ud}$ exceeds a maximum allowed number $N_{umax}$.

Another crucial issue is how to help the swarm jump out of a local optimum. When the swarm is trapped in a local optimum, the conventional solution is to reinitialize the swarm. If we abandon the global best (Gbest) by convention, then we waste a lot of early effort; on the other hand, if we use it, the swarm has a high probability of falling into this local trap again due to its powerful attraction. To address this issue, let Gbest denote the best position of the swarm of the current round of evolution (with a single initialization or reinitialization), and let Tbest denotes the best position of the swarm for all historical rounds of evolutions, thus Tbest is at least as good as Gbest. Finally, we add the Tbest term to the particle update in Equation (10), which ensures that the optimal position (Tbest) has only a moderate effect on the swarm with less attraction power.

$$\begin{array}{c}{v}_i^d\left(t+1\right)=\omega v_i^d\left(t\right)+c_1{r}_1\left(P_i^d\left(t\right)-x_i^d\left(t\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+c_2{r}_2\left(P_g^d\left(t\right)-x_i^d\left(t\right)\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+c_3{r}_3\left(P_t^d\left(t\right)-x_i^d\left(t\right)\right)\hfill \end{array}$$

(10)

where P_t is the position of Tbest.

For ease of computation, we fix c₁ = c₂ = 1.49445 based on a large set of experimental results of previous PSO variants (e.g., [23,36,71]). As for c₃, since its role is to guide the swarm to the position of Tbest in a slow manner, we can set it to a very small number c₃ = 0.01. In this way, we will update Tbest with this Gbest if the result of Gbest is better than the current Tbest; otherwise, Tbest still has the power of pulling the swarm to its position after several evolutionary generations.

3.5. Normal and Disturbance Update Modes

Note that Gbest and Pbest are more likely to be closer to the real global optimal solution in some dimensions. On the other hand, a poor particle’s current position is far away from the optimal solution, and it requires more cost (e.g., FEs) to move to a promising region.

Based on this consideration, we use different update modes for particles with excellent fitness and poor fitness to speed up the search process. We take the worst $N_w$ particles in each iteration as the particles with poor fitness. As shown in Equation (11), $N_w$ is proportional to $E_d$. The larger the value of $E_d$ is, the more dispersed the particles are. In this way, we force more particles to jump to a promising region to while reducing the waste of the FEs on poor particles.

$$N_w=N_s\times E_d/2$$

(11)

(1)

For particles with better fitness, the update mode follows the usual manner shown in Equations (2 and 10). Note that this update mode is slightly different from the traditional update due to the Tbest term in the velocity update formula.

(2)

For particles with poor fitness, we use a disturbance update mode as follows.

Step 1: Select the position of Pbest or Gbest as the seed (denoted as P) for generating new positions. Refer to Equation (12), the choice of Pbest position (denoted as P_i) or Gbest position (denoted as $P_g$) depends on the value of $E_d$. When $E_d$ is large, we tend to choose Pbest (i.e., self-cognition) to avoid fast convergence to some local optimum; when $E_d$ is small, we choose Gbest (social-cognition) to achieve a finer result.

$$P=\{\begin{array}{cc}{P}_i& r<E_d\\ P_g& otherwise\end{array}$$

(12)

where r is a random number uniformly distributed in [0, 1].

Step 2: Since P is very close to the optimal solution in some dimensions, we can randomly select a dimension d of P and perturb it into a new position, and keep the other dimensions remain the same thus to maintain the property of P as much as possible.

$$x_i=\{\begin{array}{cc}{P}_i+r_n\times \left(x_{ub}-x_{lb}\right)& i=d\\ P_i & otherwise\end{array}$$

(13)

where $r_n$ is a random number and $r_n\sim N\left(0, E_d^2\right)$.

Step 3: Replace the position of poor particles with the new position generated by the disturbance update mode.

4. Experiments and Comparisons

As shown in

Table 2. The 12 CEC2015 benchmark functions.

No.	Function Name	Fi* = Fi(x*)
1	Rotated High Conditioned Elliptic Function	100
2	Rotated Cigar Function	200
3	Shifted and Rotated Ackley’s Function	300
4	Shifted and Rotated Rastrigin’s Function	400
5	Shifted and Rotated Schwefel’s Function	500
6	Hybrid Function (N = 3)	600
7	Hybrid Function (N = 4)	700
8	Hybrid Function (N = 5)	800
9	Composition Function 1 (N = 3)	900
10	Composition Function 3 (N = 5)	1100
11	Composition Function 6 (N = 7)	1400
12	Composition Function 7 (N = 10)	1500

, to validate the effectiveness of PSO-ED, we use the same comparison set provided by a recent paper on MPSO [72] and choose 12 representative test functions from CEC2015 benchmark functions [73] as the test suite. The test suite consists of 2 unimodal functions (F₁ and F₂), 3 multimodal functions (F₃, F₄ and F₅), 3 hybrid functions (F₆, F₇ and F₈) and 4 composition functions (F₉, F₁₀, F₁₁ and F₁₂). All the guidelines of CEC2015 have been strictly followed for the experiments. For example, every function in this test suite is conducted for 30 runs independently, the search range of each dimension is set as [−100, 100], and the maximum function evaluation FEs is equal to 10,000 D. The fitness value is F_i(x) − F_i(x*) after the maximum iteration is reached, where F_i(x*) is just a number about the corresponding function for instruction.

4.1. Sensitivity Analysis

In this article, two parameters ($\alpha$ and $N_s$) are very critical to performance of PSO-ED. In order to examine the influence of the parameters on precision and efficiency, a sensitivity analysis was conducted to each parameter.

As shown in Equation (7), $\alpha$ is a user-defined threshold used to judge whether the swarm is evolving into a better result. A proper value of $\alpha$ can reflect the evolutionary state of the swarm and help the swarm choose an appropriate evolution strategy. In order to determine an appropriate value of $\alpha$, we have selected five values (1.0, 0.1, 0.01, 0.001 and 0.0001) and conducted for 30 runs independently for each value on 12 test functions. Note that the other parameters are set as follows: $N_s=40$, $N_{total}=FEs/N_s, N_{smin}=0.01N_{total}, N_{smax}=0.1N_{total}, N_{umax}=0.01N_{total}, v_{ub}=0.01\left(x_{ub}-x_{lb}\right)$.

As shown in

Table 3. Sensitivity analysis for $\alpha$.

Alpha	1		0.1		0.01		0.001		0.0001
Item	Mean	Rank	Mean	Rank	Mean	Rank	Mean	Rank	Mean	Rank
F1	9.12 × 104	4	8.33 × 104	3	3.03 × 105	5	8 × 104	1	8.27 × 104	2
F2	2.07 × 103	4	1.96 × 103	2	2.24 × 102	1	1.97 × 103	3	2.29 × 103	5
F3	2 × 101	1	2 × 101	1	2 × 101	1	2 × 101	1	2 × 101	1
F4	2.02 × 102	5	1.89 × 102	2	1.42 × 102	1	1.99 × 102	4	1.95 × 102	3
F5	3.92 × 103	3	3.91 × 103	2	3.10 × 103	1	3.95 × 103	4	3.99 × 103	5
F6	3.83 × 104	5	3.05 × 104	3	3.05 × 104	3	2.74 × 104	1	2.95 × 104	2
F7	1.22 × 101	3	1.26 × 101	5	1.04 × 101	1	1.16 × 101	2	1.25 × 101	4
F8	1.52 × 104	2	1.77 × 104	3	1.46 × 104	1	1.77 × 104	3	2.29 × 104	5
F9	1.47 × 102	4	1.34 × 102	2	1.04 × 102	1	1.59 × 102	5	1.46 × 102	3
F10	7.72 × 102	2	8.27 × 102	4	3.35 × 102	1	1.01 × 103	5	8.12 × 102	3
F11	3.30 × 104	3	3.14 × 104	2	2.54 × 104	1	3.32 × 104	4	3.35 × 104	5
F12	1 × 102	1	1 × 102	1	1 × 102	1	1 × 102	1	1 × 102	1
AR		3.08		2.50		1.50		2.83		3.25

, the statistical values (Mean and Rank) are listed and it is obvious that the result is best (smallest average ranking) when $\alpha =0.01$.

Another important parameter is the swarm size $N_s$. We choose five values (20, 30, 40, 50 and 60) to conduct experiments. And the other parameters are set as follows: $N_{total}=FEs/N_s, N_{smin}=0.01N_{total}, N_{smax}=0.1N_{total}, \alpha =0.01, N_{umax}=0.01N_{total}, v_{ub}=0.01\left(x_{ub}-x_{lb}\right)$. The results are shown in

Table 4. Sensitivity analysis for $N_s$.

SIZE	20		30		40		50		60
Item	Mean	Rank	Mean	Rank	Mean	Rank	Mean	Rank	Mean	Rank
F1	8.65 × 104	2	6.97 × 104	1	3.03 × 105	5	1.20 × 105	3	1.27 × 105	4
F2	2.31 × 103	4	2.45 × 103	5	2.24 × 102	1	2.08 × 103	3	1.94 × 103	2
F3	2 × 101	1	2 × 101	1	2 × 101	1	2 × 101	1	2 × 101	1
F4	2.21 × 102	5	1.99 × 102	4	1.42 × 102	1	1.82 × 102	3	1.76 × 102	2
F5	4.01 × 103	3	4.17 × 103	5	3.10 × 103	1	3.96 × 103	2	4.02 × 103	4
F6	2.96 × 104	4	2.28 × 104	1	3.05 × 104	5	2.86 × 104	3	2.78 × 104	2
F7	1.34 × 101	5	1.22 × 101	4	1.04 × 101	1	1.14 × 101	2	1.19 × 101	3
F8	1.84 × 104	3	1.54 × 104	2	1.46 × 104	1	2.15 × 104	4	2.62 × 104	5
F9	2.37 × 102	5	1.57 × 102	2	1.04 × 102	1	1.62 × 102	3	1.95 × 102	4
F10	9.28 × 102	3	9.47 × 102	5	3.35 × 102	1	8.79 × 102	2	9.37 × 102	4
F11	3.29 × 104	2	3.34 × 104	4	2.54 × 104	1	3.35 × 104	5	3.31 × 104	3
F12	1 × 102	1	1 × 102	1	1 × 102	1	1 × 102	1	1 × 102	1
AR		3.17		2.92		1.67		2.67		2.92

. The average ranking shows that PSO-ED performs best when $N_s=40$.

4.2. Comparison with Other PSO Variants

We use the same criteria provided by MPSO [72] to compare our PSO-ED with MPSO and its corresponding comparison algorithms for fair comparison. As shown in on

Table 5. The popular algorithms used for comparison.

No.	Algorithms	Abbreviation
1	A modified particle swarm optimizer	GPSO [49]
2	Population structure and particle swarm performance	LPSO [26]
3	Defining a standard for particle swarm optimization	SPSO [74]
4	Comprehensive learning particle swarm optimizer	CLPSO [75]
5	The fully informed particle swarm	FIPS [27]
6	Dynamic multi-swarm particle swarm optimizer with local search	DMSPSO [35]
7	Modified particle swarm optimization and its applications	MPSO [72]

, these popular algorithms are GPSO [49], LPSO [26], SPSO [74], CLPSO [75], FIPS [27], and DMSPSO [35]. The algorithms’ performances are characterized by statistical means and standard deviations. Note that the results of the seven PSO variants are directly referenced from literature [72]. For all the algorithms, the swarm size is set to 40, therefore the maximum number of iterations is 2500 for 10-D and 7500 for 30-D. The statistical results for the 12 test functions in 10-D and 30-D are summarized in

Table 6. Comparison of PSO-ED with 7 popular PSO variants for 10-D case.

		GPSO	LPSO	SPSO	CLPSO	FIPS	DMSPSO	MPSO	PSO-ED
F1	Mean	5.05 × 106	1.17 × 105	2.78 × 104	5.53 × 105	2.51 × 105	9.64 × 104	2.63 × 104	2.03 × 104
	Std	2.31 × 107	7.30 × 104	1.01 × 104	7.42 × 104	3.50 × 104	2.46 × 105	6.61 × 103	1.65 × 104
F2	Mean	6.02 × 108	2.94 × 107	6.15 × 103	4.73 × 104	6.49 × 103	1.38 × 104	6.36 × 103	5.80 × 102
	Std	1.05 × 109	7.79 × 107	2.83 × 104	8.12 × 104	3.86 × 102	5.47 × 103	2.12 × 102	9.94 × 102
F3	Mean	2.03 × 101	2.02 × 101	2.02 × 101	2.02 × 101	2.03 × 101	2.01 × 101	1.87 × 101	2 × 101
	Std	1.12 × 101	4.07 × 102	2.99 × 102	2.41	1.51 × 101	1.64 × 101	1.18 × 10−2	4.34 × 10−3
F4	Mean	1.48 × 101	1.35 × 101	4.87	1.02 × 101	6.75	9.19	3.23	1.58 × 101
	Std	1.12 × 101	9.61	4.98	3.73 × 101	1.72	6.16	1.76 × 10−2	5.94
F5	Mean	5.76 × 102	2.91 × 102	4.14 × 102	6.11 × 102	5.14 × 102	3.34 × 102	1.89 × 102	5.48 × 102
	Std	9.36 × 101	8.95 × 102	6.49 × 102	1.46 × 102	4.58 × 102	1.76 × 102	8.85 × 101	1.75 × 102
F6	Mean	4.69 × 103	5.83 × 103	1.13 × 103	1.72 × 103	7.11 × 102	1.78 × 103	5.20 × 102	4.11 × 102
	Std	6.41 × 103	1.04 × 104	5.75 × 103	3.96 × 102	7.15 × 102	1.38 × 104	3.17 × 102	2.36 × 102
F7	Mean	5.56	3.60	1.34	1.53	8.87 × 10−1	1.96	8.99 × 101	2.04
	Std	2.12	4.30 × 101	1.99 × 101	4.24 × 101	2.39 × 101	4.07 × 101	1.23 × 10−1	6.38 × 10−1
F8	Mean	6.53 × 103	1.81 × 103	1.27 × 103	4.87 × 102	6.89 × 102	1.79 × 102	4.46 × 102	3.09 × 102
	Std	4.98 × 104	3.51 × 103	2.54 × 103	2.88 × 102	1.67 × 103	6.33 × 101	1.28 × 102	2.23 × 102
F9	Mean	1.07 × 102	1.01 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102
	Std	1.79 × 101	1.01	7.99 × 102	1.39 × 102	1.92 × 101	5.41 × 101	1.06 × 10−2	7.97 × 10−2
F10	Mean	3.14 × 102	2.59 × 102	2.15 × 102	1.62 × 101	4.64 × 101	1.31 × 102	1.90 × 102	7.91 × 102
	Std	2.22 × 101	1.11 × 102	5.62 × 102	5.15	1.13 × 102	4.49 × 102	2.66 × 101	8.97 × 102
F11	Mean	6.25 × 103	5.47 × 103	6.19 × 103	2.45 × 103	2.29 × 103	3.17 × 103	2.71 × 103	6.78 × 102
	Std	4.37 × 103	6.32 × 103	8.62 × 103	4.51 × 102	1.70 × 103	2.89 × 103	7.25 × 102	1.19 × 103
F12	Mean	1.25 × 102	1.06 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102
	Std	8.43	4.05 × 101	0	0	1.73 × 10+12	2.63 × 10+13	5.68 × 10+19	2.65 × 10−5

and

Table 7. Comparison of PSO-ED with 7 popular PSO variants for 30-D case.

		GPSO	LPSO	SPSO	CLPSO	FIPS	DMSPSO	MPSO	PSO-ED
F1	Mean	2.72 × 108	3.52 × 107	2.23 × 105	5.56 × 106	4 × 106	6.72 × 106	1.79 × 106	3.03 × 105
	Std	3.54 × 108	5.92 × 107	2.42 × 105	5.80 × 106	2.42 × 105	1.15 × 107	2.38 × 105	1.47 × 105
F2	Mean	2.23 × 10+10	1.91 × 109	3.70 × 103	4.48 × 103	6.29 × 103	3.37 × 103	1.46 × 103	2.24 × 102
	Std	1.96 × 109	2.09 × 109	2.44 × 104	1.70 × 103	1.43 × 104	2.92 × 103	7.28 × 101	4.52 × 102
F3	Mean	2.08 × 101	2.08 × 101	2.09 × 101	2.09 × 101	2.10 × 101	2.05 × 101	2.03 × 101	2 × 101
	Std	7.54 × 103	3.58 × 101	8.30 × 102	1.90 × 102	9.90 × 102	1.53 × 101	2.33 × 10−3	7.33 × 10−3
F4	Mean	1.55 × 102	1.03 × 102	3.55 × 101	9.02 × 101	1.54 × 102	8.32 × 101	1.91 × 101	1.42 × 102
	Std	8.14 × 101	1.29 × 101	3.38	3.63	4.96 × 101	1.54 × 101	4.06 × 10−1	1.80 × 101
F5	Mean	3.54 × 103	3.19 × 103	3.97 × 103	4.62 × 103	6.31 × 103	3.79 × 103	2.62 × 103	3.10 × 103
	Std	3.22 × 102	8.32 × 102	1.39 × 102	6.03 × 102	1.51 × 103	5.40 × 102	1.24 × 102	3.63 × 102
F6	Mean	1 × 107	1.30 × 106	1.14 × 105	3.53 × 105	4.37 × 105	1.70 × 105	4.41 × 104	3.05 × 104
	Std	7.16 × 107	5.56 × 105	3.13 × 104	1.71 × 105	5.05 × 105	8.56 × 104	7.17 × 103	1.90 × 104
F7	Mean	4.77 × 101	2.46 × 101	9.20	9.10	1.24 × 101	1.29 × 101	9.98	1.04 × 101
	Std	3.55 × 101	3.69 × 101	1.25	8.60 × 101	4.09	9.84 × 10−2	3.15	1.36
F8	Mean	1.73 × 106	2.36 × 105	3.22 × 104	6.36 × 104	4.73 × 104	7.95 × 104	2.64 × 104	1.46 × 104
	Std	2.05 × 107	4.11 × 105	2.60 × 104	9.24 × 104	9.13 × 103	1.91 × 105	3.36 × 103	8.03 × 103
F9	Mean	2.15 × 102	1.29 × 102	1.03 × 102	1.04 × 102	1.03 × 102	1.04 × 102	1.03 × 102	1.04 × 102
	Std	8.37 × 101	5.08	1.98 × 101	1.81 × 101	8.50 × 102	7 × 102	8.07 × 10−3	2.02 × 10−1
F10	Mean	1.24 × 103	1.04 × 103	5.91 × 102	3.55 × 102	4.39 × 102	5.98 × 102	6.03 × 102	1.81 × 104
	Std	3.88 × 102	2.09 × 102	7.22 × 101	4.81 × 101	8.05 × 101	7.56 × 102	1.88 × 101	7.73 × 103
F11	Mean	4.86 × 104	3.85 × 104	3.36 × 104	2.89 × 104	2.73 × 104	3.07 × 104	2.73 × 104	2.54 × 104
	Std	4.47 × 104	4.23 × 103	3.82 × 103	3.80 × 102	2.97 × 103	1.27 × 103	9.13 × 102	1.29 × 104
F12	Mean	7.58 × 102	1.22 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102	1 × 102
	Std	3.01 × 103	2.77 × 101	0	1.88 × 10+13	3.50 × 10+10	1.59 × 105	2.12 × 10+10	1.10 × 10−5

, respectively. Following conventions, the lowest mean and standard deviation in each line are regarded as the best results and are highlighted in bold. To validate the significance of the PSO-ED, Non-parametric Wilcoxon signed-rank test is conducted between PSO-ED and other PSO variants. The symbol “+”, “0” and “-” means that the statistical mean values of the proposed PSO-ED are better, equal and worse than those of the compared algorithms.

While conducting the comparison experiments, the crucial control parameters of our PSO-ED are set as follows: $N_s=40$ (same as the setting of MPSO [72]), $N_{total}=FEs/N_s, N_{smin}=0.01N_{total}, N_{smax}=0.1N_{total}, \alpha =0.01, N_{umax}=0.01N_{total}, v_{ub}=0.01\left(x_{ub}-x_{lb}\right)$. As shown in Table 6 for the 10-D case, compared with the other 7 algorithms, out of the total of 12 functions, the mean values of our algorithm achieve better solutions than the other 7 algorithms on 4 functions (F₁, F₂, F₆ and F₁₁), and achieve exactly the same best mean values with other 5 algorithms on 2 functions (F₉ and F₁₂). However, compared with MPSO on F₃, F₄, F₅, DMSPSO on F₈, FIPS on F₇, CLPSO on F₁₀, our PSO-ED is slightly weaker.

As shown in Table 7 for 30-D case, compared to the counterparts, out of the total of 12 functions, our algorithm obtains the best mean values on 6 functions (F₂, F₃, F₆, F₈, F₁₁ and F₁₂). However, PSO-ED is slight weaker than MPSO on F₄, F₅, F₈, SPSO on F₁.

As shown in

Table 8. Statistical analysis of Wilcoxon signed-rank test between PSO-ED and other PSO variants.

	GPSO		LPSO		SPSO		CLPSO		FIPS		DMSPSO		MPSO
D	10	30	10	30	10	30	10	30	10	30	10	30	10	30
F1	+	+	+	+	+	-	+	+	+	+	+	+	+	+
F2	+	+	+	+	+	+	+	+	+	+	+	+	+	+
F3	+	+	+	+	+	+	+	+	+	+	+	+	-	+
F4	-	+	-	-	-	-	-	-	-	+	-	-	-	-
F5	+	+	-	+	-	+	+	+	-	+	-	+	-	-
F6	+	+	+	+	+	+	+	+	+	+	+	+	+	+
F7	+	+	+	+	+	-	+	-	-	+	-	+	+	-
F8	+	+	+	+	+	+	+	+	+	+	-	+	+	+
F9	+	+	+	+	0	-	0	0	0	-	0	0	0	-
F10	-	-	-	-	-	-	-	-	-	-	-	-	-	-
F11	+	+	+	+	+	+	+	+	+	+	+	+	+	+
F12	+	+	+	+	0	0	0	0	0	0	0	0	0	0
+/0/−	10/0/2	11/0/1	9/0/3	10/0/2	7/2/3	6/1/5	8/2/2	7/2/2	6/2/4	9/1/2	5/2/5	8/2/2	6/2/4	6/1/5

, in the Non-parametric Wilcoxon signed-rank test of PSO-ED and other algorithms, PSO-ED have achieved obvious advantages on 10-D and 30-D except that MPOS and PSO-ED achieved the same optimal result on 10-D.

In conclusion, although PSO-ED is weak in solving a few test functions, its results are superior to those of popular PSO variants such as MPSO, DMSPSO, FIPS, CLPSO, SPSO, LPSO, and GPSO.

5. Conclusions

In this paper, we proposed a novel measure of diversity based on sub-space encoding for the search space; a notion of exploration degree based on the diversity in the exploration, exploitation and convergence states, which efficiently evaluates the degree of demand for the dispersion of the swarm; a technique of disturbance update mode for updating the poor-performed particles’ positions to save the cost of function evaluations (FEs) on them. Since the diversity evaluation can reflect the swarm distribution very well, it can provide a better basis for adaptive parameter adjustment strategy and assist the swarm to jump out of the local traps. Therefore, this method is more suitable for the complex multimodal optimization.

The effectiveness of the developed techniques was validated through a set of benchmark functions in CEC2015. Compared with 7 popular PSO variants, out of the 12 benchmark functions, PSO-ED obtains 6 best results for both the 10-D and 30-D cases.

However, the stability of the developed PSO-ED can be further improved and is worthy of investigation in the future work. For example, for F₁₂ in 10-D and 30-D, although PSO-ED and SPSO both achieve the optimal mean, PSO-ED is slightly weaker in the std term, which means that PSO-ED suffers from risk of falling into some local optimum.