MultiKOC: Multi-One-Class Classifier Based K-Means Clustering

Abstract

In the computational biology community there are many biological cases that are considered as multi-one-class classification problems. Examples include the classification of multiple tumor types, protein fold recognition and the molecular classification of multiple cancer types. In all of these cases the real world appropriately characterized negative cases or outliers are impractical to achieve and the positive cases might consist of different clusters, which in turn might lead to accuracy degradation. In this paper we present a novel algorithm named MultiKOC multi-one-class classifiers based K-means to deal with this problem. The main idea is to execute a clustering algorithm over the positive samples to capture the hidden subdata of the given positive data, and then building up a one-class classifier for every cluster member’s examples separately: in other word, train the OC classifier on each piece of subdata. For a given new sample, the generated classifiers are applied. If it is rejected by all of those classifiers, the given sample is considered as a negative sample, otherwise it is a positive sample. The results of MultiKOC are compared with the traditional one-class, multi-one-class, ensemble one-classes and two-class methods, yielding a significant improvement over the one-class and like the two-class performance.

1. Introduction

The aim of the one-class classification model is to distinguish data belonging to the target class from other possible classes [1,2,3,4,5]. This is an interesting problem because there are many real-world situations where a representative set of labeled examples for the second class is difficult to obtain or not available at all. This situation occurs in many real-word problems, such as in medical diagnosis for breast cancer detection [6,7], in the prediction of protein–protein interactions [8], the one-class recognition of cognitive brain functions [3], text mining [9], functional Magnetic Resonance Imaging [10], signature verification [11], biometrics [12] and bioinformatics [5,13,14,15,16], and social media [17].

In the literature, a vast amount of research has been carried out to tackle the problem of how to implement a multi-class classifier by an ensemble of one-class classifiers [18,19]. Lai et al. [20] proposed a method for combining different one-class classifiers for the problem of image retrieval. They reported that combining multi-SVM-based classifiers improves the retrieval precision. In a similar way, Tax et al. [21] suggest combining different one-class classifiers to improve the performance and the robustness of the classification for the handwritten digit recognition problem.

A multi-one-class SVMs technique (OC-SVM) that combines a beforehand clustering process for detecting hidden messages in digital images was provided by Lyu et al. [22]. They showed that a multi-one-class SVM significantly simplifies the training stage of the classifiers and that even though the overall detection improves with an increasing number of hyperspheres, the false-positive rate increases considerably when the number of the hyperspheres increases. Menahem et al. [23] suggested a different multiple one-class classification approach called TUPSO, which combines multi-one-class classifiers via a metaclassifier. They showed that TUPSO outperforms existing methods such as the OC-SVM. Ban et al. [24] proposed multiple one-class classifiers to deal with the nonlinear classification and the feature space problem. The multiple one-class classifiers were trained on each class in order to extract a decision function based on minimum distance rules. This proposed method outperforms the OC-SVM, as shown in their experiments.

In the domain of the computational biology community much work exists on multiple one-class classification. A multi-one-class classification approach to detect novelty in gene expression data was proposed by Spinosa et al. [25]. The approach combined different one-class classifiers such as the OC-KNN and OC-Kmeans. For a given sample, the final classification is considered by the majority votes of all classifiers. It was shown that the robustness of the classification was increased because each classifier judges the sample from a different point-of-view. For the avian influenza outbreak classification problem, a similar approach was provided by Zhang et al. [26].

In classification we assume that two-class data consist of two pure compact clusters of data, but in many cases one of the clusters might consist of multiple subclusters. For a certain dataset, a special method is required and the one-class reveals insufficient results. In this paper we propose a new approach called MultiKOC (Multi-one-class classifier based on K-means) which is an ensemble of one-class classifiers that, as a first step, devises the positive class into clusters or-subdata using the K-means applied to the examples of the data (not on the features space) and in the second step it trains a one-class classifier for each cluster (subdata). The main idea of our approach is to execute the K-means clustering algorithm over the positive examples. Next, a one-class classifier for each cluster is constructed separately. For a given new sample, our algorithm applies all the generated one-class classifiers. If it is classified as positive by at least one of those classifiers then it will be considered as a positive sample, otherwise it is considered as a negative sample. In our experiments we show that the proposed approach outperforms the one-class. In addition, we show that MultiKOC is stable over a different number of clusters.

The most significant contributions of our research are:

• The proposed new approach in the way that it first clusters the positive data into clusters that each cluster form a subdata, before the classification process.
• The suggested preprocessing method (i.e., the clustering phase) prevents the drawback of using only a single hypersphere generated by the one-class classifier which may not provide a particularly compact support for the training data.
• Experimental results showing that our new approach significantly improves the accuracy of the classification against other OC classifieres.

The rest of this paper is organized as follows: Section 2 describes the necessary preliminaries. Our MultiKOC approach is described in Section 3 and evaluated in Section 4. Our main discussions and future work can be found in Section 5.

2. Preliminaries

2.1. One-Class Methods

In general, a binary learning (two-class) approach to a given data discovery considers both positive and negative classes by providing examples from the two-classes to a learning algorithm in order to build a classifier that will attempt to discriminate between them. The most common term for this kind of learning is supervised learning where the labels of the two-classes are known beforehand and are provided by the teacher (supervisor).

One-class uses only the information for the target class (positive class) to build a classifier which is able to recognize the examples belonging to its target and reject others as outliers. Among the many classification algorithms available, we chose four one-class algorithms to compare their one-class and two-class versions with our suggested tool. We give a brief description of different one-class classifiers and we refer to the references [27,28] for additional details including a description of the parameters and thresholds. The LIBSVM library [29] was used as implementation of the OC-SVM (one-class using the RBF kernel function). The WEKA software [30] that is integrated in Knime [31] was used for the one and two-class classifiers.

2.2. One-Class Support Vector Machines (OC-SVM)

Support Vector Machines (SVMs) are a learning machine developed as a two-class approach [32,33]. The use of one-class SVM was originally suggested by [28]. One-class SVM is an algorithmic method that produces a prediction function trained to “capture” most of the training data. For that purpose, a kernel function is used to map the data into a feature space where the SVM is employed to find the hyperplane with maximum margin from the origin of the feature space. In this use, the margin to be maximized between the two classes (in two-class SVM) becomes the distance between the origin and the support vectors which define the boundaries of the surrounding circle, (or hypersphere in high-dimensional space) which encloses the single class. The study of [34] presents a multi-class classifier based on weighted one-class support vector machines (OCSVM) operating in the clustered feature space reporting very interesting results.

2.3. One-Class Classifiers

Hempstalk et al. [35] have developed many one-class classifiers that rely on the simple idea of using the standard two-class learning algorithm by combining density and class probability estimation. They have used the reference distribution to generate artificial data to be used as the negative examples. In other word, the two-class algorithm requires both positive and negative data. We assume that the positive data are given so one need to generate artificial negative data to be subject to the two-class classifier. The idea suggested by them actually allows to convert each two-class to one-class classifiers by generating the artificial negative data.

The one-class classification, by combining density and class probability estimation, was implemented on WEKA. We have considered the related node in Knime called OneClassClassifier (version 3.7) in order to examine different OC classifiers. We have considered J48, random forest, Naïve Bayes and SVM.

3. MultiKOC—Multi-One-Class Classifiers

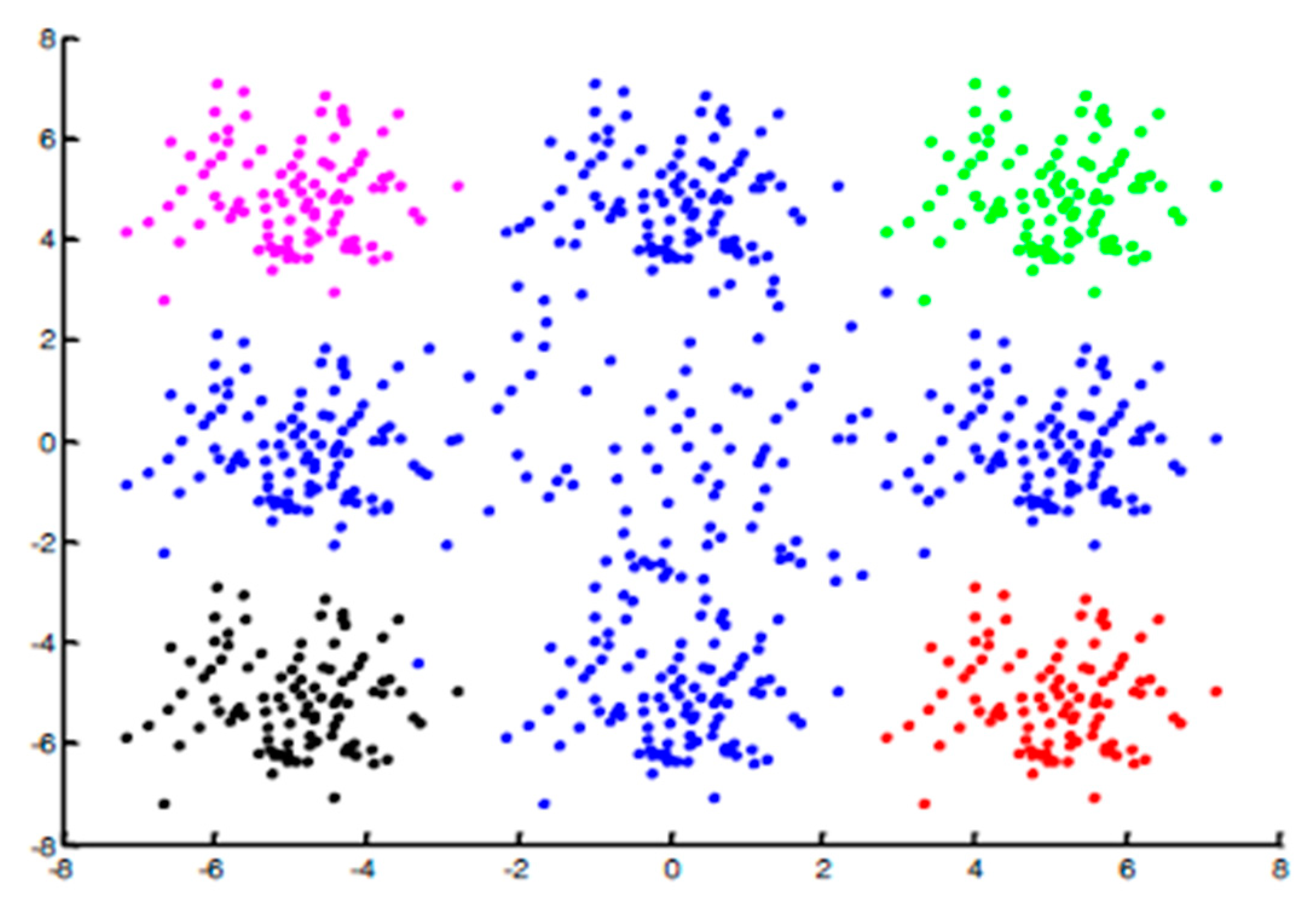
As described in the previous methods, the classifier will be trained on a positive class. However, in real-world data, the positive class might consist of different subsets (see Figure 1). The classic multi-one-class classifiers use the positive samples in order to train different classifiers, then they run the ensemble classification for new instances. As a result, if we train the classifier over all the points from those subsets then the negative class will be a part of this training procedure, yielding low performance.

The main problem with this technique (i.e., classic multi-one-class) is that the one-class classifiers do not see the negative samples (Blue points in Figure 1). As a result, the classifier will classify those points (blue points) as a positive class. To overcome this issue, we decided to train one-classifier for each subset and instead to execute one-classifier we apply multi-one-class classifiers using only one subset. For a given new instance all the one-class classifiers are employed, where if at least one of them assigns it to the positive class then it will be considered as a positive. Otherwise, it will be considered as a negative.

The main challenge of this technique is to identify the subsets. For instance, in Figure 1 we aim to identify the pink, green, black, and red subsets. Based on the fact that the points belonging to the same subset are more similar than the samples from different subsets we decided to use clustering techniques to identify the different subsets as illustrated in Figure 2. It is important to note that here: (1) we cluster only the positive class into several clusters and (2) based on our empirical experiments we see that the number of clusters is not critical. Moreover, considering two different subsets as a one subset is a more problematic situation than splitting one subset into two subsets.

To alleviate this type of data we propose the MultiKOC Classifier that works subset of the positive data. Our approach trains the one-class classifier on each subset of the positive class detected by the clustering algorithm K-means (see Figure 3) as following Algorithm 1:

Algorithm 1: MultiKOC Classifier Algorithm.

Select k—the number of the subsets; Apply the K-means clustering algorithm over the positive class (apply on the examples of the training set); For each cluster build a one-class classifier; Given an unlabeled instance $x$; Let $class\leftarrow negative$; For each classifier $cl{f}_i$do; If $cl{f}_i\left(x\right)$ is positive then i. $class\leftarrow positive$

It is important to note that the choice of the clustering algorithm and the number of the clusters is still a challenge. We have several proposed directions for dealing with this challenge, such as: (1) selecting the clustering algorithm to organize the data shapes; (2) using measures to evaluate the performance of the clustering; (3) using different hyperparameters to obtain the best clustering results (such as the K in K-means). However, selecting the clustering algorithm is the user choice based on the given data set.

Finally, although the proposed method uses the K-means clustering algorithm, it is different from the OC-Kmeans algorithm. In OC-Kmeans, the algorithm classifies each new instance based on its distance from the centroids of the clusters. In contrast, our method builds a classifier over each cluster, and then classifies new instances using those classifiers.

4. Results

We conducted experiments on three different datasets. The first dataset is syntactic which consists of two classes positive and negative samples as shown on Figure 1. Here, the data contains two classes; positive and negative of 800 samples each. The positive examples are divided into four clusters beforehand.

The second and the third data set are from the UCI repository [36]. In these data sets there are three classes. The Iris data set contains 3 classes of 50 samples each, where each class refers to a type of iris plant. The third data set is called “Thyroid gland data” which contains 150 samples from class “normal”, 35 hyper, and 30 hypo class (in our experiments we assign normal as class 1, hyper as class 2 and hypo as class 3).

For both data sets “Iris” and “Thyroid gland data”, each time in our experiments, one-class out of the three classes was considered as the negative class, while the other two classes were considered as positive class. The generated datasets are summarized in

Table 1. Description of the data sets. Positive and negative classess.

Data	Positive Class	Negative Class
SynData	blue	red
Iris-setosa-versicolor	setosa and versicolor	verginica
Iris-setosa-verginica	setosa and verginica	versicolor
Iris-versicolor-verginica	versicolor and verginica	setosa
newthyroid class 1	class 1	class 2 and class 3
class1_2_newthyroid	class 1 and class 2	class 3
class1_3_newthyroid	class 1 and class 3	class 2
class2_3_newthyroid	class 2 and class 3	class 1

.

In each experiment for the OC classifiers, the positive data were split into two subsets—one for training and the other for testing—while all the examples from the negative class were used for testing and not seen in training the OC. All algorithms were trained using 80% of the positive class and the remaining 20%, together with all the negative examples, were used for testing. Each experiment was repeated one hundred times and the averaged results were reported.

For the two-class classifiers we considered both the positive and negative data. Similarly, the data were split into training and testing sets, where 80% was used for training and 20% for testing.

We tested the performance of MultiKOC using four different classifiers: J48, SVM, Naïve Bayes, and Random Forest versus that of the classical one-class versions of these classifiers. Additionally, we tested the MultiKOC with different values of k that define the number of clusters generated by K-means. We have considered k = 1, 2, …, 6.

The first experiment was conducted using the J48 classifier, as can be seen in

Table 2. Results summary for J48 classifier. The column #clusters is the optimal number of clusters obtained for MultiKOC.

Data	#Clusters	MultiKOC(J48)	OC-J48	Two-J48
SynData	3	0.263	0.405	0.999
Iris-setosa-versicolor	3	0.325	0.000	0.960
Iris-setosa-verginica	3	0.303	0.000	0.956
Iris-versicolor-verginica	4	0.286	0.754	0.995
newthyroid class 1	2	0.330	0.275	0.947
class1_2_newthyroid	2	0.447	0.052	0.980
class1_3_newthyroid	2	0.535	0.387	0.979
class2_3_newthyroid	5	0.102	0.000	0.886
Average		0.355	0.267	0.974

. The performance of the multiKOC(J48) outperforms the classic one-class classifier.

The second experiment’s results are summarized in

Table 3. Results summary for Naïve Bayes classifier. The column #clusters is the optimal number of clusters obtained for MultiKOC.

Data	#Clusters	MultiKOC(NB)	OC-NB	Two-NB
SynData	3	0.550	0.147	0.876
Iris-setosa-versicolor	3	0.529	0.597	0.929
Iris-setosa-verginica	3	0.443	0.271	0.937
Iris-versicolor-verginica	4	0.498	0.963	1.000
newthyroid class 1	2	0.771	0.768	0.954
class1_2_newthyroid	2	0.816	0.854	0.986
class1_3_newthyroid	2	0.723	0.720	0.986
class2_3_newthyroid	5	0.083	0.081	0.873
Average		0.619	0.617	0.952

. The experiment was conducted using the Naïve Bayes classifier. The performance of the proposed method using the Naïve bayes classifier (i.e., multiKOC(J48)) outperforms the classic one-class Naïve Bayes classifier.

The third experiment was conducted using the Support Vector Machine classifier, as can be seen in

Table 4. Results summary for Support Vector Machine classifier. The column #clusters is the optimal number of clusters obtained for MultiKOC.

Data	#Clusters	MultiKOC(SVM)	OC-SVM	Two-SVM
SynData	3	0.150	0.157	1.000
Iris-setosa-versicolor	3	0.792	0.691	0.980
Iris-setosa-verginica	3	0.258	0.275	0.979
Iris-versicolor-verginica	4	0.963	0.682	1.000
newthyroid class 1	2	0.355	0.242	0.971
class1_2_newthyroid	2	0.676	0.592	0.925
class1_3_newthyroid	2	0.498	0.302	0.932
class2_3_newthyroid	5	0.082	0.088	0.944
Average		0.527	0.420	0.970

. The performance of the multiKOC(SVM) outperforms the classic one-class SVM classifier in five experiments out of eight. Moreover, as can be seen in Table 4, the averaged performance of the new proposed method outperforms the classical one by more than 10%.

The fourth experiment was conducted using the Random Forest classifier, as can be seen in

Table 5. Results summary for Random Forest classifier. The column #clusters is the optimal number of clusters obtained for MultiKOC.

Data	#Clusters	MultiKOC(RF)	OC-RF	Two-RF
SynData	3	0.167	0.357	0.999
Iris-setosa-versicolor	3	0.333	0.312	0.966
Iris-setosa-verginica	3	0.318	0.143	0.959
Iris-versicolor-verginica	4	0.433	0.367	1.000
newthyroid class 1	2	0.443	0.422	0.966
class1_2_newthyroid	2	0.610	0.747	0.987
class1_3_newthyroid	2	0.559	0.478	0.987
class2_3_newthyroid	5	0.085	0.298	0.900
Average		0.409	0.404	0.981

. The performance of the multiKOC(RF) was equivalent to the result of the classic one-class classifier.

Moreover, we can see that in all the algorithms above, the proposed MultiKOC methods outperform or are comparable to the existing methods. The results are summarized in

Table 6. Results summary for all the classifiers from the different datasets.

Classifier	MultiKOC	OC
J48	0.355	0.267
Naïve Bayes	0.619	0.617
Support Vector Machine	0.527	0.420
Random Forest	0.409	0.404

.

Another experiment was conducted to check the effectiveness of the number of the clusters on the performance of the MultiKOC as can be seen in

Table 7. Results summary for MultiKOC method with 2, 3, 4, 5 clusters on Synthetic data.

Classifier	2	3	4	5
MultiKOC(J48)	0.233	0.263	0.167	0.167
MultiKOC(SVM)	0.148	0.150	0.153	0.158
MultiKOC(NB)	0.186	0.550	0.514	0.337
MultiKOC(RF)	0.167	0.167	0.167	0.167

,

Table 8. Results summary for MultiKOC method with 2, 3, 4, 5 clusters on Iris-setosa-versicolor data.

Classifier	2	3	4	5
MultiKOC(J48)	0.344	0.325	0.290	0.272
MultiKOC(SVM)	0.770	0.792	0.679	0.695
MultiKOC(NB)	0.388	0.529	0.547	0.379
MultiKOC(RF)	0.333	0.333	0.419	0.371

and

Table 9. Results summary for MultiKOC method with 2, 3, 4, 5 clusters on new thyroid class 1 data.

Classifier	2	3	4	5
MultiKOC(J48)	0.356	0.330	0.316	0.316
MultiKOC(SVM)	0.369	0.355	0.347	0.342
MultiKOC(NB)	0.505	0.771	0.437	0.490
MultiKOC(RF)	0.385	0.443	0.373	0.347

for each dataset.

In conclusion, in general, the performance of MultiKOC algorithm does not depend in the number of the clusters. There are few cases that the performance of some classifiers was affected by the number of clusters, as a result, our future work will be focus on this issue.

5. Discussion

This study suggests MultiKOC, a novel approach for performing one-class classification that is based on partitioning the training data into clusters to model each cluster by the one-class model.

The current results show that it is possible to build up a multi-one-class classifier with a combined clustering beforehand process based only on positive examples yielding a significant improvement over the one-class and similar results as the two-class. However, the MultiKOC would include more interpretable classifiers than the two-class version as one can perform a deep analysis to explore the hidden structure of the data. Additionally, MultiKOC is robust at dealing with outliering examples, while the one-class version might add more clusters to capture those outliers and reduce their influence on the performance of the classifications.

Further research could proceed in several interesting directions. First, the suitability of the framework of our approach for different data types could be investigated. Second, it would be interesting to apply our approach to other types of classifiers and to more robust clustering methods such as Mean-Shift [37].

In the current version of MultiKOC we have considered only a one-class algorithm. One future approach is to perform an ensemble of OC and suggest a suitable voting procedure to assign the label to the new unlabeled instance.