Damage Identification of Long-Span Bridges Using the Hybrid of Convolutional Neural Network and Long Short-Term Memory Network
Abstract
1. Introduction
2. Methodology
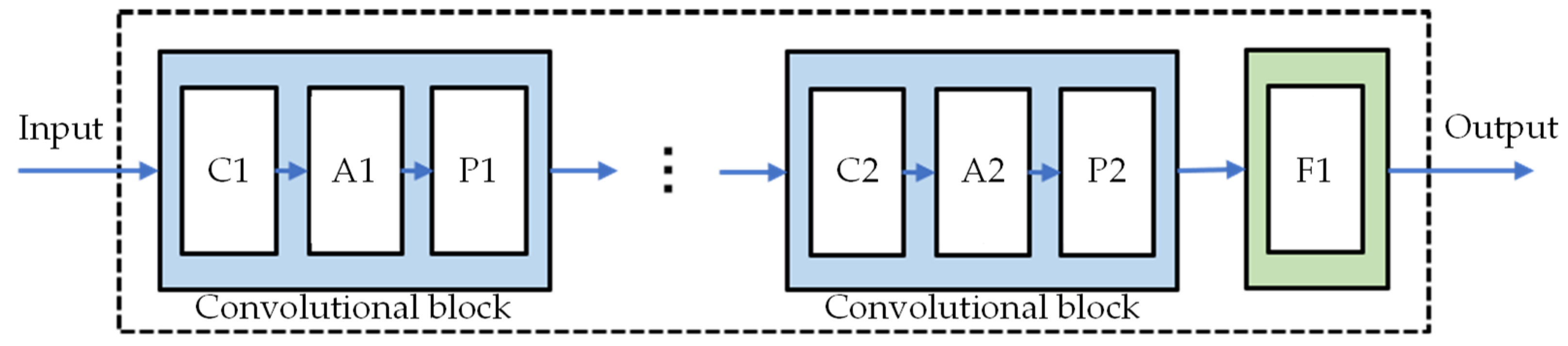
2.1. Convolutional Neural Network
2.1.1. Convolutional Layer
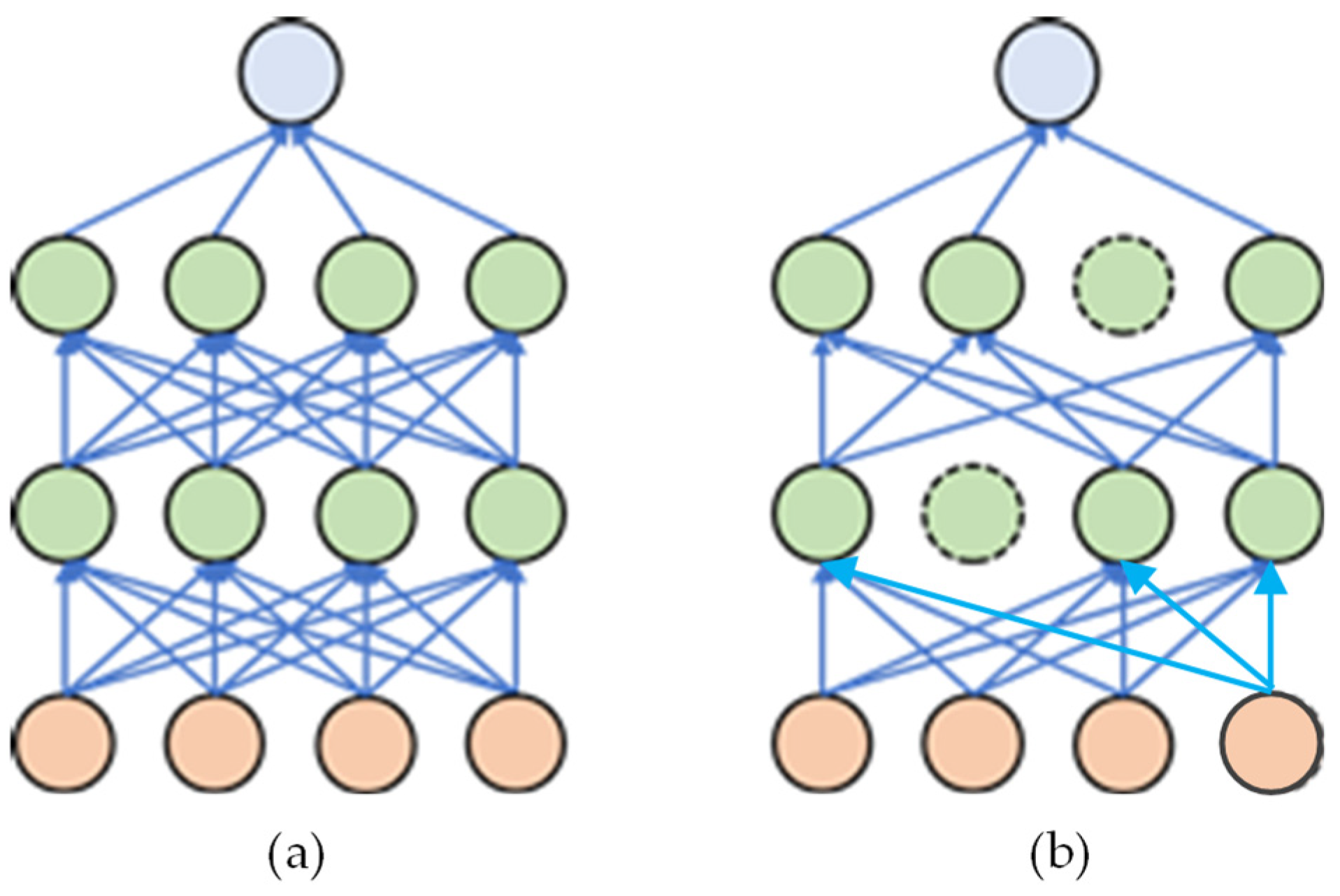
2.1.2. Pooling Layer
2.1.3. Fully Connected Layer
2.1.4. Activation Layer
2.1.5. Backpropagation Updating
- (i)
- Perform forward propagation from the input layer to the output layer:where and are the input and output of layer l, respectively. Moreover, and are the corresponding weights and biases, respectively, and is the activation function.
- (ii)
- Calculate the local gradient of the output layer:where L represents the loss function, n is the depth of the proposed CNN, and is the derivative of the activation function.
- (iii)
- According to the chain rule, calculate the local gradient of the other layers:
- (iv)
- The gradient of the weight and bias can be obtained as follows:
- (v)
- Update the weights and biases according to the learning rate and momentum m:
2.2. Long Short-Term Memory Network
2.2.1. Forget Gate
2.2.2. Input Gate
2.2.3. State Updating of Memory Unit
2.2.4. Output Gate
2.2.5. Backpropagation through Time
2.3. Optimization Technology
2.3.1. Batch Normalization
2.3.2. Dropout
2.4. Overview of the Proposed Method
- (i)
- Data acquisition and preprocessing: accelerations under different damage scenarios are obtained and normalized.
- (ii)
- Building database: accelerations of each measuring point obtained under the same damage scenario are stacked into a data matrix with dimensions , where m is the number of measuring points and n is the sequence length. Then, the data matrix is divided into k blocks with dimensions ; consequently, the number of data samples under each damage scenario expands to k. After the database is built, it is divided into a training set and a validation set.
- (iii)
- Model construction and training: the framework of the CNN-LSTM model is constructed, and the features extracted by CNN and LSTM are merged in the fully connected layer. Then, the training and validation sets are utilized to train and verify the model, and the model is optimized according to the training results to find a damage identification model with better performance.
- (iv)
- Damage identification: accelerations under an unknown state are sent to the trained model to locate damage and predict the severity.
3. Numerical Example
3.1. Details of the Long-Span Suspension Bridge
3.2. Setting Damage Scenarios and Building Database
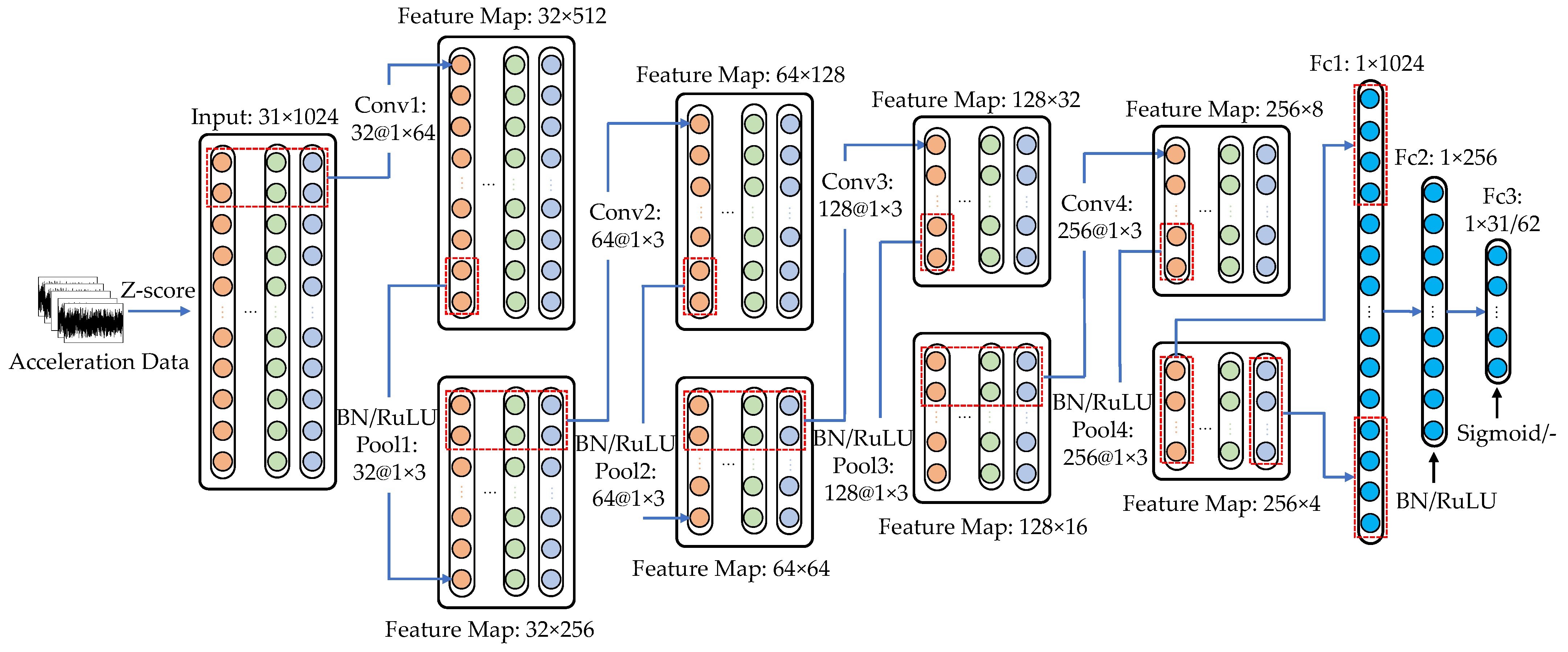
3.3. Architecture of the Proposed CNN-LSTM
3.4. Model Training and Hyperparameter Optimization
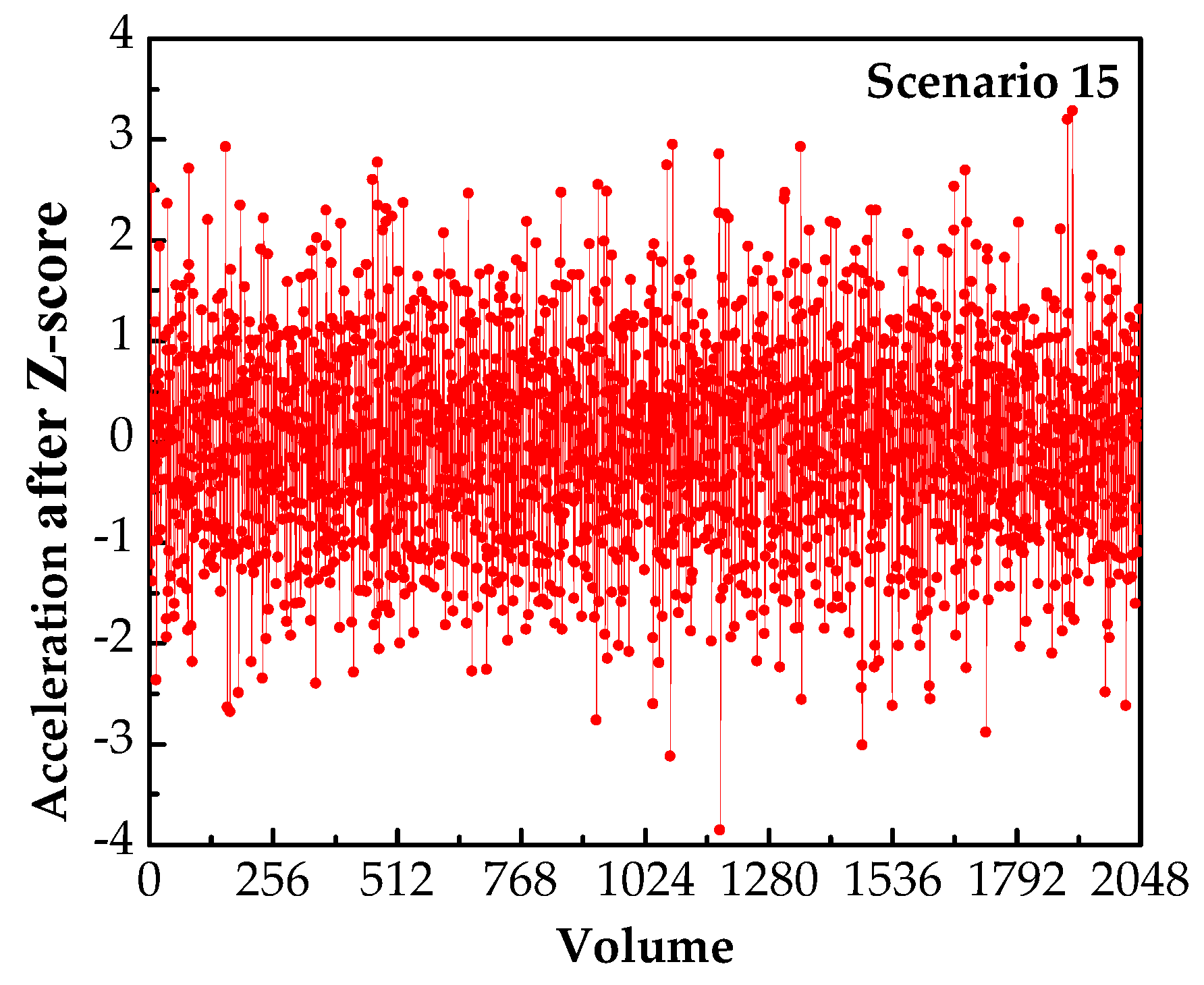
3.5. Damage Localization of Suspension Bridge Hangers
- (i)
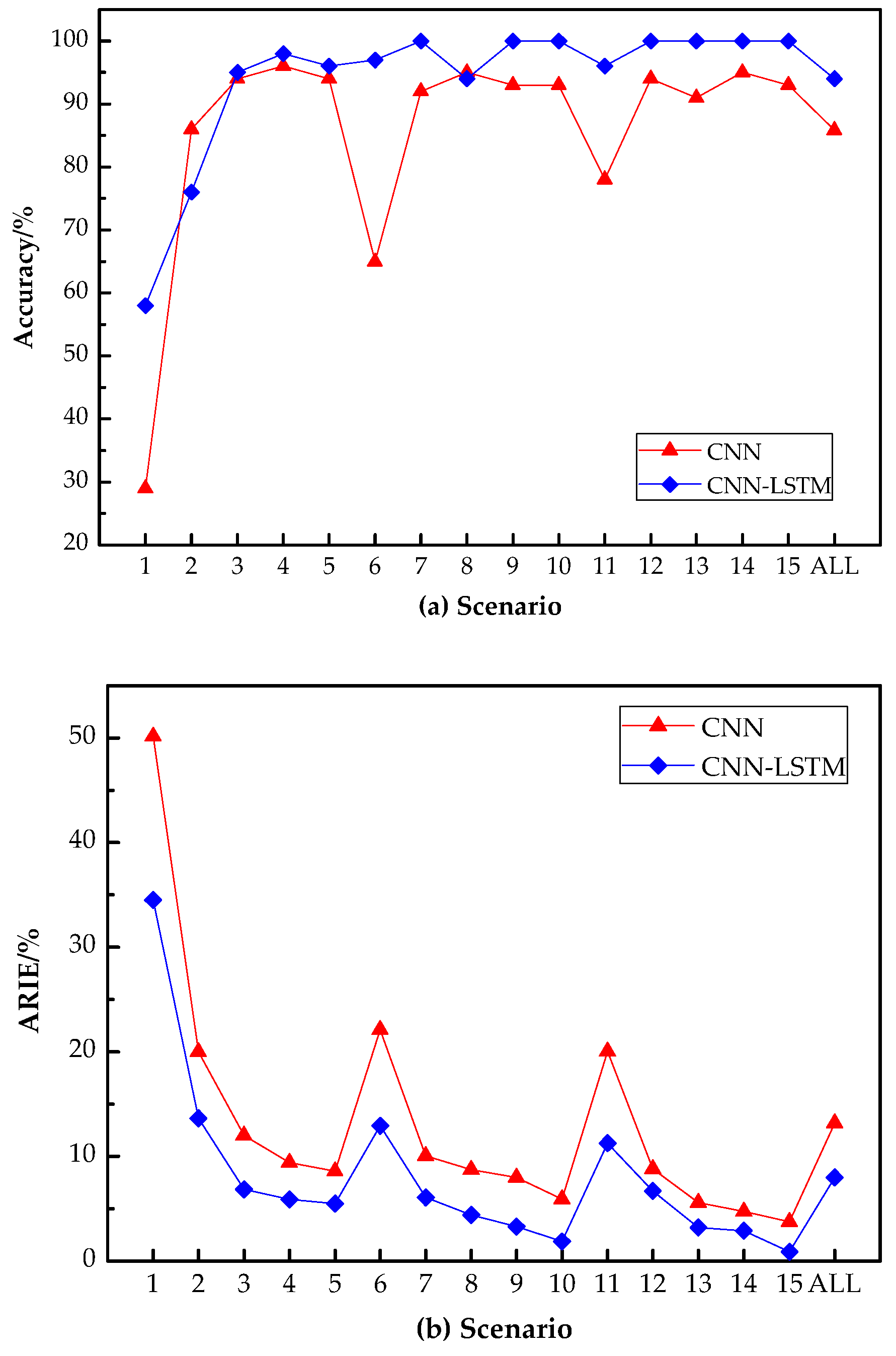
- The accuracy of damage localization of the hangers in the test set reaches 94.0%, showing that the proposed CNN-LSTM can effectively complete the task of damage localization.
- (ii)
- Comparing the recognition results of different damage scenarios, the accuracy of the CNN-LSTM model in damage localization is between 58.0 and 100%. The accuracy in scenarios 1 and 2 is relatively low, i.e., 58 and 76%, respectively, and the accuracy of the other scenarios remains above 94%. The comparison results show that except for scenarios 1 and 2, the CNN-LSTM-based damage identification method has higher accuracy in locating the damage of hangers.
- (iii)
- When comparing the recognition results of different damage types, the proposed method has little difference in the accuracy of a single damaged hanger, as well as two and three damaged hangers. The accuracy increases from 84.6 to 99.2%, which is an increase of approximately 15%. From the above results, it can be inferred that the accuracy of the proposed model in damage localization is less affected by the number of damaged hangers.
3.6. Damage Severity Prediction of Suspension Bridge Hangers
- (i)
- The ARIE of the CNN-LSTM model for the damage severity prediction of hangers is 8.0% in the test set. The ARIE under different damage scenarios is between 0.90 and 34.52%, and the ARIE under most damage scenarios is below 7.0%.
- (ii)
- For the same damage type, the ARIE decreases as the damage severity increases. The single damage scenarios decrease the fastest, with a decrease of approximately 29.03%, and the two and three damaged scenarios decrease by 11.06 and 10.37%, respectively. It can also be found from the ARIE results of the different damage severities that the CNN-LSTM model has relatively small prediction errors for larger damage severities (≥15%), while the accuracy of damage prediction for smaller damage severities (such as 5%) is poor.
- (iii)
- For the same damage severity, as the number of damaged hangers increases, ARIE shows an overall downward trend.
4. Discussion
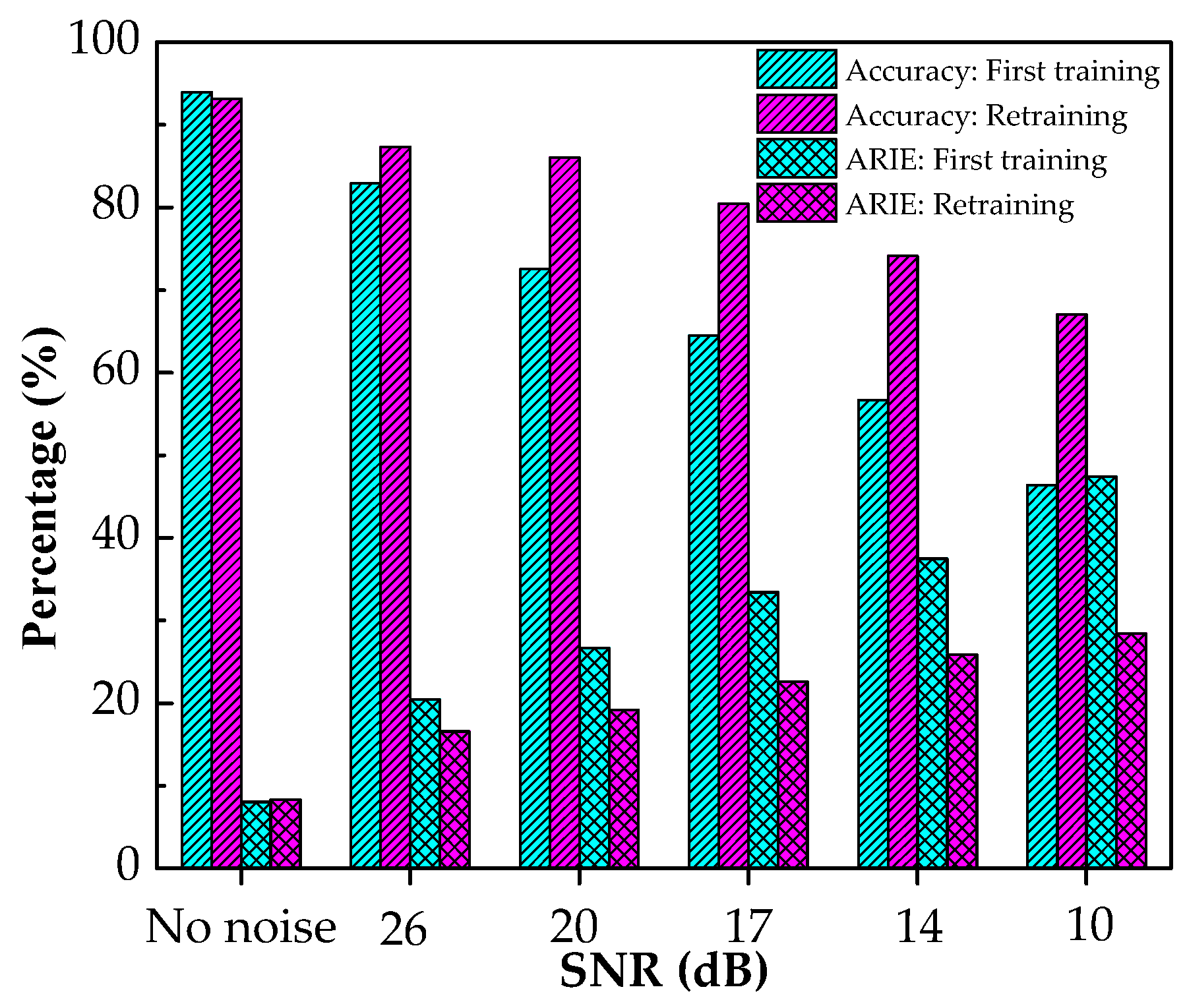
4.1. Influence of Environmental Noise on the Proposed Method
4.2. Performance Comparison
5. Conclusions
- (1)
- A database containing 8670 damage samples was constructed and divided into a training set, validation set, and test set. Afterward, the training set and the validation set were used to train and select the proposed CNN-LSTM model. For the entire test set, the accuracy of the damage localization of hangers reached 94.00%, and the ARIE of the damage severity prediction was just 8.00%.
- (2)
- To study the noise immunity of the proposed method, noise with different signal-to-noise ratios was added to the samples in the database, and then the CNN-LSTM model was retrained, and the test set after adding noise was predicted. The results show that when the SNR is 3.33, the accuracy of damage localization reached 67.06%, and the ARIE of the damage severity identification was 31%.
- (3)
- The performance improvement of the CNN-LSTM model was investigated. The damage recognition performances of the CNN and CNN-LSTM models were compared and analyzed. The results show that the accuracy of damage localization based on CNN-LSTM increased by 8.13%, and the ARIE of the damage severity prediction decreased by 5.20% compared with CNN.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Liu, T.; Zhou, J.; Chen, L.; Yang, X. Relationship between shear-stress distribution and resulting acoustic-emission variation along concrete joints in prefabricated girder structures. Eng. Struct. 2019, 196, 109319. [Google Scholar] [CrossRef]
- Wheeler, B.J.; Karimi, H.A. Deep Learning-Enabled Semantic Inference of Individual Building Damage Magnitude from Satellite Images. Algorithms 2020, 13, 195. [Google Scholar] [CrossRef]
- Xu, J.; Wang, H.; Cui, C.; Zhao, B.; Li, B. Oil Spill Monitoring of Shipborne Radar Image Features Using SVM and Local Adaptive Threshold. Algorithms 2020, 13, 69. [Google Scholar] [CrossRef]
- Xin, J.; Zhou, J.; Yang, S.X.; Li, X.; Wang, Y. Bridge Structure Deformation Prediction Based on GNSS Data Using Kalman-ARIMA-GARCH Model. Sensors 2018, 18, 298. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Zhou, J.; Xin, J.; Zhao, S.; Zhou, Y. Autoregressive Model-Based Structural Damage Identification and Localization Using Convolutional Neural Networks. KSCE J. Civ. Eng. 2020, 24, 2173–2185. [Google Scholar] [CrossRef]
- Kim, Y.; Chong, J.W.; Chon, K.H.; Kim, J. Wavelet-based AR–SVM for health monitoring of smart structures. Smart Mater. Struct. 2012, 22, 1–12. [Google Scholar] [CrossRef]
- de Lautour, O.R.; Omenzetter, P. Damage classification and estimation in experimental structures using time series analysis and pattern recognition. Mech. Syst. Signal. Process. 2010, 24, 1556–1569. [Google Scholar] [CrossRef]
- Arangio, S.; Beck, J.L. Bayesian neural networks for bridge integrity assessment. Struct. Control Health Monit. 2010, 19, 3–21. [Google Scholar] [CrossRef]
- Casciati, S.; Elia, L. Damage localization in a cable-stayed bridge via bio-inspired metaheuristic tools. Struct. Control Health Monit. 2016, 24, e1922. [Google Scholar] [CrossRef]
- Ding, Z.; Li, J.; Hao, H. Non-probabilistic method to consider uncertainties in structural damage identification based on Hybrid Jaya and Tree Seeds Algorithm. Eng. Struct. 2020, 220, 110925. [Google Scholar] [CrossRef]
- Meng, F.; Yu, J.; Alaluf, D.; Mokrani, B.; Preumont, A. Modal flexibility based damage detection for suspension bridge hangers: A numerical and experimental investigation. Smart Struct. Syst. 2019, 23, 15–29. [Google Scholar] [CrossRef]
- Guan, D.; Li, J.; Chen, J. Optimization Method of Wavelet Neural Network for Suspension Bridge Damage Identification. In Proceedings of the 2016 2nd International Conference on Artificial Intelligence and Industrial Engineering (AIIE 2016), Beijing, China, 20–21 November 2016. [Google Scholar]
- Seyedpoor, S.M.; Nopour, M.H. A two-step method for damage identification in moment frame connections using support vector machine and differential evolution algorithm. Appl. Soft Comput. 2020, 88, 106008. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous Structural Visual Inspection Using Region-Based Deep Learning for Detecting Multiple Damage Types. Comput. Civ. Infrastruct. Eng. 2017, 33, 731–747. [Google Scholar] [CrossRef]
- Gao, Y.; Mosalam, K.M. Deep Transfer Learning for Image-Based Structural Damage Recognition. Comput. Civ. Infrastruct. Eng. 2018, 33, 748–768. [Google Scholar] [CrossRef]
- Xu, Y.; Li, S.; Zhang, D.; Jin, Y.; Zhang, F.; Li, N.; Li, H. Identification framework for cracks on a steel structure surface by a restricted Boltzmann machines algorithm based on consumer-grade camera images. Struct. Control Health Monit. 2018, 25, e2075. [Google Scholar] [CrossRef]
- Lin, Y.; Nie, Z.-H.; Ma, H.-W. Structural Damage Detection with Automatic Feature-Extraction through Deep Learning. Comput. Civ. Infrastruct. Eng. 2017, 32, 1025–1046. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, C.; Gu, X.; Li, J. A novel deep learning-based method for damage identification of smart building structures. Struct. Health Monit. 2019, 18, 143–163. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning–based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Zhang, D.; Lindholm, G.; Ratnaweera, H. Use long short-term memory to enhance Internet of Things for combined sewer overflow monitoring. J. Hydrol. 2018, 556, 409–418. [Google Scholar] [CrossRef]
- Yang, R.; Singh, S.K.; Tavakkoli, M.; Amiri, N.; Yang, Y.; Karami, M.A.; Rai, R. CNN-LSTM deep learning architecture for computer vision-based modal frequency detection. Mech. Syst. Signal. Process. 2020, 144, 106885. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, C.; Peng, Z.; Dong, X.; Meng, G. Detecting the Early Damages in Structures With Nonlinear Output Frequency Response Functions and the CNN-LSTM Model. IEEE Trans. Instrum. Meas. 2020, 69, 9557–9567. [Google Scholar] [CrossRef]
- Petmezas, G.; Haris, K.; Stefanopoulos, L.; Kilintzis, V.; Tzavelis, A.; Rogers, J.A.; Katsaggelos, A.K.; Maglaveras, N. Automated Atrial Fibrillation Detection using a Hybrid CNN-LSTM Network on Imbalanced ECG Datasets. Biomed. Signal Process. Control 2021, 63, 102194. [Google Scholar] [CrossRef]
- Wigington, C.; Stewart, S.; Davis, B.; Barrett, B.; Price, B.; Cohen, S. Data Augmentation for Recognition of Handwritten Words and Lines Using a CNN-LSTM Network. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Institute of Electrical and Electronics Engineers (IEEE), Kyoto, Japan, 9–15 November 2017; Volume 1, pp. 639–645. [Google Scholar]
- Qiao, Y.; Wang, Y.; Ma, C.; Yang, J. Short-term traffic flow prediction based on 1DCNN-LSTM neural network structure. Mod. Phys. Lett. B 2021, 35, 2150042. [Google Scholar] [CrossRef]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010; pp. 92–101. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10) 2010, Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA, 2010. [Google Scholar]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Omnipress: Madison, WI, USA, 2015. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning Internal Representations by Error Propagation. Read. Cogn. Sci. 1988, 323, 399–421. [Google Scholar] [CrossRef]
- Werbos, P. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Omnipress: Madison, WI, USA, 2010. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Sun, Z.; Chang, C.C. Structural Damage Assessment Based on Wavelet Packet Transform. J. Struct. Eng. 2002, 128, 1354–1361. [Google Scholar] [CrossRef]







| Scenarios | Damage Types | Damage Severity (%) | Damage Combinations | Training Samples | Validation Samples | Test Samples |
|---|---|---|---|---|---|---|
| 1 | Single damaged hanger | 5 | 31 | 327 | 100 | 100 |
| 2 | 15 | 31 | 327 | 100 | 100 | |
| 3 | 25 | 31 | 327 | 100 | 100 | |
| 4 | 35 | 31 | 327 | 100 | 100 | |
| 5 | 45 | 31 | 327 | 100 | 100 | |
| 6 | Two damaged hangers 1 | 5 | 36 | 412 | 100 | 100 |
| 7 | 15 | 36 | 412 | 100 | 100 | |
| 8 | 25 | 36 | 412 | 100 | 100 | |
| 9 | 35 | 36 | 412 | 100 | 100 | |
| 10 | 45 | 36 | 412 | 100 | 100 | |
| 11 | Three damaged hangers 1 | 5 | 35 | 395 | 100 | 100 |
| 12 | 15 | 35 | 395 | 100 | 100 | |
| 13 | 25 | 35 | 395 | 100 | 100 | |
| 14 | 35 | 35 | 395 | 100 | 100 | |
| 15 | 45 | 35 | 395 | 100 | 100 | |
| / | / | 510 | 5670 | 1500 | 1500 |
| Layer | Size/No. | Stride | Padding | Input/Output | Activation | |
|---|---|---|---|---|---|---|
| Convolutional block 1 | Conv1 | 64 × 1/32 | 2 | SAME | 31 × 1024/32 × 512 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool1 | 3 × 1/32 | 2 | SAME | 32 × 512/32 × 256 | - | |
| Convolutional block 2 | Conv2 | 3 × 1/64 | 2 | SAME | 32 × 256/64 × 128 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool2 | 3 × 1/64 | 2 | SAME | 64 × 128/64 × 64 | - | |
| Convolutional block 3 | Conv3 | 3 × 1/128 | 2 | SAME | 64 × 64/128 × 32 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool3 | 3 × 1/128 | 2 | SAME | 128 × 32/128 × 16 | - | |
| Convolutional block 4 | Conv4 | 3 × 1/256 | 2 | SAME | 128 × 16/256 × 8 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool4 | 3 × 1/256 | 2 | SAME | 256 × 8/256 × 4 | - | |
| LSTM layer | - | - | - | 64 × 496/64 × 256 | - | |
| Fully connected block 1 | Fc1 | - | - | - | 1280/1280 | - |
| BN layer | - | - | - | 256/256 | ReLU | |
| Fully connected block 2 | Fc2 | - | - | - | 256/31(62) | - |
| Fully connected block 3 | Fc3 | - | - | - | 31(62) | Sigmoid (-) |
| Parameters to Be Adjusted | Value | Parameters to Be Adjusted | Value |
|---|---|---|---|
| Learning rate | 0.01 | Mini-batch | 32 |
| 0.005 | 64 | ||
| 0.001 | 128 | ||
| 0.0005 | Rate of dropout | 0 | |
| 0.0001 | 0.3 | ||
| BN layer | Setting | 0.5 | |
| Not Setting | 0.7 |
| Scenarios | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| No. of samples correctly identified | 58 | 76 | 95 | 98 | 96 | 97 | 100 | 94 |
| Scenarios | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| No. of samples correctly identified | 100 | 100 | 96 | 100 | 100 | 100 | 100 | 1410 |
| Scenarios | Average AIE of Undamaged Hangers (%) | Average AIE of Damaged Hangers (%) | ||
|---|---|---|---|---|
| 1 | Single damaged hanger | 5% | 0.229 | 1.726 |
| 2 | 15% | 0.068 | 2.047 | |
| 3 | 25% | 0.026 | 1.711 | |
| 4 | 35% | 0.017 | 2.070 | |
| 5 | 45% | 0.024 | 2.470 | |
| 6 | Two damaged hangers | 5% | 0.061 | 0.648 |
| 7 | 15% | 0.005 | 0.913 | |
| 8 | 25% | 0.005 | 1.102 | |
| 9 | 35% | 0.002 | 1.159 | |
| 10 | 45% | 0.010 | 0.852 | |
| 11 | Three damaged hangers | 5% | 0.018 | 0.563 |
| 12 | 15% | 0.001 | 1.006 | |
| 13 | 25% | 0.001 | 0.804 | |
| 14 | 35% | 0.003 | 1.012 | |
| 15 | 45% | 0.016 | 0.405 | |
| Layer | Size/No. | Stride | Padding | Input/Output | Activation | |
|---|---|---|---|---|---|---|
| Convolutional block 1 | Conv1 | 64 × 1/32 | 2 | SAME | 31 × 1024/32 × 512 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool1 | 3 × 1/32 | 2 | SAME | 32 × 512/32 × 256 | - | |
| Convolutional block 2 | Conv2 | 3 × 1/64 | 2 | SAME | 32 × 256/64 × 128 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool2 | 3 × 1/64 | 2 | SAME | 64 × 128/64 × 64 | - | |
| Convolutional block 3 | Conv3 | 3 × 1/128 | 2 | SAME | 64 × 64/128 × 32 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool3 | 3 × 1/128 | 2 | SAME | 128 × 32/128 × 16 | - | |
| Convolutional block 4 | Conv4 | 3 × 1/256 | 2 | SAME | 128 × 16/256 × 8 | ReLU |
| BN layer | - | - | - | - | - | |
| Pool4 | 3 × 1/256 | 2 | SAME | 256 × 8/256 × 4 | - | |
| Fully connected block 1 | Fc1 | - | - | - | 1024/1024 | - |
| BN layer | - | - | - | 256/256 | ReLU | |
| Fully connected block 2 | Fc2 | - | - | - | 256/31(62) | - |
| Fully connected block 3 | Fc3 | - | - | - | 31(62) | Sigmoid (-) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Tang, Q.; Gao, P.; Xin, J.; Zhou, J. Damage Identification of Long-Span Bridges Using the Hybrid of Convolutional Neural Network and Long Short-Term Memory Network. Algorithms 2021, 14, 180. https://doi.org/10.3390/a14060180
Fu L, Tang Q, Gao P, Xin J, Zhou J. Damage Identification of Long-Span Bridges Using the Hybrid of Convolutional Neural Network and Long Short-Term Memory Network. Algorithms. 2021; 14(6):180. https://doi.org/10.3390/a14060180
Chicago/Turabian StyleFu, Lei, Qizhi Tang, Peng Gao, Jingzhou Xin, and Jianting Zhou. 2021. "Damage Identification of Long-Span Bridges Using the Hybrid of Convolutional Neural Network and Long Short-Term Memory Network" Algorithms 14, no. 6: 180. https://doi.org/10.3390/a14060180
APA StyleFu, L., Tang, Q., Gao, P., Xin, J., & Zhou, J. (2021). Damage Identification of Long-Span Bridges Using the Hybrid of Convolutional Neural Network and Long Short-Term Memory Network. Algorithms, 14(6), 180. https://doi.org/10.3390/a14060180






