Abstract
Many mixed datasets with both numerical and categorical attributes have been collected in various fields, including medicine, biology, etc. Designing appropriate similarity measurements plays an important role in clustering these datasets. Many traditional measurements treat various attributes equally when measuring the similarity. However, different attributes may contribute differently as the amount of information they contained could vary a lot. In this paper, we propose a similarity measurement with entropy-based weighting for clustering mixed datasets. The numerical data are first transformed into categorical data by an automatic categorization technique. Then, an entropy-based weighting strategy is applied to denote the different importances of various attributes. We incorporate the proposed measurement into an iterative clustering algorithm, and extensive experiments show that this algorithm outperforms OCIL and K-Prototype methods with 2.13% and 4.28% improvements, respectively, in terms of accuracy on six mixed datasets from UCI.
1. Introduction
The main purposes of clustering analyses are to discover the implicit class structure in the data and divide the physical or abstract objects into different classes, where the similarity between a pair of objects in the same class is large and in different classes is small. As a major exploratory data analysis tool, clustering analysis has been widely researched and applied in many fields, such as sociology, biology, medicine, etc. [1,2,3]. Most current methods are designed to address single dataset types (numerical or categorical). For example, classical clustering methods, such as the k-means algorithm [4,5], the EM algorithm [6], etc., are limited to numerical datasets, while some algorithms are also proposed for clustering categorical datasets [7,8]. However, in the medical and biology fields, many datasets are collected with both numerical and categorical attributes. Hence, many researchers are dedicated to discovering clustering algorithms for mixed types of datasets with categorical and numerical attributes [9,10].
Many unsupervised clustering algorithms for mixed datasets have been proposed over the years, which can be classified into two types. The first type designs different similarity measurements for numerical and categorical data and then calculates the weighted sum of the two parts. For example, the K-Prototypes algorithm [11] for clustering mixed datasets was put forward simply by combining the k-means algorithm and the K-Modes algorithm, which are used for single types of numerical and categorical datasets, respectively. Additionally, the OCIL algorithm proposed by Cheung and Jia [12] is an iterative clustering learning algorithm based on object-cluster similarity metrics.
In the second type, the algorithms transform categorical attributes into numerical ones, and then the algorithms apply clustering methods designed for purely numerical datasets to the transformed dataset or vice versa. The most direct method is to map categorical values into numerical vectors. If a categorical attribute contains n unique values, then each value is mapped into a n-dimensional vector. This strategy increases the dataset dimensions, resulting in higher computational complexity. It could also transform numerical attributes into categorical ones. For instance, SpectralCAT, proposed by David and Averbuch [13], automatically transforms high-dimensional data into categorical data and then applies spectral clustering [14] to reduce the dimensionality of the transformed datasets through automatic non-linear transformations.
When designing clustering algorithms, the similarity or dissimilarity measurement plays an important role. Due to the different nature of numerical attributes and categorical attributes, they should be handled differently. Numerical data use a continuous variable to represent the values of each attribute, and a common distance such as the Euclidean distance usually measures the similarity between numerical objects. However, the values of the categorical data have neither a natural ordering nor a common scale. Due to this distinct nature of these two different data types, methods designed for single-type datasets cannot be applied to other types of datasets. The most direct way is the second of the two types mentioned above. However, this method ignores the similarity information in the categorical attribute values [15]. Therefore, the Hamming distance is used in many dissimilarity measurements. For example, in the K-Prototypes algorithm, the dissimilarity measurement uses the Euclidean distance for the numerical attributes and the Hamming distance for the categorical attributes. This algorithm also controls the contribution of the numerical attributes and the categorical attributes through a user-defined parameter. The K-Prototypes algorithm is simple and easy to implement, so it has been widely used in clustering mixed datasets. However, when implementing similarity measurements for categorical attributes, the Hamming distance is rough, and the clustering result is very sensitive to this parameter in the K-Prototypes algorithm. Subsequently, some improved similarity measurements for categorical attributes are proposed, which are based on the frequency of categorical values, the co-occurrence, and the conditional probability estimate [7,16,17]. Based on these improved similarity measurements for categorical attributes, some combined similarity measurements for both categorical and numerical datasets have been developed. For instance, the OCIL algorithm [12] uses the frequency of categorical object values that occur in the cluster for categorical attributes and the numerical distance for numerical attributes when measuring similarity.
It can be found that each attribute often contributes differently to the desired clustering results in many practical applications, which should be considered when measuring the similarities. For example, we want to cluster a mammographic mass dataset into two groups, corresponding to benign types and malignant types. In this task, the age attribute may play a more important role than the mass density attribute. Therefore, it is very important to identify different attribute contributions to improve the quality of the clustering results. Actually, some researchers have realized this problem and proposed several strategies. However, most research focuses on single-type datasets; e.g., for categorical attributes, the weights could be assigned based on the overall distribution of attribute values [18] or based on the frequency the class center appearances and the average distance between objects and the clustering center [19]. When handling mixed datasets, current algorithms only assign weights for single-type attributes. For example, when the OCIL algorithm [12] measuring the similarity, which only assigns weight for each categorical attribute based on information entropy, and it lets each numerical attribute take the same weight. The result is to weakens the importance of the numerical attributes. Ahmad and Dey proposed an algorithm for mixed datasets by adding weights to only numerical attributes [20]. Actually, both the numerical attributes and the categorical attributes should be evaluated when designing the similarity, and the weight strategy should be applied to both types of attributes in order to simplify the computational complexity.
In this paper, we propose a similarity measurement with entropy-based weighting for mixed datasets with both categorical and numerical attributes. First, a similarity metric for the categorical attributes is designed by assigning a different weight to each attribute based on information entropy theory. Second, we present an automatic categorization technique that transforms numerical data into categorical data, which is achieved by automatically discovering the optimal number of categorizations for each attribute based on the Calinski-Harabasz index. Then, the similarity metric for categorical data can be used to measure the similarity for transformed data. In this way, this similarity measurement can be applied to the mixed dataset containing both numerical and categorical attributes. Subsequently, this similarity measurement with entropy-based weighting is applied to the k-means framework. We accessed several datasets from UCI and compared the proposed algorithm with the OCIL and K-Prototype methods on mixed datasets as well as with the k-means algorithm on numerical datasets. The experimental results show that the iterative clustering algorithm based on the proposed similarity measurement is superior to these three algorithms.
The remainder of this paper is organized as follows. Section 2 introduces the problem formulation and then proposes a similarity measurement with entropy-based weighting for mixed datasets and applies this similarity measurement to the k-means algorithm framework. In Section 3, experiments are conducted to compare the proposed algorithm with three existing methods. Finally, we draw conclusions in Section 4.
2. Methods
2.1. Problem Formulation
Clustering means classifying the given unlabeled objects into several clusters according to certain criteria, so similar objects are classified as one cluster, and dissimilar objects are assigned to different clusters.
For a given mixed dataset X consisting of m objects, denoted as , suppose X has categorical attributes and numerical attributes. Then, can be denoted as , with and . The requirement is to cluster the dataset X into k different clusters, denoted as , with , and , ; . The optimal partition matrix can be found through the following objective function:
where is the similarity between object and cluster , is an partition matrix with and , , . indicates that object is assigned to cluster j.
According to Equation (1), the clusters can be obtained as long as the metric function of similarity between object and cluster is determined. Because implied information of each attribute is different, the contribution to cluster result is also different., we define a new similarity, in which each attribute is assigned a weight, denoted as , satisfying , and . Then the similarity between object and cluster can be measured by the following equation:
where and are the weight and similarity on the categorical attribute, respectively, and are the weight and similarity on the numerical attribute, respectively. represents the similarity on categorical attributes and represents the similarity on numerical attributes. In the following sections, we study how to calculate the weight and similarity on each attribute.
2.2. Similarity Measurement for Categorical Attributes
For categorical attributes, each pair of values chosen from the value domain are considered to have the same distance as they do not have a natural ordering. By contrast, each pair of values of a numerical attribute has a numerical distance. Due to this different characteristic, it is not appropriate to use the Euclidian distance to evaluate categorical attributes-clustering similarity. Hereby, we adopt the frequency that the value appears in the cluster for the categorical attribute , where represents the rth categorical attribute.
Definition 1.
The similarity between a categorical attribute value and cluster , where , , , is defined as
where represents the number of objects in cluster , whose value for the categorical attribute is equal to , means empty, and represents the number of objects in cluster , whose value for the categorical attribute is not empty. From Definition 1, we can find the following properties:
- ;
- only if none of the attribute ’s values of the objects belonging to cluster are equal to ;
- only if all of the Non NULL attribute ’s values of the objects belonging to cluster are equal to .
Optimizing attribute weights can improve the clustering performance. In information theory, the inhomogeneity degree of the dataset with respect to an attribute can be used to measure the significance of this attribute. In addition, according to Measure III proposed in [21], the higher the information content of an attribute, the higher the inhomogeneity degree of this attribute.
Definition 2.
Since the value domain of each attribute is definite, values of each attribute can be regarded as discrete and independent. The significance of an arbitrary categorical attribute A in dataset X can be quantified by the following entropy metric:
where A has a value domain, denoted as , which consists of all the possible values that attributes A can choose, and can be represented with , h is the total number of values in . , where is a value of attribute A, , . Therefore, is the probability density function of in dataset X for attribute A. According to Equation (4), an attribute with more varying values has higher significance. However, in practice, an attribute with too many different values may have little clustering contribution, such as the instance ID number, which is unique for each instance; however, this information is useless for clustering analysis [12]. Thus, Equation (4) can be modified with Equation (5),
Then, the weight of each attribute based on information entropy is defined as in Equation (6),
where denotes the sum of modified information entropy of all the numeric attributes, which will be described in detail in the next section. Therefore, the metric function of similarity between object and cluster on categorical attributes is modified as Equation (7).
2.3. Similarity Measurement for Numerical Attributes
Since the entropy-based weighting strategy proposed in Section 2.2 is not applicable to numerical attributes, we made numerical data discrete at first. Then, the similarity measurement was used for the discretized data which are categorical data now. Discretization of numerical data is gaining more attention from the machine learning community [22]. Discretization of a given continuous attribute is also called quantization, which divides the range of attributes into intervals. Then, an interval label marks each interval. As a result, interval labels replace the original continuous data. Obviously, discretization can reduce the number of continuous attribute values [23], thereby simplifying the original data. Discretization also makes it possible for methods of categorical data clustering to be applied to cluster numerical or mixed datasets. There are many methods for numerical dataset discretization, such as discretization by intuitive division, histogram analysis, cluster analysis and entropy-based discretization. This section defines a smart way to automatically discretize numerical data by cluster analysis so that numerical data are transformed into categorical data. This method also provides a measure to find the optimal clusters to discretize the original data.
In order to transform numerical data into categorical data, we transformed numerical data by each attribute. Formally, let be a single numerical attribute in X. is transformed into the categorical values , . As a result, each point is transformed into .
Before categorizing numerical data by applying a clustering method to the data, the optimal number of categories is required, which is critical for the success of the categorization process.
Different methods have been proposed to find the optimal number of clusters for numerical attribute data [24,25]. The most common way is to apply a clustering algorithm to the data and calculate the cluster validity index. This process is repeated with an increasing number of clusters until it achieves the first local maxima. The number of clusters corresponding to the first local maxima is chosen as the optimal number of categories.
Let q be the number of clusters, which is unknown at first, and let be a clustering function that assigns each to one of the q clusters in , where and , , . The total sum of squares of is defined as , where is the mean of , which is defined as . The within-cluster sum of squares is defined as , where the mean of each cluster is defined as . It can be found that denotes the sum of deviations from each point to the center of their associated clusters, and the of a good cluster should be a small value. The between-cluster sum of squares is defined as , which denotes the sum of the weighted distances between each center of the q clusters and the center of data, and of a good cluster result should be of a large value. It is clear that ; thus, the total sum of squares equals the sum of the within-cluster sum of squares and the between-cluster sum of squares.
The Calinski-Harabasz index is adopted to evaluate the clustering validity, which is defined as . The proof of the effectiveness of the Calinski-Harabasz index is shown in [13]. We applied a clustering method to the data and calculated the corresponding Calinski-Harabasz index of clusters, . When the validity index achieved the first local maximum, we chose the corresponding q as the optimal number of categories, denoted as .
To demonstrate the automatic categorization process, an example of the Calinski-Harabasz index calculation results is shown as Figure 1. In this example, the k-means method was chosen as . When , the k-means method was applied to the data and the validity index of the corresponding cluster result was calculated. When , the first local maxima of the Calinski-Harabasz index is found; therefore, . The automatic categorization process can be summarized as Algorithm 1.
| Algorithm 1 Automatic categorization for numerical attributes. |
| Input:: the lth numerical attribute in the dataset X; : a clustering function that partitions into q clusters and returns the corresponding assignments; : maxmum number of categories to examine; Output: : the categorical values of ;
|
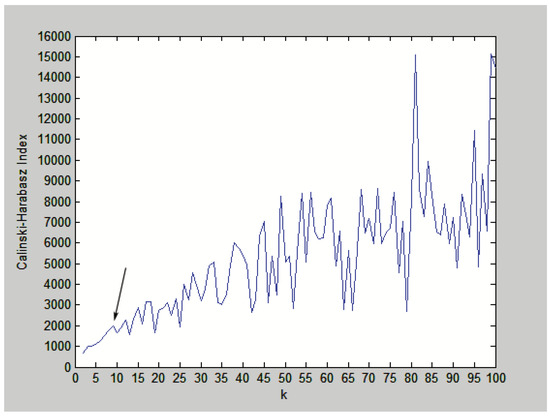
Figure 1.
The Calinski-Harabasz index for , the first local maxima of Calinski-Harabasz index is marked by the arrow.
When the optimal number of categories is found, each is allocated to one of clusters by clustering method , then the corresponding categorical value of is set as j. This process repeats for each numerical attribute in dataset X, . After this automatic categorization process, we found the optimal number of categories of each numerical attribute and transformed the original numerical data into categorical data, with , .
Since the numerical data of the original dataset X is transformed into categorical data, we can use the similarity measurement for categorical data to the transformed data. The weight of each numerical attribute is calculated based on Equation (8):
where , represents each attribute of transformed data. Therefore, the metric function of similarity between object and cluster on numerical attribute is defined as:
2.4. Similarity Measurement for Mixed Data
2.5. Iterative Clustering Algorithm
Based on Equation (10), the similarity measurement with entropy-based weighting applied to the k-means framework can be conducted as Algorithm 2.
| Algorithm 2 Iterative clustering algorithm with entropy-based weighting. |
| Input: (dataset to cluster with categorical attributes and numerical attributes); k (number of clusters); (a clustering function that partitions into q clusters and returns the corresponding assignments); (maximum number of categories to examine); Output: (an assignment of each point in X to one of k clusters);
|
Steps 1–3 utilize the automatic categorization process to obtain transformed categorical datasets based on Algorithm 1. Since the attributes of the transformed dataset are all categorical, the weight of each attribute can be calculated with the entropy-based weighting strategy, and Steps 4–9 show the process. Steps 10–21 are the iterative process that applies the similarity measurement based on Equation (10) into the k-means algorithm framework to address the transformed dataset.
3. Results and Discussion
To test the effectiveness of the similarity measurement with the entropy-based weighting proposed in this paper, two different types of datasets, mixed and numerical datasets, were selected from the UCI Machine Learning Data Repository [26], and most datasets were collected from the field of biology and medicine. The iterative clustering algorithm based on the proposed similarity measurement was compared with existing clustering algorithms, including OCIL [12], K-Prototype [9] and k-means [4]. k-means was used for dataset made of numerical variables only. In the experiments, the clustering accuracy [27] was adopted to evaluate the three mentioned methods. The clustering accuracy is defined as , where m denotes the number of instances of the dataset, denotes the provided label, denotes the obtained cluster label, is a mapping function that maps to the equivalent label from the data corpus, and the function only if ; otherwise, the value is 0. Correspondingly, the clustering error rate is defined as .
In the experiments, considering that the clustering results are affected by the selected initial centroids, we set the same initial centroids for all methods during each test, and the following experimental results were averaged from 100 random runs. In addition, k-means was chosen as the clustering method in the automatic categorization process that transforms numerical attributes into categorical attributes. Before using k-means method to cluster, the original data were normalized to be between 0 and 1.
3.1. Experiments on Mixed Datasets
In this section, we investigated the performance of the iterative clustering algorithm based on the proposed similarity measurement on mixed datasets. Table 1 shows the information of each dataset. Note that the second column presents the number of samples, the third column presents the number of the two types of attributes, and the last column presents the probability distribution of samples in different classes.

Table 1.
Description of mixed datasets.
To evaluate the performance of the iterative clustering algorithm based on the proposed similarity measurement, we compare its clustering results with OCIL and K-Prototype. The average value and standard deviation of the clustering error of these clustering algorithms are statistically summarized in Table 2. In the experiments, the weight parameter was set to 1.5 for the K-Prototypes algorithm.

Table 2.
Comparison of cluster accuracy for the proposed algorithm with OCIL and K-Prototype on mixed datasets.
From Table 2, it can be observed that the iterative clustering algorithm based on the proposed similarity measurement outperforms the OCIL and K-Prototype methods for six datasets, although the ratios of the numbers of categorical attributes to numerical attributes differ greatly, as shown in Table 1. Compared to the other two methods, the iterative clustering algorithm can improve the accuracies of clustering results by 2.13% and 4.28%, respectively. Especially in the Heart dataset, the iterative clustering algorithm improves the accuracy by 2.85% and 5.86%, respectively. This result indicates that the proposed similarity measurement is applicable to mixed datasets of variant compound styles and does not need any parameter to give weights to the two types of attributes. Furthermore, for datasets that have very uneven class distributions, the proposed similarity measurement can also achieve adequate clustering results.
To study why the iterative clustering algorithm based on the proposed similarity measurement outperforms the OCIL and K-Prototype methods, we analyzed the correlation between each attribute and the label attribute in the dataset by calculating the correlation coefficients in statistics. Since the label attribute is a categorical attribute, the Pearson correlation coefficient and the Spearman correlation coefficients are not suitable. The Kendall correlation coefficient requires that the categorical attribute be ordered; therefore, it also cannot be used to calculate the correlation between the categorical attribute and the label attribute. Here, we adopt the ReliefF algorithm, which can estimate the quality of dependencies between each attribute and label attribute [28].
To see whether the correlation between the dependencies and weights affects the clustering results, we calculate the Pearson correlation coefficient between the dependencies calculated by the ReliefF algorithm and the weights calculated by Equations (6) and (8) in each dataset. The result is shown in Table 3. Since the Dermatology dataset as well as the Zoo dataset have only one numerical attribute, calculating the correlation for numerical attribute is meaningless.

Table 3.
The correlation coefficient between dependencies and weights in each mixed dataset.
Comparing Table 2 and Table 3, it can be seen that the Dermatology dataset, with a good clustering result, has a strong correlation between dependencies and weights for categorical attributes. In addition, the Australian dataset has a strong correlation not only for categorical attributes but also for numerical attributes; this dataset also has a good clustering result. However, in the Hepatitis dataset it has a strong correlation for categorical attributes, but has a weak correlation for numerical attributes. There are only six numerical attributes and 13 categorical attributes in the Hepatitis dataset. The influence of category attributes is much greater than that of numerical attributes. So, the clustering result of Hepatitis dataset is not good, which does not violate the theory in the article. Therefore, a good clustering result may be obtained due to the reasonable weight assigned to each attribute by the proposed similarity measurement.
3.2. Experiments on Numerical Datasets
Then, we further investigated the performance of the proposed similarity measurement on pure numerical datasets. Table 4 shows the information of six numerical datasets, including the number of samples, attributes and classes, and class distribution. To evaluate the performance of the proposed similarity measurement applied to k-means on numerical datasets, we also conducted experiments compared to the most classical numerical data clustering algorithms, k-means algorithms. These two clustering algorithms were applied to different numerical datasets; Table 5 shows the mean and variance of the clustering error of clustering by applying different algorithms. In addition, before using the k-means method to cluster, the dataset was normalized to between 0 and 1.

Table 4.
Description of numerical datasets.

Table 5.
Comparison of the proposed algorithm with k-means on numerical datasets.
It can be seen that except for the Wine dataset and the Fertility dataset, the proposed similarity measurement applied to k-means outperforms the k-means method on other datasets. Normally, the clustering accuracy of the iterative clustering algorithm based on the proposed similarity measurement is 6.09% higher than that of k-means, especially for the Mass dataset, with a similarity that is 26.69% higher than that of k-means.
Similarly, the correlation coefficient between dependencies and weights was calculated to analyze why the iterative clustering algorithm outperforms the k-means method, and the correlation coefficient of each dataset is shown in Table 6. It can be found that the Mass dataset with the best clustering result has the highest correlation coefficient. Perhaps the weights of this dataset are well allocated according to the contribution of each clustering attribute.

Table 6.
The correlation coefficient between dependencies and weights in each numerical dataset.
4. Conclusions
In this paper, a similarity measurement with entropy-based weighting is proposed for mixed datasets with numerical and categorical attributes. For categorical datasets, a similarity metric is designed by assigning different weights to each attribute based on information entropy theory. For numerical datasets, the original high-dimensional numerical data are transformed to categorical data by an automatic categorization technique, so the similarity metric for categorical datasets can be applied to numerical datasets. Then, a similarity measurement for mixed datasets was obtained. Extensive experimental results show that the iterative clustering algorithm based on the proposed similarity measurement can achieve higher clustering accuracy and is superior to the existing clustering algorithms on datasets from UCI. The results also validate the feasibility of handling different types of attributes and verify that various attributes contribute differently in similarity measurements when clustering.
Author Contributions
Conceptualization, X.Q. and S.J.; methodology, J.Y.; software, S.J.; writing—original draft preparation, J.Y. and S.J.; writing—review and editing, J.Y. and X.Q.; supervision, N.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported partially by the National Natural Science Foundation of China (No. 61502135), the Programme of Introducing Talents of Discipline to Universities (No. B14025), and the Anhui Provincial Key Technologies R&D Program (No. 1804b06020378). The funding bodies had no role in study design, data collection and analysis, or preparation of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiawei, H.; Micheline, K. Data Mining: Concepts and Techniques. Data Min. Concepts Model. Methods Algorithms Second Ed. 2006, 5, 1–18. [Google Scholar]
- Rodoshi, R.T.; Kim, T.; Choi, W. Resource Management in Cloud Radio Access Network: Conventional and New Approaches. Sensors 2020, 20, 2708. [Google Scholar] [CrossRef]
- Khorraminezhad, L.; Leclercq, M.; Droit, A.; Bilodeau, J.F.; Rudkowska, I. Statistical and Machine-Learning Analyses in Nutritional Genomics Studies. Nutrients 2020, 12, 3140. [Google Scholar] [CrossRef] [PubMed]
- Macqueen, J. Some Methods for Classification and Analysis of Multivariate Observations. Berkeley Symp. Math. Stat. Probab. 1967, 1, 281–297. [Google Scholar]
- Ahmad, A.; Hashmi, S. K-Harmonic means type clustering algorithm for mixed datasets. Appl. Soft Comput. 2016, 48, 39–49. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Cao, F.; Liang, J.; Li, D.; Bai, L.; Dang, C. A dissimilarity measure for the k-Modes clustering algorithm. Knowl. Based Syst. 2012, 26, 120–127. [Google Scholar] [CrossRef]
- Guha, S.; Rastogi, R.; Shim, K. ROCK: A robust clustering algorithm for categorical attributes. Inf. Syst. 1999, 25, 345–366. [Google Scholar] [CrossRef]
- Huang, Z. Clustering large data sets with mixed numeric and categorical values. In Proceedings of the 1st Pacific-Asia Conference on Knowledge Discovery and Data Mining, Singapore, 23–24 February 1997; pp. 21–34. [Google Scholar]
- Ahmad, A.; Khan, S. Survey of State-of-the-Art Mixed Data Clustering Algorithms. IEEE Access 2019, 7, 31883–31902. [Google Scholar] [CrossRef]
- Huang, Z. Extensions to the k-means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Cheung, Y.M.; Jia, H. Categorical-and-numerical-attribute data clustering based on a unified similarity metric without knowing cluster number. Pattern Recognit. 2013, 45, 2228–2238. [Google Scholar] [CrossRef]
- David, G.; Averbuch, A. SpectralCAT: Categorical spectral clustering of numerical and nominal data. Pattern Recognit. 2012, 45, 416–433. [Google Scholar] [CrossRef]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process. Syst. 2001, 14, 849–856. [Google Scholar]
- Hsu, C.C. Generalizing self-organizing map for categorical data. IEEE Trans. Neural Netw. 2006, 17, 294–304. [Google Scholar] [CrossRef]
- Liang, J.; Chin, K.S.; Dang, C.; Yam, R.C. A new method for measuring uncertainty and fuzziness in rough set theory. Int. J. Gen. Syst. 2002, 31, 331–342. [Google Scholar] [CrossRef]
- Ng, M.K.; Li, M.J.; Huang, J.Z.; He, Z. On the impact of dissimilarity measure in k-modes clustering algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 503. [Google Scholar] [CrossRef]
- Chen, L.F.; Guo, G.D. Non-mode clustering of categorical data with attributes weighting. J. Softw. 2013, 14, 2628–2641. [Google Scholar] [CrossRef]
- Bai, L.; Liang, J.; Dang, C.; Cao, F. A novel attribute weighting algorithm for clustering high-dimensional categorical data. Pattern Recognit. 2011, 44, 2843–2861. [Google Scholar] [CrossRef]
- Ahmad, A.; Dey, L. A k-mean clustering algorithm for mixed numeric and categorical data. Data Knowl. Eng. 2007, 63, 503–527. [Google Scholar] [CrossRef]
- Basak, J.; Krishnapuram, R. Interpretable Hierarchical Clustering by Constructing an Unsupervised Decision Tree. IEEE Trans. Knowl. Data Eng. 2005, 17, 121–132. [Google Scholar] [CrossRef]
- Dougherty, J.; Kohavi, R.; Sahami, M. Supervised and Unsupervised Discretization of Continuous Features. Mach. Learn. Proc. 1995, 2, 194–202. [Google Scholar]
- Grzymala-Busse, J.W. Data reduction: Discretization of numerical attributes. Handbook of Data Mining and Knowledge Discovery; Oxford University Press, Inc.: Oxford, UK, 2002; pp. 218–225. [Google Scholar]
- Jung, Y.; Park, H.; Du, D.Z.; Drake, B.L. A Decision Criterion for the Optimal Number of Clusters in Hierarchical Clustering. J. Glob. Optim. 2003, 25, 91–111. [Google Scholar] [CrossRef]
- Bayati, H.; Davoudi, H.; Fatemizadeh, E. A heuristic method for finding the optimal number of clusters with application in medical data. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2008, 2008, 4684–4687. [Google Scholar]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 15 June 2021).
- Zhu, L.; Miao, L.; Zhang, D. Iterative Laplacian Score for Feature Selection. In Chinese Conference on Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 80–87. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).