A Comparative Study of Block Incomplete Sparse Approximate Inverses Preconditioning on Tesla K20 and V100 GPUs
Abstract
:1. Introduction
- We extend the single GPU implementation to multiple GPUs version using the Block–Jacobi preconditioner.
- A detailed multi-GPU implementation based on the open source scientific computing framework, PETSc, is introduced and investigated.
- We make detailed performance comparisons and analysis on the proposed algorithm using NVIDIA’s Tesla K20 and Tesla V100 GPUs.
2. Block–ISAI Preconditioning
3. Block–Jacobi with Block–ISAI on Multi-GPUs
3.1. Preconditioning on Multi-GPUs
| Algorithm 1 Block–Jacobi preconditioning with Block–ISAI on multi-GPUs: . |
|
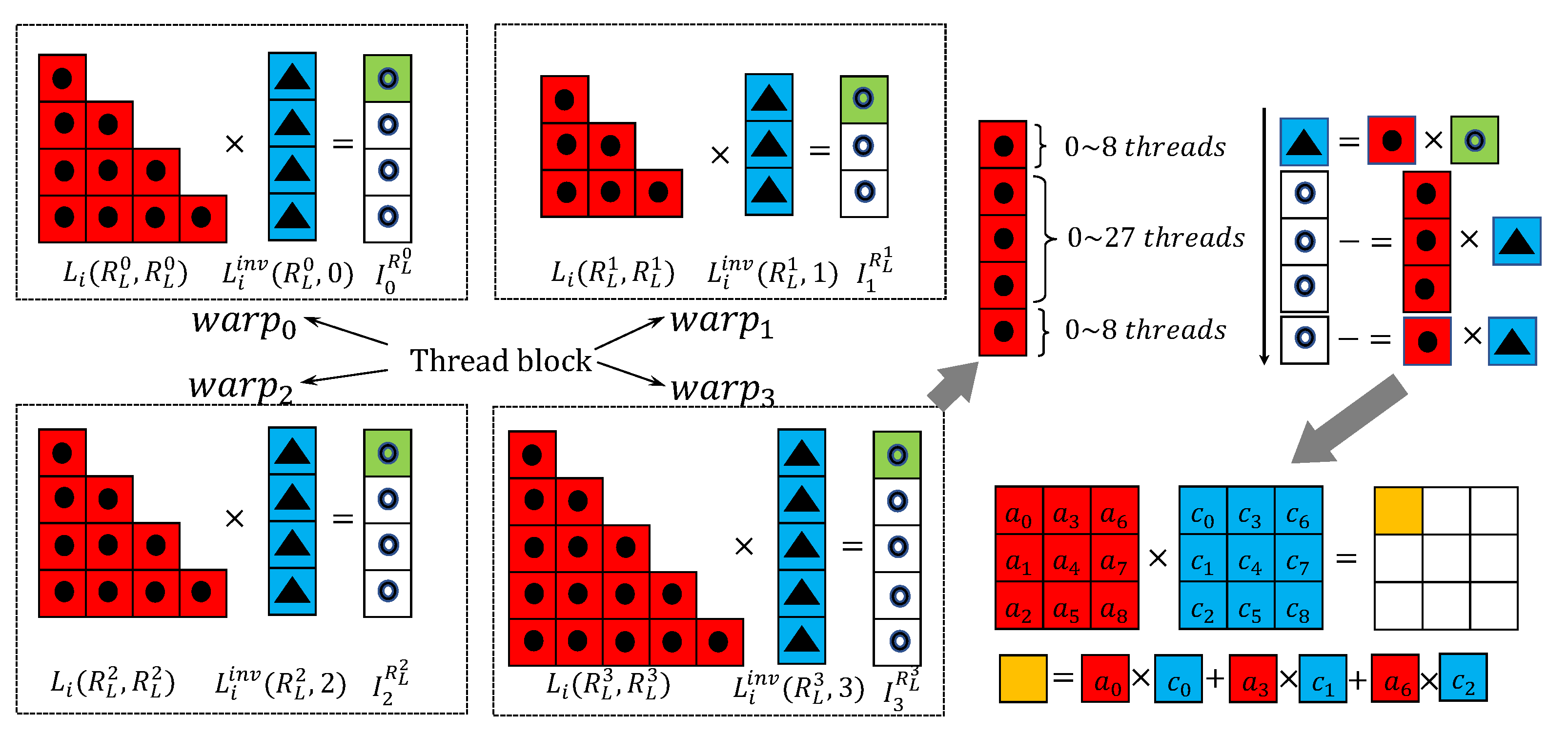
3.2. Multi-GPU Implementation
| List 1 Procedure for transforming user provided matrices to PETSc’s BCSR matrices. |
|
| List 2 Locally accessing block lower and upper factors. |
|
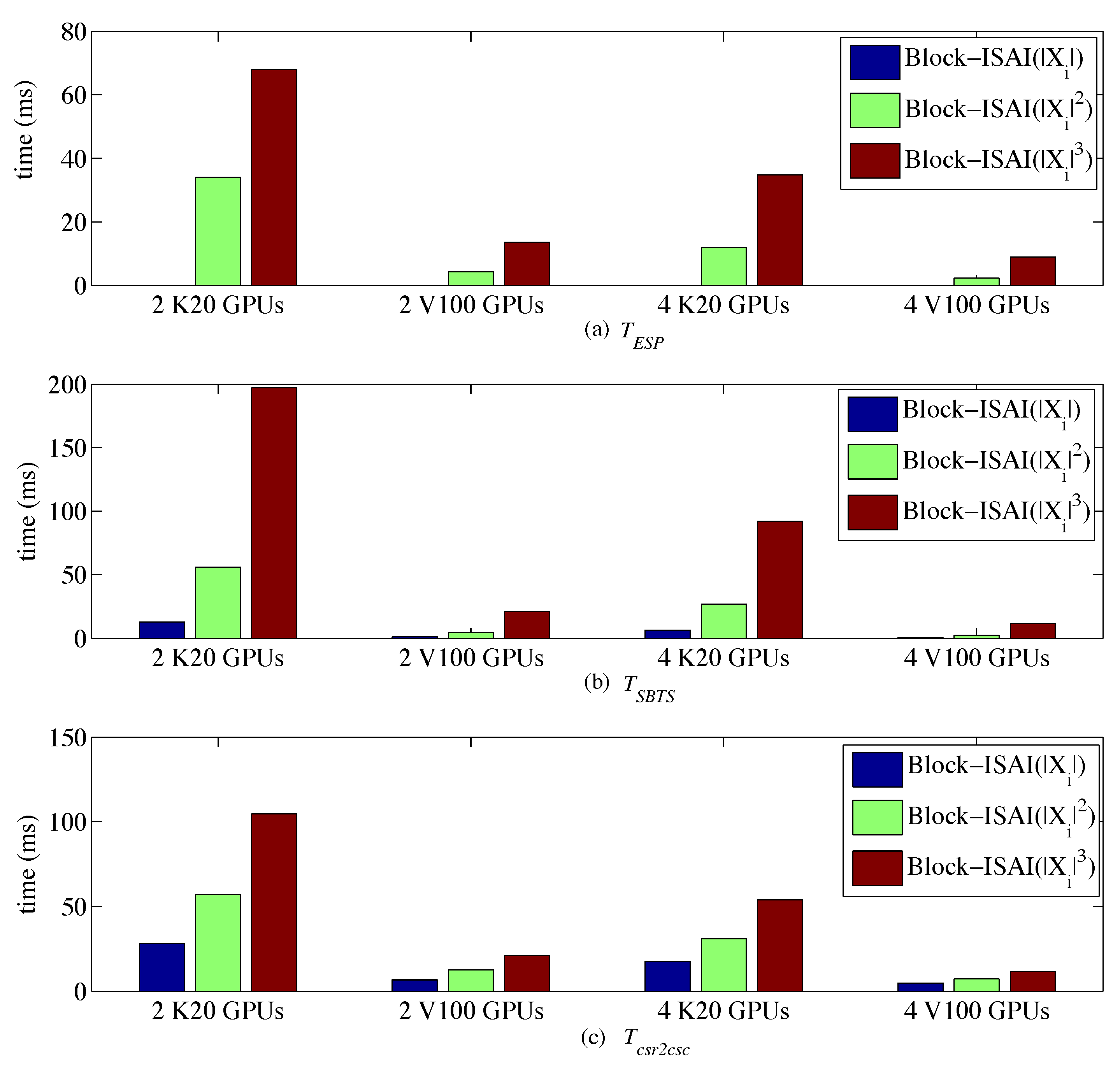
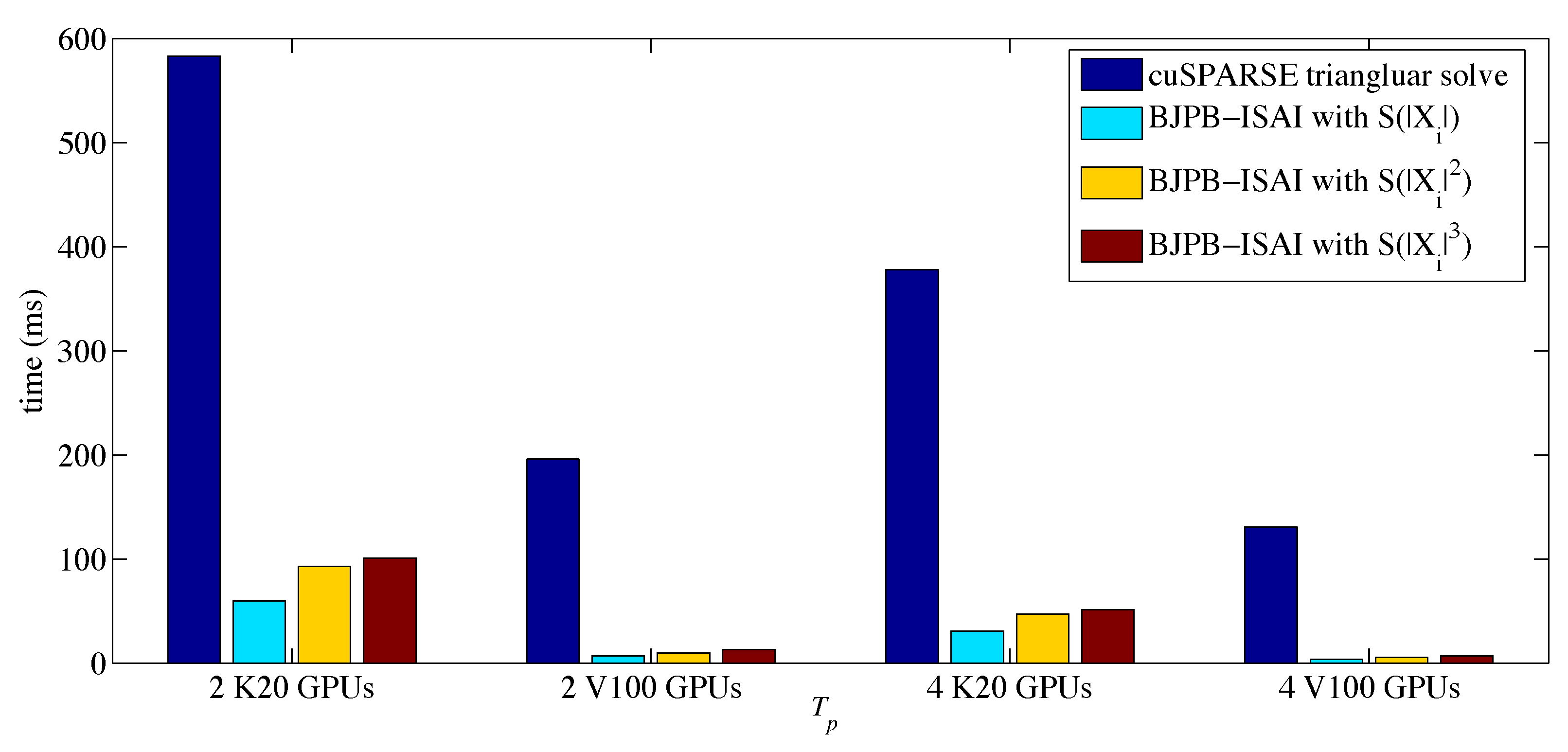
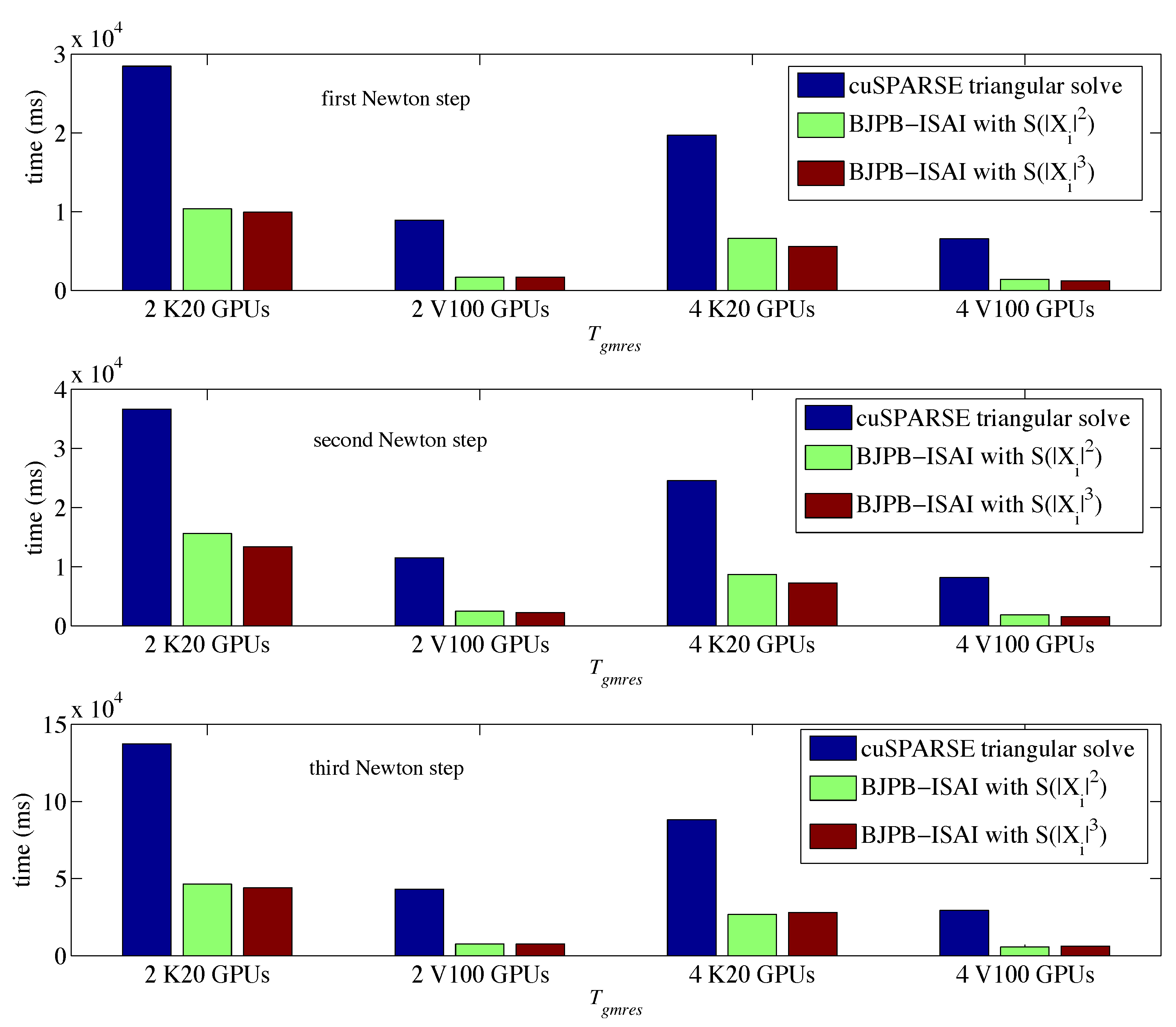
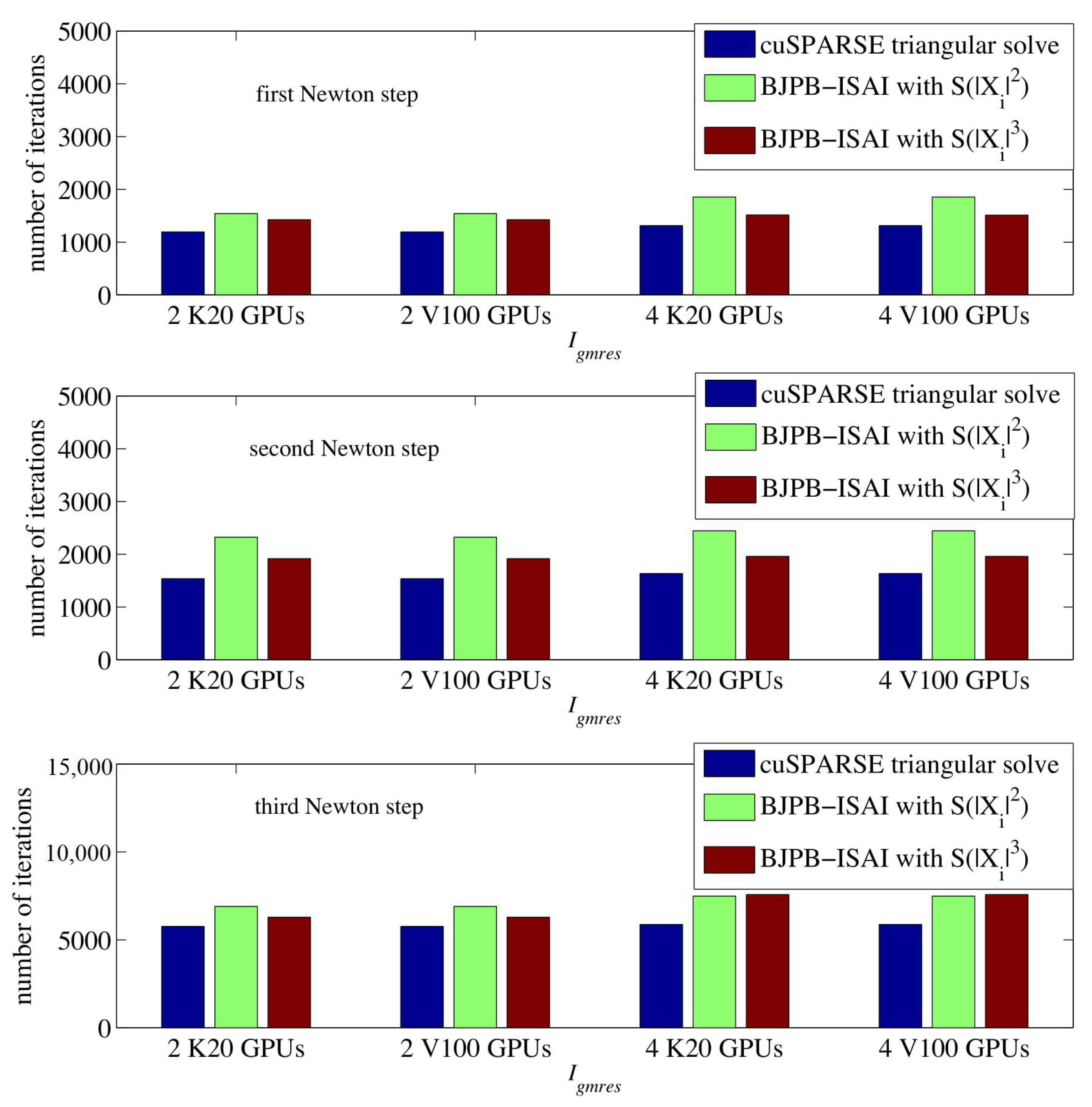
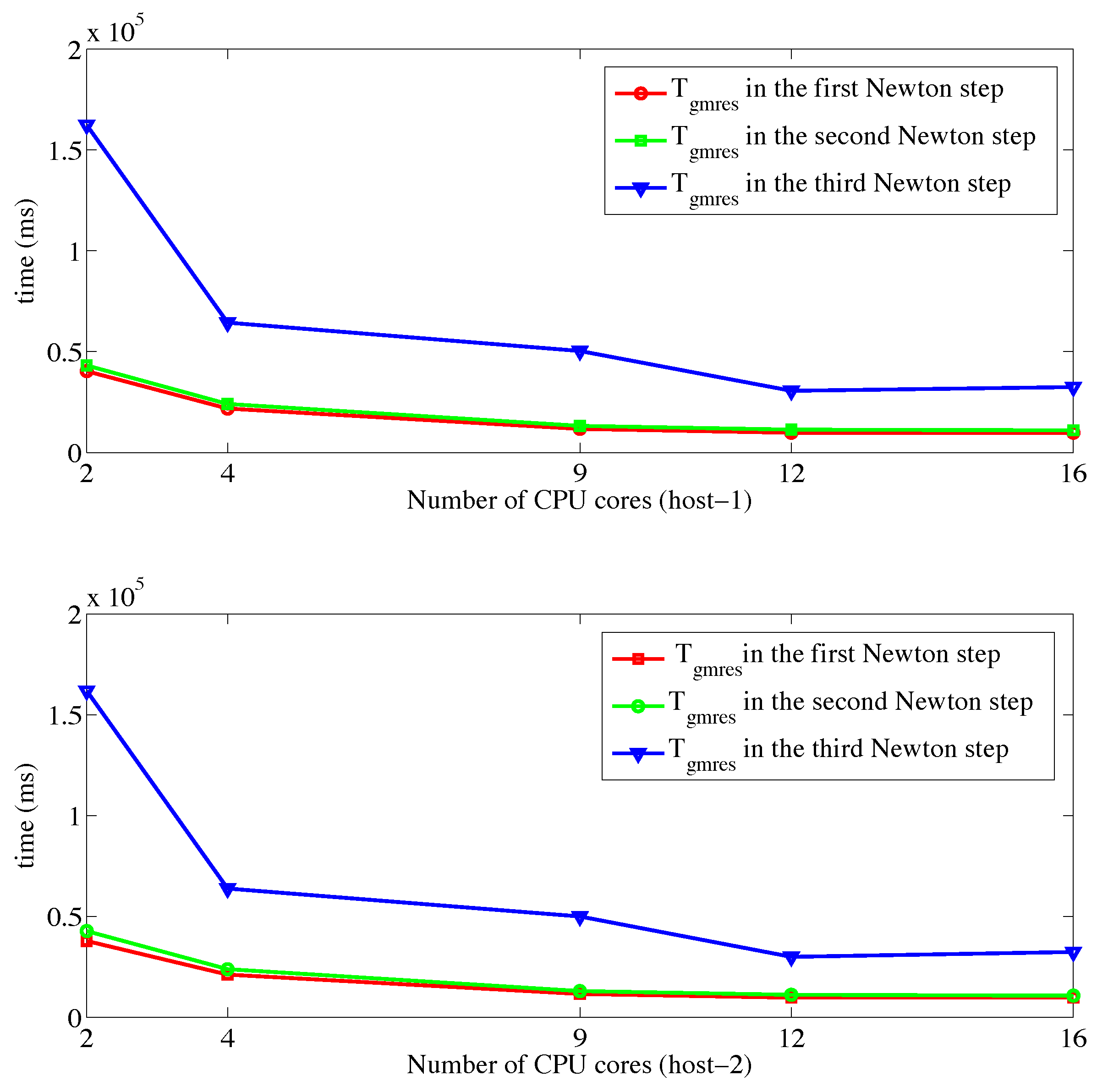
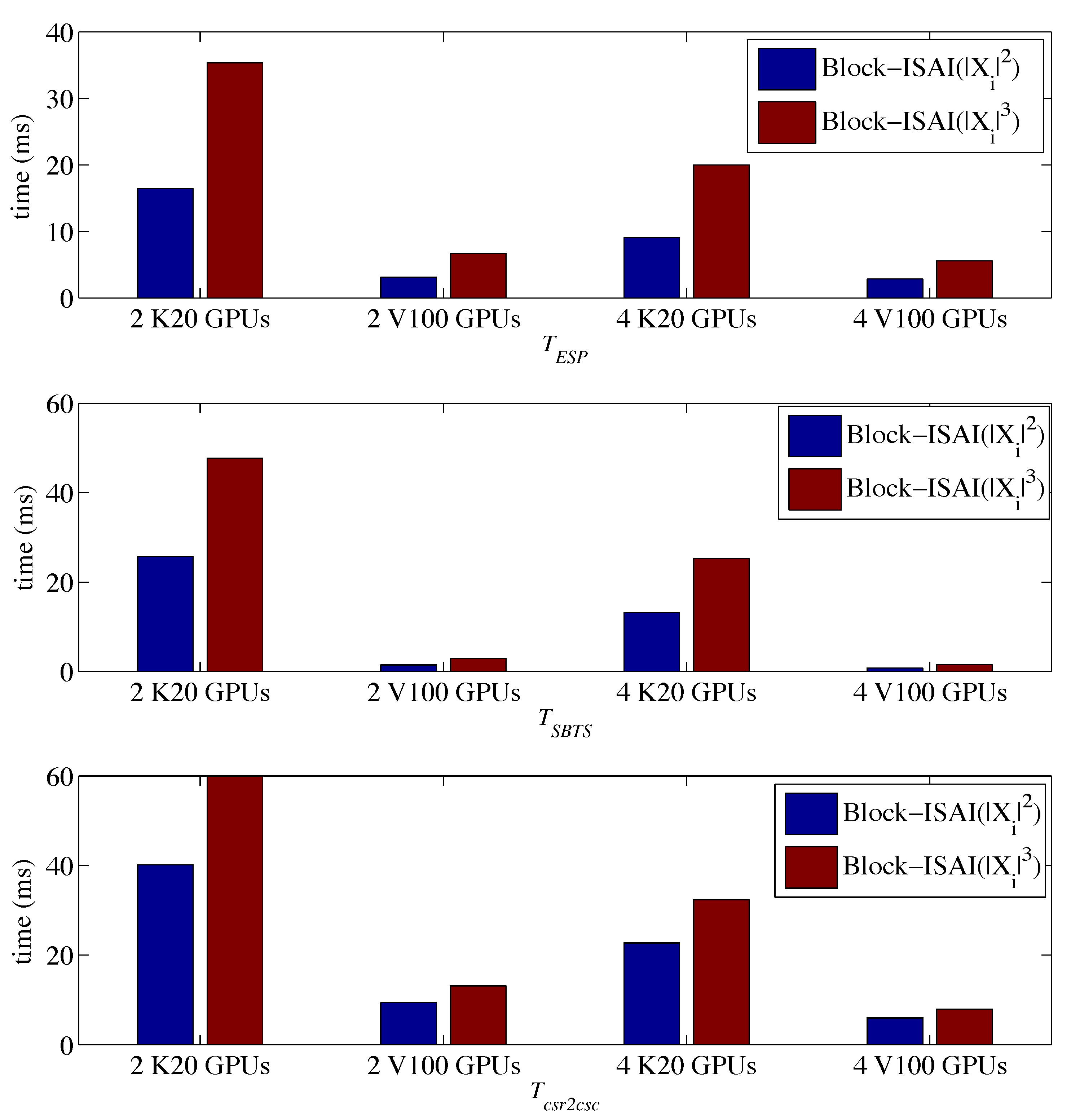
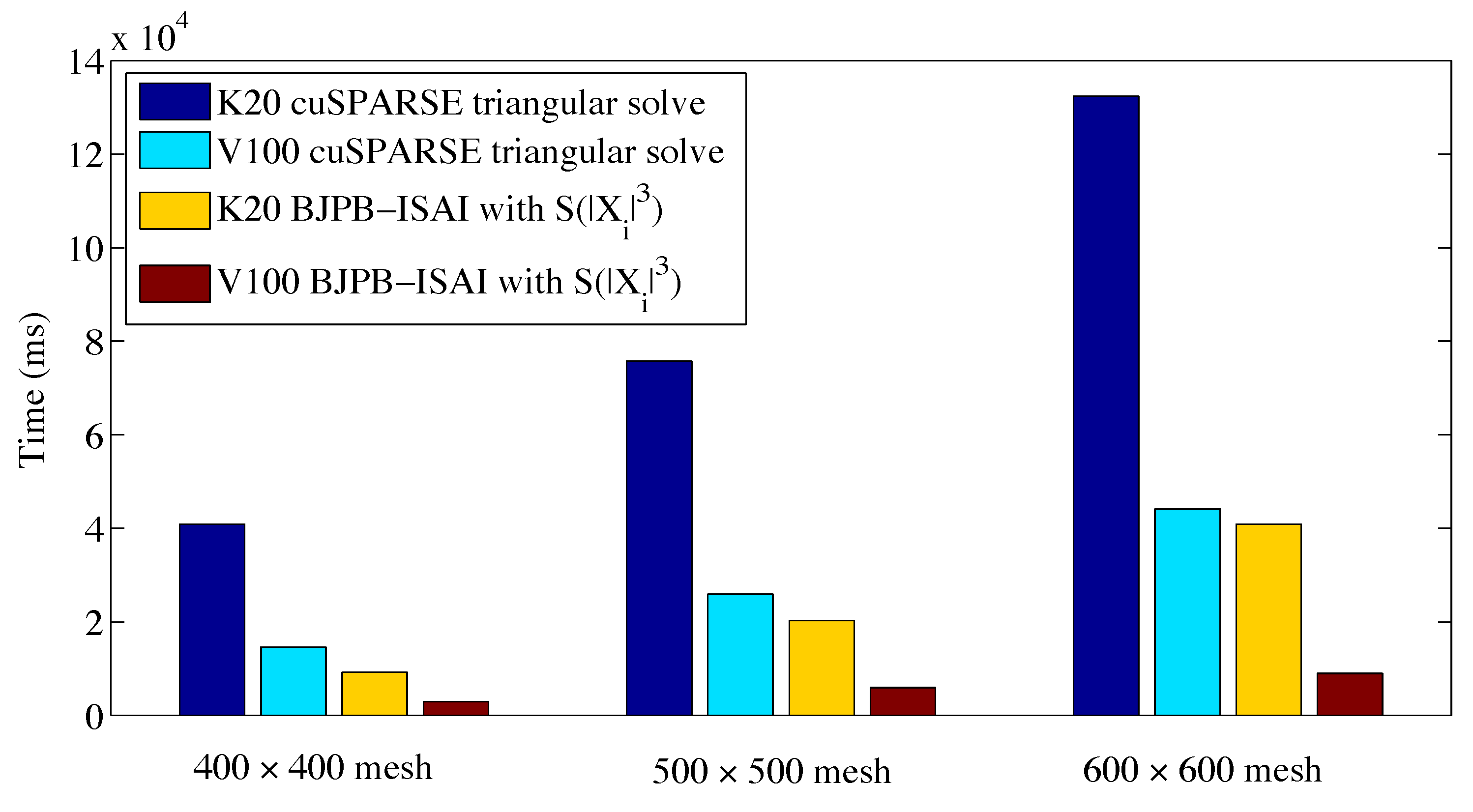
4. Experiments
4.1. Experiment Setup
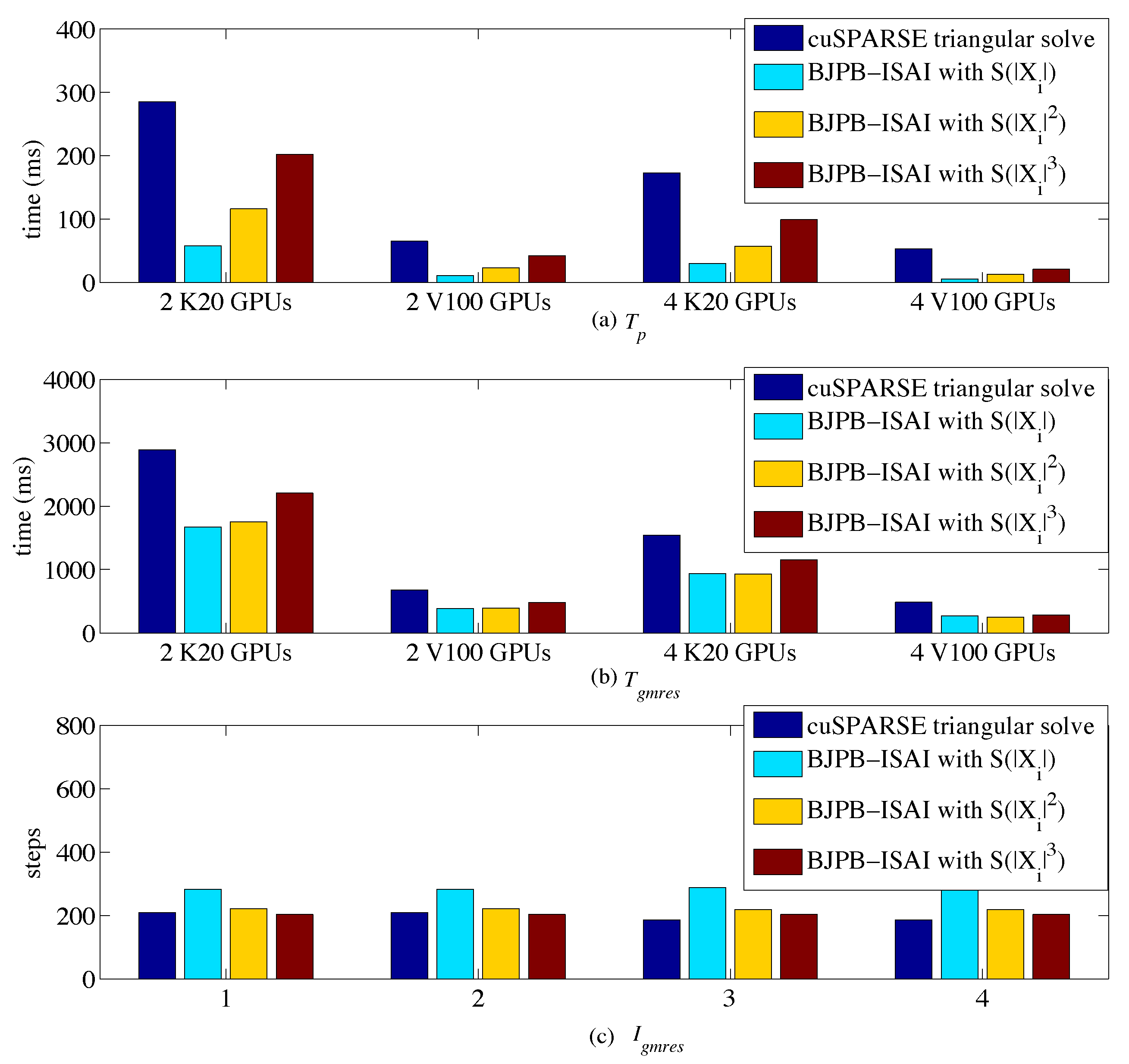
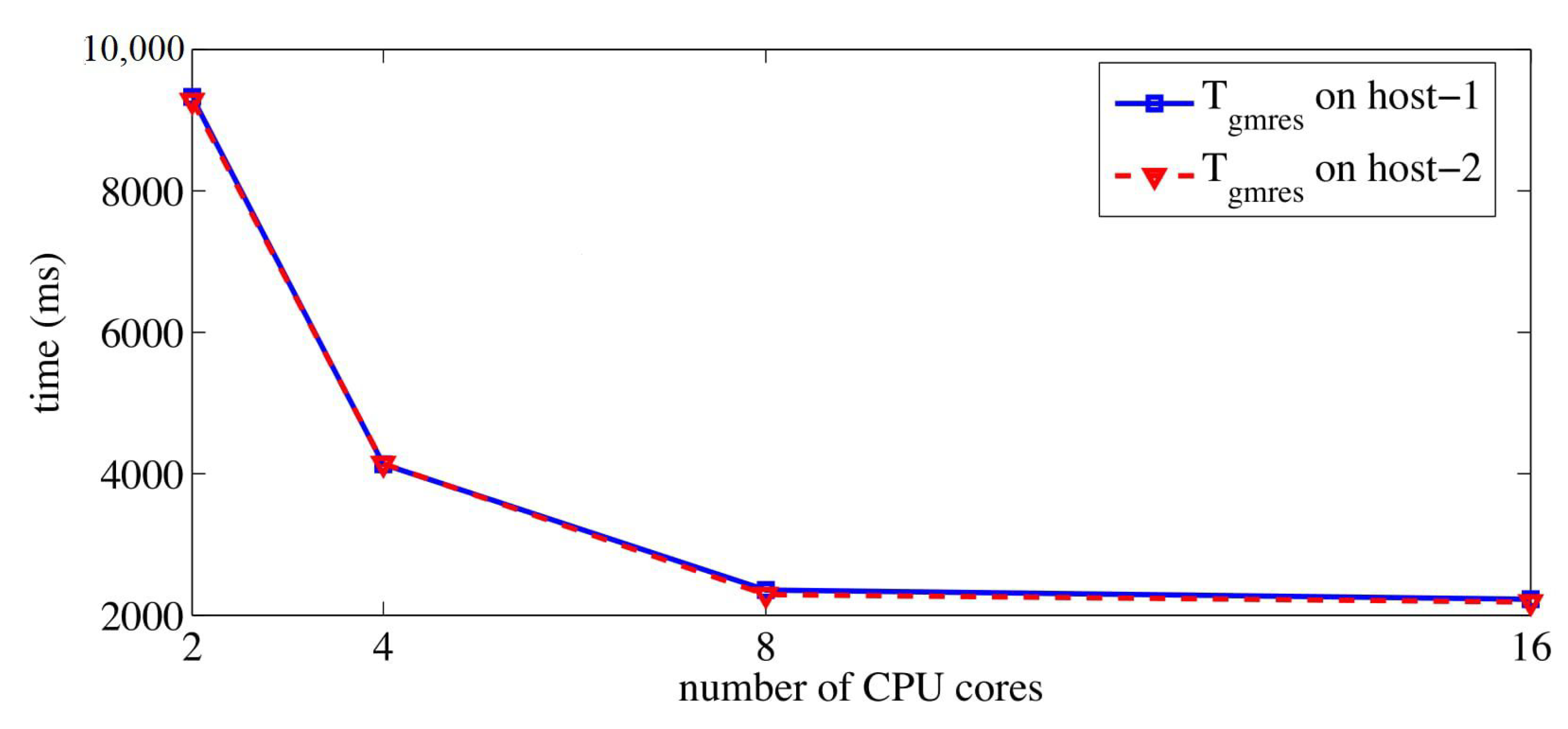
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PL, USA, 2003. [Google Scholar]
- Naumov, M. Parallel Solution of Sparse Triangular Linear Systems in the Preconditioned Iterative Methods on the GPU. Available online: https://research.nvidia.com/sites/default/files/pubs/2011-06_Parallel-Solution-of/nvr-2011-001.pdf (accessed on 29 June 2021).
- Compute Unified Device Architecture. Available online: https://developer.nvidia.com/cuda-toolkit (accessed on 20 April 2021).
- Anzt, H.; Sawyer, W.; Tomov, S.; Luszczek, P.; Dongarra, J. Optimizing Krylov Subspace Solvers on Graphics Processing Units. In Proceedings of the 2014 IEEE 28th International Parallel & Distributed Processing Symposium Workshops, Phoenix, AZ, USA, 19–23 May 2014; pp. 941–949. [Google Scholar]
- Clark, M.A.; Strelchenko, A.; Vaquero, A.; Wagner, M.; Weinberg, E. Pushing Memory Bandwidth Limitations Through Efficient Implementations of Block-Krylov Space Solvers on GPUs. Comput. Phys. Commun. 2018, 233, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Rupp, K.; Tillet, P.; Rudolf, F.; Weinbub, J.; Selberherr, S. ViennaCL-Linear Algebra Library for Multi - and Many-Core Architectures. SIAM J. Sci. Comput. 2016, 38, S412–S439. [Google Scholar] [CrossRef] [Green Version]
- Li, R.P.; Saad, Y. GPU-accelerated preconditioned iterative linear solvers. J. Supercomput. 2013, 63, 443–466. [Google Scholar] [CrossRef]
- CUDA Toolkit Documentation for cuSPARSE. Available online: https://docs.nvidia.com/cuda/cusparse/ (accessed on 5 April 2021).
- Liu, W.; Li, A.; Hogg, J.; Duff, I.S.; Vinter, B.A. Synchronization-Free Algorithm for Parallel Sparse Triangular Solves. Lect. Notes Comput. Sci. 2016, 9833, 617–630. [Google Scholar]
- Liu, W.; Li, A.; Hogg, J.D.; Duff, I.S.; Vinter, B.A. Fast synchronization-free algorithms for parallel sparse triangular solves with multiple right-hand sides. Concurrency Comput. Prac. Exp. 2017, 29, e4244. [Google Scholar] [CrossRef]
- Kashi, A.; Nadarajah, S. Fine-grain parallel smoothing by asynchronous iterations and incomplete sparse approximate inverses for computational fluid dynamics. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Chow, E.; Patel, A. Fine-grained parallel incomplete LU factorization. SIAM J. Sci. Comput. 2015, 37, C169–C193. [Google Scholar] [CrossRef]
- Chow, E.; Anzt, H.; Dongarra, J. Asynchronous Iterative Algorithm for Computing Incomplete Factorizations on GPUs. Lect. Notes Comput. Sci. 2015, 9137, 1–16. [Google Scholar]
- Dessole, M.; Marcuzzi, F. Fully iterative ILU preconditioning of the unsteady Navier-Stokes equations for GPGPU. Comput. Math. Appl. 2019, 77, 907–927. [Google Scholar] [CrossRef]
- Anzt, H.; Chow, E.; Dongarra, J. Iterative Sparse Triangular Solves for Preconditioning. Lect. Notes Comput. Sci. 2015, 9233, 650–661. [Google Scholar]
- Anzt, H.; Chow, E.; Szyld, D.B.; Dongarra, J. Domain Overlap for Iterative Sparse Triangular Solves on GPUs. In Software for Exascale Computing- SPPEXA 2013–2015; Springer: Cham, Switzerland, 2016; pp. 527–545. [Google Scholar]
- Anzt, H.; Huckle, T.K.; Bräckle, J.; Dongarra, J. Incomplete Sparse Approximate Inverses for Parallel Preconditioning. Parallel Comput. 2018, 71, 1–22. [Google Scholar] [CrossRef]
- Ma, W.P.; Hu, Y.W.; Yuan, W.; Liu, X.Z. GPU Preconditioning for Block Linear Systems Using Block Incomplete Sparse Approximate Inverses. Math. Probl. Eng. 2021, 2021, 5558508. [Google Scholar] [CrossRef]
- Kolotilina, L.Y.; Yeremin, A.Y. Factorized Sparse Approximate Inverse Preconditionings I. Theory. SIAM J. Matrix Anal. Appl. 1993, 14, 45–58. [Google Scholar] [CrossRef]
- Duin, V.; Arno, C.N. Scalable Parallel Preconditioning with the Sparse Approximate Inverse of Triangular Matrices. SIAM J. Matrix Anal. Appl. 1999, 20, 987–1006. [Google Scholar] [CrossRef] [Green Version]
- Bertaccini, D.; Filippone, S. Sparse approximate inverse preconditioners on high performance GPU platforms. Comput. Math. Appl. 2016, 71, 693–711. [Google Scholar] [CrossRef] [Green Version]
- He, G.; Yin, R.; Gao, J. An efficient sparse approximate inverse preconditioning algorithm on GPU. Concurr. Comput. Pract. Exper. 2019, 32. [Google Scholar] [CrossRef]
- Gao, J.; Chen, Q.; He, G. A thread-adaptive sparse approximate inverse preconditioning algorithm on multi-GPUs. Parallel Comput. 2021, 101, 102724. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.C.; Saad, Y. Overlapping Domain Decomposition Algorithms For General Sparse Matrices. Numer. Linear. Algebr. 1994, 3, 221–237. [Google Scholar] [CrossRef]
- OpenMPI v4.0 Series. Available online: https://www.open-mpi.org/doc/current (accessed on 24 March 2021).
- CUDA Toolkit Documentation v10.0.130. Available online: https://docs.nvidia.com/cuda/archive/10.0/ (accessed on 5 April 2021).
- Cheng, J.; Grossman, M.; McKercher, T. Professional CUDA C Programming; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Balay, S.; Abhyankar, S. PETSc Web Page. Available online: https://www.mcs.anl.gov/PETSc (accessed on 30 April 2021).
- OpenMPI v3.1 Series. Available online: https://www.open-mpi.org/doc/v3.1/ (accessed on 24 March 2021).
- CUDA 6.5 Production Release. Available online: https://developer.nvidia.com/cuda-toolkit-65 (accessed on 5 April 2021).
- Davis, T.; Hu, Y. The University of Florida Sparse Matrix Collection. ACM T. Math. Software 2011, 38, 1–25. [Google Scholar] [CrossRef]
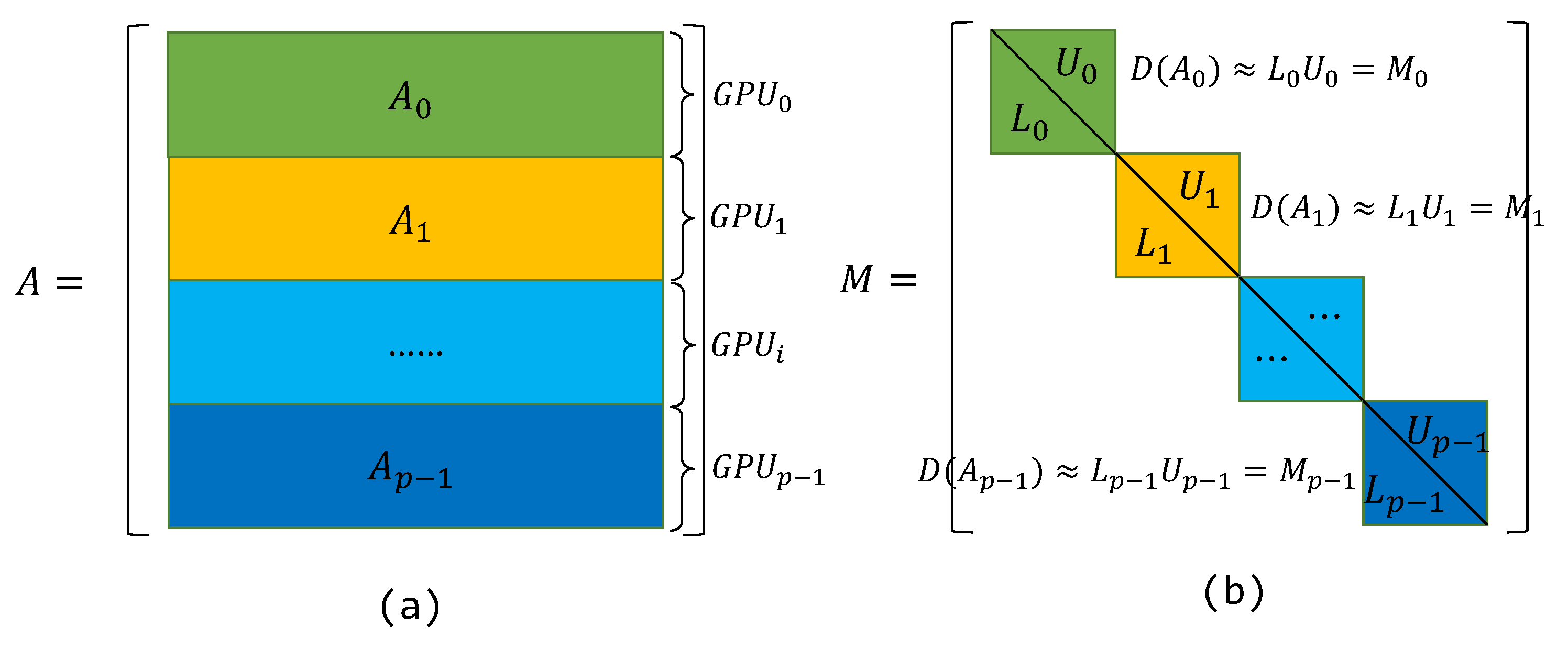
| lower and upper factors from the Block–ILU factorization | |
| sparsity pattern for the lower or upper factor | |
| factors with their absolute values | |
| estimation of the inverse of | |
| block-row indices of a block-column of | |
| block-row indices of the block-column of | |
|
block vector formed by block-rows and block-column of the identity matrix | |
| ISAI | Incomplete Sparse Approximate Inverses |
| BJPB-ISAI | Block–Jacobi preconditioning with Block–ISAI |
| BCSR, BCSC | block compressed sparse row, block compressed sparse column |
| SBTS | small block triangular systems |
| Tesla Product | Tesla K20 | Tesla V100 |
|---|---|---|
| GPU | GK110 | GV100 |
| Core Clock | 706 MHz | 1530 MHz |
| Stream Processors | 2496 | 5120 |
| Memory Interface | 320-bit DDR5 | 4096-bit HBM2 |
| Memory size | 5 GB | 16 GB |
| Peak FP32 TFLOPS | 3.52 | 15.7 |
| Peak FP64 TFLOPS | 1.17 | 7.8 |
| Shared Memory size | 16/32/48 KB | configurable up to 96 KB |
| Register File Size/SM | 256 KB | 256 KB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Yuan, W.; Liu, X. A Comparative Study of Block Incomplete Sparse Approximate Inverses Preconditioning on Tesla K20 and V100 GPUs. Algorithms 2021, 14, 204. https://doi.org/10.3390/a14070204
Ma W, Yuan W, Liu X. A Comparative Study of Block Incomplete Sparse Approximate Inverses Preconditioning on Tesla K20 and V100 GPUs. Algorithms. 2021; 14(7):204. https://doi.org/10.3390/a14070204
Chicago/Turabian StyleMa, Wenpeng, Wu Yuan, and Xiazhen Liu. 2021. "A Comparative Study of Block Incomplete Sparse Approximate Inverses Preconditioning on Tesla K20 and V100 GPUs" Algorithms 14, no. 7: 204. https://doi.org/10.3390/a14070204
APA StyleMa, W., Yuan, W., & Liu, X. (2021). A Comparative Study of Block Incomplete Sparse Approximate Inverses Preconditioning on Tesla K20 and V100 GPUs. Algorithms, 14(7), 204. https://doi.org/10.3390/a14070204






