Author Contributions
Conceptualization, E.H., M.S.H. and K.A.; methodology, P.D., E.H., M.I.H. and M.S.H.; software, P.D., E.H. and M.I.H.; validation, P.D., E.H., M.I.H., M.A.C. and M.S.A.; formal analysis, P.D., E.H., M.I.H., M.A.C. and M.S.A.; investigation, E.H., M.I.H., M.A.C., M.S.A., M.S.H. and K.A.; resources, M.I.H. and M.S.H.; data curation, P.D. and E.H.; writing—original draft preparation, P.D., E.H., M.I.H. and M.S.H.; writing—review and editing, E.H., M.A.C., M.S.A., M.S.H. and K.A.; visualization, P.D., E.H. and M.I.H.; supervision, E.H., M.S.H. and K.A. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Simple RNN Architecture.
Figure 1.
Simple RNN Architecture.
Figure 2.
A single cell LSTM architecture.
Figure 2.
A single cell LSTM architecture.
Figure 3.
A general architecture of a single GRU cell.
Figure 3.
A general architecture of a single GRU cell.
Figure 4.
System architecture of stock price prediction for different frequency domains.
Figure 4.
System architecture of stock price prediction for different frequency domains.
Figure 5.
HMC actual vs. RNN predicted for one-day interval.
Figure 5.
HMC actual vs. RNN predicted for one-day interval.
Figure 6.
HMC actual vs. LSTM predicted for one-day interval.
Figure 6.
HMC actual vs. LSTM predicted for one-day interval.
Figure 7.
HMC actual vs. GRU predicted for one-day interval.
Figure 7.
HMC actual vs. GRU predicted for one-day interval.
Figure 8.
HMC actual vs. RNN predicted for three-day interval.
Figure 8.
HMC actual vs. RNN predicted for three-day interval.
Figure 9.
HMC actual vs. LSTM predicted for three-day interval.
Figure 9.
HMC actual vs. LSTM predicted for three-day interval.
Figure 10.
HMC actual vs. GRU predicted for three-day interval.
Figure 10.
HMC actual vs. GRU predicted for three-day interval.
Figure 11.
HMC actual vs. RNN predicted for five-day interval.
Figure 11.
HMC actual vs. RNN predicted for five-day interval.
Figure 12.
HMC actual vs. LSTM predicted for five-day interval.
Figure 12.
HMC actual vs. LSTM predicted for five-day interval.
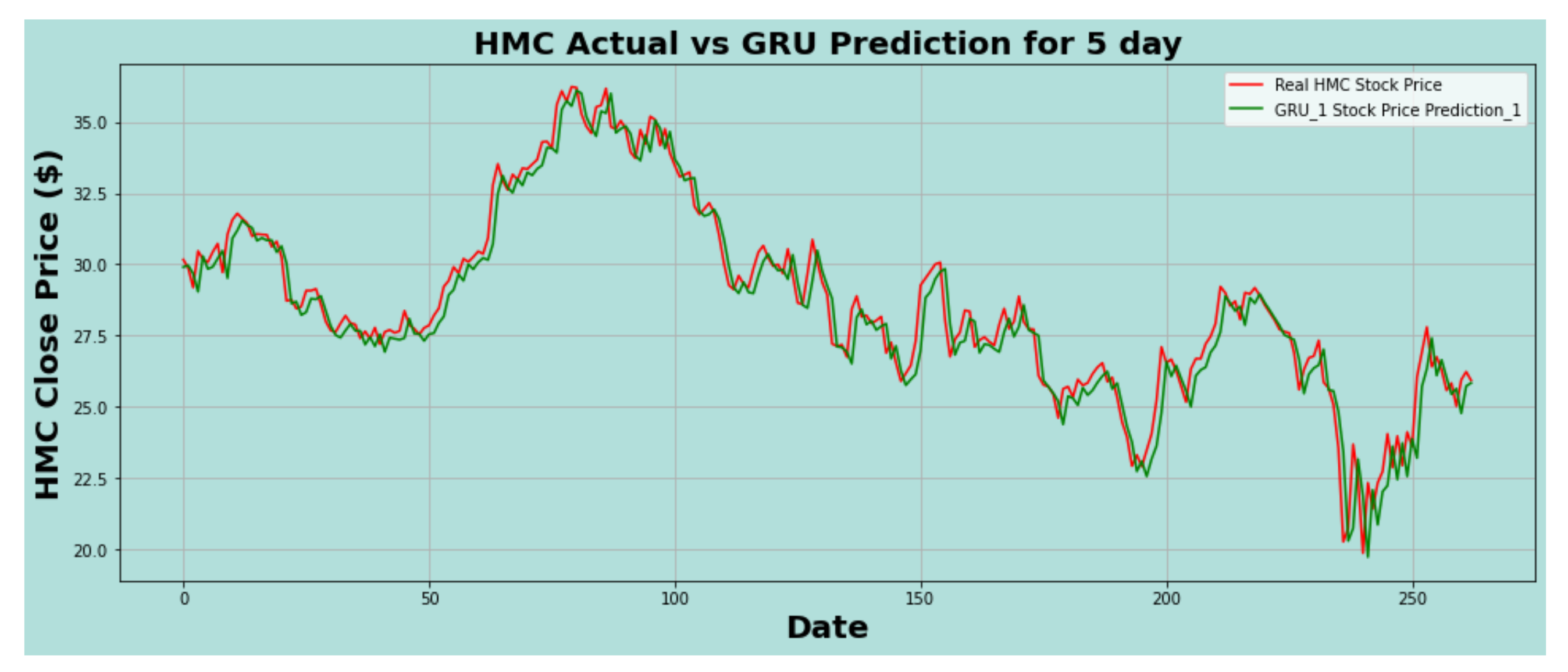
Figure 13.
HMC actual vs. GRU predicted for five-day interval.
Figure 13.
HMC actual vs. GRU predicted for five-day interval.
Figure 14.
ORCL actual vs. RNN predicted for one-day interval.
Figure 14.
ORCL actual vs. RNN predicted for one-day interval.
Figure 15.
ORCL actual vs. LSTM predicted for one-day interval.
Figure 15.
ORCL actual vs. LSTM predicted for one-day interval.
Figure 16.
ORCL actual vs. GRU predicted for one-day interval.
Figure 16.
ORCL actual vs. GRU predicted for one-day interval.
Figure 17.
ORCL actual vs. RNN predicted for three-day interval.
Figure 17.
ORCL actual vs. RNN predicted for three-day interval.
Figure 18.
ORCL actual vs. LSTM predicted for three-day interval.
Figure 18.
ORCL actual vs. LSTM predicted for three-day interval.
Figure 19.
ORCL actual vs. GRU predicted for three-day interval.
Figure 19.
ORCL actual vs. GRU predicted for three-day interval.
Figure 20.
ORCL actual vs. RNN predicted for five-day interval.
Figure 20.
ORCL actual vs. RNN predicted for five-day interval.
Figure 21.
ORCL actual vs. LSTM predicted for five-day interval.
Figure 21.
ORCL actual vs. LSTM predicted for five-day interval.
Figure 22.
ORCL actual vs. GRU predicted for five-day interval.
Figure 22.
ORCL actual vs. GRU predicted for five-day interval.
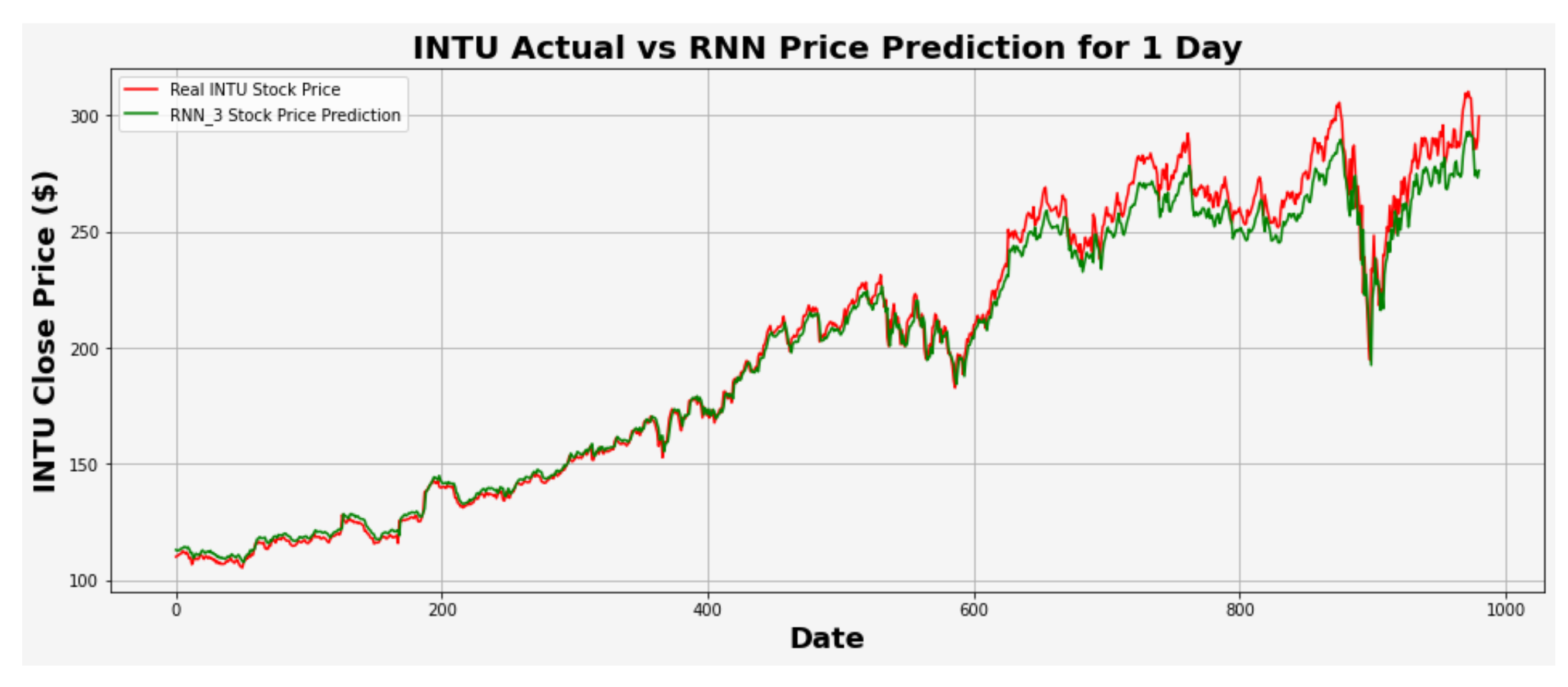
Figure 23.
INTU actual vs. RNN predicted for one-day interval.
Figure 23.
INTU actual vs. RNN predicted for one-day interval.
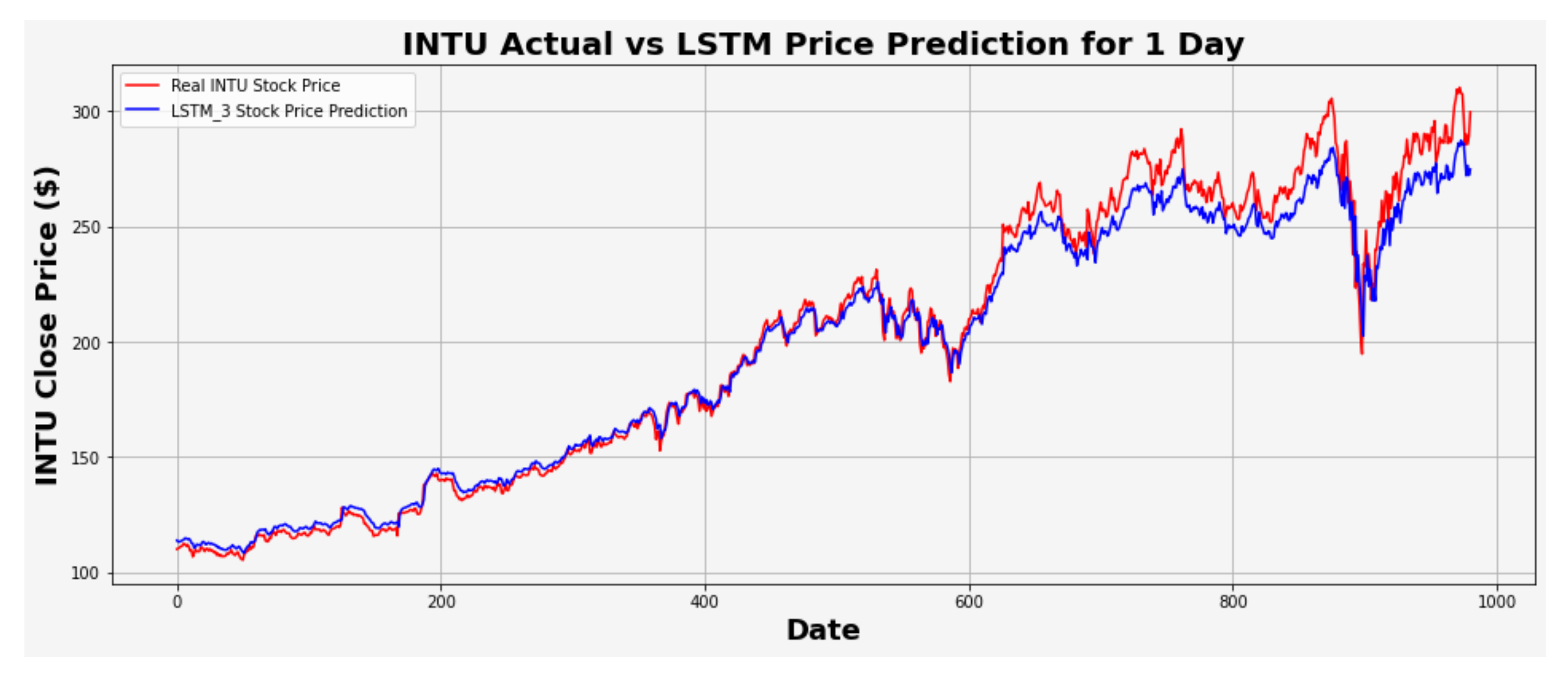
Figure 24.
INTU actual vs. LSTM predicted for one-day interval.
Figure 24.
INTU actual vs. LSTM predicted for one-day interval.
Figure 25.
INTU actual vs. GRU predicted for one-day interval.
Figure 25.
INTU actual vs. GRU predicted for one-day interval.
Figure 26.
INTU actual vs. RNN predicted for three-day interval.
Figure 26.
INTU actual vs. RNN predicted for three-day interval.
Figure 27.
INTU actual vs. LSTM predicted for three-day interval.
Figure 27.
INTU actual vs. LSTM predicted for three-day interval.
Figure 28.
INTU actual vs. GRU predicted for three-day interval.
Figure 28.
INTU actual vs. GRU predicted for three-day interval.
Figure 29.
INTU actual vs. RNN predicted for five-day interval.
Figure 29.
INTU actual vs. RNN predicted for five-day interval.
Figure 30.
INTU actual vs. LSTM predicted for five-day interval.
Figure 30.
INTU actual vs. LSTM predicted for five-day interval.
Figure 31.
INTU actual vs. GRU predicted for five-day interval.
Figure 31.
INTU actual vs. GRU predicted for five-day interval.
Table 1.
Model Architecture for Slightly Fluctuating Data (HMC).
Table 1.
Model Architecture for Slightly Fluctuating Data (HMC).
| Timeframe | Model | First Layer | Second Layer |
|---|
| one-day | RNN | 64 | 64 |
| LSTM | 256 | 256 |
| GRU | 512 | 1024 |
| three-day | RNN | 128 | 128 |
| LSTM | 256 | 256 |
| GRU | 512 | 256 |
| five-day | RNN | 128 | 32 |
| LSTM | 256 | 128 |
| GRU | 512 | 1024 |
Table 2.
Model Architecture for Moderately Fluctuating Data (ORCL).
Table 2.
Model Architecture for Moderately Fluctuating Data (ORCL).
| Timeframe | Model | First Layer | Second Layer |
|---|
| one-day | RNN | 256 | 64 |
| LSTM | 256 | 128 |
| GRU | 512 | 512 |
| three-day | RNN | 64 | 128 |
| LSTM | 256 | 256 |
| GRU | 256 | 512 |
| five-day | RNN | 256 | 64 |
| LSTM | 256 | 256 |
| GRU | 256 | 128 |
Table 3.
Model Architecture for Highly Fluctuating Data (INTU).
Table 3.
Model Architecture for Highly Fluctuating Data (INTU).
| Timeframe | Model | First Layer | Second Layer |
|---|
| one-day | RNN | 64 | 256 |
| LSTM | 256 | 128 |
| GRU | 512 | 1024 |
| three-day | RNN | 128 | 128 |
| LSTM | 1024 | 512 |
| GRU | 1024 | 512 |
| five-day | RNN | 256 | 128 |
| LSTM | 256 | 512 |
| GRU | 1024 | 512 |
Table 4.
Performance comparison of HMC one-day interval.
Table 4.
Performance comparison of HMC one-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.98321 | 0.28826 | 1.03648 | 0.40842 |
| LSTM | 0.98346 | 0.29185 | 1.04387 | 0.40531 |
| GRU
| 0.98389 | 0.28329 | 1.01502 | 0.40010 |
Table 5.
Performance comparison of HMC three-day interval.
Table 5.
Performance comparison of HMC three-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.96305 | 0.43949 | 1.58962 | 0.61541 |
| LSTM | 0.96204 | 0.44340 | 1.58702 | 0.62375 |
| GRU | 0.96413 | 0.42743 | 1.54541 | 0.60643 |
Table 6.
Performance comparison of HMC five-day interval.
Table 6.
Performance comparison of HMC five-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.94284 | 0.57858 | 2.10638 | 0.78400 |
| LSTM | 0.94093 | 0.58079 | 2.10279 | 0.79704 |
| GRU | 0.96032 | 0.56959 | 2.10013 | 0.78115 |
Table 7.
Performance comparison of ORCL one-day interval.
Table 7.
Performance comparison of ORCL one-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.96749 | 0.64351 | 1.29133 | 0.91327 |
| LSTM | 0.97345 | 0.53824 | 1.10547 | 0.82530 |
| GRU | 0.97295 | 0.55344 | 1.18299 | 0.83296 |
Table 8.
Performance comparison of ORCL three-day interval.
Table 8.
Performance comparison of ORCL three-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.95136 | 0.73144 | 1.49556 | 1.06560 |
| LSTM | 0.95364 | 0.70202 | 1.41944 | 1.04041 |
| GRU | 0.94486 | 0.83837 | 1.68504 | 1.13464 |
Table 9.
Performance comparison of ORCL five-day interval.
Table 9.
Performance comparison of ORCL five-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.90040 | 0.98882 | 1.98959 | 1.48361 |
| LSTM | 0.90153 | 0.98621 | 1.97875 | 1.39695 |
| GRU | 0.90001 | 0.99962 | 2.01920 | 1.40772 |
Table 10.
Performance comparison of INTU one-day interval.
Table 10.
Performance comparison of INTU one-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.98555 | 5.26118 | 2.34914 | 7.32498 |
| LSTM | 0.98046 | 6.20282 | 2.78882 | 8.51910 |
| GRU | 0.98983 | 3.70209 | 1.64523 | 6.14465 |
Table 11.
Performance comparison of INTU three-day interval.
Table 11.
Performance comparison of INTU three-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.94280 | 10.65475 | 4.46536 | 14.21290 |
| LSTM | 0.97453 | 6.85287 | 2.97133 | 9.48472 |
| GRU | 0.98988 | 3.91155 | 1.82053 | 5.97660 |
Table 12.
Performance comparison of INTU five-day interval.
Table 12.
Performance comparison of INTU five-day interval.
| Model | | MAE | MAPE | RMSE |
|---|
| RNN | 0.90405 | 13.57545 | 5.65341 | 17.83176 |
| LSTM | 0.96641 | 7.83521 | 3.41306 | 10.55002 |
| GRU | 0.98227 | 4.99038 | 2.31463 | 7.66498 |