QB4MobOLAP: A Vocabulary Extension for Mobility OLAP on the Semantic Web

Abstract

The accessibility of devices that track the positions of moving objects has attracted many researchers in Mobility Online Analytical Processing (Mobility OLAP). Mobility OLAP makes use of trajectory data warehousing techniques, which typically include a path of moving objects at a particular point in time. The Semantic Web (SW) users have published a large number of moving object datasets that include spatial and non-spatial data. These data are available as open data and require advanced analysis to aid in decision making. However, current SW technologies support advanced analysis only for multidimensional data warehouses and Online Analytical Processing (OLAP) over static spatial and non-spatial SW data. The existing technology does not support the modeling of moving object facts, the creation of basic mobility analytical queries, or the definition of fundamental operators and functions for moving object types. This article introduces the QB4MobOLAP vocabulary, which enables the analysis of mobility data stored in RDF cubes. This article defines Mobility OLAP operators and SPARQL user-defined functions. As a result, QB4MobOLAP vocabulary and the Mobility OLAP operators are evaluated by applying them to a practical use case of transportation analysis involving 8826 triples consisting of approximately 7000 fact triples. Each triple contains nearly 1000 temporal data points (equivalent to 7 million records in conventional databases). The execution of six pertinent spatiotemporal analytics query samples results in a practical, simple model with expressive performance for the enabling of executive decisions on transportation analysis.

1. Introduction

In this Web 2.0 era, the Semantic Web (SW) plays a significant role in data publishing with an open and interoperable nature. The SW is an extension of the World Wide Web created by the World Wide Web Consortium (W3C) to make Internet data machine-readable, and is also referred to as the Web of Data. [1]. The SW increased its position with the advanced features of complex queries such as interactive analytical queries [2]. The data availability also increased even for complex data types such as spatial data or temporal data. The representation of geospatial and temporal data on the SW is common and growing significantly [3].

Moving objects (MOs) are objects that change their locations continuously over time. The data produced by MOs have grown significantly with the availability of devices that track the position of moving objects, for example, by using smartphones and GPS [4]. MO data have triggered an interest in mobility data analysis or Mobility Online Analytical Processing (Mobility OLAP), which has been grown steadily year after year. Mobility OLAP has attracted many researchers to create mobility patterns. Mobility OLAP could be implemented, for example, in transportation, tourism, weather forecasting, and network sensor analysis [5].

Mobility OLAP utilizes data warehousing techniques that typically include a segment of trajectory or trajectory of MOs at a point in time. Generally, MO data are stored in lengthy sequences of spatiotemporal coordinates (x,y,t). These sequences are divided into smaller segments of a movement known as trajectories [5]. Moving object databases keep track of MOs’ locations over time and are designed to facilitate querying, for example, “Which cars are within fifteen minutes of Melaka Central Market?” However, they do not encourage a complicated analysis, such as, “List for each month, more than 50% of total trucks operating at speeds greater than 70 km per hour.” In this respect, integration with data warehousing technologies is necessary, which gives rise to the concept of the mobility data warehouse (DW) [6].

DW was designed according to a multidimensional (MD) modeling approach. DW could contain MOs data that can be analyzed in conjunction with other data such as city networks, road networks, agricultural data, climate observations, environmental data, and geographical data. The MOs data already exists on the SW as statistical data [6]. SW has a great vision of representing data on the web in a computer-readable way and adding semantic annotation. Information on the web could be effectively enriched, retrieved, and processed by machines or humans. SW technologies open a new model of integration data, transparency data, and semantically linked data using description logic for inference tasks [2].

The DW and SW research have been converged and are mutually beneficial. Combining these two technologies makes OLAP have more exploratory semantic sources available for interactive analytics queries and a bigger catalog worldwide. Many examples exist such as UK Environmental Data (http://environment.data.gov.uk, accessed on 5 April 2021), the Finnish LOD dataset (https://www.ldf.fi/datasets.html, accessed on 5 April 2021), Australian Linked Data (https://www.linked.data.gov.au, accessed on 5 April 2021), and European Statistic (https://ec.europa.eu/eurostat/web/nuts/linked-open-data, accessed on 5 April 2021) [7]. A vast amount of MO data containing spatial or non-spatial data have been published on the SW, yielding a need for advanced analysis of such data [8].

The abundance of open mobility data on the SW offers enhanced analytical options. Many examples web-based linked open data (LOD) created opportunities for the advanced study of such data [5,9]. These data sets contain observations and measures that are suitable for analysis (e.g., transport analysis, patient tracking, air/water quality measurements, immigration levels, etc.). However, mobility analysis on the SW still did not support the data representation and analytical query [9]. Mobility analysis on the SW still lacks a DW model with facts, measures, and dimensions for spatiotemporal/moving objects. This technology also did not support basic analytical queries for spatiotemporal/mobility operations. These operations include mobility roll-up, slice, dice, drill-down, and query functions that support mobility data types such as spatiotemporal aggregate, slice, and dice operations.

Perry et al. proposed a new query language, SPARQL-ST, an extension of SPARQL for complex spatiotemporal queries [10]. Further, a query language with the addition of geographic features on SPARQL was developed, namely GeoSPARQL. GeoSPARQL is an SW vocabulary that provides geospatial data representation. GeoSPARQL has two essential parts: an ontology for storing geospatial objects and query functions for processing relationships between the geospatial entities [11]. GeoSPARQL has some impressive features for geospatial implementation on the SW. This language did not accommodate analytical queries and had no extension for spatiotemporal and mobility data representation and queries. On the other hand, Vaisman et al. proposed a mobility DW with the concepts beyond the existing mobility analysis in the object-relational database [12], but it could not be implemented on the SW.

Mobility analysis on the SW still lacks a DW model with spatiotemporal/moving objects facts, measures, and dimensions. This technology also did not support basic analytical queries for spatiotemporal/mobility operations. These operations include mobility roll-up, slice, dice, drill-down, and query functions supporting mobility data types such as spatiotemporal aggregate and slice and dice operations [9].

This research constructs the representation of Mobility DW using the new vocabulary of QB4MobOLAP that allows the concept of Mobility DW to be defined over RDF data. Hence, the Mobility DW could be created and published on the SW. The study also defines the mobility analytics operators so that mobility analytics could be queried using SPARQL.

This paper introduces three contributions. First, QB4MobOLAP, a new vocabulary to represent Mobility DW on the SW. QB4MobOLAP extends the most recent OLAP vocabulary version with mobility concepts, including mobility facts and measures. The trajectory, level, dimensions, hierarchy, and mobility aggregation functions are also defined. Second, it introduces an extension of SPARQL query for analytical Mobility OLAP operators and functions. Third, this paper also explains the validation of the vocabulary model, operators, functions, and algorithm for the extension of SPARQL by implementing them in a practical use case.

The remainder of the paper is structured as follows: Section 2 describes related works, Section 3 consists of the material and methods involved, and Section 4 includes the results and discussion, while Section 5 concludes the paper and describes the challenges related to future work.

2. Related Works

2.1. Business Intelligence on Semantic Web

Business Intelligence (BI) is a platform that may be used to integrate, transform, and present analysis data as a means of decision-making support. BI employs proven technologies to obtain information and knowledge that is relevant to the business. These technologies are Extract Transform Loading (ETL), Data Warehouse (DW), Multidimensional Data (MD), and Online Analytical Processing (OLAP) [11].

Simultaneously, as a concept of sharing data on the Web, SW has attracted many scientists for more than a decade. SW has a great vision of representing data on the web in a computer-readable way and adding semantic annotation. Information on the Web could be effectively enriched, retrieved, and processed by machines or humans. SW technologies open a new integration data model, including transparency data and semantically linked data, using description logic for inference tasks [2]. The directions of BI and SW research have converged and are mutually beneficial. Combining these two technologies makes BI have more exploratory semantic sources available for interactive analytics queries.

The usage of BI technology over the SW begun with external source access to support BI’s decision making. These data varied from structured, semi-structured, and unstructured data formats. New terms arose, such as BI 2.0 or On-Demand BI [13], Fusion Cube [14], and Self-Service BI. [15]. BI proposed sophisticated tools to analyze vast amounts of data with outstanding performance. In contrast, the SW-linked data offered an exploratory opportunity for valuable information from big data across the internet and could be used to enrich business analytics with inferencing capability [14,16,17,18,19,20]. OLAP development using SW is categorized into three types of approaches. The first approach is an integration-based approach that focuses on data source integration; the second is an analysis-based approach that focuses on analytical processing. The third is a combination of these two approaches [9].

An integration-based approach focuses on extracting, transforming, and loading (ETL) from RDF data sources to DW. Many researchers proposed the use of this approach in their studies. Romero et al. defined a multidimensional concept of DW warehouses originating from single domain ontology representing multiple heterogeneous data sources from many business domains [21]. Niinimaki et al. developed a technique to practice ontology and the mapping of files that connect the data sources from external sources to the ontology. Then, the ETL process was performed according to the ontology and mapping files. OLAP ontology defines measures and dimensions using the Ontology Web Language (OWL) and Resource Description Framework (RDF) [22]. Likewise, Nebot et al. proposed a framework for designing a model of MD analysis with the semantic annotation stored in a Semantic DW (SDW). This approach stores the SDW as web resources, domain ontologies, and semantic annotations using XML [23].

Additionally, Jiang et al. proposed a method to handle data heterogeneity to build DW with the integration process’s domain ontology, and medical domain ontology played an important role [24]. Likewise, Bergamaschi et al. developed an ETL tool that could support semantic mappings from the data source with inter-attribute definitions to support the DW schema’s extraction and transformation process. The tool was implemented to develop DW in the food and beverage logistics area, resulting in an effective method [25].

An analysis-based approach directly focuses on analytical processes for SW/RDF data, without using the ETL process. In this approach, multidimensional data requires vocabulary to model RDF data cubes, dimensions, and measures. The de facto standard of vocabulary for the RDF Data Cube is QB [26]. Kampgen et al. proposed a querying model of statistical Linked Data using common OLAP operations on RDF data cubes. The research also found a set of OLAP query functions and operators using the SPARQL language, and improved the QB vocabulary in order to enhance multidimensional statistical data representations [27].

Moreover, Etcheverry and Vaisman developed Open Cube (OC) vocabulary using RDFS to publish multidimensional cubes on the SW. The OC was developed to support models with dimensions with multiple hierarchies, but OC had the disadvantage that it could not reuse QB vocabulary that had been used before [28]. Ibragimov et al. developed a framework called Exploratory OLAP over RDF sources. This research proposes a system that uses RDF vocabularies to define an OLAP cube with a multidimensional schema. The system intelligently executes the query to extract and summarize data and build a cube based on the vocabulary [19]. Etcheverry et al. developed an extension of QB that models multidimensional data; it is called QB4OLAP. QB4OLAP supports flat hierarchies, and is recursive, ragged, and uses many-to-many relationships in the multidimensional model [29].

Furthermore, Kalampokis et al. developed a new method to speed up query execution using a materialized view of the RDF graph. Their approach involves the physical storage of summarized triples in the system for faster processing of SPARQL queries (MARVEL). Many application tools were built using this approach and were used by governments and in industry, e.g., http://opengovintelligence.eu, accessed on 5 April 2021 [30]. On the other hand, Boumhidi et al. proposed a method for directly querying the cube data modeled by QB vocabulary with an interactive OLAP via MDX to SPARQL mapping without materialization. This research also constructed a formal algebra of OLAP operations on data cubes published as Linked Data [31].

The combination approach fully integrates SW in all layers of the BI. Several researchers proposed this combination approach: Colazzo et al. proposed a bottom-up redesign of the core data analytics concepts and RDF data tools. This design is fitted with Linked Data with a rich semantic and heterogeneous format. This design uses a full RDF warehousing approach, where the data source and the DW are in RDF graph format. This research also defines analytical schema and queries and optimization techniques with schema materialization [32]. Bansal and Kagemann created ETL tools to integrate data from various heterogeneous sources by utilizing semantic data to enrich the integration process [33]. Nath et al. proposed a programmable framework called Semantic ET (SETL) that could support the development of a Semantic Data Warehouse. SETL used TBox and QB4OLAP schema to create Multidimensional data for Semantic and Non-Semantic Data Sources [34]. Our study focuses on developing a vocabulary extension of QB4OLAP vocabulary based on an analytical approach.

2.2. Mobility Data Warehouse

Data warehousing technologies are needed to support the efficient collection, integration, storage, and analysis of the mobility pattern, yielding the notion of the Mobility Data Warehouse (DW) [7]. Mobility DW is the heart of mobility analytics, an extension of Business Intelligence (BI) that supports the collection, analysis, and presentation of information over moving object data. A Mobility DW deploys business intelligence by taking advantage of the operations associated with spatiotemporal data types to allow complex queries [7].

Trajectory DW is strongly related to mobility DW. Trajectory DW stores moving object data using base types, spatial types, and trajectories. A number of mobility analysis works that used the trajectory data warehouses (TDW) approach were published. For example, TDW was used for a recommender system for tourists [35], for road traffic analysis [36], and for finding the best location of billboard placement [37]. Further, some researchers added semantic information for TDW, such as for improving nurse productivity [38], mobility analysis [39], and modeling multiple aspect trajectories [8] to support decision making. However, according to the definition in [8], these research studies could not be classified as spatiotemporal DW since they did not support spatiotemporal queries and include moving data types [12].

Vaisman et al. defined the notion of spatiotemporal queries with aggregation extended with spatial and moving data types [10]. Based on this, they implemented Mobility DWs with spatiotemporal query support on MobilityDB, an object-relational DBMS. This implementation claimed to be supporting the spatiotemporal OLAP queries defined in [8]. Our research on this Mobility DW also supports spatiotemporal OLAP queries and moving data types represented on the SW and SPARQL.

2.3. Geospatial Semantic Web

The Spatiotemporal Multidimensional Data model on the SW starts from the Spatial SW, commonly referred to as Geospatial SW. The development of Geospatial SW began with finding a new retrieval method for geospatial data built on the semantics of spatial and ontologies developed at the University of Maine [40]. Then, the W3C SW Interest Group standardized Basic Geo Vocabulary using WGS84 as a reference datum [41].

Perry et al. stated that the web has a significant amount of spatial and temporal data, and the technology of SW could potentially make the accessibility and usefulness of data better. Because of SPARQL’s inability to query complex spatial and temporal data, Perry et al. proposed a new query language, SPARQL-ST, an extension of SPARQL for complex spatiotemporal queries. This research suggested a formal syntax and semantics and added spatial variables and constructs to manipulate temporal triples in SPARQL-ST, and was applied as a prototype built on top of a commercial DBMS [42]. Their work has many features but is still limited to essential operation for spatiotemporal operations, and is not applied for aggregation and analytical query functions.

Research on spatiotemporal data on the SW has been successfully implemented, such as Linked Geospatial Data in the UK government, followed by the manufacture of geospatial datasets by the Ordnance Survey Company for regions in the UK. These implementations could be accessed using SPARQL Endpoints [6]. Linked data are becoming popular with the advent of Geonames, a dataset in the form of linked data that collects spatial and thematic information for place names in different hemispheres and in various languages. The information stored in it is in the form of latitude, longitude, altitude, and population, and the administrative information is consistent with the 1984 World Geodetic System (WGS84) rules. Furthermore, there is LinkedGeodata, a linked data that is an SW infrastructure converted from OpenStreetMap. This linked data helps integrate and aggregate data related to maps [43] and can be easily queried with SPARQL. This approach attracts many researchers as a promising spatial linked data paradigm, but this approach still does not cover temporal data.

The temporal aspect then entered as a Spatiotemporal SW in the development of YAGO2 ontology, a continuation of YAGO knowledge-based ontology, where entities, events, and facts are combined with space-time information. YAGO2 was developed by automating Wikipedia, GeoNames, and WordNet. At present, YAGO2 contains 447 million facts and 9.8 million entities. YAGO2 uses the SPOTL model data (five tuples), an extension of SPO (3 tuples). Entities on YAGO2 are assigned a period, while the fact is assigned a time point or period [44]. YAGO2 became an excellent way to enrich large spatiotemporal knowledge-based data, but it did not have query functions for its spatiotemporal representation.

Furthermore, a query language, with the addition of geographic features to SPARQL, was developed, namely GeoSPARQL. GeoSPARQL is an SW vocabulary that provides geospatial data representation [45]. GeoSPARQL has two essential parts: an ontology for the storing of geospatial objects and query functions for the processing of relationships between the geospatial entities. The ontology was developed from the OGC standards, which have expressive concepts and terminology. The ontology of the GeoSPARQL is built to be small so that it can be easily understood and attached. The GeoSPARQL ontology has two main classes: Feature and Geometry. A Feature is an entity with spatial attributes. An example of the Feature is a building, statue, palace, lake, etc. Geometry is a shape, for example, a point, line, triangle, hexagon, etc., representing a feature’s spatial location. The third class, SpatialObject, is a superclass of both Feature and Geometry. GeoSPARQL became a geospatial RDF standard from W3C for data modeling and querying [46]. GeoSPARQL has some impressive features for geospatial implementation on the SW; this language did not accommodate analytical queries and has no extension for spatiotemporal and mobility data representation and querying.

Another proposal that is similar to GeoSPARQL is the development of stRDF/stSPARQL. The stRDF is a data model with an RDF extension and represents geospatial information that changes over time [47]. stRDF defines spatial and temporal dimensions that have literal spatial and spatial data types. stRDF also uses OGC standards such as WKT and GML for serialization. stSPARQL was developed as an extension query language for SPARQL by adding functions defined in the OpenGIS standard Simple Feature Access. These functions are in the form of basic functions (get, set), basic function access functions (equals, disjoint, intersect, touches, crosses, within, contains, overlaps, and relate), Egenhofer, RCC8, spatial analysis functions, spatial metric functions (distance and area), the spatial aggregate function (union, intersection, and extent). Strabon was then developed as an RDF store that supports semantic geospatial query languages in stSPARQL and GeoSPARQL. Strabon has expressive power in its use of these query languages with the stRDF model data. The testing of performance at strategic scales, for vast volumes of data, yielded good results [47]. stRDF/stSPARQL accommodates significant spatial data representation and query implementations, but it still lacks spatiotemporal data adoption and analytical capabilities.

Zhang et al. proposed a SPARQL extension for modeling and querying a quantitative spatiotemporal relationship. The extension model adds an event model with time and space. The query extension created 30 new query operators that could effectively find the unseen connections between event ontology entities and have excellent performance and effectiveness [48]. This approach comprehensively adds SPARQL functionality, but this approach still does not handle the spatiotemporal analytical query. On the other hand, Gur et al. proposed QB4SOLAP, a generic and extensible vocabulary (meta-model) for spatial DW on the SW. QB4SOLAP extends the QB4OLAP vocabulary with spatial concepts. They also give a formalization of QB4SOLAP. This paper defined critical spatial cube concepts, spatial hierarchies and levels, spatial measures, spatial aggregation functions, and topological relations among spatial dimension and hierarchy level members. They also defined several analytical spatial OLAP operators over QB4SOLAP, these operators’ formal semantics, and algorithms to generate spatially extended SPARQL queries [3]. This work provides a significant result in terms of the modeling and querying of spatial analytical data, but it is only limited to spatial data and does not include MOs data with more dynamic characteristics. In this study, we enhanced the QB4SOLAP capability to support mobility analysis for MOs data.

3. Research Methods

This research constructs a new vocabulary of Mobility DW on the SW that allows the definition of Mobility DW over RDF data and develops mobility query functions in SPARQL. This section explains the notions of mobility data types, operators, OLAP operators, and data sources as base concepts in this study. Hence, the last subsection describes a use case scenario for the evaluation method by implementing mobility DW in the new vocabulary and exploring descriptive, diagnostic, and discovery analysis in SPARQL.

3.1. Mobility Data Type

This research explores a new vocabulary to represent MOs on the SW for mobility analysis related to the MO data type for the purpose of query retrieval. The MO data have a data type that consists of spatial and temporal attributes. Spatial attributes describe real-world phenomena consisting of descriptive components presented with traditional data types such as integers, booleans, strings, and dates. Spatial attributes enriched with spatial extent components explain the real world in geometric data types such as Point, Multi Points, Line, Polygon, and Surface (MADS Model). Spatial attributes are stored differently and are often called thematic layers (themes).

Temporal attributes describe time and changes in time that could be defined with time types and temporal types. Guting et al. define temporal types as moving types [49]. Time types represent the time, for instance, timestamp, timestamp with time zone, period, timestamp set, and period set. Temporal types are based on time types. Temporal types include temporal integer, temporal float, temporal points, and temporal geometries. The temporal integer type could represent the evolution of employee salary. Temporal points denote the flight path of an aircraft or tourist. An example of a temporal float is the temperature of the human body.

The combination of spatial and temporal types creates new data types called temporal-spatial types [50]. This combination occurs in moving objects, such as pedestrians, trucks, moving clouds, and shrinking agricultural areas that are mostly represented using the point and polygon. Figure 1 shows an example of moving trucks in our use case of an oil palm plantation. These trucks deliver Oil Palm Fruit Fresh Bunches (FFB) from plantations to the Oil Palm Mill (OPM).

Table 1. Truck trajectories raw data.

DeliveryId	Latitude	Longitude	Time	Load (Tons)
323	−7.7737022	110.4307821	2019-09-03 07:05:04	0
	−7.7737022	110.4307821	2019-09-03 07:05:05	0
	−7.7743687	110.4306647	2019-09-03 07:05:06	0
	−7.7745781	110.430539	2019-09-03 07:05:07	0
	−7.774783	110.4306254	2019-09-03 07:05:08	0
	−7.774928	110.4306848	2019-09-03 07:05:09	0
	−7.7751657	110.4306146	2019-09-03 07:05:10	0
	−7.7753163	110.4306087	2019-09-03 07:05:11	20
	−7.7753163	110.4306087	2019-09-03 07:05:12	20
	−7.7753163	110.4306087	2019-09-03 07:05:13	20
324	−7.2132066	110.4349647	2019-09-03 09:40:00	12.3
	−7.2132063	110.4349648	2019-09-03 09:40:01	12.3
	−7.2132059	110.434965	2019-09-03 09:40:02	12.3
	−7.2132054	110.4349653	2019-09-03 09:40:03	12.3
	−7.2132049	110.4349656	2019-09-03 09:40:04	12.3
	−7.213204	110.4349662	2019-09-03 09:40:05	12.3
	−7.2132039	110.4349664	2019-09-03 09:40:06	12.3
	−7.2132039	110.4349663	2019-09-03 09:40:07	25
	−7.2132039	110.4349663	2019-09-03 09:40:08	25
	−7.2132039	110.4349663	2019-09-03 09:40:09	25

shows a sample of mobility data that have temporal-spatial types. The data contain the time, the locations of the trucks in longitude and latitude, and the float types of the truckload values. Our mobile apps captured this data to monitor the truckload and trajectory in the Oil Palm Fruit Plantation [51].

The temporal-spatial types could be extended to represent a field/region that varies in time and space. The spatiotemporal database is then used to store spatial types, temporal types, and temporal-spatial types. This database could store the position of moving objects at any point in time, changing regions continuously, and so on. Although some examples of queries could be solved, such as “When the last truck starting from Alfa Block arrive at Palm Oil Mills?”, “How fast the last truck arrived at Palm Oil Mills this morning shift?”, this kind of database does not provide a foundation for such complex analytical queries as “What is the average truckload passing the #27 road segment on the Alfa block in the X Company’s oil palm plantations this year?” or “What is the total weight of oil palm production carried by company trucks in each plantation block in the third quarter of 2020?”. These kinds of queries could be handled efficiently using Mobility DW with mobility operation capabilities. The Mobility DW has extended support for the concept of spatiotemporal data warehouses that contain spatial types, temporal types, and temporal-spatial types of data.

Implementation of the temporal types could be found on MobilityDB [52], as a data type tbool, tint, tfloat, ttext, based on the primitive data types boolean, integer, real and text, respectively. MobilityDB also has temporal-spatial types such as tgeompoint and tgeogpoint, which are based on spatial type points [53]. Because they allow the representation of values that change over time, temporal types are useful in mobility domain applications. Temporal types provide a more natural and simple representation of time-varying value. Additionally, when the values evolve over time, the operations on the base types (such as arithmetic operators and aggregation for integers and floats, and spatial relationships and distance for spatial types) can be intuitively generalized. A temporal type of instance, intuitively, represents a function from time to the base type. An example of temporal types for the representation of the truckload of DeliveryId 323 of Table 1 (Delivery323) is written by TFLOAT “(0@2019-09-03 07:05:04,20@@2019-09-03 07:05:11, 20@@2019-09-03 07:05:13)”. An example of temporal-spatial types for representing the delivery path of DeliveryId 323 of Table 1 (DeliveryPath323) is written by TGEOGPOINT “(POINT (−7.7737022 110.4307821)@2019-09-03 07:05:04, POINT (−7.7737022 110.4307821)@2019-09-03 07:05:05, ……, POINT(−7.7753163 110.4306087)@2019-09-03 07:05:13)”. In summary, Mobility analysis needs temporal-spatial types as mobility data types and a collection of related data types, including primitive types (e.g., boolean, integer, float, text), spatial types (e.g., point, line, region), and time types (e.g., periods, instant, period set).

3.2. Mobility Operator

Mobility data types have operators and functions associated with this type. These operators can be classified, including projection to a domain or range, boolean predicates, interaction with a domain or range, spatial operations, temporal operations, the rate of change, mobility aggregation, and lifting function aggregation.

Projection to a domain or range function is a function that is used to define the temporal types. These operations are DefTime, RangeValues, Trajectory, and Traverse. These operations can be defined as:

DefTime: moving(α) → periods

for α ∈ {boolean, integer, real, text, point, region}. DefTime is a function that gives moving as a constructor function that returns, for a given argument type α, the type whose values are partial functions from instant into α. An example of the DefTime function is DefTime(Delivery323), which returns {(2019-09-03 07:05:04, 2019-09-03 07:05:10), (2019-09-03 07:05:11, 2019-09-03 07:05:13)}.

RangeValues: moving(α) → range(α)

for α ∈ {boolean, integer, real, text, point, region}. The RangeValues is a projection of moving values into its range; for example, moving real returns a set of real intervals. The range is a constructor function that returns for an argument type α, the corresponding type whose values are sets of intervals over α. The RangeValues function can be instantiated, for example, to:

RangeValues:moving(integer) → range(integer)

An example of the RangeValues function is RangeValues(Delivery323), which returns {(0,20)}.

RangeValues: moving(point) → range(point)

An example of the RangeValues function is RangeValues(DeliveryPath323), which returns {(-7.7737022 110.4307821),(-7.7753163 110.4306087)}.

Trajectory: moving(point) → line

Trajectory: moving(region) → region

The Trajectory function is a function that has a moving point or a moving region as a parameter. This function projects into the range (the 2D space). For a moving point, this projection is usually a curve in the 2D plane, and for a moving region, it is a region; line and region are spatial types. For example, the Trajectory function for a moving point, Trajectory(DeliveryPath323), will return the line (−7.7737022 110.4307821, −7.7737022 110.4307821, ……, −7.7753163 110.4306087), while the Trajectory function for a moving region will return the region. Figure 2 shows another example of the trajectory of two routes, RouteT and RouteS, that intersect at time 8:20.

The boolean predicate function is a function that returns a boolean type. Examples of boolean predicate functions include IsDefinedAt and IsHasValue. These operations can be defined as:

IsDefinedAt: moving(α), time type → boolean

for α ∈ {boolean, integer, real, text, point, region}. The function IsDefinedAt will check whether the moving(α) is defined at an instant or an interval of time. For example, IsDefinedAt(DeliveryPath323,”2019-09-03 07:05:04”) returns the boolean value true.

IsHasValue: moving(α), α → boolean

Function IsHasValue will check whether the moving(α) is had a value of α. For example, IsHasValue(Delivery323,10) returns the boolean value false.

The term “interaction with a domain or range function” refers to a class of functions that access and interact with the domain and range of temporal types—the operations AtInstant and AtPeriod return values at a specified time or set of time intervals. For example, AtInstant(Delivery323, “2019-09-03 07:05:04”) returns 0 and AtPeriod(Delivery323, (“2019-09-03 07:05:04”, “2019-09-03 07:05:13”) returns a temporal float with a value of 0 at (“2019-09-03 07:05:04”, “2019-09-03 07:05:10”) and a value of 20 at (“2019-09-03 07:05:11”, “2019-09-03 07:05:13”).

InitialInstant and InitialValue return the first instant at which the function is defined and the corresponding value. For example, InitialInstant(Delivery323) returns “2019-09-03 07:05:04” and InitialValue (Delivery323) returns 0. FinalInstant and FinalValue are equivalent. For example, FinalInstant(Delivery323) returns “2019-09-03 07:05:13” and FinalValue (Delivery323) returns 20. The At Operation constrains the temporal type to a single value or a range of values within the function’s range. The AtMin and AtMax functions return to their minimal and maximal values, respectively. For example, At(Delivery323,20) returns a value of 20 at (“2019-09-03 07:05:11”, “2019-09-03 07:05:13”), AtMin(Delivery323) returns a value of 0 at (“2019-09-03 07:05:04”, “2019-09-03 07:05:10”), and AtMax(Delivery323) returns a value of 20 at (“2019-09-03 07:05:11”, “2019-09-03 07:05:13”). These operations can be summarized as follows:

AtInstant: moving(α), instant time → α

AtPeriod: moving(α), period of time → moving(α)

InitialInstant: moving(α) → instant time

InitialValue: moving(α) → α

FinalInstant: moving(α) → instant time

FinalValue: moving(α) → α

At: moving(α), α → moving(α)

AtMin: moving(α) → moving(α)

AtMax: moving(α) → moving(α)

StartSequence moving(α) → moving(α)

FinalSequence moving(α) → moving(α)

A critical property of any temporal value is its rate of change function. The rate of change function is computed using the derivation operation, which takes a temporal integer or real as an argument and returns a temporal real. Some examples of rate of change functions are:

Derivative: moving(α) → moving(real)

Speed: moving(α) → moving(real)

Temporal Aggregation operations is an operator that takes a temporal integer or real and yields a temporal real. Some temporal aggregation operations are:

$$\mathrm{Integral}: \mathrm{moving}(\mathsf{\alpha }) \to \mathrm{real} {{\displaystyle \int }}_{T}f\left(x\right)dx.$$

$$\mathrm{Duration}: \mathrm{moving}(\mathsf{\alpha }) \to \mathrm{real} {{\displaystyle \int }}_{T}dx.$$

$$\mathrm{Length}: \mathrm{moving}(\mathsf{\alpha }) \to \mathrm{real} {{\displaystyle \int }}_T\sqrt{1+{\left(\frac{dy}{dx}\right)}^2 dx}.$$

TWAvg: moving (α) → real  Integral/Duration

$$\mathrm{TWVariance}: \mathrm{moving}(\mathsf{\alpha }) \to \mathrm{real} {{\displaystyle \int }}_T\sqrt{\frac{{\left(f\left(x\right)-TAvg\right)}^2}{Duration} dx}$$

$$\mathrm{TWStDev}: \mathrm{moving}\left(\mathsf{\alpha }\right) \to \mathrm{real} \sqrt{TVariance}$$

TWMin: moving(α) → real Min(RangeValue(α))

TWMax: moving(α) → real Max(RangeValue(α))

The lifting function is a function that generalizes non-temporal data types to mobility data types. The lifting operation over non-temporal types substitutes its argument types for each time type and returns a temporal type. The operation more than and equal (≥) has lifted versions; for instance, one or both of its parameters can be of the temporal type, resulting in a time boolean.

Aggregation operations can be lifted in the same way. A lifted Avg operation, for example, merges a set of temporal reals to produce a new temporal real in which the average is computed at each instant. Figure 3 depicts a sample of the TAvg and TSum aggregation of the truckload delivery.

3.3. Mobility OLAP Operator

Mobility analysis needs OLAP operators for the expression of queries over data cubes. Mobility OLAP enhances the analytical capabilities of OLAP by taking into account the cube’s mobility information. These OLAP operators are roll-ups that aggregate measures along a hierarchical structure to obtain data with a coarser granularity. These operators are enriched with the aggregation function and operators, such as mobility aggregation, mobility spatial, and the aggregation lifting function. By selecting an individual instance at a dimension level, the slice operator removes a dimension from a cube. The dice operator reveals which cells in a cube satisfy a specified condition. The Spatial Slice and Spatial Dice enrich the OLAP operators proposed by the QB4SOLAP vocabulary [54]. Some functions enhance the spatial mobility operators: InsideGeometry, AtPeriod, AtTimeStamp, At, etc. Finally, the drill-down operator disaggregates measures along a hierarchical structure to obtain more detailed data. It is the inverse of the roll-up operation.

Table 2. The function and aggregation operators of mobility types (adapted from [50]).

Class	Operators
Projection to domain/range	DefTime, RangeValues, Trajectory
Predicates (Boolean)	IsDefinedAt, IsHasValue
Interaction with domain/range	AtTimeStamp, AtPeriod, InitialInstant, InitialValue, FinalInstant, FinalValue, At, AtMin, AtMax, startSequence, endSequence, etc
Rate of Change	Derivative, Speed, Turn
Mobility Row Aggregation	Integral, TWAvg, TWVariance, TWStDev, TWMax, TWMin
Mobility Spatial Aggregation	TCentroid, TUnion, TConvexHull, TIntersect, TMBR
Lifting Function Aggregation	TCount, TMax, TMin, TAvg, TSum
Spatial Operation	InsideGeometry, InsideRadius, Length, CumulativeLength
Temporal Operation	Duration

shows the mobility functions and operators of mobility data types.

3.4. Use Case Scenario: Oil Palm Fresh Fruit Bunches Transportation

This research utilizes the use case in the transportation of the oil palm fresh fruit bunches (FFB) in Indonesia’s plantations. This use case is applied to evaluate or prove the concept of the QB4MobOLAP Vocabulary and its query function.

The palm plantation wants to minimize transportation time, cost, and loading/unloading time to increase the quality of the fresh fruit by means of Mobility OLAP in order to find descriptive, diagnostic, and discovery information. Figure 4 depicts the FFB transportation process from harvesting until Palm Oil Mill (POM). Fruit harvesting is the first step of the crucial phase in the FFB transportation process. The fruit is then collected into the Fruit Collection Point (FCP) using such technology as the net system or the grabber system, or is collected manually. After being collected, the Fresh Fruit Bunch (FFB) will be transported to the POM according to the following steps: loading to the truck, thrilling to the POM, entering and queueing in the factory gate, weighing, and unloading into the loading ramp, and finally, the FFB will be processed in the POM. This cycle takes time and significantly affects the quality of the palm oil, especially when the fruit has bruised.

Figure 5 shows an example of the MultiDim logical model of Mobility DW for Oil Palm FFB Transportation analysis. The design has a Delivery Fact Table that has mobility measures and dimensions. The Fact Delivery has five measures. Route t( ) is a measure of the trajectory of truck positions at any point in time. The Load t() is an integer type measure that changes over time. The trajectory is a spatial type of measure represented by a line with a symbol. The other measures are Distance, as a numeric type, and Duration, as a time type.

The Route t( ) measure, as a temporal point type, allows deliveries to be aggregated along the dimensions. For example, a similar route could be merged into a single route; the route could be a union and an intersection, etc. Thus, a query such as “give me the total distance of trajectory by TruckOwner” or “give me the total truckload that passes road segment X in February” could be answered. A query such as “give the average of fruit loading time by month and plantation block”, where fruit loading time has been computed using a spatial operator within a radius, could be computed. These queries are examples of a spatial roll-up function. The delivery fact has a relationship with five dimensions, Truck, Date, and Plantation, where the latter is a spatial dimension related to the fact through many-to-many relationships. The truck dimension is composed of two levels with a one-to-many relationship. Spatial attributes or levels have an associated geometry (point, line, or region), which are indicated by symbol , and respectively.

The Plantation and FruitCollectionPoint dimensions are spatial dimensions. These dimensions share a geographical hierarchy where geometry is associated with each level in both dimensions. The FruitCollectionPoint Dimension has topological constraints that indicate an FCP in the Plantation Block, and the Plantation Block is contained in Plantation Afdeling and creates a parent–child relationship.

4. Results and Discussion

4.1. QB4MobOLAP Vocabulary

In this section, the mobility data cubes in the RDF representation are defined. The definition uses the FFB Transportation DW as an example, the logical schema of which is given in Figure 6. The QB4MobOLAP Vocabulary allows the defining of cube schemas and cube instances as RDF triples. QB4MobOLAP extends the QB4OLAP Vocabulary with mobility concepts to support Mobility OLAP operations directly over RDF data with SPARQL queries. Figure 6 shows the proposed QB4MobOLAP Vocabulary. The gray backgrounded rectangle is an extension vocabulary class, subclass, and object property from QB and QB4OLAP. These classes could be used to represent the mobility cube class. QB4MobOLAP extends the built-in function QB4OLAP, which is represented with the classes qb4mob:MobilityTemporalAggrFunction and qb4mob:MobilitySpatialAggrFunction in the vocabulary. The qb4mob:MobilityTemporalAggrFunction class has the instances qb4mob:TAvg, qb4mob:TCount, qb4mob:TMin, qb4mob:TMax, and qb4mob:TSum. The qb4mob:MobilitySpatialAggrFunction class has the instances qb4mob:TCentroid, qb4mob:TUnion, qb4mob:TConvexHull, qb4mob:TIntersect, and qb4mob:TMBR. The QB4MobOLAP also introduced the class qb4mob:MobilityObject to represent mobility data types. The qb4mob:MobilityObject has the subclasses qb4mob:MobilityBase to store temporal types and qb4mob:MobilityGeometry to store temporal-spatial types, as described in Section 3. The qb4mob:MobilityBase has the subclasses qb4mob:MobilityInteger and qb4mob:MobilityDecimal, and the qb4mob:MobilityGeometry has the subclasses qb4mob:MobilityPoint, qb4mob:MobilityCurve, and qb4mob:MobilitySurface.

4.2. Multidimensional Data Cube Definition in QB4MobOLAP

The QB4OLAP vocabulary modeled a multidimensional data cube in RDF terms. Multidimensional models are typically interpreted as data cubes, with cube cells corresponding to observational facts that are central to MD analysis. Facts have a set of properties called measures, which have aggregate functions that can be defined. To provide alternative analytic viewpoints, a data cube has n dimensions (with the attribute of contextual information) on a multidimensional space, where each dimension might have hierarchies with levels. Users can aggregate measures (of facts) at multiple levels of detail by using levels (of dimensions) (also known as granularity). Dimensions and facts are tied to the structure to assist this analysis at various detail levels. Levels also include attributes that describe the basic features of the members of the level.

These MD concepts (cube elements) and their roles and relationships are annotated at the schema level in RDF triple format using the QB4OLAP Vocabulary. Schema level (RDF) cube elements correspond to tables and columns (of tables) in an MD. Fact members with measure values and level members with attribute values are instance-level MD concepts annotated at the instance level with QB4MobOLAP Vocabulary. These instance level (RDF) cube elements correspond to the actual data rows/records annotated in triple format with QB4MobOLAP.

An RDF triple t is made up of three parts: the subject (s), the predicate (p), and the object (o), which is defined as triple (s,p,o) ∈ t = (I ∪ Bn) × I × (I ∪ Bn ∪ L), where I is the set of IRIs, Bn is the set of blank nodes, and L is the set of literals. The Cube Schema (CS), with element x defined as CS(x) ∈ (I ∪ Bn ∪ L), yields a set of triples T and is denoted by (x rdf:type ex:Property).

MD Schema. A data structure definition (DSD) contains information about the schema of a data set (i.e., a cube, an instance of the class qb:DataSet). The DSD can be applied to a variety of data sets. A data set’s DSD includes dimensions, levels, measures, and attributes, in addition to component properties. As CS = DSD, the DSD is defined by a conceptual MD cube schema CS, which includes a collection of dimension types D, a collection of measures M, and a collection of fact types as CS = (D, M, F). The following definitions apply to the cube schema elements:

Attributes. An attribute a ∈ A = {a₁, a₂, …, a_n} has a domain a:dom in the cube schema CS with a set of triples t_a ∈ T where t_a is represented as (a rdf:type qb:AttributeProperty; rdfs:domain xsd:Schema).

Levels. A level l ∈ L = {l₁, l₂, …, l_n} consists of a set of attributes A_l, which is defined by a schema l(a₁: dom₁, …, a_n: dom_n), where l is the level, and each attribute a is defined over the domain dom. For each level l ∈ L in the cube schema CS, a set of triples tl ∈ T, is represented as (l rdf:type qb4o:LevelProperty; qb4o:hasAttribute a). Relevant levels for FFB DW examples are the Plantation level and the Afdeling level, described in example 1. Afdeling is an area in a plantation that is larger than a block. An afdeling has many blocks.

Examples 1

ffb:plantation rdf:type qb4o:LevelProperty;

qb4o:hasAttribute ffb:plantationKey;

qb4o:hasAttribute ffb:plantationName;

qb4o:hasAttribute ffb:plantationGeo;

qb4o:hasAttribute ffb:PMOGeo;

qb4o:hasAttribute ffb:gateGeo.

ffb:afdeling rdf:type qb4o:LevelProperty;

qb4o:hasAttribute ffb:afdelingKey;

qb4o:hasAttribute ffb:afdelingName;

qb4o:hasAttribute ffb:afdelingGeo.

Hierarchies. A hierarchy h ∈ H = {h₁, h₂, …, h_n}, in the cube schema CS, is specified with a set of triples t_h ∈ T, and represented as (h rdf:type qb4o:HierarchyProperty; qb4o:hasLevel l; qb4o:inDimension D). h ∈ H is specified as h = (Lh, Rh) for each hierarchy, where Lh is a hierarchy level. Lh is a subset of Ld levels of the dimension D where Lh ⊆ Ld ∈ D and Ld is the dimension level. A hierarchy has a roll-up relation between its level, denoted by Rh, Rh = (Lc, Lp, c) where Lc and Lp are child and parent levels, respectively, and c is Cardinality, c ∈ {1 − 1, * − 1, 1 − *, * − *}, where * is many. For instance, Rh = (Afdeling, Plantation, *−1) shows that the roll-up relation between the child level Afdeling to the parent level Plantation is many-to-one, which means that plantation could have many afdelings. Relevant hierarchies for FFB DW examples include PlantationGeography, which is described in example 2.

Examples 2

#Hierarchies:

ffb:plantationGeography rdf:type qb4o:hierarchy;

qb4o:inDimension ffb:plantationDim;

qb4o:hasLevel ffb:fruitCollectionPoint,

ffb:block, ffb:afdeling, ffb:plantation.

Dimensions. A set of dimensions D = {d₁, d₂, …, d_n} form a cube schema with n dimensions. Each d ∈ D contains a tuple d = (L, H), where L is a Level and H is a Hierarchy. In the cube schema CS, each dimension d ∈ D has a set of triples t_d ∈ T, which are defined as (d rdf:type qb:DimensionProperty; qb4o:hasHierarchy h). Example 3 gives instances of four dimensions in FFB DW.

Example 3

#Dimensions:

ffb:plantationDim rdf:type qb:DimensionProperty;

qb4o:hasHierarchy ffb:plantationGeography.

ffb:roadDim rdf:type qb:DimensionProperty;

qb4o:hasHierarchy ffb:roadGeography.

ffb:truckDim rdf:type qb:DimensionProperty;

qb4o:hasHierarchy ffb:ownerName.

ffb:dateDim rdf:type qb:DimensionProperty;

qb4o:hasHierarchy ffb:timeHierarchy.

Measures. Facts have a property called measures. A measure m ∈ M = {m₁, m₂, …, m_n} in the cube schema CS is represented as (m rdf:type qb:MeasureProperty; rdfs:subPropertyOf sdmx-measure:obsValue; rdfs:domain xsd:schema). Measures are encoded with the sdmx definition, sdmx-measure:obsValue, which, for the attributes of rdfs:domain, specifies the schema of the measure property, and, for rdfs:range, defines the value types, i.e.,; integer, decimal, etc. For example, in FFB DW, there are duration and distance measures where the instance value is in the form of “65” ^^xsd:integer and “14.21” ^^xsd:decimal. Measures are related to facts and dimension levels.

Facts. Facts are associated with values of dimensions and measures. A fact is denoted as f ∈ F = { f₁, f₂, … , f_n}. The relation of the facts is described in components in the schema level of the definition of the facts cube, which is determined by (F rdf:type qb:DataStructureDefinition; qb:component[qb4o:level l; qb4o:cardinality c]; qb:component[qb:measure m; qb4o:aggregateFunctionAF]). Cardinality, c ∈ {1 − 1, 1 − *, * − 1, * − *} specifies the relationship cardinality between facts and level members. The definition of the cube schema requires the specification of measures’ aggregate functions. QB4OLAP defines typical aggregate functions, for example, AF ∈ {Sum, Avg, Count, Min, Max}. The facts are presented at the instance level, with each fact f having a unique IRI I, an observation. The fact is represented as (f rdf:type qb:Observation). An example of a fact instance f with its relation to measure values and dimension levels is a sale transaction from customer “Anton” (dimension level value), for a product “Digital Camera” (another dimension level value), with a unit price of “1000” (measure value) Malaysian Ringgit, and a sales amount of “2” (another measure value) units. The fact member and dimension level customers have one-to-many relationships, which means that the same customer can make multiple sales. The aggregate function can be specified to measure unit price as “Average/Avg”, and the sales amount can be specified as “Sum”

.

4.3. Defining Spatiotemporally Enhanced MD Data in QB4MobOLAP

Spatial Attributes. Spatial attributes are specified on a domain level. Each attribute with a geometry domain (sa: domgeo ∈ A) is a member of the geo:Geometry class and is referred to as a spatial attribute, which is represented in the cube schema CS as (sa rdf:type qb:AttributeProperty; rdfs:domain geo:Geometry). In the instances, each spatial attribute type (point, polygon, line, etc.) is assigned using the predicate rdfs:range.

Spatial Levels. In the cube schema CS, a spatial level ls ∈ L is defined by a set of triples t_ls ∈ T and represented as (ls rdf:type qb4o:LevelProperty; qb4o:hasAttribute a, as; geo:hasGeometry geo:Geometry). Spatial levels must be geo:Geometry class members and may have spatial attributes. Example 4 shows the Plantation level as a spatial level with spatial attributes.

Example 4

#Attributes

ffb:plantationKey rdf:type qb4o:levelAttribute;

qb4o:inLevel ffb:plantation;

rdfs:range xsd:Integer.

ffb:plantationName rdf:type qb4o:levelAttribute;

qb4o:inLevel ffb:Plantation;

rdfs:range xsd:String.

ffb:plantationGeo rdf:type qb4o:levelAttribute;

qb4o:inLevel ffb:plantation;

rdfs:subPropertyOf geo:Geometry;

rdfs:range geo:wktLiteral;

rdfs:domain geo:Polygon;

rdfs:subClassOf geo:SpatialObject;

Spatial Hierarchies. Two or more spatial levels l_s relate to each other to create a spatial hierarchy h_s ∈ H. The spatial hierarchy step describes a roll-up relation between the spatial levels. QB4SOLAP introduces topological relations, T_r, in addition to cardinalities in the roll-up relation that are encoded as R = (L_c, L_p, c, T_r) for the spatial hierarchy steps. Let t_shs ∈ T be a set of triples to represent a hierarchical step for spatial levels in hierarchies, which is given with a blank node: _sh_hs ∈ B and encoded as (:_shhs rdf:type qb4o:HierarchyStep; qb4o:childLevel slhci; qb4o:parentLevel slhpi; qb4o:cardinality c; qb4so:hasTopologicalRelation Tr) where slhci ∈ Lc, slhpi ∈ Lp. For example, a spatial hierarchy is “geography”, which should have spatial levels (e.g., FruitCollectionPoint, Block, Afdeling, and Plantation) with the roll-up relation Rh = (Block, Afdeling, many-to-one, within), which also specifies that the child-level Afdeling is “within” the parent level Plantation.

Spatial Dimensions. Dimensions are considered spatial if they contain at least one spatial hierarchy. More than one dimension can share the same spatial hierarchy and spatial levels as that hierarchy.

Spatial Measures. A Spatial measure sm ∈ M is specified by a set of triples t_sm ∈ T and represented as (sm rdf:type qb:MeasureProperty; rdfs:subPropertyOf sdmx-measure:obsValue; rdfs:domain geo:Geometry) in the cube schema CS. Spatial measures are represented by a geometry that uses geometry serialization standards in OGC schemas. For example, a spatial measure is a trajectory that contains a list of coordinates of locations, which is given as a line geometry type and is associated with an observational fact of the trajectory of delivery.

Mobility Measures. A mobility measure mm ∈ M is specified in the cube schema CS by a set of triples t_mm ∈ T and encoded as (mm rdf:type qb:MeasureProperty; rdfs:subPropertyOf sdmx-measure:obsValue; rdfs:domain qb4mob:MobilityBase/MobilityGeometry). The class of the numeric value is given with the property rdfs:domain, and rdfs:range assigns the values from the class qb4mob:MobilityBase/mobilityPoint, i.e., the temporal integer, temporal float, temporal point, temporal polygon, etc., at the instance level. Mobility measures are represented by a mobility base/geometry. These mobility measures use schema extension of OGC schemas with temporal natures that change over time.

Mobility Facts. Mobility facts F_m have mobility/spatiotemporal natures that are related across several dimensions, either spatial or temporal. The mobility fact cube has mobility measures (m_m), as its members make it possible to aggregate mobility measures with the aggregation functions M_agg. Representation of a complete mobility fact cube at the schema level in RDF is given by a set of triples t_fs ∈ T and encoded as (fs a qb:DataStructureDefinition; qb: component [qb: measure ms, sdmx-measure:obsValue; qb4mob:aggregate-functionMAF]). QB4MobOLAP extends the built-in functions of QB4OLAP with mobility aggregation functions, which are added with the class qb4mob:MobilityTemporalAggrFunc or qb4mob:MobilitySpatialAggrFunc. An example of a mobility fact instance f_m with its relation to measuring values and dimension levels is a truck route delivery of some fruits (ffb:Route), which are created routes with coordinate points of the location that change by time. The cardinality of the dimension level truck and fact member is one-to-many, where a truck could have some delivery routes. Specification of the mobility aggregate function for route (coordinate points by time) can be specified as the “Time Centroid/TCentroid” route of locations.

Example 5

#Measures

ffb:Distance rdf:type qb:MeasureProperty;

rdfs:range xsd:decimal.

ffb:Duration rdf:type qb:MeasureProperty;

rdfs:range xsd:Time.

ffb:Route rdf:type qb:MeasureProperty;

rdfs:domain qb4mob:MobilityPoint;

rdfs:range geo:wktLiteral;

rdfs:subClassOf qb4mob: MobilityObject.

ffb:Trajectory rdf:type qb:MeasureProperty;

rdfs:domain geo:Linestring;

rdfs:range geo:wktLiteral;

rdfs:subClassOf geo:SpatialObject.

ffb:Load rdf:type qb:MeasureProperty;

rdfs:domain qb4mob:MobilityInteger;

rdfs:range geo:wktLiteral;

rdfs:subClassOf qb4mob:MobilitylObject.

#Cube Definition

ffb:freshFruitBunchDelivery rdf:type qb:DataStructureDefinition;

#Lowest level for each dimension

qb:component [qb4o:level ffb:plantation;

cardinality qb4o:ManyToOne];

qb:component [qb4o:level ffb:truck;

cardinality qb4o:ManyToOne];

qb:component [qb4o:level ffb:date;

cardinality qb4o:ManyToOne];

#Cube measures

qb:component [qb:measure ffb:Duration; qb4o:aggregateFunction qb4o:Avg];

qb:component [qb:measure ffb:Distance; qb4o:aggregateFunction qb4o:Avg];

qb:component [qb:measure ffb:Trajectory; qb4o:aggregateFunction qb4so:Centroid];

qb:component [qb:measure ffb:Route; qb4o:aggregateFunction qb4mob:TCentroid];

qb:component [qb:measure ffb:Load; qb4o:aggregateFunction qb4mob:TSum];

4.4. Defining MD Data Instance in QB4MobOLAP

The previous sub-chapter has shown that the data cube schema can be represented using QB4MobOLAP in the RDF format. This sub-chapter will explain the representation of the Delivery cube instance using QB4MobOLAP. The notation Graph Instance (GI) represents the RDF Graph of the data cube instance. The notation ffbi: is used for the prefix of GI, and the subgraph that refers to the specific instance with the index i is denoted by GI (i).

Level Members. A level l has a set of level members LM (l) ={lm₁,..., lm_y}. Each level member lm_i has a unique IRI idI (lm_i) ∈ I, linked in the cube instance graph GI with the qb4o:LevelMember predicate. A level member is related to its level by the qb4o:memberOf property. The RDF graph formulation of the level members LM (l) is represented as

GI LM(I) = {(id (l_mi) rdf:type qb4o:LevelMember)} ∪ {(id (lmi) qb4o:memberOf id (l))}

Definition of Level Members’ attributes. A level member has an attribute set l_m = {a₁, a₂, …., a_p}, which is used to describe the characteristics of the level member. Each attribute a_i is linked to the level member with the identifier id (a_i).

Example: The triples below show how some level members of the FFB DW are represented in RDF.

Example 6

#Instance

ffbi:plantation_1 rdf:type qb4o:LevelMember;

qb4o:memberOf ffb:plantation;

ffb:plantationName “PT. LestariPlantation”;

ffb:plantationGeo “POLYGON((-7.7737022 110.4307821, -7.7753163 110.4306087, …. ))”^^geo:wktLiteral

ffb:PMOGeo “POINT(-7.7753163 110.435160)”ˆˆgeo:wktLiteral;

ffb:gateGeo “POINT(-7.7753163 110.4352012)”ˆˆgeo:wktLiteral.

ffbi:afdeling_2 rdf:type qb4o:LevelMember;

qb4o:memberOf ffb:afdeling;

ffb:afdelingName “Afdeling Alfa”;

ffb:afdelingGeo “POLYGON((-7.7737022 110.4307821, -7.7753163 110.4306087, …. ))”^^geo:wktLiteral;

skos:broader ffbi:plantation_1.

Fact Members. A fact F has a set of data members FM (F) = {f₁, f₂, …, f_t}, which are the instances of the data cube. Each fact f_i ∈ FM has a unique IRI id (f_i) ∈ I, which is linked in the cube instance graph GI with the qb:Observation predicate. A fact member f_i is related to a set of dimension level L(f_i) = { l₁, l₂, …., l_r }and has a set of measure M(m_i) = { m₁, m₂, …., m_r}. Each dimension level l_j is linked to level member with the identifier id-S (l_j) and each measure m_k is linked to the level member with the identifier id-S(m_k). Dimension values and measure values are associated with a fact F. Dimension values are denoted by f → v(d_i) and measure values denoted by f → v(m_j). The value of v(d_i) ∈ I, is the identifier of a level member in LM (l_j). The value of every measure m_j is a literal such that v(d_i) ∈ L. The RDF graph formulation of the fact members FM (F) is represented as:

$$GI FM\left(F\right) = {{\displaystyle \cup }}_{n=1}^m\left(G{I}_{fi}\right)$$

$$\begin{array}{c}{{\displaystyle \cup }}_{n=1}^m\left(G{I}_{fi}\right)=\left\{\right(\mathrm{id}\left({\mathrm{f}}_{\mathrm{i}}\right)\mathrm{rdf:type\; qb:Observation}\left)\right\}\cup \\ {{\displaystyle \cup }}_{I_j\in L\left(f_i\right)}\left\{\right(i{d}^I \left(f_i\right)i{d}^S \left(l_j\right)i{d}^I \left(v_{l_j}\right)|f_i \to v_{l_j})\}\cup \\ {{\displaystyle \cup }}_{m_k\in M\left(f_i\right)}\left\{\right(i{d}^I\left(f_i\right)i{d}^S\left(m_k\right)i{d}^I\left(v_{m_k}\right) | f_i \to v_{m_k})\}\end{array}$$

The RDF representation example below shows the fact member of FFB DW using the above definition. Note that the fact member and corresponding level members relating to dimensions are given with the prefix ffbi:. idS (aID) is a surrogate key that links the fact member with the corresponding dimensions.

Example 7

#Measure Instance

ffbi:delivery_071219_1 rdf:type qb:Observation;

ffb:truckKey ffbi:truck_1;

ffb:dateKey ffbi:date_1;

ffb:plantationKey ffbi:plantation_1;

ffb:Route “TGEOGPOINT((-7.7737022 110.4307821@2019-09-02 08:00:01,

-7.7753163 110.4306087@2019-09-02 08:00:01, …))^^geo:wktLiteral;

ffb:trajectory “LINESTRING((-7.7737022 110.4307821, -7.7753163 110.4306087, …. )) “^^geo:wktLiteral;

ffb:Load “TINT( 25@2019-09-02 08:00:01, 35@2019-09-02 08:00:02,…) “^^geo:wktLiteral;

ffb:Distance “15.23”^^xsd:decimal;

ffb:Duration “00:20:36”^^xsd:Time;

4.5. Querying the Fresh Fruit Bunch for Transportation and Production Analysis

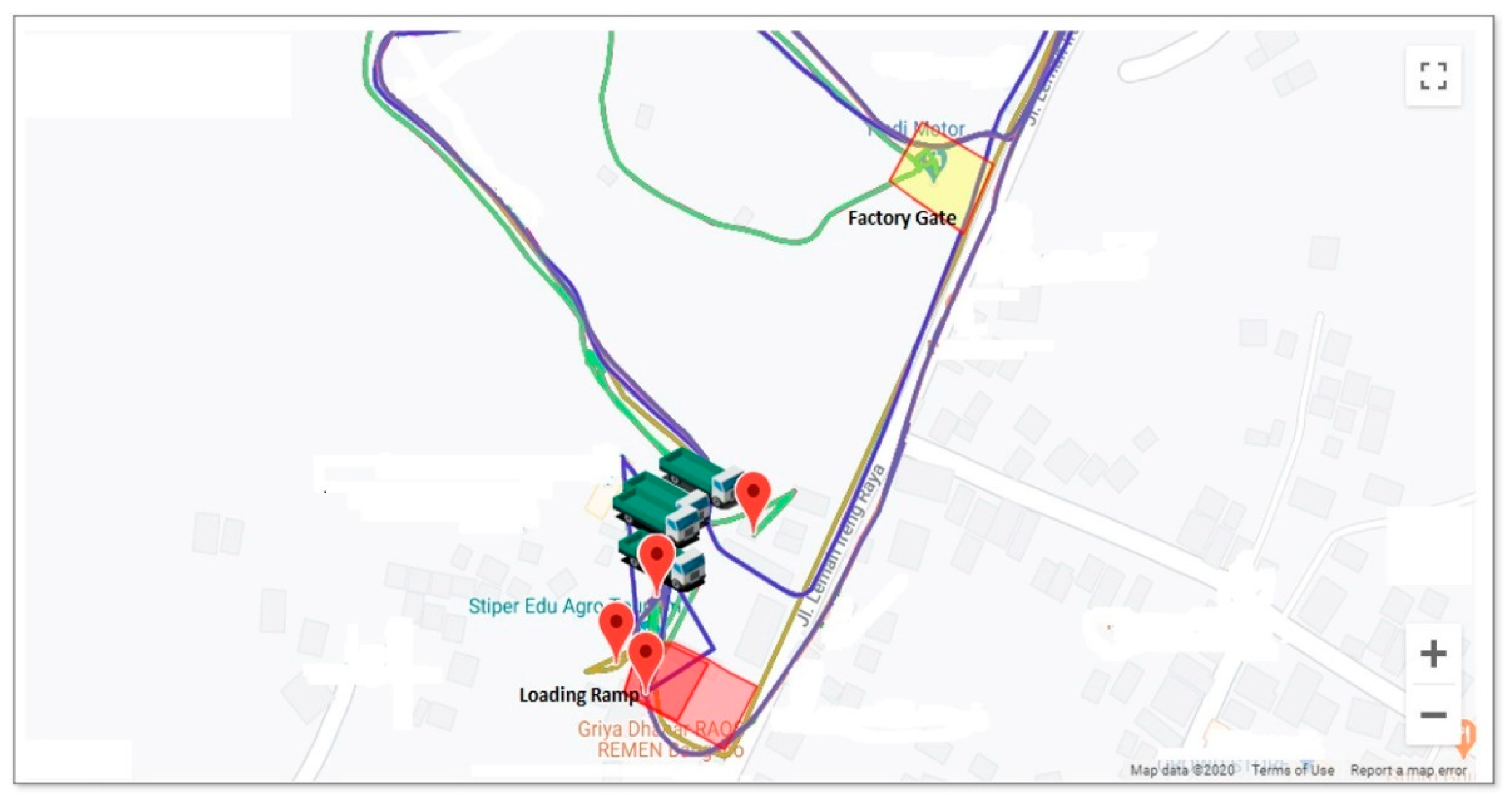
To evaluate or give proof of concept regarding how to implement mobility data cube concepts on the SW, and express queries for transportation and production analysis, the Fresh Fruit Bunch (FFB) data warehouse was explored. The FFB DW was built to support factory executives and farmers’ cooperation to analyze the transportation, loading/unloading, or even plantation productivity. The analysis aimed to reduce the transportation time to the POM to minimize the FFB quality loss, maximize the road support for effective FFB transportation, and maximize plantation productivity.

The queries are executed using the SPARQL, GeoSPARQL, and SPARQL function extensions for mobility queries that were developed in this research. These queries gather descriptive, diagnostic, and discovery analysis to know the event and phenomenon and the reason behind the event from the DW encoded in QB4MobOLAP vocabulary. The queries combine typical OLAP operations, such as roll-up, slice, spatial slice, temporal slice, and dice, with spatial and temporal operations on MOs.

The FFB DW contains 8826 triples consisting of approximately 7000 fact triples with nearly 1000 temporal data points each. In conventional data storage, the triple is equivalent to approximately 7 million records. The RDF graph is published using the GraphDB server on the Windows platform with a Pentium Core i5 8th generation with 16GB RAM computer. The server can be accessed at http://lod.if.fti.uajy.ac.id:7200/sparql, accessed on 10 June 2021.

Query#1: Give the average distance traveled by each truck per month in Q3 2019.

The query involves some operations that are rolled-up along the Time and Truck dimensions. Then, the computation of the distance on the moving object data is conducted. Finally, slicing operations are performed for the Time dimension.

SELECT ?month ?truckKey (AVG(jsfn:length(?droute)) as ?lengthRoute)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:dateKey ?dateKey;

ffb:Route ?droute.

?dateKey qb4o:memberOf ffb:date;

ffb:quarter ?quarter;

ffb:year ?year;

ffb:month ?month.

FILTER ((?quarter = 3) && (?year=2019))}

GROUP BY ?month ?truckKey

Query#2: Give the average delivery duration per truck owner in September 2019.

The query involves some operations that are rolled-up along the Truck dimension. Then, the computation of the duration of the moving objects is conducted. Finally, slicing operations are performed for the Time dimension.

SELECT ?oName (AVG(jsfn:Duration(?droute)) as ?RouteTimeSpan)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:dateKey ?dateKey;

ffb:Route ?droute.

?dateKey qb4o:memberOf ffb:date;

ffb:month ?month;

ffb:year ?year.

?truckKey qb4o:memberOf ffb:truck;

ffb:ownerName ?oName.

FILTER ((?month = 9) && (?year=2019))

} GROUP BY ?oName

Query#3: Give the average duration of FFB delivery inside the Afdeling Alfa per truck owner.

The query involves some operations that are rolled-up along the Truck dimension. Then, the computation of the duration of the moving objects and geometry operations is conducted. Finally, spatial-slicing operations are performed within areas as a spatial function, sfWithin.

SELECT ?oName

(AVG(jsfn:Duration(jsfn:insideGeometry(?droute,?afdelingGeo))) as ?x)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:Route ?droute;

ffb:plantationKey ?plantationKey.

?plantationKey qb4o:memberOf ffb:plantation;

ffb:plantationGeo ?plantationGeo.

?afdelingKey qb4o:memberOf ffb:afdeling;

ffb:afdelingGeo ?afdelingGeo;

ffb:afdelingName ‘Afdeling Alfa’.

?truckKey qb4o:memberOf ffb:truck;

ffb:ownerName ?oName.

FILTER (geof:sfWithin(?afdelingGeo,?plantationGeo))}

GROUP BY ?oName

Query#4: Compute the truck’s average speed from the farmer’s plantation to the factory.

The query involves spatiotemporal roll-up along the Truck dimension, speed computation of the delivery, and slicing of the truck and date dimension.

SELECT ?lplate (AVG(jsfn:TWAvg(jsfn:TSpeed(?droute))) as ?AvgSpeed)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:dateKey ?dateKey;

ffb:Route ?droute.

?truckKey qb4o:memberOf ffb:truck;

ffb:ownerName ?oName;

ffb:licensePlate ?lplate.

?dateKey qb4o:memberOf ffb:date;

ffb:year ?year.

FILTER ((?oName != ‘Factory’) && (?year = 2019))}

GROUP BY ?lplate

Query#5: Compute the average queue time in Palm Oil Mills (POM) by each truck owner in 2019.

The query involves some operations roll-up along the Truck dimension, computation of the queue time, and slicing operations performed for the Time dimension. The truck timespan, in a radius of 100 m from the loading ramp POM, defines the queue time.

SELECT ?oName

(AVG(jsfn:Duration(jsfn:insideRadius(?droute,?PMOGeo,100))) as ?AverageQueueTime)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:dateKey ?dateKey;

ffb:Route ?droute;

ffb:plantationKey ?plantationKey.

?dateKey qb4o:memberOf ffb:date;

ffb:year ?year.

?plantationKey qb4o:memberOf ffb:plantation;

ffb:plantationGeo ?plantationGeo;

ffb:PMOGeo ?PMOGeo.

?truckKey qb4o:memberOf ffb:truck;

ffb:ownerName ?oName.

FILTER (?year = 2019)

}

GROUP BY ?oName

Query#6: Compute the total Palm FFB harvest of each afdeling and block in the year between 2017 and 2019. This query involves some roll-up operations along the spatial dimension (afdeling and block), spatial computation of insideGeometry, slicing operations for periods, and spatial slice function.

SELECT

?afdelingName ?blockName

(SUM(jsfn:AtTimeStamp(?dload,(jsfn:EndTime

(jsfn:GetTime(jsfn:insideGeometry(?droute,?blockGeo)))))-

jsfn:AtTimeStamp(?dload,(jsfn:StartTime

(jsfn:GetTime(jsfn:insideGeometry(?droute,?blockGeo)))))) as ?PSum)

WHERE {

?obs rdf:type qb:Observation;

ffb:truckKey ?truckKey;

ffb:dateKey ?dateKey;

ffb:Load ?dload;

ffb:Route ?droute.

?dateKey qb4o:memberOf ffb:date;

ffb:year ?year.

?afdelingKey qb4o:memberOf ffb:afdeling;

ffb:afdelingGeo ?afdelingGeo;

ffb:afdelingName ?afdelingName.

?blockKey qb4o:memberOf ffb:block;

ffb:blockGeo ?blockGeo;

ffb:blockName ?blockName.

FILTER((?year >=2017)&&(?year <=2019)&&geof:sfWithin(?blockGeo,?afdelingGeo))

}

GROUP BY ?afdelingName ?blockName

The prefixes used in this query are:

• jsfn: <http://www.ontotext.com/js#>
• rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#>
• qb: <http://purl.org/linked-data/cube#>
• ffb: <http://www.uajy.ac.id/ffbi/>
• qb4o: <http://www.w3.org/2001/XMLSchema#>
• geof: <http://www.opengis.net/def/function/geosparql/>
• ffbi: <http://www.uajy.ac.id/ffbi/instance#>

Table 3. Query Execution Test.

Query	OLAP Features	Analysis Category	Execution Time (s)
			1	2	3	4	5
Q1	roll-up, dice, distance	descriptive	2.5	2.5	2.2	2.1	2.2
Q2	roll-up, dice, duration, drill-down	descriptive, diagnostic	0.8	0.7	0.7	0.7	0.7
Q3	roll-up, duration, spatial slice, slice	descriptive, diagnostic, discovery	58	57	58	58	56
Q4	roll-up, spatiotemporal aggregation, slice	descriptive, diagnostic, discovery	31	30	30	30	30
Q5	roll-up, spatial slice, slice	descriptive, diagnostic	16	9.2	9	7.8	7.8
Q6	roll-up, spatial slice, slice	descriptive, diagnostic, discovery	132	129	128	129	128

shows the experimental results for the six queries after five executions. Queries were executed many times to ensure optimal cache usage. It was shown that the Mobility DW on the SW has a convenient, simple model and expressive performance (below 3 s for regular OLAP query, below 1 min for spatiotemporal OLAP query with spatial slice combination, and approximately 2 min for OLAP query with extensive spatial slice combination). The spatial operations made the queries take a longer time. The usage of mobility fact measures in the DW adds query expressiveness and prevents extensive joining, as was the case for the previous segment trajectories proposal. Developing a detailed performance analysis as a comprehensive set of experiments is outside the scope of this paper and is planned in future work.

5. Conclusions and Future Works

This paper studied and provided a proof-of-concept of mobility modeling for the enhancement of multidimensional data cubes using RDF Semantic Web. This research presents the representation of Mobility DW with an extended mobility data type, specified user-defined mobility functions, and implemented the concept and functions in the new QB4MobOLAP vocabulary and SPARQL, respectively. QB4MobOLAP is an extension of QB4OLAP—the de facto standard Vocabulary for RDF Cube, which allows users to publish Mobility DW in the RDF format with mobility facts and measures that can be analyzed while taking into account contextual dimensions that are not restricted in pre-aggregate measures, as is the case for traditional DW representation. Integrating these mobility measures in DW realizes the notion of spatiotemporal queries defined in [55].

Users can publish Mobility multidimensional RDF data using the QB4MobOLAP Vocabulary. Thus, users can query from RDF endpoints using SPARQL’s Mobility OLAP operators. The essential Mobility OLAP operations were defined to support users in mobility analysis, and these include Mobility Row Aggregation, Mobility Spatial Aggregation, Lifting Function Aggregation, Spatial Operation, and Temporal Operation. The evaluation of the vocabulary and operations was provided by implementing a real-world mobility query for FFB transportation analysis that illustrated the comprehensive set of queries and the execution performance.

Future works will be conducted to extend and optimize the implementation of the query operators in SPARQL, which is still limited in this research. For non-technical users, the SPARQL query language is complex. So, the challenge is also to provide high-level Mobility OLAP operators to help non-technical users.