Intelligent Search of Values for a Controller Using the Artificial Bee Colony Algorithm to Control the Velocity of Displacement of a Robot
Abstract
:1. Introduction
2. Related Work
- 1.
- Initialization Phase: All the vectors of the population of food sources, ()’s, are initialized () by scout bees, and control parameters are set. Since each food source, (), is a solution vector to the optimization problem, each () vector holds variables, (), which are to be optimized so as to minimize the objective function.
- 2.
- Employed Bees Phase: New food origins are being searched (); the one that has more nectar in the food neighborhood () is put in memory. Once the food origin neighbors are found, then rentability (aptitude) is evaluated. For example, a food origin can be determined by using the formula of the following Equation (1) [27].
- 3.
- Onlooker Bees Phase: In this optimization algorithm, an observer bee chooses a food source based on the calculated fitness value with Equation (2). Data from food sources are provided by the bees employed. The roulette method is used for selection [28]. The probability value Pm with which is chosen by an observer bee can be calculated using the expression given in the Equation (3) [27]:
- 4.
- Scout Bees Phase: The bees without jobs who choose their food origins randomly are called scout bees. Then the converted scouts begin to look for new random solutions. For example, if solution has been abandoned, the new solution discovered by the scout who was the used bee can be defined using Equation (4). Therefore, all food origins with a low fitness value are abandoned due to exploitation [27].
- Is inspired by the foraging behavior of honeybees;
- Is a global optimization algorithm;
- Has been initially proposed for numerical optimization [10];
- Can be also used for combinatorial optimization problems [22];
- Uses only three control parameters (population size, maximum cycle number, and limit) that are to be pre-determined by the user;
3. Proposed Approach
Methodology
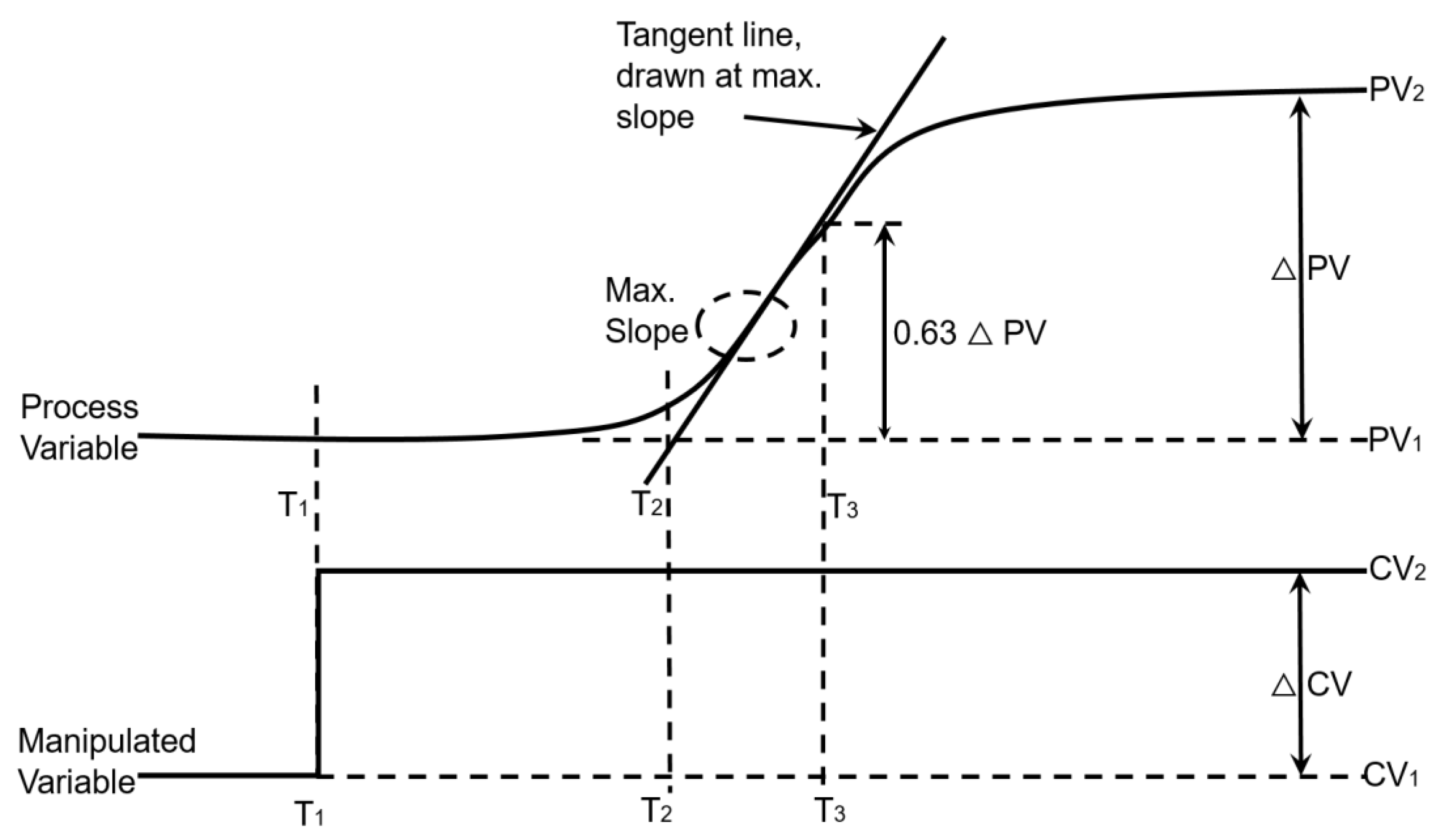
- Gain Process
- Dead time
- Time constant
4. Results Obtained from The Tests Performed
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nair, S.; Coronado, E.; Frye, M.; Goldaracena, T.; Arguello, C. Particle Swarm Optimization for the control of a swarm of biological robots. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–4. [Google Scholar]
- Ayawli, B.B.K.; Chellali, R.; Appiah, A.Y.; Kyeremeh, F. An Overview of Nature-Inspired, Conventional, and Hybrid Methods of Autonomous Vehicle Path Planning. J. Adv. Transp. 2018, 2018, 8269698. [Google Scholar] [CrossRef]
- Robert, C. Machine Learning, a Probabilistic Perspective. Chance 2014, 27, 62–63. [Google Scholar] [CrossRef]
- Misir, D.; Malki, H.A.; Chen, G. Design and analysis of a fuzzy proportional-integral-derivative controller. Fuzzy Sets Syst. 1996, 79, 297–314. [Google Scholar] [CrossRef]
- Zadeh, L.A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets Syst. 1997, 90, 111–127. [Google Scholar] [CrossRef]
- Martínez, R.; Castillo, O.; Aguilar, L.T. Optimization of interval type-2 fuzzy logic controllers for a perturbed autonomous wheeled mobile robot using genetic algorithms. Inf. Sci. 2009, 179, 2158–2174. [Google Scholar] [CrossRef]
- Amador, L.; Castillo, O. Bee Colony Optimization Algorithm. In Optimization of Type-2 Fuzzy Controllers Using the Bee Colony Algorithm; Amador, L., Castillo, O., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 23–32. [Google Scholar]
- Cuéllar, M.P.; Pegalajar, M.C. Design and implementation of intelligent systems with LEGO Mindstorms for undergraduate computer engineers. Comput. Appl. Eng. Educ. 2014, 22, 153–166. [Google Scholar] [CrossRef]
- Perez, S.R.; Gold-Veerkamp, C.; Abke, J.; Borgeest, K. A new didactic method for programming in C for freshmen students using LEGO mindstorms EV3. In Proceedings of the 2015 International Conference on Interactive Collaborative Learning (ICL), Florence, Italy, 20–24 September 2015; pp. 911–914. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B.B. A modified Artificial Bee Colony (ABC) algorithm for constrained optimization problems. Appl. Soft Comput. 2011, 11, 3021–3031. [Google Scholar] [CrossRef]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Chong, C.S.; Sivakumar, A.I.; Low, M.Y.H.; Gay, K.L. A Bee Colony Optimization Algorithm to Job Shop Scheduling. In Proceedings of the 38th Conference on Winter Simulation, Monterey, CA, USA, 3–6 December 2006; pp. 1954–1961. [Google Scholar]
- Teodorović, D.; Dell’Orco, M. Bee colony optimization—A cooperative learning approach to complex transportation problems. In Advanced OR and AI Methods in Transportation; Publishing House of Poznan Uniwersity of Technology: Poznań, Poland, 2005; pp. 51–60. [Google Scholar]
- Teodorović, D.; Lucic, P.; Markovic, G.; Orco, M.D. Bee Colony Optimization: Principles and Applications. In Proceedings of the 2006 8th Seminar on Neural Network Applications in Electrical Engineering, Belgrade, Serbia, 25–27 September 2006; pp. 151–156. [Google Scholar]
- Luyben, W.L. Tuning Proportional−Integral−Derivative Controllers for Integrator/Deadtime Processes. Ind. Eng. Chem. Res. 1996, 35, 3480–3483. [Google Scholar] [CrossRef]
- Saleh, A.L.; Hussain, M.A.; Klim, S.M. Optimal Trajectory Tracking Control for a Wheeled Mobile Robot Using Fractional Order PID Controller. J. Univ. Babylon Eng. Sci. 2018, 26, 292–306. [Google Scholar] [CrossRef]
- Onieva, E.; Milanés, V.; Pérez, J.; De Pedro, T. Genetic Fuzzy-based Steering Wheel Controller using a Mass-Produced Car. Int. J. Innov. Comput. Inf. Control. 2012, 8, 3477–3494. [Google Scholar]
- Nandam, P.K.; Sen, P.C. A comparative study of proportional-integral (P-I) and integral-proportional (I-P) controllers for dc motor drives. Int. J. Control. 1986, 44, 283–297. [Google Scholar] [CrossRef]
- Hao, M.R.; Ghani, N.M.A.; Wahid, M.S.A. Real-Time PID Control of Wireless Two-Wheeled Balancing Lego EV3 Robot. J. Telecommun. Electron. Comput. Eng. 2018, 10, 6. [Google Scholar]
- Bell, M.; Kelly, J.F. Robot Commander Remote Control App. In LEGO® MINDSTORMS® EV3; Bell, M., Kelly, J.F., Eds.; Apress: Berkeley, CA, USA, 2017; pp. 319–321. [Google Scholar]
- Ding, J.; Li, Z.; Pan, T. Control System Teaching and Experiment Using LEGO MINDSTORMS NXT Robot. Int. J. Inf. Educ. Technol. 2017, 7, 309–313. [Google Scholar] [CrossRef] [Green Version]
- Akmal, M.A.; Jamin, N.F.; Ghani, N.M.A. Fuzzy logic controller for two wheeled EV3 LEGO robot. In Proceedings of the 2017 IEEE Conference on Systems, Process and Control (ICSPC), Malacca, Malaysia, 15–17 December 2017; pp. 134–139. [Google Scholar]
- Maharuddin, M.F.; Ghani, N.M.A.; Jamin, N.F. Two-Wheeled LEGO EV3 Robot Stabilisation Control Using Fuzzy Logic Based PSO Algorithm. J. Telecommun. Electron. Comput. Eng. 2018, 10, 149–153. [Google Scholar]
- Bibi, R.; Chowdhry, B.S.; Shah, R.A. PSO based localization of multiple mobile robots employing LEGO EV3. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; pp. 1–5. [Google Scholar]
- Kast, C.; Rosenauer, B.; Meissner, H.; Aramphianlert, W.; Krenn, M.; Hofer, C.; Mayr, W. Development of a Modular Bionic Prototype Arm Prosthesis Integrating a Closed-Loop Control System. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2018, Prague, Czech Republic, 3–8 June 2018; Lhotska, L., Sukupova, L., Lacković, I., Ibbott, G.S., Eds.; Springer: Singapore, 2018; pp. 751–753. [Google Scholar]
- Jadon, S.S.; Sharma, H.; Tiwari, R.; Bansal, J.C. Self-adaptive position update in artificial bee colony. Int. J. Syst. Assur. Eng. Manag. 2017, 9, 802–810. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Ogata, K. Ingeniería de Control Moderna; Pearson Educación: London, UK, 2003. [Google Scholar]
- Meshram, P.M.; Kanojiya, R.G. Tuning of PID controller using Ziegler-Nichols method for speed control of DC motor. In Proceedings of the IEEE—International Conference on Advances in Engineering, Science and Management (ICAESM-2012), Nagapattinam, Tamil Nadu, India, 30–31 March 2012; pp. 117–122. [Google Scholar]
- Kelvin, T. Erickson. In Programmable Logic Controllers; Dogwood Valley Press: Rolla, MO, USA, 2005. [Google Scholar]







| Controller Type | |||
|---|---|---|---|
| p | ∞ | 0 | |
| PI | 0 | ||
| PID |
| NUM. | |||
|---|---|---|---|
| 1 | 3.8538 | 8.5949 | 2.0947 |
| 2 | 1.3049 | 3.3470 | 6.5614 |
| 3 | 5.5574 | 7.0028 | 3.0410 |
| 4 | 6.5373 | 7.3083 | 4.5221 |
| 5 | 7.6869 | 8.1065 | 3.1513 |
| 6 | 8.6309 | 0.6437 | 4.6822 |
| 7 | 3.8538 | 8.5949 | 3.2261 |
| 8 | 6.4815 | 7.2582 | 3.7371 |
| 9 | 3.1727 | 6.7449 | 3.5709 |
| 10 | 4.2885 | 8.6309 | 3.5917 |
| 11 | 4.1859 | 7.2531 | 4.1478 |
| 12 | 4.8299 | 8.8266 | 4.1827 |
| 13 | 3.2176 | 6.4975 | 3.1795 |
| 14 | −0.2182 | 6.1521 | 3.3044 |
| 15 | 8.1057 | 8.339 | 4.1057 |
| 16 | 7.2582 | 8.6190 | 4.5323 |
| 17 | 7.002 | 6.0428 | 3.8286 |
| 18 | 3.1726 | 6.7449 | 4.0684 |
| 19 | 0.2836 | 7.5682 | 1.2493 |
| 20 | 1.2345 | 6.4258 | 3.1565 |
| Control Type | Values Kp | Values Ti | Results Error |
|---|---|---|---|
| Integral proportional control (PI), traditional | 6.02796 | 0.50993 | 16.6874 |
| Intelligent integral proportional control | 7.5682 | 0.2836 | 1.2493 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villegas, J.M.; Caraveo, C.; Mejía, D.A.; Rodríguez, J.L.; Vega, Y.; Cervantes, L.; Medina-Santiago, A. Intelligent Search of Values for a Controller Using the Artificial Bee Colony Algorithm to Control the Velocity of Displacement of a Robot. Algorithms 2021, 14, 273. https://doi.org/10.3390/a14090273
Villegas JM, Caraveo C, Mejía DA, Rodríguez JL, Vega Y, Cervantes L, Medina-Santiago A. Intelligent Search of Values for a Controller Using the Artificial Bee Colony Algorithm to Control the Velocity of Displacement of a Robot. Algorithms. 2021; 14(9):273. https://doi.org/10.3390/a14090273
Chicago/Turabian StyleVillegas, José M., Camilo Caraveo, David A. Mejía, José L. Rodríguez, Yuridia Vega, Leticia Cervantes, and Alejandro Medina-Santiago. 2021. "Intelligent Search of Values for a Controller Using the Artificial Bee Colony Algorithm to Control the Velocity of Displacement of a Robot" Algorithms 14, no. 9: 273. https://doi.org/10.3390/a14090273
APA StyleVillegas, J. M., Caraveo, C., Mejía, D. A., Rodríguez, J. L., Vega, Y., Cervantes, L., & Medina-Santiago, A. (2021). Intelligent Search of Values for a Controller Using the Artificial Bee Colony Algorithm to Control the Velocity of Displacement of a Robot. Algorithms, 14(9), 273. https://doi.org/10.3390/a14090273








