Topological Data Analysis in Time Series: Temporal Filtration and Application to Single-Cell Genomics

Abstract

The absence of a conventional association between the cell–cell cohabitation and its emergent dynamics into cliques during development has hindered our understanding of how cell populations proliferate, differentiate, and compete (i.e., the cell ecology). With the recent advancement of single-cell RNA sequencing (RNA-seq), we can potentially describe such a link by constructing network graphs that characterize the similarity of the gene expression profiles of the cell-specific transcriptional programs and analyze these graphs systematically using the summary statistics given by the algebraic topology. We propose single-cell topological simplicial analysis (scTSA). Applying this approach to the single-cell gene expression profiles from local networks of cells in different developmental stages with different outcomes reveals a previously unseen topology of cellular ecology. These networks contain an abundance of cliques of single-cell profiles bound into cavities that guide the emergence of more complicated habitation forms. We visualize these ecological patterns with topological simplicial architectures of these networks, compared with the null models. Benchmarked on the single-cell RNA-seq data of zebrafish embryogenesis spanning 38,731 cells, 25 cell types, and 12 time steps, our approach highlights gastrulation as the most critical stage, consistent with the consensus in developmental biology. As a nonlinear, model-independent, and unsupervised framework, our approach can also be applied to tracing multi-scale cell lineage, identifying critical stages, or creating pseudo-time series.

1. Introduction

In recent years, technological developments in data visualization, especially the subfield of topological data analysis (TDA), has illuminated the structure of biological data with features such as clusters, holes, and skeletons across a range of scales [1]. The TDA approach has proven to be especially useful with recent advancements in experimental techniques at the single-cell resolution in both genomics and neuroscience, such as radiomics [2] and brain imaging [3,4]. The utility of the topology comes from the idea of persistence, which extracts the underlying structures within data while discarding noisy elements in the single-cell data collection. Unlike graph-based data such as human connectomes, most of the time, the high-dimensional data collected from single-cell techniques are similiarity-based. Under the assumption that these data were sampled from an underlying space $\mathcal{X}$, the goal is to first approximate $\mathcal{X}$ with a combinatorial representation and then compute some sort of invariant features to recover the topology of $\mathcal{X}$. For interested readers, Refs. [5,6,7] are a few recent reviews of the applications of TDA in various field of biology, Ref. [8] is a practical introduction and guide on how to apply TDA to data science and understand its results, and [9] is a gentle introduction and tutorial to the computation of a persistent homology.

Single-cell topological data analysis (scTDA) is one of the first attempts to apply topology-based computational analyses to study temporal, unbiased transcriptional regulation given the single-cell RNA sequencing data [10]. In order to visualize the most invariant features of the entire gene expression data, scTDA clusters low-dispersion genes with significant gene connectivity according to their centroid in the topological representation and visualizes the data points in a low-dimension space with the Mapper algorithm [11]. Computing the library complexity as the number of genes whose expression is detected in a cell, scTDA observes a mild dependence by the library complexity on the timescale of the single-cell data of 1529 cells collected at 5 time points. This is expected because the number of genes expressed by cells in the early stages of a developmental process is larger than in the adult case, as pointed out in [12]. As a result, in scTDA, the library complexity is not used for any purpose in the topological data analysis and not related to any topological properties.

Intuitively thinking, if we were to introduce a definition for “cell complexity” which characterizes the behaviors of cell–cell co-expression or interactions, the quantities of cell complexity should be agnostic to the number of genes expressed by the cells and should be different across differentiated cells and across the developmental process. Can we introduce a better summary statistic for the cell complexity that can capture the developmental trajectory with more distinctions between time points? To clarify, unlike the previous definition of “library complexity”, which simply quantifies the number of genes expressed in a cell, we wish to define a cell complexity measure to better model higher-order networks and dynamic interactions in single-cell data. Understanding the cell–cell interactions can help identify intercellular signaling pathways, and previous analytical studies have focused on computing a communication score between the ligand–receptor pair of interacting proteins [13]. For instance, the authors of [14,15] inferred the intercellular signaling pathways of cell–cell communications by computing the co-expression of all genes or other cell markers. The alternative would be to compute the similarity between the gene expression profiles, as in [16]. In this work, we aim to focus directly on the cell level and use the similarity between each cell’s gene expression profiles as a graph to compute a topological descriptor of the complexity. The more connected a group of cells is in this similarity graph, the higher the complexity of this group of cells is. There are two major quests in this line of research, and they are as follows.

1.1. Quest from Topological Data Analysis

Existing TDA applications usually focus on the low-dimensional graph visualization and persistent homology of the data (e.g., computing the Betti numbers or barcodes up to the second dimension), because interpreting the biophysical meaning of the geometry and higher dimensional persistent modules is a conceptual challenge. Others have proposed hybrid approaches to combine the merits of data geometry and topology by adaptively selecting the proper thresholds in the pairwise distance matrix of the data points [17,18]. Another alternative to these low-dimensional TDA methods is simplicial analysis. Simplicial architecture was studied in biological data through application in human brain connectomes [19], where each connected pair of neurons is considered an edge to create a graph, and the numbers of Rips–Vietoris simplices in up to seven dimensions are computed in static graphs compared with random graphs. Likewise, in our inquiry, we are interested in the intercellular interaction within the same type of cells (the cell complexity) rather than the relationships between different groups of cell, as in scTDA [20]. However, the filtration challenge of deriving a graph from the distance-based data by choosing the best threshold hinders the practical application of such simplicial analysis in these point cloud data.

1.2. Quest from Single-Cell Resolution Data

With the increasingly popular usage of single-cell genomic techniques, it might be possible to infer such cell–cell interaction (or cellular ecology) in a fine resolution. However, as far as we are aware, there are only a few works in the literature exploring the cellular ecology from single-cell RNA sequencing data. For instance, the authors of [21,22] applied the ecology and multi-agent models to model single-cell systems. We wish to complement this line of work by connecting it to topological data analysis, where the focus is to model the shape or manifold of the data from the similarity of the data points. For instance, simplicial complexes are high-dimensional objects or generalizations of neighboring graphs that represent the cliques of data points or, in other words, a notion of ecology. The ecology does not have to be the organisms within a physical system. In the field of data science where we represent biological cells by their measurements (e.g., gene expression profiles) as data points residing in high-dimensional feature spaces, the ecology can be how these data points are connected to one another in the feature space. If we adopt an ecology research point of view, in order to characterize the dynamic systems of a community, one needs to have knowledge or prior knowledge regarding the causal relationships between the agents (e.g., how prey and predators interact and in what ways). In order to parse out causal relationships, the temporal sequence of these events matters. Thus, the property of the synchrony and asynchrony of the events is key to translating the feature space (represented by a similarity graph) to an ecology, which has directed (e.g., causal) relationships among the agents. This is why a temporal take on topological data analysis can potentially unlock the first step, from finding a static representation of the overall shape of the data points to discovering the event-directed representations (i.e., a temporal skeleton) of the data points.

One challenge of this hybrid direction is to conceptually understand the biological meaning behind the dissimilarity of the omic data. For instance, what does it mean if two cells have similar gene expression profiles to each other? Does that indicate homogeneity if the two cells are from the same tissue, or is it an artifact from the manual labeling or classifications not being perfect? Can we measure the “complexity” of the cell populations based on the heterogeneity or diversity within populations? If we can, how do we evaluate and interpret lower-order versus higher-order “complexity”? These are some open questions we wish to engage the field to discuss and investigate together instead of answering them directly in this first work.

The other challenge is the scalability and compariablity of the single-cell data. With the advancements in multi-channel, high-throughput data collection techniques in biological fields, how do we compute the pairwise distances of the point clouds efficiently? In different trials of single-cell experiments, how do we make sure that the persistent modules are comparable to one another?

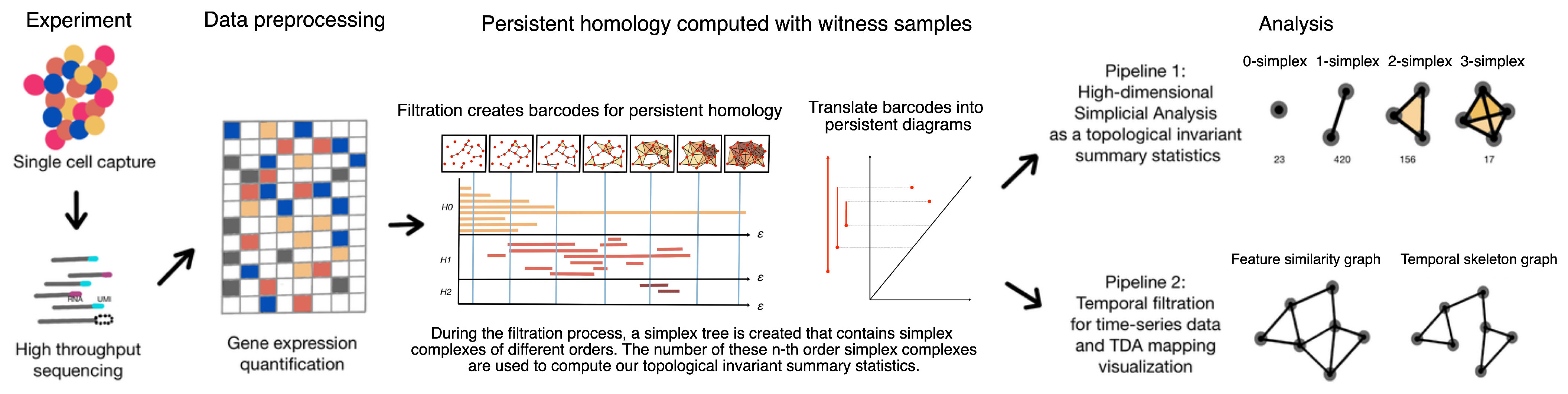
1.3. Framework: Single-Cell Topological Simplicial Analysis (scTSA)

In this study, we propose a topological simplicial analysis (TSA) pipeline (Figure 1) as an exploratory inquiry to solve three challenges. (1) With the algebraic geometry’s definitions of forming higher-order simplices, we can potentially interpret that cliques of higher orders indicate operational units of higher orders. (2) With the bootstrapping techniques to sample the data points collected at each sublevel, we can scale the analysis to large single-cell datasets and compare groups of cells quantitatively. (3) With a time delay constraint on the filtration process, we can sort the projected data points of cells into distinct groups of cells collected from the same time stamps. The framework first takes the measurements of the single-cell RNA sequencing data, which generate a similarity matrix among the cells based on their gene expression profiles. Other than performing the persistent homology to obtain lower-order topological descriptors of the data, we compute additional higher-order topological descriptors by counting the number of the simplices which emerge from the filtration process. In addition, we introduce a technique to extract the temporal skeleton of the developmental processes, called temporally filtrated TDA, and show that the developmental trajectories of cells can be better revealed in this approach compared with existing TDA mapping techniques.

We begin our presentation in Section 2 with a short overview of the mathematical definitions of the single-cell data visualization problem and an introduction of the necessary concepts and definitions in the language of computational topology. Section 2 formulates the topological simplicial analysis pipeline we are proposing as well as the numerical tricks applied in the implementation to ensure the scalablity. We apply this single-cell topological simplicial analysis (scTSA) to the zebrafish single-cell RNA sequencing data with 38,731 cells and 25 cell types over 12 time steps [23]. We select the top 103 genes based on the scTDA pipeline from the high-dimensional, high-throughput transcriptomic data. In Section 3, we introduce the dataset used to benchmark the method and present the analysis results with their mathematical interpretations for the biological insights. In the last section, we discuss the validity of using our framework to understand the higher-order cellular complexity and conclude our methods by pointing out several future work directions as the next step in this line of research.

2. Materials and Methods

2.1. Single-Cell Data in the Point Cloud Space

Genomic measurement and analysis at a single-cell resolution has enabled new understandings of complex biological phenomena, such as revealing the cellular compositions of complex tissues and organisms [24]. Single-cell RNA sequencing (scRNA-seq) techniques measure the gene expression profiles of individual cells through mechanisms such as microfludics. For instance, the benchmark dataset of zebrafish embryogenesis [23] that we use in this study applied Drop-seq, a massively parallel scRNA-seq method to profile the transcriptomes of tens of thousands of embryonic cells [25]. These single-cell data are usually point clouds in a finite metric space, where a finite point set $S\subseteq {\mathbb{R}}^d$. Let $d(·,·)$ denote the distance between two points in a metric space $\mathcal{Z}$. The assumption is that data were sampled from the underlying space $\mathcal{X}$. The goal is to recover the topology of $\mathcal{X}$. To accomplish this goal, one needs to first approximate X with a combinatorial representation (e.g., with the simplicial complex) and then compute a topological invariant summary statistics (e.g., with the persistent homology).

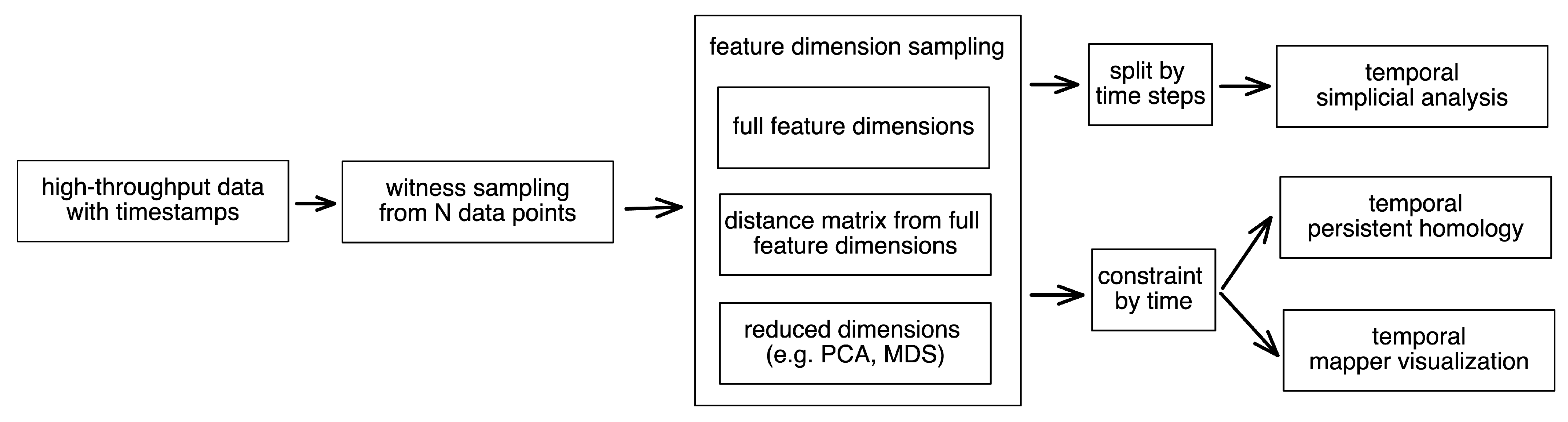
2.2. Definition of Simplicial and Temporal Filtration

Given the point cloud data, we then constructed a continuous shape on top of the data to highlight the underlying topology and geometry. The process to build such a shape is through mathematical filtration, which is often a simplicial complex or a nested family of simplicial complexes that reflects the innate structure of the point cloud data at different scales [8]. If we considered all the points in the point cloud data, each with a coordinate of their locations in certain embedding, then they each occupied a spherical space with the same radius $ϵ$ around them, which is called a nerve ball. If two nerve balls overlapped or contacted each other, then we considered an edge to be formed between them in this graph. Filtration is a process for tuning the parameter $ϵ$ from 0 to ∞ and recording the families of the simplicial complexes generated through the increasingly connected (or “complex”) graph.

Usually, the challenge is to extract relevant and useful information about the shape of the data through defining such simplicial complexes from the graph (generated through the filtration process). The Rips–Vietoris complex is one of the common choices in practice for computing the topological invariants of point clouds, which are defined as follows: given the vertex set $\mathcal{Z}$, for each pair of vertices a and b, edge a-b is included in the Rips–Vietoris complex $C(\mathcal{Z},t)$ if $d(a,b)\le t$, and a higher dimensional simplex is included in $C(\mathcal{Z},t)$ if all of its edges are included. Since $C(\mathcal{Z},t)\in C(\mathcal{Z},t^{\prime })$ whenever $t\le t^{\prime }$, the filtered Rips–Vietoris complex is a filtered simplicial complex as well as the maximal simplicial complex that can be built on top of its $1-$skeleton, and thus a clique complex or a flag complex is formed.Unlike conventional low-dimensional topological data analysis, we computed the simplices at a high dimension count (up to seven) during the entire filtration process. To record the number of cliques, we computed the filtered simplicial complexes and recorded their cumulative counts across the entire filtration process.

Since the topological data analysis usually only considers the graph constructed by the spatial proximity (i.e., the distance matrix) between the data points in the low-dimensional embedding, it is not clear how to incorporate timestamp information for meaningful inference and visualization when facing the time series data streams. One approach would be to simply consider the time stamp as the metadata for post hoc labeling of the topological representations. Another alternative would be to consider time as an additional dimension in the filtration process. We present temporal filtration as the following: alongside the conventional sweeping of the parameter $ϵ$ from 0 to ∞, we set another parameter $\tau$ to indicate a hard constraint in edge forming between two points. Alternatively and intuitively, temporal filtration is equivalent to conventional filtration by using the composite norm:

$$d((x,t_x),(y,t_y))=max(\frac{1}{{ϵ}^{\ast }}|y-x|,\frac{1}{{\tau }^{\ast }}|t_y-t_x\left|\right)$$

(1)

where ${ϵ}^{\ast }$ and ${\tau }^{\ast }$ are directly related to the spatial threshold $ϵ$ (in the feature space) and the temporal threshold $\tau$, respectively. As a practical note from this notation, it can be used without additional specialized software.

In other words, only if the time stamp difference between the two data points is within the time delay limit $\tau$ can two nerve balls, if spatially proximal enough (less than $ϵ$), form an edge in between. On the other hand, if the time stamp difference between the two data points is larger than $\tau$, then even if they are spatially proximal enough (less than $ϵ$), they cannot form an edge. Given the problem settings, one can either set a reasonable time delay limit $\tau$ given the domain knowledge or tune $\tau$ from 0 to ∞, similar to the filtration process with the spatial filtration parameter $ϵ$. The latter approach can potentially extract temporally invariant topological summary statistics.

Figure 2 is an intuitive example of the criterion of edge forming in the temporal filtration. In the example, we have seven data points, which are marked by their time stamps (when they were measured). The node marked 1 indicates it is collected at time step 1. There is a one-time step difference between each data point of consecutive numbers. To illustrate the differences between the conventional and temporal filtration, the schematic is a snapshot of the full filtration process frozen at a set of filtration thresholds. In all four cases, we consider the case where the spatial threshold $ϵ$ of the nerve ball around each data point is one (which, in our case, only contains every data point’s nearest neighbor and not the second-nearest neighbor). If we only performed spatial filtration, we would consider them all to be connected. However, that would not match the temporal skeleton. Instead, we could set a temporal constraint $\tau$ such that only if two data points that were spatially (in the feature space) proximal to each other were also measured to be temporally close to each other would their edge be included. If $\tau$ was small (e.g., one time step apart), then we would have a fine resolution temporal skeleton which separated the data points into three main phases. If $\tau$ was medium-sized (e.g., two time steps apart), then we would have a relatively crude-resolution temporal skeleton which separated the data points into two main phases. If $\tau$ was big (e.g., three time steps part), then we would have a crude temporal skeleton which grouped them all into connected components. This also demonstrates the possibility of using $\tau$ as a hierarchical mechanism to parse the persistent features of different temporal resolutions.

2.3. Topological Data Analysis with Persistent Homology

Following the definition above, an abstract simplicial complex is given by a set $\mathcal{Z}$ of vertices or 0-simplices, a set of k-simplices $\sigma =[z_0,z_1,\cdots ,z_k]$ where $z_i\in \mathcal{Z}$ for each $k\le 1$, and a set of $k+1$ faces for each k-simplex obtained by deleting one of the vertices. A filtered simplicial complex is given by filtration of a simplicial complex $\mathcal{Y}$, with a collection of subcomplexes $\left\{\mathcal{Y}\right(t\left)\right|t\in \mathbb{R}\}$ of $\mathcal{Y}$ such that $\mathcal{Y}\left(t\right)\subset \mathcal{Y}\left(t^{\prime }\right)$ whenever $t\le t^{\prime }$. The filtration value of a simplex $\sigma \in \mathcal{Y}$ is the smallest t value such that $\sigma \in \mathcal{Y}\left(t\right)$. Topological data analysis methods usually involve computing the persistent homology [26]. The Betti numbers help describe the homology of a simplicial complex $\mathcal{Y}$. The Betti number value $B{N}_k$, where $k\in \mathbb{N}$, is equal to the rank of the kth homology group of $\mathcal{Y}$. The Betti intervals over the filtration process help describe how the homology of $\mathcal{Y}\left(t\right)$ changes with t. A k-dimensional Betti interval with endpoints $[t_{\mathrm{start}},t_{\mathrm{end}})$ corresponds to a k-dimensional hole that appears at the filtration value $t_{\mathrm{start}}$, remains open for $t_{\mathrm{start}}\le t<t_{\mathrm{end}}$, and closes at value $t_{\mathrm{end}}$.

Figure 3 is a schematic diagram outlining how to perform a filtration process (by sweeping $ϵ$), document the “birth” and “death” of each complex (the colored lines of various lengths in the chart), and generate this as a barcode representation [27] or a persistence diagram [28] for the downstream analyses. In this schematic diagram, a point cloud of 19 data points is presented in a low-dimensional embedding space. In the filtration process, a parameter $ϵ$ is swept from zero to the maximum pairwise distance within the point cloud, indicating a distance threshold under which the two points can form an edge to become one connected component in the graph. For each value $ϵ$, we obtained a space $S_{ϵ}$ consisting of vertices, the edges formed among the vertices, and the higher-dimensional polytopes connected by these edges. For instance, a nerve ball of a radius $ϵ$ grows around each point cloud, and an edge will form if two nerve balls touch. Homology counts the number of essentially different cycles—linear combinations of simplices that form a cycle (for example, a loop formed by a sequence of edges)—that are not the boundary of something that can fill in the hole (for example, a combination of 2D simplices or triangles spanning the inside of the loop). We denote $H_n$ as the nth homology group (i.e., the formation of the simplex complexes of the order n), with 0-simplex as the nodes (or clusters), 1-simplex as the edges between two nodes, 2-simplex as the loops (or triangles in this case), 3-simplex as the tetrahedrons, and so on. We logged the existence of an n-simplex if and only if all of its components (e.g., (n-1)-simplex, (n-2)-simplex, ⋯, 1-simplex, and 0-simplex) were all in $S_{ϵ}$ and marked their demises when some of these topological cavities were filled with the additions of new edges (and potentially nodes). Each colored line indicates the “lifespan” of a simplex, with its starting point as its “birth” (or first appearance) and ending point as its “death” (or disappearance due to the two nerve balls fully overlapping). In this example, the persistent homology of the data cloud can be presented in the form of a “barcode” representation, which is a finite collection of intervals. The births and deaths of the simplicial complexes up to the second order were recorded when the filtration process gradually swept the distance threshold. The barcode representation is often replaced with the visualization of a 2D persistence diagram, in which the x-axis indicates the birth time (the distance threshold at which filtration appears) and the y-axis indicates its death time (the distance threshold at which filtration disappears). In most cases, only the first two orders of the filtrations are computed and included in persistent barcodes or diagrams.

By using temporal filtration in place of conventional filtration, we could extend the methods of persistent homology into one for temporal persistent homology. Our method is related to the research on multi-parameter persistence [29], which aims to construct a topological space with more than one filtered space. In other words, the computation of a persistent barcode or diagram can also be customized to use temporal filtration as its filtration criterion by either using a composite norm function as in Equation (1) or using multi-parameter filtration with a temporal constraint.

2.4. Empirical Simplicial Computation with Witness Sampling and Dimension Reduction

Overall, the witness sampling is critical for two reasons: (1) The single-cell data have different noise granularity across cell types and data collection procedures [30], and thus the number of cells collected in each time point and different cell type (as in the analyzed developmental study [23]) can vary in magnitude, making direct simplicial computation incomparable, and (2) in large-scale, high-throughput data, the large number of data points and feature sizes can make computation especially expensive and infeasible. For instance, the computation of filtration requires a comparison between a sweeping proximity threshold and the distance between two data points, and computing the distance matrix between all points is not only time-consuming but memory-exhaustive (e.g., 1 M points would require 1 T to just store the distance matrix).

For these larger datasets, if we included every data point as a vertex, the filtrated simplicial complexes could quickly contain too many simplices for efficient computation. To solve this numerical inconsistency issue, we instead extracted the lazy witness complexes by sampling m data points [26] with a sequential maxmin procedure [31], setting a nearest neighbor inclusion of two (as in the term “lazy”). The selection of m depends on the scale of the dataset. The bigger the sample size m, the better the estimate. However, different partitions of the data points have varying sizes. For instance, if there are only 50 data points collected in time step 1 while there are more than 100 points in other time steps, then the maximum m that can be picked is 50. The computation of the witness complex in high dimensions can be implemented with GUDHI [32], Ripser [33], and JPlex software [34]. The codes to reproduce the empirical results can be accessed at https://github.com/doerlbh/scTSA, accessed on 15 August 2022.

Figure 4 outlines our scalable time series topological simplicial analysis pipeline. We started with the high-throughput data points marked with their time stamps. To decrease the number of data points for efficient computation (and also comparability across time points), witness sampling was performed among these data points. Then, one could choose to reduce the dimensions or not given the noise and distribution properties of the data. The usage of dimension reduction is a useful step before filtration. Due to the “Curse of Dimensionality”, the data points in a very high-dimensional space can be very sparse, and thus the distances between them usually collapse to a constant (i.e., residing in a hyperspherical space). As a result, the filtration computation around them can be ineffective and unstable. Mapping them onto a low-dimensional space can partly solve this issue.

Then, to perform the temporal simplicial analysis, the data points were first separately grouped into different time points, and then their filtrations were computed to obtain the number of simplicial complexes in different orders. To perform the temporal persistent homology and mapper visualization, one could apply the temporal constraint onto the sampled data points thus far to obtain a temporal skeleton.

2.5. Topological Simplicial Analysis

Given the simplicial complexes of different orders from the witness sampling approach, we needed to correct for the effect of sampling. The larger the sample size, the more likely the higher-order simplicial complexes emerge. One way to correct for this amplification effect is to normalize this quantity directly to the quantity collected from a null distribution of the data. Usually, for a graph, network, or more generically, data with a binary connectivity format (e.g., a brain connectome), the Erdős–Rényi random graph [35] can be used as a control model. However, in fully connected similarity-based data, the average connectivity probability is entirely dependent on the filtration factor. To avoid this caveat, we took a different approach by permuting the pairwise distances of the data points, which is equivalent to a weighted version of the Erdős–Rényi random graph. Another strategy would be permuting the feature at each dimension. In this way, the low-dimensional embeddings computed by the multidimensional scaling could form different connectivity profiles while maintaining the same distance distribution. Then, we applied the same topological data analysis pipelines to the embeddings computed from the pairwise distance matrices from both the actual data and the control models.

To this point, we propose a formal definition of cellular complexity as the normalized n-simplicial complexity $NS{C}_n$, a family of summary statistics with an increasing order n:

$$NS{C}_n=\frac{S{C}_n^{data}}{S{C}_n^{null}}$$

(2)

where $NS{C}_n$ is computed by taking the ratio between the number of the simplicial complexes for a certain order n computed from the actual data (which we denote as $S{C}_n$) and the sum of those computed from the control models and from the actual data. An alternative would be $NS{C}_n=\frac{S{C}_n^{data}}{(S{C}_n^{data}+S{C}_n^{null})}$. A value of 0.5 would indicate that the simplicial complexity at the order n is the same in the data and the null models. Empirically, we computed the $NS{C}_n$ with the order n from 1 to 7 as the summary statistics characterizing the ecology among the data points with cliques and cavities of increasing modularities.

2.6. Topological Data Visualization with Low-Dimensional Mapping

To build and visualize the topological representation of the point cloud data, we used the Mapper algorithm [36] through the implementations provided by KeplerMapper (https://github.com/scikit-tda/kepler-mapper, accessed on 15 August 2022) with modifications for temporal filtration at https://github.com/doerlbh/tkMapper, accessed on 15 August 2022. In brief, a dissimiliarity matrix was computed from the preprocessed RNA-seq data by finding the pairwise correlation distance. This metric space was then reduced to a low-dimensional embedding with the multi-dimensional scaling [37]. Given this embedding, the point cloud data are chopped into coverings of hypercubes with 50% overlapping between the cubes. The choice of 50% was empirically determined by our dataset. We varied the overlap parameter among 25%, 50%, and 75%, and 50% gave the best clustering effect. Then, for each hypercube, the data points within the cube were clustered with the single-linkage rule. This step further aggregated all the points into a network in which each vertex corresponded to a cluster, and each edge corresponded to a non-vanishing intersection between the clusters. As defined in Section 2.2, if temporal filtration were applied, then edge forming would also controlled by the additional time delay constraint for the clusters formed with both spatial and temporal proximity, and the edges would only exist between two clusters if all points in the two clusters were within the time delay limit $\tau$. In other words, the filter function was the same one that we applied to persistent homology, which could either be single filtration with the temporal constraint, single filtration with the temporal composite norm, or multi-parameter filtration. Once we reached a network representation, the network could eventually be visualized with force-directed algorithms for insights.

3. Results

We benchmarked the scTSA method on the zebrafish single-cell RNA sequencing data with 38,731 cells and 25 cell types over 12 time steps [23]. The dataset studied the embryogenesis, which is the process where the cells gradually differentiate into distinct fates through stages of transcriptional change. The goal of this study was to facilitate a comprehensive identification of cell types with their time stamps in order to reconstruct their developmental trajectories (e.g., transcriptional states, branch points, and asyncrhony). As the gene expression profiles obtained from the vertebrate embryo were time stamped from 3.3 to 12 hours post-fertilization (hpf), they provided a perfect testbed for time series analysis to reconstruct the transcriptional trajectories and characterize the time-dependent development properties.

We processed the scRNA sequencing data into entries of 103 dimensions corresponding to the expression levels of 103 significant genes (which we selected using scTDA). We then standardized the features by removing the mean and scaling to the unit variance. Before we performed the persistent homology, we first embedded the dataset into a low-dimensional space using dimension reduction. In Figure 5, we embedded the data using principal component analysis (PCA), t-distributed stochastic neighbor embedding (TSNE) [38], and uniform manifold approximation and projection (UMAP) [39] and colored them by time step. We observed that they all demonstrated a temporal gradient.

We performed persistent homology and temporal persistent homology on the scaled dataset. In this case, $\tau$ was set to be one (meaning that we only cared about the linkage formed between consecutive time points). Figure 6 compares the persistence diagrams for the two approaches. From the persistence diagrams, the persistent features detected by persistent homology were not noticeably different from those detected by temporal persistent homology. While not a focus of this work, further study using downstream machine learning tasks can potentially pinpoint the benefits of these temporal persistent features.

For the simplicial analysis, we first grouped the data by their time steps. The data collected at the 12 time steps were highly imbalanced (1 (2225 data points), 2 (200), 3 (1158), 4 (1467), 5 (5716), 6 (1026), 7 (4101), 8 (6178), 9 (5442), 10 (5200), 11 (1614) and 12 (4404)). For each time point, we performed a witness sampling of 200 data points since it was the lowest number of samples among all time points. We identified the simplicial complexity to vary over the time, suggesting a potential better summary statistic with better distinction among the time steps (Figure 7). The normalized simplicial complexity (computed as the ratio of the number of simplicial complexes discovered within the data to the number of those discovered within the null model) suggested an abundance of high-dimensional simplices over the null models. The existence of a significant number of high-dimensional simplices was observed for the first time at the single-cell level. In all time points, the number of simplices of dimensions larger than one in the null model was far smaller than those found in the actual data. In addition, we observed relative differences between what we discovered in the null models, and the actual data increased drastically when the dimensions were higher. Furthermore, the number of low-dimensional simplices (up to three dimensions) of the data appeared to be equal to or smaller than that of the null models (with a normalized complexity less than one), suggesting a possible transfer from a lower-order clique structure to a higher-order structure.

In order to investigate the trade-off between the higher-order and lower-order simplicial complexity in the developmental stages, we mapped the normalized 3-simplicial complexity against the normalized 1-simplicial complexity. Figure 8 suggests a gradually increasing higher-order complexity starting from the fifth time point and an overall below-null lower-order complexity in a monotonically increasing direction from the second time point. Compared with the null model, the presence of a much larger number of cliques across a range of dimensions in the single-cell data suggests that the connectivity between these cells might be highly organized into numerous fundamental building blocks (e.g., proto-cell types) with increasing complexity. These two figures both suggest that the gastrulation stage (from time point 5 to time point 6) is a very critical stage in vertebrate development, matching the established understanding in developmental biology that it is a process where the embryo begins the differentiation process to develop into different cell lineages [40]. Before gastrulation, the embryo is a continuous epithelial sheet of cells. After the gastrulation stage, organogensis starts, where individual organs develop within the newly formed germ layers.

This observation is further supported by the visualization of topological data analysis mapping. Figure 9 compares the network visualizations with and without temporal filtration. We observed that, when color-labelled with the time points, the conventional topological data analysis outlined a progression of cellular development, but there were many subsequent time points in the middle of earlier time steps. For instance, we can see that there are many dark blue nodes from the 11th or 12th time points in the middle of the web, where the majority of the nodes are earlier stages from the 5th to the 7th time points. When using temporal filtration (with $\tau$ set to be just one time step), we observed that the network had much more of a skeleton and more branches, where each branching node consisted only of points of the same time stamp. The gastrulation stage, which happened between the fifth and sixth time points, appeared to belong to two separate tracks, supporting the hypothesis that after the notochord and prechordal plate territories become transcriptionally distinct, the gastrulation process refines the boundary between the two cellular populations [23].

These filtrated simplicial architectures may also offer insights into cell lineage tracing. We performed hierarchical clustering of the summary statistics computed from the transcriptome data of different cell types. We compared the results using the proposed normalized simplicial complexity versus the one using the Betti numbers (which is more conventionally used in many downstream topological data analyses). 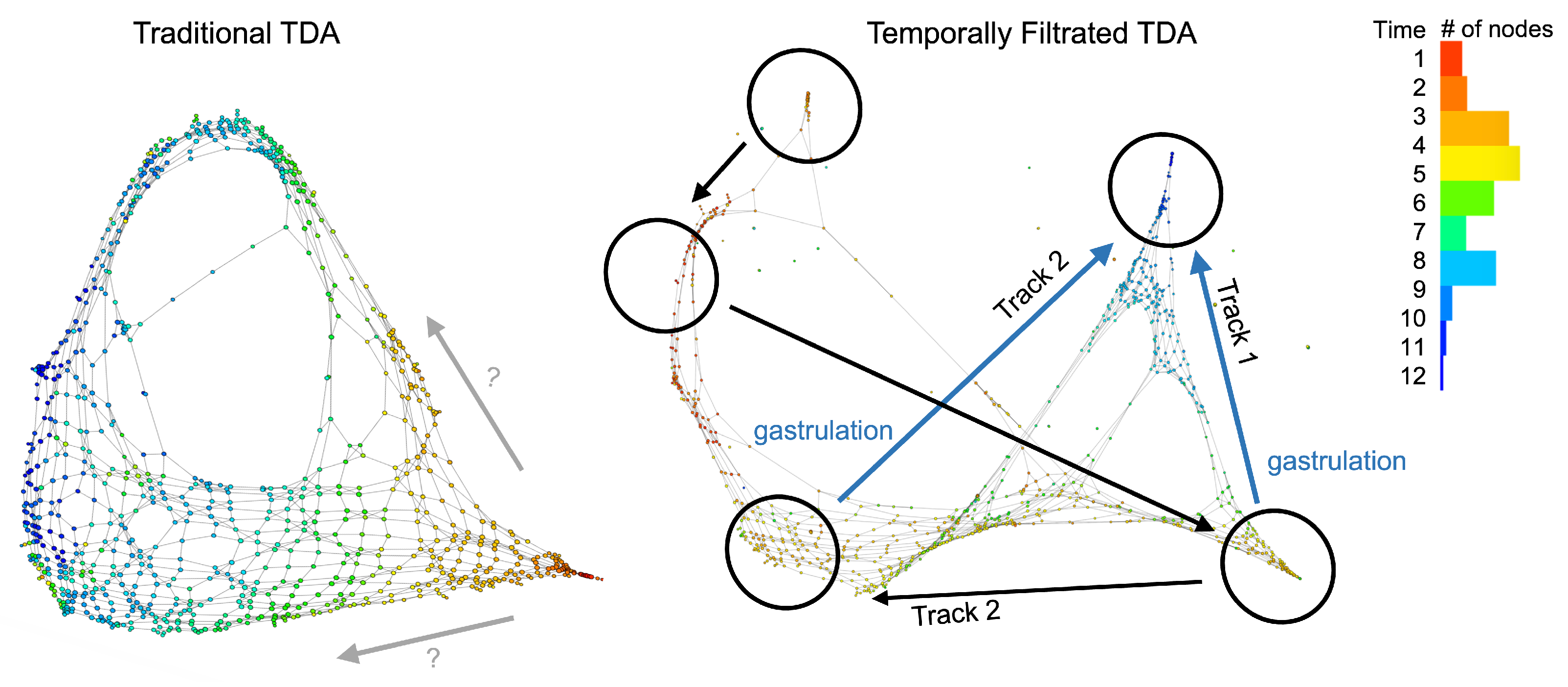As shown in Figure 10, the normalized simplicial complexity offered a more reasonable clustering performance in terms of more distinctive summary statistics than the Betti numbers by themselves.

4. Discussion

What is cellular complexity and what does higher-order complexity mean? As an inquiry to this question, we explored the possibility of introducing the mathematical notion of higher-order simplicial complexes into analyzing distance-based single-cell data. Benchmarked on single-cell gene expression data with multiple developmental stages, we proposed single-cell topological simplicial analysis and demonstrated that simplicial complexity can be a well-defined summary statistic for celluar complexity.

This investigation provides a scalable, parameter-free, expressive, and unambiguous mathematical framework to represent the cellular complexity with its underlying structure. By “parameter-free”, we mean that it does not have arbitrary hyperparameters that the users have to set in order to perform the analysis. The parameter $\tau$ is instead a user-specified parameter that is relevant to the specific application and problem of interest. An analogy for a prediction model would be that the learning rate is an arbitrary hyperparameter, and the prediction window would be a user-specified parameter relevant to the application. Locally, these structures are characterized in terms of the simplicial complexes. Globally, these structures are characterized in terms of the cavities formed by these simplices. Topological cavities are usually formed and then later filled with the addition of new edges (and potentially nodes). When computing the persistent homology, we performed a filtration process which innately tracked the formation and later filling of topological cavities of different dimensions. The temporal persistent homology characterized the information of cavities with the lifespan of these topological objects. This framework revealed an intricate topology of cellular similarity which included a vast number of cliques of cells and of the cavities that bound these cliques together. These topological summary statistics, which captured the relationships among the high-dimensional cliques, uncovered the transcriptional differences in the connectivity of cells of different types during the graph reconstruction process.

From the scTSA visualization, we discovered for the first time in any single-cell data an abundant number and variety of higher-order cliques and cavities. When compared with the control models, the framework measured a much higher number of high-dimensional cliques and cavities in the graph construction filtration process. The critical stage identified by the framework matched the current understanding in developmental biology. Compared with the statistics of the Betti numbers, the normalized simplicial complexity demonstrated better distinctions between time points and cell types.

Topological data analysis, as in many other machine learning methods, has many empirical considerations related to sample size and dimensionality selection. To demonstrate the sensitivity of persistent homology to the sampling size and reduced dimensions, we perform the following experiment. We use the full dimensions of the standard scaled dataset, varied the sampling size from 50 to 100, 500, and 1000 data points, and computed their persistence diagrams. We then set the sample size to 1000, varied the PCA dimensions to be the first 2, 10, and 103 (full) dimensions, and computed their persistence diagrams. We observed no clear difference. Then, we perform simplicial analysis with witness sampling using sample sizes from 10 to 100, 200, and 300. In this case, we observe a slightly higher number of higher-order simplical complexes, but the overall shape and distinction between the time steps were maintained (Figure 11). Future studies can investigate strategies for increasing the stability of simplicial analysis for the sample size.

In the introduction, we posed some open questions we wish to engage the field to discuss and investigate together, instead of answering them directly in this first work. Here, we will briefly share our preliminary takes on some of the specific ones.

Why does expression similarity deserve the name of complexity? To clarify, the expression similarity may not be a measure of complexity. However, the temporally connected higher order co-expression structure characterized by similarity can be a useful measure of complexity. If the task requires several agents to work together at the same time or follow a specific sequence of actions by different agents, then it is more complex than a task which only requires a few agents or does not need to follow a specific sequence. The notion of similarity is usually related to clustering and thus the separation of homogeneous groups. To expand on this understanding, the similarity relationships that are further constrained by temporal sequences would relate to functionally separating groups of homogeneous agents, thus potentially being informative of their interactions.

Is there a reason to believe gene expression similarity has something to do with interactions rather than reflecting the number of similar cells that happen to be present in the sample? This temporally constrained gene expression similarity can both reflect the number of similar cells that coexist at the same time and also potentially be related to some level of functional interaction, as discussed above. We wish to leave further investigations on the types of interaction for future works and welcome discussions on and critique of these interpretations.

Finally, there are other potentially applicable questions we can explore. Can we determine the developmental stages without physiological features? Can we generate pseudo-time series based on single-cell sequencing data? Finally, and most importantly, does the vast presence of high-dimensional cliques suggest that the interaction between these cells is organized into fundamental building blocks of increasing complexity? Through this inquiry with topological simplicial analysis, we can form a hypothesis that the cells organize themselves into high-dimensional cliques for certain functional or developmental reasons. Further research includes developing mechanistic theories behind the emergence of such high-dimensional cellular cliques and experimentally testing these hypotheses to reveal the missing link between functions and cellular complexity.

5. Conclusions

In summary, our work describes a novel, scalable, and unsupervised machine learning method that facilitates the understanding of and solutions to three main technical challenges in bioinformatics. By “machine learning”, we refer to the general goal of building a model that learns from the data. Topological data analysis is a class of unsupervised learning methods. The topological features identified from the process can be further applied to downstream machine learning tasks, such as the hierarchical clustering of cellular lineage.

5.1. A Lack of Time Series Analytical Methods in Quantifying the Underlying Temporal Skeleton within the Manifold of the Similarities among Data Points

In persistent homology and mapper visualization, our temporal filtration uses a user-specified time separation parameter $\tau$, which can be either discrete (consecutive time steps) or continuous (by a time delay quantity). This enables the computation of persistent components that are computed only on data points that are temporally proximal and thus provides a temporal skeleton representation. In simplicial analysis, we can group the data points by time step and compute the normalized simplicial complexity as a quantity to inform the ecology of cells in the transcriptomic feature space.

5.2. A Lack of Scalable Computational Methods for Characterizing Single-Cell Sequence Signals in the Scale of 10,000+ Data Points While Single-Cell Sequencing Data Have Dominated Bioinformatics in Recent Years

The usage of witness sampling and dimension reduction enable the computation of persistent homology for large numbers of high-dimensional data points. Sampling is also a required step for comparing the topological features in groups of data points with different counts. The normalization against null distribution of the data sample partly corrects for the amplification effect of higher-order topological quantities. The usage of dimension reduction techniques such as PCA helps with data management and computation without a significant loss of performance.

5.3. A Lack of Insight and Interpretation That Connects the Mathematical Language of Algebraic Topology for the Physical References to Biological Phenomena

In the introduction and discussion, we initiated the discussion of the interpretations of the topological properties. More specifically, we pointed out how the temporally directed relationships among data points can be related to functionally separating groups of homogeneous agents in the feature space and thus be potentially informative of their interactions. With our temporally directed treatment of filtration or grouping techniques, our study is a small but first step to using topological data analysis as not only a descriptor tool for static manifolds but also a discovery tool for dynamic or mechanistic components in the future. Our goal in this work was not to fully answer the question of interpreting the biological insights’ topological properties but to further motivate and facilitate our understanding of the question. As more techniques of topological data analysis are applied to biological problems, we wish to encourage discussion and critique from the biology and machine learning research communities.

5.4. Summary

In summary, we proposed a new family of filtrations for longitudinal time series multidimensional data along with auxiliary data analysis tools. We demonstrated our application to the temporal inference problems using a set of time-resolved gene expression data. The key technique, called temporal filtration, substitutes a conjunctive distance and time threshold for the conventional distance threshold for point cloud data augmented with time stamps. In addition to persistent homology, mapper constructions, and the use of witness sampling with this technique, an original set of standardized summary statistics, the normalized simplicial complexities, is proposed. These techniques were used to conduct an exploratory analysis of zebrafish embryonic development through the lens of longitudinal single-cell RNA sequencing data. The applications showcased clear improvements in the interpretability of visualizations compared with a cross-sectional approach and suggest that the key events in the evolution of a biological system can be more effectively detected using normalized simplicial complexity than using Betti numbers. Other than the biological application in single-cell genomics, the time series problem is a topic that is especially applicable beyond the application proposed in our work and thus a major interest in the unsupervised machine learning communities dealing with high-dimensional time series signals.