1. Introduction
Detecting and dealing with novelty is an inherent part of dealing with the open world. There is almost no greater source of uncertainty for a Weibull-open-world control-agent (WOW-agent) than being presented with a novel change in the world, especially novel independent agents in an uncontrolled world. While novelty is something sufficiently dissimilar to the past experience, that does not mean the WOW-agent cannot reason about the novelty. While there have been multiple papers addressing out-of-distribution detection, novel class discovery, and open-world learning, not all novelty is out-of-distribution data or a novel class. A WOW-agent could be observing known classes taking part in novel actions, known classes involved in novel interactions, or novel changes to known classes, as well as observing novel classes. We need more general models of novelty, ways of detecting that novelty, and ways of testing multiple levels of novelty. This paper address all three goals.
This paper considers the simulation domain of CartPole3D, allowing us to study different subtypes of novelty. CartPole3D is largely based on the well-known classic control task CartPole [
1], where the task is to control the cart action to keep the pole balanced for as long as possible or until an episode generally (ends 200-time-steps). The primary difference between the CartPole3D environment and classic CartPole is that CartPole3D lives in a (simulated) 3-dimensional world that has flexibility/complexity, and requires the controller to choose between Front, Back, Left, Right, and no action. While 3D Cartpole environments have been used in other RL-based control studies [
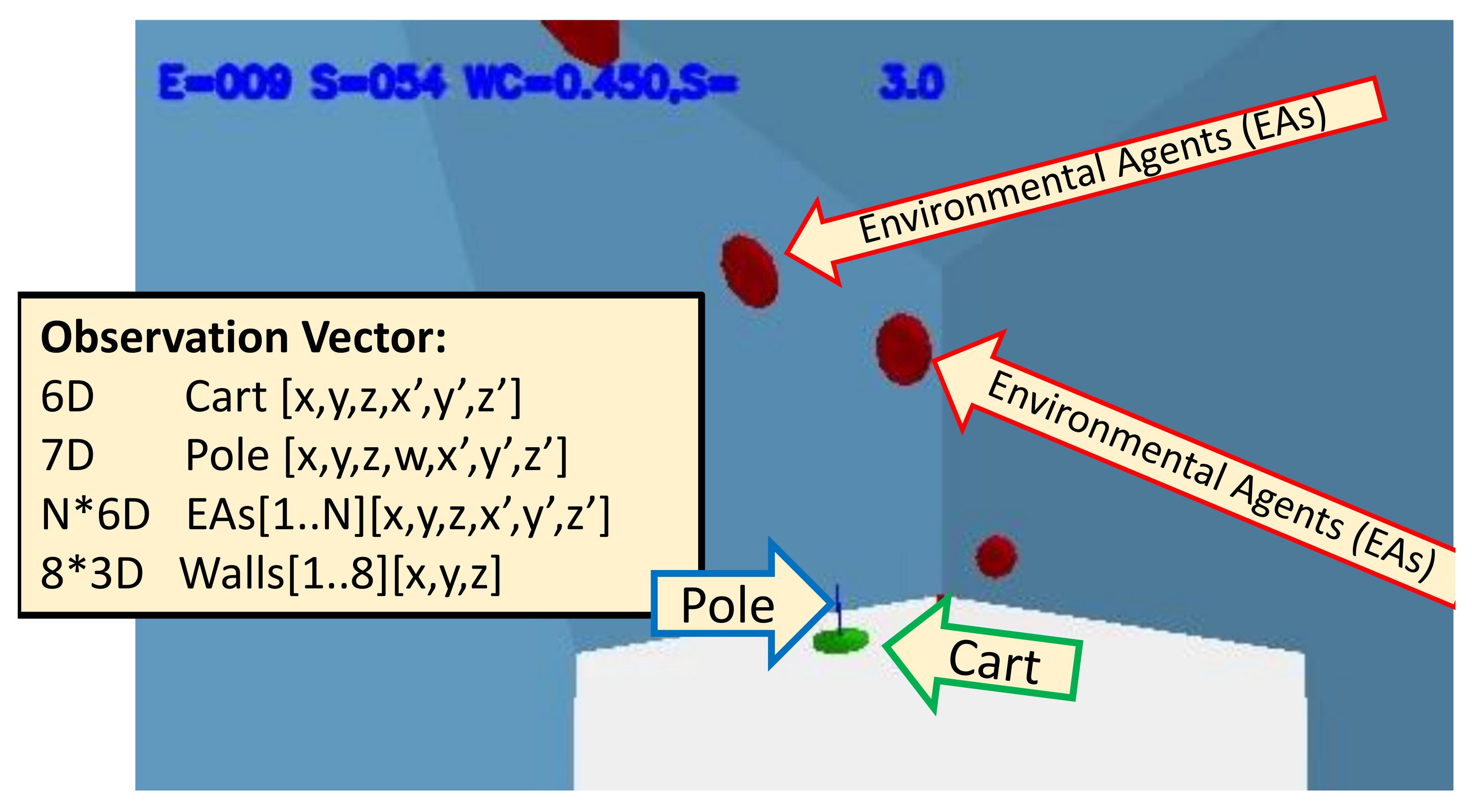
2], our usage is different because we add independently moving agents to introduce/study novelty. Different independent agents are introduced into the environment to create new types of novelty; see
Figure 1 for an example. The test environment can introduce novelties where there is a difference in the independent agents (e.g., the number, size, or stickiness of the agent), the actions of the spherical agents (e.g., random motion versus directed attacking motions), or even the interactions (if balls coordinate in action). These would all be novelties the WOW-agent needs to detect and manage. If a WOW-agent can recognize which type of novelty has been introduced, it might impact how they choose to behave (e.g., a sticky/stationary ball could help balance the pole), while attacking independent agents should be avoided. The experiments in this paper will use this domain, comparing a one- and two-step lookahead WOW-agent using Extreme Value Theory (EVT) for multi-type novelty detection with the same WOW-agent using a Gaussian-based novelty detection. We also compare a Deep-Q-learning Network (DQN)-based control algorithm [
3] that is not novelty aware.
To address the problem of multiple subtypes of novelty, this paper adopts and extends a recent framework for defining novelty theory [
4] and expands it to formalize the definition of and detection of multiple semantically different levels of novelty. In the original Boult et al. [
4] framework, novelty was defined using abstract dissimilarity measures in the world or observation spaces. However, the theory did not define “agents spaces,” which are required to build novelty detection.
The WOW-agent developed for this research seeks to detect previously unseen novelties and classify them into different semantic novelty subtypes. In particular, we consider novelty in classes, agents, actions, relations, and interactions, see
Figure 2. Thus, we extend the Boult et al. [
4] framework to include agent novelty, with a computable EVT-based dissimilarity in the agent-space. Secondly, we extend it to multi-type novelty by having multiple dissimilarity measures in all three spaces defined in that paper:
world-space, observed-space, and agent-space. These are logically defined in the associated spaces and allow us to have different dissimilarity measures defining the different subtypes of novelty. Our WOW-agent can classify previously unseen novelties using the multiple dissimilarity measures and use that classification to formulate responses.
The observation-spaces and agent-spaces include random variations, and dissimilarity measure computation will have noise. Hence, there is uncertainty in deciding if this dissimilarity is from noise or is caused by a novelty. A robust detection process is required. We show how to use EVT to determine when a measured dissimilarity is sufficiently different from training to declare something novel. Using the same dissimilarity variables/structures as our EVT-based solution, we also detect novelty using Gaussian-based uncertainty models for comparison.
The contributions of this paper include:
Extension of the Boult et al. [
4] framework to be computationally tractable, support agent-space dissimilarity, and support our formalization of multi-type novelty discovery.
Formalization of the use of per-dimension EVT for dissimilarity-based novelty discovery in the presence of uncertainty.
Formalization of multiple new dissimilarity operators for novelty in CartPole, and in general, for any simulator-based domain.
Experiments on CartPole3D with active environmental agents to evaluate how well EVT-based novelty detection works for multi-level, including comparison with Gaussian-based novelty detection and a DQN-based control agent.
2. Problem Formalization
In multi-agent problems, the term agent can become overloaded; we use the term WOW-agent to refer to our software-agent that controls the cart while detecting/managing novelty. We also have a DQN-based agent and a Gaussian-control agent, which are baseline software agents that control the cart and detect novelty, respectively. We use the term environmental agents to refer to other independently moving agents in the environment.
We also have two teams involved in the research: we refer to the Eval-Team team as the team that generated the core environment and environmental agents, as well as, ran the sequestered tests. We use Control-Team to designate the team that created the controlling agent that needs to control the cart while also detecting novelties in the open-world.
2.1. CartPole3D with Environmental Agents
As stated in the introduction, the novel CartPole3D environment has been constructed to utilize BulletPhysics [
5], with a mixed C++/Python code base. The Eval-Team and Control0Team developed a slightly modified version of pyBullet that uses a modified planar constrained joint for the cart and to support setting state of the position and joints used for the cart. The latter was a crittical function for the look-ahead controller used by the Controller-team. This was incorporated into a python environment use by both teams—in particular, this paper uses v0.7.9 of the system from
https://github.com/holderlb/WSU-SAILON-NG (accessed on 10 December 2021). The resulting CartPole3D model is a simulated environment with roughly 200 total changeable parameters/properties/attributes, some of which have easily changeable python interfaces, some of which are in model “urdf” files, and some of which are only in the C++ code.
Figure 2 shows a graphic rendering of the basic CartPole3D environment, the cart, the pole, the walls, and an example with four environmental agents. While the simulator can generate images, in this project, we do not receive images, just low-dimensional observation vectors, which is all the information the controlling agents receive about the environment.
For the cart controllers, we consider three different models,
DQN-agent: Deep-Q-learning Network (DQN)-based control algorithm, which is the baseline
GOWN-agent: Gaussian-based Open-World Novelty agent
WOW-agent: our Weibull-based Open-World controller agent
The Eval-Team-team developed trainined a DQN-based agent for CartPole3D to serve as a baseline. The baseline DQN-agent was a standard deep neural network with two layers of 512 fully connected nodes with rectified linear unit activation. The agent used DQN training, similar to that in [
3,
6,
7]. The agent was trained on non-novel CartPole3D episodes and converged after 500k steps. The final average performance reached was 0.8 out of 1.0, which represents keeping the pole balanced for 160-time steps on average out of the possible 200-time steps.
The Control-Team-team implemented the WOW-agent and GOWN-agent; see the MDPI branch of
[email protected]:Vastlab/SAILON-CartPole3D.git (accessed on 10 December 2021). Both used a lookahead-based control algorithm, where it received the current observational vector and compared that with its projected state. We noted that to support the Control-Team state setting functions needed for the WOW-agent lookahead type controller, Control-Team developed a modified pybullet. The state setting was imperfect as the test system only provided truncated position and velocity of the cart, pole, and active agents—which produced insufficient information to exactly recreate the state. Thus the lookahead state prediction was inherently noisy, and the WOW-agent must detect novelty in the presence of a noisy world model.
2.2. Formal Models of Novelty
The Boult et al. [
4] framework has critical elements defining novelty based on task-dependent dissimilarity functions
, and associated thresholds
and
for the world and observational space respectively. We generalize this by defining multiple dissimilarity measures in each space using task-semantics to provide multiple types of novelty. First, as shown in
Figure 2, we expand the definition to have four dissimilarity operators in each of the world-spaces and observed-spaces:
Agent Dissimilarity:
Motion Dissimilarity:
Relations Dissimilarity:
Interaction Dissimilarity
In the two-party evaluation used in this paper, the definitions of these dissimilarity measures are up to the Eval-Team, who defines the worlds with novelties. In the real world, we never know the actual novelty. In this formulation, the Control-Team does NOT get to know how the world/observed dissimilarity measures are defined or even what of the four dissimilarity to use. The control-team must detect novelty and estimate novelty subtype based on the combination of its own dissimilarity functions and the roughly implied semantics.
The definitions of novelty can be generalized to as many semantic subclasses of novelty as one wants for the given task. In particular, the control agent defines 64 different dissimilarity dimensions for agent-dissimilarity. Probabilities over subsets of these 64 dimensions are combined to approximate the unknown measures for world/observed dissimilarity measures.
Note that this approach is explicitly anticipating particular classes of novelty which we contend is still consistent with the idea of novelty. This approach also uses properties of the observed novelty to determine a more semantically meaningful label. While not explored in this paper, such a classification may be useful for adapting to that novelty. For example, with finer subtypes/categories such as attacking-motion versus supporting-motion (e.g., one would adapt differently by avoiding the spheres displaying former novel motions and seeking out those with the latter).
The second expansion of the Boult-et-al model is by adding dissimilarity operators for the agents. While their model provided the observed data to the agent, it defined by to the EvalTeam (our oracle) with their dissimilarity operators in the world-space. Hence, we define a dissimilarity operator for agents who can use a mixture of the observed data and the full agent state history. In particular, this allows us to define a formal process for the agent to use an EVT-based process, described in the next section, to estimate a threshold. It is worth noting that the agent-dissimilarity may declare something novel where the observed dissimilarity may not. The discrepancy can occur because the agent chooses a limited set of data for computing/normalizing its dissimilarity; in our case, we use a distributional model even if the observed-space has a large set of actual states. We also introduce an agent-space regret operator. Let be the task performance measure, which for CartPole is the percentage of time the pole was balanced. Then we define agent regret as , i.e., the failure percentage for the task performance operator.
In the Boult et al. [
4] framework, they provided a formal definition of nuisance novelties, which we also adopt as it is useful to be able to distinguish novelties for which there is a novelty but where the world and observation regret differ. For example, in the CartPole domain, using just the state interface (versus image interface), the agent can never detect a “cart-color” novelty as it is not observable. Hence, if world regret depends on the detection of that novelty, there will be inherent disagreement.
While that paper was a nice start, its model was not operationally, not precise and ignored uncertainty/variations. In this paper we propose an operational definition: a non-detection nuisance novelty occurs when the agent regret is not statistically different from its performance in the normal world but when world regret is statistically different. While there may be more general models for statistically significant testing, we use a very simple model. Let be the mean and standard deviation in a normal world of the regret of the baseline agent . Then an agent is robust if where the baseline can be the agent itself but ideally is a near-optimal algorithm so that robustness is not measured with respect to a badly performing algorithm. Let be the mean and standard deviation of normal world regret, respectively. Then we declare a novel world instance x to be a nuisance novelty, if and only if, the agent is robust on input x and Intuitively, nondetection nuisance novelty occurs when the world regret is significantly impacted by x while the agent is robust, i.e., the agent regret with respect to task performance is not impacted by the novelty.
3. Method
The problem here has three aspects. First is the core CartPole3D task—keep the pole balanced. The second is the detection of novelty, and the third is the characterization of the subtype of novelty. In this section, we describe the key methods used for each task.
3.1. Control
Our WOW-agent is a classic lookahead where we consider one-step and two-step lookaheads. To implement a lookahead WOW-agent, we had to augment the CartPole++ 3D world with a set-state function, which was more complex than it might sound. The CartPole++ environment implemented the cart using only a partially implemented (and not officially supported) planar joint, which constrains the object to move only within the x-y plane. Unfortunately, the class did not have a sufficient implementation to support even a basic set-state function. The second issue is that in the planar joint model, the cart is defined with a base position plus a joint offset but then returns position via a center-of-mass that is neither of those values. Thus, given the final position, infinitely many combinations can result in the same endpoint. The pole position is specified as attached to the “top” of the cart, but that position is unknown (e.g., because it depends on the unknown size of the cart). Unlike the 2D CartPole environment, where lookahead can have a near-perfect prediction, even in a normal world, the “set-state” function is inherently noisy, and prediction errors are non-zero and vary by variable. Thus, setting the internal state of the simulator for lookahead is inherently uncertain.
The scoring function is a combination of how far the pole is off vertical plus a novel element added to try to avoid the bouncing balls. Unlike traditional CartPole, we know there will be agents flying around the arena, and in general, if they collide, it will likely impact the pole. Hence, we compute the distance to the closest potential collision point and include an inverse weighted version of that into the score. We note that we cannot avoid collisions with fast agents aiming at the cart because they can move faster than we can get out of the way. Though not included in this paper, one way to adapt to novelty may be to adjust the scoring weight for potential collisions to start moving out of the way sooner. Others would be to change the force or angle of the push, but neither was an option in this version of CartPole3D.
3.2. EVT-Based Probability of Per-Instance Novelty and Overall Novelty Detection
As discussed in the previous section, we use dissimilarity measures + EVT for detection. We broke the dissimilarity measure computation into 34 static variables, 9 dynamic variables, and 21 prediction-error variables. The static variables are the min and max of the absolute value of the initial position of all the objects in the world. To deal with the variable number of agents, we build one static model for agents by combining variables from all agents using the appropriate min and max operators. We compute the min/max of cart/pole/block velocity for dynamic variables. For prediction-error variables, we use the per-dimensional prediction error between the predicted and the actual state after an action, and we do this for the cart and ball positions (3D*2), the cart, pole, and ball velocities (3D*2), and the pole angle (4D). Static dimensionality would include the wall locations if the novel world had different initial wall locations. Since we even hypothesized that walls could move as a potential novelty, we include it in the state. Finally, we also keep track of and utilize the collision and failure frequencies.
We run 3000 trials and collect the dynamics for the first 40 steps of control and then collect the values of all the above variables. We treat each dimension separately and do Weibull fitting using a tail size of 100, producing 64 different Weibull models. At test time, we compute the variables and sum the Weibull cumulative distribution function (CDF) probability from each for the time step. We also track which individual dimensions had significant EVT probability (>0.01) and use that to build our characterization strings discussed below.
While the above gives us a probability of the current time step being “novel,” collisions will often produce variable values unlike those seen in training. We limit training to only the first 40 timesteps to reduce the number of collisions. In 3000 trials, we only see roughly 50 collisions in the training data, which does not provide enough data to characterize the collision effect. Furthermore, since some novelties may reduce impacts, for overall novelty detection, we want something that looks at the distribution of scores independent of the subtype of novelty or variable used and incorporates a model of reliability. Looking at the literature, we decide to build roughly the approach described in [
8]. This approach builds a Kullback–Leibler (KL) divergence model, using a truncated Gaussian, from a vector of probability scores. We compute the expected KL divergence over the first 40 steps in training. Then at test time, we do the same and use the probability of exceeding that value as the overall novelty signal that the world has changed. We then accumulate that probability over trials with a blending to smooth out the impact of occasional collisions.
While we have described this use of EVT-based novelty computation in relative CartPole-specific terms, the reader should see how it can be applied to any set of variables in a simulator in both the raw form as well as their prediction error. The task-specific issues are mapping those to the different dissimilarity levels.
3.2.1. WOW Novelty Detection: EVT Per-Step Combined
When using the dissimilarity-based theory, multiple sources of uncertainty impact how to set the novelty detection threshold. The first is the normal uncertainty caused by random variations in the measure. But the second source of uncertainty would be associated with any model assumptions (e.g., if one assumes Gaussian distribution on values that may or may not hold). The important observation of this section is that we remove the second source of uncertainty by using Extreme Value Theory (EVT) because we do not need to assume much about the distribution of dissimilarity in the normal world.
In the [
4] framework, they simply declare thresholds for dissimilarity
,
, without providing any meaningful discussion on how they might be defined/estimated. Given the inherent variations and noise in real problems and the undefined scaling issues, defining these to account for uncertainty in the actual task/worlds is critical. In this section, we propose using EVT to define meaningful thresholds, including the agent threshold
.
There are two primary Extreme Value theorems, and we build from the Fisher-Tippet Theorem, also known as the statistical EVT of the first type. Just as the Central Limit Theorem dictates that the random variables generated from certain stochastic processes follow Gaussian distributions, EVT dictates that given a well-behaved initial distribution of values (e.g., a distribution that is continuous and has an inverse), the distribution of the maximum (minimum) values can assume only limited forms. We restate the core theorem here for reader convenience, and one can find proofs in many books, including in [
9].
Theorem 1 (Fisher-Tippet Theorem:). Let be a sequence of i.i.d samples. Let If a sequence of pairs of real numbers exists such that each and then if F is a non-degenerate distribution function, it belongs to the Gumbel, the Fréchet, or the Reversed-Weibull family.
Assuming dissimilarity, like distance, is bounded from below by 0, of the three distributions only the Reversed-Weibull can apply for maximum (and hence Weibull for minima). This EVT, and in particular the Weibull-based fitting, is widely used in many fields [
9], such as manufacturing (e.g., estimating time to failure), natural sciences (e.g., estimating 100- or 500-year flood levels), and finance (e.g., portfolio risks). EVT has recently been (re)introduced and applied in recognition, machine learning, and computer vision [
8,
10,
11,
12] where it is often used in open-set or open-world recognition tasks.
We note that some of the fields we will model are not bounded apriori, e.g., maximum velocity is not easily bounded. Such fields might be better modeled with a different type-1 EVT distribution (e.g., Freshet or Gumbel), or may even be better modeled with a peak-over-threshold, i.e., EVT type 2 [
13,
14], approaches. However, for simplicity we have used Weibull modeling for all fields and found it to be sufficiently effective and leave the search for better per-field models to future work.
To apply the Weibull to determine a novelty detection threshold we consider some dissimilarity measures and collect values of this measure of a large number of trials in the normal world. We can then use the largest or smallest of these scores, depending on the variable type, and fit a three-parameter Weibull distribution to them:
where
,
, and
are locations, scale, and shape parameters. Multiple libraries can compute the three-parameter Weibull, including SciPy, used for this paper. The associated CDF is given by:
which can be used to compute the probability of novelty for any given dissimilarity score
x. In our control system, we accumulate this probability over different items and then threshold (
), which simplifies processing varying numbers of dissimilarity. If desired, one can use the distributional parameters
, to compute the dissimilarity threshold
that yields a given probability
such that probability
implies novelty. We use the inverse CDF to derive
.
3.2.2. KL-Divergence over Per-Episode Novelty-Detection
The per-dimension approach produces a vector with per-time step probabilities of novelty. If the simulation and predictions were perfect, thresholding such per-time step data may be sufficient to detect novelty. However, we found probability from a single trial was too noisy to use directly. This is because the 200-time steps per episode and 100 s of episodes per trial, combined with the noise inherent in the simulation with a imperfect set-state function, have too high a probability of false detection. To improve robustness, we consider the distributions of the novelty probabilities over time and inspired by [
8] we use KL-divergence to compare the normal distribution to the distribution from the test data, see
Figure 3. To improve sensitivity for small differences, we also use the accumulation of novelty probability over time.
The Kullback–Leibler divergence is a fundamental measure of the difference between distributions. It measures the relative entropy
where
is the probability density function of the testing vector, and
is the probability density function of normal world vectors. In our case both the training and test vectors are distributions of per-time novelty probabilities, and the goal is to detect changes in that distribution. Intuitively the training vector would be all small value and the test all large values, but KL allows us to formalize “how” different is the distributions.
Making the classic Gaussian assumption for the pair of distributions, i.e., letting
and
, be the distribution parameters of the test and normal worlds respectively, the KL divergence measure is:
3.3. Overall World-Changed Novelty Detection
As an experimental trial for this task is a sequence of episodes, we compute the KL-divergence per episode and accumulate that over time. This allows small subtle changes to accumulate evidence. One issue for using KL is that, in some episodes, the environmental agents impact the cart and the temporal probability vector cannot be filled; hence KL detection becomes even noisier. To address this, we do not reduce the accumulation weight for KL for episodes that do not get at least 40/200 samples. This, however, reduces detection in highly unstable environments, so we increase the overall probability of novelty based on consecutive failures. Future work should formalize that process using EVT, but that takes way more runs to gather enough data, so for the experiments herein, it is an ad-hoc increase.
3.4. GOWN Per-Instance Novelty
The above described is the core WOW system. For novelty detection, we also developed a Gaussian-based GOWN baseline. It is identical to the EVT agent in all respects except that the per-instance novelty is based on truncating a Gaussian model. We computed the mean
and standard deviation
on each, similar to the EVT and used them in the Gaussian CDF:
We could compute probability of an outlier for each dimension as
and then could use either
-norm or
-norm, i.e., sum or max, to combine the dimensions. Unfortunately, both resulted in 100% of the test trials having false positives. Since trials have 200 episodes, with 20–40 episodes before novelty is introduced, noise makes an outlier too likely to occur randomly. To reduce the impact of the accumulation of many small- to medium-sized outliers, we modified the approach to use
which truncates the Gaussian outlier probability when the input is within
of the mean. If the data was Gaussian, this would be an effective threshold of about
of the data. We fed these probabilities into the KL-divergence detection algorithm described next with its expected mean/variance for overall change detection.
3.5. Characterization of Per-Instance Novelty
Using the per-dimension EVT-based probabilities, we can characterize the novelty into subtypes. We can combine the static variables to form our agent-dissimilarity measure while combining the “velocity” dimensions into a motion-dissimilarity measure. We use the remaining dynamic variables for relation dissimilarity, which we expected to be largely driven by prediction error. Hence, we should capture changes in relationships such as sloping of the cart, adding wind or friction, etc. The control agent outputs a string when it reports the world has changed to be novel. It summarizes the detected deviations along the lines of “Initial world off and Dominated by Balls with 18 Velocity Violations 18; 18 Agent Velocity Violations; 30 Total Agent Violations; 0 Cart Total Violations; 0 Pole Total Violations ...” which would be overall a motion violation (agent velocities).
4. Experimental Results
In our experiment, we use a sequestered evaluation methodology so that the CartPole agent subteam does not know the actual novelties. The paper’s authors represent two non-overlapping groups at different organizations. The evaluation subgroup designed/implemented the novelties and evaluated the systems, while the control agent subgroup developed the CartPole3D novelty detection agent. Our long-term goal is an automated evaluation system and baseline agent for comparison.
The experiments had 360 runs with four subtypes of novelty; with average performance plots for both the baseline DQN-agent and the WOW (EVT) agent shows each of the four subtypes of novelty are shows in
Figure 4. Each plot averages. In addition the EvalTeam defined three difficulty levels per subtype, by varying the world dissimilarity of the novelties they introduce, with smaller dissimilarity being harder to detect. Overall, there were 30 random sample runs per “subtype/difficulty” setting. Each run had 200 trials for 360*200 total trials. Each trial consisted of 200 CartPole episodes where a random
K (unknown to control agent) number of normal episodes was followed by 200-K novel episodes. For each episode
t, the performance scores
was the fraction of the 200 timesteps where agent
A kept the pole within the required range, the run terminated with performance =1 if the agent successfully reached 200 steps.
To evaluate the system, we consider the following metrics, computed over the 30*200 trials per the subtype/difficulty:
FP Rate: Fraction of trials where a false positive (or early detection) was reported. It was always zero for EVT experiments but not for Gaussian and so reported for completeness.
Detection rate: Mean ± stdev fraction of correctly detected trials. Note that a trial is considered a false positive and not a correct detection if the agent declared novelty before novelty was introduced.
Detection Delay: Mean ± stdev number of episodes after novelty was introduced before it was declared detected.
Performance: Mean ± stdev of Performance Score
OPTI: (Overall Performance Task Improvement) Mean ± stdev of relative post-novelty performance to a baseline DQN WOW-agent:
where
C is the CartPole control agent being tested (EVT or Gaussian) and
B is the baseline DQN agent.
Robust% which is the percentage of trials that were not statistically different from normal, using agent performance in a normal world.
The scoring of characterization was done by the evaluation team by matching the reported strings with the ground-truth novelty introduced for that trial. Human interpreters scored the accuracy of the objects involved (e.g., balls, cart, etc.), the property or relationship changed (e.g., movement), and the change type (e.g., increased speed or direction change). In the performance table, we list the characterization of object accuracy and characterization of property accuracy. The control agent did not attempt to report change type, so it scored zero on that dimension; we leave that dimension for future work as it allows even finer subtype detection.
5. Discussion
We report the detection, characterization, and control performance of the 1&2 step lookahead with EVT-based detection in
Table 1 for four different novelty subtypes, each with three levels of difficulty. We also report the DQN performance in that table. The DQN agent was pure control and did not report novelty. We performed a Wilcoxon signed-rank test for significance (used for all comparisons in this paper), and the difference in performance was statistically significant with
.
For relation and interaction subtypes, both baseline and control agents were robust, making detection more difficult. When the control agent was designed, the designers expected the semantics of “relations” to include things such as spatial positioning, and variations in world geometry (e.g., floor tilt, friction) would be detected in cart/pole dynamics. We failed to detect them until they were in the “hard” category; the impact of these may be below the noise inherent in the system from random collisions and the inability to exactly model the cart/pole. When the control agent was designed, the designers thought the semantics of “interaction” would be interactions between the agents and our cart. Thus, we expected our collision/failure measures would capture dissimilarity in that subtype. The experimental results show that interactions were all nuisance novelties. Collision/failure are more likely appropriate measures of action (e.g., attacking agents). We now hypothesize that interactions would be agent-to-agent measures that are not captured because we accumulated all agent data into one set of values. Future work will separate them out and look for patterns.
In
Table 2, we report the detection performance for the GOWN Gaussian-based novelty detector on the agent and action subtypes of novelty. The GOWN detection peformance for relation and interaction were zero and also not shown. The Gaussian-based detector is significantly worse than the EVT detector (
) in both FP rate and detection rate. We did not score the Gaussian detector for characterization, but given the much worse detection, we expect characterization will also be much worse. The control algorithm is the same, so not surprisingly, the robustness and performance were not statistically different and are not shown.
We attribute the significant improvement with EVT-based detection to the fact that the underlying data, such as position or velocity profiles, are not well modeled by a Gaussian. Sometimes a dimension has a much thicker tail distribution—leading to false positives when data exceeds the three sigma threshold frequently. Other times the data is bounded or very tightly defined, leading to missed detections. For example, positions cannot go beyond the walls, but smaller agents can be detected as they can get closer to the wall than agents seen in training, while larger agents never get as close. The more flexible EVT Weibull distribution naturally fits these types of uncertain data allowing better modeling and detection.
6. Related Work
A recent unifying formalization for defining novelty was introduced in [
4]. In that paper, they briefly considered 2D CartPole, but with either a simple Euclidean distance of state features or a very complex dissimilarity measure computed as expectations over the normal world. Their definition used a pairwise comparison of each new state with all training states, which was computationally impractical; in addition, that paper lacked any suggestions for defining when the dissimilarity was abnormal. The dissimilarity measures considered herein are more straightforward and support multiple subtypes of novelty. Importantly, we introduce using Extreme Value Theory as the core algorithm for deciding when dissimilarity departs from normal, which, as distributional models, are efficient while still modeling uncertainty in the decision.
Another general framework for defining novel worlds based on a generative framework is presented in [
15], which defines novelty in terms of the construction or generation of defined worlds and states. While we consider it a formally closed world model, the framework can be used in our expanded model. Other frameworks measure novelty based on the complexity of agents able to recover some level of task performance in novel worlds [
16,
17] or based on agent-independent representations of the world [
18]. The major distinction is that our approach does not have to reason about how the changes happen, just about what observations change, and how that can be used to classify subtypes of novelty.
Novelty detection has many variations among signal processing, computer vision, and machine learning [
19,
20,
21,
22,
23,
24,
25]. Still, almost all of these view novelty detection as a one-class problem—detecting things different from training. Recent work continues this one-class view but looks at how one can improve the process with learned features [
26] or by using GANs [
27]. Out-of-Distribution (OOD), similar to novelty detection, detects inputs that have not been seen before, but this body of work also treats the OOD as a single group somehow different from training [
28,
29], with substantial aspects of the work focusing on uncertainty modeling. These all differ from our work, as we focus on how to define/detect multiple subtypes of novelty.
Open-set and open-world recognition [
8] are also related problems and the most related algorithms. While that family or work has many known classes, they initially treat all “unknowns” as a single group. In open-world recognition, they detect unknowns and then get human-supplied labels and learn the new classes. In contrast, our model attempts to define a subclass of novelty based on anticipated properties of the novel, not human-supplied labels after detection. And while those papers also use EVT-based models, they convert all of the high-dimensional representations to a single dimension, while the approach in this paper uses EVT-based models per dimension, and combines probabilities over dimensions to define subtypes of novelty. For example, using agent speed dimensions for one type of novelty while using the difference between a predicted and observed position for other types of novelty detection.
The family n-step lookahead algorithm is classic AI in simulation environments, runs through different actions, and returns the one producing the most reward [
30]. It has been implemented in many CartPole models before, such as [
31] where they extract optimal cost values from optimizations, and approximate the cost-to-go for a simple one-step model predictive WOW-agent in a regular CartPole2D environment with walls. Our work uses a one- and two-step lookahead process in a 3D environment with walls and balls, which adds a new level of complexity as moving balls increase the chance for collisions and require the agent to consider them. We generally use a one-step lookahead, but when collisions are likely, or the world is novel, we use the more expensive two-step lookahead.
Novelty in the open-world has been addressed only to a very limited extent in agent-based reinforcement learning domains like CartPole. Sekar et al. [
32] approach novelty from an exploration perspective; that is, they use the world model learned so far to identify states with high uncertainty and devise plans for visiting those states. The agent performs this exploration offline, which they call “imagination.” They evaluate their approach on the DeepMind Control Suite [
33] of 20 RL domains, including 2D CartPole, to demonstrate their agent’s ability to achieve superior zero-shot performance on novel domains. Ref. [
34] takes a similar exploratory approach, but use a population of agents guided by evolutionary strategies to seek out novel states in the OpenAI Gym’s [
1] Humanoid-v1 and Atari games domains. However, the domains were presented visually to the agent, and the novelty was not characterized.
Peng et al. [
35] learn the rules and states of a game domain and store these in a rules knowledge graph (KG) and a state KG. Changes that result in changes in these KGs indicate the presence of novelty and trigger further learning by the agent. This learning can proceed offline, again as a form of “imagination”-based simulation to accelerate adaptation to the novelty. They evaluate their approach in Monopoly with novelties such as increasing the price of some properties. Results show that their approach allows an agent to adapt more quickly to novelty than a standard RL agent trained from scratch on the novel scenario. In this case, the changes to the KGs can constitute a characterization of the novelty.
Muhammad et al. [
36] describes a framework for handling novelty in agent-based domains. Their approach maintains a knowledge base of actions and beliefs, which are used to invoke a planner to achieve goals in agent-based domains and detect discrepancies between predicted and actual states. Their approach can detect, characterize, and accommodate novelty. They evaluate their approach in two agent-based environments: their NovelGridworlds environment [
37] and a variant of Minecraft called Polycraft [
38]. Their approach can handle novelties that reduce performance, but additional capabilities are needed to handle novelties that prevent task achievement.
Klenk et al. [
39] uses a model-based approach for adapting to novelty in agent-based domains. Their Hypothesis-Guided Model Revision over Multiple Aligned Representations (HYDRA) approach combines a domain-independent planner and model-based diagnosis to diagnose and repair the model when novelty is detected. HYDRA has been applied to the Angry Birds-based novelty generator [
40,
41]. Results show that the performance of the domain-independent HYDRA approach is comparable to systems designed specifically for the Angry Birds domain [
42].
7. Conclusions and Future Work
This paper introduced the idea of multiple subtypes of novelty with different dissimilarity measures computed over EVT-based distributional models of static, dynamic, and prediction errors. This is a very general concept and could be applied in other domains to help refine novelty detection. The paper also showed that the EVT-based approach to the subtype of novelty can be effective even for nuisance novelties—if the right variables/dimensions are anticipated and computed, but can fail to detect nuisance novelties when only critical control-related variables are used. When the world can present novelty, it can pay to look at things that do not seem to matter to the task at hand.
Open-world learning, which includes both the problem of detecting and learning to manage multiple types of novelty, is of growing practical interest. While this paper addressed them in a simulated and simple world, where it was easy to control/introduce novelty hidden from Control-Team, who designed the controllers, future work should address these in more realistic problems/settings. This paper results from an ongoing multi-team effort addressing learning in open worlds. Future work will continue to advance the art and also show how the extended framework used herein can be applied to other types of novelty and domains. As future work, the Eval-Team will define even more types of novelty, and Control-Team will enhance controllers to address them and improve detection—the main branch of the public code will provide those advances.