Abstract
Motivated by the transportation needs of modern-day retailers, we consider a variant of the vehicle routing problem with time windows in which each truck has a variable capacity. In our model, each vehicle can bring one or more wagons. The clients are visited within specified time windows, and the vehicles can also make multiple trips. We give a mathematical programming formulation for the problem, and a branch and price algorithm is developed to solve the model. In each iteration of branch and price, column generation is used. Different subproblems are created based on the different capacities to find the best column. We use CPLEX to solve the problem computationally and extend Solomon’s instances to evaluate our approach. To our knowledge, ours is the first such study in this field.
1. Introduction
The Vehicle Routing Problem () initially emerged when Dantzig and Ramser formulated and resolved the problem of supplying fuel to service stations around the end of the fifties of the last century [1].
The definition states that n customers with discrete quantities of goods must be served by m vehicles initially located at a depot. A is to determine the optimal routes taken by a group of vehicles while serving a group of users. The objective is to minimize the overall transportation cost. The solution to the classical problem is a set of routes visiting all the customers exactly once that all begin and end in the depot. The transportation cost is improved by reducing the total traveled distance [2].
The Multi-Trip Vehicle Routing Problem with Time Windows () is a type of the classical Vehicle Routing Problem with Time Windows () with more than one trip for a vehicle during a workday. A trip is a timed route when more than one route can be allocated to a vehicle. The multi-trip feature is needed when the vehicle fleet size is limited. In this case, a benefit is a reduced number of drivers and vehicles. Besides, in practice, industries cannot provide an unlimited number of vehicles to serve all customers, and they tend to prefer a limited number of vehicles to do more than one trip. Despite its apparent practical relevance, this variant of the classical VRP has not been the subject of a large number of studies. Refs. [3,4,5] are a few papers worked on Multi trip vehicle routing problem ().
Multi-trip vehicle routing problem with a variable number of wagons and time windows defines a variant of the classical vehicle problem in which the capacity of vehicles can be determined given the total demand of the route when a vehicle is prepared to leave the depot. In this situation, one, two, or three wagons can be attached to make a vehicle ready to service the customers. The number of wagons and vehicles is limited, and the vehicle configuration will stay the same during all vehicle trips. This new methodology is suitable to decrease time and cost by reducing the number of vehicles, drivers, and fuel consumption, which is specifically more critical in distributing goods over large distances like two different cities or from large cities to rural areas.
The main contribution of this work is to introduce a mathematical model for Multi-trip Vehicle Routing Problem with a Variable number of Wagons and Time Windows (MTVRP-VW-TW). We develop a Branch and Price method to find an optimal solution. Column generation is used for each iteration of the branch and pricing. Various subproblems are formed to choose the appropriate column based on the various capacities. We used modified Solomon’s instances [6] to test the algorithm. It is the first time the model has been presented and solved with exact methods.
The rest of the paper is organized as follows. We review the relevant research in Section 2. We give the definition and mathematical model for MTVRP-VW-TW in Section 3. Column generation for MTVRP-VW-TW is presented in Section 4. MTVRP-VW-TW is solved using the branch and price algorithm in Section 5. The detailed experimental study is discussed in Section 6. Section 7 concludes this paper with a discussion of the limitations of this work and possible future extensions.
2. Literature Review
Multi-trip vehicle routing problem () is an essential type of vehicle routing problem in the real world that is studied less than other versions of vehicle routing problem, specifically, for exact methods. Ref. [7] is a survey that categorizes and examines urban logistic flows. As a result, it outlines the three main scientific issues that must be resolved: time dependency, the arrangement of the distribution on multiple levels and trips, and dynamic information. Fleischmann [8] proposed a modification of the savings heuristic and used a Bin Packing Problem heuristic to assign the routes to vehicles with multiple uses. Taillard, Laporte, and Gendreau [9] presented a tabu search algorithm with three phases to solve the problem. Brando and Mercer [10] proposed another tabu search algorithm with a variable neighborhood to find a solution with the least cost. The algorithm is a three-phase algorithm that creates an initial solution by a heuristic and then uses tabu search (reinsertion and exchange of customers) to improve the solution and restore feasibility. Brandão and Mercer [11] also presented a more complex problem when mixed fleets and maximum overtime constraints are allowed. Salhi [12] proposed the many-to-many location-routing problem. Campbell and Savelsbergh [13] described insertion heuristics that can be used effectively when time windows constraints are added to the problem.
Petch and Salhi [5] developed a multi-phase constructive heuristic for the , which in phase one generates a solution using a savings approach, and phase 3 generates a solution by route population approach. Phase 2 is a construction and improvement stage in which an solution is constructed using bin-packing with the minimization of overtime as the objective. Salhi and Petch [14] improved their previous method to a hybrid Genetic Algorithm with the same objective. Olivera and Viera [15] presented an adaptive memory approach to minimize total routing cost. Cattaruzza et al. [16] used a hybrid genetic algorithm with a new local search operator that is a combination of standard moves and swaps between trips to minimize total traveling time. Wassan et al. [17] proposed a two-level variable Neighborhood Search to generate an - initial solution to minimize the total cost. Tirkolaee et al. [18] formulated a new model for a robust multi-trip vehicle routing problem with intermediate depots and time windows to address the uncertain nature of the demand. Anggodo et al. [19] presented a genetic algorithm for multi-trip vehicle routing problems with time windows. More heuristic approaches are in [20,21,22,23], in which a hybrid genetic algorithm, a simulated annealing, a hybrid particle swarm optimization algorithm, and a hybrid genetic algorithm are used respectively. A new impact integer programming formulation for the multi-trip vehicle routing problem with time windows is developed in [24].
A limited number of papers on the exact methods for exist. Desrosiers and Solomon [25] were the first to use column generation in a Dantzig-Wolfe decomposition framework. Halse [26] implemented Lagrangean decomposition. After that, Kohl and Madsen [27] extended Lagrangean relaxation. These approaches were further developed using Dantzig-Wolfe decomposition, including cutting planes or parallel platforms in Kohl, Desrosiers, Madsen, Solomon, and Soumis [28]; Larsen [29]; Cook and Rich [30]. A hybrid algorithm, a combination of Lagrangean relaxation and Dantzig-Wolfe decomposition, was presented by Kallehauge [31]. Chabrier, Danna and Le Pape [32]; Feillet, Dejax, Gendreau and Gueguen [33]; Rousseau, Gendreau and Pesant [34]; Larsen [29]; Chabrier [35]; Irnich and Villeneuve [36]; Danna and Le Pape (2005) [37] presented algorithms based on the subproblem methods. Hernandez et al. [3], and Nabila Azi et al. [38] suggested the branch and price algorithm with two phases. In the first phase, all paths are generated. In the second phase, the problem is solved by column generation. Macedo et al. [39] proposed an approach using a pseudo-polynomial model. Munari and Morabito [40] presented a branch-price-cut for a multi-trip vehicle routing problem; Faiz et al. [41] has two integer programs for the open vehicle routing problem and uses column generation to solve them; Azi et al. [4] gave column generation embedded in branch and price algorithm to solve multi-trip vehicle routing problem with time windows using dynamic programming to generate all non-dominated paths by label correcting algorithm which are used in the subproblem; Seixas and Mendes [42] presented a branch and price algorithm to solve the multi-trip vehicle routing problem with time windows and driver work hours. Bettinelli et al. [43] used a branch-and-cut-and-price algorithm to solve the multi-trip separate pickup and delivery problem with time windows. A branch-cut-and-price algorithm is developed in [44] for the single and multi-trip two-echelon vehicle routing problem with time windows. A new variant of the multi-trip vehicle routing problem for the case of being in a queue while the unloading capacity is full is presented in [45] which is solved using a branch-and-price-and-cut algorithm.
We are unaware of any work on exact methods for the multi-trip vehicle routing problem with time windows and the flexibility of having different wagons attached to service customers, as in this paper. In contrast to the previous works like [3,4,38] which give branch and price algorithms for , we formulate a new variant of in which the capacity can be different. This requires a modification of the branch and price algorithms. We have a different master problem compared to the previous work. There are three sub-problems with three different objective functions, and each subproblem is solved by constructing a new route graph based on the capacity of the vehicle in which we look for all the non-dominated tours.
3. Mathematical Model for Multi-Trip Vehicle Routing Problem with a Variable Number of Wagons and Time Windows
An instance of this problem is defined by a set of customers , and the depot is represented by the vertices 0 and . Depot 0 is the start depot, and is the return depot.
The set is denoted N in a complete directed graph , where A is a set of arcs . A traveling time of is associated with each arc , which we consider as the distance of two vertices i and j, where . A fleet of wagons W, with identical capacities q which can be connected as one wagon, two wagons or three wagons to organize a set of vehicles V. Vehicles in V are used to serve the customers. |V| and |W| are the number of vehicles and wagons, respectively. The set of arcs A represents all the connections between customers and the depot. There are no arcs ending at vertex 0 or originating from vertex . A traveling time of is associated with arc , where . Any customer has a demand , a service time , and a time window , which means that a vehicle must arrive at the customer before . If it arrives before the time window opens, it has to wait until to service the customer. The time windows for both depots are assumed to be , representing the scheduling horizon. The vehicles may not leave the depot before and must return at the latest time . A route of a vehicle is a closed path that starts and ends at the depot. The vehicle starts at the depot, visits several customers in a specific order, and returns to the depot again. At every point on the route, the time windows and capacity constraints are satisfied. The workday of each vehicle is a sequence of routes where each route starts and ends at the depot and we call it a tour. Multiple routes can be performed by a vehicle during one day, and these routes are collectively called a tour. These routes are denoted by the set R and the maximum number of routes in any tour (for any vehicle) is fixed in our model.
Each vehicle can be configured to use one, two, or three wagons giving it different capacities. The configuration of each vehicle must stay the same on all trips. Next, we define some of the mathematical model’s decision variables. The decision variable denotes the time that the vehicle k starts to service customer i in route r. If the vehicle k does not service customer i in route r, has no meaning; consequently, its value is considered irrelevant. Variable is one if vehicle k drives directly from customer i to customer j and zero otherwise in route r. Variable is used to determine how many wagons vehicle k needs, where n is in . If , vehicle 3 has 2 wagons. Therefore, and must be 0, which means vehicle 3 does not have 1 or 3 wagons. Moreover, finally, is the vehicle’s capacity, depending on the number of wagons attached.
We assume and therefore , for all k and r. The goal is to design a set of routes that minimizes the total distances of all routes and
- Each customer is serviced exactly once;
- Every route starts at vertex 0 and ends at vertex ;
- The time windows of the customers are satisfied;
- The total demand on a route can not exceed the capacity of the vehicle, which depends on the number of wagons attached to it (1, 2, or 3);
- Total number of the wagons used should be less than ;
- A vehicle is assigned only one configuration;
- Each vehicle must leave the depot 0;
- All vehicles must return to the depot ;
- The start time of the next route by the same vehicle should be after the finishing time of its previous route;
An unused vehicle is modeled by driving the empty route .
The mathematical model is described next.
The objective function (1) minimizes the total distances of tours. The constraints (2) ensure that each customer is visited exactly once. Equations (3) and (4) state that the total demand on a route can not exceed the capacity of each vehicle depending on the number of wagons attached. The constraint in (5) shows the number of wagons in total. Constraints (6) ensure that a vehicle is assigned only one configuration. Equations (7)–(9) indicate that each vehicle must leave the depot 0; flow conservation constraints; finally, all vehicles must return to the depot . The inequalities (10) establish the relationship between the vehicle departure time from a customer and its immediate successor. Constraints (11) assert that the time windows are observed. Constraints (12) ensure a proper trip sequencing for the workday of a vehicle that the starting time of the next trip of the vehicle must be after the finishing time of its previous trip. Equations (13) and (14) are integer variables.
4. Column Generation for --
Multi-trip vehicle routing problem with a variable number of wagons and time windows and the mathematical model was described in Section 3. In this section, we solve the problem using column generation. The master problem, pricing subproblem, and the techniques for solving the pricing subproblem will be explained.
4.1. Master Problem for --
A tour is the set of all the routes a vehicle performs during a day. So, the decision variable , which refers to a column corresponding to a tour. is the set of all feasible tours, is the total distance of tour , is the total number of wagons, is the number of the vehicles and is the number of wagons used for a vehicle that is used in tour w and . is one if customer i is in tour w, 0 otherwise. We use the following decision variable:
The master problem is:
The objective function (18) is to minimize the total distances of all tours. Constraints (19) ensure that each customer is visited at least once. The constraint (20) states that the number of all tours must be less than the number of vehicles. Constraint (21) states that the number of wagons used in all the vehicles must be less than the total number of wagons.
The solution is a subset of . As the number of columns is exponential in the number of customers, we solve the restricted master problem () with a limited number of columns for the initial solution. The columns are progressively added into . The LP-relaxation of () is solved with an solver to obtain the dual variables associated with the optimal solution of the . These dual values are sent to the subproblem to determine new tours with a negatively reduced cost, and these new tours are added to the master problem. The process will continue until there are no more tours with a negatively reduced cost. This guarantees an optimal solution to the .
4.2. Method for Constructing Tours/Columns
Once the LP relaxation of the restricted master problem is solved, Three sub-problems are defined below based on the definition of the --. The first sub-problem is to find tours of vehicles with one wagon attached; the second and third sub-problems are to find tours of vehicles with two and three wagons attached, respectively. Each sub-problem is an elementary shortest-path problem with resource constraints. The path starts at the artificial start node (depot) and to the artificial end node (depot) in the route graph. The route graph and its construction are explained in the following sections. Solving each sub-problem gives a new tour with the most negatively reduced cost. Following are the steps to solve the sub-problems.
4.3. Generating All Non-Dominated Paths
All non-dominated routes must first be generated to solve the sub-problems. The label correcting algorithm [33] is used to create all these routes. To keep track of previously visited nodes, elementary paths must be generated. A path p from an origin node to a node is labelled with . Time consumption, is the time used in the path till customer which sets to 0 at the depot, and after extending a path by visiting a new customer, it is updated as , where and are two adjacent customers on the route and represents the service time for the customer . Load consumption, is the capacity used for the path and sets to 0 at the beginning when the vehicle is at the depot, then when a customer is added to the path, it is updated by where is the quantity that must be delivered to the customer . A time interval representing the time window is associated with each customer and a load interval , where Q is the vehicle’s capacity. is the length of the path and is made negative by replacing the distance of each arc with , such that . We make the distances negative so that vehicles leave the depot. Otherwise, it would be optimal to stay at the depot; is the number of unreachable nodes and if node i is unreachable, 0 otherwise. The following dominance relation is used to determine non-dominated routes:
Dominance Relation: If two paths, p, and , extend from origin o to node j with labels and , respectively, then path p dominates if and only if [38].
In other words, a path p dominates a path if (a) it is no longer, (b) it does not use more resources for each resource taken into account, and (c) every node that is unreachable for path p is also unreachable for path [38].
Using this relation will keep only the labels for non-dominated elementary paths.
To implement the label correcting algorithm for our problem, we need to create a label which represents a path p from the depot to the customer j. All feasible non-dominated routes are generated using these labels.
During the path extension, we need to see if the current time consumption () plus the distance is less than , then is replaced by , and the extension of the path continues. Each time we extend one node or the node is unreachable, increases by one. We also eliminate the partial routes when we are extending the paths. So, at the end of the algorithm, we will have all non-dominated routes.
4.4. Creation of the Route Graph
After creating all non-dominated routes, each can be looked at as a node in a new graph called the route graph. The route graph includes these routes as nodes and two artificial nodes for the start and end of the vehicle workday. To create the route graph, if there is an edge between nodes r and , route r and must not visit the same customer, and the feasibility of servicing route after route r is determined through departure time windows as explained below.
The latest departure and arrival times and the earliest departure and arrival times need to be calculated to satisfy the second condition. To have an edge , the latest departure of route must be larger than the latest arrival of route r. There are edges between the artificial start node and all routes and from all routes to the artificial end node.
There are two time windows for each route node r which are earliest and latest departure times and earliest and latest arrival times . Routes must be started and completed in these intervals. These time windows are determined as shown below [38].
Latest departure and arrival times:
If the route r is shown as a sequence where the first and last points are the depot as well as other customers ( ones) in the middle, first the latest feasible time of each customer must be calculated using a back-ward sweep of route r starting from to . Therefore:
Finally, we will have which is the latest departure of the route r and again in a similar way we obtain the latest arrival time of the route as well as the latest feasible schedules () at each customer using a forward sweep, so each can be calculated as:
Earliest departure and arrival times:
Suppose we calculated the latest departure time (), the earliest departure time() and the latest feasible schedules to begin service at each customer() in the route r, two cases can happen:
Case 1: there is no waiting time (vehicle doesn’t arrive before time windows) in the latest feasible time of customers, then we can shift the latest times by the minimum of () and , so we can calculate it for each route as:
By deducting these units from the latest departure and arrival times, the earliest departure and arrival can be obtained. So, we have:
and,
Having all the latest departure and arrival times as well as the earliest departure and arrival times, it is possible to write the time windows for all routes as: and .
Case 2: If there are some waiting times in the latest feasible time for customers. Then, we can not leave the depot earlier, when the latest arrival times are before the time windows.
So, the earliest departure and arrival times will be the same as the latest departure and arrival times respectively.
and,
In case 2, the time windows for departure and arrival will be a single point. So, the route can be served after route r if .
Given all this information, now to create the route graph, we must note that there must not be any common customer between routes r and and the latest arrival time of the route r must be less than the latest departure time of the next route . If both conditions are met, then there is an edge from r to .
4.5. Sub-Problem for --
The subproblem is defined on the route graph where is the set of all non-dominated routes generated by the label correcting algorithm [33] plus two artificial nodes for the start and end of the tour. is the set of edges in the route graph with the time windows on each route, and .
Dual variables associated with the master problem constraints are needed to formulate the subproblem on the route graph. Let be dual the variables associated with constraints (19) in the master problem and and are the dual variables associated with (20) and (21) constraints respectively.
Let , where is the total distance of route s, and the reduced cost of arc is:
Using the binary variable which is one if the route is used and zero otherwise, and the continuous variable which is the departure time of the route r, we formulate the subproblem as follows:
The objective function (23) is to reduce the cost of the tour. Constraint (24) indicates that the vehicle must leave a route and go to the next one. Constraints (25) and (26) ensure that the tour starts and ends at the depot. The inequalities (27) establish the relationship between the vehicle departure time from a route and its immediate successor. Constraints (28) assert that the time windows of routes are observed.
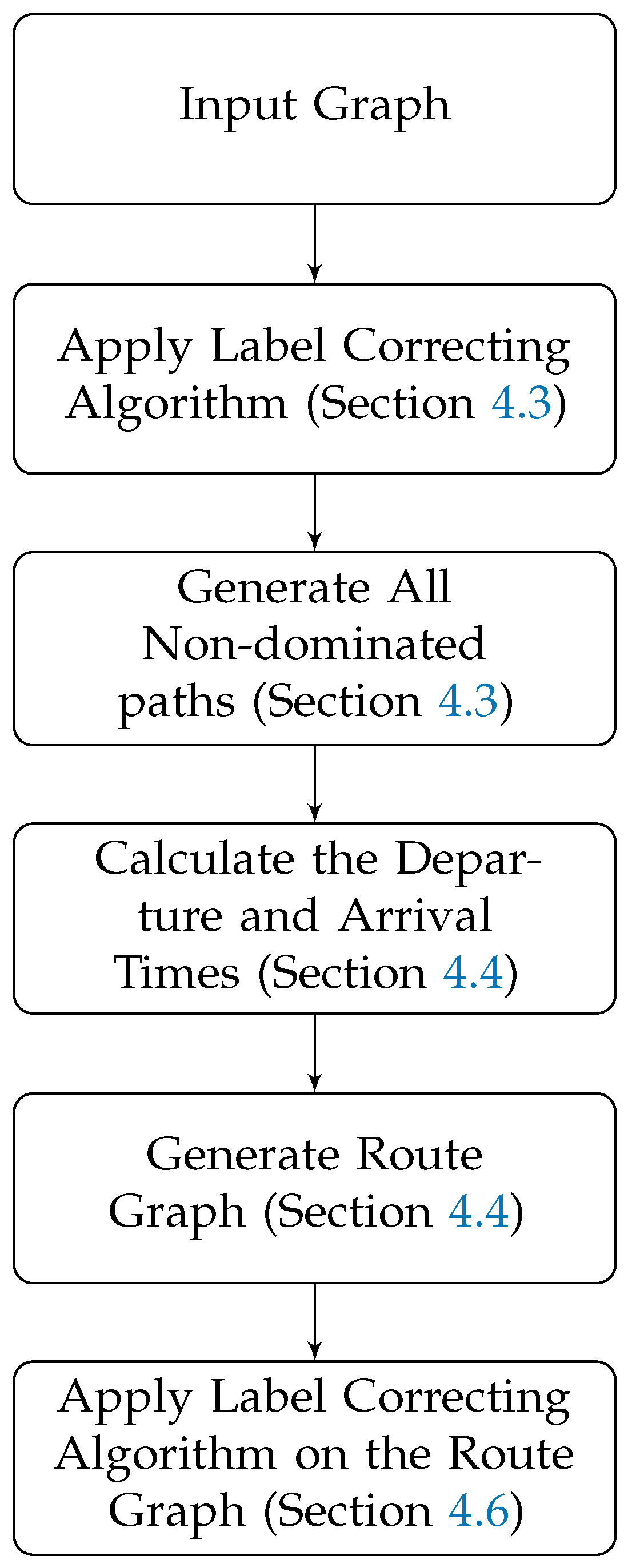
The following flowchart shows the process of generating all non-dominated tours for the sub-problem with one wagon in Figure 1. The same procedure is used for two other sub-problems.
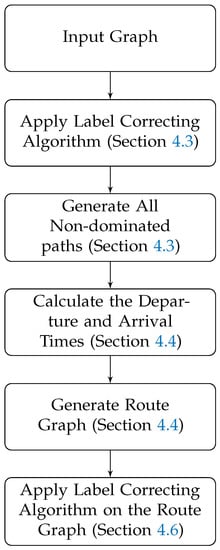
Figure 1.
Process of generating all non-dominated tours.
4.6. Solving the Pricing Subproblems
For three different capacities of the vehicles, we have three route graphs. Consequently, three subproblems will be solved. The label correcting algorithm can be applied to each of them again to find the new tour with the negative reduced cost to be added to the master problem.
Now, the label correcting algorithm can be implemented to determine all non-dominated tours of the route graph. The method described in [4] is used to implement the label-correcting algorithm on the route graph.
Using the extend and dominate function in the label correcting algorithm, all non-dominated tours will be generated. The algorithm first generates all non-dominated routes and then generate the route graph, and finally creates all non-dominated tours. The algorithm is described next.
Description of the Algorithm:
The Algorithm 1 finds all non-dominated tours on the route graph from the origin node p (depot).
We need the following notation to describe the algorithm:
- : The input graph.
- N: Set of customers and vertices 0 and as the depot.
- A: Set of all edges between vertices in N
- : List of labels on node
- : Set of successors of node .
- E: List of nodes waiting to be processed.
- : Function that returns the label resulting from the extension of label towards node when the extension is possible, nothing otherwise.
- : Procedure that removes dominated labels in the list of labels .
- : List of labels extended from to
- : To save all non-dominated routes.
- : latest departure time of .
- : latest arrival time of .
- : earliest departure time of .
- : earliest arrival time of .
- : Route graph
- : Set of all non-dominated routes which are vertices in the route graph.
- : Set of edges in the route graph
- : List of labels on node
- : Set of successors of route .
- : List of routes waiting to be processed.
- : Function that returns the label resulting from the extension of label towards node when the extension is possible, nothing otherwise.
- : Procedure that removes dominated labels in the list of labels .
- : List of labels extended from to
| Algorithm 1 Generating all non-dominated tours |
|
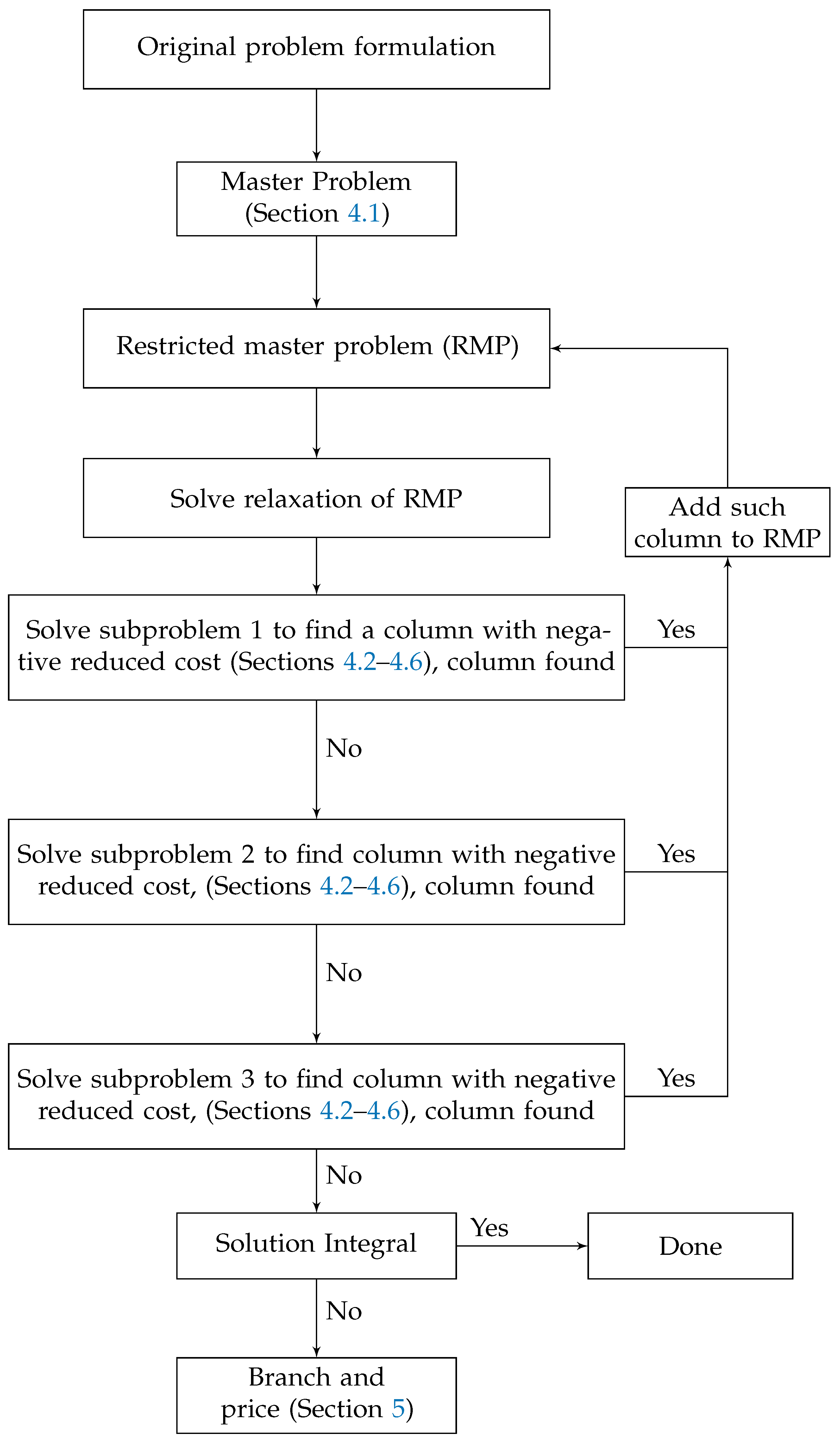
All non-dominated tours will be generated using the extend and dominate function in the label-correcting algorithm. There are three subproblems based on the various capacity. All tours will be generated for these three subproblems. First, we will see if there is a new tour with a negative reduced cost in the subproblem with one wagon. If so, the column will be added to the master problem. If not, the second subproblem will be checked. Suppose a new tour with a negative reduced cost is added to the master problem. If not, we will check the third subproblem, which uses three wagons. We solve the subproblems until all tours with the negative reduced cost are found and added to the master problem. The following flowchart shows the procedure of the algorithm in Figure 2.
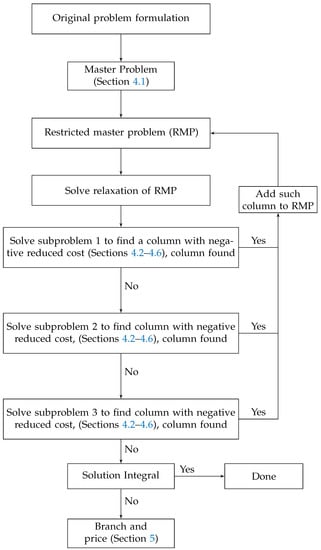
Figure 2.
Column generation procedure for various capacities.
5. Branch and Price Algorithm for --
In this section, we describe initialization, the search strategy, the branching strategy, and the upper bound that we use in our implementation of branch and price for the multi-trip VRP with variable wagons and time windows.
Initialization: At the root of the search tree, the is initialized with tours made of a single customer visit. The number of columns thus corresponds to the number of customers. For internal nodes in the search tree, the algorithm initializes the with the set of columns in the parent node considered after removing infeasible columns due to branching [4]. The minimum capacity for all vehicles that service a single customer is one wagon.
Search Strategy: The branch and price tree is explored using a depth-first search.
Lower and Upper Bound: The solution to at the root node gives a lower bound for the problem. We solve the master problem using CPLEX. The integer solution of the master problem given by the CPLEX 12.8 is used as the upper bound.
Branching Strategy: Two branching strategies are used. We branch on the number of vehicles and the arcs.
Branching on the Number of Vehicles: We sum the value of variables of the optimal solution of , so , where . If k is fractional, two branches are created. For each branch, one additional constraint is added to the master problem. These two constraints are:
and
The dual variable value corresponding to the new constraint is added to the subproblem, and the column generation is done again for this new child node.
Branching on Arcs: The branch on an arc happens when the flow on an arc is fractional. We calculate the flow on any arc that is in some column. The sum of the , on the columns that include an arc , will give the flow on the arc. The arc with fractional value is taken. So, these branches will be:
- Left branch: , which means the customer j must be visited right after customer i in all tours of and the route graph. To enforce it, all columns in the and the route graph that contains arc with and with must be deleted. Also, if , then the decision variables for vertices i and j are set to one in , and .
- Right branch: , which means the customer j must not follow the customer i immediately. So all tours must be removed, including the arc in and the route graph.
Branch and Price Process
We start at the root, and if is feasible, all possible columns from three subproblems will be added to the . The LP solution of the root is set as the lower bound, and also integer solution given by the CPLEX is used as the upper bound. Two branches on the number of vehicles are created, and we use a stack in implementation DFS, so nodes are added to the front of the stack. For each node, column generation is used again to find the LP- solution of . We check if the node must be pruned or kept. If the node is not pruned, we update the upper bound and create two new branches. After processing all nodes, we see if the sum of the value of variables of the best bound is an integer, but variable values are not, then the branching on nodes is used to generate nodes. Then, we calculate the flows on all the arcs. In the same way, we continue with the last node added to the head of the list to see if the node must be pruned or kept after using column generation. If we keep the node, two branches are created, and the upper bound is updated. The process continues until the stack is empty.
6. Experimental Evaluation for --
6.1. Mathematical Model Test
The mathematical model of MTVRP-VW-TW with the objective function of the duration of the longest route is solved with CPLEX and C++, using modified Solomon instances [46]. The algorithm is implemented in C++. The instances are a subset of Solomon’s set of CVRPTW test problems. They are type of with 25 customers. We modified the number of vehicles and capacity in type to 25 vehicles, and the capacity of 200 changed to 15 vehicles, 30 wagons, 3 routes and a capacity of 150 for each wagon. For type , 25 vehicles and a capacity of 700 are changed to 15 vehicles, 30 wagons, 3 routes, and a capacity of 500 for each wagon. For type with a capacity of 1000 changed to 15 vehicles, 30 wagons, 3 routes, and a capacity of 700 for each wagon. Table 1, Table 2 and Table 3 show the results.

Table 1.
25 Customers.

Table 2.
50 Customers.

Table 3.
10 Customers.
All the instances have a large integrality gap and it takes a lot of time to solve the mathematical model.
6.2. Branch and Price Test
Solomon’s (100 customers) instances [46] for Euclidean are modified to evaluate the model. We use the first ten customers of Solomon’s instances to test the algorithm. The Euclidean distance between two customer locations determines the travel time for these instances.
The instances of Solomon [46] that we consider of six different types , , , , , . Each data set has eight to twelve 100-node problems. Sets and have clustered customers whose time windows were generated based on a known solution. Problem sets and randomly generate the customer’s location over a square. Sets and combine randomly placed and clustered customers. Sets of type 1 have narrow time windows and small vehicle capacity. Sets of type 2 have large time windows and large vehicle capacity. Therefore, the optimal solutions for type 2 problems have very few routes and significantly more customers per route. It must be noted that the branch and price algorithm is an exact algorithm that could not solve more than 40–50 customers so far.
To use Solomon’s instances, we modify them. So, the solution to instances are routes with one trip. We need to adjust them for the multi-trip and different capacity use. We use 10 of 25 customers for the instance. Instances of type 1 that have a capacity of 200 for each vehicle now have a capacity of 50 per wagon. Instances of type 2 with a capacity of 1000 per vehicle have been modified with a capacity of 100 per wagon. The number of vehicles is limited to 10. The number of wagons is 45. A tour’s maximum number of routes is limited to three for these instances.
Experimental Results
The results of the branch and price algorithm are presented next. The program was implemented in the optimization programming language OPL, using ILOG CPLEX. CEDAR, the Compute Canada cluster, was used for experimentation, with a limit of 4 h on each solve and a maximum memory requirement of 40GB. Our algorithm was able to find optimal solutions for , , , and .
The results are in Table 4 where the column named Instances is the type of the instance. The gap is between the LP-relaxation value at the root and the optimal integer value in %. CPU time is calculated as differences between the time recorded at the root and the end of the algorithm in seconds. Obj is the total distance. Iter is the number of iterations used to solve by CPLEX. Cols is the number of columns generated during the branch and price algorithm. Node is the number of nodes explored in the search tree. The route is the max number of routes used in all tours. Tour is the number of tours used to visit customers.

Table 4.
Branch and Price for 10 Customers.
6.3. Analysis
The mathematical model was tested, and it can take hours, or days to give solutions with gaps of around 60%, this is why we need to use a method like a branch and a price, which is an exact method to have the optimal solution of the problem.
The mathematical model is a new one in that the mathematical test confirms the validation of the model and the branch and price test shows solving the model optimally. The branch and price algorithm solves the model for the small instances, but it gives the optimal solution for these instances that the model can not provide.
During experimentation, we notice that the algorithm explores more nodes if a similar capacity (one wagon) is used for all tours. Giving the algorithm the option to check more tours with two wagons and three before starting a new branch makes it faster and explores a smaller number of nodes. The number of added columns before starting a new branch increases when different capacities are used. Varying capacity can significantly affect the number of explored nodes. The upper bound that the CPLEX provides us is a good upper bound close to the optimal solution and it helps to explore fewer nodes and have a solution faster.
The algorithm solves type 2 instances where the time windows are more expansive on the horizon. It is faster and uses fewer iterations. For type C instances, branch and price could not find a solution to the time cut-off limit. All the instances listed in Table 4 were solved optimally within four hours.
We need to solve two resource constraints, the shortest path problem to determine a column with a negative reduced cost, and we need also to construct a route graph. The shortest path problem is solved using dynamic programming whose run time depends on the number of non-dominated paths which can be exponential. For large instances, this type of program run out of memory to store all the non-dominated paths. That is why we cannot solve large instances using column generation, as a part of future work we will look at other methods for solving the resource constraint shortest path problem.
7. Conclusions and Future Work
This work defines a new type of , multi-trip vehicle routing problem with a variable number of wagons and time windows. The problem is serving clients’ demands in a specific interval of time (time windows). At the same time, vehicles can make multiple daily trips, and the vehicle’s capacity can be set at the beginning of the day by adding up to three wagons for each vehicle. First, a mathematical model of the problem is developed, and then we develop a branch and price algorithm to solve the problem. The approach to solving the problem is column generation embedded in a branch and bound algorithm. We implemented the branch and price algorithm for -- on several Solomon’s instances to show the algorithm’s effectiveness. It can compute the optimal integer solution for limited customers.
We are interested in combining the column generation approach with metaheuristics to develop a faster solution for --. We will extend the model for split delivery with time windows, multiple wagons, and multiple trips per vehicle. The model can be extended to a multi-objective problem as well. In addition to these two types of the s, the model can be extended to other variants of the s. We can develop heuristic, exact and approximate approaches to solve the model.
Author Contributions
Conceptualization, L.K.; methodology, L.K.; software, validation, formal analysis L.K. and C.N.F.; writing—original draft preparation, L.K.; writing—review and editing, L.K. and C.N.F. All authors have read and agreed to the published version of the manuscript.
Funding
Funding support from NSERC, Canada, in the form of research assistantships, is gratefully acknowledged. Support for experimentation on a compute cluster from Compute Canada is also acknowledged.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Solomon’s (100 customers) instances for Euclidean VRPTW from https://www.sintef.no/projectweb/top/vrptw/100-customers/ (accessed on 20 August 2022) are modified to evaluate the model.
Acknowledgments
The authors would like to thank Robert Benkoczi and Daya Gaur for numerous discussions and helpful comments on a draft version of this manuscript.
Conflicts of Interest
There is no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VRP | Vehicle Routing Problem |
| VRPTW | Vehicle Routing Problem with Time Windows |
| MTVRP | Multi-trip vehicle routing problem |
| MTVRPTW | Multi-Trip Vehicle Routing Problem with Time Windows |
| MTVRP-VW-TW | Multi-trip VRP with a Variable number of Wagons and Time Windows |
| RMP | Restricted Master Problem |
| RLMP | LP-relaxation of RMP |
References
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Caric, T.; Gold, H. Vehicle Routing Problem; InTech: London, UK, 2008. [Google Scholar]
- Hernandez, F.; Feillet, D.; Giroudeau, R.; Naud, O. An exact method to solve the multitrip vehicle routing problem with time windows and limited duration. TRISTAN 2010, 7, 366–369. [Google Scholar]
- Azi, N.; Gendreau, M.; Potvin, J.Y. An exact algorithm for a vehicle routing problem with time windows and multiple use of vehicles. Eur. J. Oper. Res. 2010, 202, 756–763. [Google Scholar] [CrossRef]
- Petch, R.J.; Salhi, S. A multi-phase constructive heuristic for the vehicle routing problem with multiple trips. Discret. Appl. Math. 2003, 133, 69–92. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D.; González-Feliu, J. Vehicle routing problems for city logistics. EURO J. Transp. Logist. 2017, 6, 51–79. [Google Scholar] [CrossRef]
- Fleischmann, B. The Vehicle Routing Problem with Multiple Use of Vehicles. Ph.D. Thesis, Fachbereich Wirtschaftswissenschaften, Universität Hamburg, Hamburg, Germany, 1990. [Google Scholar]
- Taillard, É.D.; Laporte, G.; Gendreau, M. Vehicle routeing with multiple use of vehicles. J. Oper. Res. Soc. 1996, 47, 1065–1070. [Google Scholar] [CrossRef]
- Brandao, J.; Mercer, A. A tabu search algorithm for the multi-trip vehicle routing and scheduling problem. Eur. J. Oper. Res. 1997, 100, 180–191. [Google Scholar] [CrossRef]
- Brandão, J.C.S.; Mercer, A. The multi-trip vehicle routing problem. J. Oper. Res. Soc. 1998, 49, 799–805. [Google Scholar] [CrossRef]
- Nagy, G.; Salhi, S. The many-to-many location-routing problem. Top 1998, 6, 261–275. [Google Scholar] [CrossRef]
- Campbell, A.M.; Savelsbergh, M. Efficient insertion heuristics for vehicle routing and scheduling problems. Transp. Sci. 2004, 38, 369–378. [Google Scholar] [CrossRef]
- Salhi, S.; Petch, R. A GA based heuristic for the vehicle routing problem with multiple trips. J. Math. Model. Algorithms 2007, 6, 591–613. [Google Scholar] [CrossRef]
- Olivera, A.; Viera, O. Adaptive memory programming for the vehicle routing problem with multiple trips. Comput. Oper. Res. 2007, 34, 28–47. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D.; Vigo, D. An iterated local search for the multi-commodity multi-trip vehicle routing problem with time windows. Comput. Oper. Res. 2014, 51, 257–267. [Google Scholar] [CrossRef]
- Wassan, N.; Wassan, N.; Nagy, G.; Salhi, S. The multiple trip vehicle routing problem with backhauls: Formulation and a two-level variable neighbourhood search. Comput. Oper. Res. 2017, 78, 454–467. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Bakhsi, M.; Mahdavi, I. A robust multi-trip vehicle routing problem of perishable products with intermediate depots and time windows. Numer. Algebr. Control Optim. 2017, 7, 417–433. [Google Scholar] [CrossRef]
- Anggodo, Y.; Ariyani, A.; Ardi, M.; Mahmudy, W. Optimization of multi-trip vehicle routing problem with time windows using genetic algorithm. J. Environ. Eng. Sustain. Technol. 2017, 3, 92–97. [Google Scholar]
- Tirkolaee, E.B.; Hosseinabadi, A.A.R.; Soltani, M.; Sangaiah, A.K.; Wang, J. A hybrid genetic algorithm for multi-trip green capacitated arc routing problem in the scope of urban services. Sustainability 2018, 10, 1366. [Google Scholar] [CrossRef]
- Babaee Tirkolaee, E.; Abbasian, P.; Soltani, M.; Ghaffarian, S.A. Developing an applied algorithm for multi-trip vehicle routing problem with time windows in urban waste collection: A case study. Waste Manag. Res. 2019, 37, 4–13. [Google Scholar] [CrossRef]
- Chen, D.; Pan, S.; Chen, Q.; Liu, J. Vehicle routing problem of contactless joint distribution service during COVID-19 pandemic. Transp. Res. Interdiscip. Perspect. 2020, 8, 100233. [Google Scholar] [CrossRef]
- Zhen, L.; Ma, C.; Wang, K.; Xiao, L.; Zhang, W. Multi-depot multi-trip vehicle routing problem with time windows and release dates. Transp. Res. Part E Logist. Transp. Rev. 2020, 135, 101866. [Google Scholar] [CrossRef]
- Neira, D.A.; Aguayo, M.M.; De la Fuente, R.; Klapp, M.A. New compact integer programming formulations for the multi-trip vehicle routing problem with time windows. Comput. Ind. Eng. 2020, 144, 106399. [Google Scholar] [CrossRef]
- Desrochers, M.; Desrosiers, J.; Solomon, M. A new optimization algorithm for the vehicle routing problem with time windows. Oper. Res. 1992, 40, 342–354. [Google Scholar] [CrossRef]
- Halse, K. Modeling and Solving Complex Vehicle Routing Problems. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 1992. [Google Scholar]
- Kohl, N.; Madsen, O.B.G. An optimization algorithm for the vehicle routing problem with time windows based on Lagrangian relaxation. Oper. Res. 1997, 45, 395–406. [Google Scholar] [CrossRef]
- Kohl, N.; Desrosiers, J.; Madsen, O.B.; Solomon, M.M.; Soumis, F. 2-path cuts for the vehicle routing problem with time windows. Transp. Sci. 1999, 33, 101–116. [Google Scholar] [CrossRef]
- Larsen, J. Parallelization of the Vehicle Routing Problem with Time Windows; Citeseer: Lyngby, Denmark, 1999. [Google Scholar]
- Cook, W.; Rich, J.L. A Parallel Cutting-Plane Algorithm for the Vehicle Routing Problem with Time Windows; Technical Report; Rice University: Houston, TX, USA, 1999. [Google Scholar]
- Kallehauge, B.; Larsen, J.; Madsen, O.B. Lagrangean Duality and Non-Differentiable Optimization Applied on Routing with Time Windows-Experimental Results; Relatório interno IMM-REP-2000-8; Department of Mathematical Modeling, Technical University of Denmark: Lyngby, Denmark, 2000. [Google Scholar]
- Chabrier, A.; Danna, E.; Le Pape, C. Coopération entre génération de colonnes avec tournées sans cycle et recherche locale appliquée au routage de véhicules. In Proceedings of the Journées Nationales sur la Résolution Pratique de Problèmes NP-Complets, Nice, France, 27–29 May 2002; pp. 83–97. [Google Scholar]
- Feillet, D.; Dejax, P.; Gendreau, M.; Gueguen, C. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Netw. Int. J. 2004, 44, 216–229. [Google Scholar] [CrossRef]
- Rousseau, L.M.; Gendreau, M.; Pesant, G.; Focacci, F. Solving VRPTWs with constraint programming based column generation. Ann. Oper. Res. 2004, 130, 199–216. [Google Scholar] [CrossRef]
- Chabrier, A. Vehicle routing problem with elementary shortest path based column generation. Comput. Oper. Res. 2006, 33, 2972–2990. [Google Scholar] [CrossRef]
- Irnich, S.; Villeneuve, D. The shortest path problem with k-cycle elimination (k ≥ 3): Improving a branch and price algorithm for the VRPTW. INFORMS J. Comput. 2003, 10, 1–15. [Google Scholar]
- Danna, E.; Le Pape, C. Accelerating branch-and-price with local search: A case study on the vehicle routing problem with time windows. In Column Generation; Desaulniers, G., Desrosiers, J., Solomon, M.M., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2005; Charpter 3. [Google Scholar]
- Azi, N.; Gendreau, M.; Potvin, J.Y. An exact algorithm for a single-vehicle routing problem with time windows and multiple routes. Eur. J. Oper. Res. 2007, 178, 755–766. [Google Scholar] [CrossRef]
- Macedo, R.; Alves, C.; de Carvalho, J.V.; Clautiaux, F.; Hanafi, S. Solving the vehicle routing problem with time windows and multiple routes exactly using a pseudo-polynomial model. Eur. J. Oper. Res. 2011, 214, 536–545. [Google Scholar] [CrossRef]
- Munari, P.; Morabito, R. A branch-price-and-cut algorithm for the vehicle routing problem with time windows and multiple deliverymen. Top 2018, 26, 437–464. [Google Scholar] [CrossRef]
- Faiz, T.I.; Vogiatzis, C.; Noor-E-Alam, M. A column generation algorithm for vehicle scheduling and routing problems. Comput. Ind. Eng. 2019, 130, 222–236. [Google Scholar] [CrossRef]
- Seixas, M.P.; Mendes, A.B. A branch-and-price approach for a multi-trip vehicle routing problem with time windows and driver work hours. In Proceedings of the Congreso Latino-Iberoamericano de Investigación Operativa. Simpósio Brasileiro de Pesquisa Operacional, Rio de Janeiro, Brazil, 24–28 September 2012; pp. 3469–3480. [Google Scholar]
- Bettinelli, A.; Cacchiani, V.; Crainic, T.G.; Vigo, D. A branch-and-cut-and-price algorithm for the multi-trip separate pickup and delivery problem with time windows at customers and facilities. Eur. J. Oper. Res. 2019, 279, 824–839. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Dupas, R.; Deschamps, J.C. A branch-cut-and-price approach for the single-trip and multi-trip two-echelon vehicle routing problem with time windows. Transp. Sci. 2022. [Google Scholar] [CrossRef]
- Huang, N.; Li, J.; Zhu, W.; Qin, H. The multi-trip vehicle routing problem with time windows and unloading queue at depot. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102370. [Google Scholar] [CrossRef]
- Solomon’s Benchmark Instances. Available online: https://www.sintef.no/projectweb/top/vrptw/100-customers/ (accessed on 20 August 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).