Algorithm for Determining the Types of Inverse Kinematics Solutions for Sequential Planar Robots and Their Representation in the Configuration Space

Abstract

The work defines in a new way the different types of solutions of the inverse kinematics (IK) problem for planar robots with a serial topology and presents an algorithm for solving it. The developed algorithm allows the finding of solutions for a wide range of robots by using a geometric approach, representing points in a polar coordinate system. Inverse kinematics, which is one of the most important, most studied and challenging problems in robotics, aims to calculate the values of the joint variables, given the desired position and orientation of the robot’s end effector. Configuration space is defined by joint angles and is the basis of most motion planning algorithms. Areas in the working and configuration space are generated that are reachable with different types of solutions. Programs are created that use the proposed algorithm for robots with two and three rotational degrees of freedom, and graphically present the results in the workspace and configuration space. The possibility of transitioning from one type of solution to another by passing through a singular configuration is discussed. The results are important for planning motions in the workspace and configuration space, as well as for the design and kinematic analysis of robots.

1. Introduction

This paper presents an algorithm that examines the configuration spaces of planar serial robots and uses this information to classify inverse kinematics solutions. Examples are presented that show the benefit of dividing the workspace and configuration space into zones with different types of solutions. The algorithm is implemented in AutoCAD and can help visualize feasible trajectories. Advantages include finding solutions in singular positions and automatically generating the configuration space along with the workspace. Some limitations of the algorithm are that it is not applicable for real-time tasks and currently can be used only for serial and planar robots.

1.1. Literature Review

Serial robots are the most common industrial manipulators. They are designed as a series of links connected by motor-actuated joints that extend from a base to an end-effector. Robot kinematics deals with two types of problems—forward and inverse kinematics problems. For serial robots the forward kinematics problem is straightforward, and a single solution is easily found; the most popular method for the solution is proposed by Denavit and Hartenberg [1]. Inverse kinematics (IK) is a much more difficult problem than forward kinematics due to the presence of singularities and nonlinearities. Completely analytical solutions exist only for a small class of kinematically simple manipulators [2]. For many industrial robot designs, specific inverse kinematic solutions have been found using various algorithmic approaches that do not involve direct analytical solutions.

Deriving kinematic models for robots with a serial topology is essential for analyzing, researching and programming industrial robots. In [2], an analytical solution for a two-link robot is described, as well as for the basic structure of the Stanford Manipulator. The research in [3] investigates popular serial-structure mechanisms with two and three degrees of freedom, whose inverse kinematics permit closed-form analytical solutions. A Python program was developed for the serial-structure mechanisms. Geometric solutions of the inverse kinematics problem for robots with three and six rotational degrees of freedom are given in [4] and [5], respectively. The geometric approach is usually more intuitive and significantly reduces the complexity and time for calculations of the IK. However, it requires an individual approach to each different type of manipulator. In [6], a hybrid algorithm is proposed that combines the geometric method with an analytical one and is applied to an industrial robot PUMA 560. In [7], the inverse kinematics problem is solved with a reduced set of equations, an appropriate choice of the coordinate system associated with the end effector and an application of the principle of orthogonality in rotation. The approach does not require the calculation of the forward kinematics problem and can be used for manipulators with different geometries.

For redundant robots, determining analytically all solutions of the inverse kinematics problem is a very difficult task [8,9,10,11]. Despite the complexity, [8,9,10,11] contain several examples of finding solutions analytically. The Pioneer 2 robotic arm is a redundant robot with five degrees of freedom. The analytical equations for its inverse kinematics are derived in [8]. Article [9] presents solutions to the forward and inverse problems of a Power Cube 4-DOF redundant robot, using the Denavit and Hartenberg parameters, the law of cosines and the method of vector coordinates. It is shown that the different position and the change of an additional input variable have a significant influence on the robot configuration. The human hand is modeled as a redundant serial manipulator in [10]. The null space of the Jacobian matrix for the proposed model is determined. The results in [10] suggest that the redundancy in the human hand is used to reduce errors in trajectory and anisotropy arising from external disturbances. The authors of [11] propose a method for speeding up calculations in analytical and numerical methods for solving the inverse kinematics problem for a robot with seven degrees of freedom.

Numerical algorithms usually do not give all the solutions. In general, the choice of initial value and the searching algorithm have a big influence on the accuracy of their solution [6]. In [12], a numerical method for IK of serial robots is proposed which uses a dual quaternion formulation of kinematics in a converging paths algorithm. According to [12], the traditional algebraic, geometric and iterative methods are inadequate if the manipulator’s structure is more complex. As the complexity of the robot increases, the solution of the inverse kinematics problem requires more computational time. In [13], the ability of ANFIS (Adaptive Neuro-Fuzzy Inference System) to learn from training data is used to solve the inverse kinematics problem. Computer simulations are conducted for robots with two and three degrees of freedom that demonstrate the approach. Numerical methods based on inverse differential kinematics are effective in solving the inverse kinematics problem of robots with seven degrees of freedom with arbitrary geometric parameters. However, they offer insufficient numerical stability and take time to determine a unique solution. The research in [14] presents an approach that generates a general algorithm for a n-link planar hyper-redundant robot. This method repeatedly uses the solution of the inverse problem of a two-link robot on virtual joints, where the virtual joints are defined after a geometric proposal. In [15], Locally Recurrent Neural Networks (LRNNs) are used to solve the inverse kinematics problem. A MATLAB/Simulink simulation is presented for a manipulator with six degrees of freedom by computing the inverse kinematics with LRNN and applying complex motions. The authors of [16] present an analysis of the performance of different approaches for solving inverse kinematics with neural networks and the results are compared with the analytical approach. The main reason for using data-driven techniques such as neural networks to solve the inverse kinematics of robotic manipulators, is that it can be extended to any number of joints without much effort, while other methods have to consider the number of joints and the types of connections in advance. In [17], neural network training datasets, are created with a simulation software that uses a kinematic model of the robot. The solution of each neural network is evaluated using an analytical solution of the forward kinematics problem of the robot.

Cyclic Coordinate Descent (CCD) is a numerical method that uses only geometric considerations to derive subsequent iterations. The idea is to move each link independently, so as to minimize the error between the end-effector and the target by repeating this over all joints (repeating the process iteratively) [18,19]. This is a popular method for solving inverse kinematics that finds application in computer characters animation [18,20] and in robotics [19]. In [19], this method is combined with Newton’s method and applied with six different known robot manipulators. The CCD algorithm can be easily applied in robotics, but it can take a series of iterations before reaching a solution, and it can also generate incorrect joint rotations. The findings of [20] present an algorithm that uses a target triangle to determine the orientation and joint angles by eliminating the problems associated with incorrect and large angular rotations. The authors of [21] propose a method using the law of cosines that quickly determines the joint angles of a kinematic structure when the target is given. It combines an analytical with a numerical method.

The research in [22] proposes a model of a structured artificial neural network (ANN) and adaptive neural fuzzy inference system (ANFIS) in order to find the inverse kinematics solution of a robot. Since there is no unique inverse kinematics solution, predictive models are applied to the initial configuration. In general, IK is affected by an incorrect configuration of the links, which implies that the existence, uniqueness, and stability of its solutions are not guaranteed [23]. In [23], the authors demonstrate the effectiveness of applying network inversion with regularization, by which the incorrect positioning can be reduced. An example is given with a robotic arm with multiple joints.

1.2. Background and Related Work

The configuration space is an important concept used in motion planning algorithms. The main idea is to represent the robot as a point in a multidimensional space and to map the obstacles [24,25,26,27,28]. The concept is applicable to both mobile [24] and stationary robots [25,28]. A configuration of a stationary robot uniquely defines the mutual arrangement of its links. For this reason, this configuration is determined by the position of the controllable motors. The set of all configurations that a robot can occupy defines its configuration space. Each configuration of the robot in this space represents an n-dimensional point. Although tasks are formulated in real Cartesian space, in order for the robot to understand and execute them, they are translated in its configuration space. The movements of the robot are represented by the movement of a point in this space. A map is created with free regions and regions that are inadmissible due to collision with obstacles. The concept transforms the problem of planning the motion of a robot in an environment with obstacles (where the shape and dimensions of the robot and the obstacles must be considered) into a problem of planning the motion of a point in the robot’s free configuration space. Configuration space has played a crucial role in the development of many motion-planning algorithms for environments with obstacles [26]. Many applications in robotics, computer-aided design, and related fields can be reduced to computational problems with configuration spaces. In [24], two important challenges related to configuration spaces are addressed: how to efficiently compute an approximate representation of high-dimensional configuration spaces; and how to efficiently perform geometric proximity queries and motion planning in high-dimensional configuration spaces. Algorithms for building a configuration space, ones based on machine learning and geometric approximation techniques, are presented. The motion of a robotic arm in a rectangular tunnel and the corresponding configuration space are studied in [25]. Techniques from geometric group theory are used to find the optimal way to move the arm from one position to another. The authors of [26] propose a decomposition of the configuration space in order to check for collisions of the robot with an obstacle. The algorithm is implemented for a robot with seven degrees of freedom. The research in [27] presents a simple algorithm for approximating the free configuration space of robots with a small number of DOFs. Various approaches are applied to planning motions in the configuration space: network methods, Voronoi decomposition and artificial potential fields. In [28], a configuration space warping method and the classic Rapidly-exploring Random Tree (RRT) search method are compared in terms of their computation time and path length.

The methods for finding a solution to IK presented in [2,3,4,5,6,7,8,9,10,11] can be defined as analytical or analytically geometric. Works [12,13,14,15,16,17,18,19,20,21,22,23] present numerical methods for finding a solution to IK. Some of the presented works combine numerical, analytical and geometric approaches. Inverse kinematics is the basis for determining the configuration space of a robot. The investigations in [24,25,26,27,28] consider algorithms for generating a configuration space in the presence of obstacles, which is important for the proper implementation of robot control algorithms.

The analysis of redundant robots [9,10,11,12,13] shows that infinitely many IK solutions are possible for a single position and orientation of the end effector. For classic industrial robots such as [2,3,4,5,6,7,8], depending on their joint constraints, it is possible to have more than one solution to the inverse problem, as shown in [2]. In practice, the presented approaches for finding solutions [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], find only part of multiple possible solutions without classifying them. The problem of determining the configuration space is important for motion planning algorithms in complex environments [14,15,16,17,18]. Decomposition of the configuration space can be useful for generating motions and avoiding collisions with obstacles [27]. These conclusions are the main motivations for the present work.

Inverse kinematics has been studied extensively, with many available mathematical and algorithmic techniques. However, unlike forward kinematics, inverse kinematics cannot be solved with a closed-form expression (in general), i.e., cannot be described with a finite number of standard mathematical operations. This problem may have no solutions, multiple solutions, or even have an infinite number of solutions. As a result, the intricacies of the IK must be understood in order to apply it effectively in practice. These problems are clearly visible when looking at simple practical examples.

In [3], two types of solutions of the inverse problem are shown for a planar three-link robot with the same orientation of the end effector. These two solutions are called: Elbow up position and Elbow down position. Ref. [29] presents two analytical solutions for a SCARA-type robot. They are named “Left side solution” and “Right side solution” and are reported to be symmetric. Essentially, Refs. [3,29] highlight the same aspect—the non-uniqueness of IK solutions. A large part of the studies [2,4,5,6,7] unfortunately do not consider all possible solutions, but find only one of them. Thus, a better solution to a problem may be missed. For redundant IK robots, there are countless solutions. The same point from the workspace can be reached in different ways, i.e., with different types of configurations [9].

Almost all numerical methods [12,13,14,15,16,17,18,19,20,21,22] search for a sequence of solutions for IK starting from a previously known initial configuration and find only a part of the possible solutions. In practice, the initial configurations can be different in type and this can have a significant impact on the solution. This fact is taken into account in very few of the reviewed articles and algorithms. Ref. [23] reports the incorrect configurations for a certain task, performed by a multi-joint robotic arm.

The combination of joint angles for a particular position of the end effector may not exist, as shown in Figure 1a. Figure 1b shows an example where there are a number of combinations of joint angles ${\theta }_i$ that give the same solution, i.e., there is no unique solution. If the target point requires a near-singular robot configuration, joint angle estimation is difficult (Figure 1c; then the solution is unstable [23]. When multiple solutions exist, none of the IK approaches specify which solution is “the best”. It is also important to note that many of the solutions found with IK techniques may be unfeasible. For example, IK solutions may fall outside the joint constraints, cause the robot to collide with itself, or make the robot encounter obstacles from the environment. The requirement to produce high-quality solutions can be considered a soft constraint, while requirements such as joint constraints and obstacles in the work area are considered hard constraints. Soft constraints can be expressed as a demand of an IK solution that minimizes some scalar function. To deal with soft constraints, in the analytical case, where multiple solutions exist, one can simply go through all solutions. Hard constraints in the case of an analytical solution can only be checked after all solutions have been found. In the numerical case, it is preferable to use solution techniques that account for these additional constraints.

The configuration space is a key concept for planning robot movements in an environment with obstacles. This is a space defined by the joint angles. The robot is represented as a point in the configuration space [24], which is extremely convenient for path planning. A big challenge in inverse kinematics is that the mapping from configuration space to workspace and back (which happens with both IK and the forward kinematic problem) is non-linear. This means that straight lines in the joint space are converted to curves in the workspace and vice versa. To some extent, the present work is a continuation, complement and generalization of concepts for solving the inverse kinematics problem, [30,31,32] for a specific redundant 3D printed robot. The proposed algorithm uses ideas presented in [23,30] and develops them to account for the solution types of the inverse problem and the joint constraints of a multi-link robot. The concept of solution types in the presence of joint constraints for a particular robot is presented in [31]. The solutions are divided into left-L and right-R, depending on whether the joint angles ${\theta }_2$ and ${\theta }_3$ are positive or negative.

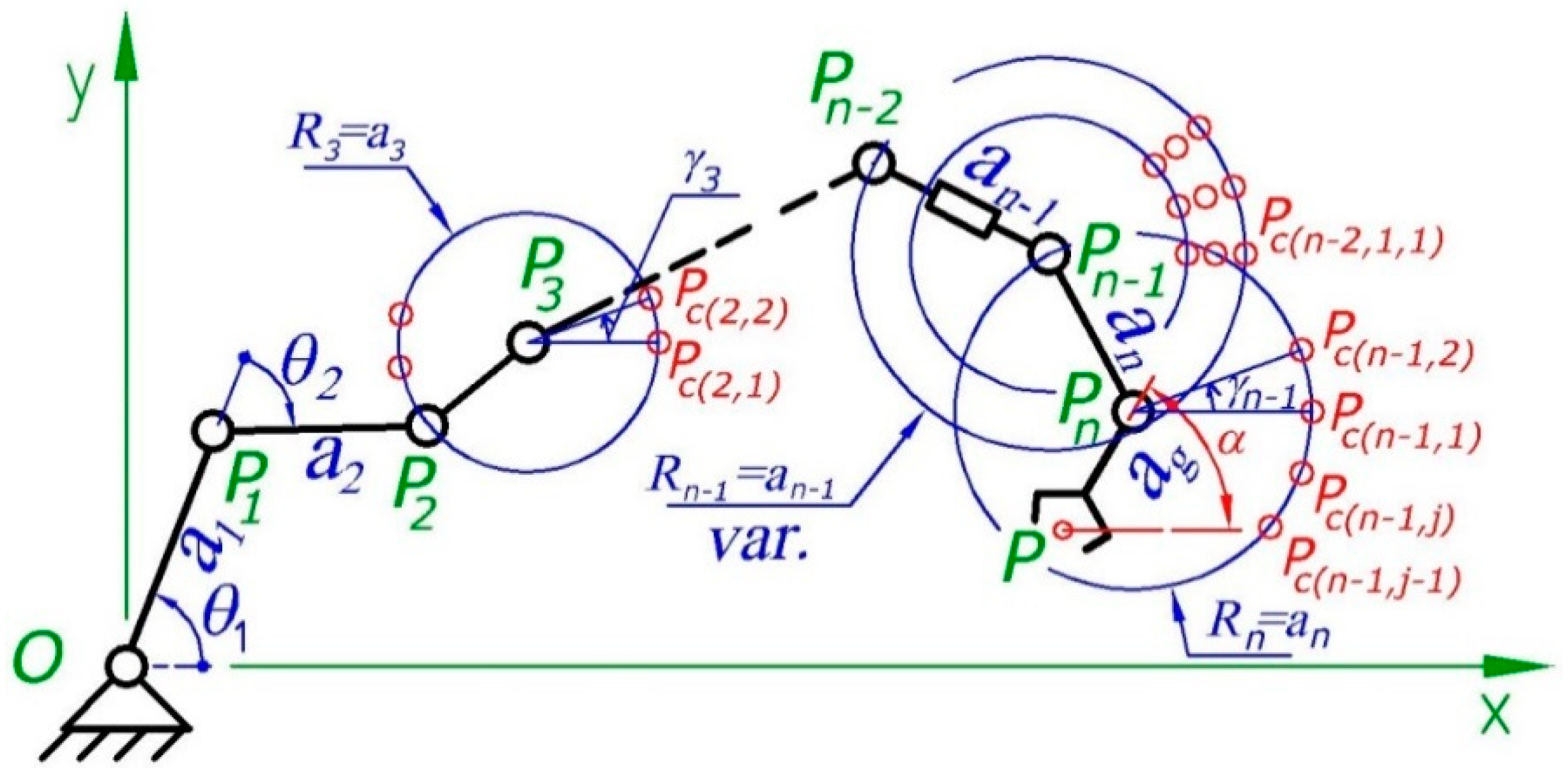
2. Definitions and Conditions for the Solution Types

Many of the stationary robots can be represented as planar [1,13]. For others, the spatial motions are obtained after rotation or translation of a planar mechanism [29], which means that the study of planar robots is important. Still, the preponderance of robots mainly use rotational and translational joints, and a planar mechanism with a serial topology can be schematically represented as in Figure 2a. Here, the axes of the rotational joints are marked with green letters $O, P_1, P_2, \dots P_n$ the center of the gripper with P, and the lengths of the links with $a_i$. The length of the gripper with $a_g$.

The axis of a translational joint can pass through the axes of two adjacent rotational joints, such as between points $P_1$ and $P_2$, or be arbitrarily located relative to adjacent rotations, such as the translation located between $P_{k-1}$ and $P_k.$ However, for both cases it can be said that the main effect of the translations is to change the distance $a_k$ between their neighboring rotations. Similar considerations can be made even for cases where there are several translations located between two rotational joints. For these reasons, in our further reasoning, it is used a simplified equivalent model of a planar serial robot, one which uses only rotational joints, and where there are translations, the effect is reflected with a variable length of the link-$var. a_k$ Thus, three definitions are introduced for an n-link robot, which can be represented as shown in Figure 2b.

Definition 1.

Right-hand relative configuration of two adjacent links (for example $a_k$and $a_{k+1}$) of the robot is called such a configuration, for which the relative angle ${\theta }_{kR}$, between the two links, is within the range:

$$0\pm 2i\pi <{\theta }_{kR}<\pi \pm 2i\pi ; i=0,1,2,3,\dots ,n.$$

(1)

Such configuration is denoted with R (Figure 3a).

For example: Usually the angles of rotation of the links, relative to each other, are less than a full revolution. Then, if the joint constraints of joint k are in the interval $0<{\theta }_{kR}<\pi$, the configuration is right-hand, and it can be said that the angle ${\theta }_{kR}$ is positive for a right-hand relative configuration of the two adjacent links. If a person bends their right arm, their shoulder and forearm will assume a right-hand configuration.

Definition 2.

Left-hand relative configuration of two adjacent links (for example $a_k$and $a_{k+1}$) of a robot is called such a configuration, for which the relative angle ${\theta }_{kL}$between the two links is within the range:

$$-\pi \pm 2i\pi <{\theta }_{kL}<0\pm 2i\pi ; i=0,1,2,3,\dots ,n.$$

(2)

Such configuration is denoted with L (Figure 4a).

Definition 3.

Relative singularity configuration ${\theta }_{ks}$, between two adjacent links of a robot, is called such a configuration, which cannot be presented, neither as right-hand, nor as left-hand. For this type, angle ${\theta }_k$between the two links ($a_k$and $a_{k+1}$) is equal to 0 or $\pi \left[rad\right]$, i.e.,: ${\theta }_{ks}=0; \pm \pi ;\pm 2\pi ;\pm 3\pi ;\dots$

The relative singularity configurations between two links are denoted with $S_0$if ${\theta }_{ks}=0; \pm 2\pi ;\pm 4\pi ;\pm 6\pi ;\dots$—fully stretched hand, and with $S_{\pi }$if ${\theta }_{ks}=\pi ; \pm 3\pi ;\pm 5\pi ;\pm 7\pi ;\dots$—fully folded hand.

Property 1.—Symmetry.

If $P_{k-1}$and $P_{k+1}$are two points in the plane where the axes k − 1 and k + 1 of the robot are located, the lengths of the links are respectively $a_k=const\ne 0$, $a_{k+1}=const\ne 0$and the existence of left- and right-handed solutions for both links is possible, then these two configurations for the links are symmetric with respect to a line passing through points $P_{k-1}$and $P_{k+1}$, and the angles ${\theta }_{kR}$and ${\theta }_{kL}$are equal in magnitude and have opposite signs i.e., ${\theta }_{kR}=-{\theta }_{kL}$(Figure 5).

This property can easily be proved using the equality of triangles $∆P_{k-1}{P}_{kR}{P}_{k+1}\equiv ∆P_{k-1}{P}_{kL}{P}_{k+1}$.

Property 2.—Uniqueness.

If the distance d between the two points $P_{k-1}$and $P_{k+1}$is

$$d_{P_{k-1}, P_{k+1}}=\left|\sqrt{{\left(P_{k+1,x}-P_{k-1,x}\right)}^2+{\left(P_{k+1,y}-P_{k-1,y}\right)}^2}\right|=a_k+a_{k+1}$$

(3)

or

$$d_{P_{k-1}, P_{k+1}}=\left|\sqrt{{\left(P_{k+1,x}-P_{k-1,x}\right)}^2+{\left(P_{k+1,y}-P_{k-1,y}\right)}^2}\right|=\left|a_k-a_{k+1}\right|$$

(4)

Then these two points ($P_{k-1}$and $P_{k+1}$) are reached by the axes of rotation for the two adjacent links with only one single configuration, which is neither left nor right, i.e., it is a relative singular configuration.

Although this can be proven geometrically, here the property is explained from a robotics perspective using the Jacobian matrix. If we imagine that the position of a rotational joint $P_{k-1}$ is fixed and consider only part of the robot, represented by the links $a_k$ and $a_{k+1}$, a well-studied structure of a two-link robot [2] is obtained, whose Jacobian matrix J has the form:

$$J=\left[\begin{array}{cc}-a_{k}sin\left({\theta }_{k-1}\right)-a_{k+1}sin\left({\theta }_{k-1}+{\theta }_k\right)& -a_{k+1}\sin \left({\theta }_{k-1}+{\theta }_k\right)\\ a_{k}cos\left({\theta }_{k-1}\right)+a_{k+1}cos\left({\theta }_{k-1}+{\theta }_k\right)& a_{k+1}\cos \left({\theta }_{k-1}+{\theta }_k\right)\end{array}\right]$$

(5)

The determinant of the Jacobian matrix is

$$\det \left(J\right)=a_k{a}_{k+1}sin\left({\theta }_k\right)$$

(6)

Since the lengths of the links are $a_k\ne 0$ and $a_{k+1}\ne 0$ then $\det \left(J\right)$ becomes 0 for ${\theta }_k=0; \pm \pi ;\pm 2\pi ;\pm 3\pi ;\dots$ a correspondence is then obtained between the generally accepted notion of singularity of a robot and the introduced relative singularity configuration between its two adjacent links. Transition of links $a_k$ and $a_{k+1}$ from left to right-hand configuration or vice versa is possible only by passing through a relative singularity configuration. When the robot has joint constraints and/or obstacles in its workspace, situations are possible for which there are different types of solutions, but the transition between them cannot be realized. This fact is important for planning robot movements.

We are looking for an algorithm to find the inverse kinematics of a planar robot that can be represented by the equivalent diagram from Figure 2b, and it is necessary to determine the type of solutions according to definitions 1 to 3 and take into account the joint constraints. As an addition, it can be checked for collisions of the robot links with obstacles. For the implementation of the algorithm to make sense, the robot must have at least two rotational joints. The solution to this problem is useful for the following purposes:

-

Detect and classify multiple inverse kinematics solutions for a single position and orientation of the gripper;

-

Generate IK solutions for a planar trajectory in the workspace with or without changing the gripper orientation;

-

Generate the configuration space and regions of it corresponding to Definitions 1–3;

-

Generate the workspace and regions of it corresponding to Definitions 1–3.

3. Materials and Methods

Consider the problem of finding the inverse kinematics at a fixed position P and orientation of the gripper at angle α (Figure 6). The algorithm for finding IK, taking into account the types of solutions, is based on the following main idea: Searching for a solution from the gripper to the base of the robot.

IK seeks an answer to the question of what joint coordinates the robot must have, in order for the gripper to reach a certain known position and orientation. Then, if a robot can be presented with an equivalent structural diagram, such as Figure 2b, the coordinates of point $P_n$, which is the axis of rotational joint n, are easily determined. The set of points $P_{c\left(n-1,j\right)}$ (j = 1, 2, …, k), that the axis $P_{n-1}$ of the n − 1th rotational link could reach, will lie on a circle with center $P_n$ and radius $R_n=a_n$—the length of link n. Therefore, if the rest of the robot can reach any of these points, there will be a solution for IK. Similar considerations can be applied to determine which points can be reached by the axes $P_{n-2}$,$P_{n-3}$,$P_{n-4}$, …. until a potential set of points $P_{c\left(3,j\right)}$ is obtained, which will belong to a circle with center $P_3$ and radius $R_3=a_3$ (Figure 6). Thus, a two-link mechanism ($a_1, a_2$) is obtained, for which IK is well known. Therefore, it is necessary to check whether point $P_{c\left(3,j\right)}$ is a solution of IK. If it is, the configuration is saved as a possible solution. It is necessary to create several nested loops to generate the set of points to be tested in sequence. In the event that the robot has a translational joint (for example, link $a_{n-2}$ from Figure 6) it is necessary to vary the corresponding radius, for example $R_{n-1}$ as shown in Figure 6. The structure of the algorithm is given in Figure 7.

Step 1. Input data.

The number of rotational joints n is known. Input: The lengths of the links $a_i$ (if there are translational connections, it is necessary to determine the change of the corresponding lengths $a_{kmin}\le a_k\le a_{kmax}$); The joint constraints ${\theta }_{imin}\le {\theta }_i\le {\theta }_{imax}$ of the rotational joints; The coordinates $P_x$ and $P_y$ of point P from the gripper; If it is necessary to take into account the orientation of the gripper, the angle α is entered, otherwise it is assumed that point $P_n\equiv P$.

Step 2. Determining point $P_n$.

If angle α is set, the coordinates of point $P_n$ are:

$$\left|\begin{array}{c}{P}_{nx}=P_x+a_{g}cos\alpha \\ P_{ny}=P_y+a_{g}sin\alpha \end{array}\right.$$

(7)

Step 3. Checking if point $P_n$ is reachable

Reachability is a problem that depends on the lengths of the links, i.e., the proportions between them and the joint constraints. It is assumed that initially no joint restrictions are imposed and the problem is divided into two parts: maximally distant points—external reachability limit—and points that cannot be reached with folded links—internal reachability limit (Figure 8). The condition for external reachability to point P_n can be intuitively determined:

$$\sqrt{P_{nx}^2+P_{ny}^2}\le R={{\displaystyle \sum }}_{i=1}^n{a}_i+a_g$$

(8)

Point $P_n$ is reachable if inequality (8) is satisfied. Here, $P_{nx}^{}$ and $P_{ny}^{}$ are the coordinates of a point $P_n$, that the robot is trying to reach. This inequality (8) defines a circle with center at the base of the robot and radius R.

The second condition—of internal reachability—is more complicated to define. If the longest link $a_{imax}$ is shorter than the sum of all other links and no joint constraints are imposed, all points of the circle with radius R (8) are reachable. An inner circle centered at the base of the robot, which is not reachable, appears if $a_{imax}$ is longer than the sum of all other links (Figure 8). The radius r of this circle is calculated from:

$$\sqrt{P_{nx}^2+P_{ny}^2}\ge r=a_{imax}-{{\displaystyle \sum }}_{i=1}^n{a}_i+a_g$$

(9)

In this case, point $P_n$ is reachable if inequalities (8) and (9) are satisfied.

In this step, a check can also be performed for a unique solution, which occurs if $P_n$ lies on a circle defined by Equations (8) or (9).

Step 4. Setting the number and distribution of points on the circles.

The number of circles for which points must be generated depends on the number n of robot links. It also determines the number of nested loops. Thus, if there are no translational connections, the number of nested loops k will be:

$$k=n-2$$

(10)

Since it is not necessary to rotate the gripper and the first two links of the robot.

The number of points and the manner of their distribution on the generated circles is set. A simple option is to set evenly distributed points along the circle. The number of points increases the precision of the algorithm, but also increases the calculations and the time for its execution.

Step 5. Nested loops for defining points of interest.

Points $P_{c\left(i,j\right)}$, belonging to a circle with center $P_i$ and radius $R_i=a_i$, are defined. In the algorithm given in Figure 7 this is done using polar coordinates and increasing the angle γ (see Figure 6). Syntax from Visual LISP for AutoCAD is used, which has built-in functions for working with geometric objects. For example, the function {polar < point angle distance>} defines a new point relative to a previous one using polar coordinates. This step only defines the idea of generating multiple points, located on a circle, using nested loops without limiting how they are obtained. Depending on the programming language used, the implementation can be adapted accordingly.

Step 6. Solution of the inverse kinematics problem for the two-link mechanism.

Finding solutions for a two-link mechanism is a classic problem that has been studied in numerous books and articles. However, most articles do not consider all possible solutions [2,4,5]. Figure 9 shows a block diagram of the complete algorithm that determines the type of IK solution for a two-link mechanism, according to Definitions 1–3. $d_{O, P_2}=\left|\sqrt{{\left(P_{2x}-O_x\right)}^2+{\left(P_{2y}-O_y\right)}^2}\right|$ is the distance between points O and $P_2$. It is assumed that the base is located at point O(0,0) which is in the origin of a fixed coordinate system.

The block “Compute two solutions” (from Figure 9) can be done in different ways. Appendix A presents a geometric solution that uses built-in functions of Visual Lisp for AutoCAD and avoids trigonometric functions. The idea boils down to determining the intersection points ($P_{1R}$ and $P_{1L}$) of two circles with radii $R_1=a_1$ and $R_2=a_2$, located according to Figure 10. First the distance $L=\overline{O{P}_2}$ between points O and $P_2$ is determined. From the law of cosines, it follows:

$$a_2^2=a_1^2+L^2-2a_{1}Lcos\left(\beta \right)$$

(11)

Distance $\overline{O{P}_h}=t=$ $a_{1}cos\left(\beta \right)$ and, considering (11), for t it follows that:

$$t=\frac{a_1^2+L^2-a_2^2}{2L}$$

(12)

The height $h=\overline{P_h{P}_{1R}}=\overline{P_h{P}_{1L}}$ is found from the Pythagorean theorem.

$$h=\sqrt{a_1^2-t^2}$$

(13)

Using the Visual LISP commands Polar and Angle, the points $P_{1R}$ and $P_{1L}$ are found. The Angle command allows you to determine the angle of inclination of a segment, defined by two points (see Appendix A).

Step 7. Check for joint constraints and configuration type.

After performing step 6, two configurations $q_{1L}={\left[{\theta }_{1L},{\theta }_{2L},{\theta }_3,{\theta }_4\dots \right]}^T$ and $q_{1R}={\left[{\theta }_{1R},{\theta }_{2R},{\theta }_3,{\theta }_4\dots \right]}^T$ are obtained, which claim to be an IK solution. We note that the angles ${\theta }_i$ are relative, i.e., are measured with respect to the axis of the previous link in a counter-clockwise direction. Thus, depending on definition 1 to 3, the remaining joint angles ${\theta }_3,{\theta }_4\dots$ can also be classified by assigning them indices L, R, $S_o$ or $S_{\pi }$.

A check is made to see if the joint angles fall within the permissible limits. As a result, one or both solutions can be rejected or accepted. Here it can also be checked for collision with an obstacle and self-collision of the robot links, if necessary. The type of configuration is taken into account and the angles ${\theta }_i$ of the approved solutions are recorded. Defining collisions between bodies is a separate topic that is beyond the scope of this work. Thus, after executing one cycle of the algorithm, one of the following results is obtained:

-

The reviewed configuration is not an IK solution.

-

There is only one solution, classified according to definitions 1, 2 and 3; for example: $q_{1L}={\left[{\theta }_{1L},{\theta }_{2L},{\theta }_{3R},{\theta }_{4L}, {\theta }_{5s0}\dots \right]}^T$.

-

There are two solutions, classified according to definitions 1, 2 and 3; for example: $q_{1L}={\left[{\theta }_{1L},{\theta }_{2L},{\theta }_{3R},{\theta }_{4L}\dots \right]}^T$ and $q_{1R}={\left[{\theta }_{1R},{\theta }_{2R},{\theta }_{3R},{\theta }_{4L},{\theta }_{5s\pi }\dots \right]}^T$.

After executing the entire program for one position and orientation of the gripper, a set of classified configurations is determined, which is the solution to the inverse kinematics problem.

4. Results

4.1. Example 1

Figure 11a shows a 3D printed model of a SCARA type robot. Its structure consists of two links and a base connected by rotational joints, so that the main movements take place in the plane. We are not interested in the vertical translation at this stage. The lengths of the links are respectively $a_1=0.15\left[\mathrm{m}\right]; a_2=0.1\left[\mathrm{m}\right];$ and the joint constraints are: $-\frac{\pi }{2}\le {\theta }_1\le \frac{\pi }{2};-\pi \le {\theta }_2\le \frac{\pi }{2}$ [rad].

Figure 11b shows the left $U_L$ and right $U_R$ hand reachability zones for this robot. The union of these two areas represents the robot’s workspace:

$$w=U_L\cup U_R$$

(14)

Section f represents a region where both left-handed and right-handed solutions can exist.

$$f=U_L\cap U_R$$

(15)

There is an area $f_L$, the points from which can only be reached with left-hand configuration:

$$f_L=w-U_R$$

(16)

And area $f_R$ which is reachable only with right-hand configuration:

$$f_R=w-U_L$$

(17)

Of course, $w=f_L\cup f_R\cup f$ Figure 12 (right) illustrates those areas in Cartesian space.

Figure 12 (left) shows a graphical representation of the configuration space. What happens at the boundaries of the configuration space, and when ${\theta }_2=0$?

The solution of the forward problem in this case is simple. The coordinates of point P are determined (see Figure 11 on the right):

$$\left|\begin{array}{c}{x}_p=a_1\cos \left({\theta }_1\right)+a_2\cos \left({\theta }_1+{\theta }_2\right)\\ y_p=a_1\sin \left({\theta }_1\right)+a_2\sin \left({\theta }_1+{\theta }_2\right)\end{array}\right.$$

(18)

When ${\theta }_2=0$ and ${\theta }_2=-\pi$ are obtained for points from the configuration space that belong to lines in this space (the red horizontal lines in Figure 12, left), they are transformed into points of circles in the real space (the red arcs on the right of Figure 12). We can verify this from the analytic dependencies as well. Indeed, from (18), for ${\theta }_2=0$ it follows:

$$\left|\begin{array}{c}{x}_p=\left(a_1+a_2\right)\cos \left({\theta }_1\right)\\ y_p=\left(a_1+a_2\right)\sin \left({\theta }_1\right)\end{array}\right.$$

(19)

After raising to the second degree and summing the two equations from system (19) it is obtained:

$${\mathrm{x}}_{\mathrm{p}}^2+{\mathrm{y}}_{\mathrm{p}}^2={\left(a_1+a_2\right)}^2\left(\sin {\left({\theta }_1\right)}^2+\cos {\left({\theta }_1\right)}^2\right)$$

(20)

or

$${\mathrm{x}}_{\mathrm{p}}^2+{\mathrm{y}}_{\mathrm{p}}^2={\left({\mathrm{a}}_1+{\mathrm{a}}_2\right)}^2$$

(21)

This is an equation of a circle with radius $R=\left(a_1+a_2\right)$ and center (0,0).

When ${\theta }_2=-\pi$, following similar considerations, it is obtained:

$${\mathrm{x}}_{\mathrm{p}}^2+{\mathrm{y}}_{\mathrm{p}}^2={\left({\mathrm{a}}_1-{\mathrm{a}}_2\right)}^2$$

(22)

This is an equation of a circle with radius $R=\left(a_1-a_2\right)$. Not all points from these red circles (Figure 12-right) are fully reachable by the robot due to the joint constraints. The points from these arcs can be reached with only one singular configuration of the robot, which means that there exists only one unique solution to both the forward and the inverse kinematics problems. In this case the arm is either fully extended or the links overlap one another.

Let us now investigate what happens to the points from the configuration space that lie on the line ${\theta }_1=\frac{\pi }{2}$. From (19) it follows that:

$$\left|\begin{array}{c}{x}_p=a_2\cos \left({\theta }_2+\frac{\pi }{2}\right)\\ y_p=a_1+a_2\sin \left({\theta }_2+\frac{\pi }{2}\right)\end{array}\right.$$

(23)

Analogously, it is obtained an equation of a circle:

$$x_p^2+{\left(y_p-a_1\right)}^2=a_2^2$$

(24)

Similarly for ${\theta }_1=-\frac{\pi }{2}$, it follows:

$$x_p^2+{\left(y_p+a_1\right)}^2=a_2^2$$

(25)

These circles correspond to the blue arcs on Figure 12 (right), and are on the boundaries of the workspace. Similarly, the equation of the green arc can be determined, which serves as the boundary of solutions with right-hand configurations.

Since the workspace of the robot is divided into areas where point P can be reached in two ways (left and right-hand—f) and those reachable with only one type of solution ($f_R$ and $f_L$), the configuration space should also be divided in a similar way. The algorithm from Figure 9 and Appendix A are used to find IK solutions.

For a point $P\left(180\left[\mathrm{m}\mathrm{m}\right],120\left[\mathrm{m}\mathrm{m}\right]\right)$ (Figure 11, right), two solutions of the inverse problem are found: for the left-hand it is obtained $q_R\left(1.06\left[\mathrm{r}\mathrm{a}\mathrm{d}\right],-1.07\left[\mathrm{r}\mathrm{a}\mathrm{d}\right]\right)$ and for the right-hand $q_L\left(0.17\left[\mathrm{r}\mathrm{a}\mathrm{d}\right],1.07\left[\mathrm{r}\mathrm{a}\mathrm{d}\right]\right)$ respectively. The result is presented graphically in Figure 12.

Using the proposed algorithm, multiple solutions are found for the inverse kinematics from the robot’s workspace. Using polar coordinates, a set of points, located in the reachable zone according to Figure 8, is generated. The results are given in Figure 13.

The algorithm removes the points outside the joint constraints. The solutions that are only possible with the left-hand (L) are depicted with small blue circles; those of type R are magenta; and where both types of solutions are possible, they are represented with green circles. Thus, the solution of the inverse problem yields a region q(ABCDEF) in the configuration space, inside which both left and right-handed solutions are possible. It can be noted that AB is a vertical segment, BC is a horizontal segment, CD is a curved line, DE is a vertical segment, EF is a horizontal segment and FA is again a curved line. Areas from the workspace are transformed into the configuration space, respectively:

$$\left|\begin{array}{c}{f}_L\stackrel{IK}{\to }{q}_L\\ f\stackrel{IK}{\to }q\\ f_R\stackrel{IK}{\to }{q}_R\end{array}\right.$$

(26)

In Figure 13 (right) two trajectories $t_1$ and $t_2$ are given, which connect point $P_1\in f_L$ with point $P_2\in f_R$. Both trajectories fall entirely within the robot’s workspace. Using the algorithm, points from $t_1$ and $t_2$ are transformed into the configuration space.

Trajectory $t_1$ is an arc of a circle with radius R = 90 [mm] and center (x = 60 [mm], y = 116 [mm]). Each point of this arc corresponds to two solutions in the configuration space, which form two red curves $q_{t1L}$ and $q_{t1R}$. Parts of these two curves go outside the joint constraints.

The trajectory $t_2$ is a spline that passes through point $P_3$, which lies on the boundary of the workspace. Each point from $t_2$ corresponds to two points in the configuration space except point $P_3$, for which there is only one solution because it is reached with a singularity configuration of type $S_0$. The two curves in which $t_2$ is transformed are given in green—$q_{t2p}$ and blue—$q_{t2i}$ color, respectively.

After solving the IK, point $P_1$ is transformed into two points $q_{P1L}$ and $q_{P1R}$ in the configuration space, where $q_{P1R}$ is outside the joint constraints (not defined).

Point $P_2$ is transformed into two points $q_{P2L}$ and $q_{P2R}$ in the configuration space, where $q_{P2L}$ is outside the joint constraints (not defined).

Point $P_3$ is transformed into a single point $q_{P3}$, which lies on the axis ${\theta }_1$. At this point, the curves $q_{t2p}$ and $q_{t2i}$ intersect. It can be said that each of the two trajectories $t_1$ and $t_2$ from the workspace is transformed into two trajectories in the configuration space, and only one of them $q_{t2p}$ (in green) falls entirely within the joint constraints of the robot.

4.2. Example 2

Figure 14 shows a 3D printed model of a redundant robot with 4 parallel axes of rotation.

The main movements take place in the plane. The rotation ${\theta }_4$ is used to change the orientation of the gripper, and ${\theta }_1, {\theta }_2, {\theta }_3$ to define its position. Here, only the gripper position is of interest and the configuration space is considered as three-dimensional. The dimensions and joint constraints of the robot are given in Figure 15a.

Octants and Types of Solutions in the Configuration Space

The joint angles ${\theta }_1, {\theta }_2, {\theta }_3$ are independently controllable, defining three mutually perpendicular axes and planes that define a three-dimensional configuration space. The three coordinate planes divide space into eight parts, and each part is known as an octant. In Figure 14c, the octants are marked with Roman numerals. The sign of the coordinates of a point in this space depends on the octant in which it is located. If the rotational joints are rotated by an angle $-\pi <{\theta }_i<\pi$, each different type of solution will fall into a precisely defined octant. The angle ${\theta }_1$ does not affect the solution type, therefore one solution type can fall into two adjacent octants.

Table 1. Decision types and octants in the robot’s configuration space.

Solution Type $\to$	RR		LR		RL		LL
Octants $\to$ Coordinates $\downarrow$	I	II	III	IV	V	VI	VII	VIII
${\theta }_1$	+	-	-	+	+	-	-	+
${\theta }_2$	+	+	-	-	+	+	-	-
${\theta }_3$	+	+	+	+	-	-	-	-

presents the signs of the coordinates of the joint angles and the solution types according to the octants.

Relative singularity configuration types are easier to define in the configuration space. The parameter ${\theta }_2=0$ means that the singularity configurations $S_{0,2}$ fall in the coordinate plane determined by the axes ${\theta }_1$ and ${\theta }_3$, and ${\theta }_3=0$ sets $S_{0,3}$ in the plane $O,{\theta }_1,{\theta }_2$ (see Figure 14c).

Using the proposed algorithm, a Visual LISP for AutoCAD program is created to determine IK solutions and divide them into types. The program runs in AutoCAD and uses dialog boxes to set the input parameters. The results are presented in the AutoCAD model space.

In the “Geometric Parameters” dialog box, Figure 15a, the lengths of the robot’s links are set, as well as the joint constraints. This is where the scope of the solution is determined, either to find a single point, to find multiple points from a segment or arc, or to define the robot’s workspace. If the “Include obstacles” option is selected, the program will check for collisions with obstacles. To define the workspace, multiple points are generated in polar coordinates. They are entered with the dialog window “Positions of end effector” (Figure 15b). The last line “Number of radial points 2” sets the number of points at which link $a_3$ will be rotated according to the algorithm. The result, based on the parameters set by the dialog windows, is given in Figure 15c. The types of solutions are represented with small circles placed in different layers with different diameter and color. For clarity, Figure 16 shows the individual types of solutions separately.

If the cross-section of these four main types of solutions (singularity configurations are not taken into account for now) is plotted, 10 regions numbered from 1 to 10 and given in Figure 17 are obtained. Since the resulting type map is symmetrical, the areas 1 through 6 are examined in more detail.

The “Point” option from the “Geometric parameters” dialog box (Figure 15a is used to find solutions for point P from the corresponding regions. The program calculates and draws multiple configurations in the workspace, as well as the corresponding points in the configuration space (Figure 18). Since ${\theta }_1$ does not influence the solution type, the configuration space is represented in the plane $O,{\theta }_2,{\theta }_3$.

Region 1—only RR type configurations are possible (illustrated in Figure 18). These solutions fall into the first and second octants of the configuration space. In the symmetric region 10, there will be only LL solutions. Regions 1 and 10 are obtained by subtracting the solution set RR from LL, or vice versa (LL-RR)—see Figure 16.

Region 2—there are both RR and RL types of solutions.

Region 3—solution types are distributed across LR, RR and RL.

Region 4—solution types are distributed across LL, RR and RL.

Region 5—there are only symmetric solutions: LL and RR.

Region 6—all types of solutions are possible.

Determining the regions for which it is possible to have a relative singularity configuration, it is easier if the forward kinematics problem is used. Since either ${\theta }_2=0=const$ or ${\theta }_3=0=const$, the mechanism can be considered as a two-link, which significantly simplifies the task. Considerations from Example 1 are used and the areas given in Figure 19 are obtained.

In the configuration space, these are part of the coordinate planes—$O, {\theta }_1, {\theta }_3$ for relative singularity configurations of type $S_{0,2}$ and plane—$O, {\theta }_1, {\theta }_2$ for type $S_{0,3}$, determined by joint constraints.

When both ${\theta }_2=0$ and ${\theta }_3=0,$ the whole robot is in a singularity configuration, i.e., $\det \left(J\right)=0$ and the possible positions in the workspace are on the red arc in Figure 19, right. These singular configurations (${\theta }_2=0$ and ${\theta }_3=0$) are presented as a segment ($-\frac{\pi }{2}\le {\theta }_1\le \frac{\pi }{2}$) along the ${\theta }_1$ axis, see Figure 14 on the right. Note that this line is an exact intersection of the relative singularity planes $S_{0,2}$ and $S_{0,3}$.

5. Discussion

5.1. Discussion of Definitions

The introduced Definitions 1–3 exhaust the possible cases of searching for different IK solutions for robots with the structure from Figure 2b and clarify what is meant by a type of solution. Singularity configurations of the robot prevent it from realizing some movements. They depend on the number of joints, their types (translational or rotational) and their geometric arrangement. Singularities occur when the calculation of IK for velocity fails (for example, when division by zero occurs) and should therefore be avoided. For each robot, a Jacobian matrix J can be defined that assigns transfer functions between the joint angle velocities and the end effector velocity. Mathematically, a singularity occurs when $\mathit{det}\left(J\right)=0$. Thus, for a particular robot, it is possible that the relative singularity configuration does not match any of the calculated singularity configurations of the entire robot. However, due to the presence of joint constraints (in some cases also when working in an environment with obstacles), some of the robot’s links are blocked and its structure changes. It is in such a case that the consideration of the newly introduced relative singularity configurations is useful. Another case for which it is useful to know the relative singular configurations is when the robot’s end effector needs to execute a trajectory and it is necessary to go from a relative left to a relative right configuration or vice versa. This transition is possible only when the robot is in an area where relative singularity is possible for the respective links. This is illustrated below in the discussion of the examples. The relative singularities are also related to the possibilities of the end effector to realize different orientations in one point (angle of service). For example, in areas three and six of Figure 18, it is shown that the angle of possible orientations at a point is continuous. This corresponds to a region where there is an intersection of two relative singularity configurations from Figure 19. In the areas without relative singularity configurations, this angle is either significantly limited (Figure 18 area 1) or divided into sectors (Figure 18 area 5). The breaking of sectors is due to the impossibility of changing the type of the solution from left-handed to right-handed and vice versa.

5.2. Discussion of Example 1

The proposed algorithm serves to determine the areas reachable by left-(L) and right-(R) hand configurations for a robot with two degrees of freedom. These areas in the workspace can be easily determined analytically, but in the configuration space, even for this simple case, this is not an easy task. The algorithm generates multiple points in the configuration space (Figure 13) and defines the three zones $q_L, q_R,q$ in which solutions of type L, R and a combination of the two are present. The location of the points in the configuration space is not uniform due to the non-linear nature of the IK and the setting of the points in polar coordinates.

Even if a trajectory falls entirely within the workspace of the robot, it may not be executed by the robot (for example, trajectory $t_1$). The transition from zone $f_L$ to $f_R$ or vice versa is possible only if passing through a singularity configuration (trajectory $t_2$). Singular configurations lie on the outer boundary of f and therefore the robot must pass through this region. Only a trajectory (for example, $q_{t2p}$) that falls entirely within the configuration space of the robot can be executed (Figure 13). The size and shape of the regions depends on the lengths of the links and is strongly influenced by the joint constraints. Graphical representation of trajectories in the configuration space helps to understand problems in motion planning or optimization.

Although it is possible to realize joints without constraints, in practice, such cases are very rare in robotics. When rotating at an angle close to or greater than $2\pi$[rad], many problems arise: a cantilever bearing of the joint between the two links is required, which is less favorable for the distribution of forces; the transmission of signals and energy becomes difficult due to the twisting of the cables; finally, control is difficult because it is necessary to check which direction of rotation is closer to the target angle and to record the rotation history. As can be seen from the examples, especially in the presence of joint constraints, the questions related to the type of initial and final desired configuration are essential.

5.3. Discussion of Example 2

Representing a configuration space with more than two dimensions is not an easy task. In the general case, it has the form of an n-dimensional parallelepiped with side lengths determined by the joint constraints. Example 2 considers a three-dimensional case. As dimensionality increases, the analytical mapping of spaces becomes complex. In such cases, it is believed that the proposed method is useful because the algorithm generates sets of points that form the map.

For the robot from Figure 14, whose dimensions and joint constraints are given in Figure 15, with the help of the proposed algorithm and the created program, 10 different main regions (Figure 17) are obtained in which the robot has different qualities. For example, if the robot moves only in region 1 or 10, it will reach the target point only with an RR or an LL configuration type, respectively.

Region 2 can be reached with both RR and RL configurations, and a transition between the two configurations is possible without the robot having to leave region 2—Figure 18. When transitioning from RR to RL, the robot passes through a relative singularity of type $S_{0,3}$. This is also confirmed by Figure 19 where it is shown that region 2 is a subset of the region with singularities of type $S_{0,3}$.

Points in region 3 can be reached with three main configuration types: RR, RL and LR. A transition through singularities of type $S_{0,2}$ and $S_{0,3}$ is possible between the different types of solutions, as the robot stays in the same region.

In the small region 4, solutions RR, RL and LL are possible. The transition between RR and RL is possible in the same area through $S_{0,3}$ (see also Figure 19). However, the transition between RR and LL or RL and LL cannot take place until the gripper is out of that region. In Figure 19, it can also be seen that region 4 is not part of region $S_{0,2}$.

Region 5—RR and LL types of solutions are possible here and it is not possible to switch from one type to the other without leaving the region.

Region 6—All solution types are possible as well as transitioning between them without leaving the zone. Analogous considerations are made for mirror zones 7,8,9 and 10.

From Figure 19, conclusions are drawn regarding the possibility of realizing trajectories that pass through several regions. The robot links can move by changing different types of configurations between the areas that are simultaneously covered by $S_{0,2}$ and $S_{0,3}$; these are in region 3, and a large part of 6 and 8. A trajectory that goes from 1 to 10, through 5, or vice versa cannot take place. To go from region 10 to 1 or vice versa the robot must pass through a region covered by $S_{0,2}$ and $S_{0,3}$.

5.4. Advantages of the Algorithm

-

Finds a set of points in the configuration space that can reach a given point in the workspace and sorts them by type. This can be used to determine the service coefficient and the robot’s mobility factor.

-

Transforms trajectories from the workspace into a corresponding set of points with possible solutions in the configuration space. This gives completeness to the solutions, unlike some numerical methods known so far, which find only one solution, one that is affected by the initial configuration;

-

Can be used to define regions from the workspace and configuration space with different types of solutions. Once created, a region map for a particular robot (environment with obstacle), can be used repeatedly by motion planning algorithms with different initial and target configurations.

-

Finds an IK solution even in singular configurations. Numerical methods based on the Jacobian matrix do not deal with this problem.

-

The algorithm is applicable to planar robots with a serial structure.

-

The resulting regions are useful for planning the placement of objects in the workspace of the robot.

5.5. Disadvantages of the Algorithm

-

It is not applicable (or difficult to apply) to real-time tasks.

-

In order to obtain a detailed and correct map for robots with more degrees of freedom or for complex obstacles in the workspace area, it is necessary to increase the number of checked points and algorithm cycles.

-

The algorithm is only suitable for robots with a serial structure. It is not applicable to parallel robots and closed structure robots.

-

The even distribution of survey points on circles requires multiple reachability checks for points that are sometimes clearly unreachable. We believe that this process can be optimized in the future.

Currently, the algorithm seeks the solutions to IK by going through every possible configuration of the robot. However, it could be determined in advance that some configurations are clearly unfeasible, which could reduce the total calculations and optimize the algorithm. In addition, if the obstacles in the environment do not change, the configuration space map for a particular robot is generated once and can be used repeatedly to determine different trajectories, even executed in real time. Often in robot control, it is not necessary to map the types of solutions. In such cases, the algorithm could be simplified to seek singular solutions by testing only a couple of configurations (which could be randomly chosen). This could improve the speed of the algorithm.

6. Conclusions

The paper presents an idea for finding and classifying multiple solutions of IK using a geometric approach. Definitions are introduced that clearly distinguish the types of solutions. An approach is proposed to determine regions in which the robot can occupy relative singularity configurations. In regions with different solution types, the robot is expected to possess qualitatively different properties.

A program has been created that uses the proposed algorithm. It works in the AutoCAD environment, which is convenient for visualizing the results in two-dimensional and three-dimensional space. Examples from the implementation of the program are also analyzed.

The algorithm is suitable for applications that do not work in real time. It can be applied in conjunction with collision detection algorithms to obtain maps that are used by algorithms to operate in a given environment with obstacles and multiple target requests. The obtained results can be useful for the design, research and motion planning of robots with a serial structure. The algorithm is useful for teaching students and Ph.D. students, because the results are presented graphically, which makes the processes easier to understand. The main steps are presented without specifying the way of their implementation, which allows for further development and improvement of the algorithm.

Singular configurations of robots are generally undesirable due to difficulties related to their control. The examples discussed show situations where traversing singular configurations is useful because it increases the reachability of the robot gripper.

The achieved results provide a foundation for further development of this work and can assist other research working in related fields. Future applications will be sought to generate multi-dimensional configuration spaces in the presence of obstacles in the workspace. The presented examples consider only a small portion of the possible applications and focus on investigating the position of the robot’s end effector. The properties of robots related to gripper orientation tasks will be investigated with the created program. The work can be developed further to solve the forward and inverse kinematics problems for robots with closed and open-closed topologies.