Thermal Conductivity of Low-GWP Refrigerants Modeling with Multi-Object Optimization

Abstract

In this paper, the procedure of finding the coefficients of an equation to describe the thermal conductivity of refrigerants low in global warming potential (GWP) is transformed into a multi-objective optimization problem by constructing a multi-objective mathematical model based on the Pareto approach. For the first time, the NSGAII algorithm was used to describe a thermophysical property such as thermal conductivity. The algorithm was applied to improve the performance of existing equations. Two objective functions were optimized by using the NSGAII algorithm. The average absolute relative deviation was minimized, while the coefficient of determination was maximized. After the minimization process, the optimal solution located on the Pareto frontier was chosen through a comparative analysis between ten selection methods available in the literature. The procedure generated a new set of coefficients of the studied equation that decreased its average absolute relative deviation by 0.24%, resulting in better performance over the entire database and for fluids with a high number of points. Finally, the system model was compared with existing literature models to evaluate its suitability for predicting the thermal conductivity of low-GWP refrigerants.

1. Introduction

The thermal conductivity (λ) of refrigerants is an essential property to describe the heat transfer in HVAC&R applications. For example, it directly affects the convection heat transfer coefficient in the heat exchangers. Therefore, this transport property is crucial for the optimization and design of these components. However, the experimentally determined λ data of refrigerants available in the literature do not cover all the temperature and pressure ranges needed for industrial applications. This is especially true for the fluids of low global warming potential (GWP) [1], also known as “fourth-generation” refrigerants [2,3,4], which have been identified as potential alternatives to high-GWP working fluids, such as several hydrofluorocarbons (HFCs). In fact, a limited number of experimental data for λ of these alternative refrigerants, mainly hydrofluoroolefins (HFOs) and hydrochlorofluoroolefins (HCFOs), were presented in the literature [5].

For this reason, several models have been developed to describe the temperature and pressure dependence of the thermal conductivity of refrigerants both in the vapor and liquid phases. Considering that no rigorous theory can accurately describe the liquid thermal conductivity [6], different semi-empirical and empirical models were proposed to calculate the λ of liquid refrigerants. Some of the main ones are extended corresponding states models, such as the ones used in REFPROP 10.0 [7]; models based on the entropy-scaling concept [8,9,10,11]; models based on equations of state [12,13]; semi-empirical correlations that describe the λ dependence on temperature [14,15,16]; and empirical equations that use specific fixed parameters [17,18,19,20,21]. Among them, some models have been specifically developed to describe the liquid thermal conductivity of low-GWP refrigerants, such as HFOs and HCFOs [11,14,20,21]. In particular, our research group recently proposed a modified version of the Di Nicola et al. [19] correlation to calculate the liquid thermal conductivity dependence of low-GWP refrigerants on temperature and pressure [20]. It has the following expression:

$$\frac{{\lambda }_L}{{\lambda }_0}=\lfloor a{T}_r+b{p}_c+c\omega +{\left(\frac{1}{M}\right)}^d\rfloor \left[1+\left(f_0+f{T}_r{}^2\right)p_r{}^g\right]$$

(1)

where λ_L is the liquid thermal conductivity in W m⁻¹ K⁻¹, T_r = T·T_c⁻¹ is the reduced temperature, T_c is the critical temperature in K, p_r = p·p_c⁻¹ is the reduced pressure, p_c is the critical pressure in bar, ω is the acentric factor, M is the molecular mass in kg kmol⁻¹, and λ₀, a, b, c, d, f₀, f and g are coefficients regressed on experimental data. In the original work, the following values for the studied alternative refrigerants were regressed by using a Random Search method [22] by minimizing the average absolute relative deviation of the liquid thermal conductivity: λ₀ = 0.43693 W m⁻¹ K⁻¹, a = −0.28725, b = 0.00372 bar⁻¹, c = 0.26967, d = 0.36436, f₀ = −0.00135, f = 0.05484 and g = 0.88049. In particular, the same dataset containing a total of 2073 experimental data for 6 low GWP refrigerants, namely R1233zd(E), R1234yf, R1234ze(E), R1234ze(Z), R1224yd(Z), and R1336mzz(Z), defined in the study [20] have been considered in the calculations reported in this work.

In this paper, a new methodology was employed to find Equation (1) coefficients using the Multi-Objective Optimization (MOO) approach. The MOO approach allows to solve complex problems [23,24] in which multiple and even conflicting objective functions exist. The classical approach of an optimization problem involves a single objective function and a single best solution. Several methods available in the literature are based on this approach, such as the Random Search method [22] or advanced intelligent algorithms [25,26]. On the other hand, the multi-objective optimization problem comprises a group of objective functions that must be simultaneously maximized or minimized. This approach is used in many engineering problems. An example is the cost minimization of a manufactured item and the simultaneous maximization of its performance. Another is the maximization of an engine’s performance with a simultaneous decrease in fuel consumption. Finding the best coefficients for an equation could be considered a MOO problem if multiple objective functions are simultaneously considered. In this particular case, we simultaneously optimize the Average Absolute Relative Deviation (AARD) and the coefficient of determination (R²). The advantage of multi-objective optimization is that it allows us to consider several criteria when designing a new equation and enables us to find a better approximation of the experimental values and a more robust equation.

In [27], it is possible to find a review of the various uses of the MOO for chemical process engineering problems and a detailed explanation of all the steps to build, resolve, and select the optimum result.

The algorithm used to solve the multi-objective problem is NSGAII [28] which is a popular nondominated genetic algorithm in genetic algorithms. NSGAII is based on multi-objective optimization. It is a very effective algorithm used in various engineering and scientific fields.

In this study, the NSGA-II is used to obtain the Pareto frontier [29,30] that solves the problem of simultaneous optimization of the two objectives, AARD and the coefficient of determination. It yields more consistent solutions to the problem, simultaneously considering more statistical parameters.

Such a method is a novelty in the field of thermophysical properties and it achieves a very good performance. In fact, the statistical parameters of AARD and Root Mean Square Error (RMSE) were improved in the entire database, and good results were also obtained for single fluids having a large number of data points.

The final result of the optimization is the Pareto front (Figure 1) which is a set of points representing the best trade-offs between the different objective functions, i.e., the most feasible solutions which satisfy the constraints while satisfying as many of the objectives as possible. A drawback of this approach is that the selection of the best solution among the ones on the Pareto front is not a trivial problem. Indeed, in a single-objective minimization problem, the best solution is the smallest. However, in a multi-objective problem, the optimal solution cannot be easily selected since some of the solutions that optimize one objective may not be satisfactory for the others. A tool developed by [31,32] that implements ten methods to select an optimal solution from the Pareto front was used in this regard. This useful tool allowed us not only to weigh the two objective functions but also to choose which weight was the most significant and which solutions were optimal in solving the problem of finding the best solution for minimizing the distance between calculated and experimental values. In this regard, the ten selection methods available in the tool were used to choose the optimal solution within the Pareto frontier regarding their capability to manage objectives with significantly different magnitudes and were able to rank among the best solutions.

In the end, the obtained model was compared with literature models to determine its effectiveness for predicting the thermal conductivity of low GWP refrigerants.

The paper has been organized as follows: after the introduction, the algorithms used to perform the MOO task are described. Then, the results obtained in different cases are presented. Finally, the main conclusions are presented with future works on the studied topic.

2. Methods

2.1. Genetic Method

One of the multi-objective optimization approaches is using genetic algorithms, which are well-suited to this problem. Genetic algorithms are based on the concepts of genetic evolution, survival of the strongest individual, and natural elimination of the weakest [33,34]. In a large time frame, the species containing the strongest genetic set will become dominant within the population. Mutatis mutandis to a mathematical problem, the solution of an optimization problem belonging to the set of possible solutions S is called a chromosome. Each chromosome has genes, expressed decimally, that control part of the behavior of the chromosomes. The genetic algorithm aims to match the chromosomes’ code to a solution by modifying their genes. This process is called encoding.

There are three mechanisms underlying genetic algorithms that can be modified: initial population choice, mutation, and crossover. The initial population choice is based on random choice algorithms, and it is essential to choose the initial population as best as possible. On the other hand, the mutation introduces random mutations within the chromosome choice algorithm to enlarge the search space and avoid local minima [33]. Finally, the crossover is one of the essential elements of the genetic algorithm and governs the combination of two parent chromosomes to produce new chromosomes [33]. This operation is repeated many times by applying crossover to generate new chromosomes and find the dominant ones appearing more frequently in the population.

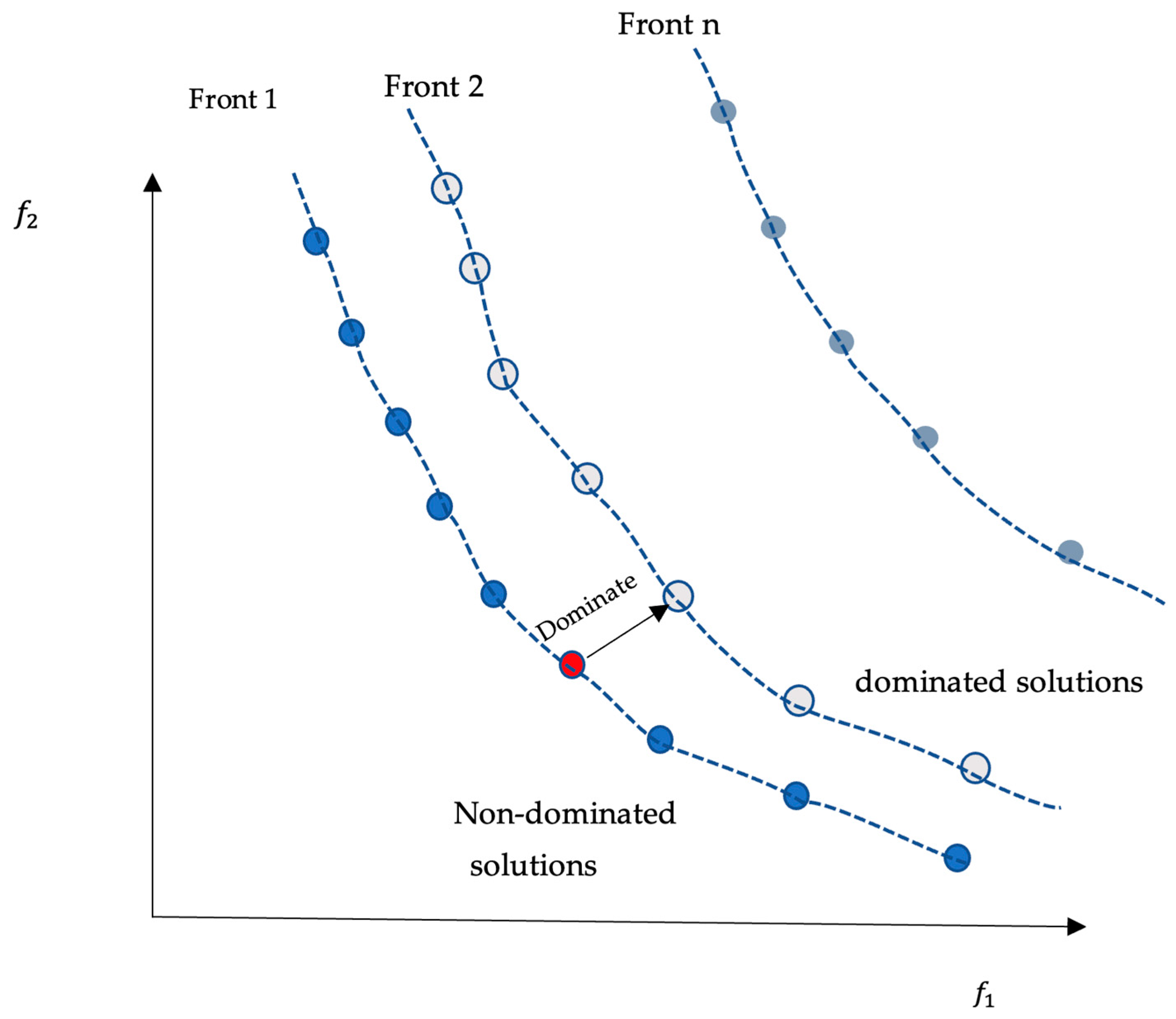
2.2. NSGAII Method

The algorithm chosen for parameter optimization is NSGA 2 [28]. It is a robust multi-objective algorithm that is efficient and highly tested in the literature [35,36,37].

Fundamentally, as also shown in Figure 2, it is based on the following steps:

• Random initialization of the base population;
• Selection of the initial population through a process of non-dominance;
• Application of crowding distance for subsequent selection of individuals;
• Selection of individuals based on crowding distance;
• Application of genetic algorithm and application of mutation and crossover;
• Recombination and population selection for building the next generation.

The crowding distance used in the NSGA II algorithm can estimate the density of the solutions surrounding a particular solution. In the NSGA II, the solutions with higher crowding distance are selected for the next population. The crowding distance is fundamental because it prevents the algorithm from searching for local minima instead of global ones. The steps to find the crowding distance are described in [28].

In the case under consideration, to describe the conductivity of low-GWP refrigerants, we started from Equation (1) by optimizing the coefficients λ₀, a, b, c, d, f₀, f, and g through the NSGA II genetic algorithm. For the initialization part and the iteration of the NSGAII algorithm, we used a commercial program called ModeFrontier [38]. In particular, the following objective functions were chosen:

1.

Average Absolute Relative Deviation

$$\mathrm{AARD}\%=\frac{100}{N}{\displaystyle \sum }_{i=1}^n\frac{\left|{\lambda }_{L,i}^{exp}-{\lambda }_{L,i}^{calc}\right|}{{\lambda }_{L,i}^{exp}}$$

(2)

2.

Coefficient of Determination

$${\mathrm{R}}^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left({\lambda }_{L,i}^{exp}-{\lambda }_{L,i}^{calc}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left({\lambda }_{L,i}^{exp}-{\overline{\lambda }}_L\right)}^2}$$

(3)

where ${\lambda }_L^{exp}$ is the experimental liquid thermal conductivity, ${\lambda }_L^{calc}$ is the calculated liquid thermal conductivity, ${\overline{\lambda }}_L$ is the mean of experimental liquid thermal conductivity, and $n$ is the number of experimental points. The two objectives conflict with each other; the optimization algorithm minimized AARD% and maximized R² at the same time.

As explained in the introduction, the 2074 points of the dataset defined by Tomassetti et al. [20] were used. The eight coefficients of the equation were optimized with the following bounds: ${\lambda }_0\in \left[0,1\right]$, $a\in \left[-0.5,0.5\right]$, $b\in \left[0,0.5\right]$, $c\in \left[0,0.5\right]$, $d\in \left[0,0.5\right]$, $g\in \left[0,1\right]$, $f\in \left[-1,0.1\right]$, and $f_1\in \left[0,0.15\right]$.

For the initialization of the optimization process, 80 points chosen as follows were used:

• 10 points by a random process;
• 10 points via a pseudo-random Sobol sequence [39];
• 60 points using the incremental space filler algorithm. This algorithm is very useful in creating the DoE to generate a uniform distribution of data in the input space [40].

The following operating parameters were used to implement the NSGA2 algorithm:

• Number of generations: 100;
• Crossover probability: 0.9;
• Mutation probability: 1.

As a final step, ten algorithms for choosing the optimal solution were compared using the tool available in [31,32]. To obtain the best results, the objective functions were given weights. The obtained results are reported in

Table 1. Comparison between the results provided by the ten algorithms for choosing the optimal solution available in [31].

Type of Algorithm	AARD% (0.5)	R2 (0.5)	AARD% (0.8)	R2 (0.2)
TOPSIS [41]	1.40733	0.991706	1.40660	0.991193
LINMAP [42]	1.40733	0.991706	1.40660	0.991193
VIKOR [43]	1.40927	0.991963	1.40833	0.991927
FUCA [44]	1.4073	0.991269	1.40660	0.991193
GRA [31]	1.40927	0.991963	1.40927	0.991963
SAW [43]	1.40660	0.991193	1.40660	0.991193
MEW [43]	1.40660	0.991193	1.40660	0.991193
ELCTRE II [45]	1.4073	0.991269	1.40678	0.991207
ELECTRE III [31]	1.40927	0.991963	1.40927	0.991963
NFM [46]	1.40927	0.991963	1.40927	0.991963

. The first attempt was to assign the same weight to the two objective functions, but then, we noticed that the coefficient of determination varied only to the fourth decimal digit, and it was decided to give more importance to the AARD% by using the following weights: 80% for AARD% and 20% for R².

3. Results and Discussion

In this section, the final result of the MOO process is described. The algorithm started with an initial guess for the solution and gradually improved it until a satisfactory result was obtained. It incorporated techniques from the NSGAII genetic algorithm to minimize the AARD% and maximize the R². After all the steps described above, the following optimal result was obtained: AARD% = 1.40660 and R² = 0.991193.

Figure 3 shows the result of the choice process of the optimal result from the Pareto frontier made with the abovementioned tool [31,32]. It shows a graphical representation of the position of the optimal solution compared to the rest of the solutions analyzed. In this figure, the best solution is indicated by the red circle located at the bottom-left corner. This solution was selected as the optimal one of the problem because it is the only one that provides the maximum of the R² and the minimum of the AARD% with respect to the weighted objective functions. Therefore, the chosen point is the best compromise between the two weighted objective functions. The parameters found at the end of the minimization procedure are: $a=-0.43751$, $b=0.0055$, $c=0.3000$, $d=0.25228$, $g=0.76287$, $f=0.0805$, $f_0=-0.0023$, and ${\lambda }_0=0.2885$.

Table 2. Comparison between the parameters obtained with the method used in [19] and the new method (NSGAII).

Parameter	Original Parameters	New Parameters	Difference	Rate of Change
${\lambda }_0$	0.43693	0.2885	0.14843	34%
$a$	−0.28725	−0.43751	0.15026	−52%
$b$	0.00372	0.0055	−0.00178	−48%
$c$	0.26967	0.3000	−0.03033	−11%
$d$	0.36436	0.25228	0.11208	31%
$f_0$	−0.00135	−0.0023	0.00095	−70%
$f$	0.05484	0.0805	−0.02566	−47%
$g$	0.88049	0.76287	0.11762	13%

shows a comparison between the old and new parameters. It is possible to see that there are a few significant differences between the old and new parameters. Nevertheless, the main differences are between the very low parameters, where the new and old parameters differ by a relatively small amount. On the other hand, we can notice that the magnitude and the sign are the same between the two parameter sets.

As shown in

Table 3. Comparison between the results of the method used in Tomassetti et al. [20] and the new approach using the NSGAII algorithm.

Statistical Parameter	Method Used in Tomassetti et al. [20]	New Method (NSGAII)
AARD%	1.45	1.41
R2	0.9922	0.9911
RMSE	0.00411	0.00406

, the new method for computing the coefficients provided better values of AARD% and RMSE (Equation (4)) with respect to the original coefficients. However, it did not ensure the best solution for R² due to the weighing in the optimal point selection on the Pareto frontiers. In fact, as we stated in the previous section, the objective functions were weighted to obtain better results of AARD%. However, the R² is very close to the previous one, with a change on the third decimal digit.

$$\mathrm{RMSE}=\frac{100}{N}{\displaystyle \sum }_{i=1}^n\sqrt{\frac{{({\lambda }_{L,i}^{exp}-{\lambda }_{L,i}^{calc})}^2 }{{\lambda }_{L,i}^{exp}}}$$

(4)

Table 4. Deviations between the experimental liquid thermal conductivity data of the low-GWP refrigerants and the results provided by Equation (1) with the new coefficients calculated using NSGAII, the original results of Equation (1) [20], and REFPROP 10.0 calculations.

		This Work		Original Results [20]		REFPROP 10.0
Fluid	Point Numbers	AARD%	MARD%	AARD%	MARD%	AARD%	MARD%
R1224yd(Z)	53	2.62	5.11	1.45	7.34	6.36	8.86
R1233zd(E)	1132	1.10	3.28	1.15	3.39	0.34	1.58
R1234yf	267	1.45	6.85	1.45	7.24	0.30	1.56
R1234ze(E)	494	1.31	3.83	1.63	5.94	0.34	2.04
R1234ze(Z)	61	3.89	7.05	1.77	5.08	1.78	5.70
R1336mzz(Z)	66	3.98	11.97	3.64	8.48	0.70	2.17
Overall	2073	1.41	-	1.45	-	0.54	-

shows the deviations between the experimental thermal conductivity data of the studied liquid refrigerants and the calculations provided by Equation (1) using the coefficients corresponding to the chosen point in the Pareto frontier. The results given by Equation (1) using the original coefficients [20] and by REFPROP 10.0 are also reported in Table 4. REFPROP 10.0 provides the thermal conductivity values using either fluid-specific correlations or a modification of the extended CSP method. In particular, these models describe the thermal conductivity dependence on temperature and pressure at different thermodynamic conditions. As expected, REFPROP 10.0 ensured the lowest deviations since it uses fluid-specific correlations or extended corresponding states models.

Regarding the results of Equation (1) with the new coefficients, the fluid with the largest deviation is R1336mzz(z). As evident from Figure 4, this equation cannot accurately reproduce the high temperatures where the deviations have a maximum of 11.97%. As can be seen in Table 4, the deviations that improve the most are those of the fluids with larger numbers of points. This result could be considered a potential limitation of the method used and could be used in the future for fluids with larger amounts of experimental data in many other applications. In addition, although better results were obtained, it must be pointed out that genetic algorithms, such as NSGAII, have other disadvantages. For example, the computational cost of this method is certainly higher than that of other minimization methods. Furthermore, genetic algorithms are very sensitive to the initial values chosen and often do not converge if the chosen values are not correct. However, if the user can optimally tune the parameters, excellent results can be achieved.

4. Conclusions and Future Works

This paper proposes an approach based on the NSGA-II method to find new coefficients of a literature equation that describes the thermal conductivity of low-GWP refrigerants. A database of 2073 points for six low-GWP refrigerants was used. The goal was to determine thermal conductivity at temperatures not investigated by the experiments, giving the user a reliable instrument to calculate the thermal conductivity of alternative refrigerants. The methodology follows a multi-objective approach to simultaneously minimize the average absolute relative deviation and maximize the coefficient of determination. The results obtained do not significantly improve those previously obtained by other methods. However, they are a novelty since the NSGAII genetic method was used for the first time to describe a thermophysical property. Nevertheless, the statistical parameters provided by the new method are better than that of previous methods, yielding a total AARD of 1.41% and a coefficient of determination of 0.0019. In particular, the new procedure produced a new set of coefficients that decreased the average absolute relative deviation of the studied equation by 0.24%, resulting in better performance over the entire database and for fluids with several data points. Moreover, the new set of parameters improved the RMSE compared to the original ones. This work may open very interesting scenarios for future applications to other thermophysical properties not yet investigated with this approach. This methodology could be applied to many other thermophysical properties, improving existing equations’ performance or investigating new ones. For example, genetic algorithms could be applied to characterize surface tension or viscosity, obtaining better results than those provided by the models available in the literature.