No Cell Left behind: Automated, Stochastic, Physics-Based Tracking of Every Cell in a Dense, Growing Colony
Abstract
:“What I cannot create, I do not understand.”—Richard P. Feynman (Nobel Prize in Physics, 1965)
1. Introduction and Motivation
2. Previous Work
Novelty
- We maintain a physically-based model of the “universe” so we “know” where every bacterium is at any given moment.
- The model has tight physical constraints over what changes are allowed between frames, so the model effectively “understands” what is possible and what is not.
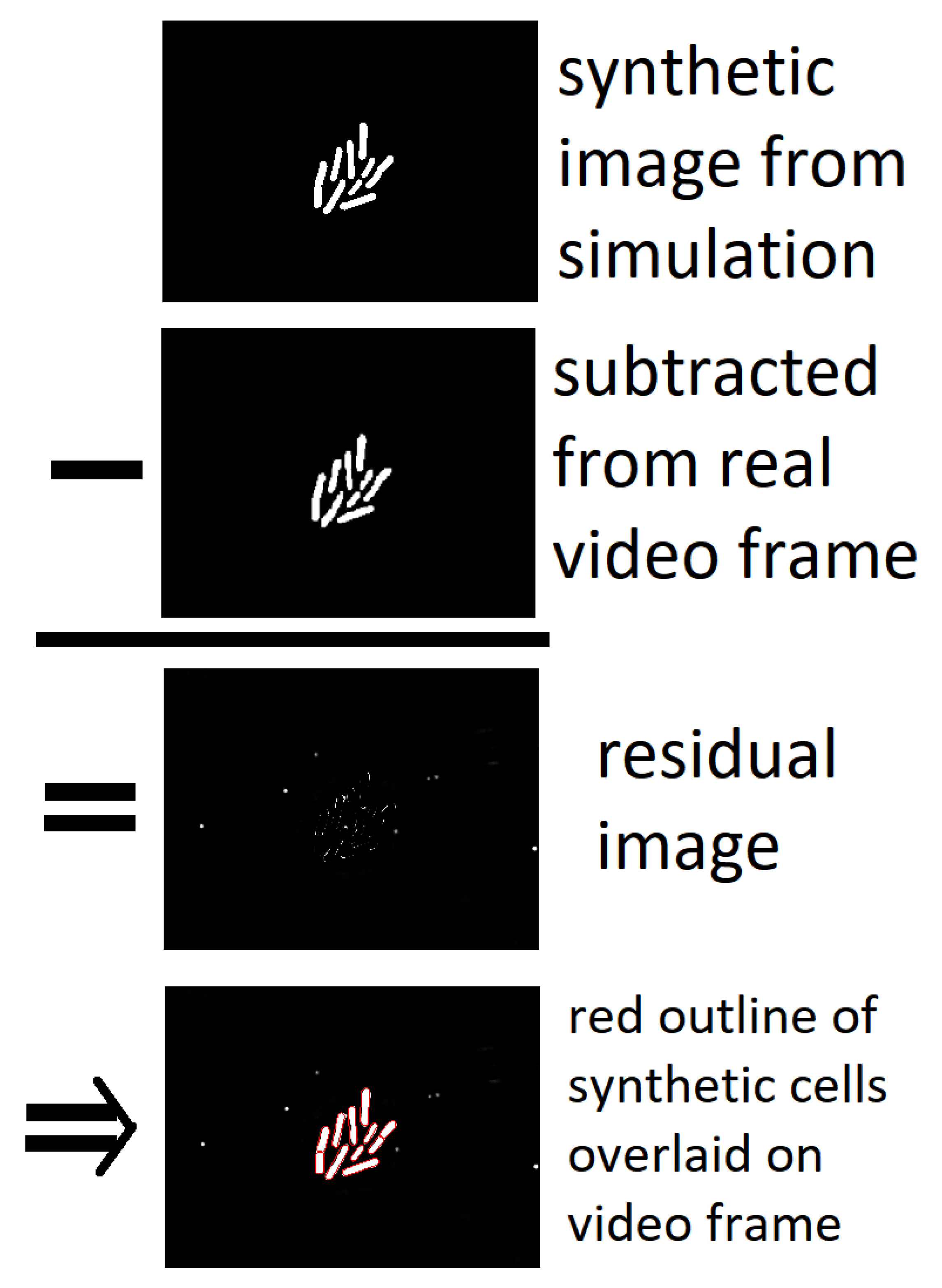
- These constraints allow us to easily disregard large amounts of noise in the image if they reflect changes that are physically impossible within the constraints of the model.
- Since each and every bacterium has a physical “presence” in our model, it’s highly unlikely to “lose track” of any individual unless even a human would have difficulty tracking the individual (e.g., if it moves off screen or becomes blurred and difficult to distinguish from closely-packed neighbors).
3. Methods
Initialization and Simulation Rules
4. Results
4.1. Bacterial Counting
4.2. Cell Lineage Trees
4.3. Precise Motility Measurements
5. Summary, Conclusions & Future Work
- Some systems can capture three-dimensional images whereas Cell Universe currently only handles two dimensions. This will require 3D models of cells to be developed, which adds to the size of the parameter space to be searched. In the case of simply-shaped cells such as bacteria, a model consisting of a cylinder with hemispherical ends would readily extend the current 2D rectangle with semi-circular ends.
- Cells can have more complex shapes than bacteria, and higher resolution images may also display interior structure of the cells. Simulating these aspects may require significantly more parameters that need to be optimized; efficiently dealing with a larger number of optimization parameters per cell could be challenging, though the increasing availability of parallel processing may alleviate some of the cost.
- The speed of Cell Universe could be greatly improved by using less costly algorithms such as simulated annealing to optimize just one universe in place of ensemble simulation.
- Its speed could also be greatly increased by moving from Python to a compiled language such as C++.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rundo, L.; Militello, C.; Vitabile, S.; Russo, G.; Sala, E.; Gilardi, M.C. A survey on nature-inspired medical image analysis: A step further in biomedical data integration. Fundam. Inform. 2020, 171, 345–365. [Google Scholar] [CrossRef]
- Li, K.; Chen, M.; Kanade, T.; Miller, E.D.; Weiss, L.E.; Campbell, P.G. Cell Population Tracking and Lineage Construction with Spatiotemporal Context. Med. Image Anal. 2008, 12, 546–566. [Google Scholar] [CrossRef] [PubMed]
- Maška, M.; Ulman, V.; Svoboda, D.; Matula, P.; Matula, P.; Ederra, C.; Urbiola, A.; España, T.; Venkatesan, S.; Balak, D.M.; et al. A benchmark for comparison of cell tracking algorithms. Bioinformatics 2014, 30, 1609–1617. [Google Scholar] [CrossRef] [PubMed]
- Meijering, E.; Dzyubachyk, O.; Smal, I.; van Cappellen, W.A. Tracking in cell and developmental biology. Semin. Cell Dev. Biol. 2009, 20, 894–902. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhou, X.; Ma, J.; Wong, S.T.C. Multiple nuclei tracking using integer programming for quantitative cancer cell cycle analysis. IEEE Trans. Med. Imaging 2010, 29, 96–105. [Google Scholar]
- Al-Kofahi, O.; Radke, R.J.; Goderie, S.K.; Shen, Q.; Temple, S.; Roysam, B. Automated cell lineage construction: A rapid method to analyze clonal development established with murine neural progenitor cells. Cell Cycle 2006, 5, 327–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gamarra, M.; Zurek, E.; Escalante, H.J.; Hurtado, L.; San-Juan-Vergara, H. Split and merge watershed: A two-step method for cell segmentation in fluorescence microscopy images. Biomed. Signal Process. Control 2019, 53, 101575. [Google Scholar] [CrossRef]
- Zhang, H.P.; Be’er, A.; Florin, E.-L.; Swinney, H.L. Collective motion and density fluctuations in bacterial colonies. Proc. Natl. Acad. Sci. USA 2010, 107, 13626–13630. [Google Scholar] [CrossRef] [Green Version]
- Padfield, D.; Rittscher, J.; Roysam, B. Coupled minimum-cost flow cell tracking for high-throughput quantitative analysis. Med. Image Anal. 2011, 15, 650–668. [Google Scholar] [CrossRef]
- Sacan, A.; Ferhatosmanoglu, H.; Coskun, H. CellTrack: An open-source software for cell tracking and motility analysis. Bioinformatics 2008, 24, 1647–1649. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Yang, H.; Huang, H.; Zhu, T. Cellcounter: Novel Open-Source Software for Counting Cell Migration and Invasion In Vitro. BioMed Res. Int. 2014, 2014, e863564. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, A.E.; Jones, T.R.; Lamprecht, M.R.; Clarke, C.; Kang, I.H.; Friman, O.; Guertin, D.A.; Chang, J.H.; Lindquist, R.A.; Moffat, J.; et al. CellProfiler: Image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 2006, 7, R100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamprecht, M.R.; Sabatini, D.M.; Carpenter, A.E. CellProfiler: Free, versatile software for automated biological image analysis. BioTechniques 2007, 42, 71–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaqaman, K.; Loerke, D.; Mettlen, M.; Kuwata, H.; Grinstein, S.; Schmid, S.L.; Danuser, G. Robust single particle tracking in live cell time-lapse sequences. Nat. Methods 2008, 5, 695–702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kan, A.; Chakravorty, R.; Bailey, J.; Leckie, C.; Markham, J.; Dowling, M. Automated and semi-automated cell tracking: Addressing portability challenges. J. Microsc. 2011, 244, 194–213. [Google Scholar] [CrossRef] [PubMed]
- Chalfoun, J.; Majurski, M.; Dima, A.; Halter, M.; Bhadriraju, K.; Brady, M. Lineage mapper: A versatile cell and particle tracker. Sci. Rep. 2016, 6, 36984. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Zimmer, C.; Olivo-Marin, J.C. Tracking fluorescent cells with coupled geometric active contours. In Proceedings of the 2004 2nd IEEE International Symposium on Biomedical Imaging: Nano to Macro, Arlington, VA, USA, 18 April 2004; pp. 476–479. [Google Scholar]
- Baker, R.M.; Brasch, M.E.; Manning, M.L.; Henderson, J.H. Automated, contour-based tracking and analysis of cell behaviour over long time scales in environments of varying complexity and cell density. J. R. Soc. Interface 2014, 11, 386. [Google Scholar] [CrossRef] [PubMed]
- Dzyubachyk, O.; Essers, J.; van Cappellen, W.A.; Baldeyron, C.; Inagaki, A.; Niessen, W.J.; Meijering, E. Automated analysis of time-lapse fluorescence microscopy images: From live cell images to intracellular foci. Bioinformatics 2010, 26, 2424–2430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maška, M.; Danek, O.; Garasa, S.; Rouzaut, A.; Munoz-Barrutia, A.; Ortiz-de Solorzano, C. Segmentation and Shape Tracking of Whole Fluorescent Cells Based on the Chan-Vese Model. IEEE Trans. Med. Imaging 2013, 32, 995–1006. [Google Scholar] [CrossRef]
- Nath, S.K.; Palaniappan, K.; Bunyak, F. Cell Segmentation Using Coupled Level Sets and Graph-Vertex Coloring. Med. Image Comput. Comput. Assist. Interv. 2006, 9 Pt 1, 101–108. [Google Scholar]
- Whitaker, J.S.; Hamill, T.M.; Wei, X.; Song, Y.; Toth, Z. Ensemble Data Assimilation with the NCEP Global Forecast System. Mon. Weather. Rev. 2008, 136, 463–482. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bellus, M.; Wittmann, C.; Steinheimer, M.; Weidle, F.; Kann, A.; Ivatek-Šahdan, S.; Tian, W.; Ma, X.; Tascu, S.; et al. The Central European limited-area ensemble forecasting system: ALADIN-LAEF. Q. J. R. Meteorol. Soc. 2011, 137, 483–502. [Google Scholar] [CrossRef]
- Demeritt, D.; Cloke, H.; Pappenberger, F.; Thielen, J.; Bartholmes, J.; Ramos, M. Ensemble predictions and perceptions of risk, uncertainty, and error in flood forecasting. Environ. Hazards 2007, 7, 115–127. [Google Scholar] [CrossRef]
- Dai, A.; Meehl, G.A.; Washington, W.M.; Wigley, T.M.; Arblaster, J.M. Ensemble simulation of twenty–first century climate changes: Business–as–usual versus CO2 stabilization. Bull. Am. Meteorol. Soc. 2001, 82, 2377–2388. [Google Scholar] [CrossRef] [Green Version]
- Chenouard, N.; Bloch, I.; Olivo-Marin, J.C. Multiple Hypothesis Tracking for Cluttered Biological Image Sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2736–3750. [Google Scholar] [CrossRef]
- Stylianidou, S.; Brennan, C.; Nissen, S.B.; Kuwada, N.J.; Wiggins, P.A. SuperSegger: Robust image segmentation, analysis and lineage tracking of bacterial cells: Robust segmentation and analysis of bacteria. Mol. Microbiol. 2016, 102, 690–700. [Google Scholar] [CrossRef] [Green Version]
- Klein, J.; Leupold, S.; Biegler, I.; Biedendieck, R.; Münch, R.; Jahn, D. Tlm-tracker: Software for cell segmentation, tracking and lineage analysis in time-lapse microscopy movies. Bioinformatics 2012, 28, 2276–2277. [Google Scholar] [CrossRef] [Green Version]
- Paintdakhi, A.; Parry, B.; Campos, M.; Irnov, I.; Elf, J.; Surovtsev, I.; Jacobs-Wagner, C. Oufti: An integrated software package for high-accuracy, high-throughput quantitative microscopy analysis. Mol. Microbiol. 2016, 99, 767–777. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676. [Google Scholar] [CrossRef] [Green Version]
- Tinevez, J.-Y.; Perry, N.; Schindelin, J.; Hoopes, G.M.; Reynolds, G.D.; Laplantine, E.; Bednarek, S.Y.; Shorte, S.L.; Eliceiri, K.W. TrackMate: An open and extensible platform for single-particle tracking. Methods 2017, 115, 80–90. [Google Scholar] [CrossRef]
- Huth, J.; Buchholz, M.; Kraus, J.M.; Mølhave, K.; Gradinaru, C.; Wichert, G.v.; Gress, T.M.; Neumann, H.; Kestler, H.A. Timelapseanalyzer: Multi-target analysis for live-cell imaging and time-lapse microscopy. Comput. Methods Programs Biomed. 2011, 104, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Winter, M.; Mankowski, W.; Wait, E.; Temple, S.; Cohen, A.R. Lever: Software tools for segmentation, tracking and lineaging of proliferating cells. Bioinformatics 2016, 32, 3530–3531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsoucas, D.; Yuan, G.-C. Recent progress in single-cell cancer genomics. Curr. Opin. Genet. Dev. 2017, 42, 22–32. [Google Scholar] [CrossRef] [PubMed]







| Program | Err. | %Err. | CPU (s) | Comment |
|---|---|---|---|---|
| SuperSegger [27] | 0.80 | 2.24 | ∼2400 | 10 min cores on 2.9 GHz Mac |
| CellProfiler [12,13] | −2.20 | −6.17 | ∼3600 | 15 min cores on 3.2 GHz Lenovo G500s i5-3230M |
| Lineage Mapper [16] | 2.84 | 7.95 | ∼300 | Required enormous effort (days) to tune its parameters |
| Cell Universe “Clean” | 2.85 | 7.99 | 9900 | 20 min cores on CentOS 2.4 GHz Opteron 6378 |
| TLM-Tracker [28] | −3.55 | 5.41 | ∼300 | 5 min; very sensitive to noise; clean images only. |
| Cell Universe “Noisy” | 5.85 | 16.40 | 17,000 | 35 min cores on CentOS 2.4 GHz Opteron 6378 |
| ImageJ Reg. Count. | −10.99 | −30.80 | ∼10,000 | 20 min cores on CentOS 2.4 GHz Opteron 6378 |
| CellCounter [11] | 14.56 | 40.82 | ∼1000 | |
| Oufti [29] | −29.08 | −89.50 | ∼1000 | |
| TrackMate/Fiji [30,31] | 37.11 | 104.30 | ∼1000 | |
| TimeLapseAnal. [32] | — | — | ? | |
| LEVER [33] | — | — | ? |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, H.; Shehada, E.R.; Stahlheber, S.; Pandey, K.; Hayes, W.B. No Cell Left behind: Automated, Stochastic, Physics-Based Tracking of Every Cell in a Dense, Growing Colony. Algorithms 2022, 15, 51. https://doi.org/10.3390/a15020051
Pham H, Shehada ER, Stahlheber S, Pandey K, Hayes WB. No Cell Left behind: Automated, Stochastic, Physics-Based Tracking of Every Cell in a Dense, Growing Colony. Algorithms. 2022; 15(2):51. https://doi.org/10.3390/a15020051
Chicago/Turabian StylePham, Huy, Emile R. Shehada, Shawna Stahlheber, Kushagra Pandey, and Wayne B. Hayes. 2022. "No Cell Left behind: Automated, Stochastic, Physics-Based Tracking of Every Cell in a Dense, Growing Colony" Algorithms 15, no. 2: 51. https://doi.org/10.3390/a15020051
APA StylePham, H., Shehada, E. R., Stahlheber, S., Pandey, K., & Hayes, W. B. (2022). No Cell Left behind: Automated, Stochastic, Physics-Based Tracking of Every Cell in a Dense, Growing Colony. Algorithms, 15(2), 51. https://doi.org/10.3390/a15020051






