1. Introduction
A
Hamiltonian path (
cycle) in a graph is a spanning path (cycle) of the graph. The
Hamiltonian path (
cycle)
problem involves deciding whether or not a graph contains a Hamiltonian path (cycle). A graph is called
Hamiltonian if it contains a Hamiltonian cycle. A graph
G is said to be
Hamiltonian connected if for each pair of distinct vertices
u and
v of
G, there is a Hamiltonian path between
u and
v in
G. It is well known that the Hamiltonian path and cycle problems are NP-complete for general graphs [
1]. In [
2], Harary outlined the important motivations and applications for Hamiltonian path problem. In addition, the Hamiltonian problems have been much studied and have numerous applications in different areas, including establishing transport routes, production launching, the on-line optimization of flexible manufacturing systems [
3], computing the perceptual boundaries of dot patterns [
4], pattern recognition [
5,
6,
7], hypercube properties [
8], molecular and physical sciences [
9,
10], biology science [
11], etc. It is worth mentioning that Twarock et al. [
11] applied the Hamiltonian path to the analysis of viral genomes, and Balasubramanian [
9,
10] pointed out that in molecular and physical sciences, the Hamiltonian path problem is related to random walks, enumeration of self-returning walks and ring perception algorithms, and peripherals of fullerenes. The
longest path problem, which finds a simple path with the maximum number of vertices in a graph, is one of the most important problems in graph theory. The Hamiltonian path problem is clearly a special case of the longest path problem. Despite the many applications of the problem, it is still open for some classes of graphs, including solid supergrid graphs and supergrid graphs with some holes [
12]. There are few classes of graphs in which the longest path problem is polynomial-time solvable [
13,
14,
15]. Because the time complexity of the longest path problem on solid supergrid graphs is still open, it is interesting to study this problem for the subcalsses of solid supergrid graphs. In this paper, we focus on
C-shaped supergrid graphs, which form a subclass of solid supergrid graphs. We will give the necessary and sufficient conditions for the Hamiltonicity and Hamiltonian connectivity of
C-shaped supergrid graphs. We also present a linear-time algorithm for finding a longest path between any two distinct vertices in a
C-shaped supergrid graph.
The
two-dimensional integer grid graph is an infinite graph whose vertex set consists of all points of the Euclidean plane with integer coordinates and in which two vertices are adjacent if the (Euclidean) distance between them is 1. The
two-dimensional supergrid graph is an infinite graph obtained from
by adding all edges on the lines traced from up-left to down-right and from up-right to down-left. A graph is a
grid graph if it is a finite induced subgraph of
. A
supergrid graph is a finite vertex-induced subgraph of
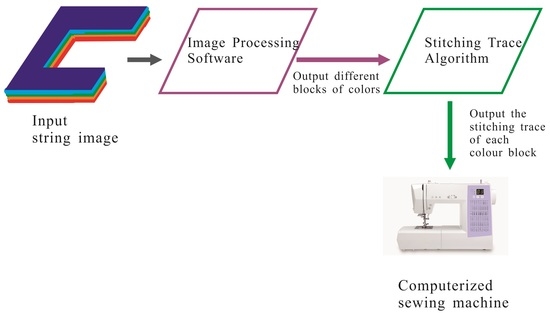
. Supergrid graphs came from our industry-university cooperative research project, and can be applied to compute the stitching trace of computerized sewing machines [
16]. A
solid supergrid graph is a supergrid graph without any hole, and a
rectangular supergrid graph is a solid supergrid graph bounded by a axis-parallel rectangle. A
L-shaped or
C-shaped supergrid graph is a supergrid graph obtained from a rectangular supergrid graph by removing a rectangular supergrid subgraph from it to form a
L-like or
C-like shape.
The Hamiltonian connectivity and longest path of shaped supergrid graphs can be applied for computing the optimal stitching trace of computer embroidery machines [
12,
16,
17]. For example, consider that a string of letters will be sewed into an object such that the number of crossed paths is minimum. The Hamiltonian connectivity and longest path of these shaped letters play an important role in deciding these sewing traces. In addition, they can be also applied to construct the minimum printing trace of 3D printers. For example, consider a 3D printer with a
C-like object being printed. The software produces a series of thin layers, designs a path for each layer, combines these paths of produced layers, and transmits the above paths to 3D printer. Because 3D printing is performed layer-by-layer (see
Figure 1a), each layer can be considered as a
C-shaped supergrid graph. Suppose that there are
k layers under the above 3D printing. If the Hamiltonian connectivity of
C-shaped supergrid graphs holds true, then we can find a Hamiltonian path, starting from
and ending at
, of a
C-shaped supergrid graph
, where
,
, represents a layer under 3D printing. Thus, we can design an optimal trace for the above 3D printing, where
is adjacent to
for
. In this application, we restrict the 3D printer nozzle to be located at integer coordinates. For example,
Figure 1a shows five layers
–
of a 3D printing for a
C-type object,
Figure 1b depicts the Hamiltonian paths of
for
, and the result of this 3D printing is shown in
Figure 1c.
Some related works in the literature are summarized as follows. Recently, Hamiltonian path (cycle) and Hamiltonian connected problems in grid and supergrid graphs have received much attention. In [
18], Itai et al. proved that the Hamiltonian path problem on grid graphs is NP-complete. They also gave necessary and sufficient conditions for a rectangular grid graph having a Hamiltonian path between two given vertices. Note that rectangular grid graphs are not Hamiltonian connected. Zamfirescu et al. [
19] gave sufficient conditions for a grid graph having a Hamiltonian cycle, and proved that all grid graphs of positive width have Hamiltonian line graphs. Later, Chen et al. [
20] improved the Hamiltonian path algorithm of [
18] on rectangular grid graphs and presented a parallel algorithm for the Hamiltonian path problem with two given endpoints in rectangular grid graphs. In addition, there is a polynomial-time algorithm for finding Hamiltonian cycles in solid grid graphs [
21]. However, the Hamiltonian problems are still open for solid supergrid graphs. In [
22], Salman introduced alphabet grid graphs and determined classes of alphabet grid graphs which contain Hamiltonian cycles. Supergrid graphs first appeared in [
16], and the authors proved that the Hamiltonian cycle and path problems on general supergrid graphs are NP-complete, and every rectangular supergrid graph always contains a Hamiltonian cycle. Recently, the Hamiltonian connectivity of
L-shaped supergrid graphs has been verified in [
17]. Note that
C-shaped supergrid graphs contain
L-shaped supergrid graphs as their subgraphs. Thus, the results of
L-shaped supergrid graphs can not be directly applied to
C-shaped supergrid graphs. However, the results in [
17] will be used in our method. In this paper, we will consider the Hamiltonian, Hamiltonian connectivity, and longest path of
C-shaped supergrid graphs.
The rest of the paper is organized as follows. In
Section 2, some notations, observations, known results, and one special Hamiltonian connected property of a special rectangular supergrid graph are given. In
Section 3, we give the necessary and sufficient conditions for the Hamiltonian and the Hamiltonian connected
C-shaped supergrid graphs. This section shows that
C-shaped supergrid graphs are always Hamiltonian and Hamiltonian connected except for a few conditions. In
Section 4, we present a linear-time algorithm to compute the longest path between any two distinct vertices in a
C-shaped supergrid graph. Finally, a conclusion is given in
Section 5.
2. Terminologies and Background Results
In this section, we will introduce some terminologies and symbols. Some observations and previously established results for the Hamiltonicity and Hamiltonian connectivity of rectangular and L-shaped supergrid graphs are also given. In addition, we also prove some Hamiltonian connectivity property of a special class of rectangular supergrid graphs that will be used in proving our result.
Suppose that G is a graph with vertex set and edge set . Let , and let . We write for the subgraph of G induced by S, and for the subgraph . In general, we write instead of . The notation (resp., ) means that vertices u and v are adjacent (resp., non-adjacent). A vertex wadjoins edge if and . For two edges and , if and then we say that and are parallel, denoted this by . A neighbor of vertex v is any vertex adjacent to v. We denote by the set of neighbors of v in G, and let . The degree of vertex v in G, denoted by , is the number of vertices adjacent to v. A path P of length in G, denoted by , is a sequence of vertices such that for , and all vertices except in it are distinct. The first and last vertices visited by P are denoted by and , respectively. We will use to denote “P visits vertex ” and use to denote “P visits edge ”. A path from to is denoted by -path. In addition, we use P to refer to the set of vertices visited by path P if it is understood without ambiguity. A cycle is a path C with and . Two paths (or cycles) and of graph G are vertex-disjoint if . If , then two vertex-disjoint paths and can be concatenated into a path, denoted by .
For a node (vertex)
v in the plane with integer coordinates, let
and
represent the
x and
ycoordinates of node
v, respectively, denoted by
. A
grid graph is a finite vertex-induced subgraph of
.
Figure 2a shows a grid graph, and it is clear that the maximum degree of all vertices is four. A
supergrid graph is a finite vertex-induced subgraph of
.
Figure 2b depicts a supergrid graph, it is clear that the maximum degree of all vertices is eight. Thus, supergrid graphs contain grid graphs as subgraphs. Notice that grid graphs are not a subclass of supergrid graphs, and the converse is also true. Obviously, all grid graphs are bipartite [
18] but supergrid graphs are not bipartite.
A
rectangular supergrid graph, denoted by
, is a supergrid graph whose vertex set is
and
. That is,
contains
m columns and
n rows of vertices in
and its shape is a rectangle. The size of
is defined to be
, and
is called
n-rectangle. The vertex
v is called the
upper-left (resp.,
upper-right,
down-left,
down-right)
corner of
if for any vertex
,
and
(resp.,
and
,
and
,
and
). The edge
is said to be
horizontal (resp.,
vertical) if
(resp.,
), and is called
crossed if it is neither a horizontal nor a vertical edge. There are four boundaries in a rectangular supergrid graph
with
. The edge in the boundary of
is called
boundary edge. A path is called
boundary of
if it visits all vertices and edges of the same boundary in
and its length equals to the number of vertices in the visited boundary. For example,
Figure 3a shows a rectangular supergrid graph
which is called 8-rectangle and contains
boundary edges.
Figure 3a also indicates the types of edges and corners. In the figures we will assume that
are coordinates of the upper-left corner in
, except when we explicitly change this assumption.
A
L-shaped supergrid graph, denoted by
, is a supergrid graph obtained from a rectangular supergrid graph
by cutting its subgraph
from the upper-right corner, where
and
. A
C-shaped supergrid graph is a supergrid graph obtained from a rectangular supergrid graph
by removing its subgraph
from its node coordinated as
while
and
have exactly one border side in common, where
,
,
,
,
, and
. The structures of
and
are explained in
Figure 3b,c, respectively.
In our method, we need to partition a rectangular or C-shaped supergrid graph into disjoint parts, where . The partition is defined as follows.
Definition 1. Assume that is a rectangular supergrid graph or a C-shaped supergrid graph . A separation operation on is a partition of into η vertex-disjoint rectangular or L-shaped supergrid subgraphs , , ⋯, , i.e., and for and , where . A separation is called horizontal if it consists of a set of vertical edges, and is called vertical if it contains a set of horizontal edges. Note that horizontal or vertical separation may be empty in our partition for the presentation of clarity. For example, Figure 3a indicates a horizontal (resp., vertical) separation of which partitions it into and (resp., and ). Let
be a rectangular supergrid graph with
,
be a cycle of
, and let
H be a boundary of
. The restriction of
to
H is denoted by
. If
, i.e.,
is a boundary path on
H, then
is called
flat face on
H. If
and
contains at least one boundary edge of
H, then
is called
concave face on
H. A Hamiltonian cycle of
is called
canonical if it contains three flat faces on two shorter boundaries and one longer boundary, and it contains one concave face on the other boundary, where the shorter boundary consists of three vertices. A Hamiltonian cycle of
with
or
is said to be
canonical if it contains three flat faces on three boundaries, and it contains one concave face on the other boundary. The following lemma states the result in [
16] concerning the Hamiltonicity of rectangular supergrid graphs.
Lemma 1 (See [
16])
. Assume that is a rectangular supergrid graph with . Then, the following statements hold true:- (1)
contains a canonical Hamiltonian cycle;
- (2)
with or contains four canonical Hamiltonian cycles with concave faces being on different boundaries.
Figure 4 shows canonical Hamiltonian cycles for rectangular supergrid graphs found in Lemma 1. Each Hamiltonian cycle constructed by this lemma contains all the boundary edges on any three sides of the rectangular supergrid graph. This shows that for any rectangular supergrid graph
with
, we can construct four canonical Hamiltonian cycles such that their concave faces are placed on different boundaries. For instance, the four distinct canonical Hamiltonian cycles of
are shown in
Figure 4b–e.
Let denote supergrid graph G with two specified distinct vertices s and t. Without loss of generality, we will assume that in the rest of the paper. We denote a Hamiltonian path between s and t in G by . We say that does exist if there is a Hamiltonian -path in G. From Lemma 1, does exist if and is an edge in the constructed Hamiltonian cycle of .
Definition 2. Assume that G is a connected supergrid graph and is a subset of the vertex set . is called a vertex cut if is disconnected. A vertex is said to be a cut vertex if is disconnected.
In [
12], the authors showed that
does not exist if the following condition hold:
s or
t is a cut vertex, or
is a vertex cut (see
Figure 5).
Assume
G is any supergrid graph. The following lemma shows that
does not exist if
satisfies condition (F1), and can be verified by the same arguments in [
23].
Lemma 2 (See [
23])
. Assume that G is a supergrid graph with two vertices s and t. If satisfies condition , then does not exist. The Hamiltonian
-path of
constructed in [
12] satisfies that it contains at least one boundary edge of each boundary, and is called
canonical.
Lemma 3 (See [
12])
. Assume is a rectangular supergrid graph and . If does not satisfy condition , then there exists a canonical Hamiltonian -path of . Lemma 4 (See [
17])
. Assume is a rectangular supergrid graph with and , and s and t are its two distinct vertices. Let , , and . If does not satisfy condition , then there exists a canonical Hamiltonian -path P of such that if does satisfy condition ; and otherwise, where condition is defined as follows: and , or and .
We then give some observations on the relations among cycle, path, and vertex. These propositions will be used in proving our results and are given in [
12].
Proposition 1 (See [
12])
. Let G be a graph. Assume and are two vertex-disjoint cycles of G, and are two vertex-disjoint paths of G, and are a cycle and a path, respectively, of G with , and assume x is a vertex in or . Then, the following statements hold true:- (1)
If there exist two edges and such that , then and can be combined into a cycle of G (see Figure 6a). - (2)
If there exist two edges and such that , then and can be combined into a path of G (see
Figure 6b). - (3)
If vertex x adjoins one edge of (resp., ), then (resp., ) and x can be merged into a cycle (resp., path) of G (see
Figure 6c). - (4)
If there exists one edge such that and , then and can be combined into a path of G (see
Figure 6d).
Next, we will discover one Hamiltonian connected property of 3-rectangle
with
that will be used in to prove our result. Let
,
, and
be three vertices of
. Assume that
and edges
,
. Assume that
. We will prove that there exists a Hamiltonian
-path
P of
such that
. Before giving this property, we first give one result in [
12] for 3-rectangle as follows.
Lemma 5 (See [
12])
. Assume is a 3-rectangle with and being its two distinct vertices. Then, contains a canonical Hamiltonian -path which contains at least one boundary edge of each boundary in . By using the above lemma, we will prove the following lemma.
Lemma 6. Assume is a 3-rectangle with and being its two distinct vertices. Let , , and , which are the three vertices of , and let edges , . If , then there exists a Hamiltonian -path of containing and .
Proof. We will prove this lemma by induction on
m. Let
. Then,
, where
. Initially, let
. Then,
and
. By considering every case, we can construct the desired Hamiltonian
-path of
, as shown in
Figure 7a–o. Assume that the lemma holds true when
. Consider that
. Then,
is a subgraph of
, where
,
,
, and
. Let
. By Lemma 5,
contains a Hamiltonian
-path
such that it contains an edge
locating to face
. Then,
and
. By Statement (4) of Proposition 1,
and
can be combined into a Hamiltonian
-path of
. The construction of such a Hamiltonian path is depicted in
Figure 7p. Thus, the lemma holds when
. By induction, the lemma holds true. □
In addition to condition (F1) (see
Figure 8a,b), in [
17], we showed that
does not exist whenever one of the following conditions is satisfied.
assume that
G is a supergrid graph, there exists a vertex
such that
,
, and
(see
Figure 8c).
,
,
,
, and
or
(see
Figure 8d).
Theorem 1 (See [
17])
. Assume that is a L-shaped supergrid graph with vertices s and t. Then, does exist if and only if does not satisfy conditions ,
, and .
The following lemma shows the Hamiltonicity of L-shaped supergrid graphs.
Theorem 2 (See [
17])
. Assume that is a L-shaped supergrid graph. Then, contains a Hamiltonian cycle if and only if it does not satisfy condition ,
where condition is defined as follows:there exists a vertex winsuch that.
Theorem 3 (See [
12,
17])
. Assume that G is or
with two distinct vertices s and t. Then, a longest -path in G can be computed in -linear time.
3. The Necessary and Sufficient Conditions for the Hamiltonicity and Hamiltonian Connectivity of C-Shaped Supergrid Graphs
In this section, we will give the necessary and sufficient conditions for C-shaped supergrid graphs containing a Hamiltonian cycle and Hamiltonian -path. First, we will verify the Hamiltonicity of C-shaped supergrid graphs. If or there exists a vertex such that , then contains no Hamiltonian cycle. Therefore, is not Hamiltonian if condition (F6) is satisfied, where condition (F6) is defined as follows:
or there exists a vertex such that .
Theorem 4. has a Hamiltonian cycle if and only if it does not satisfy condition .
Proof. Only if part : Assume that satisfies condition (F6), then we will prove that it contains no Hamiltonian cycle. Let such that if ; otherwise . It is obvious that any cycle in must pass through v twice. Therefore, contains no Hamiltonian cycle.
If part : We will prove this statement by constructing a Hamiltonian cycle of . There are two cases:
Case 1:
and
. If
, then there exists a vertex
such that
. Thus,
. We make vertical and horizontal separations on
to obtain three disjoint rectangular supergrid subgraphs
,
, and
, as depicted in
Figure 9a. Assume that
and
. By Lemma 1,
contains a canonical Hamiltonian cycle
(see
Figure 9b). We can place one flat face of
to face
and
. Thus, there exists an edge
such that
and
. By Statement (3) of Proposition 1,
v and
can be combined into a cycle
. By the same argument,
u can be merged into the cycle
to form a Hamiltonian cycle of
, as shown in
Figure 9c.
Case 2:
or
. By symmetry, assume that
. We make a horizontal separation on
to obtain two disjoint supergrid subgraphs
and
, as depicted in
Figure 9d,e, where
Figure 9d,e respectively, indicate the case of
and
. By Theorem 2 (resp. Lemma 1),
(resp.
) contains a Hamiltonian (resp. canonical Hamiltonian) cycle
(resp.
) such that its one flat face is placed to face
(resp.
). Then, there exist two edges
and
such that
; as shown in
Figure 10a,b. By Statement (1) of Proposition 1,
and
can be combined into a Hamiltonian cycle of
, as shown in
Figure 10c,d. □
Now, we give the necessary and sufficient conditions for the existence of a Hamiltonian
-path in
. In addition to condition (F1) (as depicted in
Figure 11a,b) and (F3) (as depicted in
Figure 11c), if
satisfies one of the following conditions, then it contains no Hamiltonian
-path.
,
, and
and
or
or
and
or
(see
Figure 11d).
, , and
- (1)
,
, and
(see
Figure 11e); or
- (2)
,
,
, and
(see
Figure 11f); or
- (3)
,
, and
(see
Figure 11g).
, and (
or
) (see
Figure 11h).
Lemma 7. If exists, then does not satisfy conditions , , , , and .
Proof. Assume that
satisfies one of the conditions (F1), (F3), (F7), (F8), and (F9), then we show that
does not exist. For conditions (F1) and (F3), it is clear (see
Figure 11a–c). For condition (F7), by inspecting all cases of
Figure 11d there exists no Hamiltonian
-path. For cases (1)–(2) of condition (F8), consider
Figure 11e,f. Let
v be a vertex depicted in these figures. Since
is a vertex cut of
, then
is disconnected and contains three (or two) components in which two components (or one component) consist of only one vertex. Hence, any path between
s and
t must pass through
s or
v twice. Therefore,
contains no Hamiltonian
-path. For case (3) of condition (F8), consider
Figure 11g. A simple check shows that there is no Hamiltonian
-path in
containing both of vertices
u and
v. For condition (F9), consider
Figure 11h. Let
such that
and
. Since
,
v is a cut vertex of
. Obviously, any path between
s and
t must pass through
v two times. Therefore,
contains no Hamiltonian
-path. □
In the following, we will show that has a Hamiltonian -path when does not satisfy conditions (F1), (F3), (F7), (F8), and (F9). We consider the case of in Lemma 8 and the case of in Lemmas 9 and 10.
Lemma 8. Assume thatanddoes not satisfy conditions, , and. Thendoes exist.
Proof. Notice that, here,
and
or
and
. If
,
, or
, then
satisfies condition (F1) or (F9). Without loss of generality, assume that
and
. We make a horizontal separation on
to obtain two disjoint subgraphs
,
. Let
and
such that
,
, and
if
; otherwise
(see
Figure 12a). Consider
. Condition (F1) holds, if
- (i)
, , and . Clearly, if this case holds, then satisfies condition (F1), a contradiction.
- (ii)
and . Clearly, in this case, . It contradicts that when .
Therefore,
does not satisfy condition (F1). Now, consider
. Since
and
, it is enough to show that
does not satisfy condition (F1). Condition (F1) holds, if
,
, and
. Clearly, if this case holds, then
satisfies condition (F1), a contradiction. Therefore,
does not satisfy conditions (F1), (F3), and (F4). Since
and
do not satisfy conditions (F1), (F3), and (F4), by Lemma 3 and Theorem 1, there exist Hamiltonian
-path
and Hamiltonian
-path
of
and
, respectively (see
Figure 12b). Then,
forms a Hamiltonian
-path of
, as depicted in
Figure 12c. □
Lemma 9. Assume , , and does not satisfy conditions , , , and . Then does exist.
Proof. Depending on whether , we consider the following cases:
Case 1: . Notice that, here, if , then . If and and , then satisfies (F1) or (F3). Consider the positions of s and t, as there are the following two subcases:
Case 1.1:
or
. Without loss of generality, assume that
and
. We make a vertical and a horizontal separations on
to obtain two disjoint supergrid subgraphs
and
, as depicted in
Figure 13a–c. Let
and
such that
,
, and
if
; otherwise
(see
Figure 13a–c). Here, if
(i.e.,
, then
. Consider
. Condition (F1) holds, if
and
, or
and
. Clearly, in any case, it contradicts that
when
. Condition (F3) holds, if
and
. If this case holds, then
satisfies condition (F3), a contradiction. Condition (F4) holds, if
,
,
,
, and
. It contradicts that
when
. Thus,
does not satisfy conditions (F1), (F3), and (F4). Now, consider
. Since
and
, clearly
does not satisfy condition (F1). A Hamiltonian
-path of
can be constructed by similar arguments in proving Lemma 8, as shown in
Figure 13d.
Case 1.2: . In this subcase, and hence . If , then satisfies (F3). Since does not satisfy condition (F8), . There are two subcases:
Case 1.2.1:
. Let
,
, and
. Let
and
. We make a vertical and horizontal separations on
to obtain three disjoint rectangular supergrid subgraphs
,
, and
; as depicted in
Figure 14a. Assume that
and
. By Lemma 6, where
, or Lemma 3, where
,
contains a Hamiltonian
-path
such that
(see
Figure 14b). Then,
,
u,
v can be combined into a Hamiltonian
-path of
by Statement (3) of Proposition 1 (see
Figure 14c).
Case 1.2.2:
and
. Since
does not satisfy conditions (F1), (F7), and (F8), we have that (1)
or
if
, and (2)
or
if
. Thus,
or
. By symmetry, assume that
. We make a vertical separation on
to obtain two disjoint supergrid subgraphs
and
, as depicted in
Figure 14d,e. Let
and
such that
,
, and
if
; otherwise
(see
Figure 14d,e).
Notice that, here, if , then . If and , then satisfies condition (F8). Consider . Since , , and , clearly does not satisfy conditions (F1), (F3), and (F9). Here, lies on Lemma 8. Now, consider . Condition (F1) holds, if
- (i)
and . In this case, satisfies condition (F7), a contradiction.
- (ii)
and . Clearly if , then . Hence, .
Therefore,
does not satisfy condition (F1). By Lemmas 3 and 8,
and
contain Hamiltonian
-path
and
-path
, respectively. Then,
forms a Hamiltonian
-path of
, as depicted in
Figure 14f.
Case 2:
. Since
and
, it follows that
. We make a horizontal separation on
to obtain two disjoint supergrid subgraphs
and
, where
,
, and
(see
Figure 15a–c). Since
and
, clearly
. Also since
and
, it follows that
. Depending on the positions of
s and
t, there are the following two subcases:
Case 2.1: or . Without loss of generality, assume that . Here, . If , then satisfies condition (F3).
Case 2.1.1: or and or . Since , it is enough to show that does not satisfy conditions (F1) and (F4). Condition (F1) holds, if
- (i)
. By assumption, this case does not occur.
- (ii)
and . Clearly if this case holds, then satisfies condition (F1), a contradiction.
Condition (F4) holds, if
,
,
,
,
, and
. Clearly, if this case holds, then
satisfies condition (F7), a contradiction. Therefore,
does not satisfy conditions (F1), (F3), and (F4). Since
does not satisfy conditions (F1), (F3), and (F4). By Theorem 1,
contains a Hamiltonian
-path
in which one edge
is placed to face
. By Theorem 2,
contains a Hamiltonian cycle
such that its one flat face is placed to face
. Then, there exist two edges
and
such that
(see
Figure 15d). By Statement (2) of Proposition 1,
and
can be combined into a Hamiltonian
-path of
. The construction of a such Hamiltonian path is depicted in
Figure 15e.
Case 2.1.2: and . In this case, , , , and . If , then satisfies condition (F1). Depending on whether , we consider the following two subcases:
Case 2.1.2.1:
. In this subcase, we can construct a Hamiltonian
-path by the pattern shown in
Figure 16a. Consider
Figure 16a. Since
and
, clearly
does not satisfy conditions (F1), (F3), and (F4). Thus by Theorem 1,
contains a Hamiltonian
-path
. For
, we can construct two paths
and
such that
connects
s and
p,
connects
q and
t,
,
,
, and
, as shown in
Figure 16a. Then,
forms a Hamiltonian
-path of
(see
Figure 16a).
Case 2.1.2.2:
. We make a vertical separation on
to obtain two disjoint subgraphs
and
, where
if
; otherwise
; as shown in
Figure 16b,c. First, let
and consider
Figure 16b. Clearly since
,
does not satisfy condition (F1). By Lemma 3,
contains a canonical Hamiltonian
-path
. Then, there exists one edge
that is placed to face
. By Theorem 2,
and
contain Hamiltonian cycle
and
, respectively. Using the algorithm of [
17], we can construct
and
to satisfy that one flat face of
, which is placed to face
and
, and one flat face of
, which is placed to face
(see
Figure 16d). Then, there exist four edges
,
, and
such that
and
. By Statements (1) and (2) of Proposition 1,
,
, and
can be combined into a Hamiltonian
-path of
. The construction of a such Hamiltonian path is depicted in
Figure 16e. Now, let
and consider
Figure 16c. Since
and
(in
), it is clear that
does not satisfy conditions (F1), (F3), and (F4). By similar arguments in proving
, a Hamiltonian
-path of
can be constructed (see
Figure 16f).
Case 2.2: (
and
) or (
and
). Without loss of generality, assume that
and
. Let
and
such that
, where
Consider and . Condition (F1) holds, if
- (i)
and or and . Obviously in this case, and . It contradicts that when and .
- (ii)
and . If this case holds, then satisfies condition (F1), a contradiction.
Condition (F3) holds, if and . If this case holds, then satisfies condition (F3), a contradiction. Condition (F4) holds, if and and or and . A simple check shows that these cases do not occur. Therefore, and do not satisfy conditions (F1), (F3), and (F4). A Hamiltonian -path of can be constructed by similar arguments in proving Lemma 8. Notice that, here, and are L-shaped supergrid graphs. □
Lemma 10. Assume , or , and does not satisfy conditions , , , and . Then does exist.
Proof. Without loss of generality, assume that
. Since
,
, and
, thus
. We make a horizontal separation on
to obtain two disjoint supergrid subgraphs
and
, where
and
(see
Figure 17a,b). Since
,
,
, and
, it follows that
. Depending on the positions of
s and
t, there are the following three subcases:
Case 1: . In this case, () or ( and ). If and , then satisfies condition (F3), a contradiction. Depending on the size of , we consider the following two subcases:
Case 1.1: (
) or (
and
,
, or
). In this subcase,
is not a vertex cut of
. Then,
does not satisfy condition (F1). By Lemma 3,
contains a canonical Hamiltonian
-path
. Using the algorithm of [
12], we can construct a Hamiltonian
-path
of
in which one edge
is placed to face
. By Theorem 2,
contains a Hamiltonian cycle
. Using the algorithm of [
17], we can construct
such that its one flat face is placed to face
. Then, there exist two edges
and
such that
(see
Figure 17c). By Statement (2) of Proposition 1,
and
can be combined into a Hamiltonian
-path of
. The construction of a such Hamiltonian path is depicted in
Figure 17d.
Case 1.2:
and
. In this subcase,
is a vertex cut of
. Notice that, here,
. If
and
, then
satisfies condition (F1). Without loss of generality, assume that
. We make a vertical and a horizontal separations on
to obtain two disjoint supergrid subgraphs
and
. Let
,
, and
such that
,
,
,
,
, and
(see
Figure 18a,b). A simple check shows that
,
, and
do not satisfy conditions (F1), (F3), and (F4). Thus, by Theorem 1,
,
, and
contain a Hamiltonian
-path
, Hamiltonian
-path
, and Hamiltonian
-path
, respectively. Then,
forms a Hamiltonian
-path of
. The construction of a such Hamiltonian path is depicted in
Figure 18c.
Case 2: . A Hamiltonian -path of can be constructed by similar arguments in proving Case 2.1 of Lemma 9. Notice that, in this case, is a rectangular supergrid graph.
Case 3: ( and ) or ( and ). A Hamiltonian -path of can be constructed by similar arguments in proving Case 2.2 of Lemma 9. Notice that, in this case, is a rectangular supergrid graphs. □
It immediately follows from Lemmas 7–10 that the following theorem holds true.
Theorem 5. does exist if and only if does not satisfy conditions , , , , and .
4. The Longest -Paths in -Shaped Supergrid Graphs
In this section, first for the cases where does not exist, we give the upper bounds on the lengths of the longest paths between s and t. Then, we show that these upper bounds are equal to the lengths of the longest path between s and t. Notice that the isomorphic cases are omitted. In the following, we use to denote the length of the longest -paths and to indicate the upper bound on the length of the longest -paths, where G is a rectangular, L-shaped, or C-shaped supergrid graph. By the length of a path we mean the number of vertices visited by the path. These upper bounds are given in Lemmas 11–13.
We first consider the case of , where . In this case, may satisfy conditions (F1), (F3), or (F9). We compute the upper bound of the longest -path in this case as the following lemma.
Lemma 11. Let and . Assume that satisfies one of the conditions , , and . Then, the following conditions hold:
If (resp., ), then the length of any -path cannot exceed , where (resp., ) (see Figure 19a,b). If and or and , without loss of generality assume that , then the length of any -path cannot exceed , where , , and if ; otherwise (see Figure 19c,d).
Proof. The proof is straightforward, see
Figure 19. □
Next, we consider the case of . In this case, may satisfy conditions (F1), (F3), (F7), or (F8). Depending on the sizes of c and d, we consider the subcases of (1) and (2) or . Consider that . Then, does not satisfy conditions (F3), (F7), and (F8). Thus, may satisfy condition (F1) only. We can see that s or t is not a cut vertex when . Thus, is a vertex cut when satisfies condition (F1). We can see from the structure of that a, c, or d is equal to 2 if is a vertex cut. The following lemma shows the upper bound of the longest -path under that and satisfies condition (F1).
Lemma 12. Assume that and is a vertex cut. Then, the following conditions hold:
If and , then the length of any -path cannot exceed , where , , , , and (see
Figure 20a,b). If , , and and or , and , without loss of generality assume that and , then the length of any -path cannot exceed , where and (see
Figure 20c,d).
Proof. Consider
Figure 20a,b. Removing
s and
t clearly disconnects
into two components
and
. Thus, a simple path between
s and
t can only go through one of these components. Therefore, its length cannot exceed the size of the largest component. Notice that, for (UB4), the length of any path between
s and
t is equal to
(see
Figure 20c,d). Since
, it is obvious that the length of any
-path cannot exceed
. □
In the following, we will consider that
, and (
or
). Without loss of generality, assume that
. We first make a horizontal and a vertical separation on
to obtain two disjoint subgraphs
and
, as depicted in
Figure 21a, where
,
, and
is a path graph. Depending the locations of
s and
t, we consider the following cases:
Case I:
. In this case,
,
, and
. Then,
may satisfy conditions (F1) or (F3), as depicted in
Figure 21b.
Case II:
and
. In this case,
may satisfy conditions (F1) or (F3), as depicted in
Figure 21c.
Case III:
. In this case,
may satisfy conditions (F1), (F3), (F7), or (F8), as depicted in
Figure 21d. If
,
, and
, then it is the same as Case I. Depending on whether
satisfies condition (F1), there are the following three subcases:
Case III.1: s or t is a cut vertex of . In this subcase, , and it is the same as Cases I or II.
Case III.2: is a vertex cut of . Consider the following subcases:
Case III.2.1:
. In this subcase,
or
, as shown in
Figure 22a,b. If
, then
satisfies conditions (F1) and (F3); otherwise it satisfies condition (F1).
Case III.2.2:
,
, and
. In this subcase, it is similar to condition (UB3) in Lemma 12 (see
Figure 22c).
Case III.2.3:
,
,
, and
. In this subcase, it is similar to condition (UB4) in Lemma 12 (see
Figure 22d).
Case III.3: does not satisfy condition (F1). In this subcase, s and t are not cut vertices and is not a vertex cut of . Then, may satisfy conditions (F3), (F7), or (F8). Depending on the size of k, we consider the following subcases:
Case III.3.1: . In this subcase, may satisfy conditions (F7) and (F8), as follows:
Case III.3.1.1:
satisfies condition (F7). In this subcase,
and
and
or
or
and
or
(see
Figure 23a).
Case III.3.1.2:
satisfies condition (F8). In this subcase,
and
(see
Figure 23c–e).
Case III.3.2: . In this subcase, satisfies condition (F3) but it does not satisfy condition (F1). There are the following subcases:
Case III.3.2.1:
and
and
or
or
and
or
. In this subcase, it is the same as Case III.3.1.1 (see
Figure 23b).
Case III.3.2.2:
and
and
or
and
and
(see
Figure 23e,f).
Based on the above cases, we compute the upper bounds of the longest -paths on under that and as the following lemma.
Lemma 13. Assume that and . Let . Then, the following conditions hold:
If , , and ( or ), then the length of any -path cannot exceed (see
Figure 24a,b, and refer to Case I and Case III.1). If , , and or and , then the length of any -path cannot exceed , where , , and if ; otherwise (see
Figure 24c,d, and refer to Cases II and III.1). If (resp., and ), then the length of any -path cannot exceed , where (resp., ) (see
Figure 25a,b, and refer to Case III.2.1). If , , and , then the length of any -path cannot exceed , where , , , , and (see
Figure 25c,d, and refer to Case SIII.2.2). If , , , and , then the length of any -path cannot exceed , where , , , and (see Figure 25e,f, and refer to Case III.2.3). If and or (resp., and or ), then the length of -path cannot exceed , where (resp., ) (see
Figure 26a–c, and refer to Case III.3.1.1 and Case III.3.2.1). If satisfies condition (F8), then the length of -path cannot exceed , where (see Figure 26d–f, and refer to Case III.3.1.2). If does not satisfy condition (F1), , and or and (resp., and and ), then the length of any -path cannot exceed , where (resp., ) (see Figure 26g,h, and refer to Case III.3.2.2).
Proof. For (UB5), consider
Figure 24a,b. There is only one single path between
s and
t that has the specified. For (UB6), consider
Figure 24c,d. Since
and
w is a cut vertex, it is clear that the length of any
-path cannot exceed
.
For (UB7), consider
Figure 25a,b. In
Figure 25a,b,
is a vertex cut and hence removing
s and
t clearly disconnects
into two components. Thus, a simple path between
s and
t can only go through one of these components. Therefore, its length cannot exceed the size of the largest component. Since
, the larger component will be
. For (UB8) and (UB9), consider
Figure 25c–f. The computations of their upper bounds are the same as (UB7), and (UB3) in Lemma 12.
For (UB10), consider
Figure 26a–c. A simple check shows that the length of any
-path cannot exceed
, where
,
,
p,
q are defined in
Figure 26a–c. For (UB11), consider
Figure 26d–f. In
Figure 26d–f, let
and
, where
may be one of
s and
t. Removing
r and
z clearly disconnects
into two components and a simple path between
s and
t can only go through a component that contains
s,
t,
r, and
z. Since the one disjoint component contains only one vertex, the upper bound of the longest
-path will be
. For (UB12), consider
Figure 26g,h. Since
w is a cut vertex, we can easily show that the length of any path between
s and
t cannot exceed
, where
or
. □
Assume that condition (C0) is defined as follows:
does not satisfy any of conditions (F1), (F3), (F7), (F8), and (F9).
Clearly must satisfy one of conditions (C0), (UB1), (UB2), (UB3), (UB4), (UB5), (UB6), (UB7), (UB8), (UB9), (UB10), (UB11), and (UB12). If satisfies (C0), then . Otherwise, can be computed using Lemmas 11–13. We summarize them as follows:
In the following, we will show how to obtain a longest -path for C-shaped supergrid graphs. Notice that if satisfies condition (C0), then, by Theorem 5, it contains a Hamiltonian -path.
Lemma 14. If satisfies one of the conditions –, then .
Proof. We prove this lemma by constructing a -path P such that its length equals to . Consider the following cases:
Case 1: Condition (UB1), (UB7), (UB10), or (UB11) holds. Then, by Lemma 11 (resp. Lemma 13),
, where
or
(resp.
or
) (see
Figure 19a,b,
Figure 25a,b and
Figure 26a–f). Since
is a
L-shaped supergrid graph, by the algorithm of [
17], we can construct a longest
-path in
.
Case 2: Condition (UB2) or (UB6) holds. By Lemma 11 (resp. Lemma 13),
(see
Figure 19c,d and
Figure 24c,d), where
,
(resp.
and
), and
. Then,
and
are
L-shaped and rectangular supergrid graphs, respectively. First, by the algorithms [
12,
17], we can construct a longest
-path
(resp.
) in
(resp.
) and a longest
-path
(resp.
) in
(resp.
), respectively. Then,
(resp.
) forms a longest
-path of
.
Figure 19c,d and
Figure 24c,d show the constructions of such a longest
-path.
Case 3: Conditions (UB3), (UB8), or (UB9) hold. Assume that (UB3) holds. By Lemma 12,
=
, where
,
,
,
, and
(see
Figure 20a,b). Since
and
are
L-shaped supergrid graphs, by the algorithm of [
17] we can construct a longest path between
s and
t in
and
.
Figure 20a,b depicts such a construction. For conditions (UB8) and (UB9), consider
Figure 25c–f. Then,
may be a rectangle. By the algorithm of [
12] we can construct a longest
-path in
if it is a rectangle. In addition,
is a
C-shaped supergrid graph in (UB9) (see
Figure 25e). Then,
satisfies condition (UB12). Its longest
-path can be computed by the algorithm in [
17]. Its construction is shown in Case 6 and
Figure 25e shows such a construction of the longest
-path.
Case 4: Condition (UB4) holds. By Lemma 12,
, where
and
. Consider
Figure 20c,d. Then,
is a
L-shaped supergrid graph and
is a rectangle. By the algorithm of [
17], we can construct a longest
-path
in
that contains edge
locating to face
. By Lemma 1,
contains a canonical Hamiltonian cycle
such that its one flat face is placed to face
. Thus, by Statement (2) of Proposition 1,
and
can be combined into a longest
-path of
.
Case 5: Condition (UB5) holds. By Lemma 13,
. Obviously, the lemma holds for the single possible path between
s and
t (see
Figure 24a,b).
Case 6: Condition (UB12) holds. By Lemma 13,
, where
. We make a vertical and a horizontal separation on
to obtain two disjoint supergrid subgraphs
and
, where
and
(see
Figure 27a). Note that
does not satisfy condition (F1) in this case. Depending on the positions of
s and
t, these are the following three subcases:
Case 6.1:
. A longest
-path of
can be constructed by similar arguments in proving Case 1 of Lemma 10 (see
Figure 27a,b). Then, we can construct a Hamiltonian
-path of
.
Figure 27a,b depicts such constructions. The size of constructed Hamiltonian
-path equals to
, and hence it is the longest
-path of
.
Case 6.2:
. A longest
-path of
can be constructed by similar arguments in proving Case 2 of Lemma 10 (see
Figure 27c,d). Depending on whether
is a vertex cut of
, we consider
Figure 27c,d. Then, we can construct a Hamiltonian
-path of
, as shown in
Figure 27a,b. The size of constructed Hamiltonian
-path equals to
, and hence it is the longest
-path of
.
Case 6.3: and or and . Without loos of generality, assume that and . A longest -path of can be constructed by similar arguments in proving Case 2.2 of Lemma 9 and Case 3 of Lemma 10. □
Based on Lemmas 8–10 and Lemmas 11–14, we present Algorithm 1 to solve the longest path problem on
C-shaped supergrid graph. Let the input of Algorithm 1 be a
C-shaped supergrid
and vertices
. In Algorithm 1, it needs to determine whether
satisfies conditions (F1), (F3), (F7), (F8), or (F9). Clearly, it can be done in constant time. By Lemmas 8–10,
does exist if
does not satisfy any of conditions (F1), (F3), (F7), (F8), and (F9). By the proofs of Lemmas 8–10,
can be constructed in
time. Consider that
satisfies conditions (F1), (F3), (F7), (F8), or (F9). By Theorem 5,
does not exist. By the proofs of Lemmas 11–14, the longest
-path can be constructed in
time. Thus, Algorithm 1 runs in
-linear time. We finally conclude the following main result.
| Algorithm 1: The longest -path algorithm. |
Input: A C-shaped supergrid graph with , and two distinct vertices s and t in . Output: The longest -path. if and does not satisfy the forbidden conditions (F1), (F3), (F7), (F8), and (F9), then output constructed from Lemma 8; if, , and does not satisfy the forbidden conditions (F1), (F3), (F7), and (F8), then output constructed from Lemma 9;
if, or , and does not satisfy the forbidden conditions (F1), (F3), (F7), and (F8), then output constructed from Lemma 10; if satisfies one of the forbidden conditions (F1), (F3), (F7), (F8), and (F9), then output the longest -path based on Lemma 14.
|
Theorem 6. Given a C-shaped supergrid graph and its two distinct vertices s and t, Algorithm 1 computes a longest -path in -linear time.
Let G be a graph and let . The all-pairs longest path problem is to find the longest paths between all pairs of vertices in G. The most obvious solution to the all-pairs longest path problem is to run a longest path algorithm times since there are pairs of vertices. Let . Then, . By calling Algorithm 1 times, the all-pairs longest path problem for can be solved. Thus, the following corollary holds true.
Corollary 1. Given a C-shaped supergrid graph , the all-pairs longest path problem can be solved in time by calling Algorithm 1 times.