Binary Horse Optimization Algorithm for Feature Selection
Abstract
:1. Introduction
- (1)
- Presentation of the main steps of the original version of the Horse Optimization Algorithm (HOA) introduced in [24];
- (2)
- Adaptation of the HOA to the Binary Horse Optimization Algorithm (BHOA) for feature selection optimization problems;
- (3)
- Application of the BHOA to nine state-of-the-art datasets from the UCI machine learning repository [25], which are representative for classification problems, using the classification algorithms RF, SVM, GBT, LR, K-NN, and NB;
- (4)
- Comparison of the results with the ones obtained using three other bio-inspired approaches, based on binary versions of the GWO, PSO, and Crow Search Algorithm (CSA) [26].
2. Related Work
2.1. The Horse Optimization Algorithm and Its Applications
2.2. Bio-Inspired Approaches for Feature Selection
3. Methods
3.1. HOA
- Step 1. horses are initialized randomly in the -dimensional search space.
- Step 2. The algorithm computes the fitness value of each horse using the objective function and updates the value of the best horse .
- Step 3. The value of is initialized to .
- Step 4. The best horses according to the fitness value are the leaders of the herds from the set of newly initialized herds such that .
- Step 5. The next best horses according to the fitness value are single stallions and form the set .
- Step 6. The remaining horses are assigned randomly to herds from .
- Step 7. The worst horses in terms of fitness value are distributed randomly in the -dimensional search space, their fitness values are recomputed, and the value of is updated accordingly.
- Step 8. For each herd of size from , the ranks are from such that the highest rank values are assigned to the horses with the best fitness values, which are the minimum values in case of minimization problems or the maximum values in case of maximization problems. If two horses with indices , from have the same fitness value, such that , then the horse with the index has a higher rank than the horse with the index . The center of the herd is computed as the weighted arithmetic mean of the positions of the horses such that the weights are the ranks.The instructions from Step 9 to Step 14 are performed for each horse.
- Step 9. The gait is updated to a random value from .
- Step 10. The formula for updating the position for a single stallion is:such that , are the values of the velocity in and , is a random value from , is the gait of the horse , is the center of the nearest herd, namely, the one for which the Euclidean distance between the position of the stallion and the center of the herd is minimum, and is the position of the stallion in the current .
- Step 11. If the horse belongs to a herd, then its velocity is updated using the formula:such that and are the rank of and the center of the herd, respectively.
- Step 12. The formula for the updating of the position is:where and represent the positions in and , respectively.
- Step 13. The -dimensional memory pool is updated as follows:where for any the formula for the updating of memory is:such that is the normal distribution with mean and standard deviation .
- Step 14. The new fitness value of the horse is computed as the best value between the fitness value of the position and the fitness values of the matrix elements. If an element of has a better fitness value than , then is updated to the value of that element. If has a better fitness value than , then is updated to .
- Step 15. The instructions performed in this step are the ones performed in Step 8.
- Step 16. For each single stallion from , the nearest herd is determined. If the single stallion has a better fitness value than the stallion of the herd, then the two stallions are swapped as follows: (1) the single stallion becomes the leader of the herd, (2) the leader of the herd becomes a single stallion, and (3) the positions of the two stallions are switched.
- Step 17. The value of is incremented by .
- Step 18. The algorithm returns the value of .
3.2. BHOA for Feature Selection
| Algorithm 1. BHOA for feature selection. | |
| 1: | Input , , , , , , , , |
| 2: | Output |
| 3: | initialize a population of horses in the -dimensional space |
| 4: | adjust the positions of the horses |
| 5: | apply to compute the fitness values of the horses and update |
| 6: | for to do |
| 7: | if then |
| 8: | the best horses are leaders of herds from |
| 9: | the next best horses represent set |
| 10: | the remaining horses are distributed randomly to herds from |
| 11: | the worst horses are positioned randomly |
| 12: | end if |
| 13: | compute the horse ranks and the left of each herd from |
| 14: | for each horse do |
| 15: | update the gait |
| 16: | if single then |
| 17: | update the velocity using Formula (1) |
| 18: | else |
| 19: | update the velocity using Formula (2) |
| 20: | end if |
| 21: | update the position by applying the Formula (6) to the velocity and adjust it |
| 22: | update the -dimensional memory using the Formulas (4)–(6) and adjust it |
| 23: | update the new fitness value, the position, and |
| 24: | end for |
| 25: | compute the horse ranks and the left of each herd from |
| 26: | swapping stallions operations |
| 27: | end for |
| 28: | return |
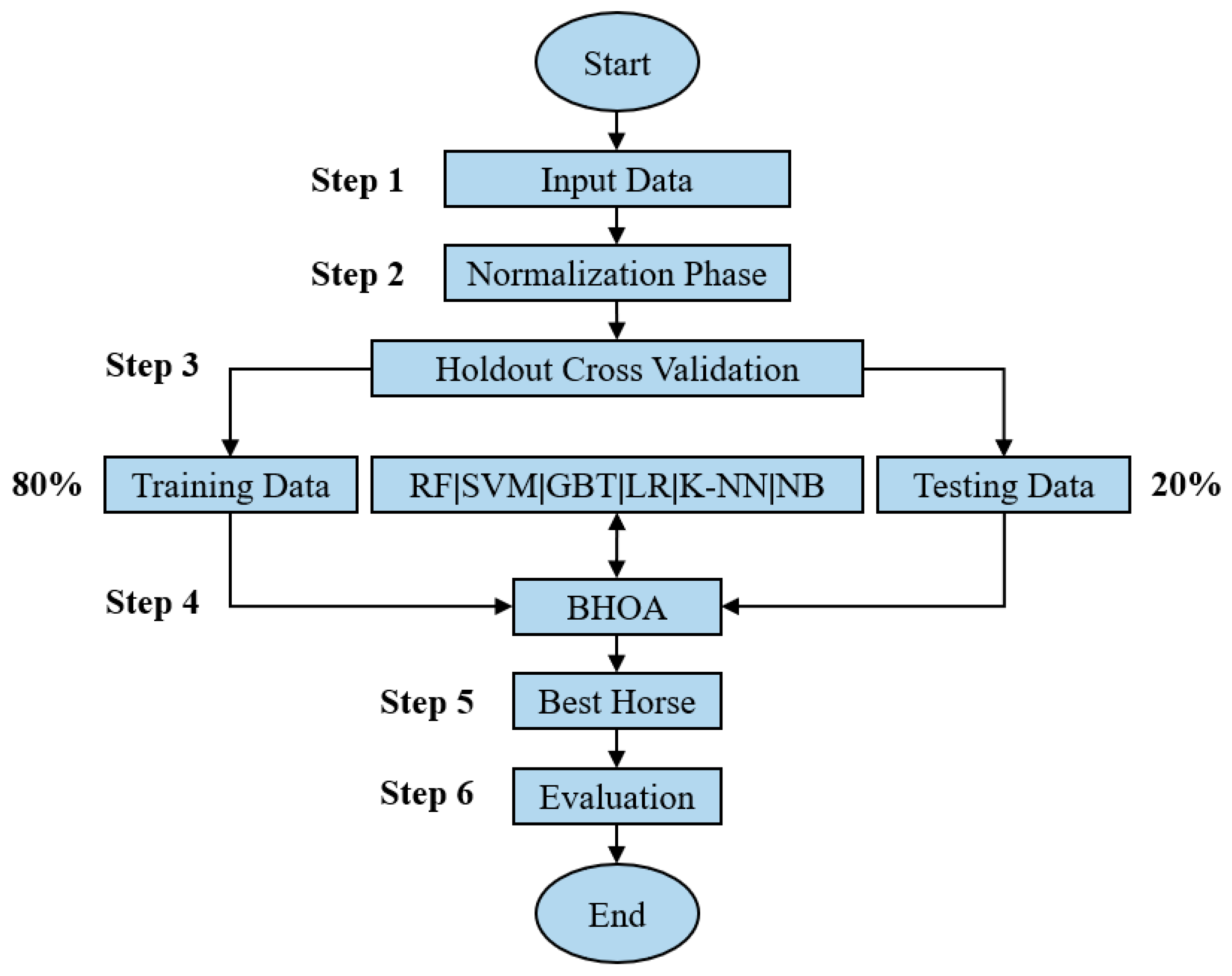
3.3. BHOA Machine Learning Methodology for Feature Selection
- (1)
- the data samples have the same number of features;
- (2)
- the number of features is greater than or equal to ;
- (3)
- each data sample has a label which is an integer value greater than or equal to ;
- (4)
- the values corresponding to the features are real numerical values.
- Step 1. The input data is represented by a dataset characterized by data samples with an equal number of features, which is a number greater than , a label which is an integer value greater than or equal to , and features described by real numerical values.
- Step 2. In the normalization phase, the values corresponding to the features are normalized to take values from , while the labels are not altered.
- Step 3. In the holdout cross-validation phase, the input data is split randomly into 80% training data and 20% testing data.
- Step 4. The BHOA algorithm is applied in feature selection. For each running of the algorithm, a different from the possible classifiers RF, SVM, GBT, LR, K-NN, and NB, is selected. The objective function is adapted to the following formula:where is the number of selected features which is equal to the number of s of the position , is equal to , which is the number of dimensions of the search space, and is the Root Mean Squared Error (RMSE), computed using as parameters the testing data and the values predicted by the when the features were selected according to .
- Step 5. The best horse is the one for which the value of is minimal, as the objective of the optimization problem is to obtain the best prediction results using as few features as possible.
- Step 6. The performance is evaluated using the standard classification metrics:where , , , and are the true positives, true negatives, false positives, and false negatives for binary classification problems. The metric was not considered because for multi-label classification problems the value of the is equal to the value of the . In particular, the values for and are computed as weighted values.
4. Results
4.1. Experimental Data Description
- (1)
- Smart Grids Data: The original data is the Electrical Grid Stability Simulated Data Dataset. The dataset was generated for a smart grid with one producer and three consumers, and the features describe the reaction time of the participants, the power consumed/produced, and the gamma coefficients of the price elasticity. The 13th feature, which represents the maximal real part corresponding to the characteristic equation root, is removed. The 14th feature is represented by the labels column. The values ‘stable’ and ‘unstable’ are converted into 1 and 0, respectively.
- (2)
- Raisin Data [39]: This dataset contains information from images of Besni and Kecimen raisin varieties that were grown in Turkey. The features describe the area, perimeter, major axis length, minor axis length, eccentricity, convex area, and extent. The labels column is represented by the ‘class’ column. The labels ‘Kecimen’ and ‘Besni’ were converted into 0 and 1, respectively.
- (3)
- Turkish Music Emotion Data [40]: The data are developed as a discrete model. The four classes of this data are ‘happy’, ‘sad’, ‘angry’, and ‘relaxed’. The dataset is prepared using non-verbal music and verbal music from various genres of Turkish music. The labels ‘happy’, ‘sad’, ‘angry’, and ‘relaxed’ are converted into 1, 2, 3, and 0, respectively.
- (4)
- Diabetes Risk Prediction Data [41]: The original data are from the Early Stage Diabetes Risk Prediction Dataset. The features contain information about the age of the monitored subjects and various conditions such as obesity, visual blurring, and delayed healing. The labels column is called ‘class’, and the two types of possible labels are ‘positive’ and ‘negative’. The categorical values are converted to numerical values as follows: ‘female’, ‘yes’, and ‘positive’ are converted to 1, while ‘male’, ‘no’, and ‘negative’ are converted to 0.
- (5)
- Rice Data [42]: The Rice (Cammeo and Osmancik) Data Set contains data about the Osmancik and Cammeo species of rice. For each grain of rice, seven morphological features were extracted, namely, the area, perimeter, major axis length, minor axis length, extent, convex area, and eccentricity. The ‘class’ column represents the labels. The values ‘Cammeo’ and ‘Osmancik’ were converted into 0 and 1, respectively.
- (6)
- Parkinson’s Disease Data [43]: The Parkinson’s Disease Classification Data Set was gathered from 108 patients with Parkinson’s Disease, as follows: 81 women and 107 men. The 64 healthy individuals are represented by 41 women and 23 men. The column ‘id’ was removed in the preprocessed data.
- (7)
- Cervical Cancer Data: The Cervical Cancer (Risk Factors) Data Set contains data which were collected at the Hospital Universitario de Caracas in Caracas, Venezuela. The data were collected from 858 patients, and describe demographic information, historical medical records, and habits. The missing values were replaced using the mean heuristic. The four target variables ‘Hinselmann’, ‘Schiller’, ‘cytology’, and ‘biopsy’ were converted into a single target variable equal to . This conversion led to the following set of labels: {0, 1, 2, 3, 4, 5, 6, 7, 8, 12, 13, 14, 15}. Then, the labels {12, 13, 14, 15} were converted into {9, 10, 11, 12}, such that the final labels were {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
- (8)
- Chronic Kidney Disease Data: These data can be used to predict chronic kidney disease, and the attributes contain information about various characteristics such as age, blood pressure, sugar, specific gravity, and red blood cell count. The values ‘abnormal’, ‘notpresent’, ‘no’, ‘poor’, and ‘notckd’ were converted to 0, while the categorical values ‘normal’, ‘present’, ‘yes’, ‘good’, and ‘ckd’ were converted to 1. The missing values were replaced using the mean heuristic.
- (9)
- Breast Cancer Coimbra Data: The data are characterized by nine features which describe quantitative data, such as age, Body Mass Index (BMI), and glucose level, and one ‘labels’ column. In the initial version of the data, the healthy controls were labeled with 1, while the patients were labeled with 2. In the processed data, the healthy controls and the patients were labeled with 0 and 1, respectively.
4.2. BHOA Experimental Results
5. Discussion
- (1)
- Binary Grey Wolf Optimizer (BGWO);
- (2)
- Binary Particle Swarm Optimization (BPSO);
- (3)
- Binary Crow Search Algorithm (BCSA).
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brodzicki, A.; Piekarski, M.; Jaworek-Korjakowska, J. The Whale Optimization Algorithm Approach for Deep Neural Networks. Sensors 2021, 21, 8003. [Google Scholar] [CrossRef]
- Rojas-Dominguez, A.; Padierna, L.C.; Valadez, J.M.C.; Puga-Soberanes, H.J.; Fraire, H.J. Optimal Hyper-Parameter Tuning of SVM Classifiers With Application to Medical Diagnosis. IEEE Access 2017, 6, 7164–7176. [Google Scholar] [CrossRef]
- Deb, S.; Gao, X.-Z.; Tammi, K.; Kalita, K.; Mahanta, P. Recent Studies on Chicken Swarm Optimization algorithm: A review (2014–2018). Artif. Intell. Rev. 2020, 53, 1737–1765. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Studies in Computational Intelligence; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Ghaemi, M.; Feizi-Derakhshi, M.R. Forest Optimization Algorithm. Expert Syst. Appl. 2014, 41, 6676–6687. [Google Scholar] [CrossRef]
- Cheraghalipour, A.; Hajiaghaei-Keshteli, M.; Paydar, M.M. Tree Growth Algorithm (TGA): A novel approach for solving optimization problems. Eng. Appl. Artif. Intell. 2018, 72, 393–414. [Google Scholar] [CrossRef]
- Zhou, M.; Lin, F.; Hu, Q.; Tang, Z.; Jin, C. AI-Enabled Diagnosis of Spontaneous Rupture of Ovarian Endometriomas: A PSO Enhanced Random Forest Approach. IEEE Access 2020, 8, 132253–132264. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Wijaya, A.P.; Santoso, H.A. Improving the Accuracy of Naïve Bayes Algorithm for Hoax Classification Using Particle Swarm Optimization. In Proceedings of the 2018 International Seminar on Application for Technology of Information and Communication, Semarang, Indonesia, 21–22 September 2018; pp. 482–487. [Google Scholar]
- Agarwal, K.; Kumar, T. Email Spam Detection Using Integrated Approach of Naïve Bayes and Particle Swarm Optimization. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 685–690. [Google Scholar]
- Lee, C.-Y.; Huang, K.-Y.; Shen, Y.-X.; Lee, Y.-C. Improved Weighted k-Nearest Neighbor Based on PSO for Wind Power System State Recognition. Energies 2020, 13, 5520. [Google Scholar] [CrossRef]
- Nagaraj, P.; Deepalakshmi, P.; Mansour, R.F.; Almazroa, A. Artificial Flora Algorithm-Based Feature Selection with Gradient Boosted Tree Model for Diabetes Classification. Diabetes Metab. Syndr. Obes. Targets Ther. 2021, 14, 2789–2806. [Google Scholar]
- Cheng, L.; Wu, X.-h.; Wang, Y. Artificial Flora (AF) Optimization Algorithm. Appl. Sci. 2018, 8, 329. [Google Scholar] [CrossRef] [Green Version]
- Ravi, V.; Madhav, V. Optimizing the Reliability of a Bank with Logistic Regression and Particle Swarm Optimization. In Data Management, Analytics and Innovation. Lecture Notes on Data Engineering and Communications Technologies; Sharma, N., Chakrabarti, A., Balas, V.E., Bruckstein, A.M., Eds.; Springer: Singapore, 2021; Volume 70, pp. 91–107. [Google Scholar]
- Li, M.-W.; Geng, J.; Wang, S.; Hong, W.-C. Hybrid Chaotic Quantum Bat Algorithm with SVR in Electric Load Forecasting. Energies 2017, 10, 2180. [Google Scholar] [CrossRef] [Green Version]
- Fang, M.; Lei, X.; Cheng, S.; Shi, Y.; Wu, F.-X. Feature Selection via Swarm Intelligence for Determining Protein Essentiality. Molecules 2018, 23, 1569. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koohestani, A.; Abdar, M.; Khosravi, A.; Nahavandi, S.; Koohestani, M. Integration of Ensemble and Evolutionary Machine Learning Algorithms for Monitoring Diver Behavior Using Physiological Signals. IEEE Access 2019, 7, 98971–98992. [Google Scholar] [CrossRef]
- Cai, J.; Wei, H.; Yang, H.; Zhao, X. A Novel Clustering Algorithm Based on DPC and PSO. IEEE Access 2020, 8, 88200–88214. [Google Scholar] [CrossRef]
- Brezocnik, L.; Fister, I., Jr.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef] [Green Version]
- Tran, M.Q.; Elsisi, M.; Liu, M.-K. Effective feature selection with fuzzy entropy and similarity classifier for chatter vibration diagnosis. Measurement 2021, 184, 109962. [Google Scholar] [CrossRef]
- Tran, M.-Q.; Li, Y.-C.; Lan, C.-Y.; Liu, M.-K. Wind Farm Fault Detection by Monitoring Wind Speed in the Wake Region. Energies 2020, 13, 6559. [Google Scholar] [CrossRef]
- Vo, T.-T.; Liu, M.-K.; Tran, M.-Q. Identification of Milling Stability by using Signal Analysis and Machine Learning Techniques. Int. J. iRobotics 2021, 4, 30–39. [Google Scholar]
- Moldovan, D. Horse Optimization Algorithm: A Novel Bio-Inspired Algorithm for Solving Global Optimization Problems. In CSOC 2020: Artificial Intelligence and Bioinspired Computational Methods; Silhavy, R., Ed.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1225, pp. 195–209. [Google Scholar]
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 19 March 2022).
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems. Knowl.-Based Syst. 2021, 213, 106711. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A New Bio-inspired Algorithm: Chicken Swarm Optimization. In Advances in Swarm Intelligence. ICSI 2014. Lecture Notes in Computer Science; Tan, Y., Shi, Y., Coello, C.A.C., Eds.; Springer: Cham, Switzerland, 2014; Volume 8794, pp. 86–94. [Google Scholar]
- Chu, S.-C.; Tsai, P.-W.; Pan, J.-S. Cat Swarm Optimization. In PRICAI 2006: Trends in Artificial Intelligence; Yang, Q., Webb, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4099, pp. 854–858. [Google Scholar]
- Moldovan, D. Horse Optimization Algorithm Based Recurrent Neural Network Method for Epileptic Seizures Classification. In Proceedings of the 7th International Conference on Advancements of Medicine and Health Care through Technology. MEDITECH 2020. IFMBE Proceedings; Vlad, S., Roman, N.M., Eds.; Springer: Cham, Switzerland, 2022; Volume 88, pp. 183–190. [Google Scholar]
- Moldovan, D.; Anghel, I.; Cioara, T.; Salomie, I. Adapted Binary Particle Swarm Optimization for Efficient Features Selection in the Case of Imbalanced Sensor Data. Appl. Sci. 2020, 10, 1496. [Google Scholar] [CrossRef] [Green Version]
- Alirezazadeh, P.; Fathi, A.; Abdali-Mohammadi, F. A genetic algorithm-based feature selection for kinship verification. IEEE Signal Process. Lett. 2015, 22, 2459–2463. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Gao, X.-Z.; Tian, T.; Sun, X.-Y. Binary differential evolution with self-learning for multi-objective feature selection. Inform. Sci. 2020, 507, 67–85. [Google Scholar] [CrossRef]
- Leutheuser, M.; Schludhaus, D.; Eskofier, B.M. Hierarchical, multi-sensor based classification of daily life activities: Comparison with state-of-the-art algorithms using a benchmark dataset. PloS ONE 2013, 8, e75196. [Google Scholar] [CrossRef] [Green Version]
- Moldovan, D.; Slowik, A. Energy consumption prediction of appliances using machine learning and multi-objective binary grey wolf optimization for feature selection. Appl. Soft Comput. 2021, 111, 107745. [Google Scholar] [CrossRef]
- Patricio, M.; Pereira, J.; Crisostomo, J.; Matafome, P.; Gomes, M.; Seica, R.; Caramelo, F. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC Cancer 2018, 18, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernandes, K.; Cardoso, J.S.; Fernandes, J. Transfer Learning with Partial Observability Applied to Cervical Cancer Screening. In Pattern Recognition and Image Analysis, IbPRIA 2017; Alexandre, L., Salvador Sánchez, J., Rodrigues, J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10255, pp. 243–250. [Google Scholar]
- Cinar, I.; Koklu, M.; Tasdemir, S. Classification of Raisin Grains Using Machine Vision and Artificial Intelligence Methods. GJES 2020, 6, 200–209. [Google Scholar]
- Er, M.B.; Aydilek, I.B. Music Emotion Recognition by Using Chroma Spectrogram and Deep Visual Features. Int. J. Comput. Intell. Syst. 2019, 12, 1622–1634. [Google Scholar]
- Faniqul Islam, M.M.; Ferdousi, R.; Rahman, S.; Bushra, H.Y. Likelihood Prediction of Diabetes at Early Stage Using Data Mining Techniques. In Computer Vision and Machine Intelligence in Medical Image Analysis; Gupta, M., Konar, D., Bhattacharyya, S., Biswas, S., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2020; Volume 992, pp. 113–125. [Google Scholar]
- Cinar, I.; Koklu, M. Classification of Rice Varieties Using Artificial Intelligence Methods. Int. J. Intell. Syst. Appl. Eng. 2019, 7, 188–194. [Google Scholar] [CrossRef] [Green Version]
- Sakar, C.O.; Serbes, G.; Gunduz, A.; Tunc, H.C.; Nizam, H.; Sakar, B.E.; Tutuncu, M.; Aydin, T.; Isenkul, M.E.; Apaydin, H. A comparative analysis of speech signal processing algorithms for Parkinson’s disease classification and the use of the tunable Q-factor wavelet transform. Appl. Soft Comput. 2019, 74, 255–263. [Google Scholar] [CrossRef]

| Classifier | Configuration |
|---|---|
| RF | 10 estimators, 42 random state |
| SVM | 0.00001 tolerance, 42 random state |
| GBT | 10 estimators, 1.0 or 0.001 learning rate |
| LR | default parameters |
| K-NN | 9 neighbors |
| NB | default or 100,000 var smoothing |
| Experimental Dataset | Labels Number | Features Number | Training Data Samples Number | Testing Data Samples Number |
|---|---|---|---|---|
| Smart Grids Data | 2 | 12 | 8000 | 2000 |
| Raisin Data | 2 | 7 | 720 | 180 |
| Turkish Music Emotion Data | 4 | 50 | 320 | 80 |
| Diabetes Risk Prediction Data | 2 | 16 | 416 | 104 |
| Rice Data | 2 | 6 | 3048 | 762 |
| Parkinson’s Disease Data | 2 | 753 | 605 | 151 |
| Cervical Cancer Data | 13 | 32 | 686 | 172 |
| Chronic Kidney Disease Data | 2 | 24 | 320 | 80 |
| Breast Cancer Coimbra Data | 2 | 9 | 93 | 23 |
| Configuration Parameter | Value |
|---|---|
| (number of iterations) | 50 |
| (number of horses) | 30 |
| (horses reorganization frequency) | 5 |
| (dominant stallions percent) | 10% |
| (horses distribution rate) | 10% |
| (horse memory pool) | 3 |
| (single stallions percent) | 10% |
| Dataset | Classifier | Accuracy | Precision | F1 Score | EvalGBest | (nf, RMSE) | Time (ms) |
|---|---|---|---|---|---|---|---|
| Smart Grids Data | RF | 0.912 | 0.912548 | 0.910972 | 0.409985 | (9, 0.296647) | 998,676 |
| SVM | 0.694 | 0.686913 | 0.666302 | 0.456546 | (2, 0.553172) | 361,459 | |
| GBT | 0.899 | 0.898627 | 0.898736 | 0.425853 | (9, 0.317804) | 1,411,226 | |
| LR | 0.6935 | 0.685425 | 0.667392 | 0.456884 | (2, 0.553624) | 127,434 | |
| K-NN | 0.897 | 0.897719 | 0.895522 | 0.407368 | (8, 0.320936) | 1,509,808 | |
| NB | 0.7005 | 0.697274 | 0.670953 | 0.452116 | (2, 0.547265) | 19,477 | |
| Raisin Data | RF | 0.85 | 0.858348 | 0.849698 | 0.361902 | (2, 0.387298) | 109,878 |
| SVM | 0.872222 | 0.880895 | 0.871965 | 0.339523 | (2, 0.357460) | 17,181 | |
| GBT | 0.866666 | 0.870097 | 0.866666 | 0.345289 | (2, 0.365148) | 89,852 | |
| LR | 0.855555 | 0.865277 | 0.855180 | 0.356472 | (2, 0.380058) | 26,454 | |
| K-NN | 0.85 | 0.860997 | 0.849513 | 0.361902 | (2, 0.387298) | 38,053 | |
| NB | 0.85 | 0.864039 | 0.849289 | 0.361902 | (2, 0.387298) | 5984 | |
| Turkish Music Emotion Data | RF | 0.9 | 0.905083 | 0.900721 | 0.545 | (34, 0.5) | 125,597 |
| SVM | 0.925 | 0.923872 | 0.922807 | 0.485473 | (39, 0.387298) | 169,451 | |
| GBT | 0.775 | 0.811160 | 0.786773 | 0.589279 | (26, 0.612372) | 797,135 | |
| LR | 0.925 | 0.929673 | 0.923135 | 0.530756 | (35, 0.474341) | 308,861 | |
| K-NN | 0.825 | 0.832499 | 0.823849 | 0.685330 | (31, 0.707106) | 40,878 | |
| NB | 0.85 | 0.857903 | 0.851368 | 0.514260 | (26, 0.512347) | 11,822 | |
| Diabetes Risk Prediction Data | RF | 0.990384 | 0.990619 | 0.990406 | 0.198543 | (8, 0.098058) | 82,800 |
| SVM | 0.942307 | 0.942307 | 0.942307 | 0.305144 | (8, 0.240192) | 15,158 | |
| GBT | 1.0 | 1.0 | 1.0 | 0.1875 | (12, 0.0) | 45,600 | |
| LR | 0.932692 | 0.933172 | 0.932842 | 0.319577 | (8, 0.259437) | 26,535 | |
| K-NN | 0.932692 | 0.935100 | 0.933101 | 0.288327 | (6, 0.259437) | 29,988 | |
| NB | 0.951923 | 0.954133 | 0.952215 | 0.305073 | (9, 0.219264) | 6495 | |
| Rice Data | RF | 0.913385 | 0.913333 | 0.913302 | 0.304060 | (2, 0.294302) | 240,551 |
| SVM | 0.923884 | 0.924280 | 0.923666 | 0.290251 | (2, 0.275890) | 36,531 | |
| GBT | 0.914698 | 0.914767 | 0.914538 | 0.302381 | (2, 0.292064) | 286,505 | |
| LR | 0.922572 | 0.922770 | 0.922397 | 0.292027 | (2, 0.278258) | 72,552 | |
| K-NN | 0.922572 | 0.922890 | 0.922366 | 0.292027 | (2, 0.278258) | 145,352 | |
| NB | 0.922572 | 0.922553 | 0.922484 | 0.292027 | (2, 0.278258) | 8526 | |
| Parkinson’s Disease Data | RF | 0.847682 | 0.852720 | 0.849814 | 0.333878 | (124, 0.390279) | 759,970 |
| SVM | 0.860927 | 0.856619 | 0.848757 | 0.300941 | (64, 0.372924) | 2,663,289 | |
| GBT | 0.860927 | 0.862374 | 0.861605 | 0.335037 | (187, 0.363937) | 4,859,351 | |
| LR | 0.860927 | 0.859675 | 0.846185 | 0.317210 | (113, 0.372924) | 845,271 | |
| K-NN | 0.860927 | 0.859675 | 0.846185 | 0.318538 | (117, 0.372924) | 1,279,114 | |
| NB | 0.821192 | 0.823018 | 0.822064 | 0.355323 | (115, 0.422856) | 519,532 | |
| Cervical Cancer Data | RF | 0.889534 | 0.908949 | 0.847967 | 1.574075 | (14, 1.952934) | 140,590 |
| SVM | 0.889534 | 0.901737 | 0.837531 | 1.732502 | (4, 2.268336) | 197,975 | |
| GBT | 0.889534 | 0.901737 | 0.837531 | 1.732502 | (4, 2.268336) | 969,271 | |
| LR | 0.889534 | 0.901737 | 0.837531 | 1.732502 | (4, 2.268336) | 214,834 | |
| K-NN | 0.889534 | 0.901737 | 0.837531 | 1.732502 | (4, 2.268336) | 70,139 | |
| NB | 0.889534 | 0.901737 | 0.837531 | 1.732502 | (4, 2.268336) | 15,678 | |
| Chronic Kidney Disease Data | RF | 1.0 | 1.0 | 1.0 | 0.09375 | (9, 0.0) | 91,848 |
| SVM | 1.0 | 1.0 | 1.0 | 0.083333 | (8, 0.0) | 13,385 | |
| GBT | 1.0 | 1.0 | 1.0 | 0.083333 | (8, 0.0) | 60,803 | |
| LR | 1.0 | 1.0 | 1.0 | 0.104166 | (10, 0.0) | 30,407 | |
| K-NN | 1.0 | 1.0 | 1.0 | 0.09375 | (9, 0.0) | 26,898 | |
| NB | 1.0 | 1.0 | 1.0 | 0.145833 | (14, 0.0) | 6673 | |
| Breast Cancer Coimbra Data | RF | 0.913043 | 0.926421 | 0.912714 | 0.304496 | (3, 0.294883) | 84,961 |
| SVM | 0.826086 | 0.826086 | 0.826086 | 0.423882 | (4, 0.417028) | 7934 | |
| GBT | 0.913043 | 0.913043 | 0.913043 | 0.360051 | (5, 0.294883) | 38,080 | |
| LR | 0.739130 | 0.826086 | 0.716304 | 0.438620 | (2, 0.510753) | 17,734 | |
| K-NN | 0.826086 | 0.869565 | 0.819185 | 0.368327 | (2, 0.417028) | 11,024 | |
| NB | 0.782608 | 0.850543 | 0.774133 | 0.460800 | (4, 0.466252) | 5248 |
| Dataset | Classifier | GBest Value |
|---|---|---|
| Smart Grids Data | RF | [111110001111] |
| SVM | [100000000010] | |
| GBT | [111100101111] | |
| LR | [100000000010] | |
| K-NN | [111100001111] | |
| NB | [100000000010] | |
| Raisin Data | RF | [1001000] |
| SVM | [10001] | |
| GBT | [1000001] | |
| LR | [110] | |
| K-NN | [10001] | |
| NB | [100001] | |
| Turkish Music Emotion Data | RF | [01011111111101111111110110101110110110101000101010] |
| SVM | [11111111101110101111011111111011101110111001100111] | |
| GBT | [01111110111010011010101101010101010101100010010000] | |
| LR | [11110010110111010111111011111101000110111011110110] | |
| K-NN | [11111101011111000001111011011101111101011000010010] | |
| NB | [01111100111101110001110000010011111110000000010011] | |
| Diabetes Risk Prediction Data | RF | [1101100000111100] |
| SVM | [0101101110110000] | |
| GBT | [1101011101110111] | |
| LR | [1101101110100000] | |
| K-NN | [1101101000010000] | |
| NB | [1101101010110010] | |
| Rice Data | RF | [100001] |
| SVM | [001010] | |
| GBT | [110000] | |
| LR | [110000] | |
| K-NN | [001010] | |
| NB | [110000] | |
| Parkinson’s Disease Data | RF | [000011000000000000001100000000001000000000000001000001000001000000101010000000000110000000100010000010000100001000011011000000000000000000010000000001000000000000000000100000001000000010010010011000000011010000100000000000000100100000000010000100001000000000100000000100000001011100000001000000001000001100000000000000000101000001000000000110000000111000100011100000000000010000100000000000001101000001110000000000000000000100001010000000000000000000000000100100100000100010000000000000000000000000100000110010100010000000010000000010000100000000000101000000000010000000000001000000100001000100000000010000010001000000000000001000101000000000011000000011001000010010000000010110000110001000000000001000000000000100100000000010010000000100000010110011000] |
| SVM | [000010000000000000000000100000010000000000000100010000000000000000000100000000000000000000000000010000010000000000001000000000010000000000010000000000000000000000000000010001001000000000010000000000001000100000000000000000000000000000000011000000000000000000000001001000000011010000000000000000000000000000000000000000000000000100000000000000000000000000000001000000100000000001000000001000000000000000000100001000100000000000000010000001001000010010000001001000001000000000000000000011000000000000000001000000000001000000000000000001000000000000000000000000000000001000000000000000000010000000000000001000000010011000100000000000000000000000000000010000000000000000000000000010001000001000000000000000000011000000100100000000100000000001010000000000100] | |
| GBT | [100001010010110000110000010001010000000010101000100001101001010000000000011010100100000010000000010100000000100110001100101001100010100001010010000001010000010110011000101000000010000001000000000000110010010000000000000000000000001010001000000110100101001001100001000001010001010001001110001000000000000100000100001000000000010000100000000010100011000100010000100000000000101000010000000011001100000001110001101000010000000001000010010000100100100100110100000000011000000000001111001000000110000010101011000100110001000000110110000010100001000000000100000010111000000001001000010100000000000100001001111100000000011000100011000100001101001000000000000001000101000001000000000010000110001010000110000000000001100000000000000000000010000001000111010110001] | |
| LR | [000010000001000000000000100000110000000001000101010001000100000000101100000010000100000000000000010000011000000000001000000000010001000001010010000000100000000000000001010001001000000000010001000001001000100000000000000000000100000000000011000000100000000000000001101000000011110000000010100000000000001000010001000000000100000100000000010000000000001000001001000001100000000001000000001000100000000000000100001000100000100000000010000001001000010010010001001000001000000000000000000011001000000001000001100000010001000000000000000001000110000000001100000000100000001000000000001000000011000100000000001000000000011000100001000000000000000000001000010000001000000000000000001010001000001000000000000000000010000000100100000000100000000001010000000000100] | |
| K-NN | [000010000100100100000001000100001001000000000000000000011000000000000000011000000010000100000000000010001000001000000001000001010000101001101000000001001000001001000000100000110000100000000100110001000100000000000010000100100000001000000000000000100000000100001000001010100000010001000000000000010000110010000000010001000001000000000010000000000000000000100001000001000000000010000101000000010000000000100000100000001100000000000000001000100000001011000000000000101101000000010010000000000000000001000001000000100000101010000000000000000001000000000000001100000000010000000000000001000010010010000000000000000001100000001000001000001000110001000100000001000000010001000100000000000100001101000000000000110000001000000000000000100001000000000000000000001] | |
| NB | [000000001000100001010000000101000000100000010001000000000000001100100000000100000000010100000100000001000000010000100000010000000000000000001000000010000000000000000000000000000010001011000000110000000010100000110110000000000100000000000000000000000000000000000100100000010000000101000000000010000010100010000110100000000000010000000000011000010010010010100000010000101000001010000000001000010000000000101000100000100000100001100010001000001000000000000000100000000011000000010000010000000000000100000000000101000000100000100000000000000000000000110000000010000101010000000000000110000000000000000000000000010100100101000000000000100110000001110001000000001000000000000001000000000001000000101000000000000000000000101010100000000010100000001000001000000] | |
| Cervical Cancer Data | RF | [11110101010001010101100100100000] |
| SVM | [00010000000100010000000000000001] | |
| GBT | [00010000000100010000000000000001] | |
| LR | [00010000000100010000000000000001] | |
| K-NN | [00100000000000000001001000000100] | |
| NB | [00010000000100010000000000000001] | |
| Chronic Kidney Disease Data | RF | [000101110000101100101000] |
| SVM | [111011010000001000001000] | |
| GBT | [101010000010110100000010] | |
| LR | [111011010100001001001000] | |
| K-NN | [000110001000011011010100] | |
| NB | [111101001011001101111000] | |
| Breast Cancer Coimbra Data | RF | [101001000] |
| SVM | [101010010] | |
| GBT | [101001011] | |
| LR | [001100000] | |
| K-NN | [100100000] | |
| NB | [111000010] |
| Configuration Parameter | Value |
|---|---|
| (number of iterations) | 50 |
| (number of wolves) | 30 |
| Configuration Parameter | Value |
|---|---|
| (number of iterations) | 50 |
| (number of particles) | 30 |
| (initial inertia value) | 0.901 |
| (cognitive component constant) | 2 |
| (social component constant) | 2 |
| Configuration Parameter | Value |
|---|---|
| (number of iterations) | 50 |
| (number of crows) | 30 |
| (flight length) | 0.9 |
| (awareness probability) | 0.5 |
| Dataset | Classifier | Accuracy | Precision | F1 score | EvalGBest | (nf, RMSE) | Time (ms) |
|---|---|---|---|---|---|---|---|
| Smart Grids Data | RF | 0.912 | 0.912548 | 0.910972 | 0.409985 | (9, 0.296647) | 25,1259 |
| SVM | 0.748 | 0.743291 | 0.739087 | 0.459830 | (4, 0.501996) | 60,674 | |
| GBT | 0.899 | 0.898627 | 0.898736 | 0.405020 | (8, 0.317804) | 332,609 | |
| LR | 0.7495 | 0.744781 | 0.741097 | 0.458708 | (4, 0.500499) | 21,082 | |
| K-NN | 0.897 | 0.897719 | 0.895522 | 0.407368 | (8, 0.320936) | 326,848 | |
| NB | 0.7315 | 0.728542 | 0.714810 | 0.451127 | (3, 0.518169) | 4087 | |
| Raisin Data | RF | 0.85 | 0.858348 | 0.849698 | 0.361902 | (2, 0.387298) | 25,023 |
| SVM | 0.861111 | 0.869622 | 0.860832 | 0.350937 | (2, 0.372677) | 3343 | |
| GBT | 0.866666 | 0.870097 | 0.866666 | 0.345289 | (2, 0.365148) | 16,658 | |
| LR | 0.855555 | 0.858942 | 0.855555 | 0.356472 | (2, 0.380058) | 6225 | |
| K-NN | 0.872222 | 0.878514 | 0.872092 | 0.339523 | (2, 0.357460) | 8892 | |
| NB | 0.844444 | 0.859980 | 0.843577 | 0.367232 | (2, 0.394405) | 1479 | |
| Turkish Music Emotion Data | RF | 0.8875 | 0.889423 | 0.886550 | 0.515756 | (32, 0.474341) | 35,934 |
| SVM | 0.9375 | 0.940368 | 0.937143 | 0.418107 | (28, 0.370809) | 31,204 | |
| GBT | 0.825 | 0.834703 | 0.828157 | 0.579262 | (32, 0.559016) | 190,036 | |
| LR | 0.9125 | 0.913035 | 0.910288 | 0.437334 | (27, 0.403112) | 68,773 | |
| K-NN | 0.85 | 0.861757 | 0.848489 | 0.544260 | (32, 0.512347) | 11,434 | |
| NB | 0.8625 | 0.861807 | 0.859248 | 0.52 | (29, 0.5) | 3132 | |
| Diabetes Risk Prediction Data | RF | 1.0 | 1.0 | 1.0 | 0.1875 | (12, 0.0) | 21,041 |
| SVM | 0.932692 | 0.935100 | 0.933101 | 0.288327 | (6, 0.259437) | 3359 | |
| GBT | 0.990384 | 0.990619 | 0.990406 | 0.229793 | (10, 0.098058) | 11,020 | |
| LR | 0.932692 | 0.942716 | 0.933453 | 0.272702 | (5, 0.259437) | 5473 | |
| K-NN | 0.942307 | 0.946037 | 0.942750 | 0.273894 | (6, 0.240192) | 6570 | |
| NB | 0.894230 | 0.894874 | 0.894467 | 0.273823 | (5, 0.260931) | 1477 | |
| Rice Data | RF | 0.910761 | 0.910761 | 0.910761 | 0.307379 | (2, 0.298728) | 47,690 |
| SVM | 0.923884 | 0.924280 | 0.923666 | 0.290251 | (2, 0.275890) | 7404 | |
| GBT | 0.916010 | 0.916127 | 0.915837 | 0.300690 | (2, 0.289809) | 51,724 | |
| LR | 0.919947 | 0.920249 | 0.919734 | 0.295534 | (2, 0.282935) | 10,566 | |
| K-NN | 0.916010 | 0.916127 | 0.915837 | 0.300690 | (2, 0.289809) | 33,522 | |
| NB | 0.921259 | 0.921400 | 0.921097 | 0.293788 | (2, 0.280606) | 2140 | |
| Parkinson’s Disease Data | RF | 0.920529 | 0.918877 | 0.918795 | 0.355813 | (462, 0.269903) | 133,329 |
| SVM | 0.947019 | 0.950437 | 0.944484 | 0.301116 | (387, 0.230174) | 637,241 | |
| GBT | 0.900662 | 0.897880 | 0.897889 | 0.358514 | (392, 0.304491) | 965,475 | |
| LR | 0.907284 | 0.906097 | 0.902848 | 0.347226 | (358, 0.304491) | 183,896 | |
| K-NN | 0.920529 | 0.920877 | 0.916727 | 0.347218 | (409, 0.281904) | 235,658 | |
| NB | 0.834437 | 0.829944 | 0.831787 | 0.430336 | (378, 0.406451) | 22,674 | |
| Cervical Cancer Data | RF | 0.889534 | 0.909969 | 0.845334 | 1.563974 | (11, 1.970715) | 32,820 |
| SVM | 0.889534 | 0.901737 | 0.837531 | 1.724689 | (3, 2.268336) | 39,130 | |
| GBT | 0.889534 | 0.901737 | 0.837531 | 1.724689 | (3, 2.268336) | 180,010 | |
| LR | 0.889534 | 0.901737 | 0.837531 | 1.724689 | (3, 2.268336) | 32,845 | |
| K-NN | 0.889534 | 0.901737 | 0.837531 | 1.724689 | (3, 2.268336) | 10,959 | |
| NB | 0.889534 | 0.901737 | 0.837531 | 1.724689 | (3, 2.268336) | 3971 | |
| Chronic Kidney Disease Data | RF | 1.0 | 1.0 | 1.0 | 0.0625 | (6, 0.0) | 20,445 |
| SVM | 1.0 | 1.0 | 1.0 | 0.0625 | (6, 0.0) | 2410 | |
| GBT | 1.0 | 1.0 | 1.0 | 0.083333 | (8, 0.0) | 13,438 | |
| LR | 1.0 | 1.0 | 1.0 | 0.052083 | (5, 0.0) | 10,193 | |
| K-NN | 1.0 | 1.0 | 1.0 | 0.052083 | (5, 0.0) | 5905 | |
| NB | 1.0 | 1.0 | 1.0 | 0.09375 | (9, 0.0) | 1539 | |
| Breast Cancer Coimbra Data | RF | 0.826086 | 0.835058 | 0.824080 | 0.396104 | (3, 0.417028) | 20,000 |
| SVM | 0.782608 | 0.801086 | 0.777523 | 0.423882 | (3, 0.454065) | 1665 | |
| GBT | 0.869565 | 0.871906 | 0.869068 | 0.409757 | (5, 0.361157) | 9323 | |
| LR | 0.826086 | 0.869565 | 0.819185 | 0.396104 | (3, 0.417028) | 4061 | |
| K-NN | 0.869565 | 0.871906 | 0.869068 | 0.409757 | (5, 0.361157) | 2635 | |
| NB | 0.782608 | 0.783946 | 0.781780 | 0.433022 | (3, 0.466252) | 1276 |
| Dataset | Classifier | Accuracy | Precision | F1 score | EvalGBest | (nf, RMSE) | Time (ms) |
|---|---|---|---|---|---|---|---|
| Smart Grids Data | RF | 0.912 | 0.912548 | 0.910972 | 0.409985 | (9, 0.296647) | 248,483 |
| SVM | 0.7575 | 0.754617 | 0.747401 | 0.452665 | (4, 0.492442) | 89,348 | |
| GBT | 0.899 | 0.898627 | 0.898736 | 0.405020 | (8, 0.317804) | 329,124 | |
| LR | 0.758 | 0.754943 | 0.748261 | 0.452284 | (4, 0.491934) | 31,514 | |
| K-NN | 0.897 | 0.897719 | 0.895522 | 0.407368 | (8, 0.320936) | 316,462 | |
| NB | 0.7755 | 0.778501 | 0.763177 | 0.438694 | (4, 0.473814) | 4771 | |
| Raisin Data | RF | 0.822222 | 0.837050 | 0.821231 | 0.361902 | (3, 0.339679) | 27,490 |
| SVM | 0.85 | 0.856079 | 0.849847 | 0.339523 | (3, 0.309841) | 4111 | |
| GBT | 0.866666 | 0.870097 | 0.866666 | 0.345289 | (2, 0.365148) | 23,406 | |
| LR | 0.855555 | 0.862789 | 0.855341 | 0.356472 | (2, 0.380058) | 6817 | |
| K-NN | 0.872222 | 0.878514 | 0.872092 | 0.339523 | (2, 0.357460) | 9630 | |
| NB | 0.855555 | 0.860681 | 0.855466 | 0.356472 | (2, 0.380058) | 1610 | |
| Turkish Music Emotion Data | RF | 0.8125 | 0.828781 | 0.817075 | 0.559279 | (20, 0.612372) | 37,558 |
| SVM | 0.875 | 0.881037 | 0.876875 | 0.518303 | (25, 0.524404) | 35,201 | |
| GBT | 0.8125 | 0.819272 | 0.813236 | 0.609341 | (27, 0.632455) | 156,980 | |
| LR | 0.8375 | 0.841059 | 0.835601 | 0.504262 | (17, 0.559016) | 53,802 | |
| K-NN | 0.7625 | 0.784397 | 0.763781 | 0.668072 | (7, 0.844097) | 8584 | |
| NB | 0.8625 | 0.862634 | 0.858907 | 0.525732 | (36, 0.460977) | 2265 | |
| Diabetes Risk Prediction Data | RF | 1.0 | 1.0 | 1.0 | 0.125 | (8, 0.0) | 20,847 |
| SVM | 0.884615 | 0.889044 | 0.885501 | 0.286012 | (2, 0.339683) | 3908 | |
| GBT | 0.990384 | 0.990532 | 0.990361 | 0.214168 | (9, 0.098058) | 11,035 | |
| LR | 0.884615 | 0.889044 | 0.885501 | 0.286012 | (2, 0.339683) | 6369 | |
| K-NN | 0.961538 | 0.962601 | 0.961702 | 0.256462 | (7, 0.196116) | 7427 | |
| NB | 0.884615 | 0.889044 | 0.885501 | 0.286012 | (2, 0.339683) | 1488 | |
| Rice Data | RF | 0.913385 | 0.913385 | 0.913385 | 0.304060 | (2, 0.294302) | 60,536 |
| SVM | 0.923884 | 0.924280 | 0.923666 | 0.290251 | (2, 0.275890) | 9229 | |
| GBT | 0.916010 | 0.916127 | 0.915837 | 0.300690 | (2, 0.289809) | 68,857 | |
| LR | 0.919947 | 0.920249 | 0.919734 | 0.295534 | (2, 0.282935) | 18,202 | |
| K-NN | 0.922572 | 0.922890 | 0.922366 | 0.292027 | (2, 0.278258) | 36,409 | |
| NB | 0.921259 | 0.921400 | 0.921097 | 0.293788 | (2, 0.280606) | 2196 | |
| Parkinson’s Disease Data | RF | 0.900662 | 0.898439 | 0.899072 | 0.295813 | (179, 0.315178) | 107,492 |
| SVM | 0.920529 | 0.920877 | 0.916727 | 0.270857 | (179, 0.281904) | 420,036 | |
| GBT | 0.907284 | 0.904998 | 0.905260 | 0.263561 | (106, 0.304491) | 743,155 | |
| LR | 0.900662 | 0.902048 | 0.893650 | 0.286184 | (150, 0.315178) | 130,233 | |
| K-NN | 0.894039 | 0.890771 | 0.890408 | 0.298585 | (164, 0.325515) | 151,805 | |
| NB | 0.847682 | 0.846218 | 0.846905 | 0.318605 | (78, 0.390279) | 17,699 | |
| Cervical Cancer Data | RF | 0.889534 | 0.894736 | 0.840116 | 1.662037 | (7, 2.143133) | 49,912 |
| SVM | 0.889534 | 0.901737 | 0.837531 | 1.716877 | (2, 2.268336) | 45,406 | |
| GBT | 0.889534 | 0.901737 | 0.837531 | 1.716877 | (2, 2.268336) | 220,140 | |
| LR | 0.889534 | 0.901737 | 0.837531 | 1.716877 | (2, 2.268336) | 40,927 | |
| K-NN | 0.889534 | 0.901737 | 0.837531 | 1.716877 | (2, 2.268336) | 16,559 | |
| NB | 0.889534 | 0.901737 | 0.837531 | 1.716877 | (2, 2.268336) | 3805 | |
| Chronic Kidney Disease Data | RF | 1.0 | 1.0 | 1.0 | 0.052083 | (5, 0.0) | 20,926 |
| SVM | 1.0 | 1.0 | 1.0 | 0.09375 | (9, 0.0) | 2718 | |
| GBT | 1.0 | 1.0 | 1.0 | 0.052083 | (5, 0.0) | 14,586 | |
| LR | 1.0 | 1.0 | 1.0 | 0.083333 | (8, 0.0) | 7743 | |
| K-NN | 1.0 | 1.0 | 1.0 | 0.083333 | (8, 0.0) | 6437 | |
| NB | 0.9875 | 0.987735 | 0.987445 | 0.167185 | (8, 0.111803) | 1539 | |
| Breast Cancer Coimbra Data | RF | 0.913043 | 0.926421 | 0.912714 | 0.332274 | (4, 0.294883) | 20,374 |
| SVM | 0.652173 | 0.652173 | 0.652173 | 0.423882 | (6, 0.342954) | 1862 | |
| GBT | 0.608695 | 0.611956 | 0.599542 | 0.360051 | (6, 0.257846) | 9458 | |
| LR | 0.826086 | 0.869565 | 0.819185 | 0.396104 | (3, 0.417028) | 7177 | |
| K-NN | 0.913043 | 0.913043 | 0.913043 | 0.332274 | (4, 0.294883) | 2644 | |
| NB | 0.782608 | 0.783946 | 0.781780 | 0.433022 | (3, 0.466252) | 1433 |
| Dataset | Classifier | Accuracy | Precision | F1 score | EvalGBest | (nf, RMSE) | Time (ms) |
|---|---|---|---|---|---|---|---|
| Smart Grids Data | RF | 0.891 | 0.891429 | 0.889478 | 0.414280 | (8, 0.330151) | 226,327 |
| SVM | 0.713 | 0.713693 | 0.685312 | 0.443459 | (2, 0.535723) | 72,052 | |
| GBT | 0.899 | 0.898627 | 0.898736 | 0.405020 | (8, 0.317804) | 258,876 | |
| LR | 0.713 | 0.712269 | 0.686781 | 0.443459 | (2, 0.535723) | 24,238 | |
| K-NN | 0.897 | 0.897719 | 0.895522 | 0.407368 | (8, 0.320936) | 188,415 | |
| NB | 0.7085 | 0.711154 | 0.676842 | 0.446597 | (2, 0.539907) | 4146 | |
| Raisin Data | RF | 0.855555 | 0.868158 | 0.854983 | 0.356472 | (2, 0.380058) | 26,458 |
| SVM | 0.872222 | 0.880895 | 0.871965 | 0.339523 | (2, 0.357460) | 3743 | |
| GBT | 0.866666 | 0.870097 | 0.866666 | 0.345289 | (2, 0.365148) | 19,151 | |
| LR | 0.855555 | 0.862789 | 0.855341 | 0.356472 | (2, 0.380058) | 6513 | |
| K-NN | 0.872222 | 0.878514 | 0.872092 | 0.339523 | (2, 0.357460) | 9179 | |
| NB | 0.855555 | 0.860681 | 0.855466 | 0.356472 | (2, 0.380058) | 1441 | |
| Turkish Music Emotion Data | RF | 0.8625 | 0.872173 | 0.862413 | 0.532142 | (26, 0.536190) | 30,483 |
| SVM | 0.925 | 0.926199 | 0.922436 | 0.454759 | (26, 0.433012) | 35,100 | |
| GBT | 0.8 | 0.816792 | 0.804053 | 0.568705 | (25, 0.591607) | 140,459 | |
| LR | 0.8875 | 0.891218 | 0.886330 | 0.530791 | (24, 0.547722) | 47,209 | |
| K-NN | 0.7625 | 0.790690 | 0.767970 | 0.630330 | (20, 0.707106) | 8163 | |
| NB | 0.8125 | 0.821741 | 0.814935 | 0.535791 | (25, 0.547722) | 1939 | |
| Diabetes Risk Prediction Data | RF | 0.990384 | 0.990532 | 0.990361 | 0.198543 | (8, 0.098058) | 20,801 |
| SVM | 0.903846 | 0.916895 | 0.905011 | 0.295065 | (4, 0.310086) | 3723 | |
| GBT | 0.990384 | 0.990619 | 0.990406 | 0.198543 | (8, 0.098058) | 10,362 | |
| LR | 0.903846 | 0.916895 | 0.905011 | 0.295065 | (4, 0.310086) | 5936 | |
| K-NN | 0.980769 | 0.981684 | 0.980851 | 0.244631 | (9, 0.138675) | 6770 | |
| NB | 0.942307 | 0.943518 | 0.942553 | 0.289519 | (7, 0.240192) | 1393 | |
| Rice Data | RF | 0.913385 | 0.913333 | 0.913302 | 0.304060 | (2, 0.294302) | 54,663 |
| SVM | 0.923884 | 0.924280 | 0.923666 | 0.290251 | (2, 0.275890) | 8067 | |
| GBT | 0.912073 | 0.912460 | 0.911803 | 0.300690 | (2, 0.289809) | 57,991 | |
| LR | 0.922572 | 0.922770 | 0.922397 | 0.292027 | (2, 0.278258) | 14,810 | |
| K-NN | 0.922572 | 0.922890 | 0.922366 | 0.292027 | (2, 0.278258) | 34,673 | |
| NB | 0.922572 | 0.922553 | 0.922484 | 0.292027 | (2, 0.278258) | 2132 | |
| Parkinson’s Disease Data | RF | 0.913907 | 0.913134 | 0.913468 | 0.337923 | (355, 0.293415) | 118,080 |
| SVM | 0.933774 | 0.932756 | 0.932329 | 0.319168 | (380, 0.257342) | 499,655 | |
| GBT | 0.907284 | 0.905061 | 0.904107 | 0.339922 | (336, 0.304491) | 864,187 | |
| LR | 0.907284 | 0.908293 | 0.901474 | 0.357186 | (388, 0.304491) | 134,454 | |
| K-NN | 0.894039 | 0.892925 | 0.887398 | 0.369634 | (378, 0.325515) | 149,951 | |
| NB | 0.821192 | 0.826924 | 0.823694 | 0.435004 | (355, 0.422856) | 13,405 | |
| Cervical Cancer Data | RF | 0.843023 | 0.841024 | 0.824169 | 1.662473 | (11, 2.102047) | 29,424 |
| SVM | 0.889534 | 0.901737 | 0.837531 | 1.755939 | (7, 2.268336) | 47,669 | |
| GBT | 0.889534 | 0.901737 | 0.837531 | 1.755939 | (7, 2.268336) | 207,039 | |
| LR | 0.889534 | 0.901737 | 0.837531 | 1.755939 | (7, 2.268336) | 38,510 | |
| K-NN | 0.889534 | 0.901737 | 0.837531 | 1.755939 | (7, 2.268336) | 14,752 | |
| NB | 0.889534 | 0.901737 | 0.837531 | 1.755939 | (7, 2.268336) | 3392 | |
| Chronic Kidney Disease Data | RF | 1.0 | 1.0 | 1.0 | 0.072916 | (7, 0.0) | 20,432 |
| SVM | 1.0 | 1.0 | 1.0 | 0.0625 | (6, 0.0) | 2326 | |
| GBT | 1.0 | 1.0 | 1.0 | 0.072916 | (7, 0.0) | 12,809 | |
| LR | 1.0 | 1.0 | 1.0 | 0.0625 | (6, 0.0) | 7381 | |
| K-NN | 1.0 | 1.0 | 1.0 | 0.0625 | (6, 0.0) | 5904 | |
| NB | 1.0 | 1.0 | 1.0 | 0.09375 | (9, 0.0) | 1415 | |
| Breast Cancer Coimbra Data | RF | 0.913043 | 0.926421 | 0.912714 | 0.304496 | (3, 0.294883) | 21,385 |
| SVM | 0.826086 | 0.826086 | 0.826086 | 0.423882 | (4, 0.417028) | 1723 | |
| GBT | 0.913043 | 0.913043 | 0.913043 | 0.304496 | (3, 0.294883) | 8984 | |
| LR | 0.826086 | 0.869565 | 0.819185 | 0.396104 | (3, 0.417028) | 4358 | |
| K-NN | 0.913043 | 0.913043 | 0.913043 | 0.332274 | (4, 0.294883) | 2646 | |
| NB | 0.782608 | 0.783946 | 0.781780 | 0.433022 | (3, 0.466252) | 1240 |
| Dataset | Classifier | GBest Value |
|---|---|---|
| Smart Grids Data | RF | [111110001111] |
| SVM | [101100000100] | |
| GBT | [111100001111] | |
| LR | [101100000100] | |
| K-NN | [111100001111] | |
| NB | [100100000100] | |
| Raisin Data | RF | [1001000] |
| SVM | [0000110] | |
| GBT | [1000001] | |
| LR | [0011000] | |
| K-NN | [1000100] | |
| NB | [0100010] | |
| Turkish Music Emotion Data | RF | [01111111111100110111101100000111010001111010011011] |
| SVM | [01110001101110001011000101011001110101110010011111] | |
| GBT | [11100110101110110111011001010001100011111101111011] | |
| LR | [11011111001111010111001101010001000100011100010110] | |
| K-NN | [10010111110111101111011101100110101111010000111010] | |
| NB | [11011110010010111010011101010111100000011001110111] | |
| Diabetes Risk Prediction Data | RF | [1001111111011011] |
| SVM | [0101101000110000] | |
| GBT | [0001101011111110] | |
| LR | [0101101000001000] | |
| K-NN | [0101001100110000] | |
| NB | [0011100000100100] | |
| Rice Data | RF | [011000] |
| SVM | [001010] | |
| GBT | [011000] | |
| LR | [011000] | |
| K-NN | [010001] | |
| NB | [011000] | |
| Parkinson’s Disease Data | RF | [111011110111000110110001010100101100100111101010010110111111011101100111011011110100111001101101001101101011111000101001001111110100100011010011000111010010111001111010100010100100100110010010010101100101000111111000110110110111111111110010111101001011111101011110100011010100001001100011111100011010110011101111011101111101001111110101110111111111111111011110001101101101011101001110110000010111010001000111110111001111011001010100011100101010011111111100010101010100010010101010100110111001010110111110100110010111111111010011111110111101111111111100011110100001011001111110110010111011011111100111111110100011001010011011111011111011101101101111101011111001101100100101010011011111111111100001010111110011101101100001101100101111011111001001101101011] |
| SVM | [010011110011111001100010110100101001100100011101010000111101010101111101111111111100000100101100001011100011011010101110111010001101111111101110100010111001011110101111000101110000110010000000000101010011100111110110110110010110010101100111100011011101101100011101111000101010110101101011100110011100000111000000100110100101011001110010001011011101101101001011010100111101101100001001110001001111100111101110100011111100101011110100001001011100000111100000110011110111110010101010000000001111110101001011010011010000011100110100000000010001010110001001111101000000010011010001001010010010111001110010011001001001101100110000001000001011000100001111010101111011110010011011110111011100101110101011110011110000010000001111010010011100101111001010111100100] | |
| GBT | [010000110110110101001000000010100101101000001111101101010001100001011101111011111101001000110111000100110010111100111110011011100000110100100100101110000010010100010101110101010101101001101010101011111101101000011100001000111110101000101001011101110011001001110100011111110001110100111011010110010101110011000011111011011011111100010110001000111001101101010011011001110000111110110011100101000001001111100000101100001011000100101100101011111001011011111111001100001011111110011010111110010100001000011110011110111011111111100011101000011000000010101010001110110100011110011101100010101000111011000110011011001001111010101110100110100111100001001100101001101011101010111100010010111110001110000100010000111000110010000111010101111111100110001010000010110] | |
| LR | [000101010111110010000111111011110010111110001011000000010110011001011111110110100111010100001100001101001111100100101000011100101100110011001111000001011011010000010001000000010100101011100000010001110111101001001100010000011110111011100011010111100101100100110100111011010011011111111110000110111010111111110010111011000011111001110010100000001101100101001110100010001110101010111000100011011001101000001010100011000111001010101000011010101000011100100100100101001110110001101001001111000011110011011000010100111010111000110000101011010001011010000001000101000100001010001011111011101100111111010000110100010110000010110011110101000010100011011100100000000001101011001010110100100101110011100100101000000101010001001000000111101000111000100100010100111] | |
| K-NN | [101000100101010010111001011111110101111011001101011010111111000001011010111100100001011110101110101100011110101110001011011101010110110111011001110011010110011010010100110001010110010111010000111100111110101001111001010010011010011011111011010101110010001101010100010101011011000011001010101011001001011110110010101001000001011001011100101000011111010010000010111001011001011001000000001010000100011011111010010000011010010011111000101011010111111100001101111010010111111111010101001001010100111011011111110110011111100011010111111011110011001101111111111100011010011100100011110111011110101011000011011001110010110000001000101110111011011100011100001010011111101010011110110011000101110011101100000101110000000001111101001101100000110010001110010111111] | |
| NB | [101110100011001010000000010001110000100100000111010111010011001011101100001000101001001110000111001111110110110100110010111000100010101110111100010100011001011000110100101010010101101101111110101110100110001001100100111010101011011001110101011111110010010001100100110100000000011110001000111101011001001111010001101000111001011101110001100100000111111011010100101011001111010100010001010101111000011001101000001011010010100000101110011111110111010101100101101111100111110011100111100000101001011000100110110111001001111010110100111100011111011111001111011100011100101101010001010111011101001001100101010010110100100001111000101000111110001000101100101010110010001001000110110100100101111100010000001001101101010010011011010101010000010100000110101101101] | |
| Cervical Cancer Data | RF | [00110010010000100010001110010010] |
| SVM | [00100000000010000001000000000000] | |
| GBT | [00100000000010000001000000000000] | |
| LR | [00100000000010000001000000000000] | |
| K-NN | [00100000000010000001000000000000] | |
| NB | [00100000000010000001000000000000] | |
| Chronic Kidney Disease Data | RF | [001100000010000001010100] |
| SVM | [001000000100101100010000] | |
| GBT | [110100000110100001000001] | |
| LR | [001000000000001110010000] | |
| K-NN | [001000000100001100010000] | |
| NB | [000101011001000101110000] | |
| Breast Cancer Coimbra Data | RF | [001001010] |
| SVM | [101100000] | |
| GBT | [111010010] | |
| LR | [001010010] | |
| K-NN | [101110010] | |
| NB | [110000010] |
| Dataset | Classifier | GBest Value |
|---|---|---|
| Smart Grids Data | RF | [111110001111] |
| SVM | [111000000001] | |
| GBT | [111100001111] | |
| LR | [111000000001] | |
| K-NN | [111100001111] | |
| NB | [111000000001] | |
| Raisin Data | RF | [1101000] |
| SVM | [1101000] | |
| GBT | [1000001] | |
| LR | [0100100] | |
| K-NN | [1000100] | |
| NB | [0011000] | |
| Turkish Music Emotion Data | RF | [10100011101101001001000100000100010001010100110101] |
| SVM | [11111011010100011010001100010001101100010011011010] | |
| GBT | [01001100111011011011000101111110001111000100100110] | |
| LR | [01110010000000001001001000110001100110011000110000] | |
| K-NN | [00001010000000000000100001010001000000000000010000] | |
| NB | [01100111011011010110011111111111111100111010110111] | |
| Diabetes Risk Prediction Data | RF | [1101000000111110] |
| SVM | [0101000000000000] | |
| GBT | [1101001111100010] | |
| LR | [0101000000000000] | |
| K-NN | [0001001100101101] | |
| NB | [0101000000000000] | |
| Rice Data | RF | [100100] |
| SVM | [001010] | |
| GBT | [011000] | |
| LR | [011000] | |
| K-NN | [001010] | |
| NB | [011000] | |
| Parkinson’s Disease Data | RF | [000011100000001011000001001000000000000000010010001000101010000000000010001001001001000000000100000000110100000001100001000110001000001100100101001010000010010001110001000000000000100101010010111000101001000000000000010100000000010100000110100100000100100000100000001010101000000001000110000000100000001000100000001000100000001010001000001110010010111101101000001101010101010010000010000000000010010000000000000010000000010010110000100001001011000000001000000100000000101000110001001101010000000000000000000000001011111010000001000000000000010010000010100000100000001000000100001100000010010001000011000010000000110000000000100011100000100000100010011000010000100001000010000000100000010010100000000110000010000000001001010000010000000001100110100001010] |
| SVM | [011010011000000011100000110100010000000010000100100000101111001000010100000111001001000010100100110100000001001000101100000011001000101000001000000010000001000101010000100011010001000010110110000000010001000000000001010000000011000000000101110000000000000100010000001010110000010000100000000000100101000000000000100000001100011010000101000000000001000000000000000000000100000000000010100000010010010000001100100000000001011011000000000000001011010000010000000010000000100000000010000000100000001010011000100100100000011101100010000101000111000100001001100000110001001100000100010000100010100010000010000110000000110000001000001001011000000000000000000000001010101000000000001000001000011000101010100011010000010100001000000000001000100001001000010000000] | |
| GBT | [000101101000000000000000000001001000000001000100110000001000000000000000000010001000000010001100100000001000000010000000000001100010001000000001000100000010000000101000010010000000000010000010000010010010001000000001000001000010001000000101010000000000000000001001000000011000000100000010100000000000001000000000010000010000000100000000001100000001000001100000000000000010000001000000000000000100000001000001010000000000010000100001000000000000100000000001110000110000000010000000000000001000000000000000000000000011000000010001100001000000000000000000000000001000100000000000010000110000110110000101000000001000000000000000100101000000000000000001000000000000000010000000000000001000000100010000000010000000000000000001000000000010000000000000010000000] | |
| LR | [100000000000000010000000010000110000000001100100100000000000000001000000001100000010000000000000000000010000001001100000011100100111000000000000000000000010100000000100000001001000100001000000110000001000100010010111001000001010000011000010000000000000100001000000000000110000000000100000110100010000000010000100100000001001010000000000100100000101000000101001000000000000010101010001010000000000000000000001000000000001000011001100000100000001011000010011000000000001001111000000000000010010000000111010000110000000000000000000000001001011000000000100100100100010001000000111010000000011000001000100010000000010000010100101000000000000000000010000010111000101000010000100010001000101000001001010001010000000000000000000010100101010010000010000001000000] | |
| K-NN | [100100000010000000000000000100000000100100000000000000001000000001100100001100000000000000000000001000100000100000001000010101100010000010000000000100000000100000000001000000001100110000110000010000000010101010011110101010000000000010000000000000000001110000001000000010011100000100100000100000110001000010001101000000101011001000110000100010000101010010000000000010100010010101000000010000110000100000000001000000001101000000000100000100001001011010110011000010000110100110000001011000010011000001111000000000000000000000000010000000000011001101000100000100010000100010010111000000000100100010100010000000000100000000100100000000010000001000100001000101000101000010000100110101000000000001010000000000000000000010000000000110100000000001010100101000000] | |
| NB | [000000000000000000000000000000000000000000000000110000000000110100000000000000001000000000010100000100001000000000000000000000000010000100000100011000000001000000000100010000000000100000000000000000000000100000000000000000000100000000010000100000001000000000000010000000100000000000000000100010010000000000000000000000100000001000100000000010000000000010000010000000000000000000001000000000000010000000001001000100000100000000100000000000010001010000000000000010100100000000000000000000000001000000000011000000000000000001000101100000000000110000100000000000000001000000000001010010000000000110000000000010000100010000000000010000000000000010000000000000010000000000000000010000000010000010000010001001000000000000000000000000000000000000000100100000000] | |
| Cervical Cancer Data | RF | [00000000100010101010000011000000] |
| SVM | [00000000000000000000000000000101] | |
| GBT | [00000000000000000000000000000101] | |
| LR | [00000000000000000000000000000101] | |
| K-NN | [00000000000000000000000000000101] | |
| NB | [00000000000000000000000000000101] | |
| Chronic Kidney Disease Data | RF | [000100010000000100010010] |
| SVM | [100010000101101010100100] | |
| GBT | [100000000001100000100010] | |
| LR | [001111000100001110000000] | |
| K-NN | [000110010010011100000001] | |
| NB | [001111000100001110000000] | |
| Breast Cancer Coimbra Data | RF | [111000010] |
| SVM | [001111110] | |
| GBT | [001111110] | |
| LR | [001010010] | |
| K-NN | [101100001] | |
| NB | [110000010] |
| Dataset | Classifier | GBest Value |
|---|---|---|
| Smart Grids Data | RF | [111100001111] |
| SVM | [001000000001] | |
| GBT | [111100001111] | |
| LR | [001000000001] | |
| K-NN | [111100001111] | |
| NB | [001000000001] | |
| Raisin Data | RF | [0011000] |
| SVM | [0010001] | |
| GBT | [1000001] | |
| LR | [0100100] | |
| K-NN | [1000100] | |
| NB | [0011000] | |
| Turkish Music Emotion Data | RF | [00111011101100011011010110010000101101101010010101] |
| SVM | [00111101110000011001001000100111011001111001100111] | |
| GBT | [01100110001001010001001100011100111110110100011101] | |
| LR | [00010101101110011011100001010010010110100001111100] | |
| K-NN | [10101011001001001011001101000001000000100001001111] | |
| NB | [11010101001110111000001110010010111010100010110001] | |
| Diabetes Risk Prediction Data | RF | [1001111110010000] |
| SVM | [0001101000100000] | |
| GBT | [0001001111100011] | |
| LR | [0001101000100000] | |
| K-NN | [0001001110111011] | |
| NB | [1101100010100100] | |
| Rice Data | RF | [100001] |
| SVM | [001010] | |
| GBT | [011000] | |
| LR | [110000] | |
| K-NN | [001010] | |
| NB | [110000] | |
| Parkinson’s Disease Data | RF | [001100010110001010101011001001011100011010110110011000110110111110010010001111000010111001010000100100000000000001010001000000010111001111001010111001101000011010101000111010001111000110011001110011111100111110100001000101110111001010101110101110011111111000011001100100101001100100000101101100000101101110010010100100111011100001010011110101000100010011010001101011010001000000011101011011001110101111010011010010010010000100011110011010100111010100001001110101100010011110010101011010001100001101001001110011110111111100111110011000010010100010111001011110000000100010110011101000110000111000100111111110000001000111011011000010011110010101101010100110111110000000011101000110001000001010110010101001101000001110011100111100010010110100100100001010000] |
| SVM | [110011001000010111111001101100110001001111010000101111010111110000101010001011111110000001110000101110100110111011010010100001010011110010110011010101100101101100011100011110110100111011010110011101100110000100101111000001111101011101000011011010000001100010001001111110001011000101110111001000010000100011100100000100010101001100000111101000100110011101111011011101001101010101010101000101010100011111111110110110010111100001000000000001110000110111011111111100100111110111110000001000101001100010110001000001111000110011010110101101010000001001001100110001010010011101000111010100111100001101010111001110101111000011100011111101011110101001100010011111101010000001000111100110101001111001010010000111100110010001100011000100010000111011111111111110010] | |
| GBT | [001101111011011000101000000001010000101001000001101001001001010110011101000111001011010010000110000110000100100101011101001011110001000101100011101010011010000011000011001010000100110101010110110000000101010110101101010010100100110000100001000101001001010011000000101000000001001001101000011010110001100111001101111100000010010100011101010111000010101010010000000011011000110000010110010001010111110000101111001000111010010101010000101000110110101011100011011100110001000011000110011100001010000001010010101010101110100000110010000110110101110110011111011001111001011010011111110000111011100010110100010000000010011110011101001101110100110001011011010011110110010110110100101111100011101100100100101000111001001100010101011000110000110001100011100001101] | |
| LR | [000010100101101001111111101010101110111110101111110110001011001000101000111101000100000111101001010110101100010010101011010000101111110001111000011100110110010011101111001101100100101011001010110101100111010000111011101101110001001110110101100001000010000111010110110010011110001100001101001110110000110000011001011111001011000010110111000000110000010011100111101011101110100000010011000001001100010100010110100111100000001001000101111111000011001011111001010000010101111010101011000010101001011101010011011101101101001110101101101101000111001001010111101100010011101101110110101100100110110111110110100011011110111101010111101011101111011000111100101101101110111100000011011000001000011111000000011011001111000011010011010010101010001111000010001111000] | |
| K-NN | [001010001000010011001111011010010001001111111111111010011001001110001101101110001010010101011110101010101101101001001110010110000100010011000011101111101001010111101000110010100010101111001010011111000001011110100110101001100011111000101001100000111101000010001111001000011100101100000000110110000101011111011101110001011111101001000110111111010111100010110001100010110011110100101010110001100000111111000010110100011001001001100011010111010000011101010101001011001000110111110001100100010101001000101110111011000010110111110010011010000000111001010101010011100100011100011001100010001011011110000101000110000010011111101000000110011010001111000100001111101100010111010101110100110010101100101011010000100011110101100111110001110010010011011111110110110] | |
| NB | [100000100000111010101100101110001111100000010101110011010011010100110010010000000101010001011101101000000101100011011110011011000011001110000101110000111111100000010100101001110100000000100010001111100000101111100111111101010011101100100110100001010100110011111010100011001011110011001111101000001001000000110010011010111110011110111011110000100001001010111000010100011011100011110101110001010001001100101010110110110100000001000110101101010010011000100110101011111101000000111011100010010011101110101000111010001111011001110001001001111101001010000010111111000001101001101011010110000011000000000110010100000001101001010011000100011001001101110100001101111000001101000111111101110000001000011110001010000100000111001010111011001101000110011011011111100] | |
| Cervical Cancer Data | RF | [10100001001110101000100000001010] |
| SVM | [00000100110100010000000010000100] | |
| GBT | [00000100110100010000000010000100] | |
| LR | [00000100110100010000000010000100] | |
| K-NN | [00000100110100010000000010000100] | |
| NB | [00000100110100010000000010000100] | |
| Chronic Kidney Disease Data | RF | [001100010100001100010000] |
| SVM | [000010000100001010101000] | |
| GBT | [110000000111000100001000] | |
| LR | [001100000100001100010000] | |
| K-NN | [000000000000001110110001] | |
| NB | [001100001011000111010000] | |
| Breast Cancer Coimbra Data | RF | [101001000] |
| SVM | [101010010] | |
| GBT | [101000001] | |
| LR | [001010010] | |
| K-NN | [101100001] | |
| NB | [110000010] |
| Dataset | Classifier | BHOA | BGWO | BPSO | BCSA |
|---|---|---|---|---|---|
| Smart Grids Data | RF | 0.912 | 0.912 | 0.912 | 0.891 |
| SVM | 0.694 | 0.748 | 0.7575 | 0.713 | |
| GBT | 0.899 | 0.899 | 0.899 | 0.899 | |
| LR | 0.6935 | 0.7495 | 0.758 | 0.713 | |
| K-NN | 0.897 | 0.897 | 0.897 | 0.897 | |
| NB | 0.7005 | 0.7315 | 0.7755 | 0.7085 | |
| Raisin Data | RF | 0.85 | 0.85 | 0.822222 | 0.855555 |
| SVM | 0.872222 | 0.861111 | 0.85 | 0.872222 | |
| GBT | 0.866666 | 0.866666 | 0.866666 | 0.866666 | |
| LR | 0.855555 | 0.855555 | 0.855555 | 0.855555 | |
| K-NN | 0.85 | 0.872222 | 0.872222 | 0.872222 | |
| NB | 0.85 | 0.844444 | 0.855555 | 0.855555 | |
| Turkish Music Emotion Data | RF | 0.9 | 0.8875 | 0.8125 | 0.8625 |
| SVM | 0.925 | 0.9375 | 0.875 | 0.925 | |
| GBT | 0.775 | 0.825 | 0.8125 | 0.8 | |
| LR | 0.925 | 0.9125 | 0.8375 | 0.8875 | |
| K-NN | 0.825 | 0.85 | 0.7625 | 0.7625 | |
| NB | 0.85 | 0.8625 | 0.8625 | 0.8125 | |
| Diabetes Risk Prediction Data | RF | 0.990384 | 1.0 | 1.0 | 0.990384 |
| SVM | 0.942307 | 0.932692 | 0.884615 | 0.903846 | |
| GBT | 1.0 | 0.990384 | 0.990384 | 0.990384 | |
| LR | 0.932692 | 0.932692 | 0.884615 | 0.903846 | |
| K-NN | 0.932692 | 0.942307 | 0.961538 | 0.980769 | |
| NB | 0.951923 | 0.894230 | 0.884615 | 0.942307 | |
| Rice Data | RF | 0.913385 | 0.910761 | 0.913385 | 0.913385 |
| SVM | 0.923884 | 0.923884 | 0.923884 | 0.923884 | |
| GBT | 0.914698 | 0.916010 | 0.916010 | 0.912073 | |
| LR | 0.922572 | 0.919947 | 0.919947 | 0.922572 | |
| K-NN | 0.922572 | 0.916010 | 0.922572 | 0.922572 | |
| NB | 0.922572 | 0.921259 | 0.921259 | 0.922572 | |
| Parkinson’s Disease Data | RF | 0.847682 | 0.920529 | 0.900662 | 0.913907 |
| SVM | 0.860927 | 0.947019 | 0.920529 | 0.933774 | |
| GBT | 0.860927 | 0.900662 | 0.907284 | 0.907284 | |
| LR | 0.860927 | 0.907284 | 0.900662 | 0.907284 | |
| K-NN | 0.860927 | 0.920529 | 0.894039 | 0.894039 | |
| NB | 0.821192 | 0.834437 | 0.847682 | 0.821192 | |
| Cervical Cancer Data | RF | 0.889534 | 0.889534 | 0.889534 | 0.843023 |
| SVM | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| GBT | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| LR | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| K-NN | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| NB | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| Chronic Kidney Disease Data | RF | 1.0 | 1.0 | 1.0 | 1.0 |
| SVM | 1.0 | 1.0 | 1.0 | 1.0 | |
| GBT | 1.0 | 1.0 | 1.0 | 1.0 | |
| LR | 1.0 | 1.0 | 1.0 | 1.0 | |
| K-NN | 1.0 | 1.0 | 1.0 | 1.0 | |
| NB | 1.0 | 1.0 | 0.9875 | 1.0 | |
| Breast Cancer Coimbra Data | RF | 0.913043 | 0.826086 | 0.913043 | 0.913043 |
| SVM | 0.826086 | 0.782608 | 0.652173 | 0.826086 | |
| GBT | 0.913043 | 0.869565 | 0.608695 | 0.913043 | |
| LR | 0.739130 | 0.826086 | 0.826086 | 0.826086 | |
| K-NN | 0.826086 | 0.869565 | 0.913043 | 0.913043 | |
| NB | 0.782608 | 0.782608 | 0.782608 | 0.782608 |
| Dataset | Accuracy Result | BHOA | BGWO | BPSO | BCSA |
|---|---|---|---|---|---|
| Smart Grids Data | mean | 0.799333 | 0.822833 | 0.833166 | 0.803583 |
| standard deviation | 0.113340 | 0.087832 | 0.076582 | 0.100919 | |
| maximum | 0.912 | 0.912 | 0.912 | 0.899 | |
| minimum | 0.6935 | 0.7315 | 0.7575 | 0.7085 | |
| Raisin Data | mean | 0.857407 | 0.858333 | 0.853703 | 0.862962 |
| standard deviation | 0.009728 | 0.010393 | 0.017450 | 0.008364 | |
| maximum | 0.872222 | 0.872222 | 0.872222 | 0.872222 | |
| minimum | 0.85 | 0.844444 | 0.822222 | 0.855555 | |
| Turkish Music Emotion Data | mean | 0.866666 | 0.879166 | 0.827083 | 0.841666 |
| standard deviation | 0.060553 | 0.041583 | 0.040633 | 0.060553 | |
| maximum | 0.925 | 0.9375 | 0.875 | 0.925 | |
| minimum | 0.775 | 0.825 | 0.7625 | 0.7625 | |
| Diabetes Risk Prediction Data | mean | 0.958333 | 0.948717 | 0.934294 | 0.951922 |
| standard deviation | 0.029584 | 0.039723 | 0.055874 | 0.041245 | |
| maximum | 1.0 | 1.0 | 1.0 | 0.990384 | |
| minimum | 0.932692 | 0.89423 | 0.884615 | 0.903846 | |
| Rice Data | mean | 0.919947 | 0.917978 | 0.919509 | 0.919509 |
| standard deviation | 0.004621 | 0.004676 | 0.004037 | 0.005293 | |
| maximum | 0.923884 | 0.923884 | 0.923884 | 0.923884 | |
| minimum | 0.913385 | 0.910761 | 0.913385 | 0.912073 | |
| Parkinson’s Disease Data | mean | 0.852097 | 0.905076 | 0.895143 | 0.896246 |
| standard deviation | 0.016040 | 0.038081 | 0.024926 | 0.038992 | |
| maximum | 0.860927 | 0.947019 | 0.920529 | 0.933774 | |
| minimum | 0.821192 | 0.834437 | 0.847682 | 0.821192 | |
| Cervical Cancer Data | mean | 0.889534 | 0.889534 | 0.889534 | 0.881782 |
| standard deviation | 1.22 × 10−16 | 1.22 × 10−16 | 1.22 × 10−16 | 0.018988 | |
| maximum | 0.889534 | 0.889534 | 0.889534 | 0.889534 | |
| minimum | 0.889534 | 0.889534 | 0.889534 | 0.843023 | |
| Chronic Kidney Disease Data | mean | 1.0 | 1.0 | 0.997916 | 1.0 |
| standard deviation | 0.0 | 0.0 | 0.005103 | 0.0 | |
| maximum | 1.0 | 1.0 | 1.0 | 1.0 | |
| minimum | 1.0 | 1.0 | 0.9875 | 1.0 | |
| Breast Cancer Coimbra Data | mean | 0.833332 | 0.826086 | 0.782608 | 0.862318 |
| standard deviation | 0.069655 | 0.038888 | 0.128977 | 0.057789 | |
| maximum | 0.913043 | 0.869565 | 0.913043 | 0.913043 | |
| minimum | 0.73913 | 0.782608 | 0.608695 | 0.782608 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moldovan, D. Binary Horse Optimization Algorithm for Feature Selection. Algorithms 2022, 15, 156. https://doi.org/10.3390/a15050156
Moldovan D. Binary Horse Optimization Algorithm for Feature Selection. Algorithms. 2022; 15(5):156. https://doi.org/10.3390/a15050156
Chicago/Turabian StyleMoldovan, Dorin. 2022. "Binary Horse Optimization Algorithm for Feature Selection" Algorithms 15, no. 5: 156. https://doi.org/10.3390/a15050156
APA StyleMoldovan, D. (2022). Binary Horse Optimization Algorithm for Feature Selection. Algorithms, 15(5), 156. https://doi.org/10.3390/a15050156






