Abstract
Scientific papers published in journals or conferences, also considered academic publications, are the manifestation of scientific research achievements. Lots of scientific papers published in digital form bring new challenges for academic evaluation and information retrieval. Therefore, research on the ranking method of scientific papers is significant for the management and evaluation of academic resources. In this paper, we first identify internal and external factors for evaluating scientific papers and propose a publication ranking method based on an analysis of a heterogeneous academic network. We use four types of metadata (i.e., author, venue (journal or conference), topic, and title) as vertexes for creating the network; in there, the topics are trained by the SentenceLDA algorithm with the metadata of the abstract. We then use the Gibbs sampling method to create a heterogeneous academic network and apply the ConNetClus algorithm to calculate the probability value of publication ranking. To evaluate the significance of the method proposed in this paper, we compare the ranking results with BM25, PageRank, etc., and homogeneous networks in MAP and NDCG. As shown in our evaluation results, the performance of the method we propose in this paper is better than other baselines for ranking publications.
1. Introduction
Scientific papers, as the carrier of knowledge dissemination, play the role of “standing on the shoulders of giants” [1] With the development of Internet technology, the increase in scientific papers being published in the digital form not only helps avoid resource waste caused by the printing process but also promotes the speed and scope of knowledge dissemination. However, the rapid development trend of digital papers has introduced new challenges for scientific resources management. One estimate puts the count at 1.8 million articles published each year in about 28,000 journals [2] Digitally published articles foster more opportunities for information retrieval but make it harder to find the appropriate resource. Therefore, more and more people have focused on the methodology of evaluating scientific papers to improve the efficiency of information retrieval, eliminate the influence of non-relevant results, and satisfy the user’s information needs. Fortunately, research on a publication ranking algorithm is one of the effective ways to solve this problem.
In fact, many studies have focused on methods of scientific publication ranking. Citation counts [3] are the most popular method (that is, the ranking result is determined by the count of citations). This method assumes that the more citations a paper has, the higher its influence tends to be; thus, the paper is ranked higher. In addition, there is one publication ranking method based on the impact factors [4] of the venue or a paper published in a journal or a conference. If the venue has a higher impact factor, the paper published in it will also have a high influence. Besides that, the author’s reputation will also determine the ranking result; that is, a paper written by well-known scholars in the field is often ranked higher than others [5] Currently, the methods mentioned above are widely used in academic paper retrieval institutions or search engines as the basic or core algorithm for scientific paper searching. However, the above methods also have limitations when used for evaluating publications. For example, self-citation may confuse the result of citation counts, which affects the evaluation of author authority. Furthermore, the recognition of the venue affects the evaluation results of scientific papers.
Fortunately, more and more methods (e.g., machine learning, text mining, network and graph, etc.) are used in bibliometrics for ranking. PageRank [6] algorithms rely on graph theory, which promotes the research of ranking and evaluating scientific papers. However, most methods only adopt a single type of network structure and neglect the influence of different types of vertexes for ranking. The single type of network structure may include a publication network by citation relationship, keyword network by co-occurrence relationship, author network by co-author relationship, etc.
Therefore, in this paper, we propose a publication ranking method based on heterogeneous academic network analysis. The metadata that affect the evaluation of scientific papers are regarded as the vertexes in the heterogeneous network (i.e., title, topic, keyword, author, venue, abstract and full text, etc.). We then use the SentenceLDA algorithm for training topics by the metadata of the abstract, and the Gibbs sampling method is proposed for creating the heterogeneous network (also known as TVKA). Finally, we apply the ConNetClus algorithm to calculate the probability value of publication ranking.
As one contribution of this paper, we propose a method for creating a heterogeneous academic network, which is topic-sensitive with four types of vertexes. The other contribution is that we use the ConNetClus algorithm to calculate the probability value in the heterogeneous network as the publication ranking result, which we compare with the classical ranking algorithm. As the result shows, the method we use in this paper is better than other baselines.
2. Literature Review
2.1. Publication Ranking
The current rapid access to digital publications can greatly accelerate research, but the information overload also challenges researchers, especially junior researchers, in finding appropriate citations for their research projects. In previous papers, to deal with this problem, bibliometric methods have focused on ranking publications by citation analysis [7] along with graph mining [8] A common and easy method based on citation frequency or citation counts has been studied for a long time. Nevertheless, there is a basic assumption in previous methods, which is easy and straightforward: if paper1 cites paper2, then paper1 and paper2 are related. This assumption is oversimplified because it treats all citations equally, regardless of sentiment, reason, topic, or motivation. Cronin [9] reviewed a variety of perspectives on citations and argued that citations have multiple articulations in that they inform their understanding of the socio-cultural, cognitive, and textual aspects of scientific communication. Besides that, Egghe and Rousseau [10] discussed the influence of the author’s authority on citation analysis from the view of the author’s point in their paper. In recent years, there are still many scholars working in this field. Abrishami and Aliakbary [11] proposed a novel method for predicting long-term citations of a paper based on the number of its citations in the first few years after publication. Small et al. [12] from a new interpretation of citation counts, found that early citations made soon after publication are more hedged than later citations.
With the development of network and graph theory, the bibliometric method has also been improved in theory. Larson [13] first presented the concept of bibliometric methods based on the WWW (World Wide Web) and has explicitly introduced the network theory into bibliometrics since 1996. The HITS (hyperlink induced topic search) algorithm was first proposed to calculate the weight of network vertexes [14] and the PageRank algorithm proposed by Google is the most widely used algorithm to solve the problem of web page ranking in the network [6].
However, PageRank is insensitive toward topics and queries. Haveliwala [15] proposed a topic-sensitive PageRank algorithm, computing a set of PageRank vectors using a set of representative topics. After that, more and more researchers began using PageRank or improved the PageRank algorithm in the field of bibliometrics for measuring publication and author importance. Qiao et al. [16] combined the characteristics of the citation network in their paper and proposed an alternative method for evaluating the value of a paper based on an improved PageRank algorithm. Reference [17] proposed an alternative hybrid algorithm based on an optimized normalization technique and content-based approach to overcome the setbacks of PageRank. Since the algorithm of the topic model (Latent Dirichlet Allocation, LDA) [18] was proposed, scholars have tried to combine this algorithm with the PageRank method to avoid PageRank’s deficiencies toward the topic. To receive paper recommendations, Tao et al. [19] calculated the probability distribution according to the LDA of papers and used the PageRank algorithm to reorder the options in the reference network to obtain the final recommendation results. Zhang et al. [20] proposed a pipeline model, named collective topical PageRank, to evaluate the topic-dependent impact of scientific papers.
2.2. Factors for Evaluating Scientific Publications
The metadata of scientific papers (i.e., title, author, abstract, keyword, full text, reference, venue, topic, and publication time) affected the evaluation result of scientific publications [21]. In this paper, we divide these metadata into two categories: internal and external factors.
The external factors refer to the objective elements other than the content of the paper; these factors decide the ranking results in a scientific paper’s evaluation. Although the external factors do not directly determine the article’s academic influence, they can provide an indirect evaluation reference basis for them. There are seven categories of external factors divided from the research on citation incentives, whereas four factors are related to the evaluation results of academic influence (i.e., venue impact, author authority, citation, and co-author factors). Regarding the venue impact factor, there is a strong common perception that high-ranking journals publish “better” or “more important” science. The assumption is that high-ranking journals are able to be highly selective and publish only the most important, novel, and best-supported scientific discoveries [22] In terms of the author authority factor, it is generally believed that papers published by authors with high popularity in specific disciplines or those who came from famous institutions will be ranked higher. “h-index” is used to quantify the research output of individual scientists [23] which is increasingly important to calculate and is used to precisely interpret the h-index along with the rapid evolution of bibliographic databases [24] Regarding the citation factor, it is generally considered that if a paper is cited more times, it often means its academic level is higher and influence is greater. Citation counts are the highest-weighted factor in Google Scholar’s ranking algorithm. Highly cited articles are found significantly more often in higher positions than articles that are cited less often [25] In terms of the co-author factor, scientific research cooperation is a scientific activity carried out by researchers to achieve their common purpose of producing new scientific knowledge. Reference [26] examined the association of author bibliographic coupling strength and citation exchange in 18 subject areas.
Internal factors refer to the correlation between the content quality of scientific papers and their academic influence. The content quality of a published paper is the most important factor in evaluating its academic level. However, it is very difficult to quantitatively analyze the content of papers. More and more researchers are focusing on abstract or full-text content analysis plus machine-learning algorithms to evaluate the contributions of a paper. Most traditional content analysis is implemented using a keyword-matching process; thus, it cannot consider the semantic contexts of items [27] As full-text publication data provide crucial content for capturing the different methods of data use, Reference [28] employed a content-analysis method to a multidisciplinary full-text corpus to gain insights into dataset mentions and citations. Reference [29] extracted data from many full-text publications and represented the results by a probability distribution over a set of predefined topics to give a new method to enhance scholarly networks.
2.3. Heterogeneous Network
The heterogeneous network was originally used in communication and belongs to a type of network. That network is composed of computers, systems, and network devices. In most cases, different protocols run on different applications or functions. The origin of heterogeneous networks can be traced back to the BARWAN (Bay Area Research Wireless Access Network) project initiated by the University of California in 1995. In [30] R.H. Katz, the leader of this project, integrated different types of networks that overlap each other to build a heterogeneous network to meet different types of business needs. It can be seen that heterogeneous networks are mostly used to study wireless communication technology. At present, many pieces of research have been established in the frontier direction of data mining, namely, heterogeneous information networks. This method of peeling off other objects and only caring about the relationship between the research objects simplifies ideas well, but it causes a significant loss of information. In today’s complex network, there are many kinds and types of connections between objects. At this time, introducing the heterogeneous information network can mine the potential value of data without losing the relationship between objects.
The heterogeneous network can be used to implement a collaborative filtering recommendation algorithm, search-ranking algorithm, abnormal data detection, and so on. Zhang et al. [31] introduced user and item attribute information and integrated the scoring matrix into the heterogeneous information network, which effectively improved the recommendation accuracy. Wang et al. [32] considered using the heterogeneous features of a 3D model that interrelated co-clustering. This method used limited semantic information—which comes from multi-channel information—to build a heterogeneous semantic network, and then converted the heterogeneous semantic network to the semantic features of a 3D model. Zhang et al. [33] proposed an improved meta path-based collaborative filtering algorithm for weighted heterogeneous information networks. The method was evaluated with the extended MovieLens dataset, and experimental results showed that our approach outperformed several traditional algorithms and made the result of recommendation more accurate. Mu et al. [34] used complex heterogeneous information network simulation experiments to detect abnormal data so that the algorithm had a high anti-interference ability. Reference [35] proposed a method of combining meta-path selection and user preference Top-k correlation query on heterogeneous information networks to measure the correlation between different types of objects.
There are many different types of vertexes in a heterogeneous network, some of which are more important. Such vertexes often affect the structure and function of the network to a greater extent. In recent years, more and more people have been paying attention to the ranking method of vertex importance, not only because of the theoretical research significance of this method but also because of its strong practical application value [36] Among the ranking results-based algorithms, most of the current ranking functions are defined based on homogeneous networks, such as PageRank and HITS, and there are also some ranking algorithms based on heterogeneous networks, such as dual-type rankClus [37] multi-type netClus [38] and other algorithms [39] In sorting methods such as heterogeneous networks, the relationship between different types of objects and objects of the same type is important. By moving from a single homogeneous network level to the analysis of multiple types of heterogeneous network objects, the analysis of sorting algorithms is also transformed from a specific webpage to an object-oriented level of operation. However, the netClus algorithm cannot analyze references between target objects, and the network used must be a star network, which has limitations, so it leads to the optimization method that we use, and at the same time, introduces the calling relationship between homogeneous networks papers. There are increasingly more types of objects in the network, and research using a pure homogeneous network can no longer express the relationship between different types of objects. Therefore, a heterogeneous network can better reflect relationships and provide a large number of opportunities for mining research. Heterogeneous network analysis is essential to studying the relationship between different types of objects.
3. Methodology
3.1. SentenceLDA for Training Topics based on the Abstract
LDA [18] is a generative probabilistic model for collecting discrete data, such as text corpora. LDA is a three-level hierarchical Bayesian model in which each item of a collection is modeled as a finite mixture over an underlying set of topics. The limitations of LDA stem from the use of the Dirichlet distribution to model the variability among the topic proportions. One assumption is the interchangeability among words, which ignores the coherence of contents. In fact, the sentences in a text are coherent, so there is a logical relationship between sentences. We also hope that only a limited number of potential topics will appear after each sentence is processed. Therefore, we use SentenceLDA [40] as an extension of LDA, which aims to overcome this limitation by incorporating the structure of the text in the generative and inference processes.
An abstract is a brief summary of a research article, thesis, review, conference proceeding, or any in-depth analysis of a particular subject and is often used to help the reader quickly ascertain the paper’s purpose. The abstract, as one of the metadata of the publication, is the embodiment of the content of the paper, regarded as the internal factor for evaluating publications.
Considering the content of an abstract is text data, we must transform it into smaller granularity topics. This means that the content presented in the abstract will be displayed in the form of topic distributions. On the other hand, abstracts are composed of sentences, and there is a logical relationship among those sentences, so we use SentenceLDA for training topics based on the abstract to avoid the limitations of LDA.
Therefore, abstract can be expressed as the distributions of topics:
where represents a topic trained from the topic model, and n is the number of topics. The probability of each topic is . This means each topic () has its own weight score () and = 1.
3.2. Construction of the Heterogeneous Academic Network
The network is generally composed of vertexes and edges. Vertexes represent the objects in the network, and edges represent the relationship between objects. In order to explain the construction of heterogeneous academic networks, the notations and their interpretations are shown in Table 1.

Table 1.
The notations and their interpretations.
For the homogeneous network, is composed of the set of vertexes and set of edges, where V represents the vertex set, , E represents the edge set, and . Each edge represents the connection between two vertexes,, where N represents the total number of vertexes and M represents the total number of edges. In this paper, we put the focus on the heterogeneous network, , where C represents the vertex-type set, , S represents the total number of vertex types. If S = 1, there is only one type of vertex in the network, which belongs to the homogeneous network. If S > 1, there are two or more vertex-types, and the network is a heterogeneous network.
In the heterogeneous network, for each vertex, , and its type is . For each edge, if , which means the vertex is connected to the vertex , and these two vertexes have the same vertex type, . If , which means the vertex is connected to the vertex , because the vertex types of and are and respectively. and have the different vertex type. For a heterogeneous network G, we can disassemble it into several homogeneous sub-networks, . The number of sub-networks disassembled from the heterogeneous network is determined by the number of vertex types. Therefore, the heterogeneous network dividing into a collection of sub-networks:
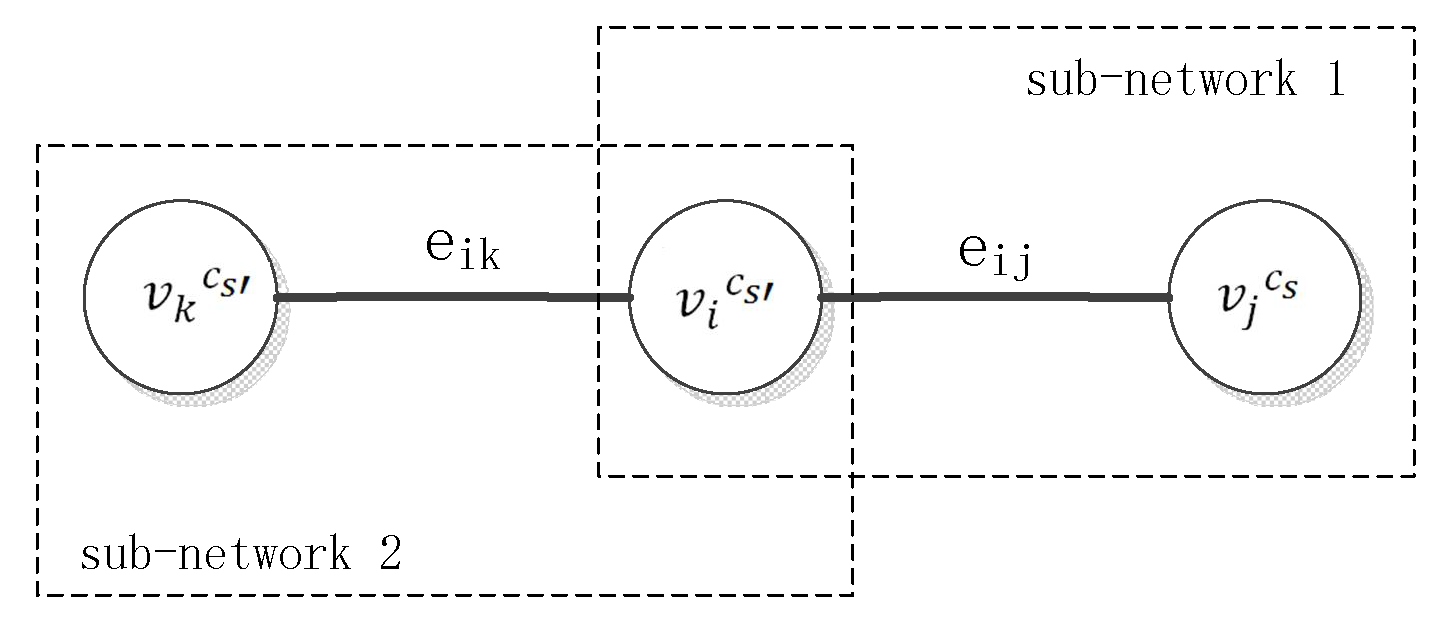
As a simple example, in the heterogeneous network (shown in Figure 1), we assumed there are two edges, and ; three vertexes,, and ; and two vertex types, and . We can obtain two sub-networks from this heterogeneous network, and . Where , and , , , . , and , . =, and = {}, = {}.
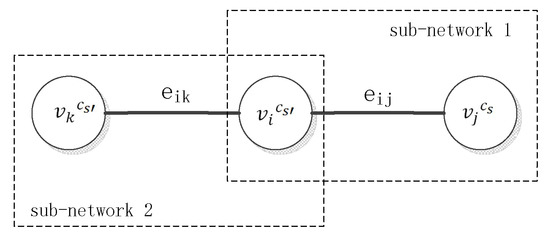
Figure 1.
A simple example of the heterogeneous network.
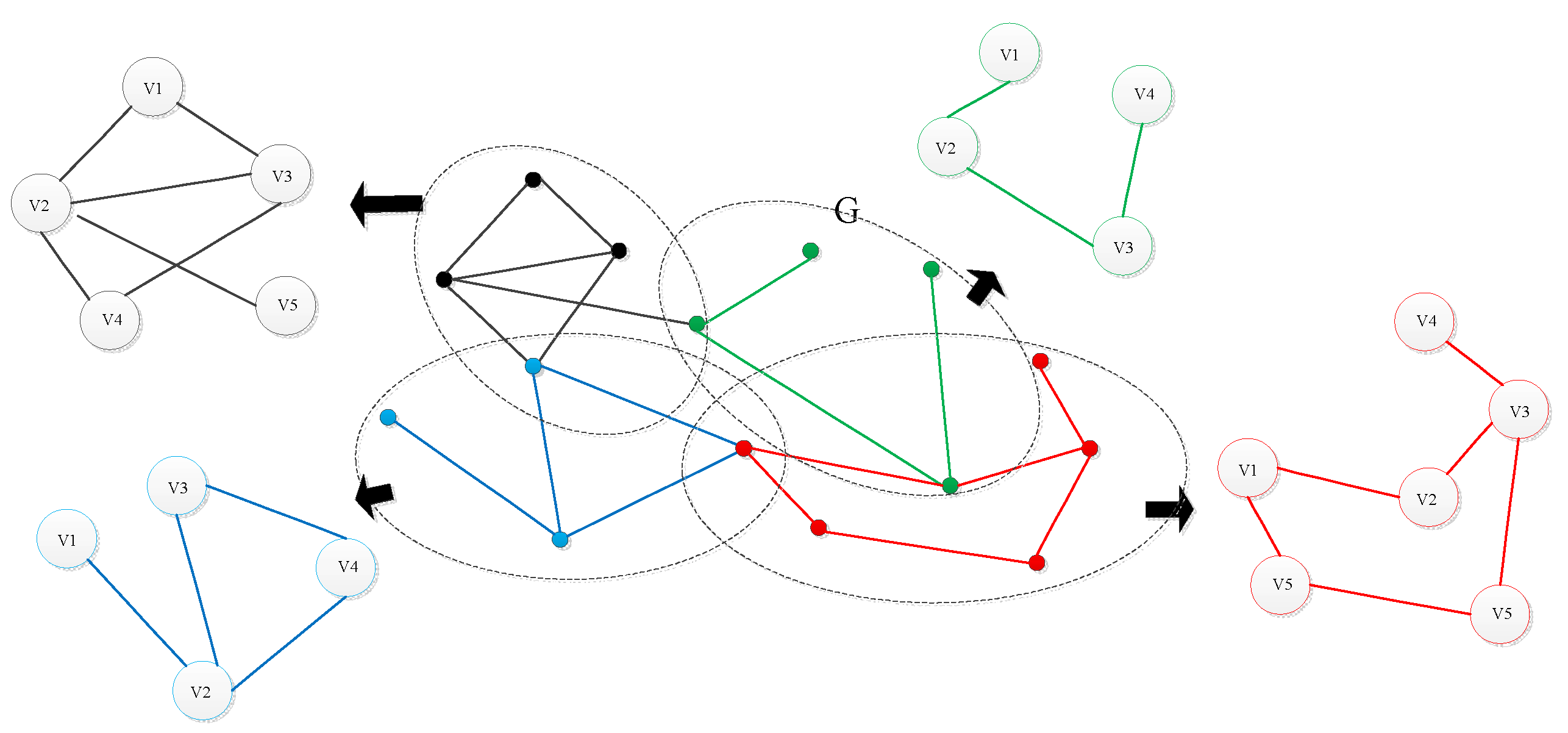
In order to better explain this question, Figure 2 shows the process of a heterogeneous network disassembling into several homogeneous sub-networks. The heterogeneous network has four types of vertexes, so we can obtain four sub-networks according to the relationships of edges and vertexes.
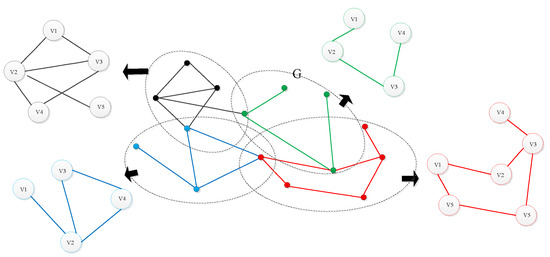
Figure 2.
Sub-networks disassembled from a heterogeneous network.
In this paper, the reason for designing the heterogeneous academic network is based on users’ requirements for academic information. This means users are not only eager to obtain the ranking of papers but also want to understand the influence of related topics, the authority of authors, the impact factor of venues, as well as the highly relevant topics with search terms.
Considering the internal and external factors of scientific publication evaluation, we construct a heterogeneous academic network. The external factors include venue impact, author authority, citation relationship, and co-author. The internal factors include the title, abstract, and keyword. Because there are certain dependencies between these metadata, and there is a one-to-one relationship between title and abstract, we convert the metadata into topics for analysis in processing.
Therefore, the heterogeneous academic network in this paper has four types of vertexes (i.e., publication (title), venue, author, and topic). The types of edges include publication to publication (created by a citation relationship), author to author (created by a co-author relationship), topic to topic (created by a co-occurrence relationship), publication to venue (the paper is published in the venue), publication to author (the paper is created by an author), and publication to topic (the paper includes a topic). The list is shown in Table 2. Considering that this paper aims to propose an algorithm for publication ranking, the vertex in the network is mainly about publications. The co-author relationship and keyword co-occurrence relationship are ignored in the latter part of this paper.

Table 2.
Types of vertex and edge.
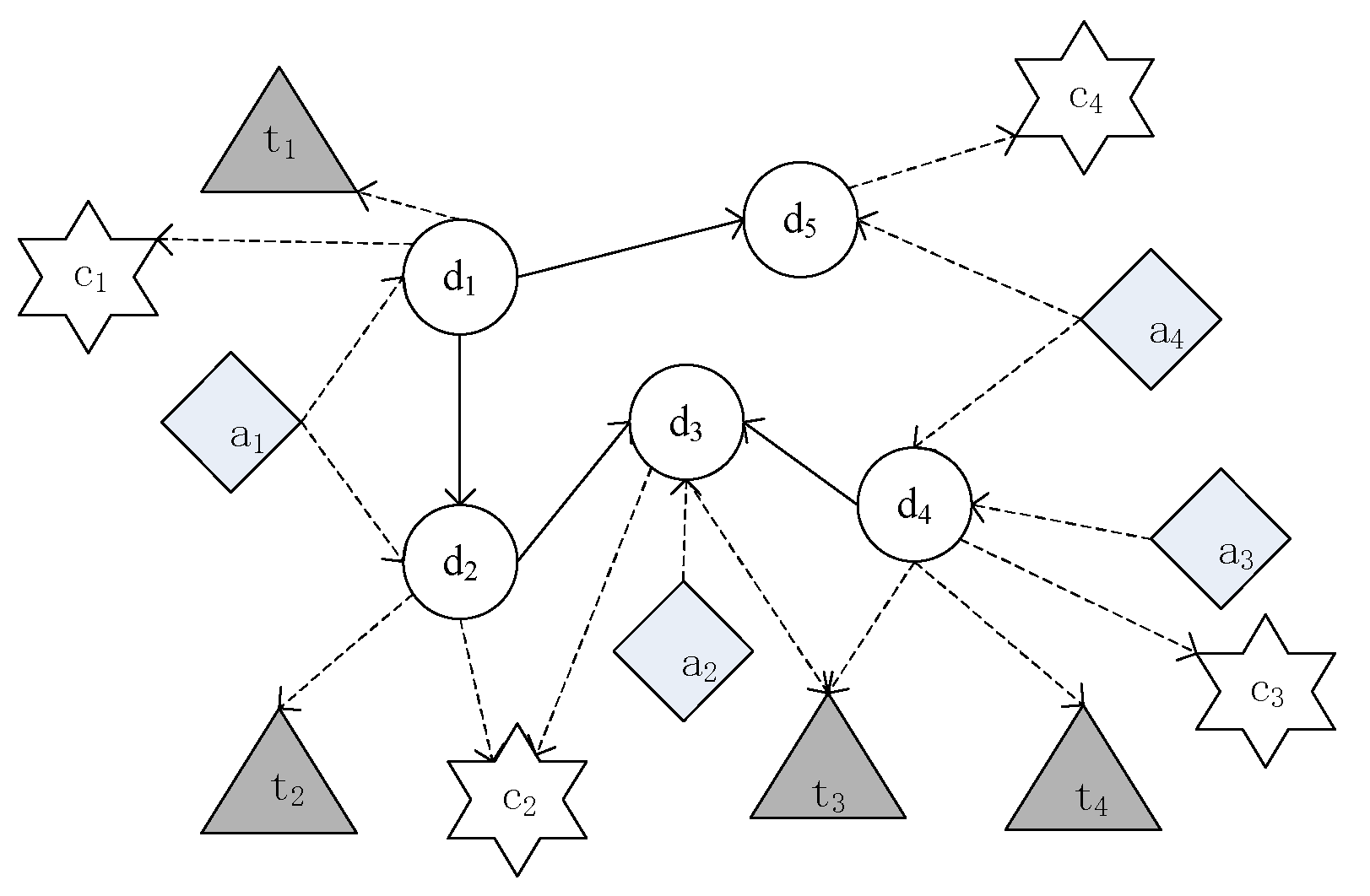
We also take an example in Figure 3 to illustrate the heterogeneous academic network. Author writes two papers, and . Paper is cited by paper . The topic is included in , and topic is included in . and are published in venue and , respectively. Paper is written by author with the topic and published in venue . Author and author jointly complete paper , which includes the topics and . Paper is published in venue . Paper is cited by papers and . Paper is created by author , and published in venue . By considering the correlation of the heterogeneous network, this computing structure offsets the limitations of the homogeneous network.
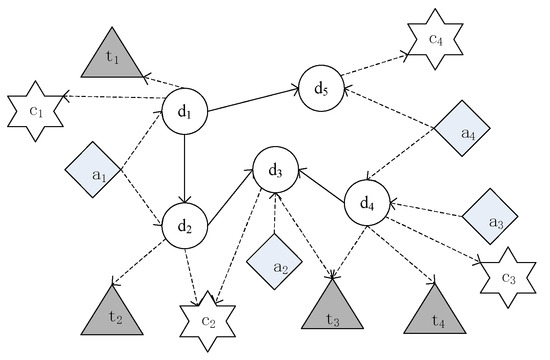
Figure 3.
An example of heterogeneous academic network object relationships.
When constructing the heterogeneous academic network, we introduced the Gibbs sampling model to represent the topic relevance. When different authors work together to complete a paper, they may contribute to different topics of the paper. At the same time, the topic of this paper also determines which journals the paper can be submitted to and which topics are relevant.
In this model, the generation of topics is determined by the words. Therefore, we can extract an author from all authors and determine the topic generated by that author, that is, the implicit distribution of the topic. Then, we extract a topic from the probability distributions of all words and obtain the topic of venues and keywords from the distributions of all journals and keywords.
The overall process can be divided into the following steps:
① For each topic , randomly extract the probabilistic for generating words for the topic of each document; the probabilistic of venue is generated, along with the probabilistic for generating keywords for the topic. The three probability distributions are based on Dirichlet distributions with prior parameters , , and , respectively.
② For each word in document :
Extract author from author :
- A topic that follows the multinomial distribution is generated by the author ( follows a prior distribution);
- Word ;
- Venue ;
- Keywords .
In the calculation, the Gibbs sample in the LDA method is to be used. First, we calculate the probability that the author generates a topic , the topic generates a word , the topic generates a keyword , and the topic generates a venue ; the i-th word , venue , and keyword in paper d are attached to topic and author . The calculated joint probability calculation formula is as follows:
where represents the frequency of the topic that was sampled based on author distribution, represents the frequency of the word that was sampled based on the topic distribution, represents the frequency of the venue (journal or conference) that was sampled based on the topic z distribution, and represents the frequency of the keyword r. The Dirichlet prior distribution of the , , distributions are considered in calculation, and we can obtain the probability .
After the unified modeling of the heterogeneous network, we can use the calculation results as the retrieval feedback of the author, venue, keyword, and publication. Under the premise of a certain topic, the probability that a paper d generates a word w can be expressed as follows:
The language model is used to represent the correlation between the document and query word, which is represented by the probability that the document generates the query word:
For a query , it is usually assumed that the words contained in it all exist independently:
Among them, represents the -th word in the query word and represents the probability that document generates word .
In the same way, P(q|a), P(q|c), and P(q|r) can obtain the probability under the relevant topic. Variable a represents all papers published by the author, thereby calculating the probability of the author for the query word; variable c represents the journal or conference in which the paper was published, thereby calculating the probability of the journal or conference for the query word; and variable r represents the corresponding keyword related to the paper, thereby calculating the probability of the relevant keyword for the query word.
3.3. Ranking Algorithm for Heterogeneous Academic Networks
The NetClus algorithm is a ranking algorithm suitable for star heterogeneous networks; it divides different types of vertexes into attribute and target objects and uses the association between different types of vertexes in the clustering ranking process. In a star heterogeneous academic network, papers are defined as target objects, and authors, venues, and keywords are defined as attribute objects. During this operation, the NetClus algorithm uses the relationship between papers and authors, the relationship between papers and keywords, and the relationship between papers and venues but ignores the citation relationship between papers and papers. The citation relationship between papers is equally important for heterogeneous academic networks. Therefore, this paper hopes to use the relationship between papers and papers and the relationship between papers and the attribute types of authors, keywords, and venues. Therefore, the ConNetClus algorithm optimized by the NetClus algorithm is adopted.
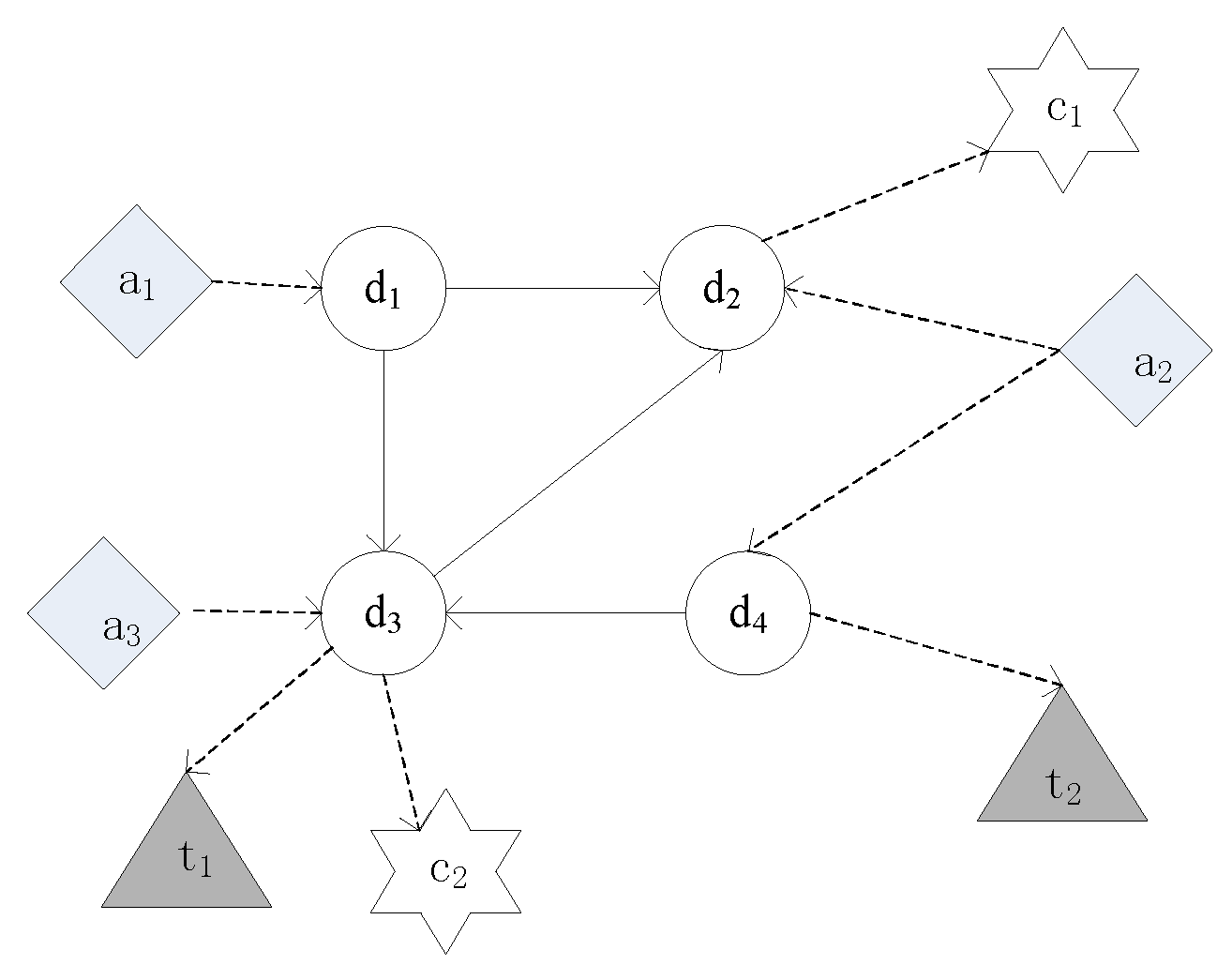
A sample data relationship in this paper Is shown in Figure 4. Suppose there are four papers (D) as the target type, and there is a citation relationship between the papers; meanwhile, the papers have a link relationship with the attribute types of author (A), keyword (T), and venue (C), respectively.
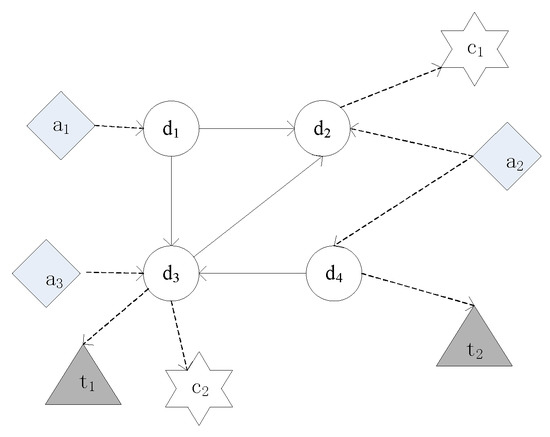
Figure 4.
Star heterogeneous academic network.
The ConNetClus algorithm framework is as follows:
① The target object is initially divided into clusters, and the initial network clustering is generated according to the partition, that is . The superscript 0 represents the 0th round, and represents the target object included in the initialization cluster .
② Calculate a ranking-based probabilistic generative model for each target object under each cluster, .
③ Calculate the posterior probability of each target object under each cluster and adjust the cluster assignment result according to the evaluation of the posterior probability.
④ Repeat steps ② and ③ until all clustering results no longer change significantly. That is, .
⑤ After the results are obtained for the target objects, the probability distributions of different types of attribute objects are obtained in each cluster so as to obtain the sorting results.
Generating probability model of target and attribute objects.
To simplify different types of objects in heterogeneous networks, different types of objects are decomposed, and then the generation behavior of the paper of the target object is modeled. If the probability of the authors, journals, and keywords of the paper being accessed is high, or the probability of the papers cited in the paper being accessed is high, it can be considered that the paper is highly likely to be accessed. The idea of decomposing heterogeneous networks is that for a heterogeneous network G, the access probabilities of objects of different attribute types are independent of each other. For example, author , can be decomposed into two parts: , where indicates the type of access author and represents the probability of facing all authors but accessing object . Therefore, for an attribute object and its type , the probability of accessing in network is defined as follows:
Among them, represents the probability that the type is accessed in the network, and represents the probability that the object is accessed in this type. The accessed probabilities of any two attribute objects are independent. Therefore, the joint probability is defined as follows:
Among them, .
Then, we build a generative model of the target object. Taking the scientific research network as an example, the multiple authors who have completed the paper , the journals that the paper is published in, and the keywords contained in the paper will all affect the generation probability of the target object paper . Therefore, the probability of generating a paper under the cluster in the network G is defined as follows:
where represents the set of attribute objects associated with the target object paper ; represents whether the paper is related to the attribute object ; represents the generation probability of a paper citing other papers, using the results of the previous round; represents the product of the generation probabilities of all attribute objects related to the target object; and represents the product of all the generation probabilities of the target object papers in the previous round.
Because the generation probability of the attribute object may be 0, a parameter is referenced to make it smooth. The formula is as follows:
Among them, represents the probability that the attribute object is accessed in the cluster. represents the access probability of attribute object in heterogeneous network G. Because the generation probability of the target object as the center point will not be 0, no parameters are added for smoothing.
The posterior probability of the target object.
It is obtained by the Bayesian formula. This probability is the probability that each target object belongs to cluster k:
Among them, represents the probability of cluster k in network G and represents the last round of calculation of the probability that the paper belongs to cluster k.
In each round of iteration, each target object can calculate the posterior probability of each dimension; then, we can compose a K-dimensional vector that can be represented as each target object, that is, . The center point of the K-dimensional vector of the cluster can be obtained according to the average value of the K-dimensional vector of the papers in this cluster. We can calculate the distance of each paper from the center point using the cosine similarity and then use this as an adjustment. We stop the iteration when the target object in the cluster no longer changes. Finally, we have the result of comprehensive sorting.
After the clustering and ranking of ConNetClus, the clustered classifiers and sorting results of each type of vertex are obtained. Then, we use the word similarity of Wikipedia [41] to calculate the similarity between the clustered classifiers and words under the topic calculated.
For a paper , consider that authority of the paper’s vertex is the sum of the products of the similarity under each cluster word and authority under each category:
Similarly, the authority of authors, conferences, and keywords is also calculated by this formula.
Then, we can apply the calculated authority of the object under the vertex type to the retrieval task of the object. This section intends to use the combined method of multiplication. We used the addition method, but the experimental results were not as good as the product. For a query word, the final score of a paper is the product of relevance and authority :
Similarly, the final scores for authors, venues, and keywords are:
If the user gives more than one query word, the proportion probability between the query words must be given; it is not a simple comparison between query words. Suppose query keywords are given; then, we set the weight value to decrease from the first keyword to the nth keyword, with the weight . The weights before and after are incremented and decremented, respectively. Because there are no more than 10 query keywords in general, the increasing and decreasing trends are increased or decreased by 0.01, respectively. Therefore, at this time, the final score of a paper is:
Similarly, the final scores for authors, conferences, and keywords are also derived from this.
4. Experiments
4.1. Data Description
In this paper, we use the dataset of high-energy physics-based theoretical papers published on the SNAP website [42] The dataset includes a paper’s number, title, author, venue, abstract, and other metadata. There are 27,770 publications with 35,702 authors published in 118 venues (journals or conferences) with 200 keywords. The citation relationships of publication-to-publication are 352,807 edges. The publications are written by 35,702 authors; therefore, the edges of publication-to-author are 40,327. Besides that, the edges of publication-to-venue are 20,956. There are 55,540 edges of publication-to-keyword.
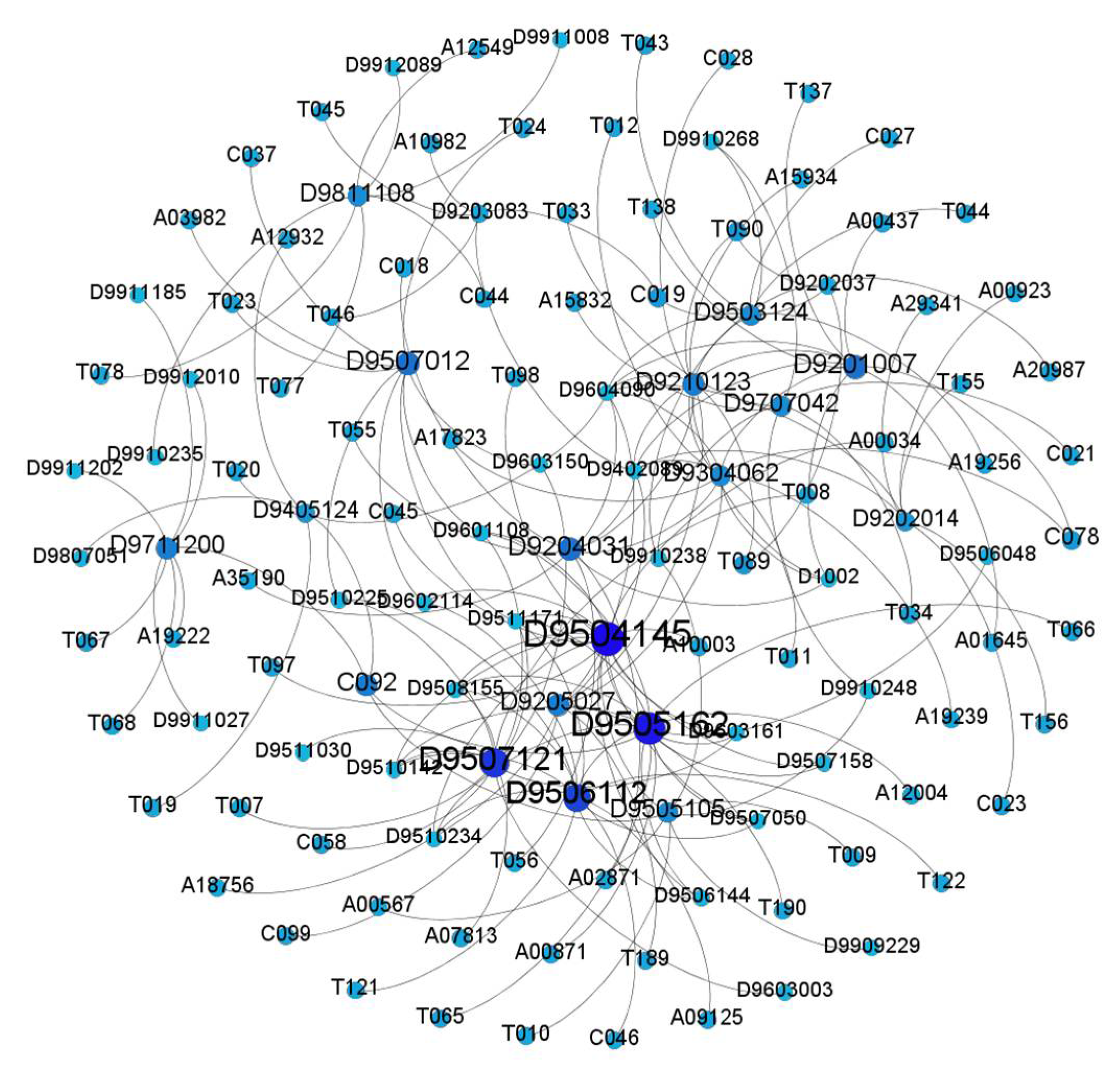
As shown in Figure 5, we visualized an example of sampling data with the software Gephi to illustrate the heterogeneous academic network. There are 105 publications as paper vertexes (D), 25 authors as author vertexes (A), 19 venues as venue vertexes (C), 38 keywords as topic vertexes (T), and 170 edges between the vertexes. In the figure, the larger vertexes with a darker color indicate that the higher its penetration, the more times it is connected.
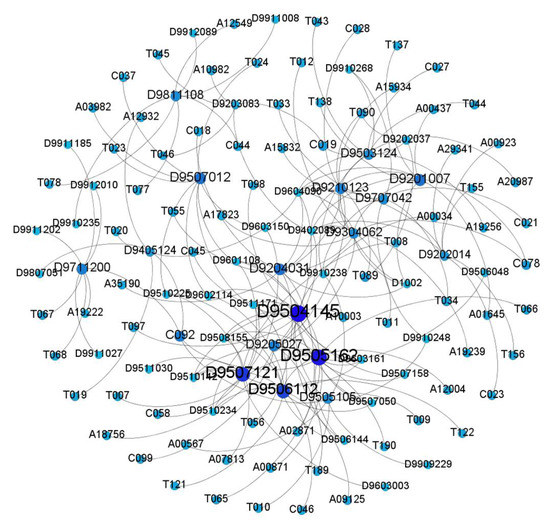
Figure 5.
Sampling example of the heterogeneous academic network (visualized by the software Gephi).
In this paper, we first use Python 3.7 as the application environment when processing the dataset. The topic model SentinceLDA is implemented in Python language, which comes from a semantic-matching calculation tool in Baidu’s open source project Familia [43] in 2017.
Based on the SentinceLDA model, we can obtain the probability distributions of the abstract data for different topics, in which we define the number of topics as 100, and 2 words of each topic are considered. These selected topics are used to create the heterogeneous academic network, and then we calculate the probability distributions of each vertex in the heterogeneous academic network under different topics. After that, we select 50 topics and 5 words corresponding to each topic. Finally, the ConNetClus algorithm is used to cluster and sort the vertexes in the network. The probability value calculated by ConNetClus is used for ranking different types of vertexes.
4.2. Data Processing
For the dataset used in this paper, we must preprocess the text data, especially for the abstract and title, to effectively carry out the data analysis. The preprocessing includes word segmentation, removing stop words, utilizing WordNet, and so on.
Firstly, for the metadata in the dataset, the authors, venues, abstracts, and keywords are extracted. The data extracted by Java programming code are stored in the MySQL database. Then, we remove the stop words because there are many meaningless semantic words in the dataset. These words occupy storage space and reduce efficiency in the retrieval process. In this paper, we use the stop words in nltk corpus.
In a text paragraph, a word may appear several times in different parts of speech, such as a verb, noun, and adjective. The topic model may treat the word as different words and calculate them repeatedly. To solve this problem, WordNet is needed for text processing. WordNet is a huge English vocabulary database. A word may have many expressions, such as nouns, verbs, adjectives, and so on. This method can associate synonyms with each other through concept and semantic relationships. For example, the words ‘environment’ and ‘environmental’ have similar meanings. If they are not processed, the calculation of topic model will be redundant. Therefore, WordNet, a natural language processing tool, is used for processing.
WordNet can not only eliminate similar words in font, but also merge the same words in semantics. This paper uses the jar file of “edu.princeton.cs.algs4” from Princeton to solve the WordNet problem.
4.3. Evaluation Methods
Two indicators were used in this paper to measure algorithm performance: mean average precision (MAP) and normalized discounted cumulative gain (nDCG) [44].
MAP: Average precision is the average accuracy of each related document in a single topic. As an indicator, MAP reflects the performance of the system for all relevant documents. If no relevant documents are returned, the default accuracy is 0.
Generally, multiple query statements are used to calculate the performance, and we calculate the average value of these performances, where Q represents the total number of queries q.
NDCG: In the indicator of MAP, there are only two statuses of documents: relevant or irrelevant. In NDCG, documents can be evaluated at different levels according to their relevance. In the process of evaluation, the results with a high correlation degree are more important than those with a low correlation degree.
NDCG estimates the cumulative relevance gain a user receives by examining retrieval results up to a given rank on the list. In this research, we use the importance score, −1, 0, 1, 2, as the relevance label to calculate NDCG scores.
where reli refers to the relevance level of the document i, which is divided into four values: 2 means very relevant, 1 means relevant, 0 means irrelevant, and -1 means noise file.
IDCG is the maximum value of DCG.
where |REL| refers to taking the first p documents, and the sorting order is from large to small according to the relevance. Because the query results are different from each other, the length of p is not same, which also has a great impact on the calculation results of DCG.
4.4. Evaluation Results
To verify the influence of the heterogeneous academic network analysis for the academic paper ranking algorithm, this paper first compares the method proposed in this paper with the classical algorithm.
PLSA is the probabilistic latent semantic analysis model. Its main goal is to reduce the dimension and map the document from the sparse, high-dimensional word space to low-dimensional vector space. This method can create a model by a single vertex as publication, author, journal, or keyword, separately, and cannot build a heterogeneous network. Therefore, PLSA was compared with the method proposed in this paper (SenLDA + ConNetClus) to verify if there are advantages to heterogeneous network analysis.
BM25 is a classical language model method of information retrieval, which is realized by calculating the correlation between network objects and query keywords. BM25 + ConNetClus is also compared to test if the SenLDA + ConNetClus method is better than the language model for publication ranking.
PageRank is a global page ranking algorithm based on the intuition that links from important pages are more significant than links from other pages. This method has been widely used in citation analysis for evaluating the importance of vertexes in the network; however, it is independent of topics. Therefore, LDA + PageRank, as used in this paper, is tested to prove that the SenLDA + ConNetClus method is more significant in heterogeneous academic network computing and analysis.
The ground truth in this paper is from the manual annotation of physics students and gives the ranking results for papers, venues, keywords, and authors in a specific topic. Considering that users may pay more attention to the top results in information retrieval, the labeling process takes 5 results as the standard. Then, using the search intersection of the algorithm proposed in this paper, BM25 and hep-th system, the search words are selected for experimental comparison. The evaluation results in MAP and NDCG are shown in Table 3 and Table 4.

Table 3.
Experimental results of MAP.

Table 4.
Experimental results of NDCG.
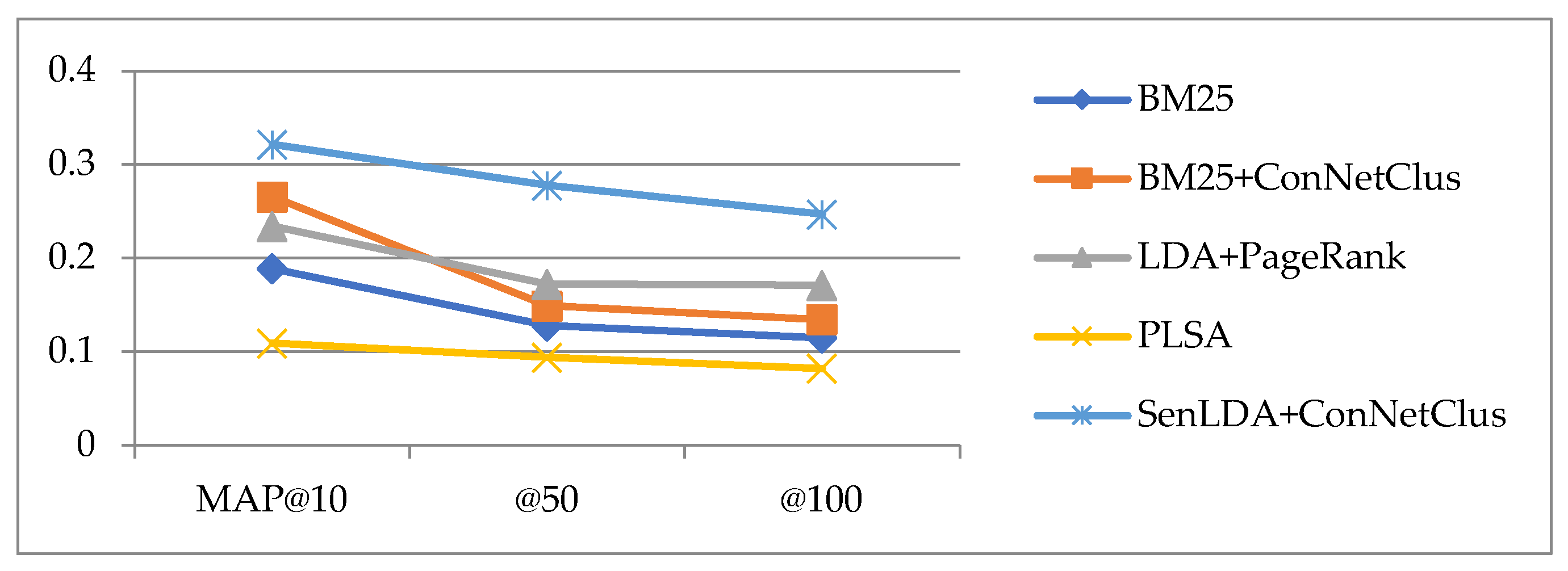
From the experimental results of MAP shown in Table 3 and Figure 6, it can be found that the higher the MAP value, the more similar the ranking result is close to the ground truth. It can be clearly seen in Figure 5 that the senLDA + ConNetClus method proposed in this paper obtains better calculation results, and its MAP value is higher than other algorithms, in MAP@10, @50, and @100.
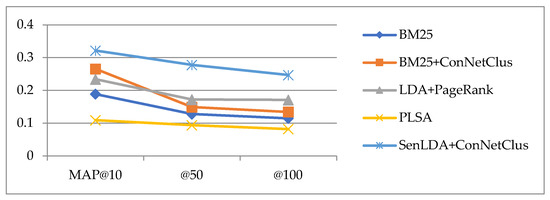
Figure 6.
Experimental results of average scores in MAP.
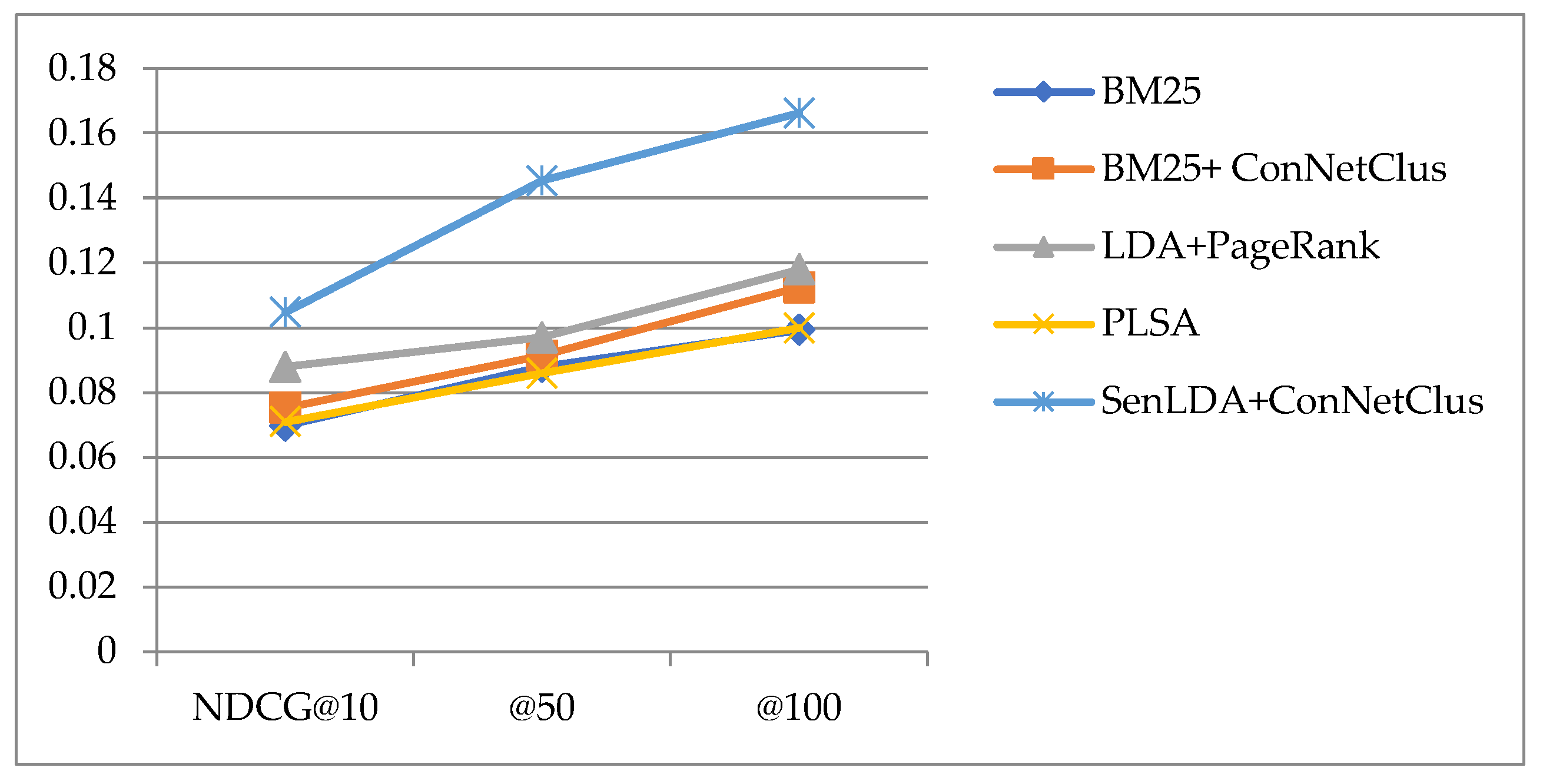
The NDCG evaluation index considers the influence of the relative importance of different contents in the search results. A higher NDCG means that the more important results will be listed at the top of search results. From the experimental results of NDCG shown in Table 4 and Figure 7, we found that the NDCG evaluation results of the method proposed in this paper are better than other comparison methods in NDCG@10, @50, and @100.
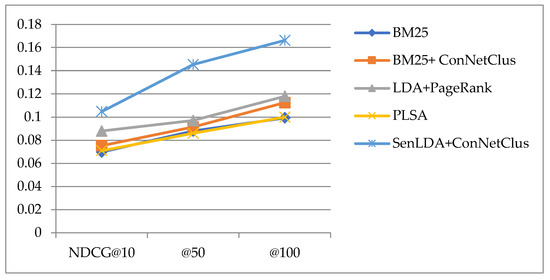
Figure 7.
Experimental results of average scores in NDCG.
Based on the above experimental results, the method for publication ranking proposed in this paper, which considers the relevance of sentences in the process of topic training by sentenceLDA, is compared with the traditional language model analysis. In addition, this method is constructed by four types of vertexes (i.e., publication, venue, author, and topic) as the heterogeneous academic network, which was contrasted with the homogeneous network for calculating and evaluating. After that, we used a heterogeneous network analysis method named ConNetClus to calculate the probability of each vertex and the ranking result. Finally, this method achieved better results than the publication ranking algorithm. Additionally, this algorithm not only realizes the ranking questions but also supports the discovery of authors, venues, and topics with high authority and relevance.
5. Conclusions
With the development of electronic scientific publications, research on the evaluation and ranking of publications has become very important for managing academic resources. The factors affecting the evaluation of publications include internal and external factors, which are also consistent with the goal of academic evaluation. Academic evaluation not only lies in the evaluation of academic papers but also includes the analysis of venues, authors, and topics. In this paper, we realized the research objects of the topic model, network construction, and weight calculation in network analysis and explored these objects and methods with the analysis of a heterogeneous academic network. As seen in the experiments, we found that the method proposed in this paper is better than the comparative methods in MAP and NDCG.
However, there are still some limitations to this paper. For example, we only selected the four most important metadata as the vertexes in the heterogeneous academic network. However, there are more metadata affecting the evaluation results of scientific publications. In addition, the calculation of edge weights can better reflect the complexity and authenticity of social networks [45] but this paper only considered the vertex weight of heterogeneous academic networks and ignored edge weights. The reason for this comes from the limitation of the dataset. In this experiment, we only took the abstract as the content of the publication from the dataset, which lacked the support of the full-text data. In a further study, we may build a heterogeneous academic network as a complex weighted network [46] using full-text data analysis; in there, the edge weights can be calculated by a full-text analysis and topics model. During the experimental comparison, the selection of ground truth data was also limited by the dataset. More open datasets should be used for further study.
Author Contributions
Conceptualization: J.Z. and Y.C.; methodology: B.J.; validation: B.J.; formal analysis: J.S. and Y.Z.; investigation: J.Z.; resources: B.J.; data curation: J.S.; writing—original draft preparation: B.J. and Y.Z.; writing—review and editing: J.Z. and Y.Z.; visualization: B.J.; supervision: J.Z. and Y.C.; project administration: J.Z; funding acquisition: J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, grant number 3132022289, the Liaoning Revitalization Talents Program, grant number XLYC1907084, the China Postdoctoral Science Foundation, grant number 2016M591421 and the Collaborative Education Project of Industry University Cooperation of the Ministry of Education, grant number 201902323007.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vom Brocke, J.; Simons, A.; Riemer, K.; Niehaves, B.; Plattfaut, R.; Cleven, A. Standing on the shoulders of giants: Challenges and recommendations of literature search in information systems research. Commun. Assoc. Inf. Syst. 2015, 37, 9. [Google Scholar] [CrossRef]
- Eveleth, R. Academics Write Papers Arguing Over How Many People Read (and Cite) Their Papers. Available online: https://www.smithsonianmag.com/smart-news/half-academic-studies-are-never-read-more-three-people-180950222/?no-ist (accessed on 1 June 2021).
- Garfield, E. Citation analysis as a tool in journal evaluation: Journals can be ranked by frequency and impact of citations for science policy studies. Science 1972, 178, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Garfield, E. Journal impact factor: A brief review. CMAJ 1999, 161, 979–980. [Google Scholar] [PubMed]
- Zhang, J.; Liu, X. Citation Oriented AuthorRank for Scientific Publication Ranking. Appl. Sci. 2022, 12, 4345. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Stanford InfoLab: Stanford, CA, USA, 1999. [Google Scholar]
- MacRoberts, M.H.; MacRoberts, B.R. Problems of citation analysis: A critical review. J. Am. Soc. Inf. Sci. 1989, 40, 342–349. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Guo, C. Full-text citation analysis: Enhancing bibliometric and scientific publication ranking. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 1975–1979. [Google Scholar]
- Cronin, B. Metatheorizing citation. Scientometrics 1998, 43, 45–55. [Google Scholar] [CrossRef]
- Egghe, L.; Rousseau, R.; Van Hooydonk, G. Methods for accrediting publications to authors or countries: Consequences for evaluation studies. J. Am. Soc. Inf. Sci. 2000, 51, 145–157. [Google Scholar] [CrossRef]
- Abrishami, A.; Aliakbary, S. Predicting citation counts based on deep neural network learning techniques. J. Informetr. 2019, 13, 485–499. [Google Scholar] [CrossRef]
- Small, H.; Boyack, K.W.; Klavans, R. Citations and certainty: A new interpretation of citation counts. Scientometrics 2019, 118, 1079–1092. [Google Scholar] [CrossRef]
- Larson, R.R. Bibliometrics of the World Wide Web: An exploratory analysis of the intellectual structure of cyberspace. In Proceedings of the Annual Meeting—American Society for Information Science, Baltimore, MD, USA, 19–20 October 1996; Volume 33, pp. 71–78. [Google Scholar]
- Gibson, D.; Kleinberg, J.; Raghavan, P. Inferring web communities from link topology. In Proceedings of the Ninth ACM Conference on Hypertext and Hypermedia: Links, Objects, Time and Space—Structure in Hypermedia Systems: Links, Objects, Time and Space—Structure in Hypermedia Systems, Pittsburgh, PA, USA, 20–24 June 1998; pp. 225–234. [Google Scholar]
- Haveliwala, T.H. Topic-sensitive pagerank: A context-sensitive ranking algorithm for web search. IEEE Trans. Knowl. Data Eng. 2003, 15, 784–796. [Google Scholar] [CrossRef]
- Qiao, H.; Wang, Y.; Liang, Y. A value evaluation method for papers based on improved PageRank algorithm. In Proceedings of the 2012 2nd International Conference on Computer Science and Network Technology, Changchun, China, 29–31 December 2012; pp. 2201–2205. [Google Scholar]
- Hasan, F.; Ze, K.K.; Razali, R.; Buhari, A.; Tadiwa, E. An improved PageRank algorithm based on a hybrid approach. Sci. Proc. Ser. 2020, 2, 17–21. [Google Scholar] [CrossRef]
- Chauhan, U.; Shah, A. Topic modeling using latent Dirichlet allocation: A survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Tao, M.; Yang, X.; Gu, G.; Li, B. Paper recommend based on LDA and pagerank. In International Conference on Artificial Intelligence and Security; Springer: Singapore, 2020; pp. 571–584. [Google Scholar]
- Zhang, Y.; Ma, J.; Wang, Z.; Chen, B.; Yu, Y. Collective topical PageRank: A model to evaluate the topic-dependent academic impact of scientific papers. Scientometrics 2018, 114, 1345–1372. [Google Scholar] [CrossRef]
- Kanellos, I.; Vergoulis, T.; Sacharidis, D.; Dalamagas, T.; Vassiliou, Y. Impact-based ranking of scientific publications: A survey and experimental evaluation. IEEE Trans. Knowl. Data Eng. 2019, 33, 1567–1584. [Google Scholar] [CrossRef]
- Brembs, B.; Button, K.; Munafò, M. Deep impact: Unintended consequences of journal rank. Front. Hum. Neurosci. 2013, 7, 291. [Google Scholar] [CrossRef] [PubMed]
- Bornmann, L.; Daniel, H.D. What do we know about the h index? J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1381–1385. [Google Scholar] [CrossRef]
- Hu, G.; Wang, L.; Ni, R.; Liu, W. Which h-index? An exploration within the Web of Science. Scientometrics 2020, 123, 1225–1233. [Google Scholar] [CrossRef]
- Beel, J.; Gipp, B. Google Scholar’s ranking algorithm: The impact of citation counts (an empirical study). In Proceedings of the 2009 Third International Conference on Research Challenges in Information Science, Fez, Morocco, 22–24 April 2009; pp. 439–446. [Google Scholar]
- Gazni, A.; Didegah, F. The relationship between authors’ bibliographic coupling and citation exchange: Analyzing disciplinary differences. Scientometrics 2016, 107, 609–626. [Google Scholar] [CrossRef]
- Son, J.; Kim, S.B. Academic paper recommender system using multilevel simultaneous citation networks. Decis. Support Syst. 2018, 105, 24–33. [Google Scholar] [CrossRef]
- Zhao, M.; Yan, E.; Li, K. Data set mentions and citations: A content analysis of full-text publications. J. Assoc. Inf. Sci. Technol. 2018, 69, 32–46. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Guo, C. Full-text citation analysis: A new method to enhance scholarly networks. J. Am. Soc. Inf. Sci. Technol. 2013, 64, 1852–1863. [Google Scholar] [CrossRef]
- Randy, H.K.; Eric, A.B. The Case for Wireless Overlay Networks; Springer: Boston, MA, USA, 1996. [Google Scholar]
- Shi, C.; Zhang, Z.; Ji, Y.; Wang, W.; Yu, P.S.; Shi, Z. SemRec: A personalized semantic recommendation method based on weighted heterogeneous information networks. World Wide Web 2019, 22, 153–184. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Wang, Y.; Jie, X. 3D model features co-clustering based on heterogeneous semantic network. In Proceedings of the 2014 4th IEEE International Conference on Information Science and Technology (ICIST), Shenzhen, China, 26–28 April 2014. [Google Scholar]
- Shi, C.; Liu, J.; Zhuang, F.; Yu, P.S.; Wu, B. Integrating heterogeneous information via flexible regularization framework for recommendation. Knowl. Inf. Syst. 2016, 49, 835–859. [Google Scholar] [CrossRef]
- Mu, L.W.; Peng, X.B.; Huang, L. Abnormal Data Detection Algorithm in Heterogeneous Complex Information Network. Comput. Sci. 2015, 42, 34–137. [Google Scholar]
- Zhang, M.; Hu, H.; He, Z.; Wang, W. Top-k similarity search in heterogeneous information networks with x-star network schema. Expert Syst. Appl. 2015, 42, 699–712. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, G. Efficient identification of node importance in social networks. Inf. Process. Manag. 2016, 52, 911–922. [Google Scholar] [CrossRef]
- Sun, Y.; Han, J.; Zhao, P.; Yin, Z.; Cheng, H.; Wu, T. Rankclus: Integrating clustering with ranking for heterogeneous information network analysis. In Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology, Saint Petersburg, Russia, 24–26 March 2009; pp. 565–576. [Google Scholar]
- Pio, G.; Serafino, F.; Malerba, D.; Ceci, M. Multi-type clustering and classification from heterogeneous networks. Inf. Sci. 2018, 425, 107–126. [Google Scholar] [CrossRef]
- Han, J.; Sun, Y.; Yan, X.; Yu, P.S. Mining heterogeneous information networks. In Proceedings of the Tutorial at the 2010 ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD’10), Washington, DC, USA, 24–28 July 2010. [Google Scholar]
- Balikas, G.; Amini, M.R.; Clausel, M. On a topic model for sentences. In Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval, Pisa, Italy, 17–21 July 2016; pp. 921–924. [Google Scholar]
- Hwang, W.; Hajishirzi, H.; Ostendorf, M.; Wu, W. Aligning sentences from standard wikipedia to simple Wikipedia. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, CO, USA, 31 May–5 June 2015; 2015; pp. 211–217. [Google Scholar]
- Available online: http://snap.stanford.edu/data/ (accessed on 15 June 2019).
- Available online: https://github.com/baidu/Familia (accessed on 11 May 2018).
- Jrvelin, K.; Keklinen, J. Cumulated Gain-Based Evaluation of IR Techniques. ACM Trans. Inf. Syst. 2002, 20, 422–446. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Alfieri, R.; Nguyen, Q.; Montepietra, D.; Cassi, D. Link and node removal in real social networks: A review. Front. Phys. 2020, 8, 228. [Google Scholar] [CrossRef]
- Nguyen, Q.; Nguyen, N.K.K.; Cassi, D.; Bellingeri, M. New Betweenness Centrality Node Attack Strategies for Real-World Complex Weighted Networks. Complexity 2021, 2021, 1–17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).