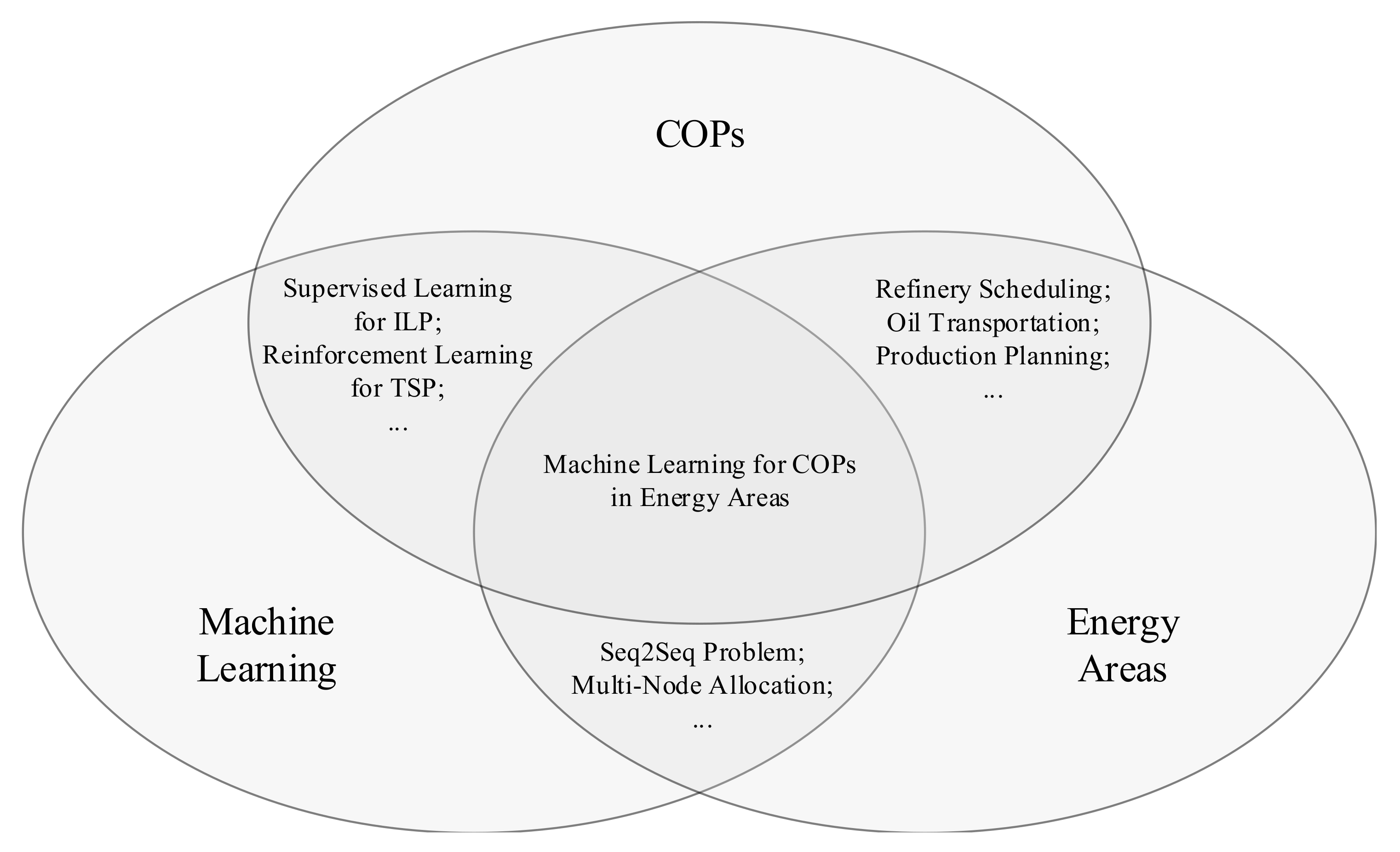
A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas
Abstract
:1. Introduction
2. Background
2.1. Combinatorial Optimization Problem
2.1.1. Traveling Salesman Problem
2.1.2. Maximum Independent Set
2.1.3. Minimum Spanning Tree
2.1.4. Maximum Cut Problem
2.1.5. Bin Packing Problem
2.2. Deep Learning
2.2.1. Attention Mechanism
- (1)
- Additive Attention
- (2)
- Pointer Networks
- (3)
- Multiplicative Attention
2.2.2. Graphic Neural Networks
- (1)
- Graph Classification Problem
- (2)
- Graph Grouping Problem
- (3)
- Node Classification Problem
- (4)
- Link Prediction Problem
2.3. Reinforcement Learning
2.3.1. Single-Agent Reinforcement Learning
2.3.2. Multi-Agent Reinforcement Learning
2.3.3. Multi-Agent Reinforcement Learning with Game Theory
- (1)
- Cooperative MARL [216]
- (2)
- Competitive MARL [221]
- (3)
- Mixed MARL [226]
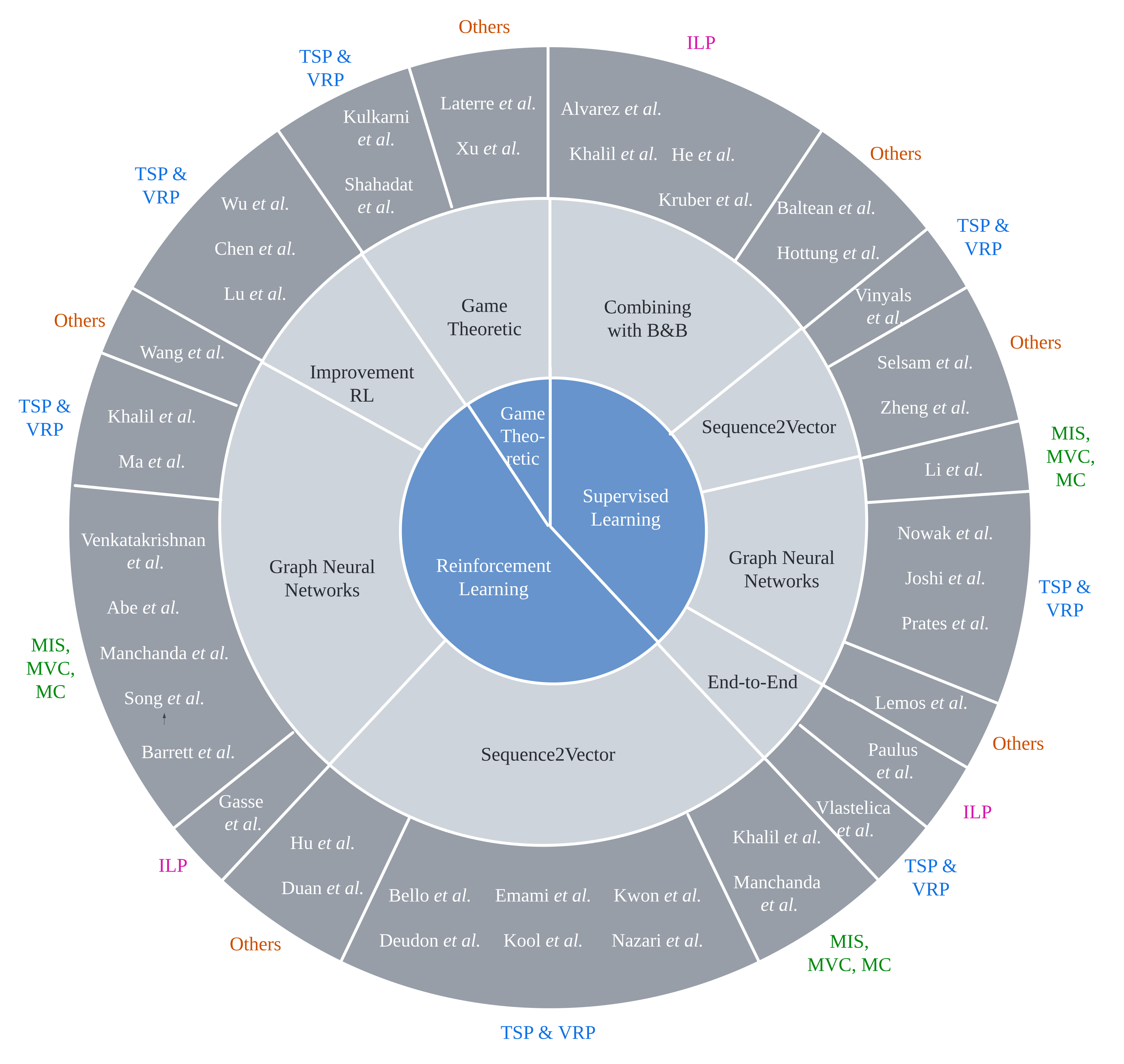
3. Learning to Solve COPs
3.1. Methods
3.1.1. Supervised Learning
Combining with Branch and Bound
Sequence2Vector
Graph Neural Networks
End-to-End Architecture
3.1.2. Reinforcement Learning
Parameterization of Policy Network
Reinforcing Methods
Improvement RL
3.1.3. Game Theoretic Methods
Single-Player Game
Competitive Game
Cooperative Game
3.2. Problems
3.2.1. Integer Linear Programming
3.2.2. MIS, MVC, MC
3.2.3. Traveling Salesman Problems
4. Applications in Energy Field
4.1. Petroleum Supply Chain
4.1.1. Refinery Production Planning
4.1.2. Refinery Scheduling
4.1.3. Oil Transportation
4.2. Steel-Making
4.3. Electric Power System
4.4. Wind Power
5. Challenge
5.1. Developing Game Theoretic Learning Methods
5.2. Challenge of Application in Energy Field
5.3. Application Gap
6. Conclusions
Future Work
- 1.
- Further investigation of the application of approaches based on game theory to tackle systematic problems is of vital significance. Currently, there are limited applications in petroleum supply chain. Refineries can be modeled as rational independent agents, while it is possible to model oil fields, pipelines, or transportation tasks as agents as well. Building such a system by approaches based on game theory in which each scene in the petroleum supply chain is a game dependent on each other is worth expecting.
- 2.
- Studies on a systematic framework to handle the increasing uncertainty in CO scheduling problems in the energy field are worth investigating. With the development of complexity caused by uncertainty in real-world problems, the algorithms also need to consider adapting to the trend.
- 3.
- It is worth studying the application of ML approaches to COPs without the framework of a traditional COP solver. Subtle modification may not be able to fully demonstrate the strengths of ML algorithms. By resolving the problem of complexity due to the large scale, ML algorithms may have better performance on COPs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korte, B.H.; Vygen, J.; Korte, B.; Vygen, J. Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Schrijver, A. On the history of combinatorial optimization (till 1960). Handbooks Oper. Res. Manag. Sci. 2005, 12, 1–68. [Google Scholar]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Courier Corporation: North Chelmsford, MA, USA, 1998. [Google Scholar]
- Schrijver, A. Combinatorial Optimization: Polyhedra and Efficiency; Springer: Berlin/Heidelberg, Germany, 2003; Volume 24. [Google Scholar]
- Panda, D.; Ramteke, M. Preventive crude oil scheduling under demand uncertainty using structure adapted genetic algorithm. Appl. Energy 2019, 235, 68–82. [Google Scholar] [CrossRef]
- Yang, H.; Bernal, D.E.; Franzoi, R.E.; Engineer, F.G.; Kwon, K.; Lee, S.; Grossmann, I.E. Integration of crude-oil scheduling and refinery planning by Lagrangean Decomposition. Comput. Chem. Eng. 2020, 138, 106812. [Google Scholar] [CrossRef]
- Qin, H.; Han, Z. Crude-oil scheduling network in smart field under cyber-physical system. IEEE Access 2019, 7, 91703–91719. [Google Scholar] [CrossRef]
- Panda, D.; Ramteke, M. Dynamic hybrid scheduling of crude oil using structure adapted genetic algorithm for uncertainty of tank unavailability. Chem. Eng. Res. Des. 2020, 159, 78–91. [Google Scholar] [CrossRef]
- Fragkogios, A.; Saharidis, G.K. Modeling and solution approaches for crude oil scheduling in a refinery. In Energy Management—Collective and Computational Intelligence with Theory and Applicat; Springer: Berlin/Heidelberg, Germany, 2018; pp. 251–275. [Google Scholar]
- Mostafaei, H.; Ghaffari Hadigheh, A. A general modeling framework for the long-term scheduling of multiproduct pipelines with delivery constraints. Ind. Eng. Chem. Res. 2014, 53, 7029–7042. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Liao, Q.; Wu, M.; Yan, X. A hybrid computational approach for detailed scheduling of products in a pipeline with multiple pump stations. Energy 2017, 119, 612–628. [Google Scholar] [CrossRef]
- Mostafaei, H.; Castro, P.M.; Ghaffari-Hadigheh, A. A novel monolithic MILP framework for lot-sizing and scheduling of multiproduct treelike pipeline networks. Ind. Eng. Chem. Res. 2015, 54, 9202–9221. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Song, W.; Chen, A. A real-time electricity scheduling for residential home energy management. IEEE Internet Things J. 2018, 6, 2602–2611. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Fang, Z.; Liu, W. Electricity scheduling strategy for home energy management system with renewable energy and battery storage: A case study. IET Renew. Power Gener. 2018, 12, 639–648. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Fang, J.; Liu, Z.; Zhang, H. Electricity scheduling optimisation based on energy cloud for residential microgrids. IET Renew. Power Gener. 2019, 13, 1105–1114. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, C.; Zhu, Z. Inter-hours rolling scheduling of behind-the-meter storage operating systems using electricity price forecasting based on deep convolutional neural network. Int. Elect. Power Energy Syst. 2021, 125, 106499. [Google Scholar] [CrossRef]
- Griffin, P.W.; Hammond, G.P. The prospects for green steel making in a net-zero economy: A UK perspective. Glob. Transit. 2021, 3, 72–86. [Google Scholar] [CrossRef]
- Song, G.W.; Tama, B.A.; Park, J.; Hwang, J.Y.; Bang, J.; Park, S.J.; Lee, S. Temperature Control Optimization in a Steel-Making Continuous Casting Process Using a Multimodal Deep Learning Approach. Steel Res. Int. 2019, 90, 1900321. [Google Scholar] [CrossRef]
- Adetunji, O.; Seidu, S.O. Simulation and Techno-Economic Performance of a Novel Charge Calculation and Melt Optimization Planning Model for Steel Making. J. Miner. Mater. Charact. Eng. 2020, 8, 277–300. [Google Scholar] [CrossRef]
- Ren, L.; Zhou, S.; Peng, T.; Ou, X. A review of CO2 emissions reduction technologies and low-carbon development in the iron and steel industry focusing on China. Renew. Sustain. Energy Rev. 2021, 143, 110846. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Zhu, P.; Wang, X.; Jia, D.; Guo, Y.; Li, S.; Chu, C. Investigating the co-evolution of node reputation and edge-strategy in prisoner’s dilemma game. Appl. Math. Comput. 2020, 386, 125474. [Google Scholar] [CrossRef]
- Shen, C.; Chu, C.; Shi, L.; Perc, M.; Wang, Z. Aspiration-based coevolution of link weight promotes cooperation in the spatial prisoner’s dilemma game. R. Soc. Open Sci. 2018, 5, 180199. [Google Scholar] [CrossRef] [Green Version]
- Bian, J.; Lai, K.K.; Hua, Z.; Zhao, X.; Zhou, G. Bertrand vs. Cournot competition in distribution channels with upstream collusion. Int. J. Prod. Econ. 2018, 204, 278–289. [Google Scholar] [CrossRef]
- Lundin, E.; Tangerås, T.P. Cournot competition in wholesale electricity markets: The Nordic power exchange, Nord Pool. Int. J. Ind. Organ. 2020, 68, 102536. [Google Scholar] [CrossRef]
- Dyson, B.J.; Musgrave, C.; Rowe, C.; Sandhur, R. Behavioural and neural interactions between objective and subjective performance in a Matching Pennies game. Int. J. Psychophysiol. 2020, 147, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Dolgova, T.; Bartsev, S. Neural networks playing “matching pennies” with each other: Reproducibility of game dynamics. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 537, p. 42002. [Google Scholar]
- Fiez, T.; Chasnov, B.; Ratliff, L. Implicit learning dynamics in stackelberg games: Equilibria characterization, convergence analysis, and empirical study. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 3133–3144. [Google Scholar]
- Jacobsen, H.J.; Jensen, M.; Sloth, B. Evolutionary learning in signalling games. Games Econ. Behav. 2001, 34, 34–63. [Google Scholar] [CrossRef] [Green Version]
- Allen, F.; Morris, S. Game theory models in finance. In Game Theory and Business Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 17–41. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised learning. In Machine Learning Techniques for Multimedia; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]
- Barlow, H.B. Unsupervised learning. Neural Comput. 1989, 1, 295–311. [Google Scholar] [CrossRef]
- Ghahramani, Z. Unsupervised learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 72–112. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. Unsupervised learning. In The Elements of Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2009; pp. 485–585. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Wiering, M.A.; Van Otterlo, M. Reinforcement learning. Adapt. Learn. Optim. 2012, 12, 729. [Google Scholar]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Sengupta, S.; Kambhampati, S. Multi-agent reinforcement learning in bayesian stackelberg markov games for adaptive moving target defense. arXiv 2020, arXiv:2007.10457. [Google Scholar]
- Zheng, L.; Fiez, T.; Alumbaugh, Z.; Chasnov, B.; Ratliff, L.J. Stackelberg actor-critic: Game-theoretic reinforcement learning algorithms. arXiv 2021, arXiv:2109.12286. [Google Scholar]
- Shi, D.; Li, L.; Ohtsuki, T.; Pan, M.; Han, Z.; Poor, V. Make Smart Decisions Faster: Deciding D2D Resource Allocation via Stackelberg Game Guided Multi-Agent Deep Reinforcement Learning. IEEE Trans. Mob. Comput. 2021. [Google Scholar] [CrossRef]
- Han, C.; Huo, L.; Tong, X.; Wang, H.; Liu, X. Spatial anti-jamming scheme for internet of satellites based on the deep reinforcement learning and Stackelberg game. IEEE Trans. Veh. Technol. 2020, 69, 5331–5342. [Google Scholar] [CrossRef]
- Modares, A.; Somhom, S.; Enkawa, T. A self-organizing neural network approach for multiple traveling salesman and vehicle routing problems. Int. Trans. Oper. Res. 1999, 6, 591–606. [Google Scholar] [CrossRef]
- Fagerholt, K.; Christiansen, M. A travelling salesman problem with allocation, time window and precedence constraints—An application to ship scheduling. Int. Trans. Oper. Res. 2000, 7, 231–244. [Google Scholar] [CrossRef]
- Debnath, D.; Hawary, A. Adapting travelling salesmen problem for real-time UAS path planning using genetic algorithm. In Intelligent Manufacturing and Mechatronics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 151–163. [Google Scholar]
- Filip, E.; Otakar, M. The travelling salesman problem and its application in logistic practice. WSEAS Trans. Bus. Econ. 2011, 8, 163–173. [Google Scholar]
- Wang, P.; Sanin, C.; Szczerbicki, E. Evolutionary algorithm and decisional DNA for multiple travelling salesman problem. Neurocomputing 2015, 150, 50–57. [Google Scholar] [CrossRef]
- Uchida, A.; Ito, Y.; Nakano, K. Accelerating ant colony optimisation for the travelling salesman problem on the GPU. Int. J. Parallel Emergent Distrib. Syst. 2014, 29, 401–420. [Google Scholar] [CrossRef]
- Zhang, R.; Prokhorchuk, A.; Dauwels, J. Deep reinforcement learning for traveling salesman problem with time windows and rejections. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Zhang, Y.; Han, X.; Dong, Y.; Xie, J.; Xie, G.; Xu, X. A novel state transition simulated annealing algorithm for the multiple traveling salesmen problem. J. Supercomput. 2021, 77, 11827–11852. [Google Scholar] [CrossRef]
- Larranaga, P.; Kuijpers, C.M.H.; Murga, R.H.; Inza, I.; Dizdarevic, S. Genetic algorithms for the travelling salesman problem: A review of representations and operators. Artif. Intell. Rev. 1999, 13, 129–170. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef] [Green Version]
- Gendreau, M.; Laporte, G.; Semet, F. A tabu search heuristic for the undirected selective travelling salesman problem. Eur. J. Oper. Res. 1998, 106, 539–545. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inform. Process. Syst. 2014, 27, 1–9. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inform. Process. Syst. 2017, 30, 1–15. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [Green Version]
- Deisenroth, M.; Rasmussen, C.E. PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 465–472. [Google Scholar]
- Çalışır, S.; Pehlivanoğlu, M.K. Model-free reinforcement learning algorithms: A survey. In Proceedings of the 2019 27th Signal Processing and Communications Applications Conference (SIU), Sivas, Turkey, 24–26 April 2019; pp. 1–4. [Google Scholar]
- Moerland, T.M.; Broekens, J.; Jonker, C.M. Model-based reinforcement learning: A survey. arXiv 2020, arXiv:2006.16712. [Google Scholar]
- Kaiser, L.; Babaeizadeh, M.; Milos, P.; Osinski, B.; Campbell, R.H.; Czechowski, K.; Erhan, D.; Finn, C.; Kozakowski, P.; Levine, S.; et al. Model-based reinforcement learning for atari. arXiv 2019, arXiv:1903.00374. [Google Scholar]
- Zhao, D.; Wang, H.; Shao, K.; Zhu, Y. Deep reinforcement learning with experience replay based on SARSA. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–6. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Konda, V.; Tsitsiklis, J. Actor-critic algorithms. In Proceedings of the Advances in Neural Information Processing Systems 12 (NIPS 1999), Denver, CO, USA, 29 November–4 December 1999. [Google Scholar]
- Land, A.H.; Doig, A.G. An automatic method for solving discrete programming problems. In 50 Years of Integer Programming 1958–2008; Springer: Berlin/Heidelberg, Germany, 2010; pp. 105–132. [Google Scholar]
- Alvarez, A.M.; Louveaux, Q.; Wehenkel, L. A Supervised Machine Learning Approach to Variable Branching in Branch-and-Bound. In ecml. 2014. Available online: https://orbi.uliege.be/handle/2268/167559 (accessed on 1 May 2022).
- He, H.; Daume, H., III; Eisner, J.M. Learning to search in branch and bound algorithms. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Khalil, E.; Le Bodic, P.; Song, L.; Nemhauser, G.; Dilkina, B. Learning to branch in mixed integer programming. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Baltean-Lugojan, R.; Bonami, P.; Misener, R.; Tramontani, A. Selecting Cutting Planes for Quadratic Semidefinite Outer-Approximation via Trained Neural Networks; Technical Report; CPLEX Optimization, IBM: New York, NY, USA, 2018. [Google Scholar]
- Hottung, A.; Tanaka, S.; Tierney, K. Deep learning assisted heuristic tree search for the container pre-marshalling problem. Comput. Oper. Res. 2020, 113, 104781. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Zheng, P.; Zuo, L.; Wang, J.; Zhang, J. Pointer networks for solving the permutation flow shop scheduling problem. In Proceedings of the 48th International Conference on Computers & Industrial Engineering (CIE48), Auckland, New Zealand, 2–5 December 2018; pp. 2–5. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 2, pp. 729–734. [Google Scholar]
- Nowak, A.; Villar, S.; Bandeira, A.S.; Bruna, J. A note on learning algorithms for quadratic assignment with graph neural networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; Volume 1050, p. 22. [Google Scholar]
- Bresson, X.; Laurent, T. Residual gated graph convnets. arXiv 2017, arXiv:1711.07553. [Google Scholar]
- Vlastelica, M.; Paulus, A.; Musil, V.; Martius, G.; Rolínek, M. Differentiation of blackbox combinatorial solvers. arXiv 2019, arXiv:1912.02175. [Google Scholar]
- Paulus, A.; Rolínek, M.; Musil, V.; Amos, B.; Martius, G. Comboptnet: Fit the right np-hard problem by learning integer programming constraints. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 8443–8453. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Deudon, M.; Cournut, P.; Lacoste, A.; Adulyasak, Y.; Rousseau, L.M. Learning heuristics for the tsp by policy gradient. In Proceedings of the International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research, Vienna, Austria, 21–24 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 170–181. [Google Scholar]
- Emami, P.; Ranka, S. Learning permutations with sinkhorn policy gradient. arXiv 2018, arXiv:1805.07010. [Google Scholar]
- Kool, W.; Van Hoof, H.; Welling, M. Attention, learn to solve routing problems! arXiv 2018, arXiv:1803.08475. [Google Scholar]
- Laterre, A.; Fu, Y.; Jabri, M.K.; Cohen, A.S.; Kas, D.; Hajjar, K.; Dahl, T.S.; Kerkeni, A.; Beguir, K. Ranked reward: Enabling self-play reinforcement learning for combinatorial optimization. arXiv 2018, arXiv:1807.01672. [Google Scholar]
- Drori, I.; Kharkar, A.; Sickinger, W.R.; Kates, B.; Ma, Q.; Ge, S.; Dolev, E.; Dietrich, B.; Williamson, D.P.; Udell, M. Learning to solve combinatorial optimization problems on real-world graphs in linear time. In Proceedings of the 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA), Virtual, 14–17 December 2020; pp. 19–24. [Google Scholar]
- Shahadat, A.S.B.; Ayon, S.I.; Khatun, M.R. SSGTA: A novel swap sequence based Ggame theory algorithm for traveling salesman problem. In Proceedings of the 2021 24th International Conference on Computer and Information Technology (ICCIT), Dalian, China, 5–7 May 2021; pp. 1–5. [Google Scholar]
- Kulkarni, A.J.; Tai, K. Probability collectives: A multi-agent approach for solving combinatorial optimization problems. Appl. Soft Comput. 2010, 10, 759–771. [Google Scholar] [CrossRef]
- Gasse, M.; Chételat, D.; Ferroni, N.; Charlin, L.; Lodi, A. Exact combinatorial optimization with graph convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Tang, Y.; Agrawal, S.; Faenza, Y. Reinforcement learning for integer programming: Learning to cut. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 9367–9376. [Google Scholar]
- Khalil, E.; Dai, H.; Zhang, Y.; Dilkina, B.; Song, L. Learning combinatorial optimization algorithms over graphs. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Karalias, N.; Loukas, A. Erdos goes neural: An unsupervised learning framework for combinatorial optimization on graphs. Adv. Neural Inform. Process. Syst. 2020, 33, 6659–6672. [Google Scholar]
- Chen, X.; Tian, Y. Learning to perform local rewriting for combinatorial optimization. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Tominac, P.; Mahalec, V. A game theoretic framework for petroleum refinery strategic production planning. Aiche J. 2017, 63, 2751–2763. [Google Scholar] [CrossRef]
- Ravinger, F. Analyzing Oil Refinery Investment Decisions: A Game Theoretic Approach. Ph.D. Thesis, Central European University, Vienna, Austria, 2007. [Google Scholar]
- Tominac, P.A. Game Theoretic Approaches to Petroleum Refinery Production Planning—A Justification for the Enterprise Level Optimization of Production Planning. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2017. [Google Scholar]
- Babaei, M.; Asgarian, F.; Jamali, M.B.; Rasti-Barzoki, M.; Piran, M.J. A game theoretic approach for pricing petroleum and determining investors’ production volume with the consideration of government and intermediate producers. Sustain. Energy Technol. Assess. 2020, 42, 100825. [Google Scholar] [CrossRef]
- Shah, N.K.; Sahay, N.; Ierapetritou, M.G. Efficient decomposition approach for large-scale refinery scheduling. Ind. Eng. Chem. Res. 2015, 54, 9964–9991. [Google Scholar] [CrossRef]
- Liang, Y.; Liao, Q.; Zhang, H.; Nie, S.; Yan, X.; Ma, J. Research progress on production scheduling optimization of refi nery. Oil Gas Storage Transp. 2017, 36, 646–650. [Google Scholar]
- Wang, J.; Rong, G. Robust Optimization Model for Crude Oil Scheduling under Uncertainty. Ind. Eng. Chem. Res. 2010, 49, 1737–1748. [Google Scholar] [CrossRef]
- Li, S.; Su, D. Establishment and solution of refinery multi-stage production scheduling model based on dynamic programming. Control Inst. Chem. Ind. 2009, 36, 6. [Google Scholar]
- Cheng, L.; Duran, M.A. Logistics for world-wide crude oil transportation using discrete event simulation and optimal control. Comput. Chem. Eng. 2004, 28, 897–911. [Google Scholar] [CrossRef]
- Wang, L.; Kinable, J.; Woensel, T.V. The fuel replenishment problem: A split-delivery multi-compartment vehicle routing problem with multiple trips. Comput. Oper. Res. 2020, 118, 104904. [Google Scholar] [CrossRef]
- Lin, S.; Xu, A.; Liu, C.; Kai, F.; Li, J. Crane scheduling method in steelmaking workshop based on deep reinforcement learning. China Metall. 2021, 31, 7. [Google Scholar]
- Zhou, Y. Application Research of Improved Gray Wolf Optimization Algorithm in Optimal Scheduling of Ateelmaking and Continuous Casting. Ph.D. Thesis, Qingdao University of Science and Technology, Qingdao, China, 2021. [Google Scholar]
- Jia, C. Deep Reinforcement Learning for Batch Machine Scheduling Problem with Non-Identical Job Sizes. Ph.D. Thesis, Hefei University of Technology, Heifei, China, 2021. [Google Scholar]
- Ma, Y.; Liu, X.; Jiang, S. Machine Learning-Based Scheduling Approach for Steelmaking-Continuous Casting Production. Metall. Ind. Autom. 2022, 46, 2. [Google Scholar]
- Yan, D.; Peng, G.; Gao, H.; Chen, S.; Zhou, Y. Research on distribution network topology control based on deep reinforcement learning combinatorial optimization. Power Syst. Technol. 2021, 1–9. [Google Scholar] [CrossRef]
- Dong, L.; Liu, Y.; Qiao, J.; Wang, X.; Wang, C.; Pu, T. Optimal dispatch of combined heat and power system based on multi-agent deep reinforcement learning. Power Syst. Technol. 2021, 45, 9. [Google Scholar]
- Cao, J.; Zhang, W.; Xiao, Z.; Hua, H. Reactive Power Optimization for Transient Voltage Stability in Energy Internet via Deep Reinforcement Learning Approach. Energies 2019, 12, 1556. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Qiu, C.; Zhang, D.; Xu, S.; He, X. A Coordinated Control Method for Hybrid Energy Storage System in Microgrid Based on Deep Reinforcement Learning. Power Syst. Technol. 2019, 6, 1914–1921. [Google Scholar] [CrossRef]
- Li, Z.; Hou, X.; Liu, Y.; Sun, H.; Zhu, Z.; Long, Y.; Xu, T. A capacity planning method of charging station based on depth learning. Power Syst. Prot. Control 2017, 45, 67–73. [Google Scholar]
- Huang, C.M.; Huang, Y.C. Combined Differential Evolution Algorithm and Ant System for Optimal Reactive Power Dispatch. Energy Procedia 2012, 14, 1238–1243. [Google Scholar] [CrossRef] [Green Version]
- Yuce, B.; Rezgui, Y.; Mourshed, M. ANN-GA smart appliance scheduling for optimised energy management in the domestic sector. Energy Build. 2016, 111, 311–325. [Google Scholar] [CrossRef]
- Huang, X.; Guo, R. A multi-agent model of generation expansion planning in electricity market. Power Syst. Prot. Control 2016. Available online: http://en.cnki.com.cn/Article_en/CJFDTOTAL-JDQW201624001.htm (accessed on 1 May 2022).
- Marden, J.R.; Ruben, S.D.; Pao, L.Y. A model-free approach to wind farm control using game theoretic methods. IEEE Trans. Control Syst. Technol. 2013, 21, 1207–1214. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Incorporating wind power forecast uncertainties into stochastic unit commitment using neural network-based prediction intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 2123–2135. [Google Scholar] [CrossRef] [PubMed]
- Mei, S.; Zhang, D.; Wang, Y.; Liu, F.; Wei, W. Robust optimization of static reserve planning with large-scale integration of wind power: A game theoretic approach. IEEE Trans. Sustain. Energy 2014, 5, 535–545. [Google Scholar] [CrossRef]
- Liu, W.; Ling, Y.; Zhao, T. Cooperative game based capacity planning model for wind power in low-carbon economy. Autom. Electr. Power Syst. 2015, 39, 68–74. [Google Scholar]
- Kuçukoglu, I.; Dewil, R.; Cattrysse, D. Hybrid simulated annealing and tabu search method for the electric travelling salesman problem with time windows and mixed charging rates. Expert Syst. Appl. 2019, 134, 279–303. [Google Scholar] [CrossRef]
- Zhou, A.H.; Zhu, L.P.; Hu, B.; Deng, S.; Song, Y.; Qiu, H.; Pan, S. Traveling-salesman-problem algorithm based on simulated annealing and gene-expression programming. Information 2018, 10, 7. [Google Scholar] [CrossRef] [Green Version]
- Dewantoro, R.W.; Sihombing, P. The combination of ant colony optimization (ACO) and tabu search (TS) algorithm to solve the traveling salesman problem (TSP). In Proceedings of the 2019 3rd International Conference on Electrical, Telecommunication and Computer Engineering (ELTICOM), Medan, Indonesia, 16–17 September 2019; pp. 160–164. [Google Scholar]
- Arapoglu, O.; Akram, V.K.; Dagdeviren, O. An energy-efficient, self-stabilizing and distributed algorithm for maximal independent set construction in wireless sensor networks. Comput. Stand. Interfaces 2019, 62, 32–42. [Google Scholar] [CrossRef]
- Kose, A.; Ozbek, B. Resource allocation for underlaying device-to-device communications using maximal independent sets and knapsack algorithm. In Proceedings of the 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, 9–12 September 2018; pp. 1–5. [Google Scholar]
- López-Ramírez, C.; Gómez, J.E.G.; Luna, G.D.I. Building a Maximal Independent Set for the Vertex-coloring Problem on Planar Graphs. Electron. Notes Theor. Comput. Sci. 2020, 354, 75–89. [Google Scholar] [CrossRef]
- Tarjan, R.E.; Trojanowski, A.E. Finding a maximum independent set. SIAM J. Comput. 1977, 6, 537–546. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G.; Smith, S.H. A greedy randomized adaptive search procedure for maximum independent set. Oper. Res. 1994, 42, 860–878. [Google Scholar] [CrossRef] [Green Version]
- Berman, P.; Furer, M. Approximating maximum independent set. In Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, VA, USA, 23–25 January 1994; Volume 70, p. 365. [Google Scholar]
- Reba, K.; Guid, M.; Rozman, K.; Janežič, D.; Konc, J. Exact Maximum Clique Algorithm for Different Graph Types Using Machine Learning. Mathematics 2021, 10, 97. [Google Scholar] [CrossRef]
- Ghaffari, M. Distributed maximal independent set using small messages. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 6–9 January 2019; pp. 805–820. [Google Scholar]
- Andrade, D.V.; Resende, M.G.; Werneck, R.F. Fast local search for the maximum independent set problem. J. Heuristics 2012, 18, 525–547. [Google Scholar] [CrossRef]
- Xiao, M.; Nagamochi, H. Exact algorithms for maximum independent set. Inform. Comput. 2017, 255, 126–146. [Google Scholar] [CrossRef] [Green Version]
- Zetina, C.A.; Contreras, I.; Fernandez, E.; Luna-Mota, C. Solving the optimum communication spanning tree problem. Eur. Oper. Res. 2019, 273, 108–117. [Google Scholar] [CrossRef]
- Akpan, N.; Iwok, I. A minimum spanning tree approach of solving a transportation problem. Int. J. Math. Stat. Invent. 2017, 5, 9–18. [Google Scholar]
- Bartolín, H.; Martínez, F.; Cortés, J.A. Topological GIS-based analysis of a water distribution network model. Applications of the minimum spanning tree. In Proceedings of the Computing and Control for the Water Industry, Exeter, UK, 5–7 September 2005. [Google Scholar]
- Liao, X.Q.; Su, T.; Ma, L. Application of neutrosophic minimum spanning tree in electrical power distribution network. CAAI Trans. Intell. Technol. 2020, 5, 99–105. [Google Scholar] [CrossRef]
- Dong, M.; Zhang, X.; Yang, K.; Liu, R.; Chen, P. Forecasting the COVID-19 transmission in Italy based on the minimum spanning tree of dynamic region network. PeerJ 2021, 9, e11603. [Google Scholar] [CrossRef]
- Kireyeu, V. Cluster dynamics studied with the phase-space minimum spanning tree approach. Phys. Rev. C 2021, 103, 54905. [Google Scholar] [CrossRef]
- Mashreghi, A.; King, V. Broadcast and minimum spanning tree with o (m) messages in the asynchronous CONGEST model. Distrib. Comput. 2021, 34, 283–299. [Google Scholar] [CrossRef]
- Jin, Y.; Zhao, H.; Gu, F.; Bu, P.; Na, M. A spatial minimum spanning tree filter. Meas. Sci. Technol. 2020, 32, 15204. [Google Scholar] [CrossRef]
- Ochs, K.; Michaelis, D.; Solan, E. Wave digital emulation of a memristive circuit to find the minimum spanning tree. In Proceedings of the 2019 IEEE 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019; pp. 351–354. [Google Scholar]
- Farashi, S.; Khosrowabadi, R. EEG based emotion recognition using minimum spanning tree. Phys. Eng. Sci. Med. 2020, 43, 985–996. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Wang, J.; Wang, C.; Qi, Z.; Ding, Z. Graphical Minimax Game and Off-Policy Reinforcement Learning for Heterogeneous MASs with Spanning Tree Condition. Guid. Navig. Control 2021, 1, 2150011. [Google Scholar] [CrossRef]
- Dey, A.; Son, L.H.; Pal, A.; Long, H.V. Fuzzy minimum spanning tree with interval type 2 fuzzy arc length: Formulation and a new genetic algorithm. Soft Comput. 2020, 24, 3963–3974. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, S.; Gu, Y.; Shun, J. Fast parallel algorithms for euclidean minimum spanning tree and hierarchical spatial clustering. In Proceedings of the 2021 International Conference on Management of Data, Virtual, 20–25 June 2021; pp. 1982–1995. [Google Scholar]
- Gyoten, H.; Hiromoto, M.; Sato, T. Area efficient annealing processor for ising model without random number generator. IEICE Trans. Inform. Syst. 2018, 101, 314–323. [Google Scholar] [CrossRef] [Green Version]
- Cook, C.; Zhao, H.; Sato, T.; Hiromoto, M.; Tan, S.X.D. GPU-based ising computing for solving max-cut combinatorial optimization problems. Integration 2019, 69, 335–344. [Google Scholar] [CrossRef]
- Patel, S.; Chen, L.; Canoza, P.; Salahuddin, S. Ising model optimization problems on a FPGA accelerated restricted Boltzmann machine. arXiv 2020, arXiv:2008.04436. [Google Scholar]
- Tu, K.N. Recent advances on electromigration in very-large-scale-integration of interconnects. J. Appl. Phys. 2003, 94, 5451–5473. [Google Scholar] [CrossRef]
- Wang, J.; Paesani, S.; Ding, Y.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mančinska, L.; Bacco, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef] [Green Version]
- Noé, F.; De Fabritiis, G.; Clementi, C. Machine learning for protein folding and dynamics. Curr. Opin. Struct. Biol. 2020, 60, 77–84. [Google Scholar] [CrossRef]
- Rodriguez, A.; Wright, G.; Emrich, S.; Clark, P.L. %MinMax: A versatile tool for calculating and comparing synonymous codon usage and its impact on protein folding. Protein Sci. 2018, 27, 356–362. [Google Scholar] [CrossRef] [Green Version]
- Poljak, S.; Rendl, F. Solving the max-cut problem using eigenvalues. Discrete Appl. Math. 1995, 62, 249–278. [Google Scholar] [CrossRef] [Green Version]
- Festa, P.; Pardalos, P.M.; Resende, M.G.; Ribeiro, C.C. Randomized heuristics for the MAX-CUT problem. Optim. Methods Softw. 2002, 17, 1033–1058. [Google Scholar] [CrossRef]
- Kim, Y.H.; Yoon, Y.; Geem, Z.W. A comparison study of harmony search and genetic algorithm for the max-cut problem. Swarm Evol. Comput. 2019, 44, 130–135. [Google Scholar] [CrossRef]
- Martí, R.; Duarte, A.; Laguna, M. Advanced scatter search for the max-cut problem. INFORMS J. Comput. 2009, 21, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Blum, C.; Schmid, V. Solving the 2D bin packing problem by means of a hybrid evolutionary algorithm. Procedia Comput. Sci. 2013, 18, 899–908. [Google Scholar] [CrossRef] [Green Version]
- Hifi, M.; Kacem, I.; Nègre, S.; Wu, L. A linear programming approach for the three-dimensional bin-packing problem. Electron. Notes Discret. Math. 2010, 36, 993–1000. [Google Scholar] [CrossRef]
- Yu, A.B.; Zou, R.; Standish, N. Modifying the linear packing model for predicting the porosity of nonspherical particle mixtures. Ind. Eng. Chem. Res. 1996, 35, 3730–3741. [Google Scholar] [CrossRef]
- Biro, P.; Manlove, D.F.; Rizzi, R. Maximum weight cycle packing in directed graphs, with application to kidney exchange programs. Discret. Math. Algorithms Appl. 2009, 1, 499–517. [Google Scholar] [CrossRef] [Green Version]
- Epstein, L.; Levin, A. Bin packing with general cost structures. Math. Program. 2012, 132, 355–391. [Google Scholar] [CrossRef] [Green Version]
- Lai, P.; He, Q.; Abdelrazek, M.; Chen, F.; Hosking, J.; Grundy, J.; Yang, Y. Optimal edge user allocation in edge computing with variable sized vector bin packing. In Proceedings of the International Conference on Service-Oriented Computing, Hangzhou, China, 12–15 November 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 230–245. [Google Scholar]
- Mohiuddin, I.; Almogren, A.; Al Qurishi, M.; Hassan, M.M.; Al Rassan, I.; Fortino, G. Secure distributed adaptive bin packing algorithm for cloud storage. Future Gener. Comput. Syst. 2019, 90, 307–316. [Google Scholar] [CrossRef]
- Baldi, M.M.; Manerba, D.; Perboli, G.; Tadei, R. A generalized bin packing problem for parcel delivery in last-mile logistics. Eur. J. Oper. Res. 2019, 274, 990–999. [Google Scholar] [CrossRef]
- Witteman, M.; Deng, Q.; Santos, B.F. A bin packing approach to solve the aircraft maintenance task allocation problem. Eur. J. Oper. Res. 2021, 294, 365–376. [Google Scholar] [CrossRef]
- Qomi, T.; Hamedi, M.; Tavakkoli-Moghaddam, R. Optimization of Crude Oil Transportation using a Variable Cost and Size Bin Packing Problem (VCSBPP). 2021. Available online: https://www.trijournal.ir/article_121959.html?lang=en (accessed on 1 May 2022).
- Frenk, J.G.; Galambos, G. Hybrid next-fit algorithm for the two-dimensional rectangle bin-packing problem. Computing 1987, 39, 201–217. [Google Scholar] [CrossRef] [Green Version]
- Mao, W. Tight worst-case performance bounds for next-k-fit bin packing. SIAM J. Comput. 1993, 22, 46–56. [Google Scholar] [CrossRef] [Green Version]
- Xia, B.; Tan, Z. Tighter bounds of the First Fit algorithm for the bin-packing problem. Discrete Appl. Math. 2010, 158, 1668–1675. [Google Scholar] [CrossRef] [Green Version]
- El-Ashmawi, W.H.; Abd Elminaam, D.S. A modified squirrel search algorithm based on improved best fit heuristic and operator strategy for bin packing problem. Appl. Soft Comput. 2019, 82, 105565. [Google Scholar] [CrossRef]
- Dhahbi, S.; Berrima, M.; Al-Yarimi, F.A. Load balancing in cloud computing using worst-fit bin-stretching. Clust. Comput. 2021, 24, 2867–2881. [Google Scholar] [CrossRef]
- Bansal, N.; Han, X.; Iwama, K.; Sviridenko, M.; Zhang, G. A harmonic algorithm for the 3D strip packing problem. SIAM J. Comput. 2013, 42, 579–592. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.; Chen, G.; Xu, Y. Deep performance analysis of refined harmonic bin packing algorithm. J. Comput. Sci. Technol. 2002, 17, 213–218. [Google Scholar] [CrossRef]
- Raj, P.H.; Kumar, P.R.; Jelciana, P.; Rajagopalan, S. Modified first fit decreasing method for load balancing in mobile clouds. In Proceedings of the 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 1107–1110. [Google Scholar]
- Jin, S.; Liu, M.; Wu, Y.; Xu, Y.; Zhang, J.; Xu, Y. Research of message scheduling for in-vehicle FlexRay network static segment based on next fit decreasing (NFD) algorithm. Appl. Sci. 2018, 8, 2071. [Google Scholar] [CrossRef] [Green Version]
- Coffman, E.G.; Garey, M.R.; Johnson, D.S. Approximation algorithms for bin-packing—An updated survey. In Algorithm Design for Computer System Design; Springer: Berlin/Heidelberg, Germany, 1984; pp. 49–106. [Google Scholar]
- Labbé, M.; Laporte, G.; Martello, S. An exact algorithm for the dual bin packing problem. Oper. Res. Lett. 1995, 17, 9–18. [Google Scholar] [CrossRef]
- Cheuk, K.W.; Luo, Y.J.; Benetos, E.; Herremans, D. Revisiting the onsets and frames model with additive attention. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Wu, C.; Wu, F.; Qi, T.; Huang, Y.; Xie, X. Fastformer: Additive attention can be all you need. arXiv 2021, arXiv:2108.09084. [Google Scholar]
- Li, X.; Xu, Q.; Chen, X.; Li, C. Additive Attention for CNN-based Classification. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 55–59. [Google Scholar]
- Tian, Y.; Newsam, S.; Boakye, K. Image Search with Text Feedback by Additive Attention Compositional Learning. arXiv 2022, arXiv:2203.03809. [Google Scholar]
- Graves, A.; Wayne, G.; Danihelka, I. Neural turing machines. arXiv 2014, arXiv:1410.5401. [Google Scholar]
- Ma, X.; Hu, Z.; Liu, J.; Peng, N.; Neubig, G.; Hovy, E. Stack-pointer networks for dependency parsing. arXiv 2018, arXiv:1805.01087. [Google Scholar]
- Li, J.; Wang, Y.; Lyu, M.R.; King, I. Code completion with neural attention and pointer networks. arXiv 2017, arXiv:1711.09573. [Google Scholar]
- Yavuz, S.; Rastogi, A.; Chao, G.L.; Hakkani-Tur, D. Deepcopy: Grounded response generation with hierarchical pointer networks. arXiv 2019, arXiv:1908.10731. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Trueman, T.E.; Cambria, E. A convolutional stacked bidirectional lstm with a multiplicative attention mechanism for aspect category and sentiment detection. Cogn. Comput. 2021, 13, 1423–1432. [Google Scholar]
- Cui, R.; Wang, J.; Wang, Z. Multiplicative attention mechanism for multi-horizon time series forecasting. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–6. [Google Scholar]
- Gan, J.; Liu, H.; He, T. Prediction of air pollutant concentration based on luong attention mechanism Seq2Seq model. In Proceedings of the 2021 7th Annual International Conference on Network and Information Systems for Computers (ICNISC), Guiyang, China, 23–25 July 2021; pp. 321–325. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive graph convolutional recurrent network for traffic forecasting. Adv. Neural Inform. Process. Syst. 2020, 33, 17804–17815. [Google Scholar]
- Wu, L.; Chen, Y.; Shen, K.; Guo, X.; Gao, H.; Li, S.; Pei, J.; Long, B. Graph neural networks for natural language processing: A survey. arXiv 2021, arXiv:2106.06090. [Google Scholar]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph neural networks for social recommendation. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Ioannidis, V.N.; Marques, A.G.; Giannakis, G.B. Graph neural networks for predicting protein functions. In Proceedings of the 2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Guadeloupe, France, 15–18 December 2019; pp. 221–225. [Google Scholar]
- Tsitsulin, A.; Palowitch, J.; Perozzi, B.; Muller, E. Graph clustering with graph neural networks. arXiv 2020, arXiv:2006.16904. [Google Scholar]
- Abu-El-Haija, S.; Kapoor, A.; Perozzi, B.; Lee, J. N-gcn: Multi-scale graph convolution for semi-supervised node classification. In Uncertainty in Artificial Intelligence. 2020, pp. 841–851. Available online: http://proceedings.mlr.press/v115/abu-el-haija20a.html (accessed on 1 May 2022).
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef] [Green Version]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Schafer, J.B.; Konstan, J.; Riedl, J. Recommender systems in e-commerce. In Proceedings of the 1st ACM Conference on Electronic Commerce, Denver, CO, USA, 3–5 November 1999; pp. 158–166. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage control for mobile sensing networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar] [CrossRef]
- Choi, J.; Oh, S.; Horowitz, R. Distributed learning and cooperative control for multi-agent systems. Automatica 2009, 45, 2802–2814. [Google Scholar] [CrossRef] [Green Version]
- Adler, J.L.; Blue, V.J. A cooperative multi-agent transportation management and route guidance system. Transp. Res. Part Emerg. Technol. 2002, 10, 433–454. [Google Scholar] [CrossRef]
- Wang, S.; Wan, J.; Zhang, D.; Li, D.; Zhang, C. Towards smart factory for industry 4.0: A self-organized multi-agent system with big data based feedback and coordination. Comput. Netw. 2016, 101, 158–168. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.W.; Zhang, B.T. Stock trading system using reinforcement learning with cooperative agents. In Proceedings of the Nineteenth International Conference on Machine Learning, San Francisco, CA, USA, 8–12 July 2002; pp. 451–458. [Google Scholar]
- Lee, J.W.; Park, J.; Jangmin, O.; Lee, J.; Hong, E. A multiagent approach to Q-learning for daily stock trading. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2007, 37, 864–877. [Google Scholar] [CrossRef] [Green Version]
- Castelfranchi, C. The theory of social functions: Challenges for computational social science and multi-agent learning. Cogn. Syst. Res. 2001, 2, 5–38. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Berlin/Heidelberg, Germany, 2021; pp. 321–384. [Google Scholar]
- Rădulescu, R.; Legrand, M.; Efthymiadis, K.; Roijers, D.M.; Nowé, A. Deep multi-agent reinforcement learning in a homogeneous open population. In Proceedings of the Benelux Conference on Artificial Intelligence, 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 90–105. [Google Scholar]
- Yu, Y.; Wang, T.; Liew, S.C. Deep-reinforcement learning multiple access for heterogeneous wireless networks. IEEE J. Sel. Areas Commun. 2019, 37, 1277–1290. [Google Scholar] [CrossRef] [Green Version]
- Gupta, J.K.; Egorov, M.; Kochenderfer, M. Cooperative multi-agent control using deep reinforcement learning. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 66–83. [Google Scholar]
- OroojlooyJadid, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. arXiv 2019, arXiv:1908.03963. [Google Scholar]
- Liu, Y.; Nejat, G. Multirobot cooperative learning for semiautonomous control in urban search and rescue applications. J. Field Robot. 2016, 33, 512–536. [Google Scholar] [CrossRef]
- Liu, I.J.; Jain, U.; Yeh, R.A.; Schwing, A. Cooperative exploration for multi-agent deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021; pp. 6826–6836. [Google Scholar]
- Khan, M.I.; Alam, M.M.; Moullec, Y.L.; Yaacoub, E. Throughput-aware cooperative reinforcement learning for adaptive resource allocation in device-to-device communication. Future Internet. 2017, 9, 72. [Google Scholar] [CrossRef] [Green Version]
- Abramson, M.; Wechsler, H. Competitive reinforcement learning for combinatorial problems. In Proceedings of the International Joint Conference on Neural Networks. Proceedings (Cat. No. 01CH37222), Washington, DC, USA, 15–19 July 2001; Volume 4, pp. 2333–2338. [Google Scholar]
- Crawford, V.P. Learning the optimal strategy in a zero-sum game. Econom. J. Econom. Soc. 1974, 42, 885–891. [Google Scholar] [CrossRef]
- McKenzie, M.; Loxley, P.; Billingsley, W.; Wong, S. Competitive reinforcement learning in atari games. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 14–26. [Google Scholar]
- Kutschinski, E.; Uthmann, T.; Polani, D. Learning competitive pricing strategies by multi-agent reinforcement learning. J. Econ. Dyn. Control 2003, 27, 2207–2218. [Google Scholar] [CrossRef]
- Movahedi, Z.; Bastanfard, A. Toward competitive multi-agents in Polo game based on reinforcement learning. Multimed. Tools Appl. 2021, 80, 26773–26793. [Google Scholar] [CrossRef]
- McKee, K.R.; Gemp, I.; McWilliams, B.; Duéñez-Guzmán, E.A.; Hughes, E.; Leibo, J.Z. Social diversity and social preferences in mixed-motive reinforcement learning. arXiv 2020, arXiv:2002.02325. [Google Scholar]
- Brown, N.; Sandholm, T. Superhuman AI for multiplayer poker. Science 2019, 365, 885–890. [Google Scholar] [CrossRef] [PubMed]
- Ye, D.; Chen, G.; Zhang, W.; Chen, S.; Yuan, B.; Liu, B.; Chen, J.; Liu, Z.; Qiu, F.; Yu, H.; et al. Towards playing full moba games with deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 621–632. [Google Scholar]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef]
- Selsam, D.; Lamm, M.; Bunz, B.; Liang, P.; de Moura, L.; Dill, D.L. Learning a SAT solver from single-bit supervision. arXiv 2018, arXiv:1802.03685. [Google Scholar]
- Li, Z.; Chen, Q.; Koltun, V. Combinatorial optimization with graph convolutional networks and guided tree search. Adv. Neural Inform. Process. Syst. 2018, arXiv:1810.10659. [Google Scholar]
- Lemos, H.; Prates, M.; Avelar, P.; Lamb, L. Graph colouring meets deep learning: Effective graph neural network models for combinatorial problems. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 879–885. [Google Scholar]
- Prates, M.; Avelar, P.H.; Lemos, H.; Lamb, L.C.; Vardi, M.Y. Learning to solve np-complete problems: A graph neural network for decision tsp. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4731–4738. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inform. Process. Syst. 2016, arXiv:1606.09375. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hu, H.; Zhang, X.; Yan, X.; Wang, L.; Xu, Y. Solving a new 3d bin packing problem with deep reinforcement learning method. arXiv 2017, arXiv:1708.05930. [Google Scholar]
- Nazari, M.; Oroojlooy, A.; Snyder, L.; Takác, M. Reinforcement learning for solving the vehicle routing problem. Adv. Neural Inform. Process. Syst. 2018, arXiv:1802.04240. [Google Scholar]
- Venkatakrishnan, S.B.; Alizadeh, M.; Viswanath, P. Graph2seq: Scalable learning dynamics for graphs. arXiv 2018, arXiv:1802.04948. [Google Scholar]
- Manchanda, S.; Mittal, A.; Dhawan, A.; Medya, S.; Ranu, S.; Singh, A. Gcomb: Learning budget-constrained combinatorial algorithms over billion-sized graphs. Adv. Neural Inform. Process. Syst. 2020, 33, 20000–20011. [Google Scholar]
- Dai, H.; Dai, B.; Song, L. Discriminative embeddings of latent variable models for structured data. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 24–26 June 2016; pp. 2702–2711. [Google Scholar]
- Song, J.; Lanka, R.; Yue, Y.; Ono, M. Co-Training for Policy Learning. Uncertainty in Artificial Intelligence. 2020, pp. 1191–1201. Available online: https://arxiv.org/abs/1907.04484 (accessed on 1 May 2022).
- Ma, Q.; Ge, S.; He, D.; Thaker, D.; Drori, I. Combinatorial optimization by graph pointer networks and hierarchical reinforcement learning. arXiv 2019, arXiv:1911.04936. [Google Scholar]
- Abe, K.; Xu, Z.; Sato, I.; Sugiyama, M. Solving np-hard problems on graphs with extended alphago zero. arXiv 2019, arXiv:1905.11623. [Google Scholar]
- Kwon, Y.D.; Choo, J.; Kim, B.; Yoon, I.; Gwon, Y.; Min, S. Pomo: Policy optimization with multiple optima for reinforcement learning. Adv. Neural Inform. Process. Syst. 2020, 33, 21188–21198. [Google Scholar]
- Barrett, T.; Clements, W.; Foerster, J.; Lvovsky, A. Exploratory combinatorial optimization with reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3243–3250. [Google Scholar]
- Wu, Y.; Song, W.; Cao, Z.; Zhang, J.; Lim, A. Learning Improvement Heuristics for Solving Routing Problems. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, X.; Yang, S. A learning-based iterative method for solving vehicle routing problems. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xu, R.; Lieberherr, K. Learning self-game-play agents for combinatorial optimization problems. arXiv 2019, arXiv:1903.03674. [Google Scholar]
- Kruber, M.; Lubbecke, M.E.; Parmentier, A. Learning when to use a decomposition. In Proceedings of the International Conference on AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Padova, Italy, 5–8 June 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 202–210. [Google Scholar]
- Gomory, R. An Algorithm for the Mixed Integer Problem; Technical Report; RAND Corp.: Santa Monica, CA, USA, 1960. [Google Scholar]
- Joshi, C.K.; Laurent, T.; Bresson, X. An efficient graph convolutional network technique for the travelling salesman problem. arXiv 2019, arXiv:1906.01227. [Google Scholar]
- Golmohamadi, H. Operational scheduling of responsive prosumer farms for day-ahead peak shaving by agricultural demand response aggregators. Int. J. Energy Res. 2020, 45, 938–960. [Google Scholar] [CrossRef]
- Mouret, S.; Grossmann, I.E.; Pestiaux, P. A new Lagrangian decomposition approach applied to the integration of refinery planning and crude-oil scheduling. Comput. Chem. Eng. 2011, 35, 2750–2766. [Google Scholar] [CrossRef]
- Li, M. Modeling Method Research on Refinery Process Production Shceduling. Ph.D. Thesis, Shandong University, Jinan, China, 2011. [Google Scholar]
- Yue, X.; Wang, H.; Zhang, Y.; Shi, B. Optimization of refinery crude oil scheduling based on heuristic rules. Comput. Appl. Chem. 2020, 2, 147–154. [Google Scholar]
- Hou, Y.; Wu, N.Q.; Li, Z.W.; Zhang, Y.; Zhu, Q.H. Many-Objective Optimization for Scheduling of Crude Oil Operations based on NSGA-III with Consideration of Energy Efficiency. Swarm Evol. Comput. 2020, 57, 100714. [Google Scholar] [CrossRef]
- Assis, L.S.; Camponogara, E.; Grossmann, I.E. A MILP-based clustering strategy for integrating the operational management of crude oil supply. Comput. Chem. Eng. 2020, 145, 107161. [Google Scholar] [CrossRef]
- Beach, B.; Hildebrand, R.; Ellis, K.; Lebreton, B. An Approximate Method for the Optimization of Long-Horizon Tank Blending and Scheduling Operations. Comput. Chem. Eng. 2020, 141, 106839. [Google Scholar] [CrossRef]
- Li, M. Refinery Operations Optimization Integrated Production Process and Gasoline Blending. J. Phys. Conf. Ser. 2020, 1626, 12111. [Google Scholar] [CrossRef]
- Bayu, F.; Shaik, M.A.; Ramteke, M. Scheduling of crude oil refinery operation with desalting as a separate task. Asia-Pac. J. Chem. Eng. 2020, 15, e2539. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Q. Refinery continuous-time crude scheduling with consideration of long-distance pipeline transportation. Comput. Chem. Eng. 2015, 75, 74–94. [Google Scholar] [CrossRef]
- Oliveira, F.; Nunes, P.M.; Blajberg, R.; Hamacher, S. A framework for crude oil scheduling in an integrated terminal-refinery system under supply uncertainty. Eur. J. Oper. Res. 2016, 252, 635–645. [Google Scholar] [CrossRef]
- Wang, H. Batch Optimization Combined with AI Ideas for Refinery Oil Pipeline Networks. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Gao, H.; Xie, Y.; Ma, J.; Zhang, B. Optimization of refined oil distribution with multiple trips and multiple due time. Control Decis. 2021, 1–10. [Google Scholar] [CrossRef]
- Li, M.; Huang, Q.; Zhou, L.; Ni, S. Research on modeling of petroleum products distribution system based on object-oriented Petri nets. Comput. Eng. Appl. 2015, 51, 55–61. [Google Scholar]
- Li, Z.; Su, T.; Zhang, L. Application Analysis and Prospect of Artificial Intelligence Technology in Smart Grid. Telecom Power Technol. 2020, 37, 2. [Google Scholar]
- Sheikhi, A.; Rayati, M.; Bahrami, S.; Ranjbar, A.M.; Sattari, S. A cloud computing framework on demand side management game in smart energy hubs. Int. J. Elect. Power Energy Syst. 2015, 64, 1007–1016. [Google Scholar] [CrossRef]
- Fan, S.; Li, Z.; Wang, J.; Longjian, P.; Ai, Q. Cooperative Economic Scheduling for Multiple Energy Hubs: A Bargaining Game Theoretic Perspective. IEEE Access 2018, 6, 27777–27789. [Google Scholar] [CrossRef]
- Peng, X.; Tao, X. Cooperative game of electricity retailers in China’s spot electricity market. Energy 2018, 145, 152–170. [Google Scholar] [CrossRef]
- Chen, J.; Bo, Y.; Guan, X. Optimal demand response scheduling with Stackelberg game approach under load uncertainty for smart grid. In Proceedings of the IEEE Third International Conference on Smart Grid Communications, Tainan, Taiwan, 5–8 November 2012. [Google Scholar]
- Li, Y.; Wang, C.; Li, G.; Chen, C. Optimal Scheduling of Integrated Demand Response-Enabled Integrated Energy Systems with Uncertain Renewable Generations: A Stackelberg Game Approach. Energy Convers. Manag. 2021, 235, 113996. [Google Scholar] [CrossRef]
| Reference | Year | Advantage or Novelty |
|---|---|---|
| Alvarez et al. [70] | 2014 | approximated SB with supervised learning |
| He et al. [71] | 2014 | formulated B&B as sequential decision-making process and learned it with imitation learning |
| Khali et al. [72] | 2016 | solved the scoring problem of SB with a learning-to-rank algorithm, online algorithm |
| Baltean et al. [73] | 2018 | used supervised learning to select quadratic semi-definite outer approximation of cutting planes |
| Hottung et al. [74] | 2020 | learned the container pre-marshaling problem (CPMP) |
| Reference | Year | Advantage or Novelty |
|---|---|---|
| Nowak et al. [81] | 2017 | encode source and target graphs |
| Joshi et al. [82] | 2017 | just encode source graph |
| Selsam et al. [230] | 2018 | model SAT as an undirected graph |
| Li et al. [231] | 2018 | solve SAT, MIS, MVC and MC with GNNs |
| Lemos et al. [232] | 2019 | solve graph coloring problem (GCP) with GNNs |
| Prates et al. [233] | 2019 | solve problems involving numerical information |
| Reference | Year | Advantage or Novelty |
|---|---|---|
| Bello et al. [85] | 2016 | used evaluation as reward feedback in RL paradigm |
| Hu et al. [238] | 2017 | solved the 3D BPP problem using RL |
| Nazari et al. [239] | 2018 | the properties of the input sequence is not static |
| Khalil et al. [95] | 2017 | formulated partial solutions as decision sequence |
| Venkatakrishnan et al. [240] | 2018 | improved scalability on larger testing graph than training set |
| Manchanda et al. [241] | 2020 | billion-sized graphs |
| Song | 2020 | combined information from both graph-based representation and ILP-form representation |
| Reference | Year | Advantage or Novelty |
|---|---|---|
| Deudon et al. [86] | 2018 | enhanced the framework with 2-opt |
| Emami et al. [87] | 2018 | learned permutation instead of decision sequences point by point |
| Kool et al. [88] | 2018 | re-designed the baseline of REINFORCE algorithm as the cost of a solution from the policy defined by the best model |
| Ma et al. [244] | 2019 | solved COPs with constraints |
| Abe et al. [245] | 2019 | used CombOpt inspired by AlphaGo Zero to replace Q-learning |
| Barrett | 2020 | explored the solution space during test time |
| Kwon et al. [246] | 2020 | handled equally optimal solutions |
| Method | Reference | Year | Description | Scale |
|---|---|---|---|---|
| Alvarez [70] | 2014 | learning SB scoring decisions on binary MILP | hundreds variables, 100 constraints | |
| He [71] | 2014 | using Dagger to learn binary branching and pruning policy on MILP | 200–1000 variables, 100–500 constraints | |
| SL | Khalil [72] | 2016 | learning ranking policy derived by SB, on-the-fly | 50,000 and 500,000 nodes |
| Kruber [251] | 2017 | learning to decide whether a decomposition of MIP is suitable | − | |
| Gasse [93] | 2019 | using GCNN to encode the bipartite graph | − | |
| Paulus [84] | 2021 | an end-to-end trainable architecture to learn constraints and cost terms of ILP | 1–8 variables, 2–16 constraints | |
| RL | Tang [94] | 2020 | learning to cut plane with RL on IP | variables × constraints = 200, 1000, 5000 |
| Method | Reference | Year | Problem | Description | Scale (Vertice) |
|---|---|---|---|---|---|
| SL | Li [231] | 2018 | MIS, MC, MVC | using GCN to generate multiple probability maps and doing tree-search on them | 1000–100,000 |
| Khalil [95] | 2017 | MC, MVC | using S2V-DQN to select desired node once a time | 50–2000 | |
| Venka-takrish-nan [240] | 2018 | MIS, MC, MVC | using Graph2Seq to handle variable graph size trained by Q-learning | 25–3200 | |
| Abe [245] | 2019 | MC, MVC | using CombOpt to solve the problem of limited exploration space | 100–5000 | |
| RL | Barrett [247] | 2020 | MC | using ECO-DQN to improve the solution during test time | 20–500 |
| Song [243] | 2020 | MVC | co-training algorithms with graph-based and ILP-based representations | 100–500 | |
| Manch-anda [241] | 2020 | MC, MVC | learning to prune poor nodes in order to generalize to larger graph | 50 K–65 M | |
| Karal-ias [96] | 2020 | MC | traing GNN in unsupervised way by constructing a differentiable loss function | up to 1500 |
| Problem | Method | Reference | Year | Description | Scale |
|---|---|---|---|---|---|
| S2V | Vinyals [76] | 2015 | Ptr-Net | <50 | |
| Bello [85] | 2016 | Ptr-Net + REINFORCE | 20, 50, 100 | ||
| Deudon [86] | 2018 | attention+REIN-FORCE+2-opt | 20, 50, 100 | ||
| Emami [87] | 2018 | attention+Sinkhorn Policy Gradient | 20 | ||
| Kool [88] | 2019 | Transformer+REIN-FORCE with baseline relating to the best model so far | 20, 50, 100 | ||
| Kwon [246] | 2020 | attention+REINFORCE | 20, 50, 100 | ||
| TSP | G2V | Nowak [81] | 2017 | GNNs | 20 |
| Khalil [95] | 2017 | GNNs + Q-learning, S2V-DQN | 50–2000 | ||
| Joshi [253] | 2019 | GCNs + beam search | 20, 50, 100 | ||
| Prates [233] | 2019 | GNNs, message passing | 20–40 | ||
| Ma [244] | 2019 | Graph pointer Network+hierarchical RL | 250, 500, 750, 1000 | ||
| improve-ment RL | Wu [248] | 2021 | transformer+AC | 20, 50, 100 | |
| end-to-end | Vlaste-lica [83] | 2020 | an end-to-end trainable architecture to learn cost terms of ILP | 5, 10, 20, 40 | |
| game | Kulkar-ni [92] | 2009 | Probability Collectives | 3 depots, 3 vehicles | |
| Shaha-dat [91] | 2021 | competitive game among strategies | - | ||
| S2V | Nazari [239] | 2018 | RNN + attention + policy gradient | 10, 20, 50, 100 customers, 20, 30, 40, 50 vehicle capacity | |
| Kwon [246] | 2020 | attention + REIN-FORCE | 20, 50, 100 | ||
| VRP | improve-ment RL | Chen [97] | 2019 | using NeuRewriter to find a local region and the associated rewriting rule | 20, 50, 100 |
| Lu [249] | 2020 | use RL to choose operators | 20, 50, 100 | ||
| Wu [248] | 2021 | transformer + AC | 20, 50, 100 |
| Senario | Problem | Reference | Year | Approach |
|---|---|---|---|---|
| refinery product profits | [99] | 2007 | stochastic algorithm | |
| Refinery Production Planning | strategic refinery production planning | [98] | 2017 | Cournot oligopoly- type game |
| refinery operation problem | [100] | 2017 | Cournot oligopoly model | |
| gasoline industry investment | [101] | 2020 | three-phase Stackelberg game | |
| refinery production and operation | [105] | 2009 | DP + mixed genetic | |
| crude oil scheduling | [104] | 2010 | fuzzy and chance-constrained programming | |
| refinery planning and crude oil operation scheduling | [255] | 2011 | Lagrangian decomposition | |
| scheduling refinery problem | [256] | 2011 | logic-expressed heuristic rules | |
| oil-refinery scheduling | [102] | 2015 | heuristic algorithm | |
| Refinery Scheduling | refinery crude oil scheduling | [257] | 2020 | line-up competition algorithm |
| crude oil operation scheduling | [258] | 2020 | NSGA-III | |
| crude oil supply problem | [259] | 2020 | MILP clustering | |
| tank blending and scheduling | [260] | 2020 | discretization- based algorithm | |
| oil blending and processing optimization | [261] | 2020 | discrete-time- presented multi- periodic MILP model | |
| crude oil refinery operation | [262] | 2020 | unit-specific event-based time representation | |
| refinery product profits | [99] | 2007 | stochastic algorithm | |
| long-term multi-product pipeline scheduling | [10] | 2014 | MILP-based continuous-time approach | |
| multi-product treelike pipeline scheduling | [12] | 2015 | continuous-time MILP | |
| Oil Transportation | long-distance pipeline transportation | [263] | 2015 | outer-approximation- based iterative algorithm |
| crude oil pipeline scheduling | [264] | 2016 | two-stage stochastic algorithm | |
| pipeline scheduling | [11] | 2017 | SM + ACO | |
| fuel replenishment problem | [107] | 2020 | adaptive large neighborhood search | |
| refined oil pipeline transportation | [265] | 2020 | parallel computation + heuristic rules + adaptive search | |
| refined oil transportation | [266] | 2021 | improved variable neighborhood search |
| Problem | Reference | Year | Approach |
|---|---|---|---|
| crane scheduling problem | [108] | 2021 | deep RL-based algorithm + DQN |
| scheduling of steelmaking and continuous casting | [109] | 2021 | DDPG-GWO |
| batch machine scheduling | [110] | 2021 | Ptr-Net |
| steel-making operation and scheduling | [111] | 2022 | integrated framework + ML |
| Problem | Reference | Year | Approach |
|---|---|---|---|
| energy-consuming device optimization | [118] | 2000 | ANN-GA |
| optimal reactive power dispatch | [117] | 2012 | DE + ant system |
| DR scheduling optimization | [272] | 2012 | Stachelberg-ML mechanism |
| energy system efficiency | [269] | 2015 | CC |
| generation expansion planning | [119] | 2016 | Q-learning + GA |
| charging stations scheduling | [116] | 2017 | NN + DL |
| multi-neighbor cooperative economic scheduling | [270] | 2018 | bargaining cooperative game |
| electricity pricing | [271] | 2018 | bottom-up inter-regional transaction model |
| power supply- demand | [114] | 2019 | RL + CNN |
| hybrid energy storage | [115] | 2019 | RL + NN |
| distribution network fault recovery | [112] | 2021 | improved Ptr-Net |
| optimization dispatch | [113] | 2021 | AC + deep deterministic policy gradient algorithm |
| DR energy system | [273] | 2021 | Stachelberg-ML optimization |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wang, Z.; Zhang, H.; Ma, N.; Yang, N.; Liu, H.; Zhang, H.; Yang, L. A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas. Algorithms 2022, 15, 205. https://doi.org/10.3390/a15060205
Yang X, Wang Z, Zhang H, Ma N, Yang N, Liu H, Zhang H, Yang L. A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas. Algorithms. 2022; 15(6):205. https://doi.org/10.3390/a15060205
Chicago/Turabian StyleYang, Xinyi, Ziyi Wang, Hengxi Zhang, Nan Ma, Ning Yang, Hualin Liu, Haifeng Zhang, and Lei Yang. 2022. "A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas" Algorithms 15, no. 6: 205. https://doi.org/10.3390/a15060205
APA StyleYang, X., Wang, Z., Zhang, H., Ma, N., Yang, N., Liu, H., Zhang, H., & Yang, L. (2022). A Review: Machine Learning for Combinatorial Optimization Problems in Energy Areas. Algorithms, 15(6), 205. https://doi.org/10.3390/a15060205






